
Funkcje uogólnione
Funkcje uogólnione
•Sygnały nie spełniające warunku Dirichleta
•Dystrybucja (funkcja uogólniona)
•Delta (impuls) Diraca
•Właściwość próbkująca delty Diraca
•Inne właściwości Delty Diraca
•Dystrybucja grzebieniowa
•Transformaty Fouriera funkcji specjalnych
•Podsumowanie
Sygnały nie spełniające warunku
Dirichleta
( )
∞
≈
∫
∞
∞
−
dt
t
x
•Sygnały x(t) są bardzo często wykorzystywane w dziedzinie
czasu, więc wskazanym byłoby jednak podać sposób ich
transformacji fourierowskiej.
•Rozszerzenie zbioru sygnałów, dla których istnieje trans-
formata Fouriera można otrzymać korzystając
z koncepcji dystrybucji (funkcji uogólnionych).
( )
( ) ( )
( )
( )
t
t
x
t
t
x
const
t
x
sgn
=
=
=
1
( )
( )
t
t
x
t
t
x
0
0
sin
cos
ω
ω
=
=
Dystrybucje (funkcje uogólnione)
Dystrybucja (funkcja uogólniona) D(t) przypisuje dowolnej
funkcji
ϕ
(t) liczbę V
D
{
ϕ
(t)}:
( )
( )
( )
{ }
t
V
t
D
t
D
ϕ
ϕ
→
Przykłady dystrybucji:
( )
( )
( )
{ } ( )
( )
( )
( )
{ }
( )
( )
( )
( )
{ }
( )
(
)
dt
dt
t
d
t
V
t
dt
t
t
V
t
t
t
V
t
b
a
D
t
D
b
a
D
t
D
D
t
D
∫
∫
+
=
→
=
→
=
→
2
0
1
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ

Zapis całkowy dystrybucji
Dystrybucja (funkcja uogólniona) D(t) przypisuje dowolnej
funkcji
ϕ
(t) liczbę V
D
{
ϕ
(t)}:
( )
( )
( )
{ }
t
V
t
D
t
D
ϕ
ϕ
→
Dystrybucję zapisujemy w postaci całkowej:
( )
( )
( )
{ }
( ) ( )
dt
t
t
D
t
V
t
df
D
t
D
ϕ
ϕ
ϕ
∫
∞
∞
−
=
→
w celu zachowania właściwości liniowości:
( )
( )
{
}
( )
{
}
( )
{
}
t
V
t
V
t
t
V
D
D
D
2
1
2
1
ϕ
ϕ
ϕ
ϕ
+
=
+
Delta Diraca (impuls Diraca)
Delta Diraca
δ
(t) przypisuje dowolnej funkcji
ϕ
(t)
liczbę
ϕ
(0):
( )
( )
( )
{ }
( ) ( )
( )
0
ϕ
ϕ
δ
ϕ
ϕ
δ
δ
∫
∞
∞
−
=
=
→
dt
t
t
t
V
t
t
Definicja delty Diraca jest też
utożsamiana z właściwością
próbkującą delty Diraca.
( )
t
ϕ
t
0
=
t
( )
0
ϕ

Paul Adrien Maurice DIRAC ( 1902 - † 1993)
Dirac Paul Adrien Maurice (1902-1993), wybitny angielski fizyk-
teoretyk, współtwórca mechaniki kwantowej, przewidział istnienie
pozytonu i wniósł istotny wkład w rozwój elektrodynamiki kwantowej.
Był profesorem uniwersytetów w Cambridge i Oksford i członkiem
Royal Society. W 1933 otrzymał (wraz z E. Schrödingerem) Nagrodę
Nobla za rozwinięcie mechaniki kwantowej.
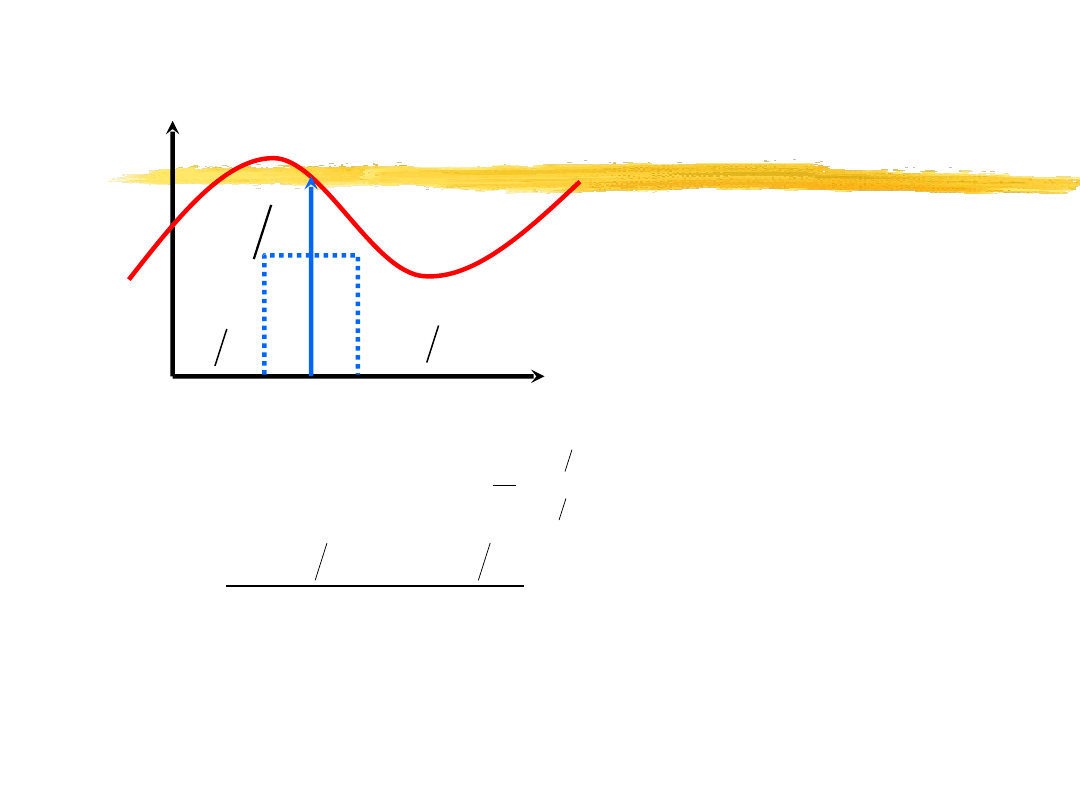
Delta Diraca (impuls Diraca)
0
=
t
( )
t
ϕ
t
( )
0
ϕ
2
ε
+
2
ε
−
ε
1
( ) ( )
( )
(
) (
)
( ) ( )
0
0
2
2
lim
1
lim
lim
0
2
2
0
0
ϕ
ε
ε
ε
ϕ
ε
ϕ
π
ε
ε
ε
ε
ε
ε
=
Φ ′
=
−
Φ
−
+
Φ
=
=
=
→
+
−
→
∞
∞
−
→
∫
∫
dt
t
dt
t
t
( ) ( )
t
t
ϕ
=
Φ ′
( ) ( )
( )
[
]
( )
( )
( ) ( )
( )
0
lim
lim
0
0
ϕ
ϕ
δ
ϕ
π
ϕ
π
δ
ε
ε
ε
ε
=
=
=
∫
∫
∫
∞
∞
−
∞
∞
−
→
∞
∞
−
→
dt
t
t
dt
t
t
dt
t
t
t
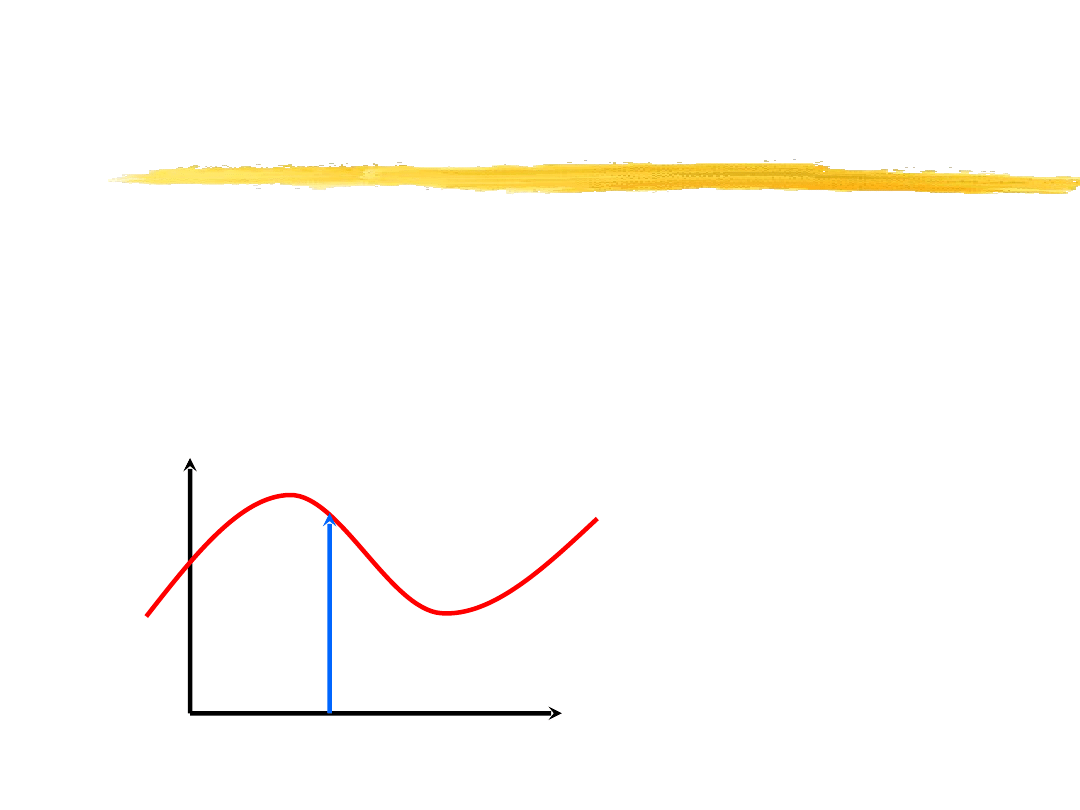
Właściwość próbkująca delty Diraca
( )
( )
( )
{ }
( ) ( )
( )
0
ϕ
ϕ
δ
ϕ
ϕ
δ
δ
∫
∞
∞
−
=
=
→
dt
t
t
t
V
t
t
(
) ( )
( )
0
0
t
dt
t
t
t
ϕ
ϕ
δ
∫
∞
∞
−
=
−
( )
t
ϕ
t
0
t
t
=
( )
0
t
ϕ
(
)
0
t
t
−
δ
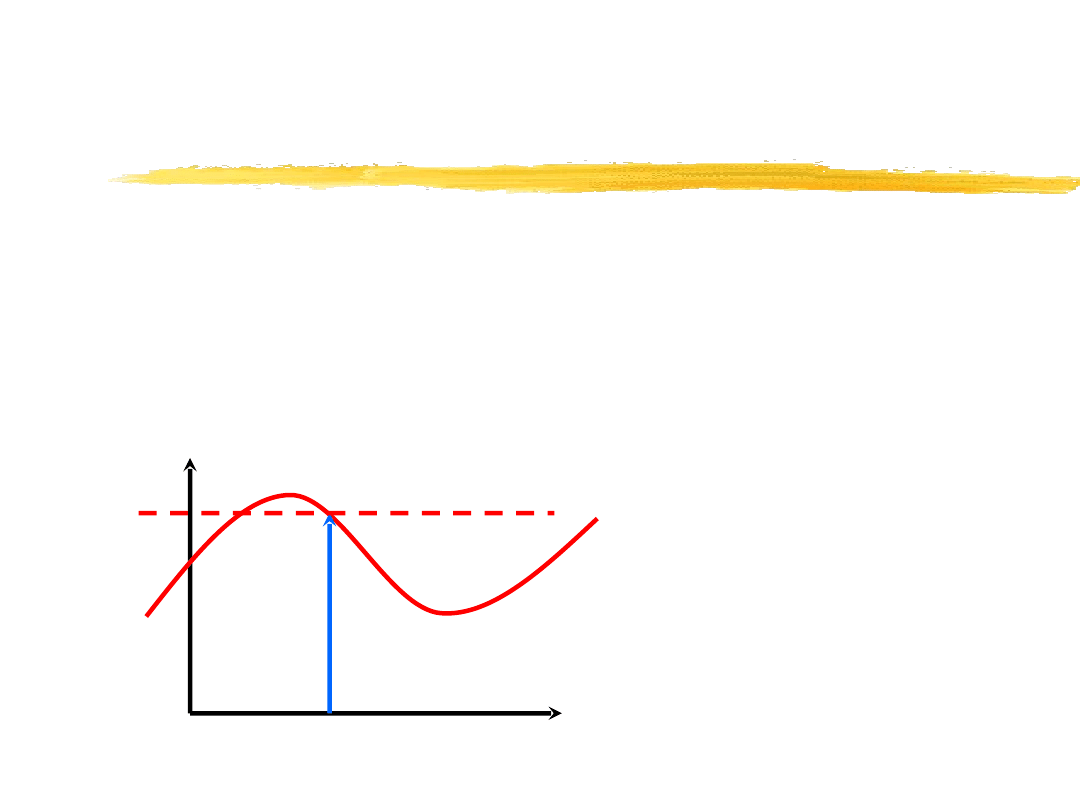
Właściwość próbkująca delty Diraca
( )
( )
( )
{ }
( ) ( )
( )
0
ϕ
ϕ
δ
ϕ
ϕ
δ
δ
∫
∞
∞
−
=
=
→
dt
t
t
t
V
t
t
( ) (
) ( ) (
)
0
0
0
t
t
t
t
t
t
−
=
−
δ
ϕ
δ
ϕ
0
t
t
=
( )
t
ϕ
t
( )
0
t
ϕ
(
)
0
t
t
−
δ
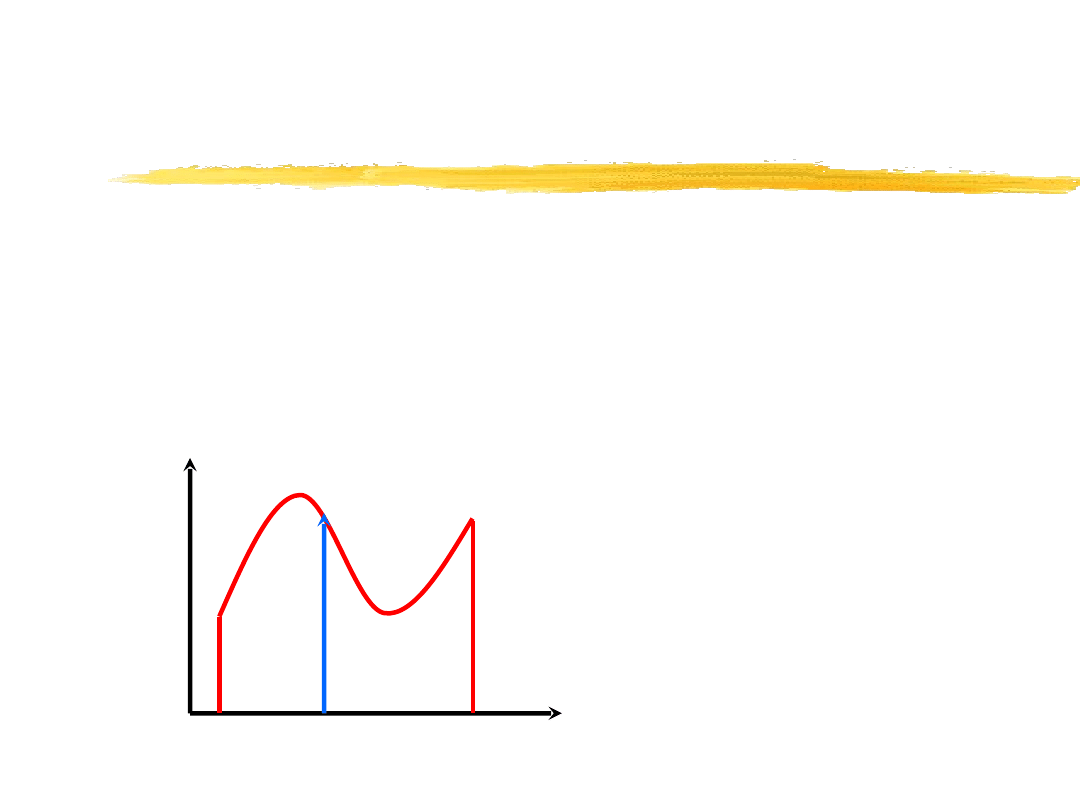
Właściwość próbkująca delty Diraca
( )
( )
( )
{ }
( ) ( )
( )
0
ϕ
ϕ
δ
ϕ
ϕ
δ
δ
∫
∞
∞
−
=
=
→
dt
t
t
t
V
t
t
(
) ( )
( )
[ ]
[ ]
∉
∈
=
−
∫
b
a
t
b
a
t
t
dt
t
t
t
b
a
,
,
0
,
,
0
0
0
0
ϕ
ϕ
δ
( )
t
ϕ
t
( )
0
t
ϕ
(
)
0
t
t
−
δ
a
b
0
t
t
=
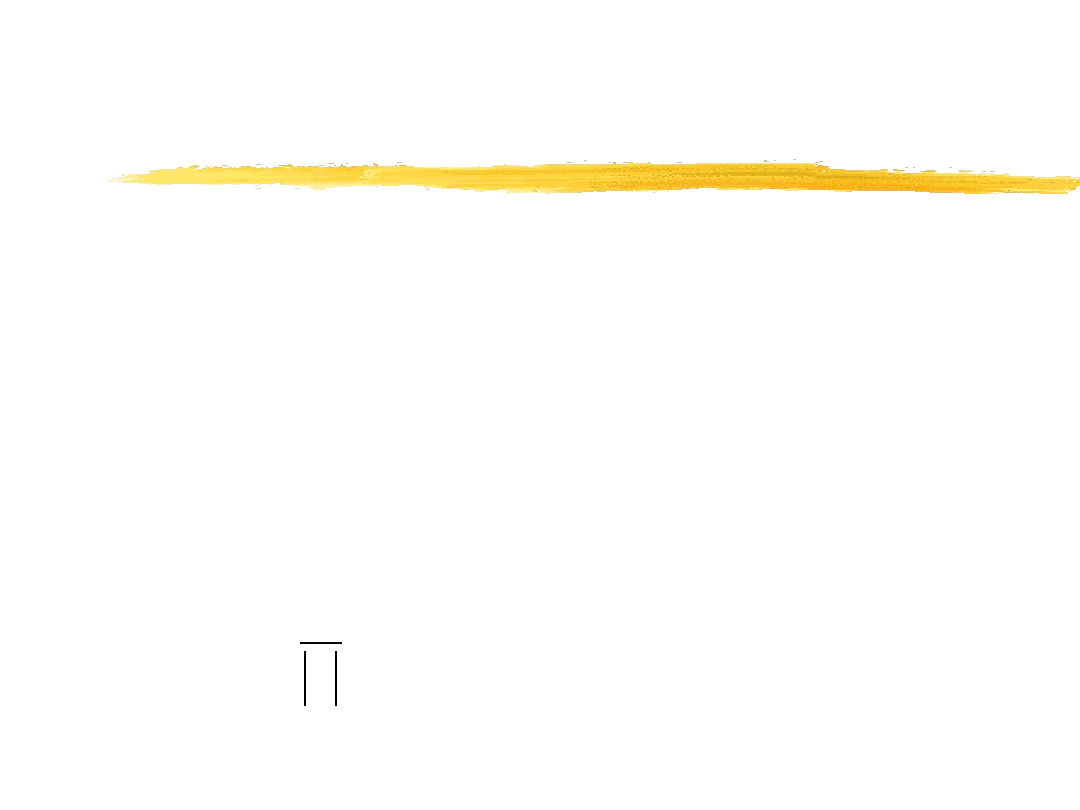
Inne właściwości delty Diraca
( ) ( )
( ) (
)
( )
t
d
t
t
t
ϕ
τ
τ
ϕ
τ
δ
ϕ
δ
∫
∞
∞
−
=
−
=
∗
Splot sygnału z deltą Diraca
„Pole” delty Diraca
( )
1
∫
∞
∞
−
=
dt
t
δ
( )
( )
t
a
at
δ
δ
1
=
„Symetria” delty Diraca
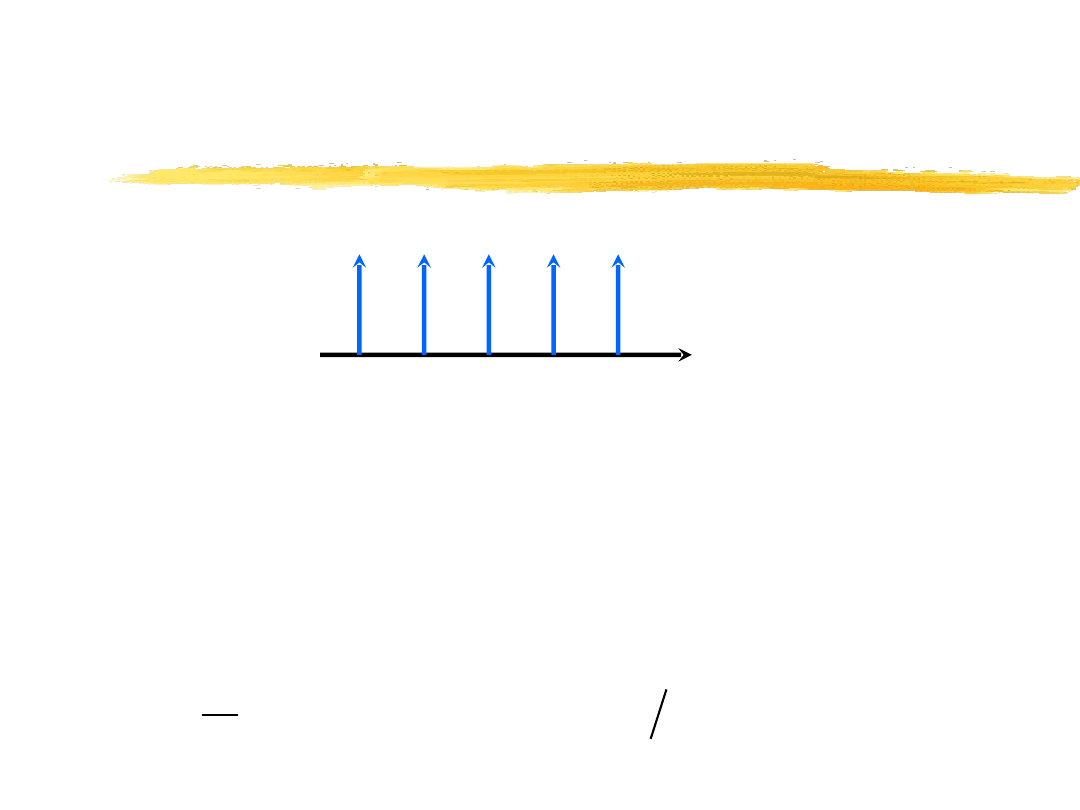
Dystrybucja grzebieniowa
t
(
)
nT
t
−
δ
( )
(
)
∑
∞
∞
−
−
=
nT
t
t
T
δ
δ
( )
(
)
T
e
T
nT
t
t
n
t
jn
T
π
ω
δ
δ
ω
2
,
1
0
0
=
=
=
−
=
∑
∑
∞
− ∞
=
∞
∞
−
Wykładniczy szereg Fouriera
dystrybucji grzebieniowej
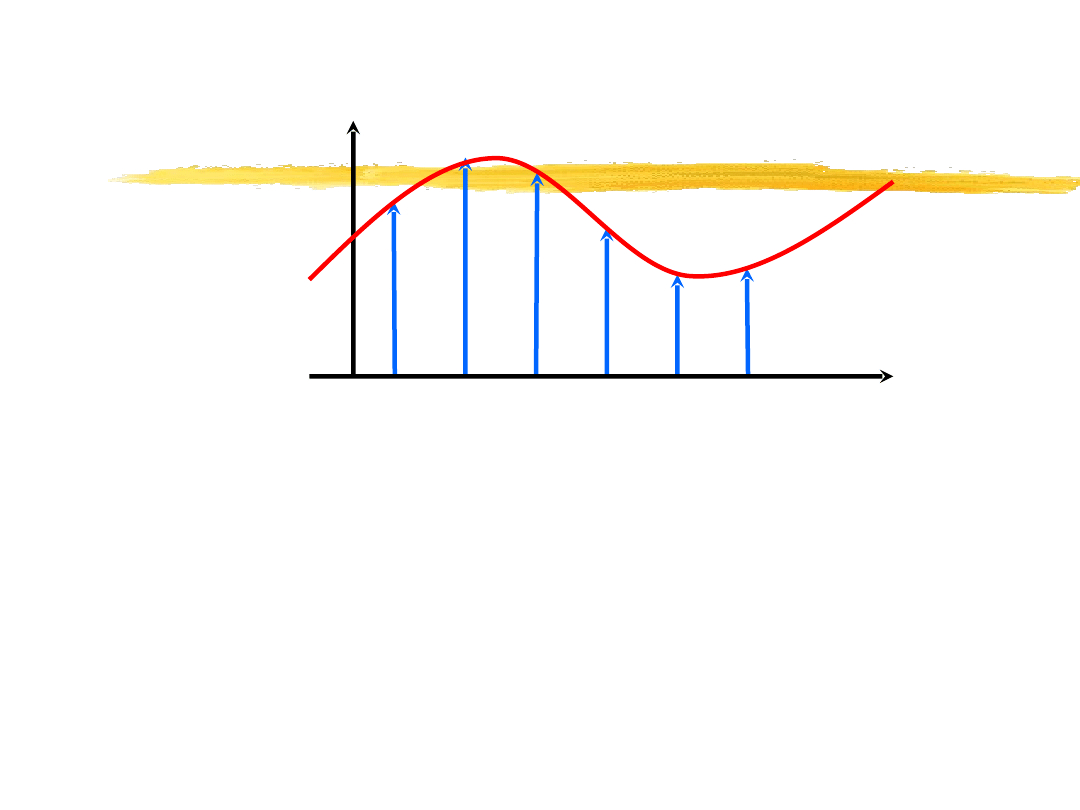
Próbkowanie sygnałów
t
nT
( ) (
)
nT
t
nT
x
−
δ
( )
( ) (
)
( )
(
) ( ) ( )
t
t
x
nT
t
t
x
nT
t
nT
x
t
x
T
δ
δ
δ
=
−
=
−
=
∑
∑
∞
∞
−
∞
∞
−
s
Zapis sygnału spróbkowanego za pomocą
dystrybucji grzebieniowej

Transformaty Fouriera funkcji specjalnych
Delta Diraca
( )
{ }
( ) (
)
( )
1
1
exp
↔
=
−
=
∫
∞
∞
−
t
dt
t
j
t
t
δ
ω
δ
δ
F
Sygnał stały
( )
ω
π δ
2
1
↔
Skok jednostkowy
( )
( )
( )
( )
( )
ω
ω
π δ
ω
j
t
j
t
t
t
1
2
sgn
,
sgn
2
1
2
1
+
↔
↔
+
=
1
1
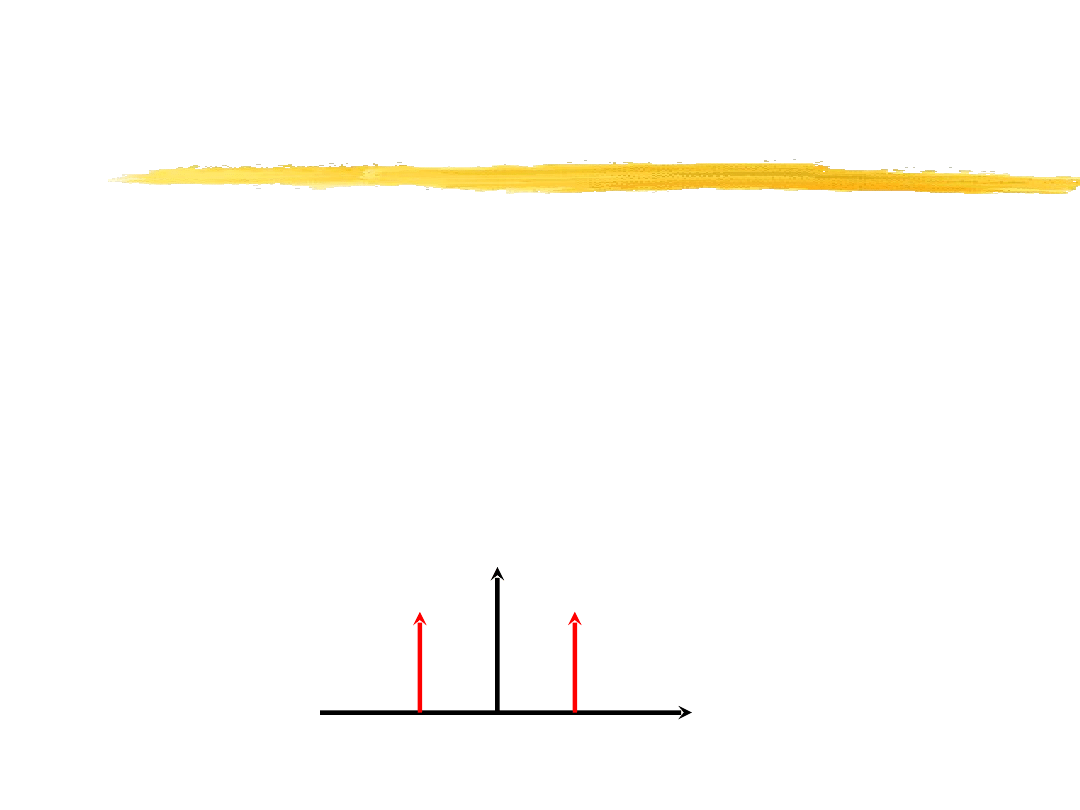
Transformaty Fouriera funkcji specjalnych
Sygnał harmoniczny
( )
(
)
(
)
(
)
(
)
±
+
↔
−
−
↔
+
↔
0
0
0
0
2
exp
2
exp
2
1
ω
ω
π δ
ω
ω
ω
π δ
ω
ω
π δ
t
j
t
j
(
) (
)
[
]
(
) (
)
[
]
0
0
0
0
0
0
sin
cos
ω
ω
δ
ω
ω
δ
π
ω
ω
ω
δ
ω
ω
δ
π
ω
+
−
−
−
↔
+
+
−
↔
j
t
t
ω
0
ω
ω
−
=
0
ω
ω
+
=
Transformaty Fouriera funkcji specjalnych
Funkcja grzebieniowa Diraca
( )
(
)
T
e
T
nT
t
t
n
t
jn
T
π
ω
δ
δ
ω
2
,
1
0
0
=
=
=
−
=
∑
∑
∞
− ∞
=
∞
∞
−
( )
(
)
∑
∑
∞
− ∞
=
∞
− ∞
=
−
↔
=
n
n
t
jn
T
n
T
e
T
t
0
2
1
0
ω
ω
δ
π
δ
ω
( )
( )
ω
δ
ω
δ
ω
0
0
↔
t
T
Podsumowanie
•Szereg sygnałów, stosowanych w praktyce laboratoryjnej,
nie posiada transformat Fouriera (nie spełniają warunku
Dirichleta).
•Konstrukcja transformat Fouriera dla tej klasy sygnałów
korzysta z definicji delty Diraca (funkcji uogólnionej).
•Delta Diraca przyporządkowuje sygnałowi – w zapisie
całkowym – wartość jego próbki.
•Funkcja grzebieniowa Diraca – ciąg okresowo powtarzanych
impulsów Diraca – umożliwia zapis operacji próbkowania
sygnałów oraz wyznaczenie transformaty Fouriera sygnału
spróbkowanego.
Document Outline
- Slajd 1
- Slajd 2
- Slajd 3
- Slajd 4
- Slajd 5
- Slajd 6
- Slajd 7
- Slajd 8
- Slajd 9
- Slajd 10
- Slajd 11
- Slajd 12
- Slajd 13
- Slajd 14
- Slajd 15
- Slajd 16
- Slajd 17
- Slajd 18
Wyszukiwarka
Podobne podstrony:
Funkcja opisujaca pop1 id 18182 Nieznany
Elektronika W10 id 159018 Nieznany
funkcje transporterow ABC id 18 Nieznany
FUNKCJE JEDNEJ ZMIENNEJ id 1820 Nieznany
PodstEle w10 id 369039 Nieznany
Funkcja blony otrzewnowej id 18 Nieznany
Funkcja opisujaca pop1 id 18182 Nieznany
5 ekstrema funkcji id 40709 Nieznany (2)
Antropologia kulturowa W10 id 6 Nieznany (2)
7 Funkcjonalizm id 44874 Nieznany (2)
Funkcje 5 id 181902 Nieznany
Funkcje 6 id 181903 Nieznany
Funkcje tworzace id 182133 Nieznany
AMI 14 Funkcje c d id 59050 Nieznany (2)
5 Badanie funkcji id 39644 Nieznany (2)
generator funkcji (1) id 187188 Nieznany
więcej podobnych podstron