Funkcje
Niech X, Y będą ustalonymi zbiorami niepustymi.
Def. Funkcją odwzorowującą (przekształcającą) zbiór X w zbiór Y
nazywamy dowolne przyporządkowanie, które każdemu elementowi
x ze zbioru X przyporządkowuje dokładnie jeden element y ze zbioru Y
i zapisujemy f: X → Y.
Elementy x zbioru X nazywamy argumentami, a zbiór X – dziedziną
funkcji. Często dziedzinę funkcji f będziemy oznaczad D
f
. Element y ze
zbioru Y taki, że y=f(x) dla pewnego x ze zbioru X nazywamy wartością
funkcji f dla argumentu x. Zbiór Y nazywamy przeciwdziedziną
funkcji f. W przeciwdziedzinie Y wyróżniamy podzbiór f(X), gdzie
i nazywamy go zbiorem wartości funkcji f.
Def.Funkcję f: X → Y nazywamy funkcją odwzorowującą zbiór X
na zbiór Y ( lub inaczej surjekcją) i zapisujemy wtedy i tylko
wtedy, gdy każdy element zbioru Y jest wartością funkcji f, tzn. f(X)=Y.•
Y
X
f
na
:
}
:
)
(
{
)
(
X
x
x
f
X
f
def
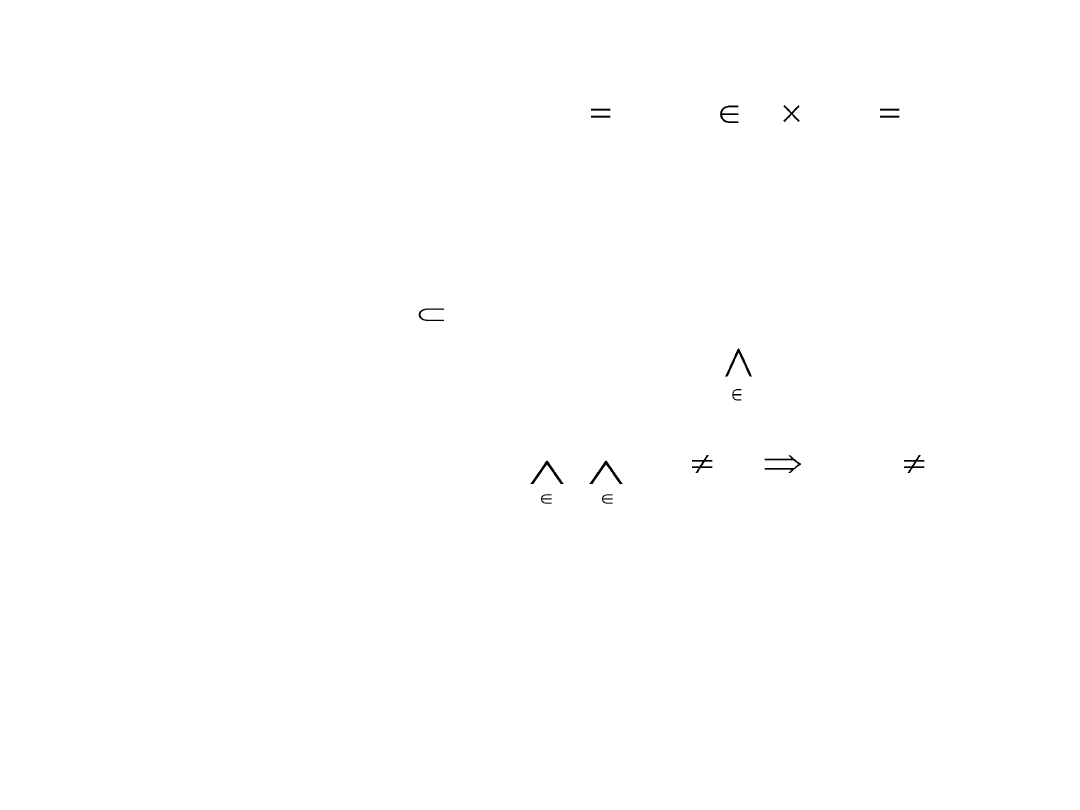
Def. Jeżeli f: X → Y, to wykresem funkcji f nazywamy podzbiór
zbioru X × Y określony równością •
Def. Dwie funkcje nazywamy równymi wtedy i tylko wtedy, gdy
mają tę samą dziedzinę oraz w każdym punkcie dziedziny mają tę
samą wartośd.•
Def. Niech f: X → Y oraz A X, A ≠ ø. Obcięciem funkcji f do
zbioru A nazywamy taką funkcję f
|A
: A → Y, że f
|A
(x) = f(x). •
Def. Funkcję f: X → Y nazywamy różnowartościową ( lub inaczej
injekcją) wtedy i tylko wtedy, gdy
Definicja Funkcję f: X → Y nazywamy wzajemnie jednoznaczną( lub
inaczej bijekcją) wtedy i tylko wtedy, gdy jest ona różnowartościowa
i odwzorowuje X na Y. Mówimy wtedy, że funkcja f przekształca
wzajemnie jednoznacznie zbiór X na zbiór Y.
)).
(
)
(
(
2
1
2
1
2
1
x
f
x
f
x
x
X
x
X
x
A
x
)}.
(
:
)
,
{(
x
f
y
Y
X
y
x
W
f
Def. Niech f: D
f
→ Y i g: D
g
→ Z oraz niech f(D
f
) D
g
.
Funkcję h: D
f
→Z określoną wzorem h(x) = g(f(x)) nazywamy złożeniem
funkcji f z funkcją g i oznaczamy symbolem g f. Funkcję f nazywamy
funkcją wewnętrzną, natomiast g – funkcją zewnętrzną złożenia g f.
Uwaga Jeżeli jednak nie jest spełniony warunek f(D
f
) D
g
, ale
jednocześnie zbiór D
h
{x D
f
: f(x) D
g
- jest niepusty, to funkcję
h: D
h
→Z określoną wzorem h(x) = g(f(x)) również nazywamy złożeniem
funkcji f z funkcją g i oznaczamy symbolem g f.
Przykład Wyznaczyd g f oraz f g, jeżeli funkcje f oraz g są określone
wzorami: f(x)= , g(x)=2 x - 4. D
g
= R, więc f(D
f
) D
g
. Funkcja g f
jest zatem określona na D
f
i (g f)(x) = g(f(x)) = g( ) = 2 - 4.
W przypadku złożenia f g mamy g(D
g
) D
f
. Należy zatem sprawdzid,
czy D
h
= {x D
g
: g(x) D
f
- ≠ ø. D
f
= <0, ∞), więc ,x D
g
: g(x) D
f
} =
= {x R: 2x - 4 <0, ∞)- = ,x R : 2x – 4 ≥ 0- = <2,∞) ≠ ø.
Zatem D
f g
= <2,∞) i (f g)(x) = f(g(x)) = f(2x - 4) = dla x D
f g
.
x
x
def
x
4
2x
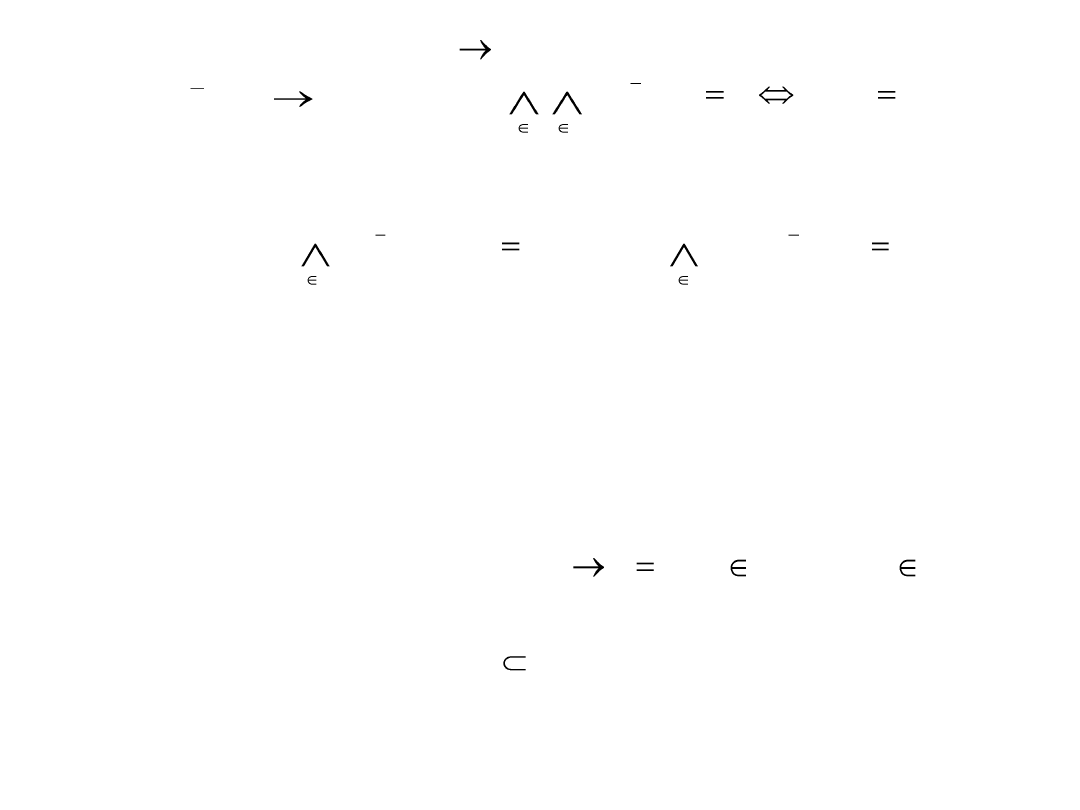
Def. Załóżmy, że funkcja jest funkcją różnowartościową.
Funkcję taką, że
nazywamy funkcją odwrotną względem f.
Z definicji wynika, że jeżeli f: X → Y jest funkcją wzajemnie
jednoznaczną, to
Definicja Niech f: X → Y. Jeżeli X oraz Y są podzbiorami R, to funkcję
f nazywamy funkcją rzeczywistą zmiennej rzeczywistej .
W dalszym ciągu będziemy zajmowad się tylko takimi funkcjami.
Zapis f: X → Y nie daje pełnej informacji o funkcji f, gdyż nie zawiera
opisu sposobu przyporządkowania. Z tego powodu będziemy czasem
posługiwad się pełnym zapisem
gdzie y = f(x) jest wzorem opisującym funkcję f.
Jeżeli funkcja f: X → Y, gdzie X ,Y R, jest funkcją wzajemnie
jednoznaczną oraz f
-1
jest funkcją względem niej odwrotną, to wykresy
funkcji f oraz f
-1
są symetryczne do siebie względem prostej y = x.
X
Y
f
na
:
1
)
)
(
)
(
(
1
y
x
f
x
y
f
X
x
Y
y
.
)
)(
(
)
)(
(
1
1
y
y
f
f
oraz
x
x
f
f
Y
y
X
x
,
)
(
:
X
x
dla
Y
x
f
y
x
f
Y
X
f
na
:
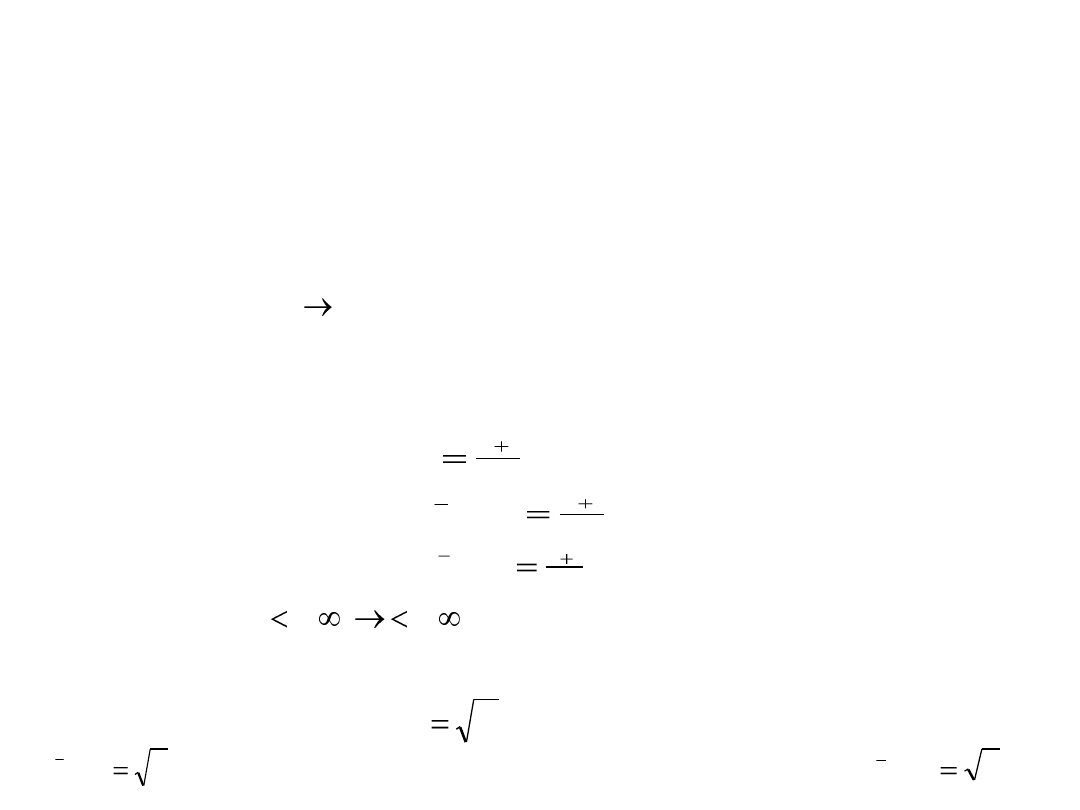
Tw. Funkcja f: X → Y ma funkcję odwrotną wtedy i tylko
wtedy, gdy f jest funkcją wzajemnie jednoznaczną.
Przykład Wyznaczyd funkcję odwrotną do:
1) funkcji f danej wzorem f(x) = 3x – 1
2) funkcji g danej wzorem g(x) = x
2
dla x ≥ 0.
Ad 1) Funkcja jest różnowartościowa, więc istnieje funkcja
do niej odwrotna. Aby znaleźd wzór opisujący funkcję do niej
odwrotną trzeba rozwiązad równanie y = 3x – 1 względem
zmiennej x. Otrzymujemy . Ostatni wzór opisuje właśnie
funkcję odwrotną. Zatem Zamieniając nazwy
zmiennych otrzymujemy
Ad 2) Funkcja jest różnowartościowa, więc istnieje
funkcja do niej odwrotna. Rozwiązując równanie y = x
2
względem
zmiennej x otrzymujemy Ostatni wzór opisuje g
-1
. Zatem
Zamieniając nazwy zmiennych otrzymujemy
.
)
(
3
1
1
x
x
f
.
)
(
3
1
1
y
y
f
3
1
y
x
.
y
x
.
)
(
1
y
y
g
R
R
na
f :
)
,
0
)
0
:
na
g
,
.
)
(
1
x
x
g
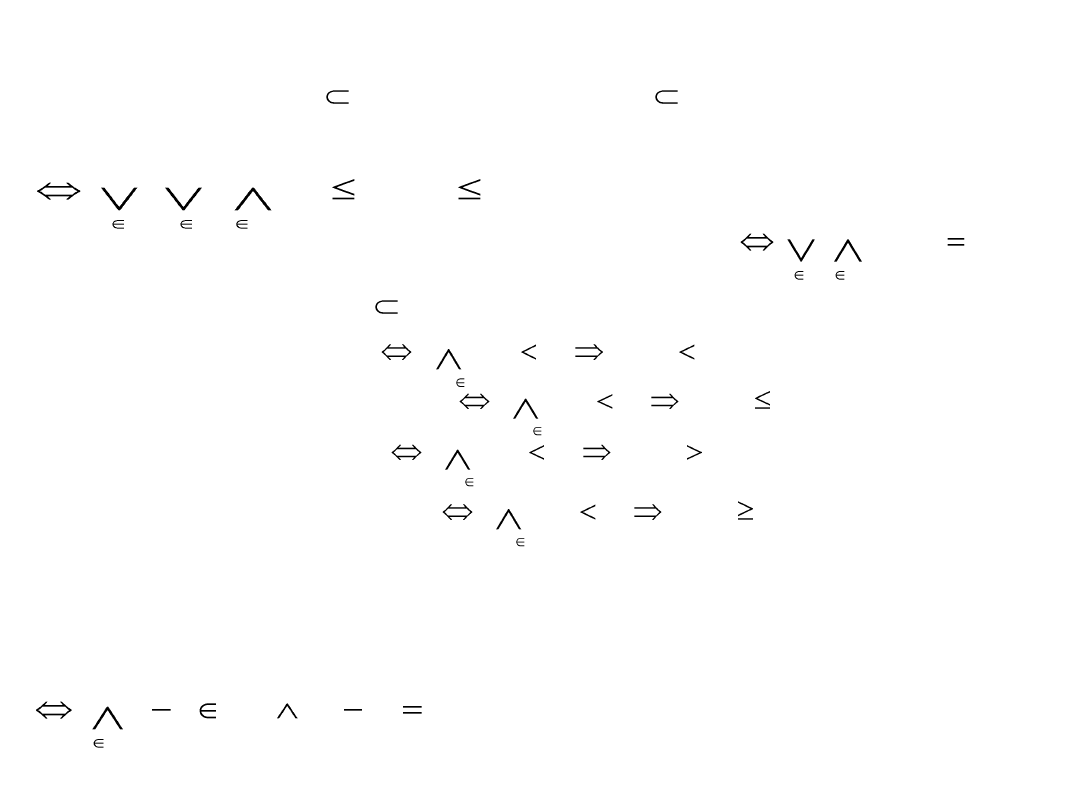
Własności funkcji
Niech f: D
f
→ R, D
f
R i g: D
g
→ R, D
g
R.
Def. Funkcję f: D
f
→ R nazywamy funkcją ograniczoną
Def. Funkcję f: D
f
→ R nazywamy funkcją stałą
Def. Niech f: D
f
→ R, A D
f
. Funkcję f nazywamy funkcją:
(a) rosnącą w zbiorze A
(b) niemalejącą w zbiorze A
(c) malejącą w zbiorze A
(d) nierosnącą w zbiorze A
Funkcje zdefiniowane powyżej nazywamy funkcjami monotonicznymi,
natomiast zdefiniowane w punktach (a) i (c)- ściśle monotonicznymi•
Def. Funkcję f: D
f
→ R nazywamy funkcją parzystą
Wykres funkcji parzystej jest osiowo symetryczny względem osi Oy.•
.
)
(
M
x
f
m
f
D
x
M
m
R
R
.
)
(
a
x
f
f
D
x
a R
)).
(
)
(
(
2
1
2
1
,
2
1
x
f
x
f
x
x
A
x
x
)).
(
)
(
(
2
1
2
1
,
2
1
x
f
x
f
x
x
A
x
x
)).
(
)
(
(
x
f
x
f
D
x
f
D
x
f
)).
(
)
(
(
2
1
2
1
,
2
1
x
f
x
f
x
x
A
x
x
)).
(
)
(
(
2
1
2
1
,
2
1
x
f
x
f
x
x
A
x
x
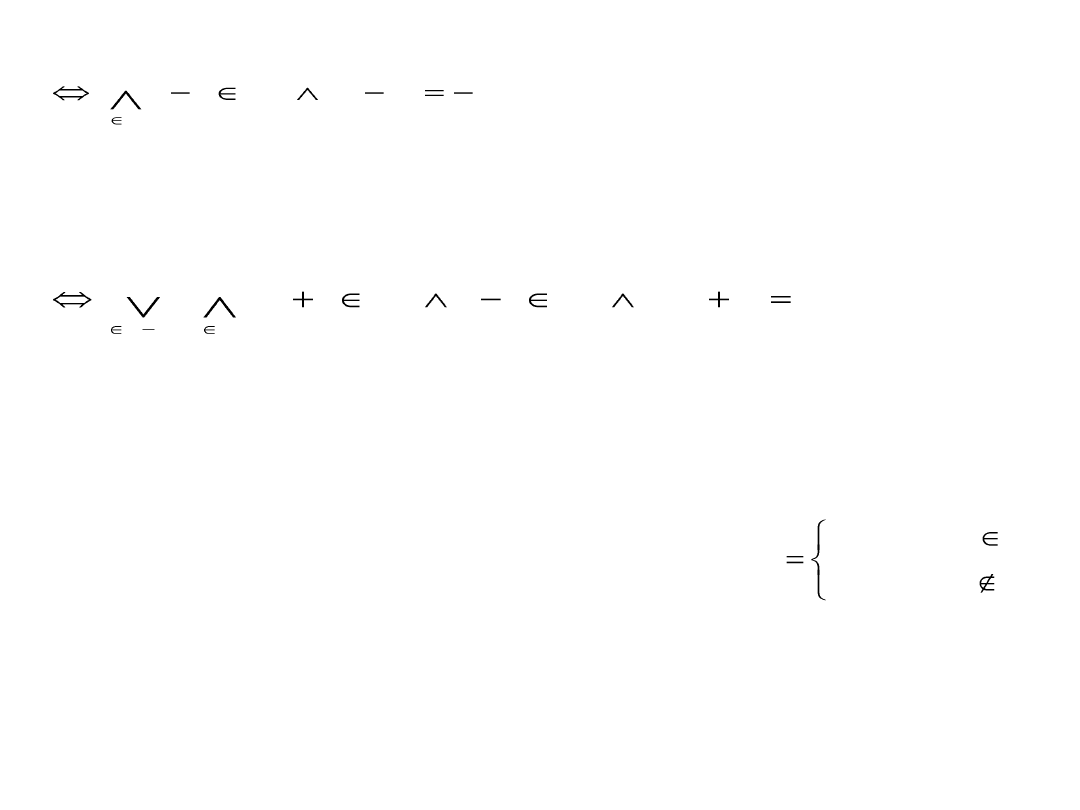
Def. Funkcję f: D
f
→ R nazywamy funkcją nieparzystą
Wykres funkcji nieparzystej jest środkowo symetryczny względem
początku układu.•
Def. Funkcję f: D
f
→ R nazywamy funkcją okresową
liczbę t nazywamy okresem funkcji f.
Def. Jeżeli wśród okresów dodatnich funkcji f istnieje
najmniejszy, to nazywamy go okresem podstawowym i oznaczamy
symbolem T.•
Przykład Rozważmy funkcję f opisaną wzorem
Jest to funkcja okresowa i każda liczba wymierna jest jej okresem.
Jednak wśród liczb wymiernych dodatnich nie istnieje liczba
najmniejsza.
)).
(
)
(
(
x
f
x
f
D
x
f
D
x
f
)).
(
)
(
(
}
0
{
x
f
t
x
f
D
t
x
D
t
x
f
f
D
x
t
f
R
W.
W
x
gdy
x
gdy
x
f
,
0
,
1
)
(
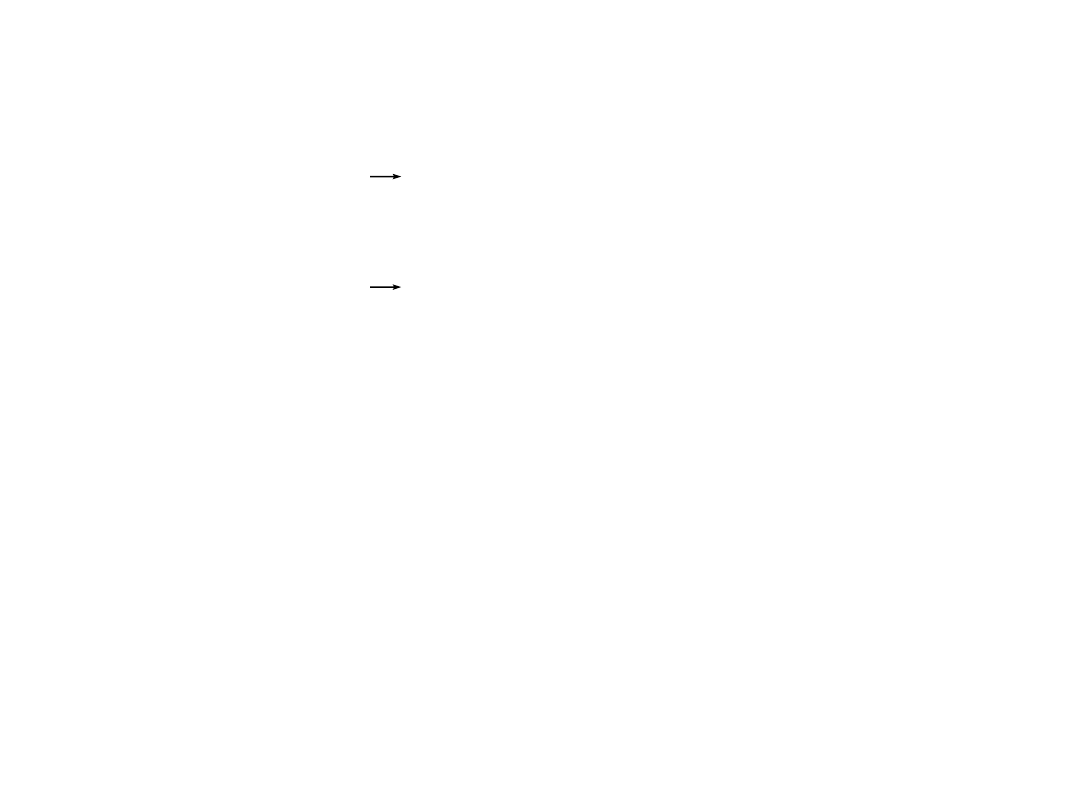
Przekształcenia wykresów
Załóżmy, że znamy wykres W
f
funkcji danej wzorem y = f(x).
1) Wykres funkcji g(x) = f(x) + q powstaje z wykresu W
f
przez
przesunięcie o wektor = *0, q+.
2) Wykres funkcji g(x) = f(x + p) powstaje z wykresu W
f
przez
przesunięcie o wektor = *-p, 0].
3) Wykres funkcji g(x) = k∙f(x ) (k > 0) powstaje z wykresu W
f
przez k-krotne „rozciągnięcie” wzdłuż osi Oy (powinowactwo
prostokątne o skali k i osi Ox).
4) Wykres funkcji g(x) = f(k∙x) (k > 0) powstaje z wykresu W
f
przez 1/k-krotne „rozciągnięcie” wzdłuż osi Ox (powinowactwo
prostokątne o skali 1/k i osi Oy).
5) Wykres funkcji g(x) = - f(x) powstaje z wykresu W
f
przez symetrię
osiową względem osi Ox, natomiast wykres funkcji g(x) = f(-x)
powstaje z wykresu W
f
przez symetrię osiową względem osi Oy.
w
w
Funkcje elementarne
Rozważmy funkcję stałą y = c, c R, funkcję tożsamościową y = x ,
wykładniczą y = a
x
, a > 0 i a ≠ 1 oraz trygonometryczną y = sinx.
Każdą funkcję, którą można otrzymad z wyżej wymienionych przez
dokonanie na nich skooczonej liczby operacji dodawania, mnożenia,
dzielenia, odwracania, składania, obcięcia nazywamy funkcją
elementarną.
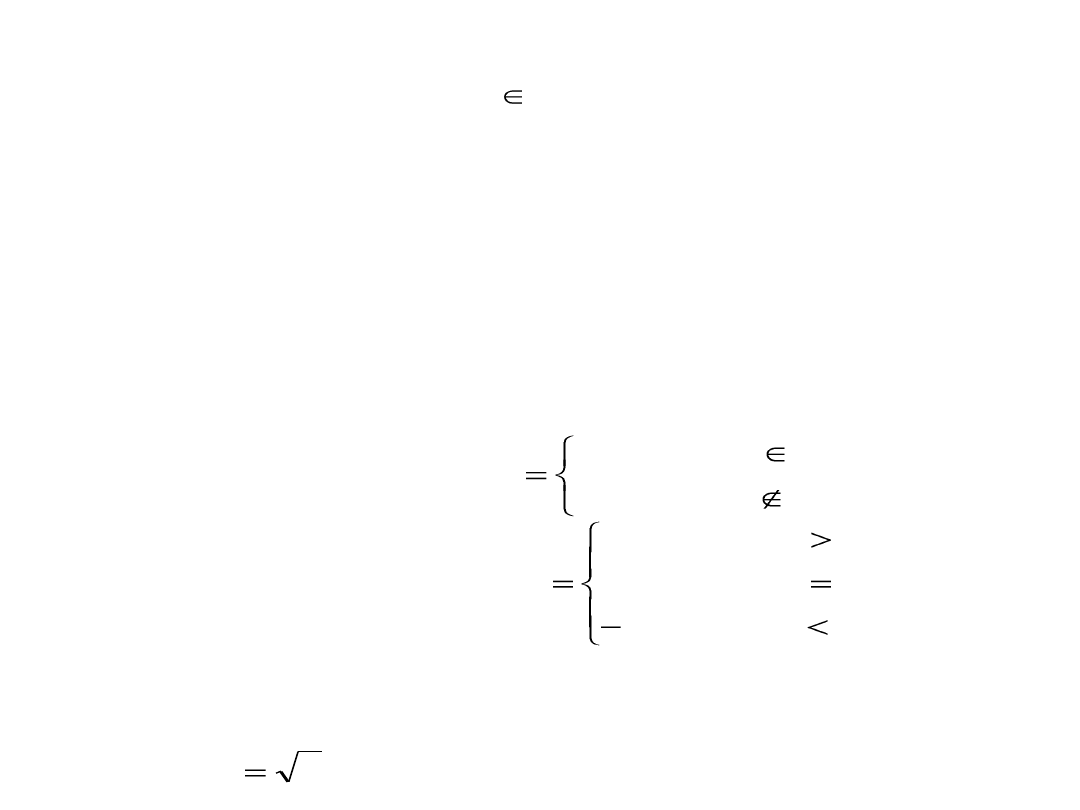
Przykłady funkcji nieelementarnych:
( 1) funkcja Dirichleta:
(2) funkcja znaku sgn:
Mówimy, ze D jest dziedziną naturalną funkcji f, jeżeli D jest zbiorem
wszystkich x, dla których funkcja f ma sens, np. dziedziną naturalną
funkcji jest zbiór D = <0,∞).
W.
W
x
gdy
x
gdy
x
f
,
0
,
1
)
(
0.
x
gdy
,
1
0
x
gdy
,
0
0
x
gdy
,
1
)
sgn(
def
x
x
x
f
)
(
Logarytm i jego własności.
Def. Niech a > 0 i a ≠ 1. Logarytmem dodatniej liczby x przy
podstawie a nazywamy taką liczbę y, że a
y
= x. Logarytm liczby x przy
podstawie a oznaczamy symbolem log
a
x.
Symbolicznie możemy zapisad
Jeżeli a = 10, to logarytm nazywamy dziesiętnym i w symbolicznym
zapisie opuszczamy podstawy tzn.
Tw. Dla dowolnych dodatnich liczb x, y, dowolnej liczby
rzeczywistej c oraz dowolnych dodatnich liczb a, b takich, że a, b ≠ 1
prawdziwe są wzory
Wzór 4) oraz wynikający z niego 4’) noszą nazwę wzorów na zamianę
podstaw logarytmów.
.
)
5
log
1
log
)
'
4
log
log
log
)
4
log
log
)
3
log
log
)
(
log
)
2
log
log
)
(
log
)
1
log
x
a
a
b
b
x
x
x
c
x
y
x
y
x
y
x
x
b
a
a
a
b
a
c
a
a
a
y
x
a
a
a
a
a
.
log
x
a
y
x
y
a
.
log
log
10
x
x