
Granice funkcji jednej zmiennej
Przypomnienie:
Zmienna
y
jest funkcją zmiennej x , jeżeli każdej z dopuszczalnych wartości x odpowiada
dokładnie jedna wartość zmiennej
y
.
Dla skrócenia zapisu stosujemy symboliczne oznaczenia funkcji, np.
)
(x
f
y
=
,
itd.
)
(t
F
s
=
Jeżeli
to dla
wartość tej funkcji jest równa:
3
2
)
(
+
= x
x
f
4
=
x
11
3
4
2
)
4
(
=
+
×
=
f
Podstawowymi funkcjami elementarnymi nazywamy funkcje:
1) potęgową
n
x
y
=
2) wykładniczą
x
a
y
=
3) logarytmiczną
dla
i
x
y
a
log
=
0
>
a
≠
a
1
4) trygonometryczne
,
x
y
sin
=
x
y
cos
=
,
tgx
y
=
,
ctgx
y
=
5) cyklometryczne
,
x
y
arcsin
=
x
y
arccos
=
,
arctgx
y
=
,
arcctgx
y
=
Funkcjami elementarnymi nazywamy funkcje, które można wyrazić jednym wzorem, w
których występuje skończona ilość działań arytmetycznych i skończona ilość operacji
oznaczanych przez symbole podstawowych funkcji elementarnych.
Wszystkie pozostałe funkcje nazywamy nie elementarnymi.
Przykłady:
Funkcja
nie jest funkcją elementarną.
⎩
⎨
⎧
>
+
≤
=
0
2
0
3
x
dla
x
x
dla
x
y
Funkcja
jest funkcją elementarną.
x
x
y
sin
5
=
Funkcję
o własności
)
(x
f
)
(
)
(
x
f
x
f
−
=
nazywamy funkcją parzystą, np.
, bo
2
x
y
=
2
2
)
( x
x
−
=
Funkcja jest nieparzysta, jeżeli
)
(
)
(
x
f
x
f
−
−
=
, np.
, bo
3
x
y
=
3
3
)
( x
x
−
−
=
Funkcje:
czy
x
a
x
nie są parzyste ani nieparzyste.
Pierwiastkami (albo miejscami zerowymi) funkcji nazywamy takie wartości argumentu, dla
których funkcja przyjmuje wartość zero. Pierwiastki funkcji
znajdujemy, przyrównując
funkcję do zera i rozwiązując równanie
)
(x
f
0
)
(
=
x
f
.
Aby znaleźć miejsca zerowe funkcji
rozwiązujemy równanie:
. Liczby:
,
9
10
)
(
2
+
+
=
x
x
x
f
0
9
10
2
=
+
+ x
x
9
1
−
=
x
1
2
−
=
x
są rozwiązaniami tego równania, czyli miejscami
zerowymi funkcji.
Dziedziną funkcji nazywamy zbiór tych wszystkich jej argumentów, dla których funkcja ma
określoną wartość. Dziedziny podstawowych funkcji elementarnych:
Funkcja potęgowa
o wykładniku wymiernym dodatnim
n
x
y
=
β
α
=
n
dla nieparzystych β
jest określona na całej osi liczbowej, natomiast dla parzystych β jest określona dla
0
≥
x
Funkcja wykładnicza
jest określona na całej osi liczbowej.
0)
(
>
=
a
a
y
x
Funkcja logarytmiczna
jest określona dla
0)
(
log
>
=
a
x
y
a
0
>
x
Funkcje trygonometryczne
,
x
y
sin
=
x
y
cos
=
są określone na całej osi liczbowej. Funkcja
jest określona na całej osi z wyjątkiem punktów:
tgx
y
=
(
)
2
1
2
π
+
= k
x
k
(k=…‐2, ‐1, 0, 1, 2.
…). Funkcja
jest określona na całej osi z wyjątkiem punktów:
ctgx
y
=
π
k
x
k
=
.
Funkcje kołowe (odwrotne do trygonometrycznych
x
y
arcsin
=
,
x
y
arccos
=
są określone
dla
, a
,
są określone na całej osi liczbowej.
1
1
≤
≤
−
x
arctgx
y
=
arcctgx
y
=

Przy wyznaczaniu dziedziny funkcji elementarnej należy zwrócić uwagę na:
1) Pierwiastki stopnia parzystego; funkcja będzie określona tylko dla takich wartości
argumentu x , dla których wyrażenie pod pierwiastkiem jest nieujemne.
2) Na mianowniki wyrażeń ułamkowych. Funkcja będzie określona dla tych wartości x , dla
których mianowniki są różne od zera.
Definicje:
1) Liczbę nazywamy granicą zmiennej
a
x
, jeżeli dla każdej dodatniej liczby
ε
istnieje
taka wartość
zmiennej
0
x
x
poczynając, od której dla wszystkich następnych wartości
zmiennej bezwzględna wartość różnicy
|
|
x
a
−
jest mniejsza od
ε
.
2) Zmienną nazywamy nieskończenie małą, jeżeli dla każdej, dodatniej liczby
a
ε
istnieje taka wartość
zmiennej a , poczynając, od której wszystkie następne
wartości zmiennej są, co do wartości bezwzględnej mniejsze od
0
a
ε
.
3) Zmienną z nazywamy nieskończenie dużą, jeżeli dla każdej dodatniej liczby N istnieje
taka wartość
zmiennej z poczynając, od której wszystkie następne wartości
zmiennej są, co do wartości bezwzględnej większe od N.
0
z
Jeżeli jest granicą zmiennej
a
x
, to mówimy, że x dąży do i piszemy
lub
a
a
x
=
lim
a
x
→
Wielkość nieskończenie wielka nie ma granicy, dla skrócenia zapisu mówimy umownie,
że z dąży do nieskończoności. i piszemy:
∞
→
z
lub
∞
=
z
lim
z definicji granicy wielkości zmiennej oraz z definicji wielkości nieskończenie małych
i nieskończenie wielkich wynika, że:
1) granicą nieskończenie małej wielkości jest zero (a więc jeśli jest wielkością
nieskończenie małą to
)
a
0
lim
=
a
2) różnica zmiennej i jej granicy jest wielkością nieskończenie małą( a więc jeśli
,
to
)
a
x
=
lim
0
=
− a
x
3) odwrotność wielkości nieskończenie dużej jest wielkością nieskończenie małą
(a więc jeśli
0
z
1
to
→
∞
→
z
)
4) odwrotność wielkości nieskończenie małej jest wielkością nieskończenie dużą
(a więc jeżeli
∞
→
→
a
to
a
1
,
0
)
Definicja.
Jeżeli
, gdy
b
x
f
→
)
(
a
x
→ (nie przybierając wartości ), to liczbęb nazywamy granicą
funkcji
w punkcie .
a
)
(x
f
a
Granicę funkcji można też określić bez odwoływania się do pojęcia granicy zmiennej..
Definicja
Liczba b nazywa się granicą funkcji
dla
)
(x
f
a
x
→ jeżeli dla każdej liczby
ε
>0 można
dobrać taką liczbę
δ
>0, że
|
będzie mniejsze od
)
(
|
b
x
f
−
ε
gdy
|
|
a
x
−
dla
a
x
≠ będzie
mniejsze od
δ
.
Jeżeli liczba jest granicą funkcji
dla
b
)
(x
f
x
dążących do , to piszemy:
a
b
x
f
a
x
=
→
)
(
lim
, gdy x dąży do w dowolny sposób.
a
b
x
f
a
x
=
−
→
)
(
lim
0
, gdy x dąży do z lewej strony, czyli tak, że x jest stale mniejsze od ;
a
a
b
x
f
a
x
=
+
→
)
(
lim
0
, gdy x dąży do z prawej strony, czyli tak, że x jest stale większe od ;
a
a
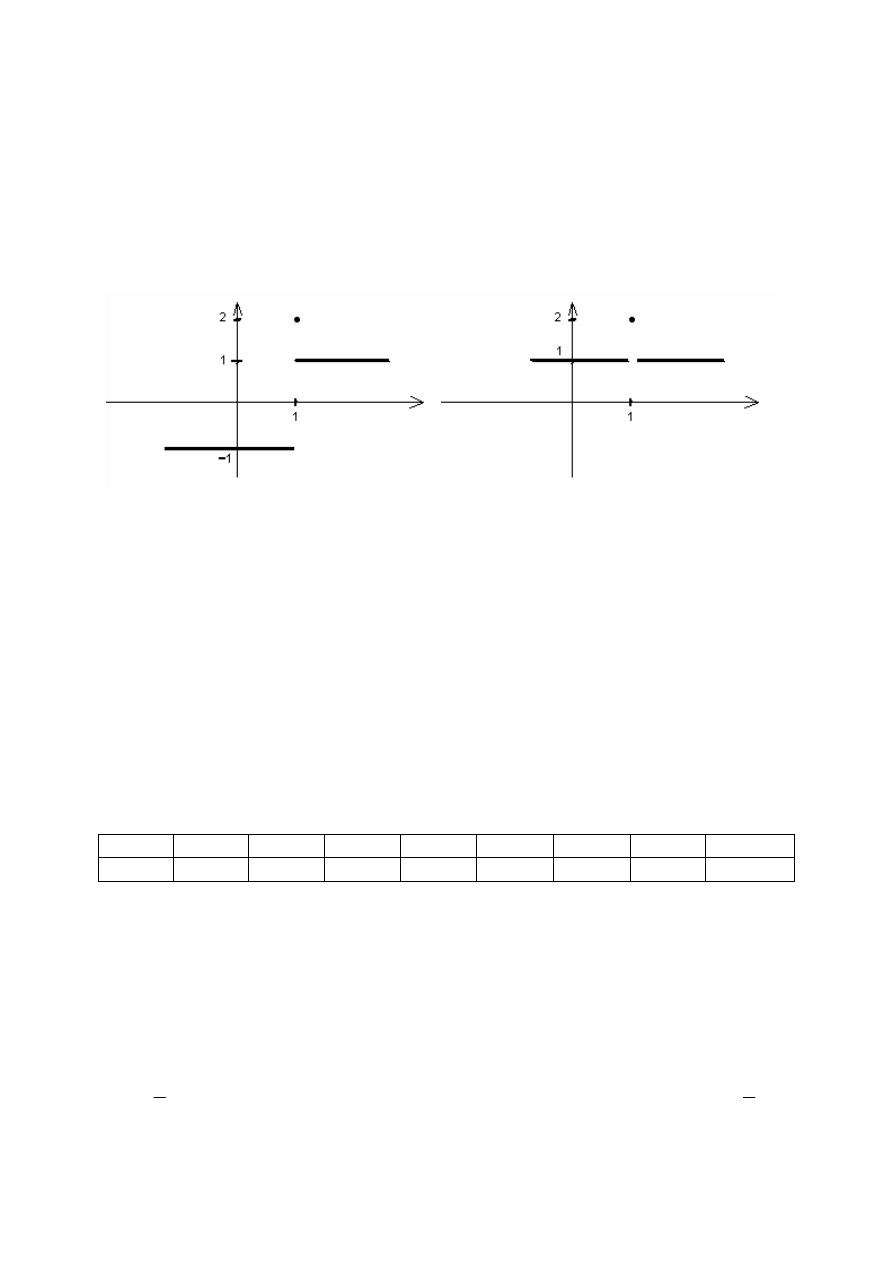
Jeśli istnieje granica funkcji, gdy
a
x
→ w dowolny sposób, to również istnieją i mają taką
samą wartość granice jednostronne tej funkcji, gdy
a
x
→ tylko z lewej strony lub tylko
z prawej strony, a więc:
Jeżeli
, to
=
b
x
f
a
x
=
→
)
(
lim
)
(
lim
0
x
f
a
x
−
→
b
x
f
a
x
=
+
→
)
(
lim
0
Natomiast, jeżeli granice jednostronne są różne lub jedna z nich nie istnieje, to granica
funkcji dla
a
x
→ nie istnieje.
Przykłady
RYS 1) Niech funkcja
ma wartość 2 dla
)
(x
f
1
=
x
, dla
wartości funkcji są równe 1,
1
>
x
dla
wartości funkcji są równe ‐1.
1
<
x
Funkcja
nie ma granicy w punkcie 1, ponieważ granica prawostronna i lewostronna
funkcji są różne.
)
(x
f
1
)
(
lim
0
1
−
=
−
→
x
f
x
1
)
(
lim
0
1
=
+
→
x
f
x
RYS 2) Funkcja
ma wartość 2 dla argumentu
)
(x
f
1
=
x
, dla argumentów różnych od 1
wartości funkcji są równe 1.
Funkcja
ma granicę w punkcie
)
(x
f
1
=
x
, ponieważ granice lewostronna i prawostronna
funkcji są sobie równe.
1
)
(
lim
0
1
=
−
→
x
f
x
, a zatem
1
)
(
lim
0
1
=
+
→
x
f
x
1
)
(
lim
1
=
→
x
f
x
Ćwiczenie 1
Biorąc n =0,1,2,3... ułożyć tabelkę wartości zmiennej:
oraz określić zachowanie
się tej zmiennej przy n rosnącym nieograniczenie, czyli dla
n
y
1
,
0
1
+
=
∞
→
n
.
n
0
1
2
3
4
5
…
∞
→
n
y
2
1,1
1,01
1,001
1,0001 1,00001
…
0
1
+
→
y
Wraz ze wzrostem n kolejne wartości zmiennej dążą do jedności, zatem dla dostatecznie
dużych wartość bezwzględna różnicy
y
|
1
|
−
y
będzie mniejsza od dowolnie małej liczby
dodatniej
ε
, co można udowodnić.
Dowód.
Niech będzie dana liczba
0
>
ε
.Można wykazać, że dla pewnych wartości n: |y‐1|<
ε
Ponieważ
, więc wystarczy wykazać, że:
w tym celu logarytmujemy obie
strony nierówności i rozwiązujemy nierówność.
n
y
1
,
0
|
1
|
=
−
ε
<
n
1
,
0
ε
lg
1
,
0
lg
<
n
⇒
ε
lg
1
,
0
lg
<
n
⇒
ε
lg
1
<
− n
⇒
ε
lg
−
>
n
⇒
1
lg
−
>
ε
n
⇒
ε
1
lg
>
n
, co oznacza, że
będzie mniejsza od
|
1
|
−
y
ε
gdy tylko n będzie większe od
ε
1
lg
.
Wobec tego zgodnie z definicją (1), zmienna
y
ma granicę równą jedności:
1
lim
=
∞
→
y
n

Ćwiczenie 2
Wykazać, że
3
2
3
3
2
lim
=
+
∞
→
x
x
x
Rozwiązanie: Utwórzmy różnicę
x
x
x
x
x
x
x
1
3
3
3
2
3
2
3
2
3
3
2
=
=
−
+
=
−
+
Gdy
∞
→
x
różnica ta jest wielkością nieskończenie małą(jako odwrotność wielkości
nieskończenie wielkiej). Jeżeli zmienna
x
x
3
3
2
+
różni się od stałej
3
2
o wielkość nieskończenie
małą, to stała ta jest granicą zmiennej.
Twierdzenia o nieskończenie małych i o granicach.
1. Suma skończonej ilości wielkości nieskończenie małych jest także wielkością
nieskończenie małą.
2. Iloczyn wielkości nieskończenie małej i wielkości ograniczonej jest także wielkością
nieskończenie małą.
3. Granica stałej jest równa wartości tej stałej.
4. Granica sumy skończonej liczby składników jest równa sumie ich granic.
lim(u+v‐w)=lim u+lim v‐lim w
5. Granica iloczynu skończonej liczby czynników jest równa iloczynowi ich granic.
w
v
u
uvw
lim
lim
lim
)
lim(
×
×
=
6. Granica ilorazu jest równa ilorazowi granic dzielnej i dzielnika, jeśli granica dzielnika
jest różna od zera.
0
lim
,
lim
lim
lim
≠
=
v
v
u
v
u
Przykład 1
Znaleźć granice funkcji
a)
⎟
⎠
⎞
⎜
⎝
⎛
−
−
→
x
x
x
1
3
2
lim
1
=
2
1
1
3
1
2
lim
1
lim
3
lim
lim
2
lim
1
1
1
1
1
−
=
−
−
×
=
−
−
×
→
→
→
→
→
x
x
x
x
x
x
x
b)
x
x
x
1
sin
lim
0
→
Gdy
argument
0
→
x
∞
→
x
1
a czynnik
x
1
sin
będzie przyjmował wartości od ‐1 do 1,
nie dążąc do żadnej określonej granicy, czyli czynnik ten nie ma granicy, ale jest wielkością
ograniczoną, bo
1
1
sin
≤
x
. Dlatego, zgodnie z twierdzeniem 2, dana funkcja, jako iloczyn
wielkości nieskończenie małej x i ograniczonej wielkości
x
1
sin
, będzie wielkością
nieskończenie małą i jej granica będzie równa zeru.
0
1
sin
lim
0
=
→
x
x
x
c) Wyznaczyć granicę lewostronną i prawostronną funkcji
x
y
1
2
=
Jeżeli zmienna x będzie zmierzać do zera z lewej strony poprzez ujemne wartości, czyli gdy
x
będzie nieskończenie małą wielkością ujemną, to
x
1
będzie nieskończenie wielką
wielkością ujemną, a
x
1
−
nieskończenie wielką wielkością dodatnią.

Po wstawieniu za liczbę
1
2
1
2
−
⎟
⎠
⎞
⎜
⎝
⎛
=
otrzymamy
0
2
1
2
1
lim
2
lim
1
1
0
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
=
∞
+
−
−
→
x
x
x
.
Jeżeli
(z prawej strony) to
0
+
→
x
+∞
→
x
1
i
+∞
=
=
∞
+
+
→
2
2
lim
1
0
x
x
Granice: lewostronna i prawostronna funkcji są różne, czyli funkcja nie ma granicy,
gdy
.
0
→
x
Uwaga: W programie omega (
), po narysowaniu wykresu tej funkcji i
naciśnięciu klawisza
ustawiamy x=0, a następnie po wybraniu opcji: gp (granica
prawostronna) lub gl (granica lewostronna) i ponownym naciśnięciu klawisza
znajdziemy
potwierdzenie powyższego rozumowania.
Obliczanie granic
Granica funkcji w danym punkcie nie zależy od tego, czy funkcja jest określona w tym
punkcie czy też nie.
a) Jeżeli rozpatrywana funkcja jest funkcją elementarną i jeżeli wartość graniczna
argumentu należy do dziedziny funkcji, to obliczanie granicy sprowadza się do
podstawienia wartości granicznej argumentu, czyli
)
(
)
(
lim
a
f
x
f
a
x
=
→
b) Jeżeli argument dąży do nieskończoności lub do liczby nie należącej do dziedziny
funkcji, to w każdym z tych przypadków poszukiwanie granicy wymaga specjalnego
badania.
Warto też wykorzystywać twierdzenia dotyczące najczęściej występujących granic przy
obliczaniu innych granic i odgrywają one rolę wzorów, które warto pamiętać.
Te podstawowe twierdzenia, to:
(stała jest wszędzie dodatnia)
a
∞
=
∞
→
ax
x
lim
∞
=
∞
→
a
x
x
lim
−∞
=
−
→
x
a
x
0
lim
+∞
=
+
→
x
a
x
0
lim
0
lim
=
∞
→
x
a
x
⎪
⎩
⎪
⎨
⎧
−
<
∞
>
∞
+
<
=
+∞
→
1)
1
gdy
1
gdy
1
|
|
gdy
0
lim
a
a
a
a
x
x
)
1
Gdy a<0 zmienna x może przyjmować tylko wartości całkowite.
⎪
⎩
⎪
⎨
⎧
<
<
∞
<
<
∞
+
>
=
−∞
→
1)
0
1
-
gdy
1
0
gdy
1
|
|
gdy
0
lim
a
a
a
a
x
x
)
1
Gdy a<0 zmienna x może przyjmować tylko wartości całkowite.
⎩
⎨
⎧
<
<
∞
+
>
∞
−
=
+∞
→
1
0
gdy
1
gdy
log
lim
a
a
x
a
x
⎩
⎨
⎧
<
<
∞
+
>
∞
−
=
+
→
1
0
gdy
1
gdy
log
lim
0
a
a
x
a
x
1
sin
lim
0
=
→
x
x
x
71828
,
2
)
1
(
lim
1
1
lim
1
0
≈
=
+
=
⎟
⎠
⎞
⎜
⎝
⎛ +
→
∞
→
e
x
x
x
α
α
α

Bardziej złożone przypadki znajdowania granic funkcji to takie, gdy funkcja jest typu:
1)
0
0
,
2)
∞
∞
,
3)
,
4)
∞
×
0
∞
−
∞
,
5)
∞
1
Przystępując do wyznaczenia granicy funkcji należy najpierw sprawdzić, jakiego typu jest
to funkcja w tym celu podstawiamy w miejsce argumentu wartość, do której ten argument
ma zmierzać.
Ad 1)
W przypadku tym przekształcamy wyrażenie tak, aby ułamek można było skrócić przez
czynnik dążący do zera.
Przykład 1
4
1
2
1
lim
)
2
)(
2
(
2
lim
4
2
lim
2
2
2
2
=
+
=
−
+
−
=
−
−
→
→
→
x
x
x
x
x
x
x
x
x
Przykład 2
5
3
1
3
5
lim
2
5
3
2
10
3
2
lim
3
4
2
2
3
4
2
4
5
2
−
=
−
+
−
+
=
−
+
+
+
−
−
+
+
−
→
−
→
x
x
x
x
x
x
x
x
x
x
x
x
x
x
(dzielimy licznik i mianownik przez x+2)
Ogólnie, jeżeli wyznaczamy granicę ułamka, którego licznik i mianownik są wielomianami,
wielomianami miejscach zerowych w punkcie granicznym x=a, to na podstawie twierdzenia
Bezouta wiemy, że wielomiany te dzielą się bez reszty przez x‐a.
Przykład 3
3
2
cos
cos
1
cos
1
lim
)
cos
cos
1
)(
cos
1
(
cos
1
lim
cos
1
sin
lim
2
2
2
3
2
=
+
−
−
=
+
−
+
−
=
+
→
→
→
x
x
x
x
x
x
x
x
x
x
x
x
π
π
π
(rozkładamy licznik i mianownik na czynniki i skracamy ułamek przez
x
cos
1
+
)
Przykład 4
2
1
1
1
1
lim
)
1
1
(
)
1
1
)(
1
1
(
lim
1
1
lim
0
0
0
−
=
+
+
−
=
+
+
+
+
+
−
=
+
−
→
→
→
x
x
x
x
x
x
x
x
x
x
(usuwamy niewymierność w liczniku mnożąc licznik i mianownik przez
1
1
+
+ x
,
a następnie dzielimy licznik i mianownik ułamka przez x)
Przykład 5
(
)
(
)
2
1
1
lim
1
1
1
1
lim
1
1
lim
0
0
0
−
=
+
+
−
=
−
−
+
+
=
+
−
→
→
→
tgx
tgx
tgx
tgx
tgx
tgx
x
x
x
(mnożymy licznik i mianownik przez
tgx
+
+ 1
1
, a następnie skracamy ułamek przez czynnik
)
tgx
Przykład 6
3
1
3
3
3
sin
lim
3
3
3
sin
3
lim
3
sin
lim
0
3
0
0
=
×
=
=
=
→
→
→
x
x
x
x
x
x
x
x
x
(przekształcamy funkcję tak, aby móc skorzystać z jednej z podstawowych granic,
mianowicie:
1
sin
lim
0
=
→
α
α
α
)

Przykład 7
2
1
2
2
sin
2
lim
2
2
sin
2
lim
cos
1
lim
2
0
2
2
0
2
0
=
×
=
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
=
=
−
→
→
→
x
x
x
x
x
x
x
x
x
(korzystamy ze wzoru trygonometrycznego
2
sin
2
cos
1
2
x
x
=
−
)
Przykład 8
4
1
4
sin
lim
cos
4
lim
)
4
(
lim
4
)
2
(
lim
)
2
(
4
lim
0
0
0
2
0
2
2
−
=
×
−
=
×
−
=
−
=
−
−
=
+
−
→
→
→
→
−
→
v
v
v
tgv
v
tgv
tgv
v
tgv
x
arctg
x
x
ν
ν
ν
ν
(podstawiając
v
x
arctg
=
+ )
2
(
otrzymamy
tgv
x
=
+ 2
, przy czym: gdy
, to
)
2
−
→
x
0
→
v
Ad 2)
Przykład 1
5
3
0
5
0
3
2
5
1
3
lim
2
5
1
3
lim
2
2
2
=
−
−
=
+
−
=
+
−
∞
→
∞
→
x
x
x
x
x
x
x
(Dzielimy licznik i mianownik ułamka przez
czyli przez najwyższą z występujących potęg x)
2
x
Zadanie to można także rozwiązać inaczej, za pomocą zamiany zmiennej. Podstawiając
mianowicie
α
1
=
x
otrzymamy:
0
→
α
, gdy
∞
→
x
, zatem
5
3
2
5
3
lim
2
5
1
3
lim
2
5
1
3
lim
2
0
2
2
0
2
2
=
+
−
=
+
−
=
+
−
→
→
∞
→
α
α
α
α
α
α
α
x
x
x
x
Ogólnie, przejście graniczne dla
∞
→
x
można zawsze sprowadzić do przejścia granicznego
dla
0
→
α
jeśli za nową zmienną przyjmie się odwrotność zmiennej wyjściowej, czyli
x
1
=
α
.
Przykład 2
1
1
1
1
1
1
lim
1
lim
2
2
−
=
−
=
+
−
=
+
−∞
→
−∞
→
n
n
n
n
n
(dzielimy licznik i mianownik przez n)
Przykład 3
1
1
1
1
lim
1
lim
)
1
(
2
1
2
1
2
2
2
lim
)
1
2
(
...
5
3
1
2
...
6
4
2
lim
=
+
=
+
=
+
+
+
×
+
=
+
+
+
+
+
+
+
+
+
+∞
→
+∞
→
+∞
→
+∞
→
n
n
n
n
n
n
n
n
n
n
n
n
n
(Licznik jest tu sumą n wyrazów ciągu arytmetycznego, mianownik sumą n+1 wyrazów
innego ciągu arytmetycznego. Należy zsumować oba wyrażenia według znanego wzoru na
sumę wyrazów ciągu arytmetycznego.)

Ad 3)
Ten przypadek wyznaczania granicy funkcji typu
∞
×
0
, można sprowadzić do przypadku
0
0
lub
∞
∞
Przykład 1
=
⎟
⎠
⎞
⎜
⎝
⎛ −
−
×
=
−
=
−
=
−
→
→
→
→
→
2
2
sin
1
lim
1
2
cos
1
lim
2
sin
lim
2
cos
2
sin
)
1
(
lim
2
)
1
(
lim
1
1
1
1
1
x
x
x
x
x
x
x
x
x
tg
x
x
x
x
x
x
π
π
π
π
π
π
π
π
π
π
π
π
2
1
2
)
1
(
2
sin
1
2
lim
2
1
=
×
=
−
⎟
⎠
⎞
⎜
⎝
⎛
=
→
x
x
x
(Wyrażenie przekształcamy na ułamek w którym licznik i mianownik dążą do zera)
Przykład 2
1
sin
lim
)
(
cos
lim
4
3
cos
4
lim
0
0
4
=
=
−
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛ −
→
→
→
t
t
t
ec
t
x
ec
x
t
t
x
π
π
π
π
(Podstawiamy:
t
x
=
−
4
π
)
Przykład 3
1
sin
lim
cos
lim
sin
cos
lim
lim
lim
0
0
0
0
=
×
=
=
=
+
→
+
→
+
→
+
→
+∞
→
α
α
α
α
α
α
α
α
α
α
α
a
ctg
xarctgx
x
(Podstawiamy
α
=
arctgx
i otrzymujemy
α
ctg
x
=
, przy czym
0
+
→
α
gdy
+∞
→
x
)
Ad 4)
Ten przypadek wyznaczania granicy funkcji typu
∞
−
∞
, można sprowadzić do przypadku:
0
0
lub
∞
∞
.
Przykład 1
4
1
2
1
lim
4
2
lim
4
4
2
1
lim
2
2
2
2
2
=
+
=
−
−
=
⎟
⎠
⎞
⎜
⎝
⎛
−
−
−
→
→
→
x
x
x
x
x
x
x
x
(Odejmujemy ułamki i otrzymany ułamek skracamy przez x‐2.)
Przykład 2
(
)
(
)
=
+
+
−
=
+
+
+
+
+
−
=
+
−
+∞
→
+∞
→
+∞
→
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
n
n
n
5
5
lim
5
5
)(
5
lim
5
lim
2
2
2
2
2
2
5
5
1
1
5
lim
−
=
+
+
−
=
+∞
→
x
n
(Rozpatrujemy funkcję jako ułamek o mianowniku 1, pozbywamy się niewymierności
w liczniku, a następnie dzielimy licznik i mianownik ułamka przez x.)
Ad 5)
W tym przypadku w celu znalezienia granicy korzystamy z następującej granicy podstawowej
e
n
n
n
=
+
=
⎟
⎠
⎞
⎜
⎝
⎛ +
→
∞
→
α
α
α
1
0
)
1
(
lim
1
1
lim
(Logarytm o podstawie e nazywa się logarytmem naturalnym i oznaczamy przez ln.
Logarytmy naturalne i dziesiętne są związane wzorami:
x
e
x
ln
lg
lg
=
oraz
e
x
x
lg
lg
ln
=
)
Przykład 1
a
a
a
n
a
n
a
a
n
n
n
n
e
n
a
n
a
n
a
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛ +
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛ +
=
⎟
⎠
⎞
⎜
⎝
⎛ +
∞
→
∞
→
∞
→
1
lim
1
lim
1
lim
lub inaczej, podstawiając
, mamy
ax
n
=
∞
→
x
gdy
∞
→
n
a
a
x
x
a
x
x
ax
x
n
n
e
x
x
x
n
a
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛ +
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛ +
=
⎟
⎠
⎞
⎜
⎝
⎛ +
=
⎟
⎠
⎞
⎜
⎝
⎛ +
∞
→
∞
→
∞
→
∞
→
1
1
lim
1
1
lim
1
1
lim
1
lim
Przykład 2
(
)
2
2
1
0
2
0
0
1
lim
)
1
(
lim
2
1
lim
−
−
→
−
→
→
=
⎥⎦
⎤
⎢⎣
⎡
+
=
+
=
−
e
x
x
x
α
α
α
α
α
α
(Podstawiając:
α
=
− x
2
mamy
0
→
α
gdy
)
0
→
x
Reguła de l’Hospitala i jej zastosowanie przy obliczaniu granic funkcji.
Skutecznym środkiem wyznaczania granicy funkcji w przypadkach, gdy jest ona typu:
0
0
(ilorazem dwóch wielkości nieskończenie małych) lub typu
∞
∞
(ilorazem dwóch wielkości
nieskończenie dużych) jest reguła de l’Hospitala, która mówi: Granica stosunku dwu
wielkości nieskończenie małych lub nieskończenie wielkich wielkości jest równa granicy
stosunku pochodnych tych wielkości, pod warunkiem, że ostatnia granica istnieje lub zmierza
do nieskończoności.
a)
Gdy okaże się, że iloraz pochodnych jest też wyrażeniem typu
0
0
lub
∞
∞
, to regułę
de l’Hospitala można stosować ponownie, a nawet wielokrotnie (jeśli jest to celowe).
Przykład 1
13
16
26
32
6
10
3
4
lim
16
6
5
16
lim
2
3
2
2
3
4
2
=
=
−
+
=
−
−
+
−
→
→
x
x
x
x
x
x
x
x
x
Przykład 2
n
m
n
m
a
x
n
n
m
m
a
x
a
n
m
nx
mx
a
x
a
x
−
−
−
→
→
=
=
−
−
1
1
lim
lim
(Po stwierdzeniu, że są to przypadki ilorazów typu:
0
0
stosujemy regułę de l’Hospitala)
Przykład 3
2
2
2
2
0
0
0
cos
cos
lim
sin
sin
lim
cos
1
cos
1
lim
b
a
bx
b
ax
a
bx
b
ax
a
bx
ax
x
x
x
=
=
=
−
−
→
→
→
(Po stwierdzeniu, że jest to przypadek ilorazu typu:
0
0
stosujemy regułę de l’Hospitala
dwukrotnie)
Czasami stosowanie reguły de l’Hospitala nie prowadzi do celu.
Przykład 4
x
tgx
tgx
x
xtgx
x
x
tgx
x
x
x
x
sec
lim
sec
lim
sec
sec
lim
sec
lim
2
2
2
2
2
π
π
π
π
→
→
→
→
=
=
=
(Granicę wyznaczamy za pomocą elementarnego przekształcenia)
1
sin
lim
cos
cos
sin
lim
sec
lim
2
2
2
=
=
=
→
→
→
x
x
x
x
x
tgx
x
x
x
π
π
π
Przykład 5
2
lim
cos
1
cos
1
lim
sin
sin
lim
2
x
tg
x
x
x
x
x
x
x
x
x
∞
→
∞
→
∞
→
=
+
−
=
+
−
(Stosowanie reguły de l’Hospitala nie prowadzi do
wyniku, ponieważ granica nie istnieje. Szukaną granicę można wyznaczyć w sposób
elementarny)
1
sin
1
sin
1
lim
sin
sin
lim
=
+
−
=
+
−
∞
→
∞
→
x
x
x
x
x
x
x
x
x
x
, gdyż
1
|
sin
|
≤
x
b)
Kiedy funkcja jest typu
lub
∞
×
0
∞
−
∞
przekształcamy funkcję do postaci ułamka
i wyznaczanie granicy sprowadzamy do przypadku:
0
0
lub
∞
∞
.
Przykład 1
2
1
2
sec
2
1
lim
2
lim
2
lim
2
0
0
0
=
=
=
→
→
→
x
x
tg
x
x
xctg
x
x
x
Przykład 2
(
)
0
lim
3
lim
ln
lim
ln
lim
3
0
3
1
1
0
1
0
3
0
3
4
3
=
−
=
−
=
=
+
→
+
→
+
→
+
→
x
x
x
x
x
x
x
x
x
x
x
(Po sprowadzeniu do przypadku
0
0
stosujemy regułę de l’Hospitala)
Przykład 3
0
sin
cos
2
sin
lim
cos
sin
cos
1
lim
sin
sin
lim
1
sin
1
lim
0
0
0
0
=
−
=
+
−
=
−
=
⎟
⎠
⎞
⎜
⎝
⎛
=
→
→
→
→
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
(Po sprowadzeniu do przypadku
0
0
stosujemy regułę de l’Hospitala dwukrotnie.
c) Przypadki funkcji typu:
,
,
także sprowadzamy do przypadków:
∞
1
0
∞
0
0
0
0
lub
∞
∞
w następujący sposób: Daną funkcję logarytmujemy i znajdujemy granicę jej logarytmu,
a następnie, gdy znamy granicę logarytmu funkcji, wyznaczamy granicę samej funkcji.
Przykład 1
( )
x
tg
x
tgx
a
2
4
lim
π
→
=
Stwierdziwszy, że zachodzi przypadek
, logarytmujemy funkcję
∞
1
i szukamy granicy jej logarytmu.
( )
x
tg
x
tgx
a
2
4
lim
π
→
=
x
ctg
tgx
tgx
x
tg
tgx
a
x
x
x
tg
x
2
ln
lim
ln
2
lim
)
ln(
lim
ln
4
4
2
4
π
π
π
→
→
→
=
×
=
=
(sprowadziliśmy poszukiwanie granicy
do przypadku
0
0
, a następnie stosując regułę de l’Hospitala, otrzymamy:
1
)
2
cos
2
(
:
sec
lim
ln
2
2
4
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
→
x
ec
tgx
x
a
x
π
Znając granicę logarytmu funkcji, znajdujemy granicę
funkcji
1
−
= e
a
Przykład 2
( )
x
x
x
1
ln
lim
+∞
→
Po ustaleniu, że zachodzi przypadek
0
∞ , obliczamy granicę logarytmu funkcji.
( )
x
x
x
a
1
ln
lim
+∞
→
=
x
x
a
x
)
ln(ln
lim
ln
+∞
→
=
Otrzymaliśmy przypadek
∞
∞
więc stosujemy regułę
de l’Hospitala
0
1
:
ln
1
lim
ln
=
⎟
⎠
⎞
⎜
⎝
⎛
=
+∞
→
x
x
a
x
skąd wynika, że poszukiwana granica
1
0
=
= e
a
Przykład 3
x
x
x
ln
2
1
6
0
lim
+
+
→
Stwierdziwszy, że zachodzi przypadek
, wyznaczamy granice:
0
0
x
x
x
a
ln
2
1
6
0
lim
+
+
→
=
x
x
a
x
ln
2
1
ln
6
lim
ln
0
+
=
+
→
i otrzymaliśmy przypadek
∞
∞
. Stosujemy regułę
de l’Hospitala
3
2
1
6
2
:
1
lim
6
ln
0
=
×
=
⎟
⎠
⎞
⎜
⎝
⎛
=
+
→
x
x
a
x
a więc poszukiwana granica wynosi
.
3
e
a
=
Wyszukiwarka
Podobne podstrony:
5 ekstrema funkcji id 40709 Nieznany (2)
7 Funkcjonalizm id 44874 Nieznany (2)
Funkcje 5 id 181902 Nieznany
Funkcje 6 id 181903 Nieznany
AMI 14 Funkcje c d id 59050 Nieznany (2)
5 Badanie funkcji id 39644 Nieznany (2)
generator funkcji (1) id 187188 Nieznany
Pochdne funkcji id 364356 Nieznany
C Typy Funkcje id 96656 Nieznany
6 funkcje id 44102 Nieznany (2)
cwiczenia4 funkcje id 124969 Nieznany
Funkcje 7 id 181904 Nieznany
Laboratorium nr 3 funkcje id 26 Nieznany
CV typ funkcjonalny id 121110 Nieznany
AMI 10 Granice funckji id 5904 Nieznany (2)
Pochodne funkcji 4 id 364442 Nieznany
3 granice i proctor id 33689 Nieznany
5 ekstrema funkcji id 40709 Nieznany (2)
granica i ciaglosc funkcji id 1 Nieznany
więcej podobnych podstron