62
POCHODNE FUNKCJI
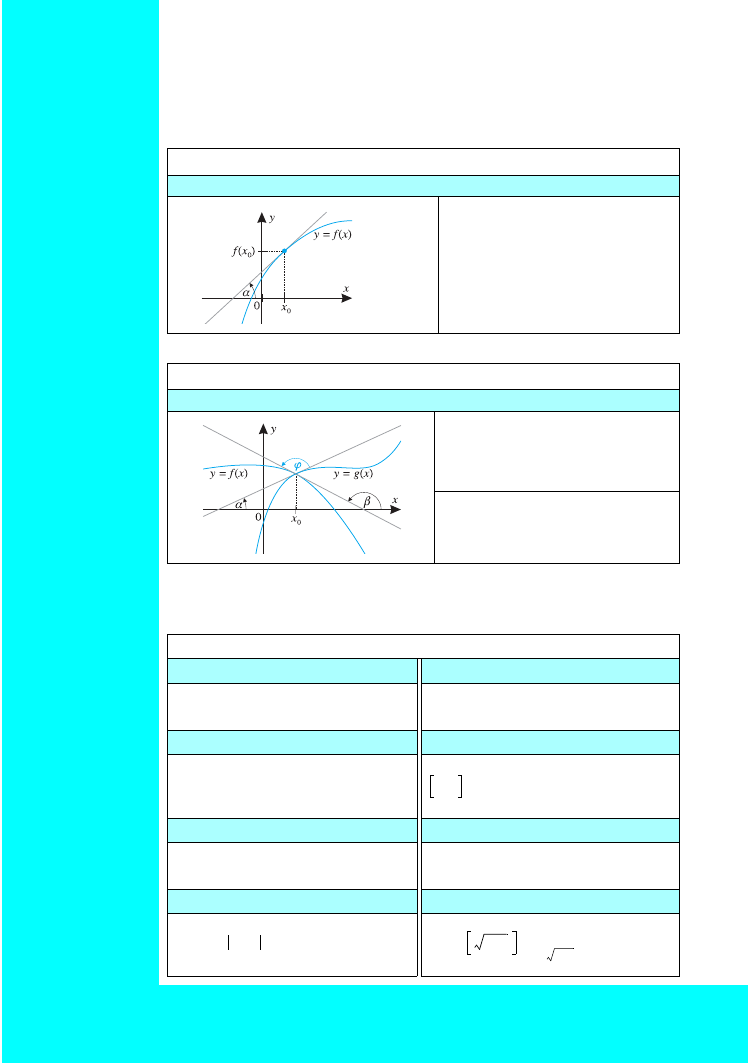
STYCZNA DO WYKRESU FUNKCJI
RÓŻNICZKOWANIE FUNKCJI
Dla funkcji f określonej w otoczeniu U(x
0
,
G) i różniczkowalnej w punkcie x
0
Równanie stycznej do wykresu funkcji
y
– f(x
0
) = f '(x
0
)(x – x
0
)
Dla funkcji f i g określonych w otoczeniu U(x
0
,
G) i różniczkowalnych w x
0
Kąt przecięcia wykresów dwóch funkcji
tg
M =
,
gdy f '(x
0
) · g'(x
0
)
z –1
M = 90°,
gdy f '(x
0
) · g'(x
0
) = –1
Dla funkcji f i g różniczkowalnych w punkcie x
∈
X i dla c
∈
R
Pochodna sumy funkcji
Pochodna różnicy funkcji
[f(x) + g(x)]' = f '(x) + g'(x)
[f(x) – g(x)]' = f '(x) – g'(x)
Pochodna iloczynu funkcji
Pochodna ilorazu funkcji
[f(x) · g(x)]' = f '(x) · g(x) + f(x) · g'(x)
=
, g(x)
z 0
Pochodna iloczynu stałej i funkcji
Pochodna funkcji stałej
[c · f(x)]' = c · f '(x)
c
' = 0
Pochodna logarytmiczna
Pochodna pierwiastka z funkcji
[ln f(x) ]' =
, f(x)
z 0
=
, f(x) > 0
Równanie stycznej
do wykresu funkcji
Kąt
między krzywymi
tg
D = f '(x
0
)
f
' x
0
( )
g
' x
0
( )
1
f
' x
0
( )
g
' x
0
( )
⋅
+
------------------------------------------
Reguły
różniczkowania
f x
( )
g x
( )
-----------
'
f
' x
( )
g x
( )
⋅
f x
( )
g
' x
( )
⋅
g x
( )
[
]
2
-----------------------------------------------------------
f
' x
( )
f x
( )
-----------
f x
( )
'
f
' x
( )
2 f x
( )
-----------------
63
Wzór
Założenie
Wzór
Założenie
(ax + b)' = a
a
, b
∈
R
(ln x )' =
x
z 0
(x
n
)' = nx
n – 1
n
∈
N, n > 1
(sin x)' = cos x
(x
D
)' =
Dx
D – 1
x
∈
R
+
,
D
∈
R
(cos x)' = –sin x
(ax
2
+ bx + c)' = 2ax + b
a
, b, c
∈
R
(tg x)' =
x
z
+
k
S,
k
∈
C
=
x
∈
R
+
(ctg x)' = –
x
z kS, k
∈
C
= –
x
z 0, a
∈
R
(arcsin x)' =
x
∈
(–1; 1)
(a
x
)' = a
x
· ln a
a
∈
R
+
\ {1}
(arccos x)' = –
x
∈
(–1; 1)
(e
x
)' = e
x
(arctg x)' =
(log
a
x )' =
x
z 0,
a
∈
R
+
\ {1}
(arcctg x)' = –
Wzór
Założenie
Wzór
Założenie
(sin x)
(n)
=
sin x + n
(cos x)
(n)
=
cos x + n
(a
x
)
(n)
= a
x
·
(ln a)
n
a
∈
R
+
\ {1}
(e
x
)
(n)
= e
x
=
(–1)
n
·
x
z 0
(ln (1 + x))
(n)
=
= (–1)
n + 1
·
x
∈
(–1; +
f)
Dla złożenia f g i funkcji g różniczkowalnej w punkcie x
∈
X oraz funkcji f
różniczkowalnej w punkcie g(x)
Pochodna funkcji złożonej
[f(g(x))]' = f '(g(x)) · g'(x)
Pochodne funkcji
elementarnych
– wzory
Pochodne rzędu n
wybranych funkcji
– wzory
Pochodna funkcji
złożonej
1
x
---
1
x
2
cos
----------------
S
2
---
x
'
1
2 x
----------
1
x
2
sin
--------------
a
x
---
'
a
x
2
-----
1
1
x
2
------------------
1
1
x
2
------------------
1
1
x
2
+
--------------
1
x
a
ln
-------------
1
1
x
2
+
--------------
S
2
---
S
2
---
1
x
---
n
( )
n
!
x
n
1
+
-----------
n
1
(
)
!
1
x
+
(
)
n
-------------------
64
ZASTOSOWANIA POCHODNEJ
Dla funkcji f mającej pochodną f ' w dowolnym przedziale otwartym X = (a; b)
lub w zbiorze X = R
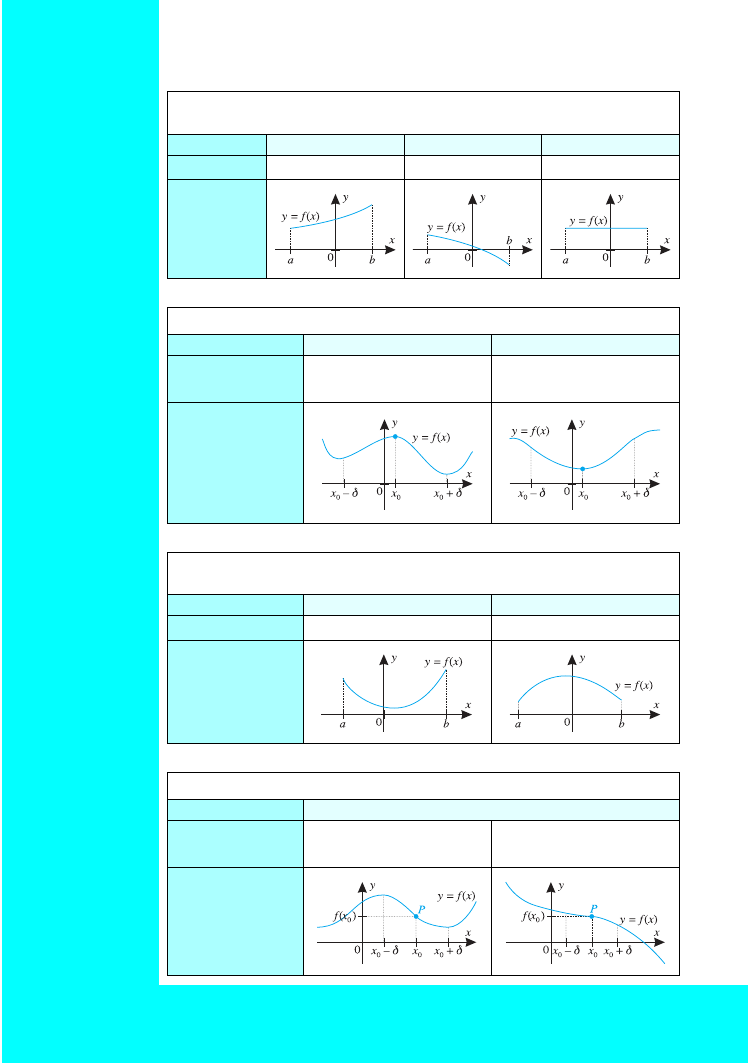
Monotoniczność
funkcja f rosnąca
funkcja f malejąca
funkcja f stała
Warunek
f
'(x) > 0
f
'(x) < 0
f
'(x) = 0
Interpretacja
geometryczna
Dla funkcji f mającej pochodną f ' w otoczeniu U(x
0
,
G) i f '(x
0
) = 0
Ekstrema lokalne
maksimum
minimum
Warunki
f
'(x) > 0 dla x
∈
S
–
(x
0
,
G)
f
'(x) < 0 dla x
∈
S
+
(x
0
,
G)
f
'(x) < 0 dla x
∈
S
–
(x
0
,
G)
f
'(x) > 0 dla x
∈
S
+
(x
0
,
G)
Interpretacja
geometryczna
Dla funkcji f mającej pochodną f '' w dowolnym przedziale otwartym X = (a; b)
lub w zbiorze X = R
Funkcja wypukła
Funkcja wklęsła
Warunki
f
''(x) > 0
f
''(x) < 0
Interpretacja
geometryczna
Dla funkcji f mającej pochodną f '' ciągłą w otoczeniu U(x
0
,
G) i f ''(x
0
) = 0
Punkt przegięcia wykresu funkcji
Warunki
f
''(x) > 0 dla x
∈
S
+
(x
0
,
G)
f
''(x) < 0 dla x
∈
S
–
(x
0
,
G)
f
''(x) < 0 dla x
∈
S
+
(x
0
,
G)
f
''(x) > 0 dla x
∈
S
–
(x
0
,
G)
Interpretacja
geometryczna
Monotoniczność
funkcji
Ekstrema lokalne
funkcji
Funkcja wypukła
i wklęsła
Punkt przegięcia
wykresu funkcji
65
CAŁKI
CAŁKOWANIE FUNKCJI
Dla funkcji f i g całkowalnych w przedziale X i dla c
∈
R
Całka sumy
Całka różnicy
[f(x) + g(x)]dx = f(x)dx + g(x)dx
[f(x) – g(x)]dx = f(x)dx – g(x)dx
Całka iloczynu stałej i funkcji
Pochodna całki
[c · f(x)]dx = c · f(x)dx
f
(x)dx = f(x)
Dla funkcji f i g mających pochodne f ' i g' ciągłe w przedziale X
Całkowanie przez części
f
(x) · g'(x)dx = f(x) · g(x) – f '(x) · g(x)dx
Dla funkcji f ciągłej w przedziale X i dla funkcji g: T
X mającej pochodną g'
ciągłą w przedziale T
Całkowanie przez podstawienie
f
(x)dx = f(g(t))g'(t)dt, gdzie x = g(t)
Dla funkcji f mającej pochodną f ' ciągłą w przedziale X i C
∈
R
Całka pochodnej funkcji
Całka pochodnej logarytmicznej
Całka pochodnej pierwiastka
z funkcji
f
'(x)dx = f(x) + C
dx
= ln f(x) + C,
f
(x)
z 0
dx
=
+ C,
f
(x) > 0
Dla dowolnych a, p, q, C
∈
R, k
∈
N
+
\ {1} i
' = p
2
– 4q < 0
dx
=
(x – a)
1 – k
+ C
dx
=
arctg
+ C
dx
= ln x +
+ C
dx
= arcsin
+ C, a
z 0
Reguły całkowania
∫
∫
∫
∫
∫
∫
∫
∫
∫
'
Całkowanie
przez części
Całkowanie
przez podstawienie
Całki
pochodnych funkcji
Całki
wybranych funkcji
wymiernych
i niewymiernych
∫
∫
na
∫
∫
∫
∫
f
' x
( )
f x
( )
-----------
∫
f
' x
( )
2 f x
( )
-----------------
f x
( )
∫
1
x
a
(
)
k
------------------
1
1
k
-----------
∫
1
x
2
px
q
+
+
---------------------------
2
'
-----------
2x
p
+
'
---------------
∫
1
x
2
a
+
------------------
x
2
a
+
∫
1
a
2
x
2
--------------------
x
a
-----
66
Wzór
Wzór
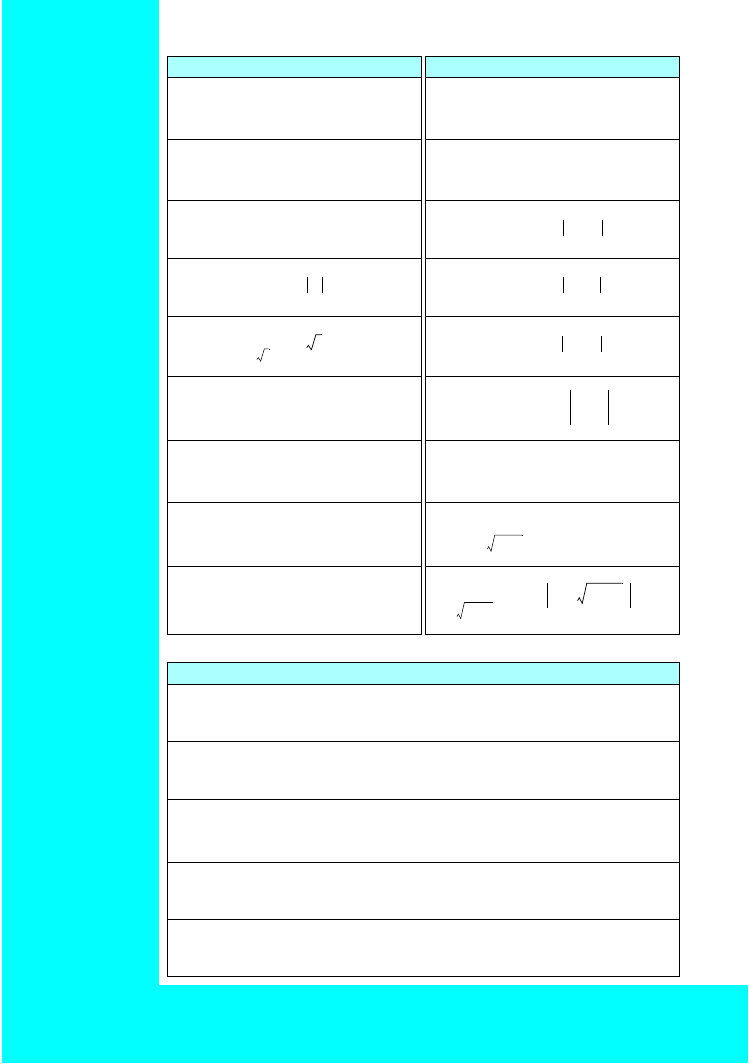
0dx = C
dx
= tg x + C
adx
= ax + C, a = const
dx
= –ctg x + C
x
D
dx
=
x
D + 1
+ C,
D z –1
tg xdx = –ln cos x + C
dx
= ln x + C
ctg xdx = ln sin x + C
dx
=
+ C
dx
= ln a + x + C
a
x
dx
=
+ C, a > 0, a
z 1
dx
= ln
+ C
e
x
dx
= e
x
+ C
dx
= arctg x + C
sin xdx = –cos x + C
dx
= arcsin x + C
cos xdx = sin x + C
dx
= ln x +
+ C
Wzory rekurencyjne na całki wybranych funkcji
sin
n
xdx = – sin
n – 1
xcos x +
sin
n – 2
xdx, n
∈
N
+
tg
n
xdx =
tg
n – 1
x – tg
n – 2
xdx, n
∈
N
+
\ {1}
dx
=
·
+
dx
, n
∈
N
+
\ {1}
x
n
· cos xdx = x
n
· sin x – n x
n – 1
sin xdx, n
∈
N
+
x
n
· sin xdx = –x
n
· cos x + n x
n – 1
cos xdx, n
∈
N
+
Całki nieoznaczone
– wzory
Wzory
rekurencyjne
na całki
wybranych funkcji
∫
∫
1
x
2
cos
---------------
∫
∫
1
x
2
sin
--------------
∫
1
D 1
+
------------
∫
∫
1
x
---
∫
∫
1
2 x
----------
x
∫
1
a
x
+
------------
∫
a
x
a
ln
----------
∫
1
1
x
2
--------------
1
2
---
1
x
+
1
x
------------
∫
∫
1
1
x
2
+
--------------
∫
∫
1
1
x
2
------------------
∫
∫
1
1
x
2
+
------------------
1
x
2
+
∫
1
n
---
n
1
n
------------
∫
∫
1
n
1
------------
∫
∫
1
1
x
2
+
(
)
n
---------------------
1
2n
2
---------------
x
1
x
2
+
(
)
n
1
---------------------------
2n
3
2n
2
---------------
∫
1
1
x
2
+
(
)
n
1
---------------------------
∫
∫
∫
∫
67
ZASTOSOWANIA CAŁKI OZNACZONEJ
Dla funkcji f ciągłej w przedziale a; b
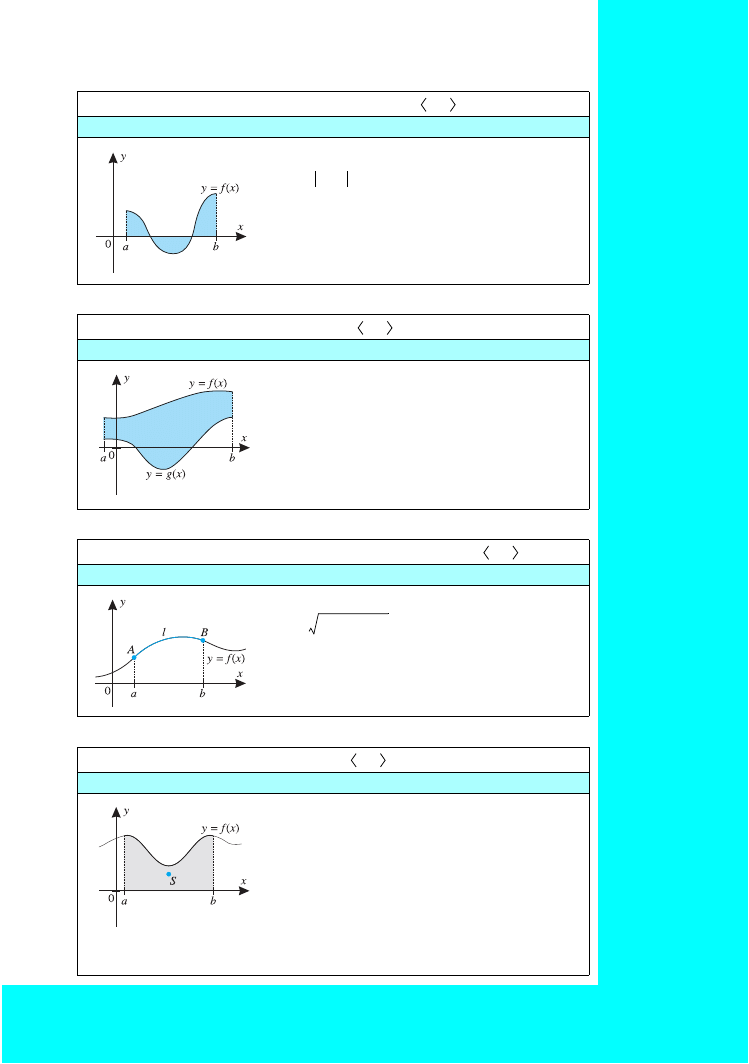
Pole figury ograniczonej wykresem funkcji
P
=
f
(x) dx
P
– pole figury ograniczonej wykresem funkcji
y
= f(x), osią Ox i prostymi x = a i x = b
Dla funkcji f i g ciągłych w przedziale a; b o wartościach f(x) > g(x)
Pole figury ograniczonej dwoma wykresami funkcji
P
= [f(x) – g(x)]dx
P
– pole figury ograniczonej wykresami funkcji
y
= f(x) i y = g(x) oraz prostymi x = a i x = b
Dla funkcji f mającej ciągłą pochodną f ' w przedziale a; b
Długość łuku wykresu funkcji
l
=
dx
l
– długość łuku AB wykresu funkcji y = f(x)
Dla funkcji f ciągłej w przedziale a; b o wartościach f(x) > 0
Współrzędne środka ciężkości figury płaskiej
x
S
=
y
S
=
S
– środek ciężkości figury ograniczonej
wykresem funkcji y = f(x), osią Ox i prostymi
x
= a i x = b
Pole figury
ograniczonej
wykresem funkcji
Pole figury
ograniczonej
dwoma wykresami
funkcji
Długość łuku
wykresu funkcji
Współrzędne
środka ciężkości
figury płaskiej
a
b
∫
a
b
∫
a
b
∫
1
f
' x
( )
[
]
2
+
x f x
( )
⋅
x
d
a
b
∫
f x
( )
x
d
a
b
∫
--------------------------
f x
( )
[
]
2
x
d
a
b
∫
2 f x
( )
x
d
a
b
∫
--------------------------
68
CAŁKI EULERA
Dla funkcji f mającej ciągłą pochodną f ' w przedziale a; b
o wartościach f(x)
t 0
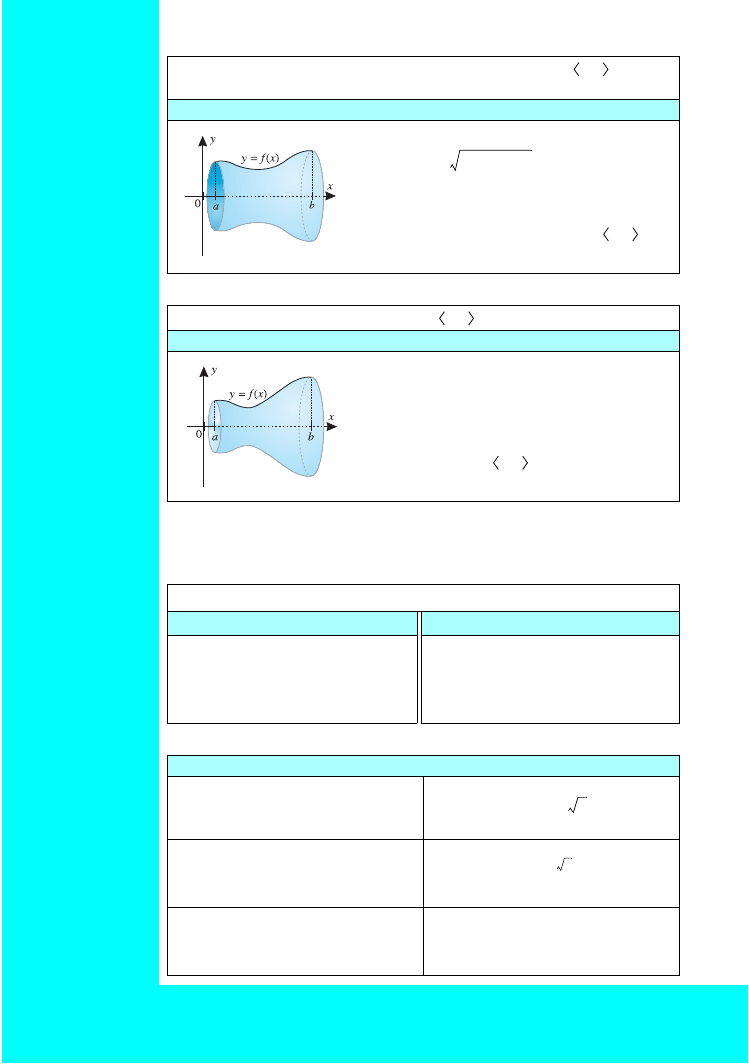
Pole powierzchni bocznej bryły obrotowej
P
b
= 2
S f(x)
dx
P
b
– pole powierzchni bocznej bryły powstałej
z obrotu wykresu funkcji y = f(x), x
∈
a; b ,
dookoła osi Ox
Dla funkcji f ciągłej w przedziale a; b o wartościach f(x)
t 0
Objętość bryły obrotowej
V
=
S f
2
(x)dx
V
– objętość bryły powstałej z obrotu wykresu
funkcji y = f(x), x
∈
a; b , dookoła osi Ox
Dla x, y
∈
R
+
Całka Eulera II rodzaju
Całka Eulera I rodzaju
*(x) = t
x – 1
e
–t
dt
E(x, y) = t
x – 1
(1 – t)
y – t
dt
Własności całek Eulera
*(x + 1) = x · *(x), x
∈
R
+
*
=
*(n) = (n – 1)!, n
∈
N
+
*(x) · * x + =
*(2x), x
∈
R
+
*(x) · *(1 – x) =
, x
∈
(0; 1)
E(x, y) =
Pole powierzchni
bocznej bryły
obrotowej
Objętość
bryły obrotowej
a
b
∫
1
f
' x
( )
[
]
2
+
a
b
∫
Funkcje
gamma i beta
Własności
całek Eulera
0
∞
∫
0
1
∫
1
2
---
S
1
2
---
S
2
2x
1
-------------
S
Sx
sin
---------------
* x
( )
* y
( )
⋅
* x y
+
(
)
---------------------------