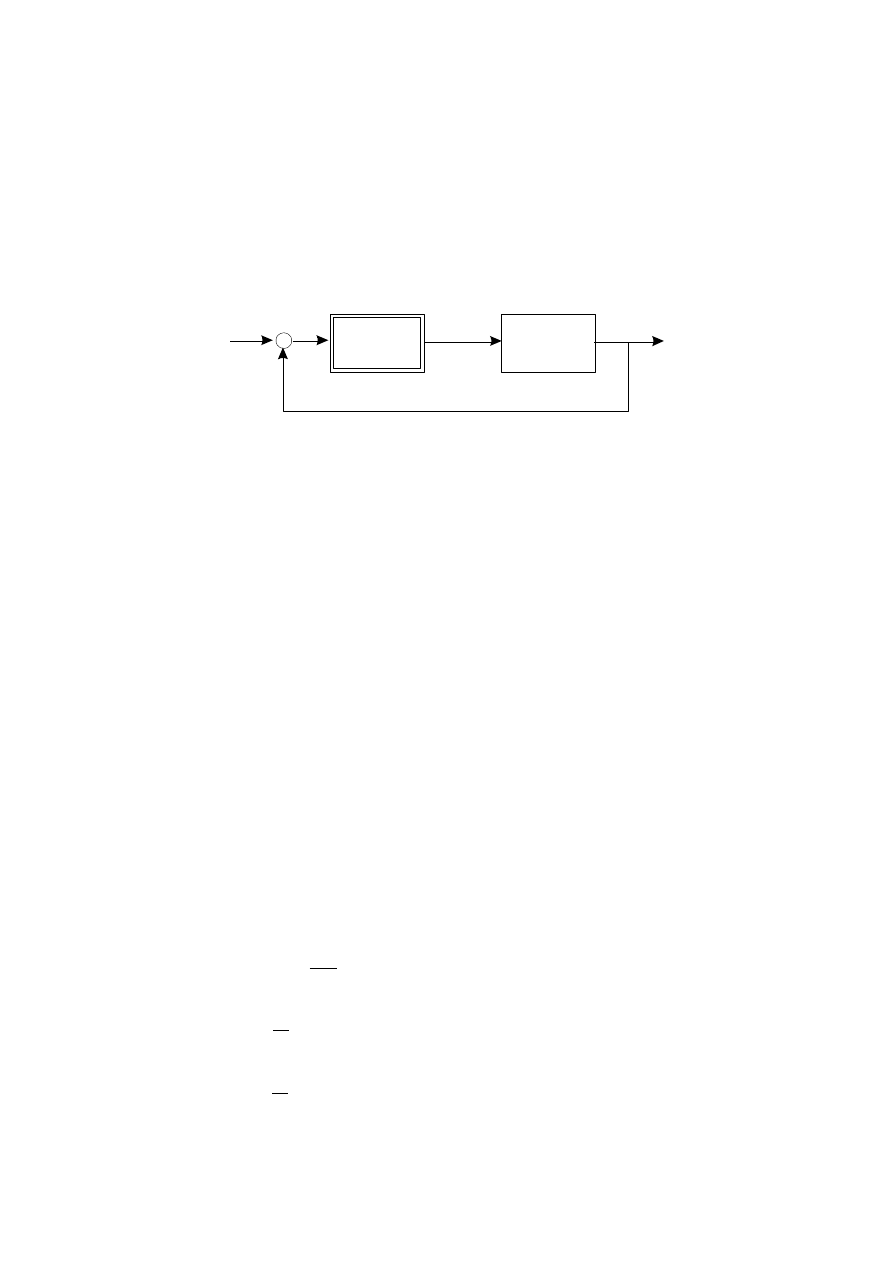
1

METODA FUNKCJI OPISUJĄCEJ

Metoda funkcji opisującej jest metodą przybliżoną.
Istotą metody jest pominięcie wyższych harmonicznych odpowiedzi członu nieliniowego na

wymuszenie sinusoidalne.
Funkcja opisująca jest przybliżoną transmitancją elementu przy założeniu, że sygnał wejściowy
elementu nieliniowego jest sinusoidalny. Zależność ta jest spełniona, jeżeli część liniowa układu ma
silne właściwości filtru dolnoprzepustowego.

Element

nieliniowy

-

e

x

u

y

Obiekt

Rys. 1. Schemat blokowy rozpatrywanego nieliniowego układu

automatycznej regulacji

Stosując metodę funkcji opisującej można określić charakter układu przedstawionego na rys. 1, a

także znaleźć jego cykle graniczne.
Przy założeniu, że element nieliniowy układu z rys.1 można opisać nieliniowym równaniem
różniczkowym:

)

t

(

x

a

...

)

t

(

x

a

)

t

(

x

a

c

)

t

(

y

b

...

)

t

(

y

b

)

t

(

y

b

)

m

(

m

)

1

(

1

0

)

n

(

n

)

1

(

1

0

















(1)

gdzie: b

k

,a

i

– współczynniki równania dla k=0,1,...,n oraz i=0,1,...,m

oraz uchyb układu jest harmoniczny

)

t

sin(

A

)

t

(

e





(2)

to wyjście y elementu nieliniowego można zapisać w postaci funkcji zależnej od amplitudy A, pulsacji



i współczynników równania





i

k

a

,

b

,

t

,

,

A

F

)

t

(

y





dla











m

i

n

k

,...,

2

,

1

,

0

,...,

2

,

1

,

0

(3)

Funkcję (3) można rozwinąć w szereg Fouriera

















1

0

)

cos(

)

sin(

)

(

r

r

r

t

r

C

t

r

B

C

t

y





(4)

gdzie:

















2

0

i

k

0

t

d

a

,

b

,

t

,

,

A

F

2

1

C

(5)



















2

0

i

k

r

t

d

)

t

r

sin(

a

,

b

,

t

,

,

A

F

1

B

(6)



















2

0

i

k

r

t

d

)

t

r

cos(

a

,

b

,

t

,

,

A

F

1

C

(7)

Dla charakterystyki statycznej elementu nieliniowego, symetrycznej względem początku układu

współrzędnych składowa stała sygnału wyjściowego C

0

=0.

2

Jeżeli rozpatrywane są nieliniowe elementy statyczne, współczynniki B

r

i C

r

zależą tylko od

amplitudy sygnału wejściowego i od współczynników a

i

, b

k

i c

0

równania opisującego te elementy.

W ogólnym przypadku współczynniki rozwinięcia w szereg Fouriera zależą od amplitudy i

pulsacji sygnału wymuszającego .

Jeżeli część liniowa układu z rys. 1 wykazuje właściwości filtru dolnoprzepustowego tłumiące

wyższe harmoniczne, to rozwinięcie w szereg Fouriera sygnału wyjściowego y(t) można ograniczyć do
jego pierwszej składowej.

)

cos(

)

,

(

)

sin(

)

,

(

)

(

)

(

1

1

1

t

A

C

t

A

B

t

y

t

y















(8)

gdzie:















2

0

1

t

d

)

t

sin(

)

t

(

y

1

)

,

A

(

B

(9)















2

0

1

t

d

)

t

cos(

)

t

(

y

1

)

,

A

(

C

(10)

Funkcją opisującą J(A,



) elementu nieliniowego nazywamy iloraz

A

)

,

A

(

jC

)

,

A

(

B

)

,

A

(

J

1

1

def











(11)

gdzie: A – amplituda wymuszenia sinusoidalnego o pulsacji



,

B

1

,C

1

– współczynniki opisane wzorami (9,10).

Dla nieliniowych elementów statycznych funkcja opisująca nie zależy od pulsacji



wymuszenia

e(t). Wtedy wzór (11) sprowadzić można do:

A

)

A

(

jC

)

A

(

B

)

,

A

(

J

1

1







.

(11)

Dla statycznych elementów nieliniowych, których charakterystyki statyczne są jednoznaczne,

współczynnik C

1

=0. Ich funkcje opisujące są więc funkcjami rzeczywistymi zależnymi od amplitudy A

i od kształtu charakterystyki statycznej elementu nieliniowego.

















2

0

1

t

d

)

t

sin(

)

t

sin

A

(

y

A

1

A

)

A

(

B

)

A

(

J

(12)

Przykład 1
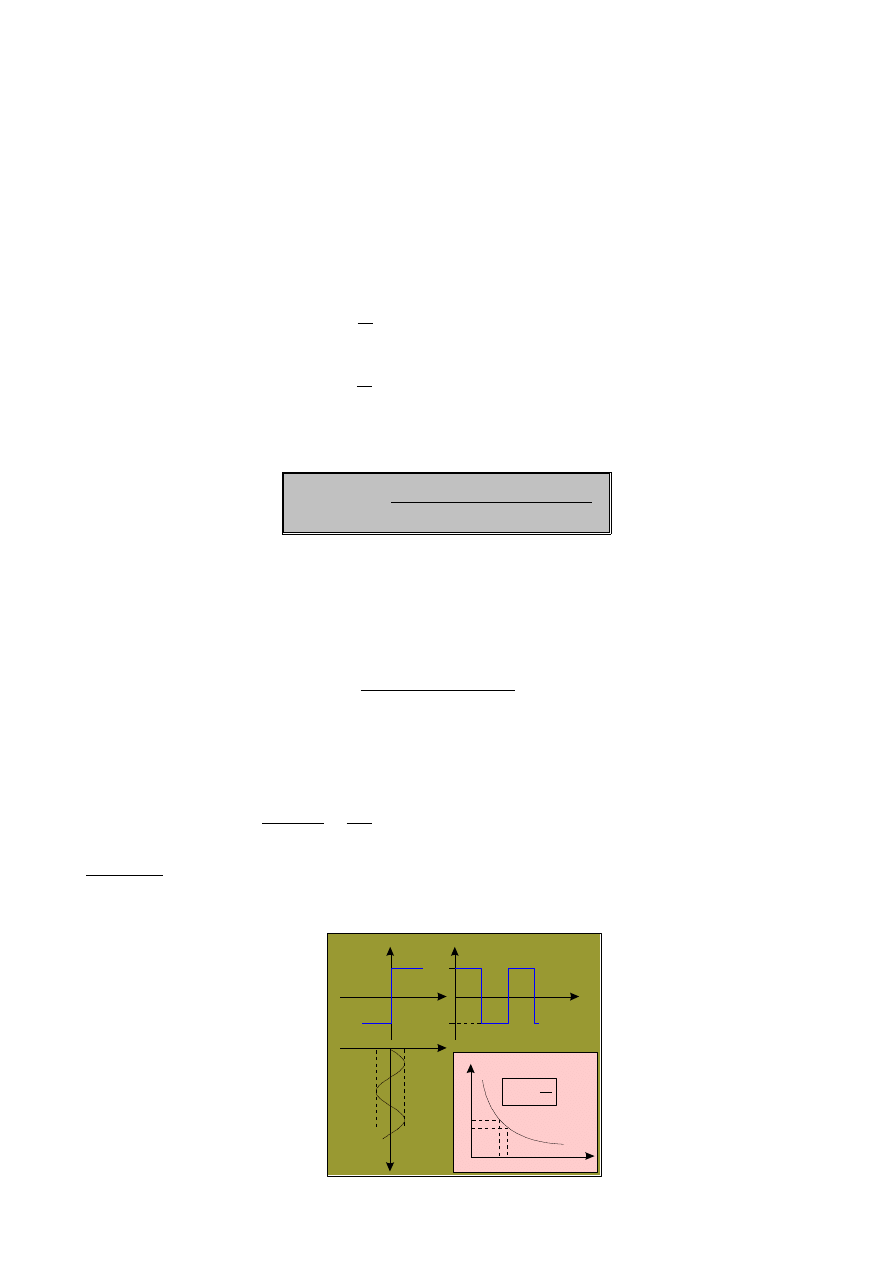
Odpowiedzią idealnego przekaźnika na wymuszenie harmoniczne jest fala prostokątna o wypełnieniu

50% i amplitudzie B (rys.2)

-B

B

A



2



0



2



0



 

= t

 

= t

-B

B

y

y( )



a

b

1

1

J (A)

0

J (A)=

0

4



A

4/





3

Rys.2 Odpowiedź przekaźnika na wymuszenie harmoniczne (a) i
wykres znormalizowanej funkcji opisującej idealnego przekaźnika
(b)

Charakterystyka statyczna przekaźnika jest jednoznaczna, więc jego funkcja opisująca jest równa:

A

B

A

J



4

)

(



, gdyż

(13)









































B

B

d

B

t

td

t

td

B

t

d

t

t

y

A

B

4

)

cos

(

2

)

(

sin

2

)

(

sin

)

(

sin

1

)

(

)

sin(

)

(

1

)

(

0

0

2

0

0

2

0

1







































,

(14)

Dla dowolnej amplitudy przekaźnika B można znormalizować funkcję opisującą, wtedy

A

A

J



4

)

(



(15)

Wykres znormalizowanej funkcji opisującej przekaźnika został przedstawiony na rysunku (2b).

Badanie nieliniowych UAR metodą funkcji opisującej

Badany jest układ regulacji automatycznej o strukturze jak na rys. (3).

J(A, )



G(j )



-

e

x

y

y

1

Rys. 3. Badany nieliniowy układ regulacji automatycznej

Funkcja opisująca członu nieliniowego jest odpowiednikiem transmitancji widmowej członu

liniowego. W ogólnym przypadku funkcja opisująca zależy od amplitudy i pulsacji sygnału
wejściowego. Równanie charakterystyczne układu ma postać:

0

1

)

,

a

(

J

)

j

(

G









(16)

Z tego równania można wyprowadzić warunek powstawania drgań harmonicznych (cyklu

granicznego)

)

,

A

(

J

1

)

j

(

G









(17)

Przedstawiając na płaszczyźnie zmiennej zespolonej charakterystykę G(j



) części liniowej oraz

krzywą –1/J(A,



) można znaleźć punkt krytyczny leżący na przecięciu się obu wykresów. Określa on

amplitudę i pulsację drgań harmonicznych; układ jest wówczas stabilny ale nieasymptotycznie
(stabilny w sensie Lapunowa, na granicy stabilności).

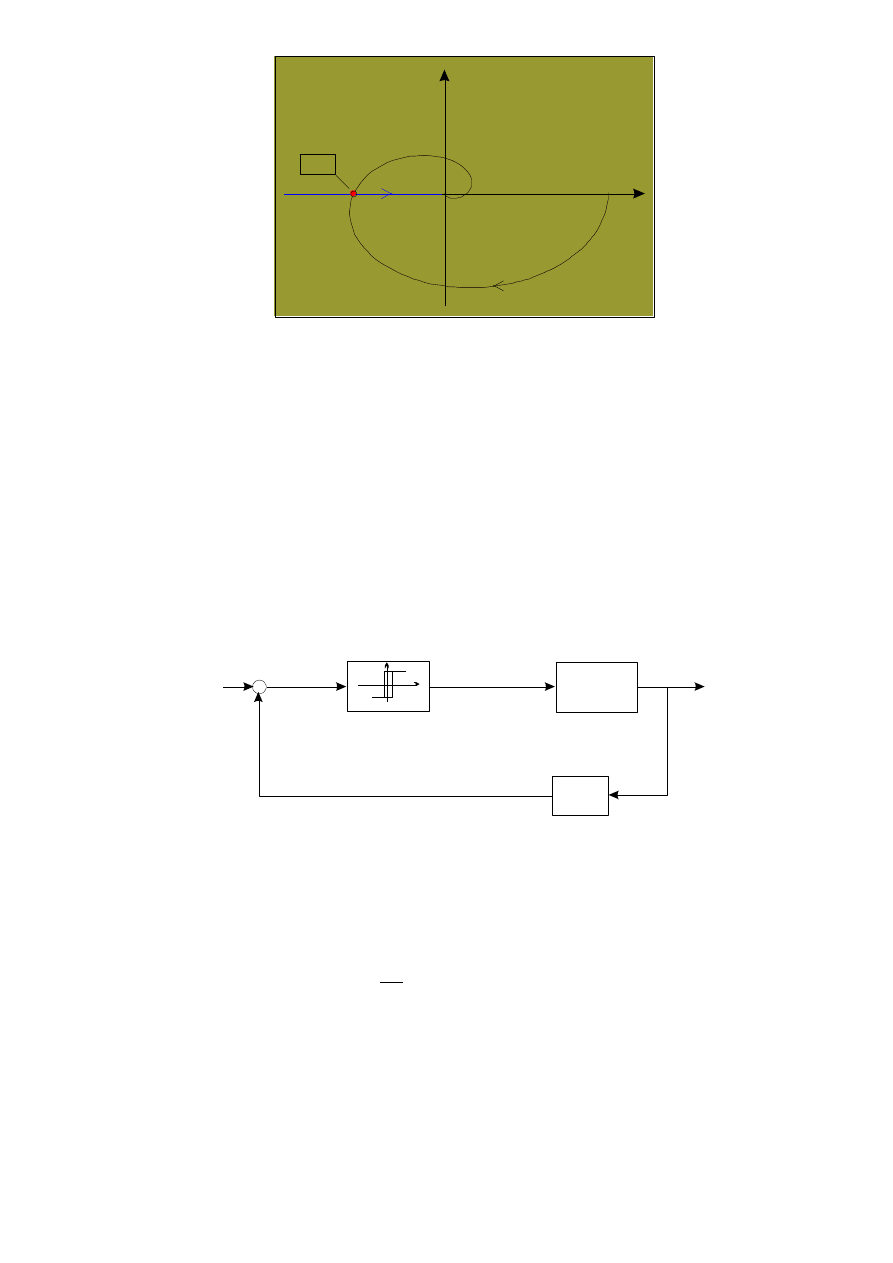
4

0

Im

Re

KR

-1/J(A)

G(j )



Rys. 4. Charakterystyki układu z funkcją opisującą J(A) równą
funkcji opisującej idealnego przekaźnika. KR – punkt określający cykl
stabilny

Idea metody funkcji opisującej jest np. wykorzystywana w realizacji automatycznego doboru

nastaw regulatorów cyfrowych (samonastrajanie STR ) w tzw. algorytmie oscylacji wymuszonych
zaproponowanym pierwotnie przez Åströma-Häglunda. Bazuje on na założeniu, że obiekt o
opóźnieniu fazowym przynajmniej



, przy wysokich częstotliwościach, może osiągnąć oscylacje o

okresie t

c

pod kontrolą przekaźnika. Obiekt jest połączony w pętli sprzężenia zwrotnego

z przekaźnikiem (rys. 5).

-1

Obiekt

x

u

y

Element

realizujący

funkcję

przekaźnika

Rys. 5. Schemat blokowy układu samonastrajania metodą oscylacji wymuszonych

Uchyb staje się sygnałem oscylującym o okresie t

c

. Jeżeli przyjmiemy amplitudę przekaźnika

równą B, to z rozwinięcia w szereg Fouriera można dowieść, że pierwsza harmoniczna sygnału
wyjściowego przekaźnika u ma amplitudę 4B/



. Jeżeli A jest amplitudą odpowiedzi obiektu

y, to wzmocnienie krytyczne obiektu jest równe:

A

B

k

k



4



(18)

Zaletą tej metody jest to, że można łatwo kontrolować amplitudę cykli krytycznych, dobierając

odpowiednio amplitudę przekaźnika. Znając punkt krytyczny charakterystyki Nyquista można
dobrać nastawy regulatora PID według tradycyjnych reguł Zieglera-Nicholsa lub innych.

Często zamiast idealnego stosuje się przekaźnik z histerezą. Układ z takim przekaźnikiem jest

mniej czuły na zakłócenia pomiarów.
Funkcja opisująca przekaźnika z histerezą jest równa:

5











j

A

B

4

)

A

(

J

2

2







,

(19)

gdzie: B – amplituda przekaźnika,



- histereza przekaźnika,

A – amplituda sygnału wyjściowego obiektu
Jak można zauważyć dla



=0 równanie jest równoważne funkcji opisującej idealnego przekaźnika.

Dla

0





wzmocnienie i okres wyznaczone z oscylacji nie są dokładnie wzmocnieniem i okresem

krytycznym. Jeśli porównać obie funkcje opisujące, jak pokazano na rys. 6 widać, że histereza
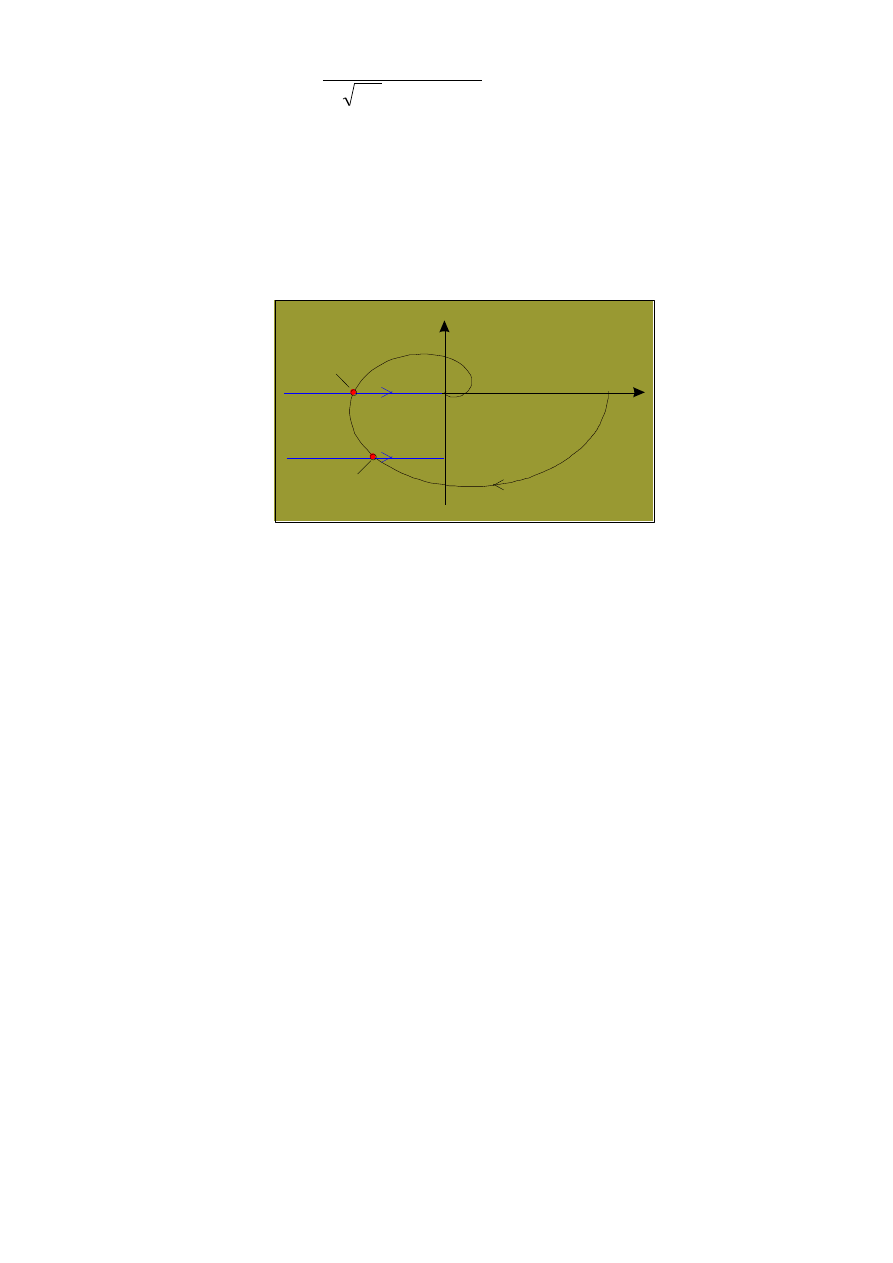
powoduje błąd w określeniu punktu krytycznego na krzywej Nyquista.

0

Im

Re

G(j )



Punkt krytyczny

dla idealnego

przekaźnika

Punkt krytyczny

przy wprowadzonej

histerezie

Rys. 6. Przesunięcie punktu krytycznego przy wprowadzeniu histerezy