38 Â

WIAT

N

AUKI

Grudzieƒ 1996

K

a˝dego, kto jest przekonany, ˝e
umys∏ ludzki jest nieograniczo-
ny w udzielaniu odpowiedzi na

wszelkie pytania, muszà mocno niepo-
koiç wnioski wyp∏ywajàce z przeglàdu
XX-wiecznej matematyki. W 1931 roku
Kurt Gödel wykaza∏ twierdzenie o nie-
zupe∏noÊci, które stanowi, ˝e ˝aden sys-
tem dedukcyjny nie jest w stanie dostar-
czyç odpowiedzi na wszystkie pytania
dotyczàce systemów liczbowych. Kilka
lat póêniej Alan M. Turing poda∏ rów-

nowa˝ne twierdzenie o programach
komputerowych, które orzeka, i˝ nie ist-
nieje algorytm pozwalajàcy stwierdziç,
czy program przetwarzajàcy pewien
konkretny zestaw danych kiedykolwiek
zakoƒczy swà prac´. Ca∏kiem niedaw-
no Gregory J. Chaitin z IBM znalaz∏ takie
stwierdzenia arytmetyczne, których
prawdziwoÊci nie da si´ nigdy wypro-
wadziç w sposób czysto dedukcyjny.

Te odkrycia kwestionujà nasze mo˝li-

woÊci naukowego poznania w dziedzi-
nie matematyki i logiki. Czy istniejà po-
dobne ograniczenia w rozwiàzywaniu
problemów spo∏ecznych lub przyrodni-
czych? Pierwszym i zapewne najbardziej
dyskusyjnym punktem jest rozstrzygni´-
cie, co w∏aÊciwie mamy na myÊli, mó-
wiàc o „naukowym poznaniu”. Aby
przeciàç ten filozoficzny w´ze∏ gordyj-
ski, przyjmijmy umiarkowanie kontro-

Jak przekroczyç

logiczne ograniczenia nauki

Modele matematyczne stosowane obecnie w wielu dziedzinach nauki

niezbyt dobrze opisujà rzeczywistoÊç. Byç mo˝e jednak

znajdà si´ sposoby obejÊcia tego problemu

John L. Casti

wersyjny poglàd, ˝e istotà metody na-
ukowego rozwiàzywania problemów
jest mo˝liwoÊç uj´cia jej w postaci zbio-
ru regu∏ post´powania, na podobieƒ-
stwo programu komputerowego. Po
prostu wprowadzamy dane poczàtko-
we problemu do zbioru regu∏, kr´cimy
korbkà dedukcji logicznej i czekamy na
ukazanie si´ odpowiedzi.

Przekonanie, ˝e metod´ naukowà

mo˝na przyrównaç do dzia∏ania progra-
mu komputerowego, wprowadza do
rozwa˝aƒ poj´cie z∏o˝onoÊci obliczenio-
wej. Stopieƒ trudnoÊci rozwiàzania zna-
nego problemu podró˝ujàcego komiwo-
ja˝era, polegajàcy na wyznaczeniu
najkrótszej drogi ∏àczàcej du˝à liczb´
miast, roÊnie – jak si´ uwa˝a – wyk∏ad-
niczo ze wzrostem liczby punktów prze-
znaczenia. Na przyk∏ad wytyczenie naj-
lepszej marszruty dla komiwoja˝era
odwiedzajàcego 100 miast wymaga∏oby
zbadania 100 x 99 x 98 x 97 x...x 1 mo˝-
liwoÊci. Jest to zadanie, które nawet naj-
szybszemu komputerowi zaj´∏oby mi-
liardy lat.

Jednak˝e przeprowadzenie takich ob-

liczeƒ jest mo˝liwe, przynajmniej teore-
tycznie. Skoncentrujmy uwag´ na pro-
blemach, dla których nie istnieje ˝aden
program umo˝liwiajàcy otrzymanie od-
powiedzi. Jak wyglàda∏by Êwiat, gdyby
przejawia∏o si´ w nim zjawisko braku
logicznych odpowiedzi, które obserwu-
jemy w matematyce? Twierdz´, ˝e wów-
czas przyroda musia∏aby byç wewn´trz-
nie sprzeczna (niekonsystentna) lub
niepe∏na w nast´pujàcym znaczeniu tych
s∏ów. Brak sprzecznoÊci w przyrodzie
oznacza, i˝ nie wyst´pujà w niej praw-

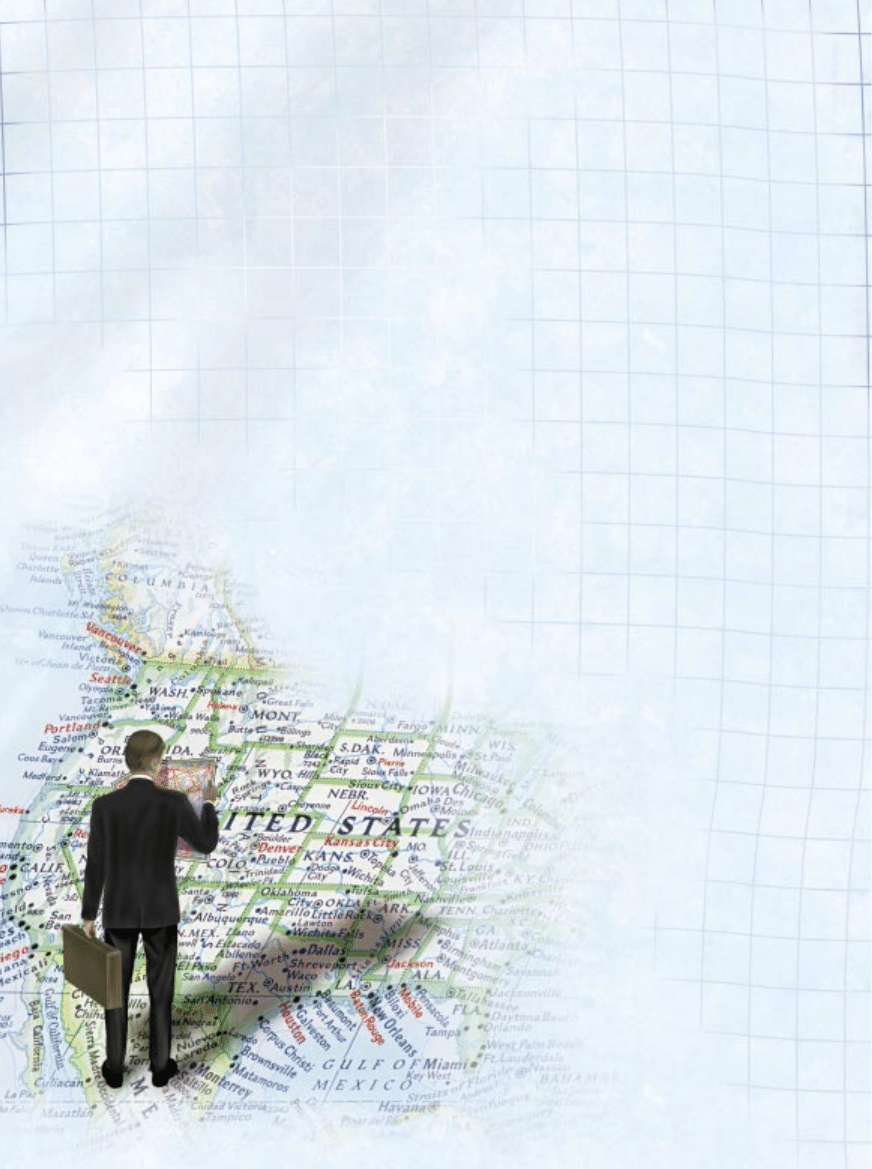
PODRÓ˚UJÑCY KOMIWOJA˚ER potrze-
bowa∏by miliardów lat pracy najszybszego
kumputera Êwiata, by obliczyç najkrótszà
drog´ mi´dzy 100 punktami przeznaczenia.
Naukowcy próbujà obecnie znaleêç sposoby
obejÊcia tego zniech´cajàcego problemu.

Â

WIAT

N

AUKI

Grudzieƒ 1996 39

dziwe paradoksy. Zazwyczaj gdy napo-
tykamy efekty Êwiadczàce o podobnych
paradoksach – takie jak strugi gazu wy-
rzucane z kwazarów z pr´dkoÊcià po-
zornie wi´kszà od pr´dkoÊci Êwiat∏a –
dalsze badania przynoszà rozwiàzanie.
(Te „nadÊwietlne” strugi okaza∏y si´ z∏u-
dzeniem wynikajàcym z efektów relaty-
wistycznych.)

Zupe∏noÊç przyrody oznacza, ˝e ˝a-

den stan fizyczny nie mo˝e powstaç bez
powodu, czyli – mówiàc krótko – ka˝-
de zjawisko ma jakàÊ przyczyn´. Nie-
którzy badacze mogliby ripostowaç:
mechanika kwantowa przeczy temu, ˝e
przyroda jest konsystentna i zupe∏na.
Jednak równanie opisujàce funkcj´ falo-
wà zjawiska kwantowego daje przyczy-
nowà interpretacj´ ka˝dej obserwacji
(zupe∏noÊç) i jest dobrze okreÊlone w
ka˝dej chwili (konsystencja). Powszech-
nie znane „paradoksy” mechaniki kwan-
towej powstajà wtedy, gdy usi∏ujemy
traktowaç obiekty kwantowe tak, jakby
by∏y klasyczne.

Trzy zagadki

W moim przekonaniu przyroda jest

zarówno zupe∏na, jak i niesprzeczna.
Z drugiej jednak strony, zale˝noÊç na-
uki od matematyki ogranicza nasze mo˝-
liwoÊci opisu zjawisk Êwiata przyrody.
Ilustracjà niech b´dà trzy dobrze znane
problemy z dziedziny fizyki, biologii
i gospodarki.

• StabilnoÊç Uk∏adu S∏onecznego. Naj-

bardziej znanym problemem mechani-
ki klasycznej jest problem n-cia∏. Mówiàc
najogólniej, chodzi w nim o opis zacho-
wania pewnej liczby n punktów mate-
rialnych, których ruch podlega newto-
nowskiemu prawu powszechnego cià-
˝enia. Jedno z pytaƒ, na które staramy

ganizmie. Oszacowano, ˝e superkom-
puter, stosujàcy w obliczeniach przy-
puszczalne regu∏y zwijania si´ bia∏ek,
potrzebowa∏by a˝ 10

127

lat, by wyzna-

czyç ostateczny kszta∏t nawet stosunko-
wo krótkiego ∏aƒcucha zawierajàcego
zaledwie 100 aminokwasów. I rzeczy-
wiÊcie, w 1993 roku Aviezri S. Fraenkel
z University of Pennsylvania wykaza∏,
˝e matematyczne rozwiàzanie proble-
mu zwijania si´ bia∏ek jest obliczeniowo
równie „trudne” jak problem podró˝u-
jàcego komiwoja˝era. W jaki sposób ra-
dzi sobie z tym natura?

• EfektywnoÊç rynku. Jeden z filarów,

na których wspiera si´ klasyczna teoria
finansów, to przekonanie, ˝e rynek jest
„efektywny”. Oznacza to, ˝e przetwa-
rza on niezw∏ocznie wszelkie informa-
cje wp∏ywajàce na cen´ akcji i towarów
i uwzgl´dnia je w bie˝àcej cenie gie∏do-
wej. W konsekwencji ceny powinny
zmieniaç si´ w zasadniczo nieprzewidy-
walny, przypadkowy sposób, pomijajàc

si´ znaleêç odpowiedê, dotyczy tego,
czy dwa cia∏a lub wi´cej zderzà si´, czy
te˝ któreÊ z nich osiàgnie dowolnie du-
˝à pr´dkoÊç w skoƒczonym czasie. W ro-
ku 1988 Zhihong (Jeff) Xia z Northwe-
stern University wykaza∏, w jaki sposób
pojedyncze cia∏o poruszajàce si´ tam
i z powrotem pomi´dzy dwoma po-
dwójnymi uk∏adami (ca∏y uk∏ad sk∏ada
si´ z pi´ciu mas punktowych) mo˝e osià-
gnàç dowolnie du˝à pr´dkoÊç i w rezul-
tacie wyrwaç si´ z uk∏adu. Ten wynik,
który wyprowadzony zosta∏ z uwzgl´d-
nieniem specyficznej geometrycznej kon-
figuracji cia∏, nie daje ˝adnej informacji
o szczególnym przypadku Uk∏adu S∏o-
necznego, ale sugeruje, ˝e nasz Uk∏ad
S∏oneczny wcale nie musi byç trwa∏y.
Co wi´cej, odkrycie to mo˝e zaowo-
cowaç nowymi metodami badawczy-
mi pomocnymi w rozwiàzaniu tego
problemu.

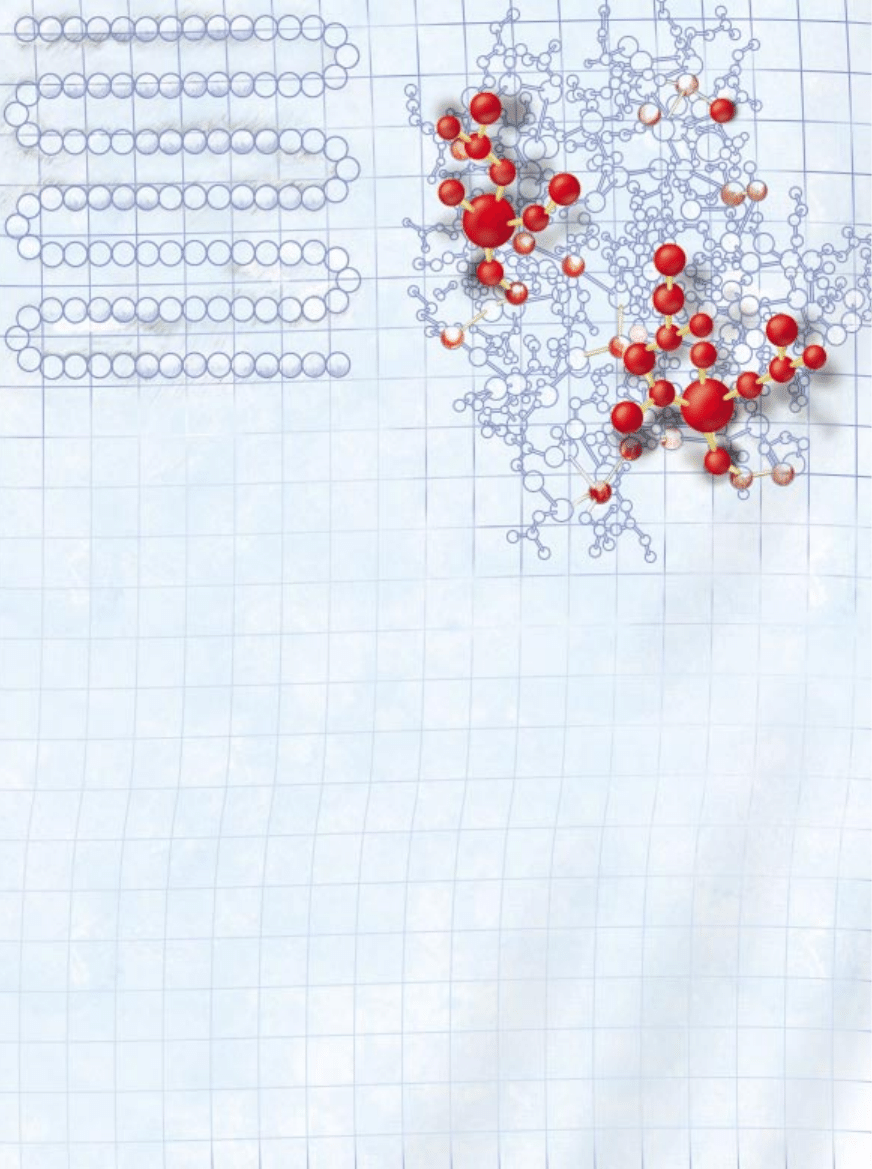
• Zwijanie si´ bia∏ek. Bia∏ka, b´dàce

podstawowymi sk∏adnikami wszystkich
organizmów ˝ywych, tworzà si´ z wiel-
kiej liczby sk∏adników, czyli ∏aƒcuchów
aminokwasów przypominajàcych kora-
liki na sznurku. Kiedy koraliki zostanà
u∏o˝one we w∏aÊciwym porzàdku, czà-
steczka bia∏ka gwa∏townie zwija si´
w wysoce specyficznà trójwymiarowà
struktur´, która okreÊla jej funkcj´ w or-

ZWIJANIE BIA¸EK to problem, w którym
rozwa˝a si´, w jaki sposób ∏aƒcuch amino-
kwasów

(z lewej) przechodzi niemal natych-

miast w nies∏ychanie skomplikowanà trój-
wymiarowà struktur´ bia∏ka

(z prawej).

Obecnie biolodzy usi∏ujà rozszyfrowaç te
zawi∏e biochemiczne regu∏y.

Wszystkie ilustracje LAURIE GRACE

40 Â

WIAT

N

AUKI

Grudzieƒ 1996

efekty inflacji. To z kolei oznacza, ˝e
strategie handlowe oparte na dost´p-
nych publicznie informacjach, takich jak
zmiany cen, powinny byç bezu˝ytecz-
ne; nie mo˝e istnieç ˝adna strategia, któ-
ra dzia∏a∏aby lepiej ni˝ rynek w d∏u˝-
szym czasie. Jednak˝e rzeczywiste rynki
zdajà si´ nie mieç nic wspólnego z aka-
demickà teorià. Literatura ekonomiczna
jest pe∏na opisów takich rynkowych
„anomalii” jak efekt niskiego wspó∏-
czynnika cena–zysk, który pokazuje, ˝e
niskie ceny akcji firm w stosunku do ich
zysków systematycznie przewy˝szajà
Êrednià rynkowà.

NierzeczywistoÊç matematyki

Analiza powy˝szych trzech proble-

mów zdaje si´ prowadziç do nast´pu-
jàcych wniosków: Uk∏ad S∏oneczny jest
byç mo˝e niestabilny, zwijanie si´ bia-
∏ek to problem obliczeniowo z∏o˝ony,
a rynki finansowe prawdopodobnie nie
sà ca∏kowicie efektywne. Wspólnym
wyznacznikiem tych domniemanych
odpowiedzi jest zagadnienie matema-
tycznej przedstawialnoÊci rzeczywiste-
go Êwiata, a nie sama jego istota. Na
przyk∏ad podane przez Xia rozwiàza-
nie problemu n-cia∏ nie t∏umaczy, w ja-
ki sposób rzeczywiste cia∏a uk∏adu pla-
netarnego poruszajà si´ pod wp∏ywem
si∏ grawitacyjnych. Podobnie wniosek
Fraenkla, ˝e zwijanie si´ bia∏ek jest ob-
liczeniowo z∏o˝one, nie wyjaÊnia, w ja-
ki sposób bia∏ka wykonujà swoje zada-
nia w ciàgu sekund raczej ni˝ eonów.
No, a obrotni maklerzy z Wall Street od
dziesiàtków lat mieli w nosie hipotez´
o efektywnoÊci rynku. Zanim jednak
wysnujemy wnioski o niezdolnoÊci na-
uki do wyjaÊnienia takich problemów,
trzeba albo wykazaç, ˝e model matema-
tyczny jest wiernym odbiciem rzeczy-
wistoÊci, albo te˝ odrzuciç go ca∏kowicie.
Rozwa˝my oba te warianty.

Podane przyk∏ady Êwiadczà, ˝e jeÊli

chcemy szukaç nierozwiàzywalnych
problemów rzeczywistego Êwiata, mu-
simy wprowadziç staranne rozró˝nie-
nie pomi´dzy rzeczywistoÊcià przyrod-
niczych i spo∏ecznych zjawisk z jednej
strony, a ich matematycznymi i oblicze-
niowymi modelami z drugiej. W zakres
obserwowalnych obiektów Êwiata fi-
zycznego wchodzà zazwyczaj bezpo-
Êrednio mierzalne wielkoÊci, jak czas lub
po∏o˝enie, albo wielkoÊci takie jak ener-
gia, które dajà si´ z nich wyprowadziç.
W ten sposób obiektem naszych rozwa-
˝aƒ sà parametry takie jak wyznaczone
po∏o˝enia planet lub rzeczywiÊcie ob-
serwowane konfiguracje bia∏ek. Te ob-
serwowalne wielkoÊci stanowià zazwy-
czaj dyskretny zbiór, a ich wartoÊci

tworzà skoƒczony zbiór liczb. Co wi´-
cej, tego rodzaju pomiary zazwyczaj sà
niedok∏adne.

Z kolei w Êwiecie matematyki te re-

alnie obserwowane wielkoÊci sà repre-
zentowane symbolicznie i cz´sto przy-
jmuje si´, ˝e ich wartoÊci nale˝à do
kontinuum przestrzennego i czasowe-
go. Symbole matematyczne reprezentu-
jàce takie atrybuty, jak po∏o˝enie czy
pr´dkoÊç, zwykle wyra˝a si´ liczbami
naturalnymi, rzeczywistymi lub zespo-
lonymi pochodzàcymi ze zbiorów nie-
skoƒczonych. W∏aÊciwym poj´ciem ma-
tematycznym charakteryzujàcym nie-
pewnoÊç jest losowoÊç.

I wreszcie jest te˝ Êwiat „obliczeƒ”,

który zajmuje nienaturalnà pozycj´,
tkwiàc cz´Êciowo w rzeczywistym Êwie-
cie przyrzàdów fizycznych, a cz´Êcio-
wo w abstrakcyjnym Êwiecie obiektów
matematycznych. Gdy myÊlimy o obli-
czeniach jako o wykonywaniu ciàgu po-
leceƒ, czyli algorytmu, mamy wówczas
do czynienia z procesem czysto mate-
matycznym i nale˝àcym do Êwiata
obiektów symbolicznych. Gdy nato-
miast patrzymy na obliczenia jako na
proces polegajàcy na kolejnym w∏àcza-
niu i wy∏àczaniu prze∏àczników w pa-
mi´ci realnej maszyny liczàcej, to wtedy
jest on mocno zakotwiczony w Êwiecie
obserwacji fizycznych.

Jednym ze sposobów wykazania, ˝e

na dane pytanie nie mo˝na daç logicznej
naukowej odpowiedzi, jest ogranicze-
nie dyskusji i argumentów wy∏àcznie
do Êwiata zjawisk przyrodniczych. Gdy-
byÊmy wybrali t´ drog´, to nie wolno
by∏oby przek∏adaç pytania: „Czy Uk∏ad
S∏oneczny jest stabilny?”, na j´zyk ma-
tematyki i tym samym oczekiwaç od-
powiedzi, która da∏aby si´ wyprowa-
dziç z logicznych schematów mate-
matyki. MusielibyÊmy bowiem w real-
nym Êwiecie znaleêç substytut dowodu
matematycznego.

Dobrym kandydatem jest poj´cie

przyczynowoÊci. Mo˝na by w zasadzie
uznaç, ˝e problem jest naukowo rozwià-
zywalny, gdyby da∏o si´ skonstruowaç
ciàg argumentów przyczynowych, któ-
rego ostatnim ogniwem by∏oby rozwià-
zanie postawionego problemu. Argu-
mentacja przyczynowa nie musi byç
wyra˝ona w j´zyku matematyki. Stan-
dardowy przyk∏ad argumentu deduk-
cyjnego: „Wszyscy ludzie sà Êmiertelni;
Sokrates jest cz∏owiekiem, a zatem So-
krates jest Êmiertelny”, jest takim w∏a-
Ênie ∏aƒcuchem przyczynowym. Nie za-
wiera on ˝adnej matematyki, jedynie
prosty wywód logiczny. Z drugiej stro-
ny, konstrukcja przekonujàcego argu-
mentu przyczynowego bez uciekania
si´ do matematyki mo˝e okazaç si´

przedsi´wzi´ciem zniech´cajàcym.
W przypadku stabilnoÊci Uk∏adu S∏o-
necznego nale˝a∏oby znaleêç przekonu-
jàce niematematyczne definicje grawita-
cji i planet.

W obliczu tych trudnoÊci rozsàdne

wydaje si´ zastosowanie metody ∏àczà-
cej Êwiat matematyki ze Êwiatem real-
nym. Gdy chcemy odwo∏aç si´ do do-
wodowej maszynerii matematyki w celu
rozstrzygni´cia jakiejÊ kwestii dotyczà-
cej Êwiata rzeczywistego, musimy naj-
pierw „zakodowaç” problem w postaci
formu∏y z jakiegoÊ dzia∏u matematyki,
na przyk∏ad równania ró˝niczkowego,
wykresu czy gry z n-uczestnikami. Roz-
wiàzujemy matematycznà wersj´ zagad-
nienia za pomocà techniki w∏aÊciwej te-
mu obszarowi Êwiata matematycznego
i ewentualnie mo˝emy „rozkodowaç”
odpowiedê (jeÊli taka istnieje) z powro-
tem na j´zyk Êwiata rzeczywistego. Cie-
kawe przy tym by∏oby wykazanie, ˝e
matematyczna wersja problemu wiernie
obrazuje sytuacj´ wyst´pujàcà w real-
nym Êwiecie. Skàd wiadomo, ˝e model
matematyczny uk∏adu fizycznego i sam
uk∏ad majà ze sobà cokolwiek wspólne-
go? To odwieczne pytanie filozofii da∏o
impuls do powstania teorii modeli usi∏u-
jàcej udzieliç na nie odpowiedzi. Co wi´-
cej, argumenty matematyczne mogà
podlegaç ograniczeniom odkrytym
przez Gödla, Turinga i Chaitina, a do-
tychczas nie wiadomo, czy podobnym
podlega Êwiat realny.

Umys∏ nie obliczajàcy

Byç mo˝e istniejà sposoby obejÊcia

tych k∏opotów. Problemy odkryte przez
Gödla i innych pojawiajà si´ w przy-
padku systemów liczbowych o nieskoƒ-
czonej iloÊci elementów, takich jak zbiór
liczb ca∏kowitych. Lecz w wielu rzeczy-
wistych problemach, choçby podró˝u-
jàcego komiwoja˝era, u˝ywa si´ jedynie
skoƒczonej liczby parametrów, które ma-

jà tylko skoƒczonà liczb´ dopuszczal-
nych wartoÊci.

Podobnie niededukcyjne sposoby ro-

zumowania – na przyk∏ad indukcja, któ-
ra pozwala wyprowadziç ogólny wnio-
sek na podstawie skoƒczonej liczby
specyficznych obserwacji – mogà nas za-
prowadziç poza obszar logicznej nieroz-
strzygalnoÊci. JeÊli wi´c zdo∏amy ogra-
niczyç formalizm matematyczny,
u˝ywajàc skoƒczonych uk∏adów liczb
czy niededukcyjnej logiki bàdê te˝ obu
naraz, na ka˝de pytanie matematyczne
powinna istnieç odpowiedê; mo˝na wi´c
oczekiwaç, ˝e otrzymany po rozkodo-
waniu takiego pytania jego odpowied-
nik w realnym Êwiecie te˝ nie pozostanie
bez odpowiedzi.

Badania ludzkiego umys∏u mogà do-

prowadziç do odkrycia innych dróg ob-
chodzenia tych trudnoÊci. Niektórzy
zwolennicy sztucznej inteligencji sugero-
wali, ˝e nasze mózgi sà niezwykle skom-
plikowanymi komputerami, które wy-
konujà obliczenia w taki sam algoryt-
miczny sposób, jak to robià konwencjo-
nalne maszyny (czy nawet procesory
równoleg∏e lub sieci neuronowe). Jed-
nak wielu teoretyków, a zw∏aszcza fizyk

Â

WIAT

N

AUKI

Grudzieƒ 1996 41

Informacje o autorze

JOHN L. CASTI jest profesorem na Politechnice w Wiedniu i w Santa Fe Insti-

tute ([e-mail]). Pomocà w sformu∏owaniu problemów poruszonych

w tym artykule s∏u˝yli Joseph F. Traub, Piet Hut, James B. Hartle i •ke E. An-

dersson, a tak˝e Institute for Future Studies w Sztokholmie, cz´Êciowo finan-

sujàcy te badania, za co autor wyra˝a wszystkim podzi´kowanie.

Literatura uzupe∏niajàca

SEARCHING FOR CERTAINTY.

John L. Casti; William Morrow, 1991.

RANDOMNESS AND UNDECIDABILITY IN PHYSICS.

K. Svozil; World

Scientific, Singapore, 1944.

BOUNDARIES AND BARRIERS.

Red. John L. Casti i A. Karlqvist;

Addison-Wesley, 1996.

UK¸AD

N-CIA¸, sk∏adajàcy si´ z punktu

materialnego oscylujàcego mi´dzy dwoma
uk∏adami podwójnymi

(z lewej), zgodnie

z twierdzeniem wykazanym przez Zhihong
Xia z Northwestern University jest niestabil-
ny. Ten wynik mo˝e doprowadziç do wnio-
sku, ˝e Uk∏ad S∏oneczny wyrzuci kiedyÊ jed-
nà ze swych planet w przestrzeƒ kosmicznà.

teoretyk Roger Penrose z University of
Oxford, argumentuje, ˝e ludzka aktyw-
noÊç poznawcza nie jest oparta na ˝ad-
nych znanych regu∏ach dedukcyjnych,
a wi´c nie podlega te˝ ograniczeniom
gödlowskim.

Ostatnio ten punkt widzenia nieocze-

kiwanie wspar∏y moje badania pod egidà
Institute for Future Studies w Sztokhol-
mie prowadzone wespó∏ z psychologiem
Margaret A. Boden z University of Sus-
sex, matematykiem Donaldem G. Saarim
z Northwestern University, ekonomistà
•ke E. Anderssonem (dyrektorem insty-
tutu) i innymi. Âwiadczà one przekony-
wajàco, ˝e zarówno w dziedzinie sztuk
pi´knych, jak i nauk przyrodniczych czy
nawet matematyki twórcze mo˝liwoÊci
ludzkie nie sà kr´powane ˝adnymi wi´-
zami, tak jak algorytmy komputerowe.
Penrose i inni teoretycy wysun´li przy-
puszczenie, ˝e zdolnoÊci twórcze cz∏o-
wieka opierajà si´ na jakimÊ dotychczas
nie znanym mechanizmie lub regu∏ach,
byç mo˝e powiàzanych z mechanikà

kwantowà. Odkrywajàc te mechanizmy
i w∏àczajàc je do arsena∏u metod nauko-
wych, badacze b´dà mogli rozwiàzywaç
problemy dziÊ nie do przezwyci´˝enia.

OczywiÊcie mo˝liwoÊci nauki w zg∏´-

bianiu tajemnic natury sà ograniczone
wieloma praktycznymi czynnikami – ta-
kimi jak b∏àd pomiaru, d∏ugoÊç czasu
obliczeƒ, fizyczne i finansowe zasoby,
decyzje polityczne czy wartoÊci kultu-
rowe. Jednak ˝aden z nich nie ma zwiàz-
ku z istnieniem logicznych barier w na-
szych mo˝liwoÊciach otrzymania od-
powiedzi na pewne pytania dotyczàce
Êwiata przyrody. W moim przekonaniu
nie ma takich barier. A zatem wnioski
wyp∏ywajàce z przeglàdu XX-wiecz-
nej matematyki wcale nie sà a˝ takie
zniech´cajàce.

T∏umaczy∏

Aleksander Strasburger

Ziemia

Merkury

S∏oƒce

Wenus

Mars