Obwody prądu stałego lub zmiennego

zawierające rezystory

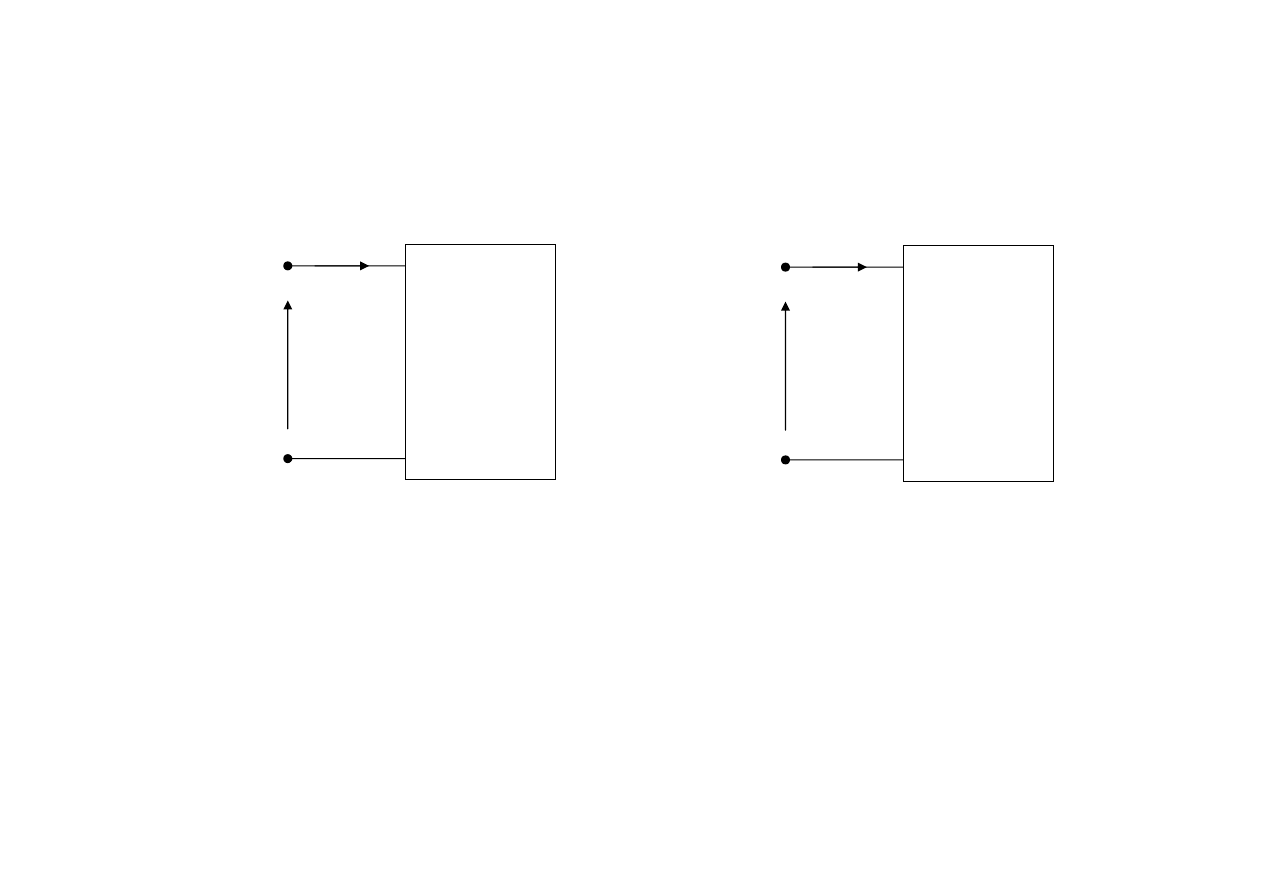
Obwody I i II są równoważne wtedy i tylko wtedygdy spełnione są zależności:

u

1

(t) = u

2

(t)

oraz

i

1

(t) = i

2

(t)

u

1

(t)

Obwód

I

i

1

(t)

≡

Obwody równoważne

u

2

(t)

Obwód

II

i

2

(t)

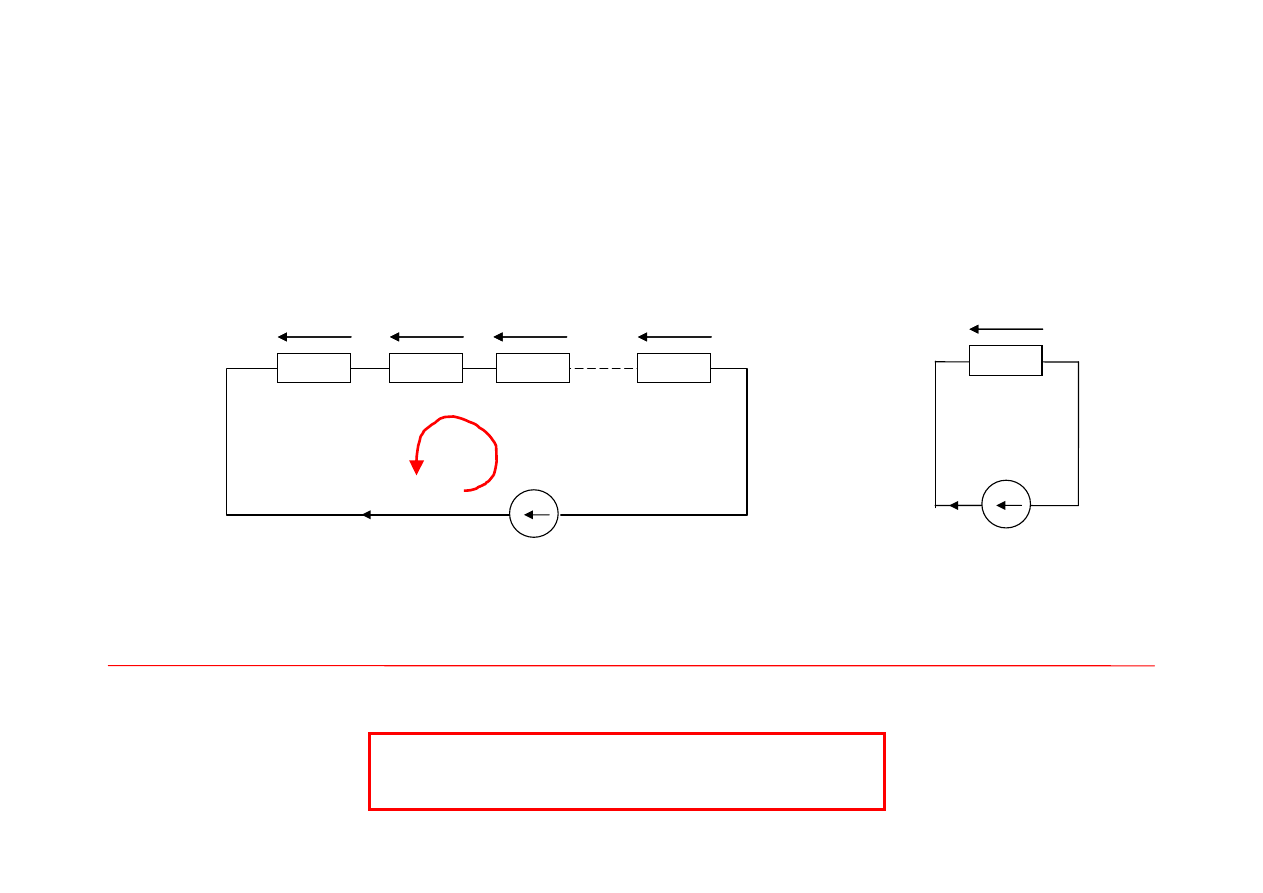
Obwody zawierające rezystory

Szeregowe łączenie rezystorów

Rezystancja zastępcza n rezystorów połączonych szeregowo jest równa sumie

algebraicznej ich rezystancji

Prawo Ohma:

u

j

(t) = i(t)R

j

u(t) = i(t)R

Z

II prawo Kirchhoffa:

u

1

(t) + u

2

(t) + u

3

(t) + ……. + u

n

(t) = u(t)

u(t) = u

Z

(t)

i(t)R

1

+ i(t)R

2

+ i(t)R

2

+ ….. + i(t)R

n

= i(t)R

Z

i(t)

u

Z

(t)

R

1

R

Z

u(t)

≡

≡

n

Z

R

R

R

R

R

+

+

+

+

=

.......

3

2

1

u

1

(t)

R

1

R

1

u

3

(t)

u

2

(t)

R

1

R

2

u

n

(t)

R

n

u(t)

i(t)

R

1

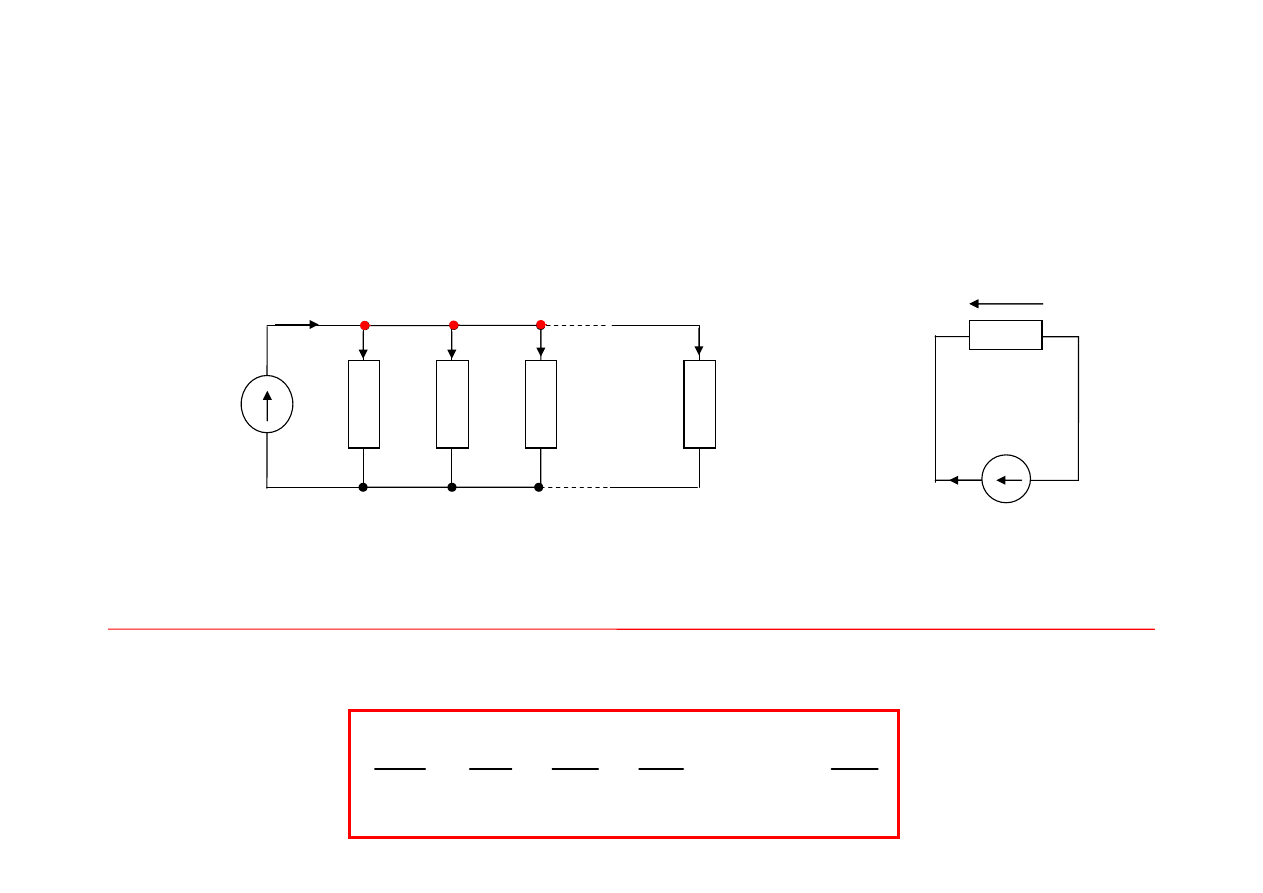
Obwody zawierające rezystory

równoległe łączenie rezystorów

Odwrotność rezystancji zastępczej n rezystorów połączonych równolegle jest równa

sumie algebraicznej odwrotności ich rezystancji

Prawo Ohma:

i

j

(t) = u(t)/R

j

i(t) = u(t)/R

Z

Węzeł w:

i

1

(t) + i

2

(t) + i

3

(t) + ……. + i

n

(t) = i(t)

u(t) = u

Z

(t)

u(t)/R

1

+ u(t)/R

2

+ u(t)/R

2

+ ….. + u(t)/R

n

= u(t)/R

Z

i(t)

u

Z

(t)

R

1

R

Z

u(t)

≡

≡

u(t)

i(t)

R

1

i

1

(t)

R

2

R

3

i

n

R

n

w

i

2

(t)

i

3

(t)

i

n

(t)

n

Z

R

R

R

R

R

1

.......

1

1

1

1

3

2

1

+

+

+

+

=

Obwody zawierające rezystory

Łączenie rezystorów w gwiazdę i w trójkąt

Połączenie rezystorów w gwiazdę będzie równoważne połączeniu rezystorów w trójkąt

jeżeli będą spełnione następujące zależności:

u’

G

(t) = u’

T

(t)

u’’

G

(t) = u’’

T

(t)

i

1G

(t) = i

1T

(t)

i

2G

(t) = i

2T

(t)

i

3G

(t) = i

3T

(t)

R

1

u

2

(t)

u

1

(t)

u

3

(t)

R

2

R

3

i

2G

(t)

i

3G

(t)

i

1G

(t)

w

u’’

G

(t)

u’

G

(t)

I

II

Gwiazda

Trójkąt

u

x

(t)

R

13

i

12

(t)

i

3T

(t)

i

1T

(t)

w1

u’’

T

(t)

u’

T

(t)

w2

R

12

R

23

i

2T

(t)

i

13

(t)

i

23

(t)

≡

Gwiazda

Trójkąt

Węzeł w:

i

1G

(t) + i

2G

(t) = i

3G

(t)

Oczko II:

u’’

G

(t) = u

2

(t) + u

3

(t)

Prawo Ohma:

u

2

(t) = i

2G

(t) R

2

u

3

(t) = i

3G

(t) R

3

Węzeł w 1

:

i

1T

(t)

=

i

12

(t)

+

i

13

(t)

Węzeł w 2

:

i

2T

(t)

=

i

23

(t)

-

i

12

(t)

Oczko:

u’’

T

(t) = u’(t) - u

x

(t)

u’

T

(t) = i

13

(t) R

12

Prawo Ohma:

u’’

T

(t) = i

23

(t) R

23

u

x

(t) = i

12

(t) R

13

Obwody zawierające rezystory

Łączenie rezystorów w gwiazdę i w trójkąt

Z pierwszego i drugiego prawa Kirchhoffa otrzymujemy:

( )

( )

( )(

)

3

2

2

3

1

''

R

R

t

i

R

t

i

t

u

G

G

G

+

+

=

( )

( )

( ) (

)

23

13

12

12

13

23

2

23

13

12

23

13

1

''

R

R

R

R

R

R

t

i

R

R

R

R

R

t

i

t

u

T

T

T

+

+

−

+

+

+

=

Dla obwodów równoważnych współczynniki występujące przy prądach i

1G

i i

1T

, oraz i

2G

i i

2T

,

należy przyrównać:

(

)

23

13

12

12

13

23

3

2

23

13

12

23

13

3

R

R

R

R

R

R

R

R

R

R

R

R

R

R

+

+

−

=

+

+

+

=

23

13

12

23

13

3

23

13

12

23

12

2

23

13

12

13

12

1

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

+

+

=

+

+

=

+

+

=

2

3

1

3

1

31

1

3

2

3

2

23

3

2

1

2

1

12

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

+

+

=

+

+

=

+

+

=

Układ równań umożliwiający zamianę
obwodu gwiazda --> trójkąt

Układ równań umożliwiający zamianę
obwodu trójkąt --> gwiazda

Gdy R

1

= R

2

= R

3

= R

G

,

to

R

12

= R

23

= R

13

= 3R

G

,

Obwody zawierające rezystory

Równoważność połączeń w gwiazdę i w trójkąt

Stosując prawa Kirchhoffa dla obu obwodów i porównując odpowiednie współczynniki

można trzymać następujące zależności pomiędzy rezystancjami R

1

, R

2

, R

3

, R

12

, R

13

i R

23

:

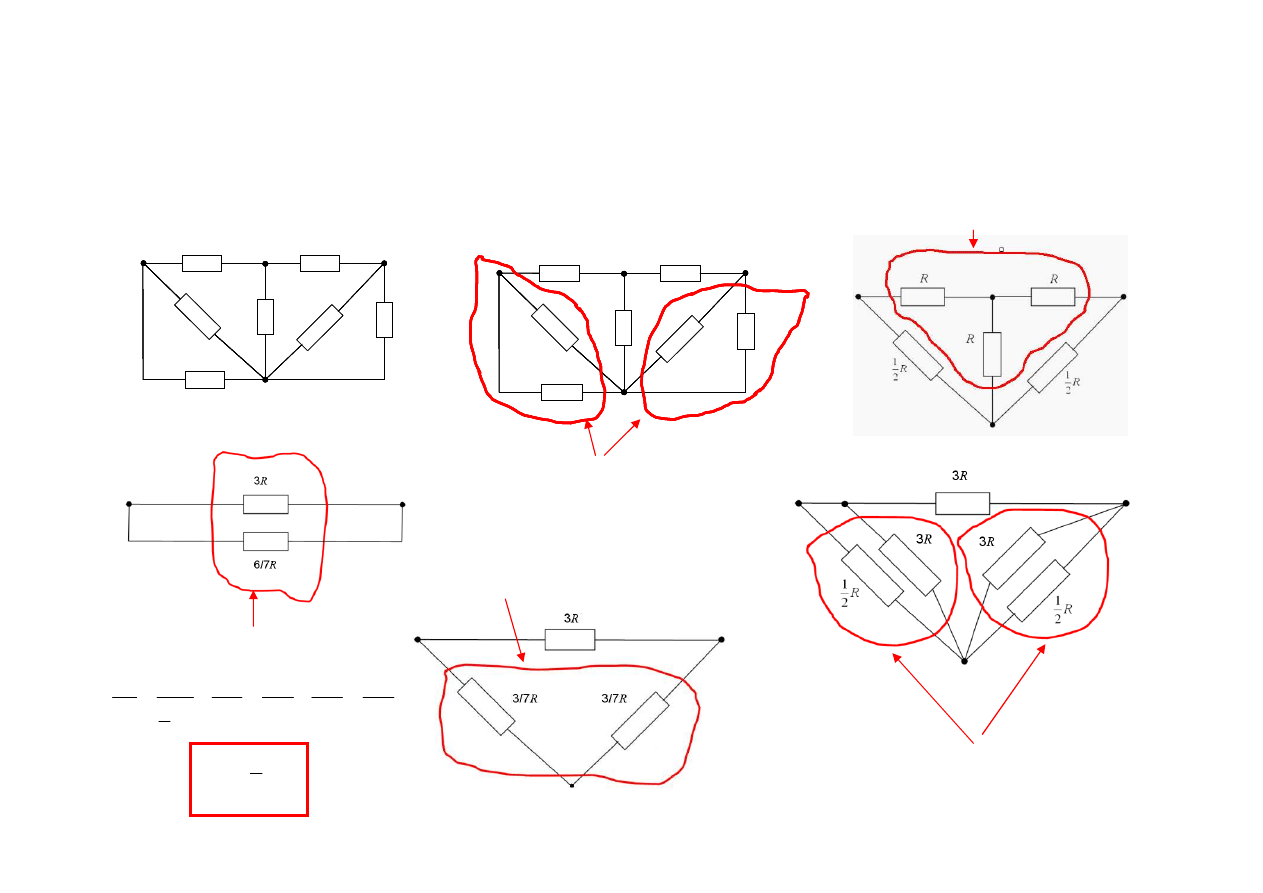
Przykład:

Obliczyć rezystancję R

Z

zastępczą pomiędzy punktami A i B dla sieci siedmiu rezystorów przedstawionej

na rysunku.

Obwody zawierające rezystory

R

R

R

R

R

R

R

R

R

R

R

R

R

R

A

B

R

R

R

R

R

R

R

R

R

R

R

R

R

R

A

B

R

R

R

R

R

R

R

R

R

R

R

R

R

R

A

B

R

R

R

R

R

R

R

R

R

R

R

R

R

R

A

B

A

B

A

B

A

B

A

B

A

B

A

B

A

B

A

B

≡

≡

≡

≡

≡

Połączenia równoległe

Połączenie szeregowe

Połączenia równoległe

Połączenie w gwiazdę

Połączenie równoległe

R

R

R

R

R

R

R

R

Z

Z

3

2

6

9

6

2

6

7

3

1

7

6

1

1

=

=

+

=

+

=

Obwody zawierające rezystory

Rezystancyjny dzielnik napięciowy

( )

( )

( )

( )

( )

( ) ( )

( )

( )

2

1

1

1

2

2

1

R

R

R

R

t

u

t

i

R

t

i

t

u

t

u

t

u

t

u

t

u

t

u

Z

Z

wej

wyj

wej

+

=

=

=

=

+

=

( )

( )

( )

( )

( )

1

0

2

1

2

2

1

2

2

1

1

≤

≤

+

=

+

=

+

+

=

K

R

R

R

K

R

R

R

t

U

t

U

t

U

R

R

R

t

U

t

U

wej

wyj

wyj

wej

wej

Współczynnik podziału napięcia - K

II prawo Kirhchoffa:

Prawo Ohma:

Rezystancja zastępcza w
połączeniu szeregowym

R

2

u

1

(t)

R

1

u

wyj

(t)

u

wej

(t)

u

2

(t)

i(t)

Bocznik prądowy

( )

( )

( )

( )

( )

( )

( )

( )

( )

oraz

0

1

to

,

gdy

0

0

0

t

u

t

u

t

u

K

R

R

R

R

R

K

t

u

t

Ku

t

u

t

u

t

u

t

u

wej

wyj

B

B

B

wej

wej

B

wej

wyj

B

≈

≈

≈

<<

+

=

−

=

−

=

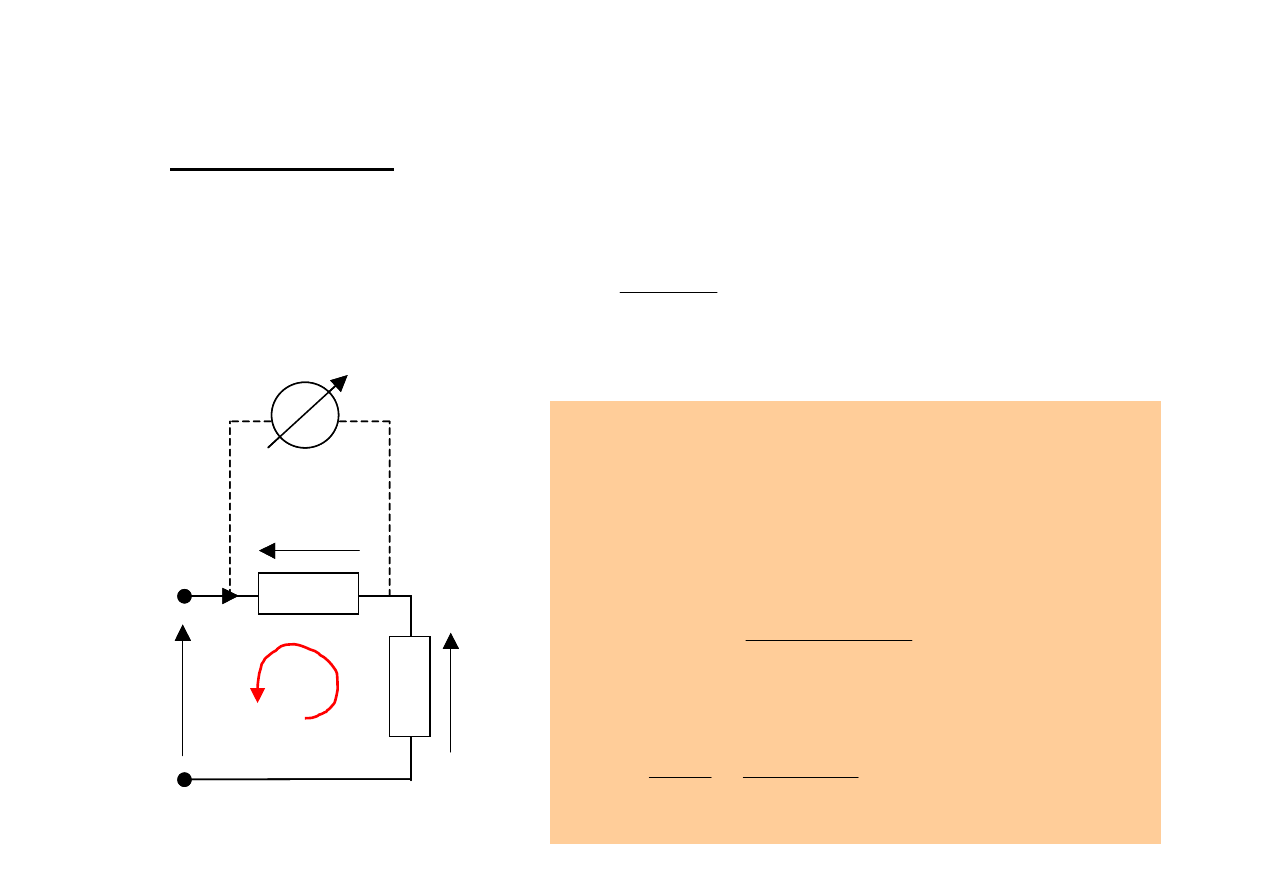
Rezystor R

B

nazywany jest

bocznikiem prądowym i służy
do pomiaru prądu płynącego w
obwodzie za pomocą
woltomierza.

( )

( )

( )

( )

( )

A

99

,

9

0,01

V

0999

,

0

V

901

,

99

V

0999

,

0

-

V

100

V

0999

,

0

10

01

,

0

01

,

0

V

100

=

Ω

=

=

≈

=

=

=

Ω

+

Ω

Ω

=

B

B

wej

wyj

B

R

t

u

t

i

t

u

t

u

t

u

Przykład:

Należy zmierzyć natężenie prądu (10A) płynącego
w obwodzie (R

0

= 10

Ω

; u

wej

(t) = 100 V) za pomocą

woltomierza i rezystora bocznikującego o
rezystancji R

B

= 0,01

Ω

II prawo Kirhchoffa:

V

R

0

u

B

(t)

R

B

u

wyj

(t)

u

wej

(t)

i(t)

V

R

0

u

B

(t)

R

B

u

wyj

(t)

u

wej

(t)

i(t)

Obwody zawierające rezystory

Rezystancyjny dzielnik napięciowy

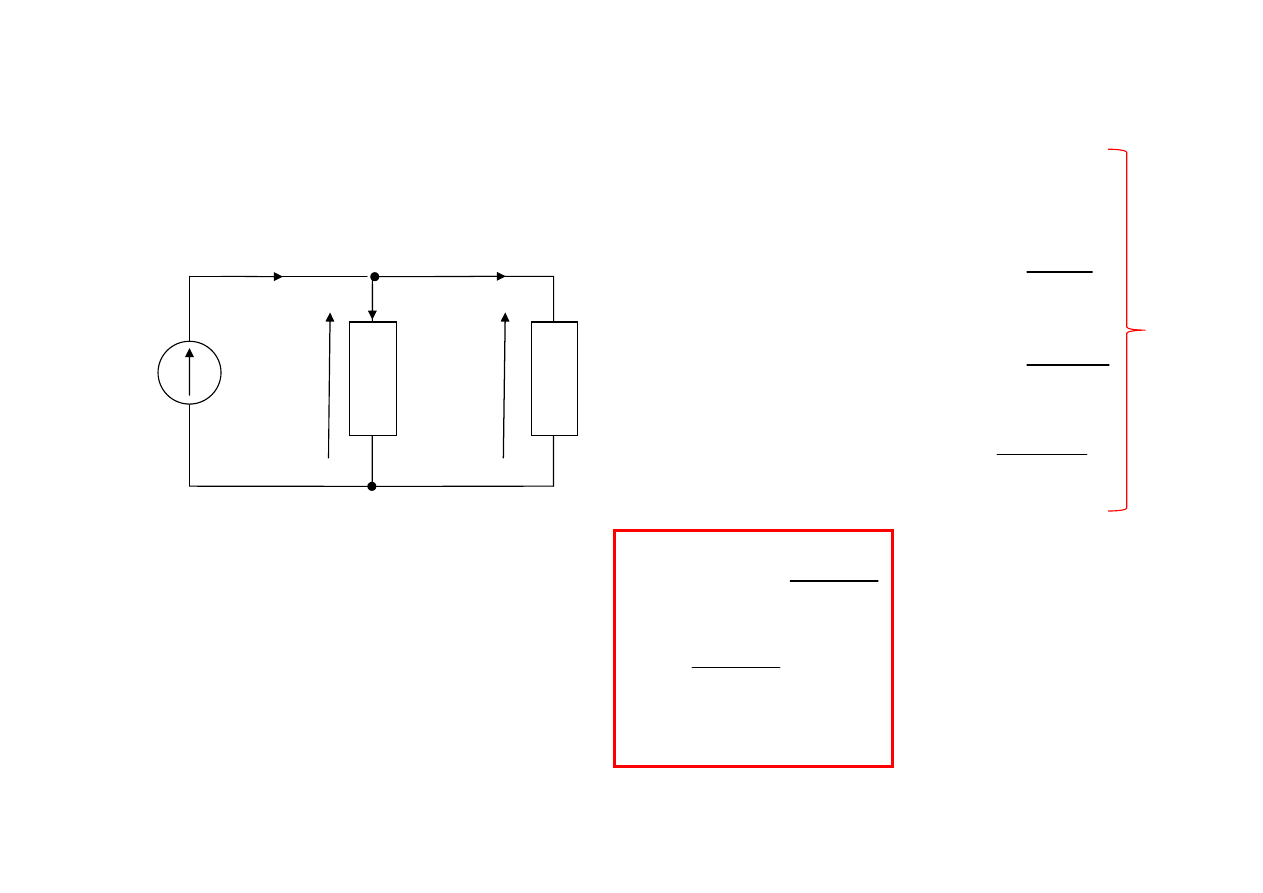
Obwody zawierające rezystory

Rezystancyjny dzielnik prądowy

( )

( )

( )

( )

( )

( )

2

1

2

1

2

2

2

R

R

R

R

R

R

t

U

t

i

R

t

U

t

i

t

U

t

U

Z

Z

wej

wej

wyj

wej

+

=

=

=

=

Współczynnik podziału prądu - K

i

II prawo Kirhchoffa

Rezystancja zastępcza w
połączeniu równoległym

( )

( )

1

0

2

1

1

2

1

1

≤

≤

+

=

+

=

i

i

wej

wyj

K

R

R

R

K

R

R

R

t

i

t

i

R

1

i

1

(t)

R

2

i

wyj

(t)

u

1

(t)

u

2

(t)

i

wej

(t)

u(t)

prawo Ohma

Jeżeli odbiornikami są rezystory, to zgodnie z prawem Ohma:

u(t) = Ri(t)

Dla prądu zmiennego moc chwilowa wyraża się wzorem:

p(t) = Ri

2

(t)

lub

p(t) = u

2

(t)/R

Dla prądu stałego moc jest niezależna od czasu i wynosi:

P= RI

2

lub

P= U

2

/R

Obwody zawierające rezystory

Moc prądu elektrycznego

Praca wyrażona powyższym wzorem zamienia się na ciepło i powoduje nagrzewanie rezystora.

Jest to tzw. ciepło Jule’a.

Jeżeli przez rezystor R w ciągu czasu t płynie prąd stały o natężeniu I, to praca tego prądu

wyniesie:

W = Pt = RI

2

t

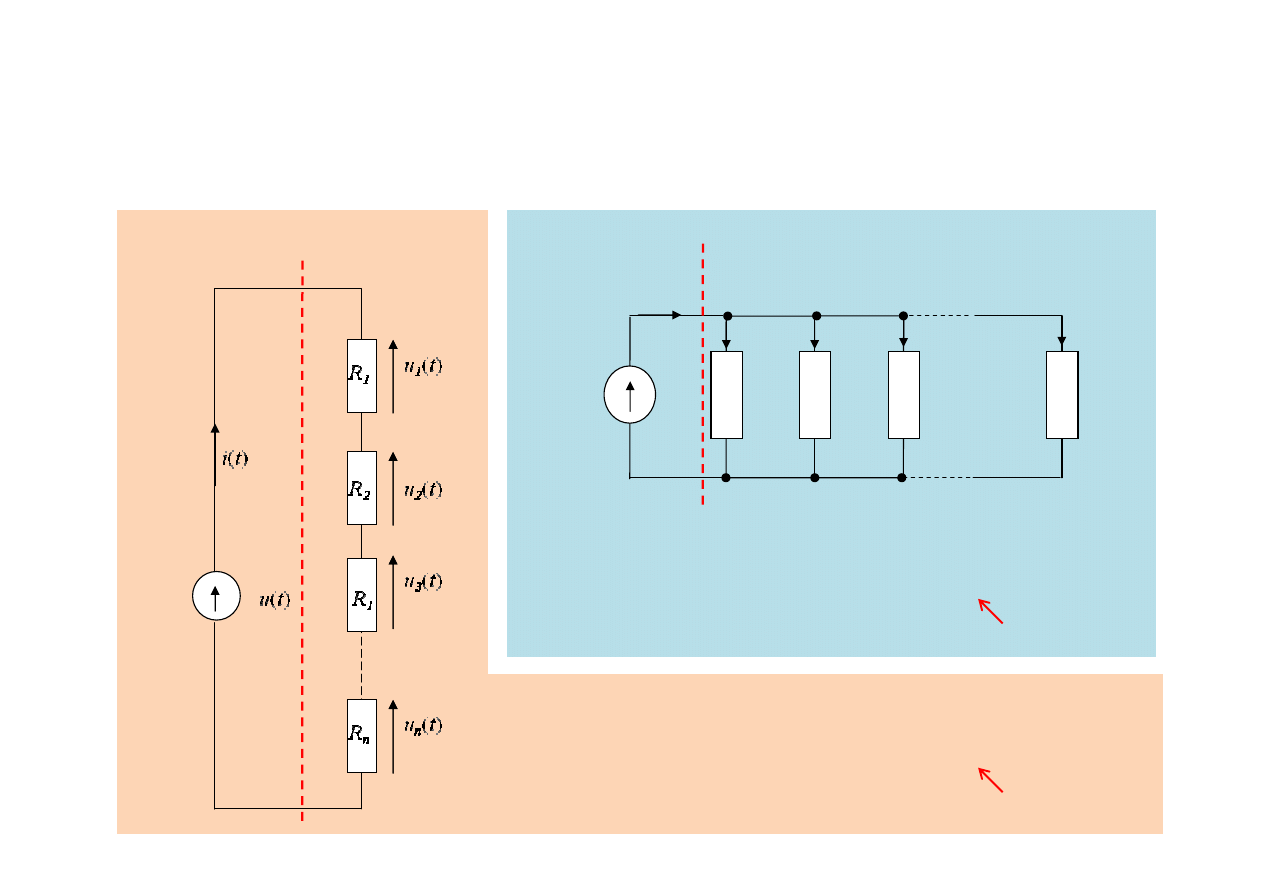
Suma mocy pobieranej przez wszystkie rezystory równa się mocy

dostarczonej ze źródła

Obwody zawierające rezystory

Bilans mocy elektrycznej

i

1

(t)

i

3

(t)

u(t)

i(t)

R

1

R

2

R

3

i

n

R

n

i

2

(t)

i

n

(t)

R

1

R

1

Połączenie szeregowe rezystorów

Połączenie równoległe rezystorów

moc dostarczona moc pobierana

moc dostarczona moc pobierana

moc pobierana:

moc dostarczona:

( ) ( )

( ) ( )

( ) ( )

( ) ( ) ( ) ( )

( )

[

]

( ) ( )

t

i

t

u

t

i

t

i

t

i

t

i

t

u

t

i

t

u

t

i

t

u

t

i

t

u

n

n

n

=

=

+

+

+

+

=

=

+

+

+

....

....

3

2

1

2

2

1

1

moc pobierana:

moc dostarczona:

( ) ( )

( ) ( )

( ) ( )

( ) ( )

( ) ( )

( )

[

]

( ) ( )

t

i

t

u

t

u

t

u

t

u

t

u

t

i

t

i

t

u

t

i

t

u

t

i

t

u

n

n

n

=

=

+

+

+

+

=

=

+

+

+

....

....

3

2

1

2

2

1

1

I prawo Kirchhoffa

II prawo Kirchhoffa