Politechnika Poznańska ► Instytut Konstrukcji Budowlanych ► Zakład Mechaniki Budowli
Układy statycznie niewyznaczalne – linie wpływu w belkach ciągłych
Zad.1
www.ikb.poznan.pl/anita.kaczor 2006
1
4.0
4.0
P=1.0
B
C
X
1
A
X
1
=1
1/4
B
C
X
1
=1
M
1
1/4
x
1
/4
1/4
1/4
1-x
2
/4
1
x
2
x
1
A
4.0m
4.0m
P=1.0
B
C
A
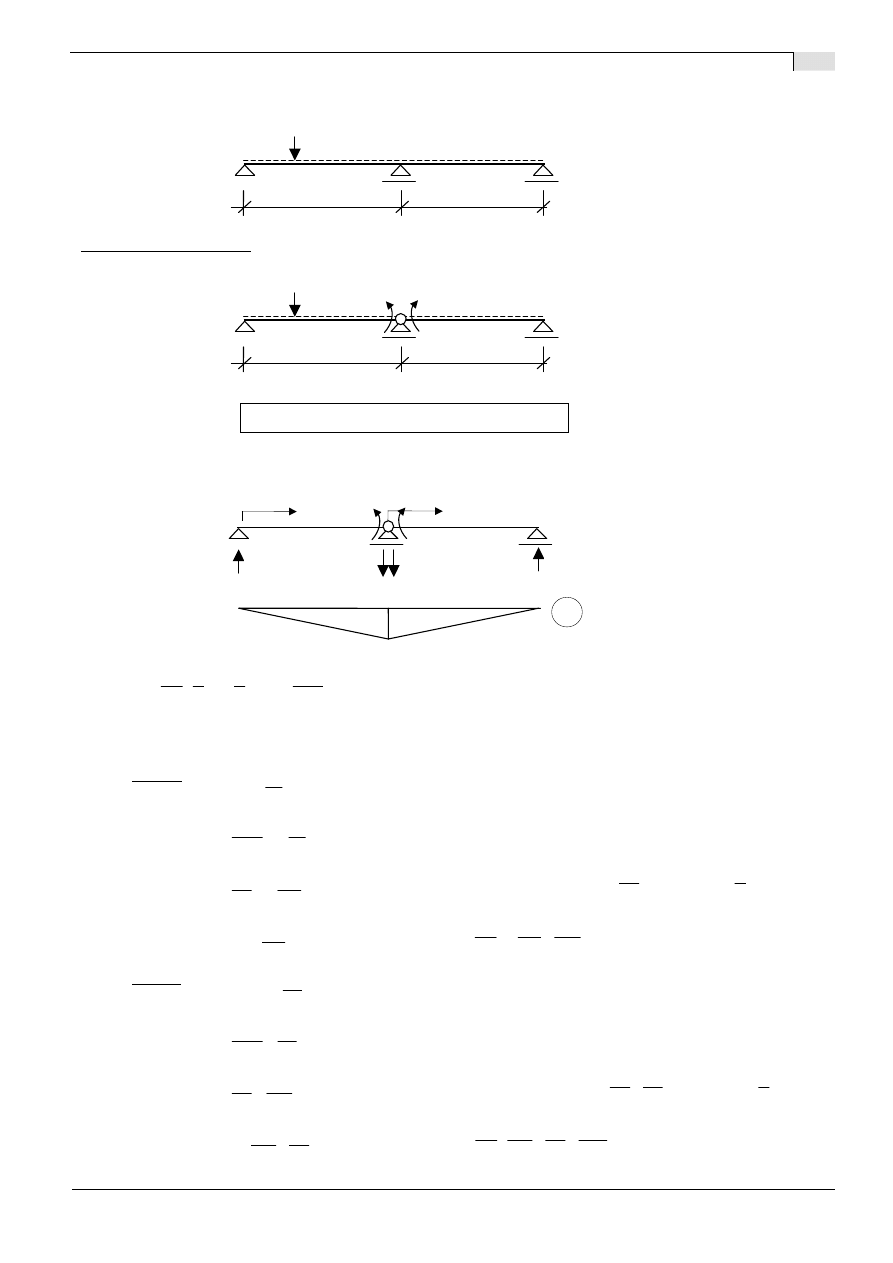
Zad. Wyznaczyć linie wpływu reakcji R
B
dla belki (EI=const):
Rozwiązanie - wersja I:
Układ podstawowy:
SSN=1
URK:
0
)
(
1
1
11
=
+
x
LwX
P
δ
δ
2
)
1
2
(
1
)
1
1
(
0
LwX
R
LwX
R
LwR
LwR
X
B
X
B
B
B
⋅
+
⋅
+
=
=
=
Stan X
1
=1
EI
EI
3
8
2
1
3
2
1
4
2
1
1
11
=
⋅
⋅
⋅
⋅
⋅
=
δ
)
(
)
(
1
1
x
x
P
P
δ
δ
=
linia ugi
ę
cia belki wywołana działaniem siły X
1
=1; wyznaczamy korzystaj
ą
c z
ró
ż
niczkowego równania linii ugi
ę
cia
(
)
y
x
P
=
)
(
1
δ
:
<A;B>
D
Cx
x
EIy
C
x
dx
dy
EI
x
dx
y
d
EI
x
x
M
+
+
−
=
+
−
=
−
=
=
1
3
1
2
1
1
2
2
1
24
8
4
4
)
(
+
−
=
=
⇒
+
−
=
⇒
=
→
=
=
⇒
=
→
=
3
2
24
1
)
(
3
2
4
24
4
0
0
4
)
2
0
0
0
)
1
:
brzegowe
war.
1
3
1
1
3
1
1
x
x
EI
x
C
C
y
x
D
y
x
AB
P
δ
<B;C>
D
Cx
x
x
EIy
C
x
x
dx
dy
EI
x
dx
y
d
EI
x
x
M
+
+
−
=
+
−
=
−
=
−
=
2
2
2
3
2
2
2
2
2
2
2
2
2
24
8
1
4
4
1
)
(
+
−
=
=
⇒
+
−
=
⇒
=
→
=
=
⇒
=
→
=
3
4
2
24
1
)
(
3
4
4
2
4
24
4
0
0
4
)
2
0
0
0
)
1
:
brzgowe
war.
2
2
2
3
2
1
2
3
2
2
x
x
x
EI
x
C
C
y
x
D
y
x
BC
P
δ
Politechnika Poznańska ► Instytut Konstrukcji Budowlanych ► Zakład Mechaniki Budowli
Układy statycznie niewyznaczalne – linie wpływu w belkach ciągłych
Zad.1
www.ikb.poznan.pl/anita.kaczor 2006
2
x
1
x
2
B
C
R
B
x
1
/4
1-x
2
/4
1
LwR
B
0
[-]
P=1.0
A
4.0
4.0
P=1.0
B
C
X
1
A
-2+x
2
/2
X
1
=1
B
C
M
1
1/2
-x
1
/2
1/2
2
x
2
x
1
A
2
16
3
64
3
4
2
24
1
8
3
)
(
4
64
3
2
24
1
8
3
)
(
2
2
2
3
2
2
2
2
3
2
11
1
1
1
3
1
1
3
1
11
1
1
x
x
x
x
x
x
EI
EI
x
LwX
x
x
x
x
EI
EI
x
LwX
BC
P
BC
AB
P
AB
−
+
−
=
+
−
⋅
−
=
−
=
−
=
+
−
⋅
−
=
−
=
δ
δ
δ
δ
1
32
3
128
2
16
3
64
2
1
4
1
;
8
3
128
4
64
2
1
4
;
2
2
3
2
2
2
2
3
2
2
1
)
1
1
(
0
1
3
1
1
3
1
1
1
)
1
1
(
0
+
−
=
−
+
−
⋅
−
−
=
⋅
+
=
>
<
+
−
=
−
⋅
−
=
⋅
+
=
>
<
=
=
x
x
x
x
x
x
LwX
R
LwR
LwR
C
B
x
x
x
x
x
LwX
R
LwR
LwR
B
A
BC
X
B
BC
B
BC
B
AB
X
B
AB
B
AB
B
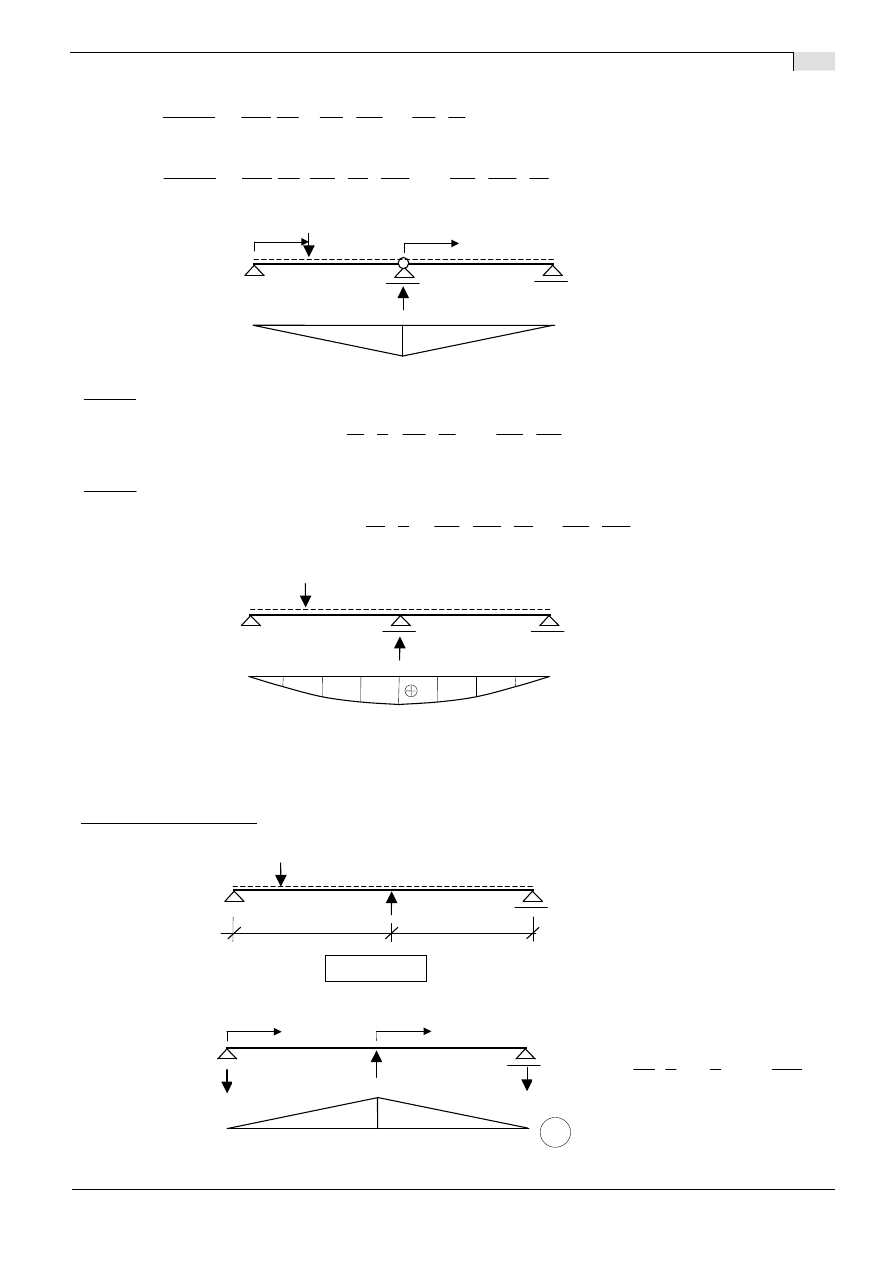
- z uwagi na symetri
ę
układu wystarczyłoby wyznaczy
ć
lini
ę
wpływu R
B
w przedziale <A;B>
Rozwi
ą
zanie - wersja II:
Układ podstawowy:
SSN=1
URK:
0
)
(
1
1
11
=
+
x
LwX
P
δ
δ
1
LwX
LwR
B
=
Stan X
1
=1
)
(
)
(
3
32
2
2
3
2
2
4
2
1
1
1
1
11
x
x
EI
EI
P
P
δ
δ
δ
=
=
⋅
⋅
⋅
⋅
⋅
=
1,00
0,688
0,914
Lw R
B
[-]
0,367
B
C
R
B
symetria
P=1.0
A
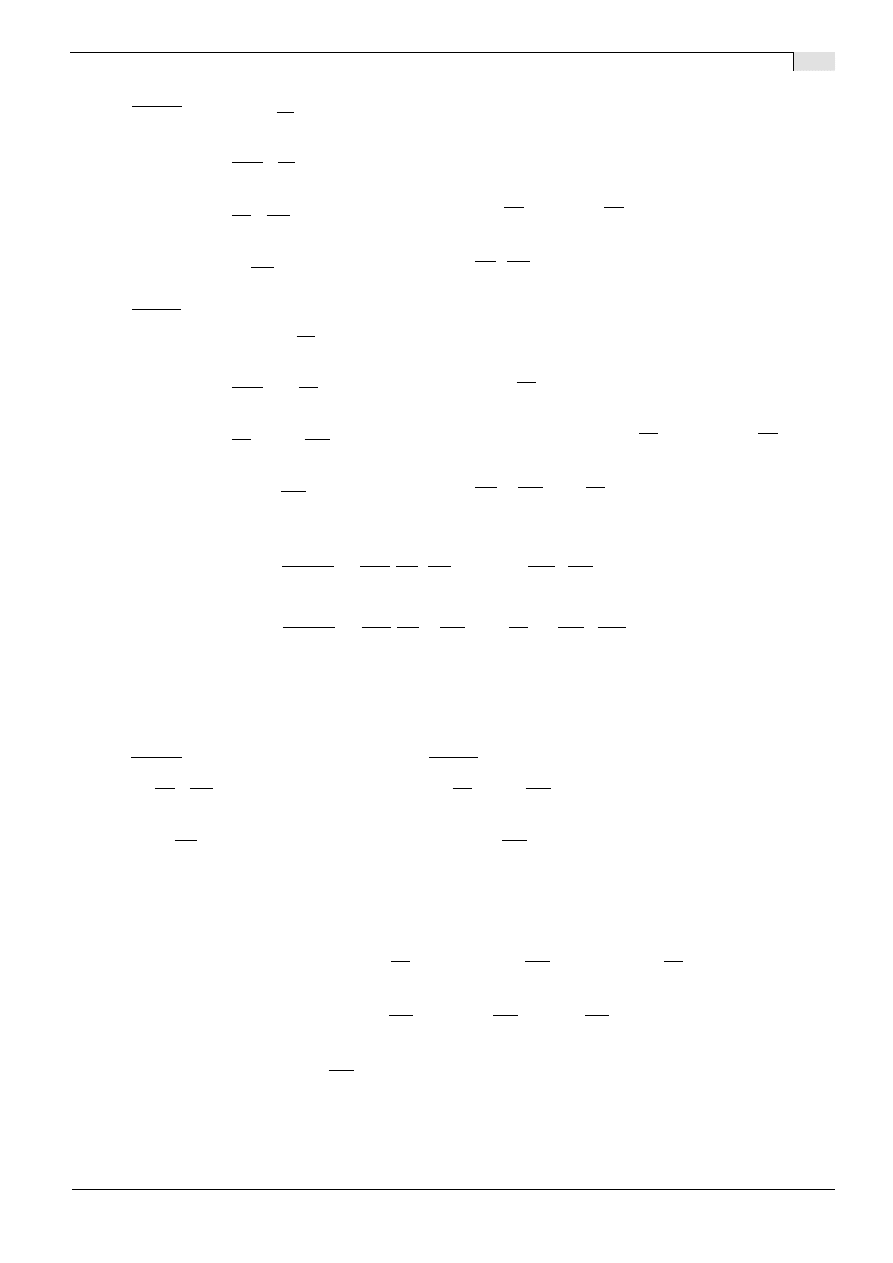
Politechnika Poznańska ► Instytut Konstrukcji Budowlanych ► Zakład Mechaniki Budowli
Układy statycznie niewyznaczalne – linie wpływu w belkach ciągłych
Zad.1
www.ikb.poznan.pl/anita.kaczor 2006
3
<A;B>
D
Cx
x
EIy
C
x
dx
dy
EI
x
dx
y
d
EI
x
x
M
+
+
=
+
=
=
−
=
1
3
1
2
1
1
2
2
1
12
4
2
2
)
(
0
0
0
)
1
:
brzegowe
war.
1
=
⇒
=
→
=
D
y
x
2) ze wzgl
ę
du na symetri
ę
obci
ąż
enia i geometrii
układu
*
obrót przekroju w p.B wynosi 0:
−
=
−
=
⇒
+
=
⇒
=
→
=
1
3
1
1
2
1
4
12
1
)
(
4
4
4
0
0
4
x
x
EI
x
C
C
dx
dy
x
AB
P
δ
<B;C>
D
Cx
x
x
EIy
C
x
x
dx
dy
EI
x
dx
y
d
EI
x
x
M
+
+
−
=
+
−
=
−
=
+
−
=
2
3
2
2
2
2
2
2
2
2
2
2
12
4
2
2
2
2
2
)
(
−
−
−
=
−
=
⇒
+
−
=
⇒
=
→
=
=
⇒
=
→
=
3
32
12
1
)
(
3
32
12
4
4
0
0
4
)
2
0
0
0
)
1
:
brzegowe
war.
2
2
3
2
1
3
2
2
2
x
x
EI
x
D
D
y
x
C
dx
dy
x
BC
P
δ
1
32
3
128
3
32
12
1
32
3
)
(
8
3
128
4
12
1
32
3
)
(
2
2
3
2
2
2
3
2
11
1
1
1
3
1
1
3
1
11
1
1
+
−
=
−
+
−
⋅
−
=
−
=
=
+
−
=
−
⋅
−
=
−
=
=
x
x
x
x
EI
EI
x
LwX
LwR
x
x
x
x
EI
EI
x
LwX
LwR
BC
P
BC
BC
B
AB
P
AB
AB
B
δ
δ
δ
δ
(czyli j/w :)
*)
w przypadku układu niesymetrycznego (ró
ż
ne przekroje lub rozpi
ę
to
ś
ci):
<A;B>
<B;C>
1
1
1
3
1
1
2
1
12
4
D
x
C
x
EIy
C
x
dx
dy
EI
+
+
=
+
=
2
2
2
3
2
2
2
2
2
2
2
12
4
2
D
x
C
x
x
EIy
C
x
x
dx
dy
EI
+
+
−
=
+
−
=
komplet warunków brzegowych:
0
4
12
4
4
0
4
)
4
4
4
4
0
0
2
4
4
)
0
(
4
)
3
4
12
4
0
12
0
0
4
12
4
)
0
(
4
)
2
0
0
0
)
1
2
2
3
2
2
2
1
2
1
2
2
1
2
1
2
1
2
1
3
2
2
3
2
1
1
3
2
1
1
1
=
+
⋅
+
−
⇒
=
→
=
=
+
⇒
+
−
⋅
=
+
⇒
=
→
=
=
=
+
⇒
+
⋅
+
−
=
+
+
⇒
=
→
=
=
=
⇒
=
→
=
D
C
y
x
C
C
C
C
x
x
D
C
D
C
D
C
y
y
x
x
D
y
x
P
B
L
B
P
B
L
B
ϕ
ϕ
- po rozwi
ą
zaniu powy
ż
szego układu równa
ń
otrzymujemy:
3
/
32
;
0
;
0
;
4
2
2
1
1
−
=
=
=
−
=
D
C
D
C
, co
prowadzi do tych samych wyników :)
Wyszukiwarka
Podobne podstrony:
linie wpływu sił tnących do ścinania
Linie wpływu belka z teleskopem
Linie wpływu Metoda przemieszczeń mmp belka lw
linie wpływu belka
Linie wpływu metoda kinematyczna belka
Linie wpływu belka z teleskopem
Linie wpływu Metoda przemieszczeń mmp belka lw
Linie wpływu belka z teleskopem
linie wpływu belka
4 Linie wpływu wielkości statycznych w ustrojach prętowych
Mechanika budowli Metoda sił belka
linie wpływu zadanie
Linie wplywu id 268681 Nieznany
Linie wpływu MARKA
Linie wpływu, Linie wpływu
2 Linie wplywuid 20498 Nieznany
Mechanika Budowli - Linie wpływu, BUDOWNICTWO, Mechanika budowli
więcej podobnych podstron