K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

XII.

SPIN I WŁASNY MOMENT MAGNETYCZNY ELEKTRONU

Dwa podpoziomy odległe od siebie o pewną wartość Δ – struktura subtelna. (Więcej na
ten temat – patrz rozdział V.2.)

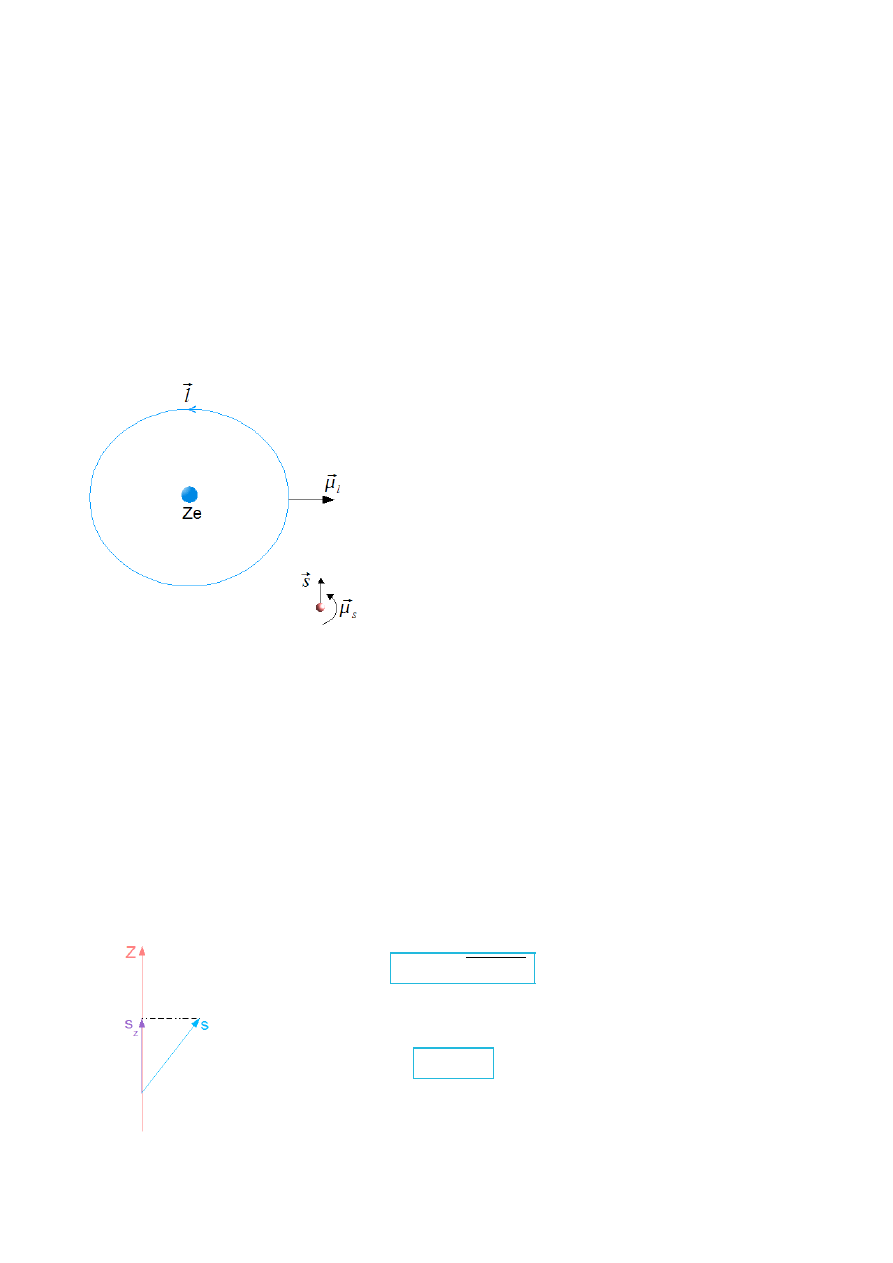
Goudsmit, Uhlenbeck (1925r.) żeby wyjaśnić strukturę subtelną podali hipotezę, że
elektron posiada spin (klasycznie: obrót wokół własnej osi).

Aby wyjaśnić zmierzony moment magnetyczny, prędkość musiałaby wynosić 300c na jego
równiku. Klasyczny obraz spinu jest nierealny, współczesna fizyka nie dopuszcza
prędkości większych od prędkości światła.
Doświadczenia pokazują, że elektron rzeczywiście posiada spin. Jego istnienie jednak nie
wynika z równania Schrödingera.

XII.1. SPIN W MECHANICE KWANTOWEJ

s

– wielkość wektorowa, podlega analogicznym prawom jak kręt.

s

– s (nie mylić ze stanem „s” dla l=0)

|

s| = ℏ



s

s + 1

(XII.1.1)

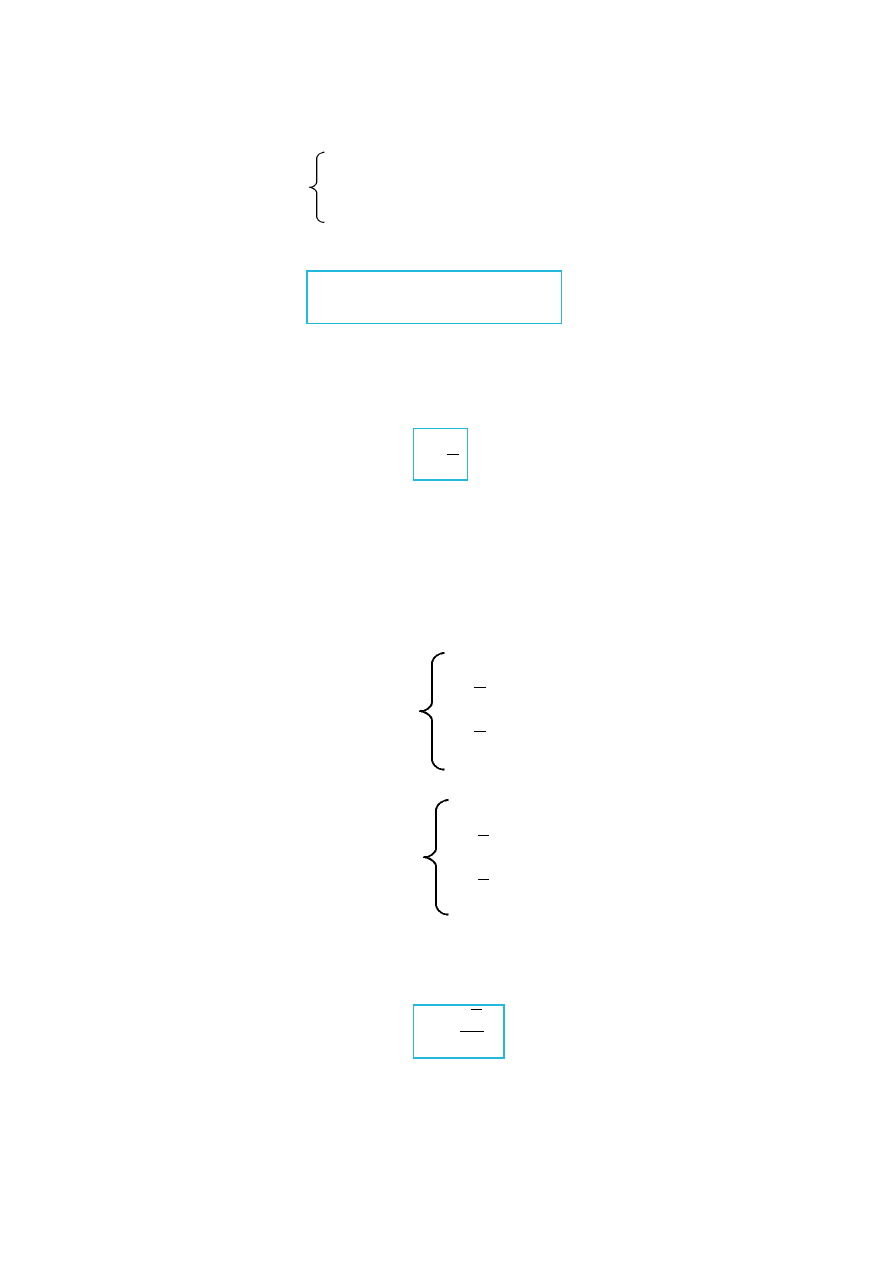
s

Z

=m

s

ℏ

(XII.1.2)

– 1 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

m – magnetyczna liczba kwantowa

m

m

L



Z

=m

L

ℏ rzut krętu na oś

m

s

s

Z

=m

s

ℏ rzut spinu na oś

Rzut spinu względem osi z ( kierunek kwantyzacji) może posiadać 2s+1 wartości.

m

s

= −s , −s1,... , s−1, s



2s +1 wartości

(XII.1.3)

Z doświadczenia Sterna – Gerlacha (S – G):

2s1 = 2 Stąd wynika, że:

s

=

1

2

(XII.1.4)

fermiony – spin połówkowy (np. elektron), podlegają zakazowi Pauliego

bozony – spin całkowity

Statystyka wszystkich cząstek jest oparta na spinach.

Z równań (XII.1.3) i (XII.1.4) wynika:

m

s

=



1
2

−

1
2

Z równań (XII.1.2) oraz (XII.1.3) wynika:

s

Z

=



1
2

ℏ

−

1
2

ℏ

Jeżeli znamy liczbę kwantową spinu możemy wyliczyć np. długość spinu.

Ze wzorów (XII.1.1) i (XII.1.4) wynika:

|

s |=



3

2 ℏ

(XII.1.5)

– 2 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

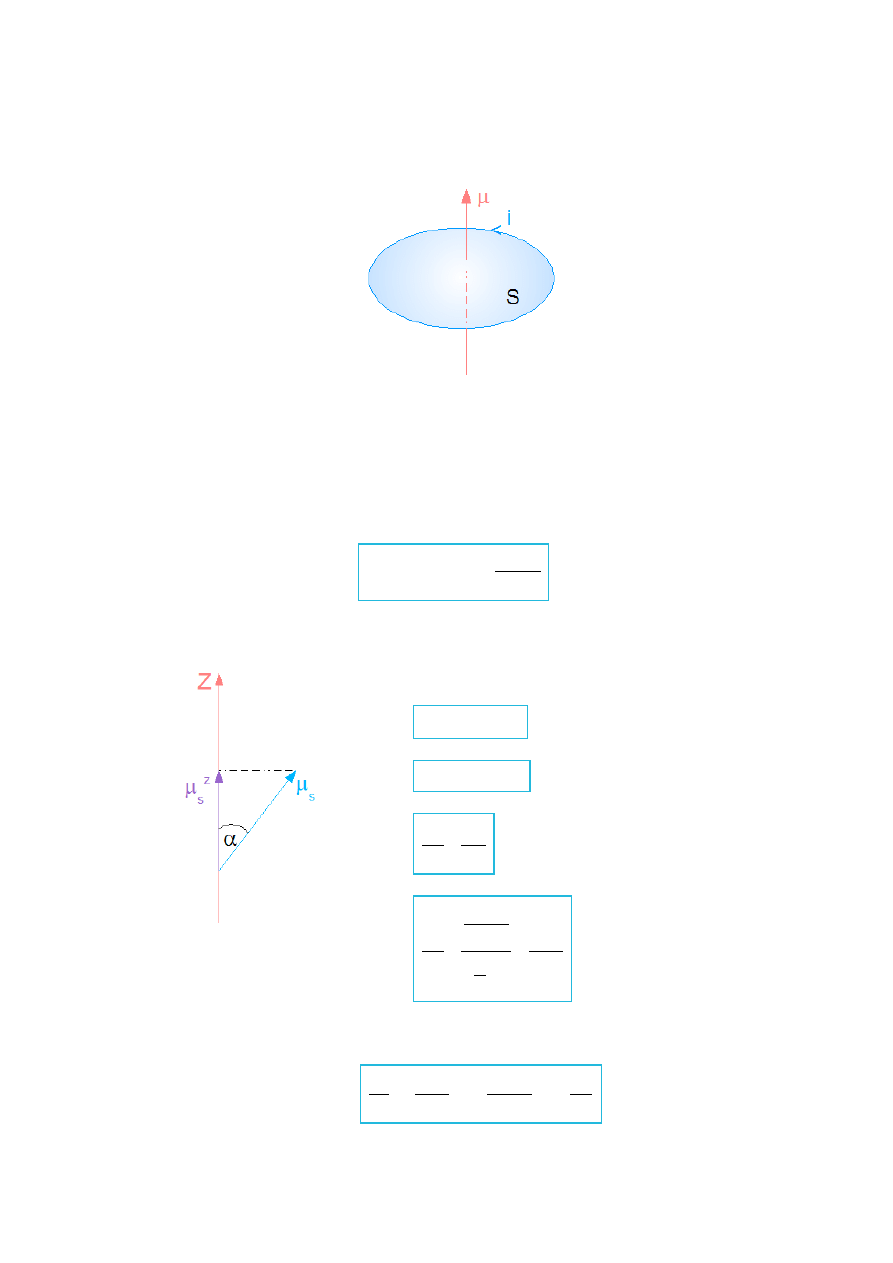
Z zamkniętym obwodem prądu związany jest moment magnetyczny.

=i S

gdzie S – powierzchnia obwodu.

Z doświadczenia S – G





s

;



s

Z

= ±1

B

= ±

e

ℏ

2m

e

c

(XII.1.6)

Różnica między spinowym i magnetycznym momentem magnetycznym.



s

Z

=

s

⋅cos

(XII.1.7)

s

Z

=|s |⋅cos 

(XII.1.8)



s

Z

s

Z

=



s

|s |

(XII.1.9)



s

Z

s

Z

=

e

ℏ

2m

e

c

1

2

ℏ

=

e

m

e

c

(XII.1.10)

Z równań (XII.1.9) oraz (XII.1.10) wynika, że:



s

∣s∣

=

e

m

e

c

= 2

e

2m

e

c

= 2



l

∣L∣

(XII.1.11)

– 3 –

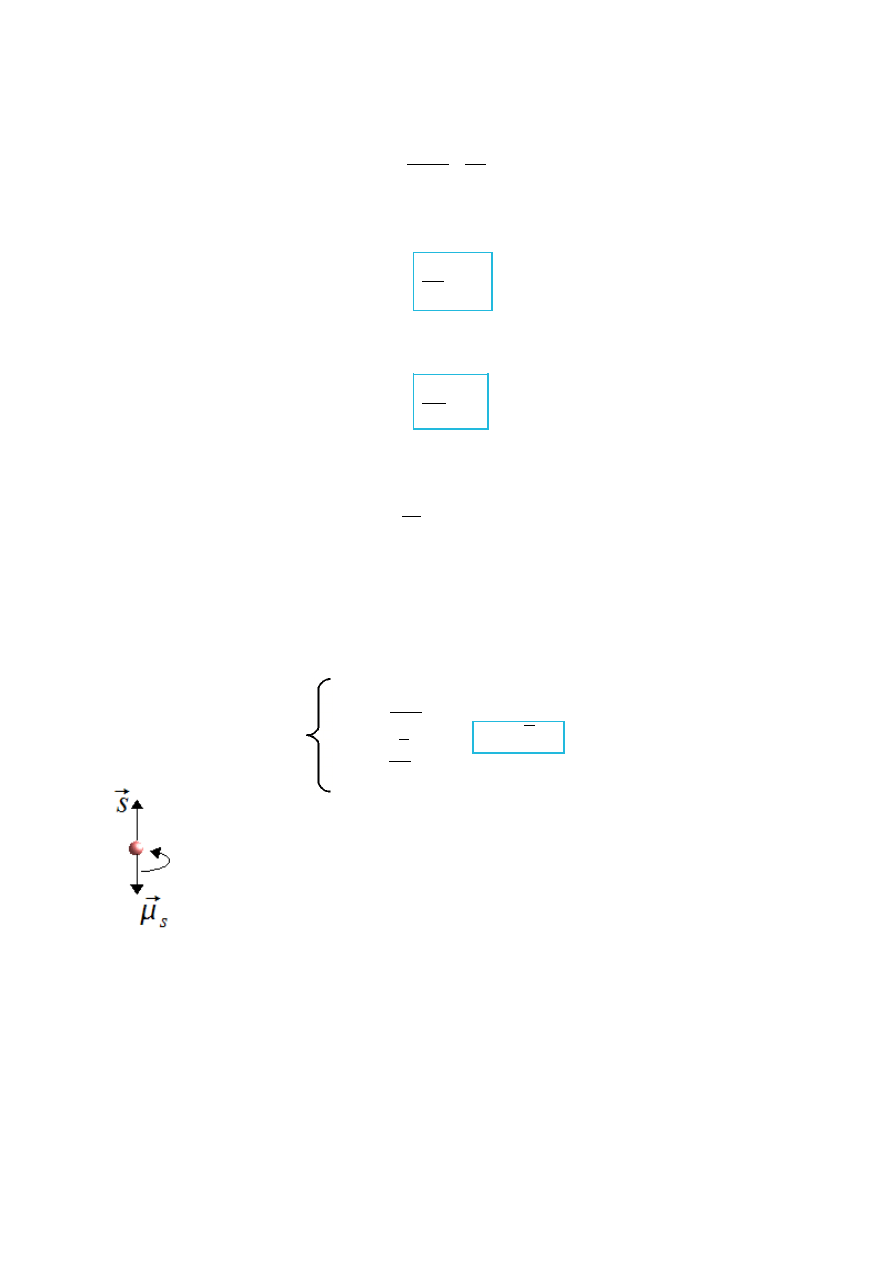
K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

e

2m

e

c

=



l

∣L∣

Stosunek żyromagnetyczny dla krętu:



l

∣L∣

= 

l

(XII.1.12)

Stosunek żyromagnetyczny dla spinu:



s

|s |

=

s

(XII.1.13)

Z wzorów (XII.1.11), (XII.1.12) oraz (XII.1.13) wynika, że czynnik Landego g

s

wynosi:



s



l

= g

s

= 2

Jest to wartość teoretyczna. Eksperymentalnie czynnik Landego jest równy:

g

s

eks

=2,023

Z (XII.1.11) wynika:



s

∣s∣⋅

e

m

e

c

∣s∣=



3

2

ℏ

→



s

=



3



B

(XII.1.14)

Funkcja falowa elektronu ze spinem:

(n, l, m) → (n, l, m, m

s

)



nlm

 x , y , z s 

nl m

l

m

s

 x , y , z , 

– 4 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

współrzędna spinowa σ =



1
2

−

1
2

Istnienie spinu wynika z teorii Diraca.

– 5 –