25
IV. RACHUNEK CAŁKOWY
4.1 Całka nieoznaczona.
Funkcję F(x) nazywamy funkcją pierwotną funkcji f(x) na przedziale X wtedy i tylko wtedy,
gdy dla każdego
X
x
∈
jest
( )
( )
x
f
x
F
=
'
.
Z powyższego wynika, że ogólną postać funkcji pierwotnej funkcji f(x) można zapisać nst.:
F(x) + C, gdzie „C” jest dowolną stałą.
Całką nieoznaczoną nazywamy zbiór wszystkich funkcji pierwotnych funkcji f(x) i
oznaczamy symbolem:
( )
∫
dx
x
f
, zatem
( )
( )
C
x
F
dx
x
f
+
=
∫
, przy czym dowolną stałą „C”
będziemy nazywali
stałą całkowania.
4.2 Całka oznaczona.
Jeżeli z przedziału X wydzielimy podprzedział
X
b
a
∈
;
, przy czym funkcja f(x) jest ciągła,
określona i monotoniczna na
X
b
a
∈
;
, to całka funkcji f(x) na podprzedziale
X
b
a
∈
;
będzie nosić nazwę całki oznaczonej, a jej symbolem jest nst. zapis:
( )
∫
b
a
dx
x
f
, zatem
( )
( )
( )
a
F
b
F
dx
x
f
b
a
−
=
∫
, przy czym F(a) oraz F(b) są wartościami funkcji pierwotnej F(x)
odpowiednio w punktach „a” i „b”.
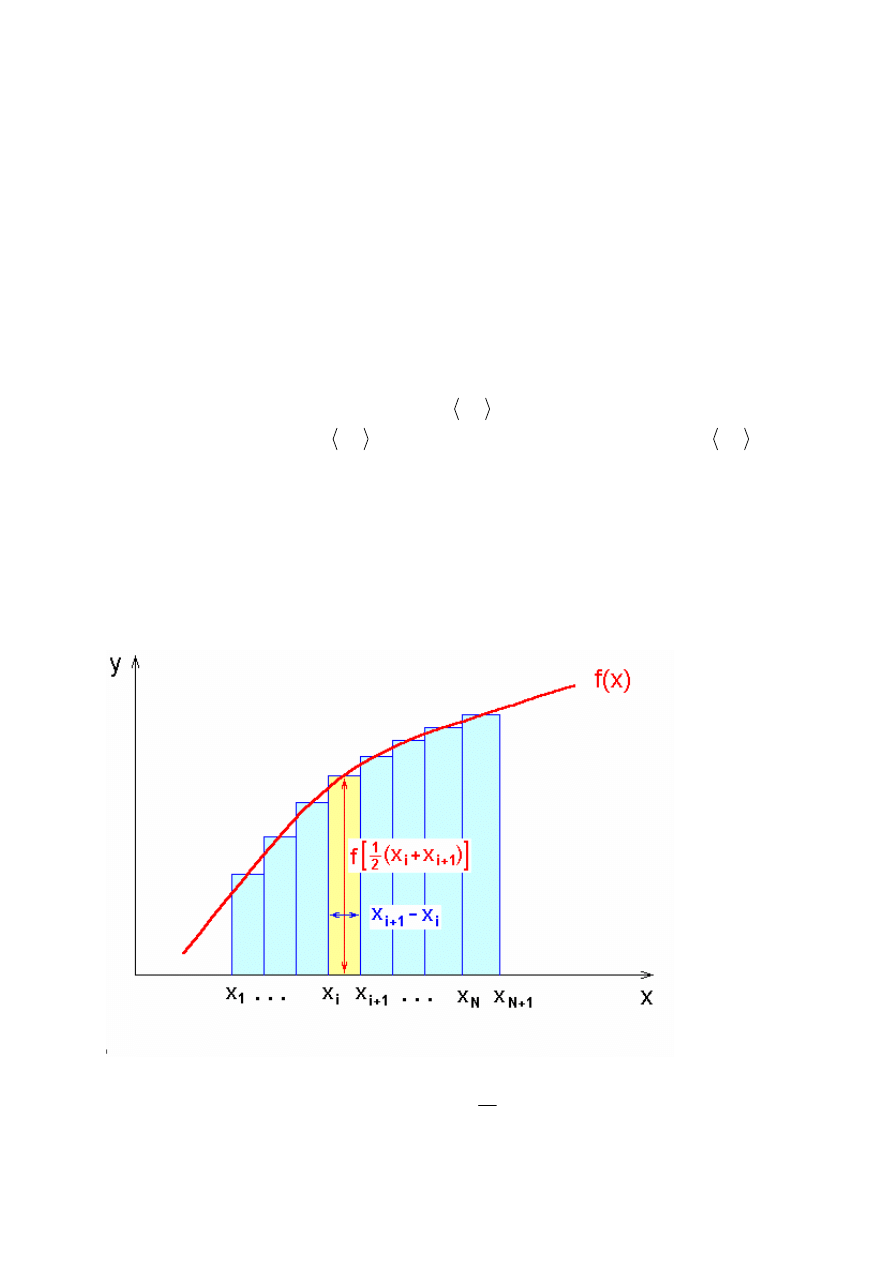
4.3 Interpretacja geometryczna całki.
( )
(
)
(
) (
)
i
i
x
b
x
a
N
i
i
i
x
x
x
x
x
x
f
dx
x
f
N
i
i
N
−
+
=
+
=
=
=
+
→
−
=
∫
∑
+
+
1
1
1
0
*
2
1
lim
1
1
1
δ

26
4.4 Własności całek
( ) ( )
[
]
( )
( )
( )
( )
∫
∫
∫
∫
∫
=
±
=
±
dx
x
f
k
dx
x
f
k
dx
x
g
dx
x
f
dx
x
g
x
f
*
*
( ) ( )
[
]
( )
( )
( )
( )
∫
∫
∫
∫
∫
=
±
=
±
b
a
b
a
b
a
b
a
b
a
dx
x
f
k
dx
x
f
k
dx
x
g
dx
x
f
dx
x
g
x
f
*
*
4.5 Obliczanie całek – metody.
1.
wykorzystując przekształcenia funkcji, własności całek oraz wzorów na całki funkcji
podstawowych
2.
przez części
( ) ( )
( ) ( )
( ) ( )
∫
∫
−
=
x
v
x
u
x
v
x
u
dx
x
v
x
u
*
*
*
'
'
dla całki nieoznaczonej
( ) ( )
( ) ( )
(
)
( ) ( )
∫
∫
−
=
b
a
b
a
b
a
dx
x
v
x
u
x
v
x
u
dx
x
v
x
u
*
*
*
'
'
przy czym wyrażenie
( ) ( )
(
)
b
a
x
v
x
u
*
oznacza nst. różnicę:
( ) ( ) ( ) ( )
a
v
a
u
b
v
b
u
*
*
−
3.
przez podstawienie
( )
(
) ( )
( )
∫
∫
=
dt
t
f
dx
x
g
x
g
f
'
*
przy czym w całce nieoznaczonej po prawej stronie
równania obowiązuje podstawienie g(x) = t
( )
(
)
( )
( )
∫
∫
=
b
a
dt
t
f
dx
x
g
x
g
f
β
α
'
*
przy czym
( )
( )
b
g
a
g
=
=
β
α
;
Przykłady:
ad. 1
całka nieoznaczona
(
)
C
x
x
x
x
C
x
x
x
x
dx
x
dx
x
dx
x
dx
x
dx
x
x
dx
x
x
dx
x
x
dx
x
dx
x
x
x
x
dx
x
x
+
−
+
−
=
=
+
−
+
−
=
−
+
−
=
=
−
+
−
=
−
+
−
=
−
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
−
7
5
3
2
7
2
5
2
3
2
1
2
5
2
3
2
1
2
1
2
1
3
2
1
2
2
1
2
1
2
1
3
2
3
7
2
5
6
2
2
7
2
5
2
*
3
3
2
*
3
2
3
3
3
3
1
3
3
1
1
całka oznaczona
(
)
(
) (
)
35
32
7
2
5
6
0
7
2
0
5
6
0
2
0
2
7
2
5
6
2
2
7
2
5
2
*
3
3
2
*
3
2
3
3
3
3
1
3
3
1
1
1
0
7
1
0
5
1
0
3
1
0
1
0
2
7
1
0
2
5
1
0
2
3
1
0
2
1
1
0
1
0
1
0
1
0
2
5
2
3
2
1
2
1
1
0
1
0
1
0
1
0
1
0
2
1
3
2
1
2
2
1
2
1
2
1
3
2
1
0
3
=
−
=
−
−
−
+
−
−
−
=
−
+
−
=
=
−
+
−
=
−
+
−
=
=
−
+
−
=
−
+
−
=
−
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
−
x
x
x
x
x
x
x
x
dx
x
dx
x
dx
x
dx
x
dx
x
x
dx
x
x
dx
x
x
dx
x
dx
x
x
x
x
dx
x
x
27
całka nieoznaczona
∫
∫
∫
∫
∫
∫
∫
∫
+
+
=
+
+
=
+
=
=
+
=
+
=
+
=
+
−
C
x
x
C
x
x
dx
x
dx
x
dx
x
x
dx
x
x
dx
x
x
dx
x
x
dx
x
x
x
x
dx
x
x
x
4
3
6
7
4
3
6
7
4
1
6
1
2
1
4
1
2
1
3
2
4
3
2
4
3
2
4
3
2
4
7
12
3
4
*
3
7
6
*
2
3
2
3
2
3
2
3
2
3
2
całka oznaczona
(
)
4
3
4
3
6
7
6
7
4
3
6
7
4
1
6
1
2
1
4
1
2
1
3
2
4
3
2
4
3
2
4
3
2
4
4
7
12
7
12
3
4
*
3
7
6
*
2
3
2
3
2
3
2
3
2
3
2
a
b
a
b
x
x
dx
x
dx
x
dx
x
x
dx
x
x
dx
x
x
dx
x
x
dx
x
x
x
x
dx
x
x
x
b
a
b
a
b
a
b
a
b
a
b
a
b
a
b
a
b
a
b
a
−
+
−
=
+
=
+
=
=
+
=
+
=
+
=
+
∫
∫
∫
∫
∫
∫
∫
∫
−
całka nieoznaczona
∫
∫
∫
∫
∫
∫
∫
+
−
−
=
−
=
−
=
=
−
=
−
=
C
tgx
ctgx
dx
x
dx
x
dx
x
x
x
dx
x
x
x
dx
x
x
x
x
x
x
dx
x
x
x
x
dx
x
x
x
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
cos
1
sin
1
sin
*
cos
sin
sin
*
cos
cos
sin
*
cos
sin
sin
*
cos
cos
sin
*
cos
sin
cos
sin
*
cos
2
cos
całka oznaczona
( )
(
)
3
3
1
2
1
3
3
1
1
1
3
1
3
1
cos
1
sin
1
sin
*
cos
sin
sin
*
cos
cos
sin
*
cos
sin
sin
*
cos
cos
sin
*
cos
sin
cos
sin
*
cos
2
cos
3
4
3
4
3
4
3
4
3
4
3
4
2
2
2
2
2
2
2
2
3
4
3
4
3
4
2
2
2
2
2
2
2
2
2
2
2
2
−
−
=
+
−
−
=
−
−
−
−
−
=
=
−
−
=
−
=
−
=
=
−
=
−
=
∫
∫
∫
∫
∫
∫
∫
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
tgx
ctgx
dx
x
dx
x
dx
x
x
x
dx
x
x
x
dx
x
x
x
x
x
x
dx
x
x
x
x
dx
x
x
x
ad. 2
całka nieoznaczona
(
)
(
)
(
)
(
)
(
)
C
x
x
x
C
x
x
x
xdx
x
x
x
v
u
x
v
x
u
xdx
x
+
+
+
=
=
+
−
−
+
=
−
+
=
=
=
=
+
=
=
+
∫
∫
cos
sin
*
1
cos
sin
*
1
sin
*
1
sin
*
1
sin
1
cos
1
cos
1
'
'
całka oznaczona
(
)
(
)
(
)
(
)
(
)
(
)
1
2
sin
*
1
2
0
cos
2
cos
0
sin
*
1
0
2
sin
*
1
2
cos
sin
*
1
sin
*
1
sin
*
1
sin
1
cos
1
cos
1
2
0
2
0
2
0
2
0
2
0
'
'
−
+
=
−
+
+
−
+
=
=
−
−
+
=
−
+
=
=
=
=
+
=
=
+
∫
∫
π
π
π
π
π
π
π
π
π
π
x
x
x
xdx
x
x
x
v
u
x
v
x
u
xdx
x
28
całka nieoznaczona
(
)
(
)
(
)
(
)
( )
x
F
x
x
x
x
x
x
x
x
x
dx
x
x
x
x
x
x
x
dx
x
x
xdx
x
x
x
x
x
x
dx
x
x
xdx
x
x
x
x
x
x
xdx
x
x
x
x
x
x
xdx
x
xdx
xdx
x
x
x
dx
x
x
xdx
x
x
x
x
xdx
x
xdx
x
x
x
x
dx
x
x
x
x
x
x
x
xdx
x
x
x
x
x
x
x
v
x
x
x
u
x
v
x
x
u
dx
x
x
=
+
+
=
+
+
=
⇒
+
+
=
⇒
−
+
+
=
⇒
⇒
−
+
+
=
−
+
−
−
=
=
−
+
−
=
−
+
−
=
=
+
−
=
−
−
=
=
−
−
=
=
−
=
=
=
=
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
'
'
2
4
1
2
cos
8
1
2
sin
*
4
1
2
1
2
cos
4
1
cos
*
sin
*
*
2
1
cos
*
2
1
2
cos
4
1
cos
*
sin
*
cos
*
2
cos
*
2
1
2
cos
4
1
cos
*
sin
*
cos
*
cos
*
2
1
2
cos
4
1
cos
*
sin
*
cos
*
2
1
2
cos
2
1
*
2
1
cos
*
sin
*
cos
*
2
sin
2
1
cos
*
sin
*
cos
1
*
cos
*
sin
2
2
1
cos
*
sin
*
sin
*
cos
*
sin
cos
*
sin
*
sin
*
sin
*
cos
cos
*
sin
*
sin
*
sin
*
cos
sin
*
cos
*
sin
sin
*
cos
cos
cos
*
cos
*
całka oznaczona
{
cos
*
2
=
∫
b
a
xdx
x
przy tak długich obliczeniach, całkę oznaczoną można policzyć jako
nieoznaczoną (obliczona powyżej), a granice całkowania <a;b> wstawić do ostatecznej
postaci funkcji scałkowanej F(x)}
=
+
+
=
b
a
x
x
x
x
2
4
1
2
cos
8
1
2
sin
*
4
1
+
+
−
+
+
=
2
2
4
1
2
cos
8
1
2
sin
*
4
1
4
1
2
cos
8
1
2
sin
*
4
1
a
a
a
a
b
b
b
b
całka nieoznaczona
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
x
F
C
x
x
x
C
x
x
x
x
x
dx
x
x
x
x
x
dx
x
x
x
x
x
x
x
v
x
u
x
v
x
u
dx
x
x
x
x
dx
x
x
x
x
x
dx
x
x
x
x
x
x
v
x
x
u
x
v
x
u
dx
x
x
=
+
+
−
=
+
−
−
=
=
−
−
=
−
−
=
=
=
=
=
=
=
−
=
−
=
−
=
=
=
=
=
=
∫
∫
∫
∫
∫
∫
8
1
ln
2
1
ln
4
1
4
1
*
4
1
4
1
*
ln
2
1
4
1
*
ln
4
1
4
1
*
ln
2
1
4
1
*
ln
4
1
*
1
4
1
*
ln
2
1
4
1
*
ln
4
1
1
ln
*
ln
2
1
4
1
*
ln
*
1
*
ln
2
1
4
1
*
ln
4
1
*
1
*
ln
2
4
1
*
ln
4
1
1
*
ln
2
ln
ln
*
2
4
4
4
4
2
3
4
4
2
4
4
4
2
4
'
3
'
3
4
2
4
4
2
4
4
2
4
'
3
'
2
2
3
29
całka oznaczona
( )
∫
=
b
a
dx
x
x
2
3
ln
*
{zamiana całki oznaczonej na nieoznaczoną}
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
x
F
C
x
x
x
C
x
x
x
x
x
dx
x
x
x
x
x
dx
x
x
x
x
x
x
x
v
x
u
x
v
x
u
dx
x
x
x
x
dx
x
x
x
x
x
dx
x
x
x
x
x
x
v
x
x
u
x
v
x
u
dx
x
x
=
+
+
−
=
+
−
−
=
=
−
−
=
−
−
=
=
=
=
=
=
=
−
=
−
=
−
=
=
=
=
=
=
∫
∫
∫
∫
∫
∫
8
1
ln
2
1
ln
4
1
4
1
*
4
1
4
1
*
ln
2
1
4
1
*
ln
4
1
4
1
*
ln
2
1
4
1
*
ln
4
1
*
1
4
1
*
ln
2
1
4
1
*
ln
4
1
1
ln
*
ln
2
1
4
1
*
ln
*
1
*
ln
2
1
4
1
*
ln
4
1
*
1
*
ln
2
4
1
*
ln
4
1
1
*
ln
2
ln
ln
*
2
4
4
4
4
2
3
4
4
2
4
4
4
2
4
'
3
'
3
4
2
4
4
2
4
4
2
4
'
3
'
2
2
3
Zatem
( )
( )
( )
( )
+
−
−
+
−
=
+
−
=
∫
8
1
ln
2
1
ln
4
1
8
1
ln
2
1
ln
4
1
8
1
ln
2
1
ln
4
1
ln
*
2
4
2
4
2
4
2
3
a
a
a
b
b
b
x
x
x
dx
x
x
b
a
b
a
ad. 3
całka nieoznaczona
(
)
C
x
C
t
tdt
dt
dx
t
x
xdx
+
−
=
+
−
=
=
=
=
=
∫
∫
5
cos
5
1
cos
5
1
sin
5
1
5
5
5
sin
całka oznaczona
(
)
5
2
5
1
5
1
0
cos
5
1
5
cos
5
1
cos
*
5
1
sin
5
1
5
0
sin
5
1
5
5
5
sin
5
0
5
0
0
=
+
=
−
−
−
=
=
−
=
=
=
=
=
=
=
=
=
∫
∫
∫
π
π
β
α
π
π
β
α
π
t
tdt
tdt
dt
dx
t
x
xdx
Uwaga:
stosując metodę zamiany całki oznaczonej na „roboczą” całkę nieoznaczoną i powrót do całki
oznaczonej z policzoną funkcją
( )
x
F
; nie zmieniamy granic całkowania!
=
∫
π
0
5
sin xdx
{przejście z całki oznaczonej na nieoznaczoną}
(
)
( )
x
F
C
x
C
t
tdt
dt
dx
t
x
xdx
=
+
−
=
+
−
=
=
=
=
=
∫
∫
5
cos
5
1
cos
5
1
sin
5
1
5
5
5
sin
Zatem
5
2
5
1
5
1
0
cos
5
1
5
cos
5
1
5
cos
5
1
5
sin
0
0
=
+
=
−
−
−
=
−
=
∫
π
π
π
x
xdx
całka nieoznaczona
(
)
(
)
∫
∫
+
+
=
+
=
=
=
=
+
=
+
C
x
C
t
tdt
dt
dx
t
x
dx
x
5
4
sin
4
1
sin
4
1
cos
4
1
4
5
4
5
4
cos
30
całka oznaczona
(
)
(
)
(
)
(
)
(
)
0
24
,
0
24
,
0
28
,
11
sin
4
1
57
,
17
sin
4
1
5
2
sin
4
1
5
4
sin
4
1
sin
4
1
cos
4
1
5
4
5
2
cos
4
1
4
5
4
5
4
cos
5
4
sin
4
1
sin
4
1
cos
4
1
4
5
4
5
4
cos
5
4
5
2
5
4
5
2
2
≅
+
−
=
−
=
+
−
+
=
=
=
=
+
=
+
=
=
=
=
=
+
=
+
+
+
=
+
=
=
=
=
+
=
+
+
+
+
+
∫
∫
∫
∫
∫
π
π
π
β
π
α
π
π
π
π
β
α
π
π
t
tdt
tdt
dt
dx
t
x
dx
x
C
x
C
t
tdt
dt
dx
t
x
dx
x
POZOSTAŁE PRZYKŁADY (WRAZ Z ODPOWIEDZIAMI) ZNAJDUJĄ SIĘ W
PODANEJ LITERATURZE NA STRONACH 104 – 107 (całka nieoznaczona) ORAZ
114 – 115 (całka oznaczona).
4.6 Całka oznaczona – obliczanie pól powierzchni.
Całkę oznaczoną możemy wykorzystywać do obliczania pól powierzchni ograniczonych
krzywymi (funkcjami); w szczególnych przypadkach możemy policzyć pole zawarte
pomiędzy krzywą (funkcją) a osią OX.
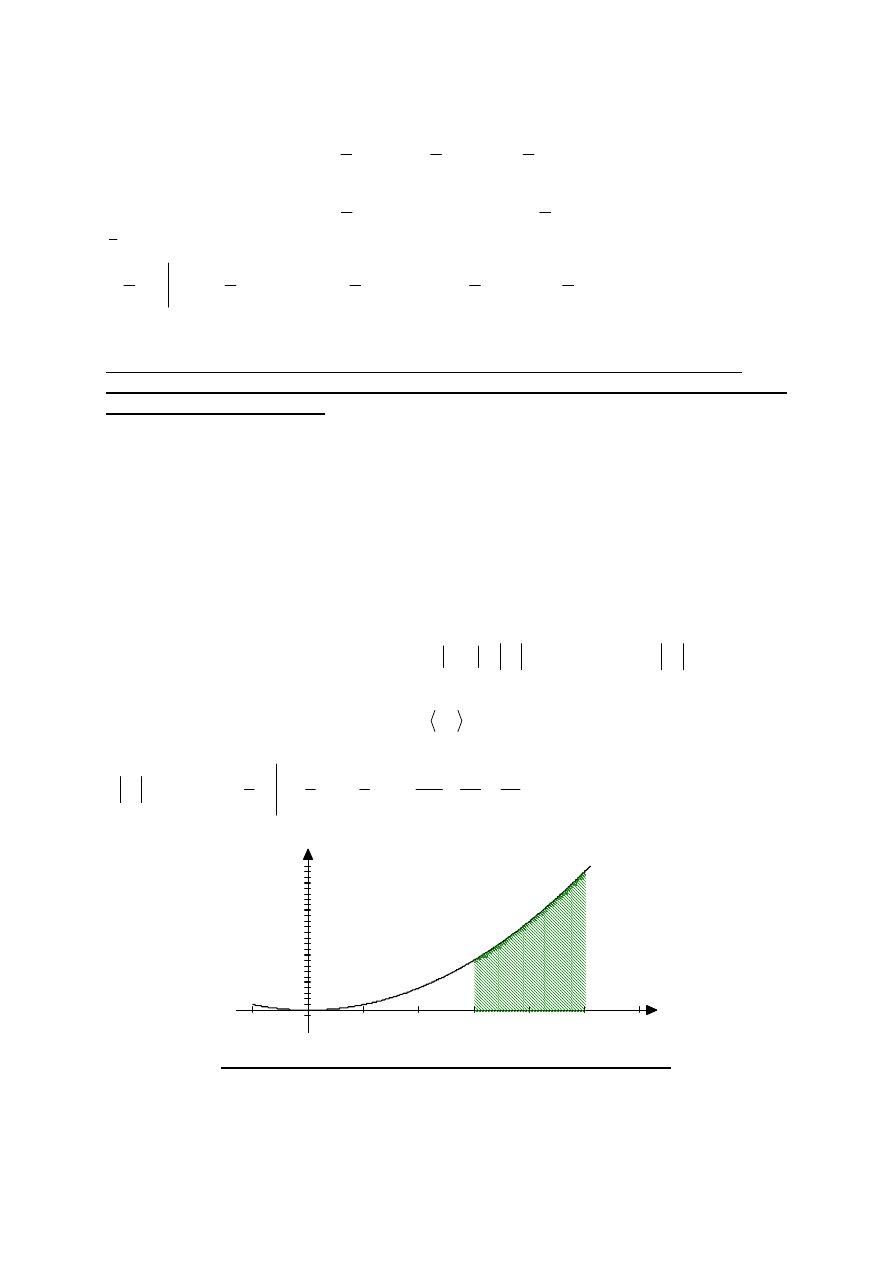
Przykład 1
: obliczyć pole powierzchni zawarte pomiędzy krzywą
( )
2
x
x
f
=
(poniższy
wykres), a osią OX, w granicach od 3 do 5.
W celu obliczenia wartości pola, należy skorzystać własności całki oznaczonej, przy czym
funkcją podcałkową f(x) będzie funkcja
( )
2
x
x
f
=
; stąd mamy:
∫
5
3
2
dx
x
; całkę tę
rozwiązujemy zgodnie z poznanymi wcześniej metodami oraz wykorzystując definicję
wartości bezwzględnej; tutaj
0
2
>
x
dla
5
;
3
∈
x
, zatem:
2
3
3
5
3
3
5
3
2
5
3
2
3
98
3
27
3
125
3
3
1
5
3
1
3
1
j
x
dx
x
dx
x
=
−
=
⋅
−
⋅
=
=
=
∫
∫
pole zakreskowane poniżej
X
Y
-1
1
2
3
4
5
6
0
Created with a trial version of Advanced Grapher - http:/ / www.alentum.com/ agra
31
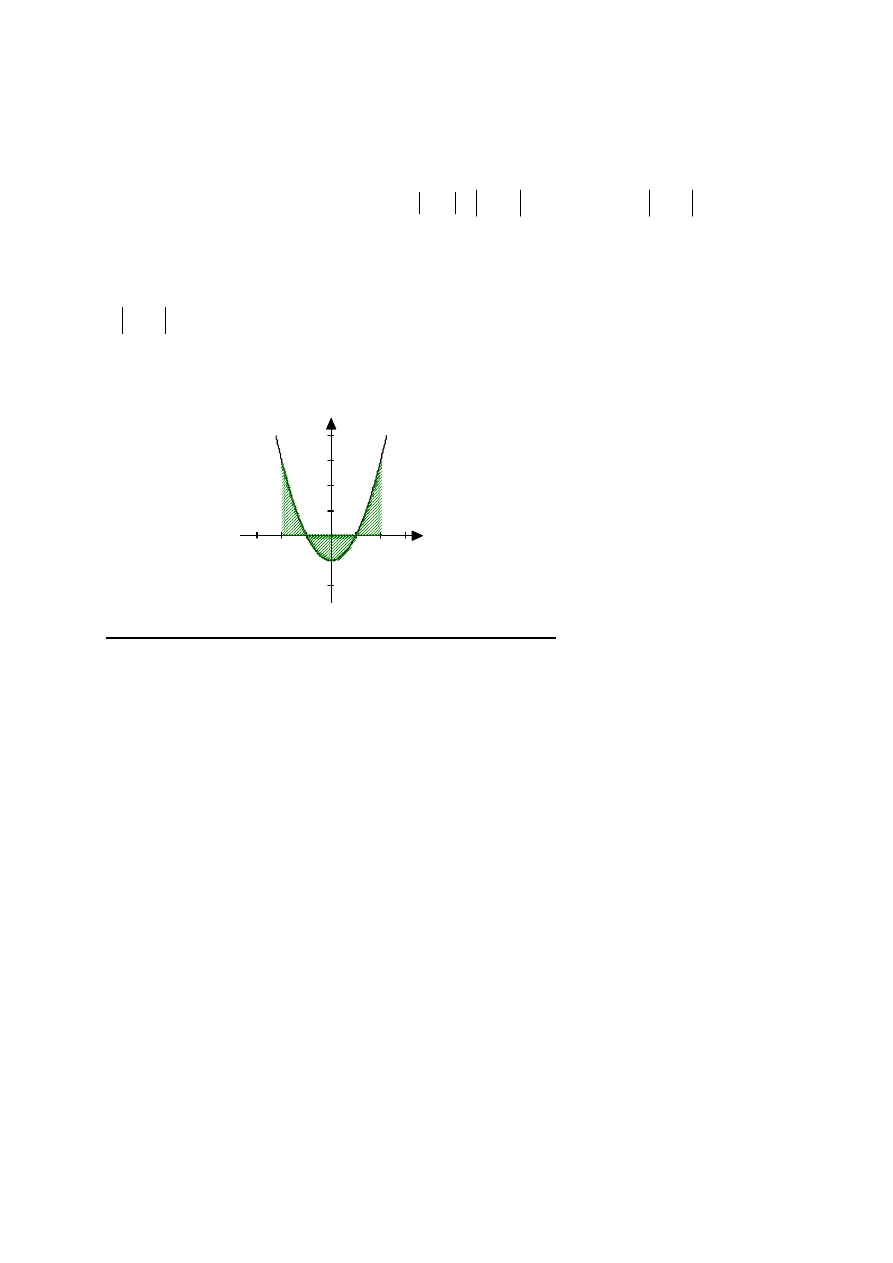
Przykład 2
: obliczyć pole powierzchni zawarte pomiędzy krzywą
( )
1
2
−
= x
x
f
(poniższy
wykres), a osią OX, w granicach od -2 do 2.
W celu obliczenia wartości pola, należy skorzystać własności całki oznaczonej, przy czym
funkcją podcałkową f(x) będzie funkcja
( )
1
2
−
= x
x
f
; stąd mamy:
∫
−
−
2
2
2
1dx
x
; całkę tę
rozwiązujemy zgodnie z poznanymi wcześniej metodami oraz wykorzystując definicję
wartości bezwzględnej, która w tym przykładzie „rozbije” naszą funkcję podcałkową na sumę
trzech funkcji w odpowiednich granicach całkowania;
(
)
(
)
(
)
(
)
(
)
(
)
∫
∫
∫
∫
∫
∫
∫
−
−
−
−
−
−
−
=
−
+
−
−
−
=
−
+
−
−
+
−
=
−
1
2
1
1
2
1
2
2
2
1
2
1
1
2
1
2
2
2
2
2
2
1
1
1
1
1
1
1
dx
x
dx
x
dx
x
dx
x
dx
x
dx
x
dx
x
= {każdą całkę rozwiązujemy zgodnie z poznanymi metodami}= 4j
2
(zakreskowane pole
poniżej)
X
Y
-3
-2
-1
1
2
3
0
Created with a trial version of Advanced Grapher - http:/ / w
Wyszukiwarka
Podobne podstrony:
Pochodna troch teorii zadania
Macierze troch teorii zadania
Funkcja troch teorii zadania
Funkcja wielu zmiennych troch teorii zadania
Logika troch teorii zadania
Ca ka niew a ciwa
Ca ka niew a ciwa
2 Ca ka potrojna 2
3 Ca ka krzywoliniowa skierowana
więcej podobnych podstron