45
VI. FUNKCJA WIELU ZMIENNYCH
6.1 Pochodna cząstkowa.
Niech dana będzie funkcja
(
)
z
x
x
x
f
n
=
,...,
,
2
1
; wówczas symbolami:
( )
( )
( )
y
x
f
x
f
y
x
f
x
f
y
x
f
x
f
n
x
n
x
x
,
...
,
,
'
'
2
'
1
2
1
≡
∂
∂
≡
∂
∂
≡
∂
∂
określamy tzw. pochodne cząstkowe
funkcji „f” względem odpowiedniej zmiennej x
1
, x
2
,…,x
n
.
Sposób obliczania funkcji pochodnych jest analogiczny do przypadku funkcji jednej
zmiennej; chcąc wyznaczyć funkcję pochodną do danej funkcji względem i – tej zmiennej,
pozostałe zmienne traktujemy jako „stałe”.
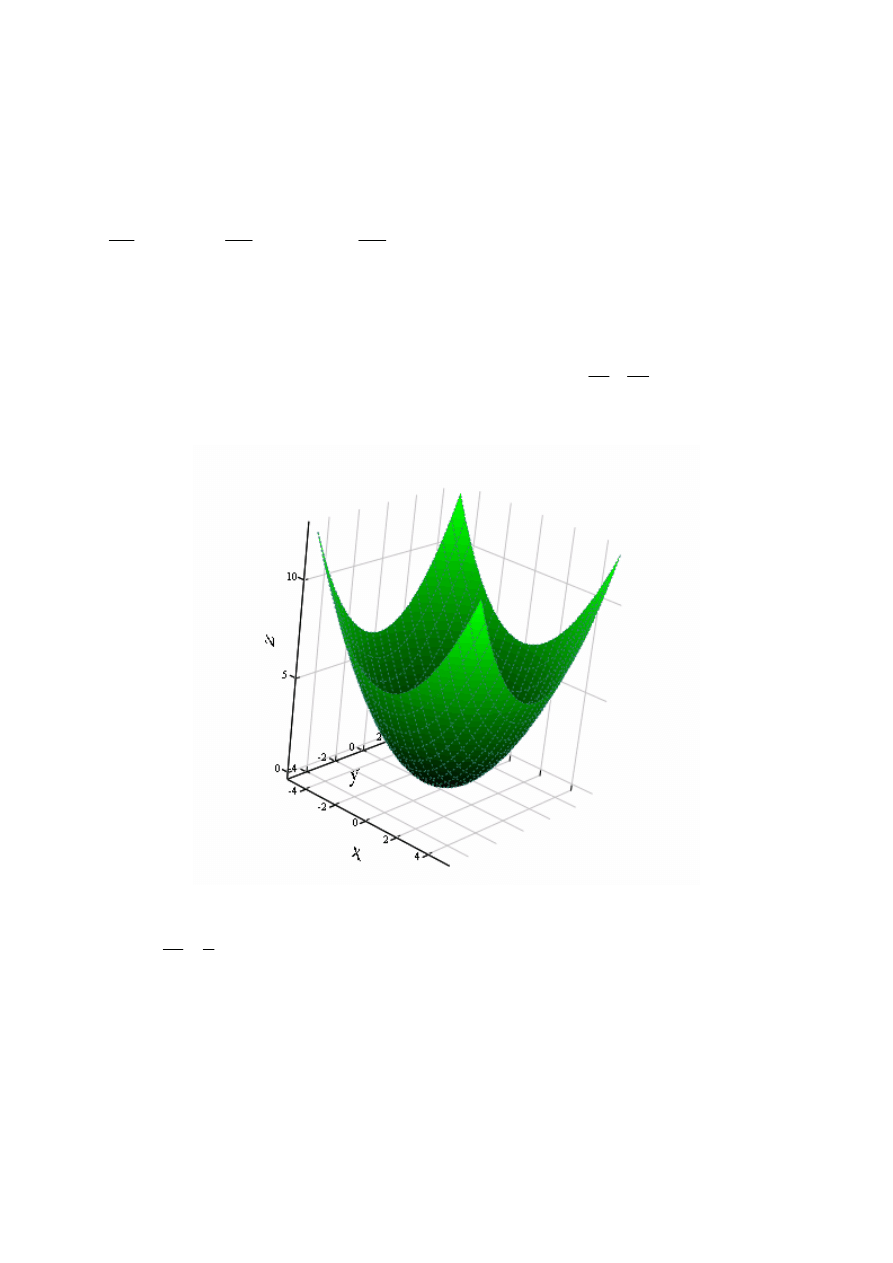
Rozpatrzmy funkcję dwóch zmiennych:
( )
z
y
x
f
=
,
; np.
( )
4
4
,
2
2
y
x
y
x
f
+
=
(poniższy
wykres)
y
x
x
x
≡
≡
2
1
;
:
Rozpatrzmy pochodne cząstkowe tej funkcji:
x
x
f
2
1
=
∂
∂
, np. wybierzmy
1
0
=
y
(tutaj można wybrać dowolną wartość), wówczas
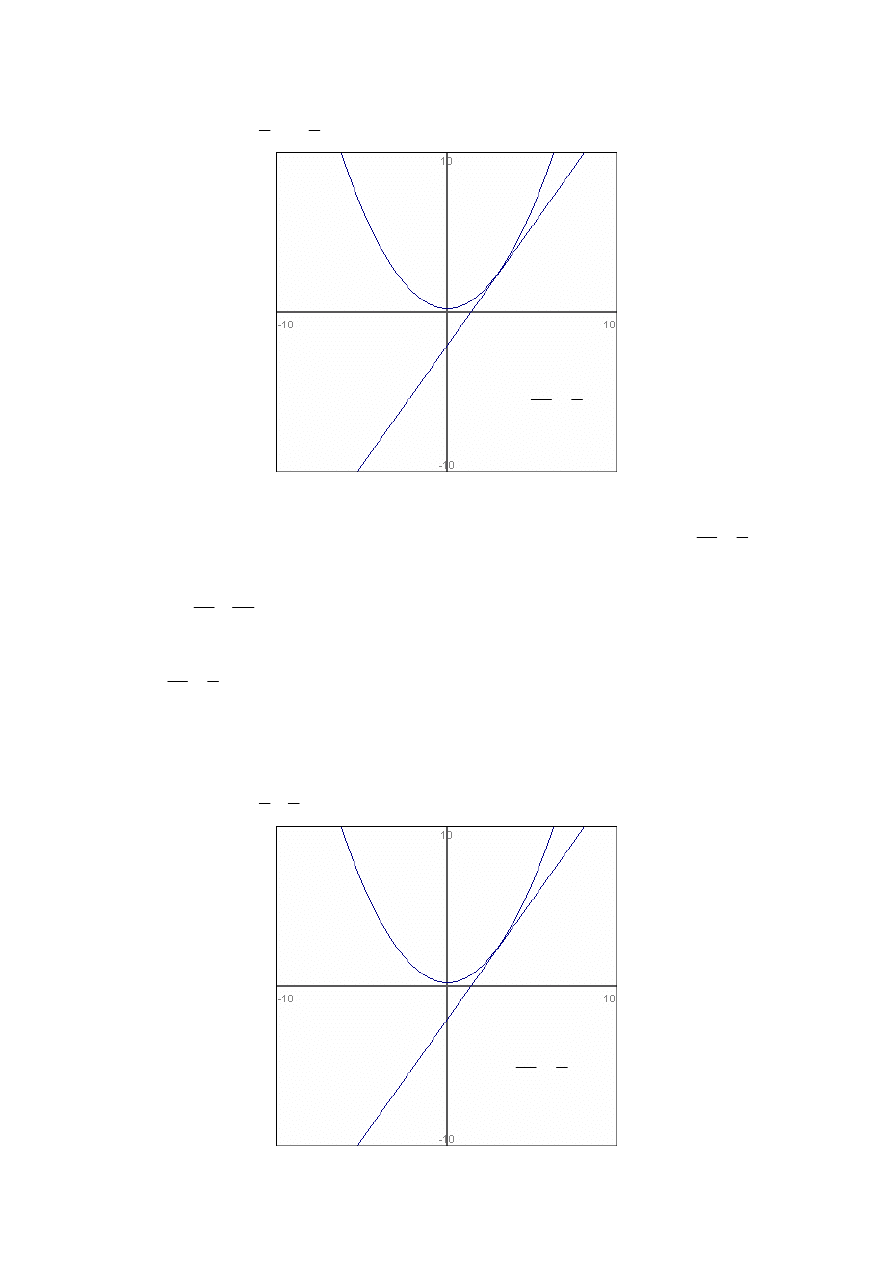
otrzymamy wzór funkcji jednej zmiennej „x” – jest to krawędź powstała przez
przecięcie naszej funkcji
( )
z
y
x
f
=
,
płaszczyzną równoległą do płaszczyzny XZ w
1
0
=
y
(wykres poniżej)
46
wykres
(
)
4
1
4
1
1
,
2
+
=
=
x
y
x
f
interpretacja geometryczna jest analogiczna jak dla funkcji jednej zmiennej; tzn.
x
x
f
2
1
=
∂
∂
jest „przepisem” na tangens kąta zawartego pomiędzy styczną do krzywej
„
(
)
4
4
,
2
0
2
0
y
x
y
x
f
+
=
” (krzywą wyznaczamy poprzez ustalenie - wybranie wartości „y
0
”, np.
tutaj 1
0
=
y
) w punkcie
(
)
0
0
; z
x
, a dodatnią półosią osi X;
y
y
f
2
1
=
∂
∂
np. wybierzmy
1
0
=
x
(tutaj można wybrać dowolną wartość), wówczas
otrzymamy wzór funkcji jednej zmiennej „y” – jest to krawędź powstała przez
przecięcie naszej funkcji
( )
z
y
x
f
=
,
płaszczyzną równoległą do płaszczyzny YZ w
1
0
=
x
(wykres poniżej)
wykres
(
)
2
4
1
4
1
,
1
y
y
x
f
+
=
=
X
(
)
1
;
=
y
x
f
Y
(
)
y
x
f
;
1
=
x
dx
df
tg
2
1
=
=
α
α
y
dy
df
tg
2
1
=
=
β
β
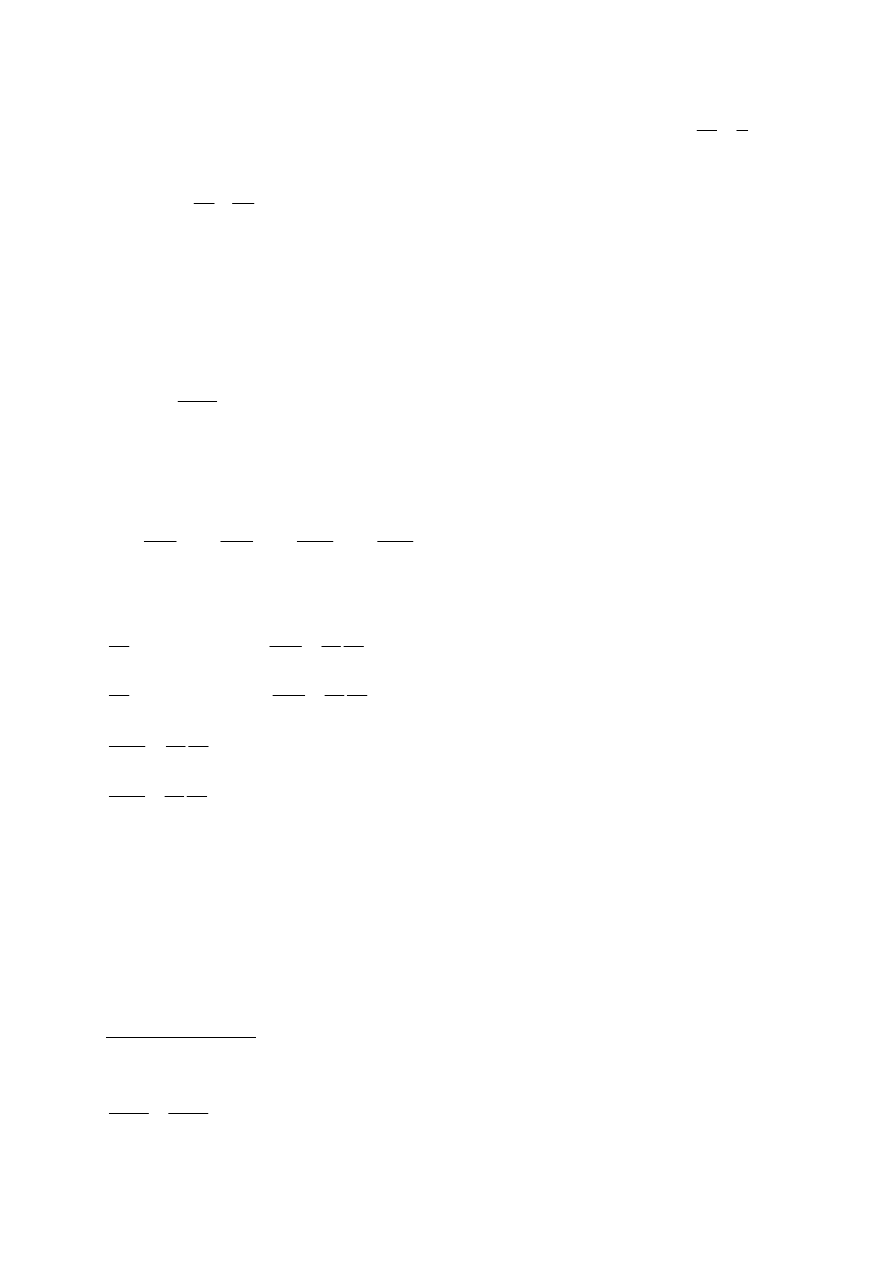
47
interpretacja geometryczna jest analogiczna jak dla funkcji jednej zmiennej; tzn.
y
y
f
2
1
=
∂
∂
jest „przepisem” na tangens kąta zawartego pomiędzy styczną do krzywej
„
(
)
4
4
,
2
2
0
0
y
x
y
x
f
+
=
” ( krzywą wyznaczamy poprzez ustalenie - wybranie wartości „x
0
”, np.
tutaj 1
0
=
x
) w punkcie
(
)
0
0
; z
y
, a dodatnią półosią osi Y;
Ćwiczenia:
Określ wzór pochodnych cząstkowych do poniższych funkcji:
( )
( )
( )
( )
2
2
;
cos
sin
;
sin
cos
;
;
y
x
e
y
x
f
y
x
y
x
f
x
y
y
x
y
x
f
y
x
xy
y
x
f
xy
⋅
=
⋅
=
⋅
−
⋅
=
+
=
6.2 Pochodna cząstkowa wyższych rzędów.
Pochodnymi cząstkowymi drugiego rzędu funkcji
( )
z
y
x
f
=
,
nazywamy funkcje określone
nst.:
x
y
f
y
x
f
y
f
x
f
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
2
2
2
2
2
2
;
;
;
; dwie ostatnie nazywa się również pochodnymi
mieszanymi.
Np.:
( )
2
;
xy
e
y
x
f
=
⇒
⋅
=
∂
∂
2
2
y
e
x
f
xy
4
2
2
2
2
2
2
2
0
y
e
e
y
y
e
x
f
x
x
f
xy
xy
xy
⋅
=
⋅
+
⋅
⋅
=
∂
∂
∂
∂
=
∂
∂
⇒
⋅
=
∂
∂
xy
e
y
f
xy
2
2
2
2
2
2
2
4
2
2
2
2
2
2
2
xy
xy
xy
xy
e
x
y
x
e
x
e
xy
xy
e
y
f
y
y
f
⋅
+
⋅
=
⋅
+
⋅
⋅
=
∂
∂
∂
∂
=
∂
∂
=
∂
∂
∂
y
x
f
y
e
xy
e
y
e
y
xy
e
x
f
y
xy
xy
xy
xy
2
2
2
2
2
2
2
2
3
2
⋅
+
⋅
=
⋅
+
⋅
⋅
=
∂
∂
∂
∂
y
e
xy
e
y
e
xy
y
e
y
f
x
x
y
f
xy
xy
xy
xy
2
2
2
2
2
2
2
2
3
2
⋅
+
⋅
=
⋅
+
⋅
⋅
=
∂
∂
∂
∂
=
∂
∂
∂
Ćwiczenia:
Oblicz pochodne drugiego rzędu (wszystkie) nst. funkcji:
( )
(
)
( )
xy
y
x
f
y
x
y
x
f
sin
;
;
;
3
2
2
=
+
=
6.3 Ekstremum lokalne funkcji dwóch zmiennych.
Warunek konieczny:
Jeżeli funkcja
( )
z
y
x
f
=
;
ma w punkcie
(
)
0
0
0
; y
x
P
=
ekstremum lokalne i istnieją w tym
punkcie obie pochodne cząstkowe pierwszego rzędu, to:
( )
( )
0
0
0
=
∂
∂
=
∂
∂
P
P
y
f
x
f
; przy czym punkt
(
)
0
0
0
; y
x
P
=
nazywamy punktem stacjonarnym.
48
Warunek dostateczny (wystarczający):
Jeżeli istnieją drugie pochodne funkcji
( )
z
y
x
f
=
;
oraz
( )
0
0
0
0
0
2
2
2
2
2
2
0
>
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
P
P
P
P
y
f
x
y
f
y
x
f
x
f
P
W
, to
funkcja
( )
z
y
x
f
=
;
ma w punkcie
(
)
0
0
0
; y
x
P
=
ekstremum lokalne.
Jeżeli
0
2
2
<
∂
∂
x
f
, to funkcja
( )
z
y
x
f
=
;
ma w punkcie
(
)
0
0
0
; y
x
P
=
maksimum
Jeżeli
0
2
2
>
∂
∂
x
f
, to funkcja
( )
z
y
x
f
=
;
ma w punkcie
(
)
0
0
0
; y
x
P
=
minimum
Jeżeli
( )
0
0
<
P
W
, to ekstremum nie istnieje
Jeżeli
( )
0
0
=
P
W
, to sytuacja jest nierozstrzygnięta
Przykład
: zbadać ekstremum lokalne funkcji
( )
x
y
x
y
x
f
4
;
2
4
−
+
=
1. stosujemy warunek konieczny istnienia ekstremum:
0
4
4
3
=
−
=
∂
∂
x
x
f
i
0
2
=
=
∂
∂
y
y
f
(
) ( )
0
;
1
;
0
2
0
4
4
0
0
0
3
=
=
⇒
=
=
−
⇒
y
x
P
y
x
2. stosujemy warunek dostateczny istnienia ekstremum:
( )
( )
12
12
0
;
1
2
2
2
0
=
=
∂
∂
x
x
f
P
( )
( )
2
2
0
;
1
2
2
0
=
=
∂
∂
P
y
f
( )
( )
0
0
0
;
1
2
0
=
=
∂
∂
∂
P
y
x
f
( )
( )
0
0
0
;
1
2
0
=
=
∂
∂
∂
P
x
y
f
( )
( )
0
24
2
0
0
12
0
;
1
0
>
=
=
= W
P
W
, zatem w punkcie
( )
0
;
1
0
=
P
istnieje ekstremum lokalne.
( )
( )
12
12
0
;
1
2
2
2
0
=
=
∂
∂
x
x
f
P
>0, czyli jest to minimum lokalne.
Ćwiczenia:
Zbadaj czy istnieją ekstrema lokalne oraz podaj ich charakter nst. funkcji:
( )
2
2
4
4
2
4
2
;
y
xy
x
y
x
y
x
f
−
+
−
+
=
( )
(
)
( )
( )
( )
y
x
xy
x
y
x
f
y
x
xy
y
x
f
x
xy
y
x
y
x
f
y
x
e
y
x
f
x
12
15
3
;
20
50
;
48
6
;
;
2
3
2
3
2
−
−
+
=
+
+
=
−
−
+
=
+
=
−