
WPROWADZENIE
DO SZTUCZNEJ INTELIGENCJI
POLITECHNIKA WARSZAWSKA
WYDZIAŁ MECHANICZNY ENERGETYKI I LOTNICTWA
MEL
MEL
NS 586
Dr in
ż
. Franciszek Dul
© F.A. Dul 2007

9. WNIOSKOWANIE W LOGICE
PIERWSZEGO RZĘDU
© F.A. Dul 2007
PIERWSZEGO RZĘDU

Wnioskowanie w logice pierwszego rz
ę
du
Poka
ż
emy, w jaki sposób uogólni
ć
algorytmy wnioskowania rachunku
zda
ń
tak, aby wnioskowa
ć
w logice
© F.A. Dul 2007
zda
ń
tak, aby wnioskowa
ć
w logice
pierwszego rz
ę
du.

• Sprowadzenie wnioskowania w logice pierwszego rz
ę
du
do wnioskowania w rachunku zda
ń
• Unifikacja
• Uogólniona reguła odrywania (modus ponens)
• Wnioskowanie w przód i wstecz
• Rezolucja
• Automatyczne dowodzenie twierdze
ń
Plan rozdziału
© F.A. Dul 2007

Jak wnioskowa
ć
z kwantyfikatorami...
W j
ę
zyku logiki pierwszego rz
ę
du mo
ż
na opisa
ć
ś
wiat w sposób
ś
cisły, a zarazem bardzo zwi
ę
zły.
Zwi
ę
zło
ść
opisu osi
ą
ga si
ę
poprzez u
ż
ycie obiektów,
relacji mi
ę
dzy nimi, funkcji oraz
kwantyfikatorów
.
Wyst
ę
powanie kwantyfikatorów uniemo
ż
liwia
jednak prowadzenie wnioskowania w taki sposób,
jak w rachunku zda
ń
.
©
F.A. Dul 2007
jak w rachunku zda
ń
.
Zdania zapisane w j
ę
zyku logiki pierwszego rz
ę
du
musz
ą
wi
ę
c najpierw by
ć
przekształcone do postaci
umo
ż
liwiaj
ą
cej wnioskowanie.
Zdania FOL mo
ż
na przekształci
ć
do postaci
rachunku zda
ń
, albo te
ż
do takich postaci, które
umo
ż
liwiaj
ą
wnioskowanie bezpo
ś
rednie w FOL
za pomoc
ą
przekształconych metod wnioskowania.

9.1. Sprowadzenie wnioskowania logiki pierwszego
rz
ę
du do wnioskowania w rachunku zda
ń
Wnioskowanie w logice pierwszego rz
ę
du mo
ż
e by
ć
sprowadzone do wnioskowania w rachunku zda
ń
.
Idea: nale
ż
y zast
ą
pi
ć
zdania kwantyfikowne przez zbiór zda
ń
bez kwantyfikatorów.
Zbiór zda
ń
zdekwantyfikowanych powinien by
ć
równowa
ż
ny
wyj
ś
ciowemu zbiorowi zda
ń
kwantyfikowanych lub co najmniej
spełnialny.
© F.A. Dul 2007
• Eliminacja kwantyfikatorów ogólnych
Zast
ą
pienie zmiennej przez
symbol podstawowy
(ground term)
• Eliminacja kwantyfikatorów szczegółowych
skolemizacja
spełnialny.

Podstawienie ogólne (universal instantiation, UI)
Ka
ż
de podstawienie do zdania z kwantyfikatorem ogólnym
pewnego wyra
ż
enia za zmienn
ą
kwantyfikowan
ą
wynika
z tego zdania, tj.
∀
v
α
—————————
Subst( {v/g},
α
)
dla ka
ż
dej zmiennej v i ka
ż
dego wyra
ż
enia g.
Subst(
θ
,
α
)
= podstawienie
θ
do
α
.
9.1. Sprowadzenie FOL do PL
© F.A. Dul 2007
Przykład Podstawienie do zdania
∀
x Król(x)
∧
Chciwy(x)
⇒
Zły(x)
wyra
ż
e
ń
: {x/Jan}, {x/Ryszard} i {x/Ojciec(Jan)} daje zdania:
Król(Jan)
∧
Chciwy(Jan)
⇒
Zły(Jan)
Król(Ryszard)
∧
Chciwy(Ryszard)
⇒
Zły(Ryszard)
Król(Ojciec(Jan))
∧
Chciwy(Ojciec(Jan))
⇒
Zły(Ojciec(Jan))
Zdanie z kwantyfikatorem ogólnym jest równowa
ż
ne zbiorowi
zda
ń
z podstawieniami
wszystkich
obiektów z dziedziny.

9.1. Sprowadzenie FOL do PL
Podstawienie szczegółowe (existential instantiation, EI)
Dla ka
ż
dego zdania
α
, zmiennej v i stałej k która
nie wyst
ę
puje
w bazie wiedzy KB zachodzi wynikanie
∃
v
α
—————————
Subst( {v/k},
α
)
Przykład Podstawienie stałej C
1
do zdania
∃
x Korona(x)
∧
NaGłowie(x,Jan)
© F.A. Dul 2007
∃
x Korona(x)
∧
NaGłowie(x,Jan)
daje zdanie
Korona(C1)
∧
NaGłowie(C1,Jan)
Stała C
1
nazywa si
ę
stał
ą
Skolema
, za
ś
procedura jej
podstawienia –
skolemizacj
ą
.
Warunek niewyst
ę
powania w bazie KB stałej Skolema której
chcemy u
ż
y
ć
jest bardzo wa
ż
ny!
Niespełnienie tego warunku powoduje,
ż
e relacja wynikania
zbioru zda
ń
skolemizowanych z bazy KB nie jest spełniona.

9.1. Sprowadzenie FOL do PL
Ró
ż
nice pomi
ę
dzy podstawieniami: ogólnym (UI)
oraz szczegółowym (EI)
• Podstawienie ogólne (UI) mo
ż
e by
ć
wykonane wielokrotnie
w celu
dodania
nowych zda
ń
do bazy wiedzy.
Nowa baza wiedzy KB jest równowa
ż
na logicznie bazie
starej.
• Podstawienie szczegółowe (EI) mo
ż
e by
ć
wykonane
tylko raz
, w celu eliminacji kwantyfikatora szczegółowego.
© F.A. Dul 2007
tylko raz
, w celu eliminacji kwantyfikatora szczegółowego.
Nowa baza wiedzy KB
nie jest
równowa
ż
na logicznie bazie
starej, ale jest spełnialna (tj. prawdziwa dla
pewnych
modeli)
je
ż
eli baza wyj
ś
ciowa była spełnialna.

9.1. Sprowadzenie FOL do PL
Sprowadzenie wnioskowania FOL do wnioskowania
w rachunku zda
ń
Załó
ż
my,
ż
e baza wiedzy KB zawiera nast
ę
puj
ą
ce zdania
i wyra
ż
enia:
Wykonanie
wszystkich
mo
ż
liwych podstawie
ń
, tutaj:
∀
x Król(x)
∧
Chciwy(x)
⇒
Zły(x)
Król(Jan)
Chciwy(Jan)
Brat(Ryszard,Jan)
© F.A. Dul 2007
Król(Jan)
∧
Chciwy(Jan)
⇒
Zły(Jan)
Król(Ryszard)
∧
Chciwy(Ryszard)
⇒
Zły(Ryszard)
Król(Jan)
Chciwy(Jan)
Brat(Ryszard,Jan)
{x/Jan}, {x/Ryszard}
daje w wyniku now
ą
baz
ę
KB:
Nowa baza wiedzy jest ju
ż
czysto
predykatowa
(KB PL)
– nie ma w niej kwantyfikatorów.
Predykatami s
ą
:
Król(Jan), Chciwy(Jan), Zły(Jan),
etc.

9.1. Sprowadzenie FOL do PL
• Ka
ż
da baza wiedzy zapisana w logice pierwszego rz
ę
du
(KB FOL) mo
ż
e by
ć
sprowadzona do bazy predykatowej
(KB PL) w taki sposób,
ż
e wynikanie jest zachowane, tj,
Zdanie wynika z przekształconej bazy KB wtedy
i tylko wtedy, gdy wynika z bazy pierwotnej.
• Zasada: przedstawienie w postaci predykatowej bazy
wiedzy KB PL, zapyta
ń
, rezolucji, odpowiedzi.
• Problem: funkcje generuj
ą
niesko
ń
czone ci
ą
gi wyra
ż
e
ń
, np.
© F.A. Dul 2007
• Problem: funkcje generuj
ą
niesko
ń
czone ci
ą
gi wyra
ż
e
ń
, np.
Ojciec(Ojciec(Ojciec(Jan)))...
Twierdzenie (Turing, Church 1936) Wynikanie w logice
pierwszego rz
ę
du jest
półrozstrzygalne
(semidecidable).
Oznacza to,
ż
e :
istniej
ą
algorytmy
które daj
ą
odpowied
ź
twierdz
ą
c
ą
na ka
ż
de
zdanie wynikaj
ą
ce z bazy KB FOL, ale
nie ma algorytmów
które odpowiadaj
ą
przecz
ą
co na ka
ż
de
zdanie nie wynikaj
ą
ce z bazy KB FOL.

9.1. Sprowadzenie FOL do PL
Problemy ze sprowadzeniem FOL do PL
• Sprowadzenie bazy FOL do postaci predykatowej prowadzi
do utworzenia wielu nieistotnych zda
ń
.
Przykład Z bazy
∀
x Król(x)
∧
Chciwy(x)
⇒
Zły(x)
Król(Jan)
∀
y Chciwy(y)
Brat(Ryszard,Jan)
wynika w sposób oczywisty zdanie
© F.A. Dul 2007
wynika w sposób oczywisty zdanie
Zły(Jan),
ale równie
ż
wiele zda
ń
nieistotnych, np.
Zły(Ryszard).
• Problem liczby podstawie
ń
.
Dla p zda
ń
k-krotnych i n stałych istnieje
p·n
k
podstawie
ń
.

Wnioskowanie w bazie predykatowej
Przekształcenie bazy zapisanej w j
ę
zyku logiki
pierwszego rz
ę
du do bazy predykatowej pozwala
prowadzi
ć
wnioskowanie metodami rachunku zda
ń
.
Jednak takie post
ę
powanie mo
ż
e by
ć
wysoce
nieefektywne, gdy
ż
eliminacja kwantyfikatorów
ogólnych mo
ż
e spowodowa
ć
lawinowy wzrost liczby
zda
ń
w bazie przekształconej.
©
F.A. Dul 2007
zda
ń
w bazie przekształconej.
Lepszym rozwi
ą
zaniem jest
modyfikacja algorytmów
wnioskowania
w taki sposób, aby mo
ż
na było
prowadzi
ć
wnioskowanie bezpo
ś
rednio w bazie FOL.
Osi
ą
ga si
ę
to poprzez zastosowanie operacji
podniesienia i unifikacji oraz wykorzystanie
uogólnionej reguły odrywania i algorytmu eliminacji
(rezolucji).

9.2. Podniesienie i unifikacja
Zamiast przekształca
ć
baz
ę
FOL do postaci PL, mo
ż
na
przedefiniowa
ć
reguły wnioskowania tak, aby były słuszne
dla logiki pierwszego rz
ę
du u
ż
ywaj
ą
cej kwantyfikatorów:
ogólnych i szczegółowych.
Unifikacja
jest to procedura rekurencyjna pozwalaj
ą
ca
sprawdzi
ć
, czy istnieje podstawienie sprowadzaj
ą
ce dwa
wyra
ż
enia do takiej samej postaci.
Unifikacja pozwala cz
ę
sto istotnie zredukowa
ć
liczb
ę
zda
ń
© F.A. Dul 2007
Unifikacja pozwala cz
ę
sto istotnie zredukowa
ć
liczb
ę
zda
ń
zawartych w bazie wiedzy KB.
Podniesienie
(lifting) - wykonanie podstawie
ń
które pozwalaj
ą
prowadzi
ć
wnioskowanie w bazie FOL.
Przykład liftingu - uogólniona reguła odrywania (Generalized
Modus Ponens).

9.2. Podniesienie i unifikacja
Unifikacja
Unifikacja
jest to procedura rekurencyjna pozwalaj
ą
ca
sprawdzi
ć
, czy istnieje podstawienie sprowadzaj
ą
ce dwa
wyra
ż
enia do takiej samej postaci.
Przykłady:
• Kobieta(Anna)
i
M
ęż
czyzna(Jan)
nie unifikuj
ą
si
ę
;
• Kobieta(Anna)
i
Kobieta(Anna)
unifikuj
ą
si
ę
trywialnie;
• Kobieta(Anna)
i
Kobieta(Maria)
nie unifikuj
ą
si
ę
, gdy
ż
maj
ą
© F.A. Dul 2007
• Kobieta(Anna)
i
Kobieta(Maria)
nie unifikuj
ą
si
ę
, gdy
ż
maj
ą
ró
ż
ne argumenty;
• Król(x)
i
Chciwy(x)
oraz
Król(Jan)
i
Chciwy(y).
Podstawienie
α
= { x/Jan, y/Jan }
unifikuje obie pary zda
ń
.
Unifikacja zda
ń
α
,
β
za pomoc
ą
podstawienia
θ
mo
ż
e by
ć
zdefiniowana nast
ę
puj
ą
co
Unify(
α
,
β
) =
θ
je
ż
eli Subst(
θ
,
α
) = Subst(
θ
,
β
)

Unifikacja
p
q
θθθθ
Zna(Jan,x)
Zna(Jan,Maria)
9.2. Podniesienie i unifikacja
Przykłady problemów unifikacji:
© F.A. Dul 2007

Unifikacja
p
q
θθθθ
Zna(Jan,x)
Zna(Jan,Maria)
{x/Maria}
9.2. Podniesienie i unifikacja
Przykłady problemów unifikacji:
© F.A. Dul 2007

Unifikacja
p
q
θθθθ
Zna(Jan,x)
Zna(Jan,Maria)
{x/Maria}
Zna(Jan,x)
Zna(y,OJ)
9.2. Podniesienie i unifikacja
Przykłady problemów unifikacji:
© F.A. Dul 2007

Unifikacja
p
q
θθθθ
Zna(Jan,x)
Zna(Jan,Maria)
{x/Maria}
Zna(Jan,x)
Zna(y,OJ)
{x/OJ,y/Jan}
9.2. Podniesienie i unifikacja
Przykłady problemów unifikacji:
© F.A. Dul 2007

Unifikacja
p
q
θθθθ
Zna(Jan,x)
Zna(Jan,Maria)
{x/Maria}
Zna(Jan,x)
Zna(y,OJ)
{x/OJ,y/Jan}
Zna(Jan,x)
Zna(y,Matka(y))
9.2. Podniesienie i unifikacja
Przykłady problemów unifikacji:
© F.A. Dul 2007

Unifikacja
p
q
θθθθ
Zna(Jan,x)
Zna(Jan,Maria)
{x/Maria}
Zna(Jan,x)
Zna(y,OJ)
{x/OJ,y/Jan}
Zna(Jan,x)
Zna(y,Matka(y))
{y/Jan,x/Matka(Jan)}
9.2. Podniesienie i unifikacja
Przykłady problemów unifikacji:
© F.A. Dul 2007

Unifikacja
p
q
θθθθ
Zna(Jan,x)
Zna(Jan,Maria)
{x/Maria}
Zna(Jan,x)
Zna(y,OJ)
{x/OJ,y/Jan}
Zna(Jan,x)
Zna(y,Matka(y))
{y/Jan,x/Matka(Jan)}
Zna(Jan,x)
Zna(x,OJ)
9.2. Podniesienie i unifikacja
Przykłady problemów unifikacji:
© F.A. Dul 2007

Unifikacja
p
q
θθθθ
Zna(Jan,x)
Zna(Jan,Maria)
{x/Maria}
Zna(Jan,x)
Zna(y,OJ)
{x/OJ,y/Jan}
Zna(Jan,x)
Zna(y,Matka(y))
{y/Jan,x/Matka(Jan)}
Zna(Jan,x)
Zna(x,OJ)
{brak}
9.2. Podniesienie i unifikacja
Przykłady problemów unifikacji:
© F.A. Dul 2007
Nie mo
ż
na podstawi
ć
{x/Jan}
bo otrzymamy
Zna(Jan,Jan)
niezgodne ze
Zna(Jan,OJ)
- wyst
ą
piło nakładanie si
ę
nazw
zmiennych.
Aby usun
ąć
konflikt nazw zast
ę
pujemy zmienn
ą
x w jednym
ze zda
ń
(np. w drugim) inn
ą
zmienn
ą
, np.
z
17
. Otrzymujemy
Zna(Jan,x) , Zna(z
17
,OJ)
Jest to
standaryzacja
która eliminuje konflikty nazw.

Unifikacja
• Aby zunifikowa
ć
Zna(Jan,x)
oraz
Zna(y,z),
mo
ż
na u
ż
y
ć
ró
ż
nych podstawie
ń
(unifikatorów), np.:
α
= { y/Jan, x/z }
→
Zna(Jan,z)
oraz
Zna(Jan,z),
lub
α
= { y/Jan, x/Jan, z/Jan }
→
Zna(Jan,Jan)
oraz
Zna(Jan,Jan)
9.2. Podniesienie i unifikacja
Przykłady problemów unifikacji:
© F.A. Dul 2007
→
Zna(Jan,Jan)
oraz
Zna(Jan,Jan)
• Pierwszy unifikator jest
ogólniejszy
ni
ż
drugi.
• Istnieje jedyny
unifikator najogólniejszy
(most general
unificator, MGU) okre
ś
lony z dokładno
ś
ci
ą
do zmiany
nazw zmiennych.
MGU = { y/Jan, x/z }

Algorytm unifikacji
9.2. Podniesienie i unifikacja
© F.A. Dul 2007

Uogólniona reguła odrywania (Generalized Modus
Ponens)
p
1
', p
2
', … , p
n
', ( p
1
∧
p
2
∧
…
∧
p
n
⇒
q)
Subst(
θ
,q)
gdzie Subst(
θ
,p
i
’) = Subst(
θ
,p
i
) dla ka
ż
dego i.
9.2. Podniesienie i unifikacja
Przykład
p
1
'
oznacza
Król(Jan)
p
1
oznacza
Król(x)
p '
oznacza
Chciwy(y)
p
oznacza
Chciwy(x)
© F.A. Dul 2007
p
2
'
oznacza
Chciwy(y)
p
2
oznacza
Chciwy(x)
θ
oznacza
{x/Jan,y/Jan}
q
oznacza
Zły(x)
Subst(
θ
,q)
oznacza
Zły(Jan)
• Uogólniona reguła odrywania (GMP) jest u
ż
ywana dla
bazy wiedzy zło
ż
onej z
klauzul Horna
(tj. zawieraj
ą
cych
dokładnie jeden
literał niezanegowany)
• Zakłada si
ę
,
ż
e wszystkie zmienne s
ą
kwantyfikowane
ogólnie.

Poprawno
ść
uogólnionej reguły odrywania
p
1
', p
2
', … , p
n
', ( p
1
∧
p
2
∧
…
∧
p
n
⇒
q) l= Subst(
θ
,q)
przy zało
ż
eniu,
ż
e Subst(
θ
,p
i
’) = Subst(
θ
,p
i
) dla ka
ż
dego i.
9.2. Podniesienie i unifikacja
Nale
ż
y wykaza
ć
,
ż
e
Lemat Dla ka
ż
dego zdania p zachodzi p
l=
Subst(
θ
,p)
poprzez podstawienie uniwersalne.
Dowód poprawno
ś
ci GMP (
oznaczenie: Subst(
θ
,p)
≡
p
θ
)
© F.A. Dul 2007
• (p
1
∧
…
∧
p
n
⇒
q)
l=
(p
1
∧
…
∧
p
n
⇒
q)
θ
(z lematu)
• (p
1
∧
…
∧
p
n
⇒
q)
θ
= (p
1
θ ∧
…
∧
p
n
θ
⇒
q
θ
)
• p
1
', …, p
n
'
l=
p
1
'
∧
…
∧
p
n
'
• p
1
'
∧
…
∧
p
n
'
l=
p
1
'
θ ∧
…
∧
p
n
'
θ
(z lematu)
• st
ą
d, i na mocy zwykłej reguły odrywana wynika
p
1
', p
2
', … , p
n
', ( p
1
∧
p
2
∧
…
∧
p
n
⇒
q)
l=
q
θ
Dowód poprawno
ś
ci GMP (
oznaczenie: Subst(
θ
,p)
≡
p
θ
)

9.3. Algorytmy FOL wnioskowania w przód i wstecz
Algorytmy wnioskowania w przód i wstecz dla FOL i logiki
zda
ń
s
ą
identyczne.
Wnioskowanie w przód dla KB FOL
• Zaczynamy od zda
ń
w bazie KB FOL opisuj
ą
cych fakty;
• Stosujemy uogólnion
ą
reguł
ę
odrywania dla FOL
do wyprowadzenia nowych zda
ń
;
• Dodajemy nowe zdania do bazy KB FOL;
• Wnioskowanie ko
ń
czymy, je
ż
eli wyprowadzimy udowadnia-
© F.A. Dul 2007
Wnioskowanie wstecz dla KB FOL
• Zaczynamy od zdania, które jest zapytaniem do KB FOL;
• Stosujemy uogólnion
ą
reguł
ę
odrywania dla FOL
znajduj
ą
c zdania z których wynika udowadniane zdanie;
• Wnioskowanie ko
ń
czymy, je
ż
eli przesłankami zdania
aktualnie dowodzonego b
ę
d
ą
zdania bazy KB FOL
które opisuj
ą
fakty dowiedzione;
• Wnioskowanie ko
ń
czymy, je
ż
eli wyprowadzimy udowadnia-
ne zdanie lub gdy dalsze wnioskowanie nie jest mo
ż
liwe;

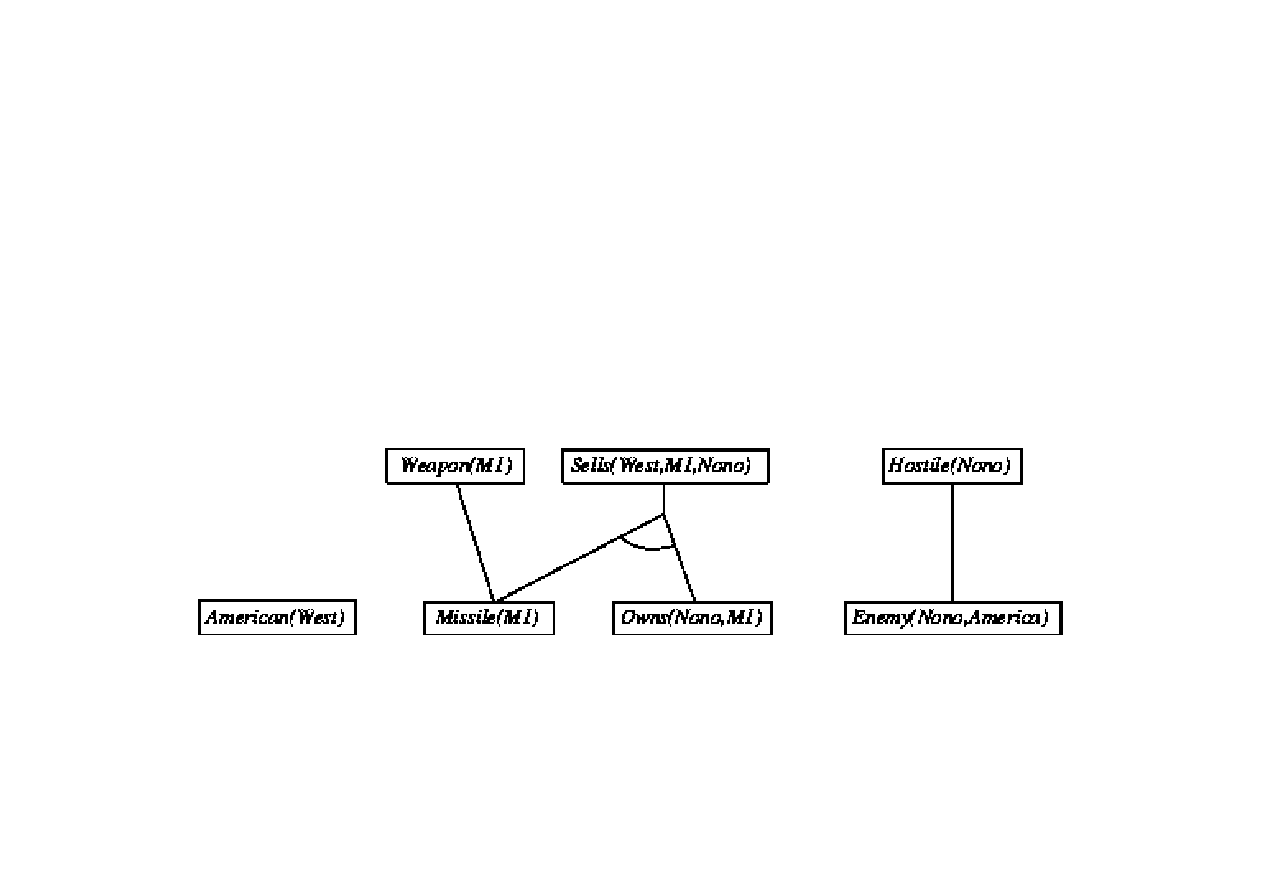
Przykład wnioskowania z bazy wiedzy FOL
9.3. Algorytmy FOL wnioskowania w przód i wstecz
• Prawo USA stanowi,
ż
e przest
ę
pstwem jest sprzeda
ż
broni do krajów wrogich.
• Kraj Nono, wróg USA, posiada pewn
ą
liczb
ę
rakiet.
• Wszystkie te rakiety zostały sprzedane Nono przez
niejakiego pułkownika Westa.
• Pułkownik West jest Amerykaninem.
Baza wiedzy KB FOL zawiera nast
ę
puj
ą
ce zdania:
© F.A. Dul 2007
• Pułkownik West jest Amerykaninem.
Dowie
ść
,
ż
e w
ś
wietle prawa ameryka
ń
skiego pułkownik
West jest przest
ę
pc
ą
.

Przykład wnioskowania z bazy wiedzy FOL
9.3. Algorytmy FOL wnioskowania w przód i wstecz
Baza wiedzy w postaci zda
ń
FOL:
... jest przest
ę
pstwem gdy Amerykanin sprzedaje bro
ń
krajom wrogim:
American(x
∧
Sells(x,y,z) )
∧
Weapon(y)
∧
Hostile(z)
⇒
Criminal(x)
Nono … posiada pewn
ą
liczb
ę
rakiet, tj.,
∃
x Owns(Nono,x)
∧
Missile(x)
Owns(Nono,M
1
) i Missile(M
1
)
… wszystkie rakiety zostały sprzedanie Nono prze pułkownika Westa
Missile(x)
∧
Owns(Nono,x)
⇒
Sells(West,x,Nono)
© F.A. Dul 2007
Missile(x)
∧
Owns(Nono,x)
⇒
Sells(West,x,Nono)
Rakiety s
ą
broni
ą
:
Missile(x)
⇒
Weapon(x)
Wróg Ameryki jest wrogiem:
Enemy(x,America)
⇒
Hostile(x)
West jest Amerykaninem …
American(West)
Kraj Nono, wróg Ameryki …
Enemy(Nono,America)

Algorytm wnioskowania w przód
9.3. Algorytmy FOL wnioskowania w przód i wstecz
© F.A. Dul 2007

Dowód poprzez wnioskowanie w przód
9.3. Algorytmy FOL wnioskowania w przód i wstecz
© F.A. Dul 2007
Dowód poprzez wnioskowanie w przód
9.3. Algorytmy FOL wnioskowania w przód i wstecz
© F.A. Dul 2007
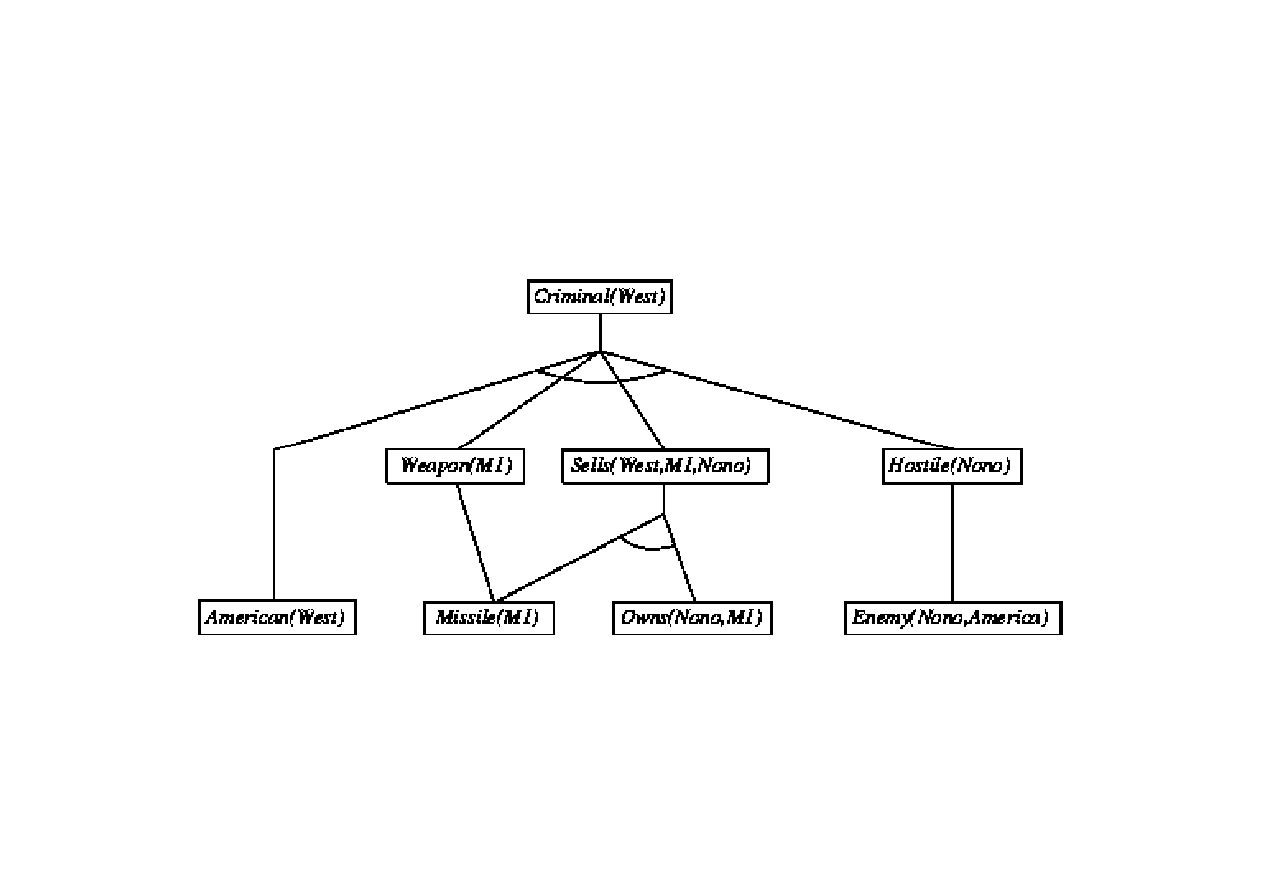
Dowód poprzez wnioskowanie w przód
9.3. Algorytmy FOL wnioskowania w przód i wstecz
© F.A. Dul 2007

Własno
ś
ci wnioskowania w przód
9.3. Algorytmy FOL wnioskowania w przód i wstecz
• Wnioskowanie w przód jest poprawne i zupełne dla bazy
w postaci klauzul Horna pierwszego rz
ę
du.
• Wnioskowanie w przód dla klauzuli Horna pierwszego
rz
ę
du
nie zawieraj
ą
cych funkcji
wymaga sko
ń
czonej
liczby kroków.
• Wnioskowanie w przód w przypadku ogólnym mo
ż
e si
ę
nie zako
ń
czy
ć
je
ż
eli zapytanie nie wynika z bazy FOL.
• Nie mo
ż
na temu zaradzi
ć
; wynikanie z klauzulami Horna
© F.A. Dul 2007
• Nie mo
ż
na temu zaradzi
ć
; wynikanie z klauzulami Horna
pierwszego rz
ę
du jest półrozstrzygalne (patrz twierdzenie
Turinga-Churcha).

Efektywno
ść
wnioskowania w przód
9.3. Algorytmy FOL wnioskowania w przód i wstecz
• Przyrostowe wnioskowanie w przód nie musi
dopasowywa
ć
reguł w k-tym kroku je
ż
eli w kroku k-1
nie została dodana nowa przesłanka.
• Dopasowanie reguł nast
ę
puje wtedy, gdy przesłanka
zawiera nowo dodany literał pozytywny.
• Dopasowanie jest kosztowne.
• Indeksowanie
bazy wiedzy pozwala uzyska
ć
informacje
o znanych faktach kosztem O(1).
© F.A. Dul 2007
• Indeksowanie
bazy wiedzy pozwala uzyska
ć
informacje
o znanych faktach kosztem O(1).
Np. zapytanie Missile(x) zwraca Missile(M
1
).
• Dopasowanie przesłanek do znanych faktów jest
zadaniem NP-hard.
• Wnioskowanie w przód jest szeroko u
ż
ywane
w
dedukcyjnych bazach wiedzy
.
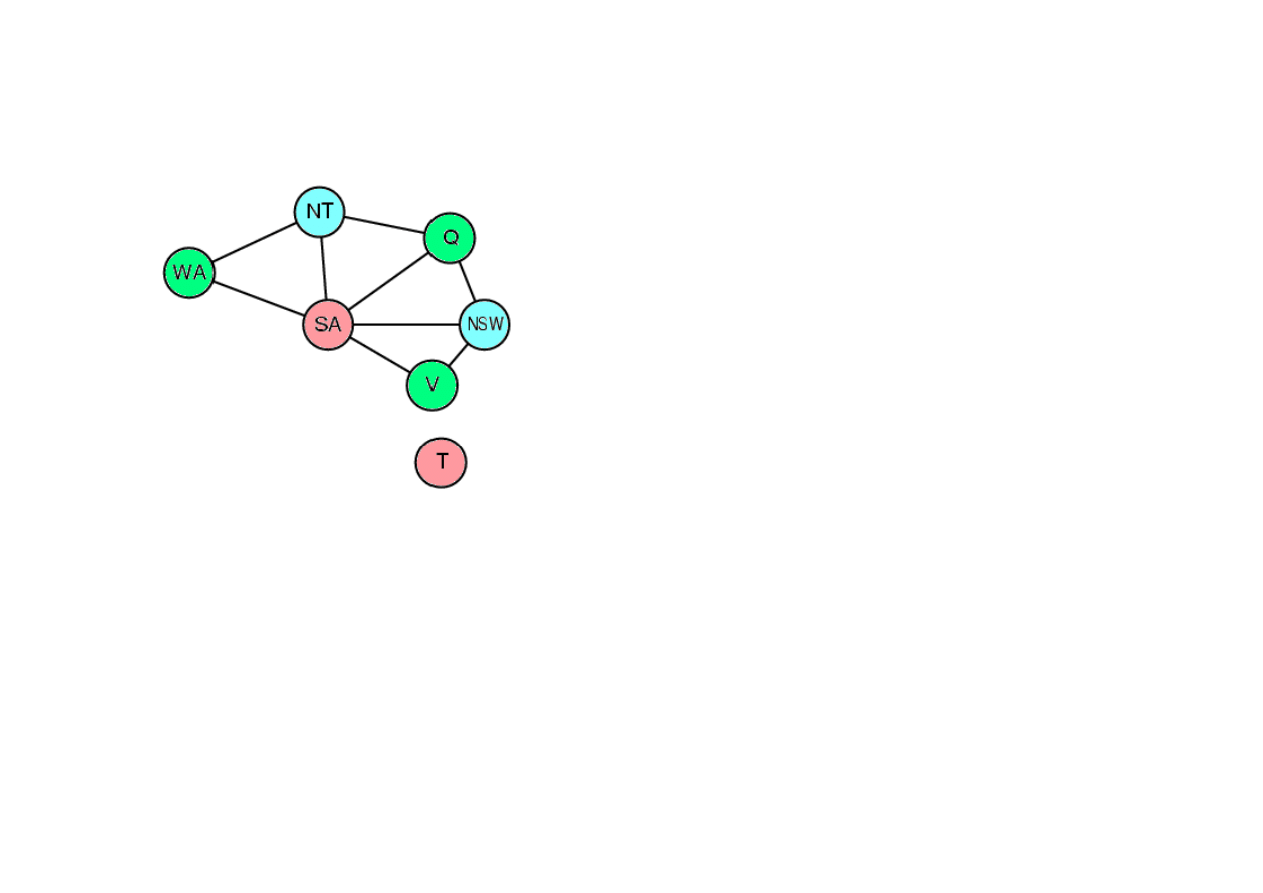
Przykład zadania trudno dopasowalnego
9.3. Algorytmy FOL wnioskowania w przód i wstecz
Diff(wa,nt)
∧
Diff(wa,sa)
∧
Diff(nt,q)
∧
Diff(nt,sa)
∧
Diff(q,nsw)
∧
Diff(q,sa)
∧
Diff(nsw,v)
∧
Diff(nsw,sa)
∧
Diff(v,sa)
⇒
Colorable()
Diff(Red,Blue)
Diff (Red,Green)
Diff(Green,Red) Diff(Green,Blue)
© F.A. Dul 2007
• Colorable()
wynika z bazy wiedzy KB FOL wtedy i tylko
wtedy gdy zadanie poszukiwania z ograniczeniami
(CSP) ma rozwi
ą
zanie.
• Zadanie CSP zawiera zadanie 3SAT jako przypadek
szczególny, zatem dopasowanie jest zadaniem NP-hard.
Diff(Blue,Red)
Diff(Blue,Green)

Algorytm wnioskowania wstecz
9.3. Algorytmy FOL wnioskowania w przód i wstecz
© F.A. Dul 2007
Subst( Compose(
α
1
,
α
2
) , p) = Subst(
α
2
,Subst(
α
1
, p))

Dowód poprzez wnioskowanie wstecz
9.3. Algorytmy FOL wnioskowania w przód i wstecz
© F.A. Dul 2007
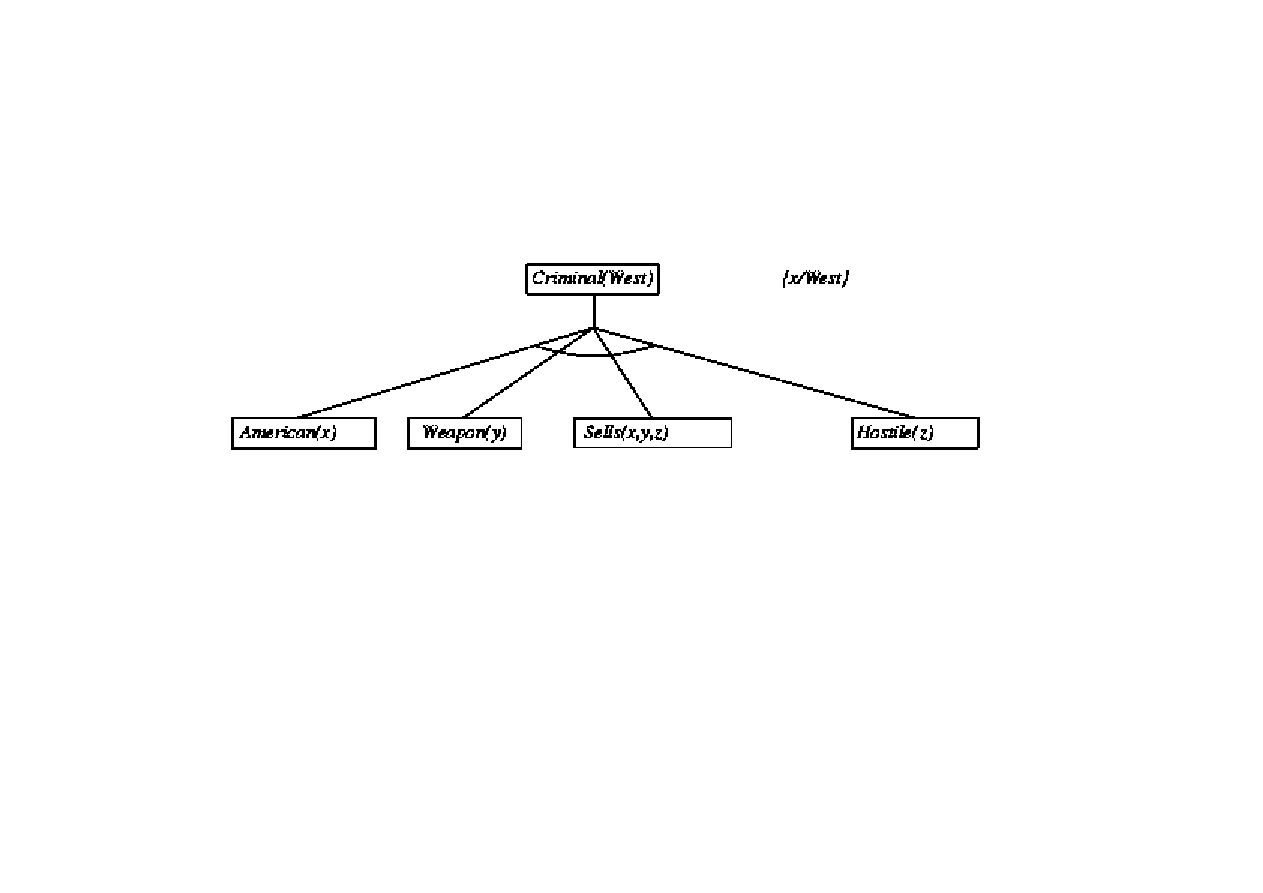
Dowód poprzez wnioskowanie wstecz
9.3. Algorytmy FOL wnioskowania w przód i wstecz
© F.A. Dul 2007
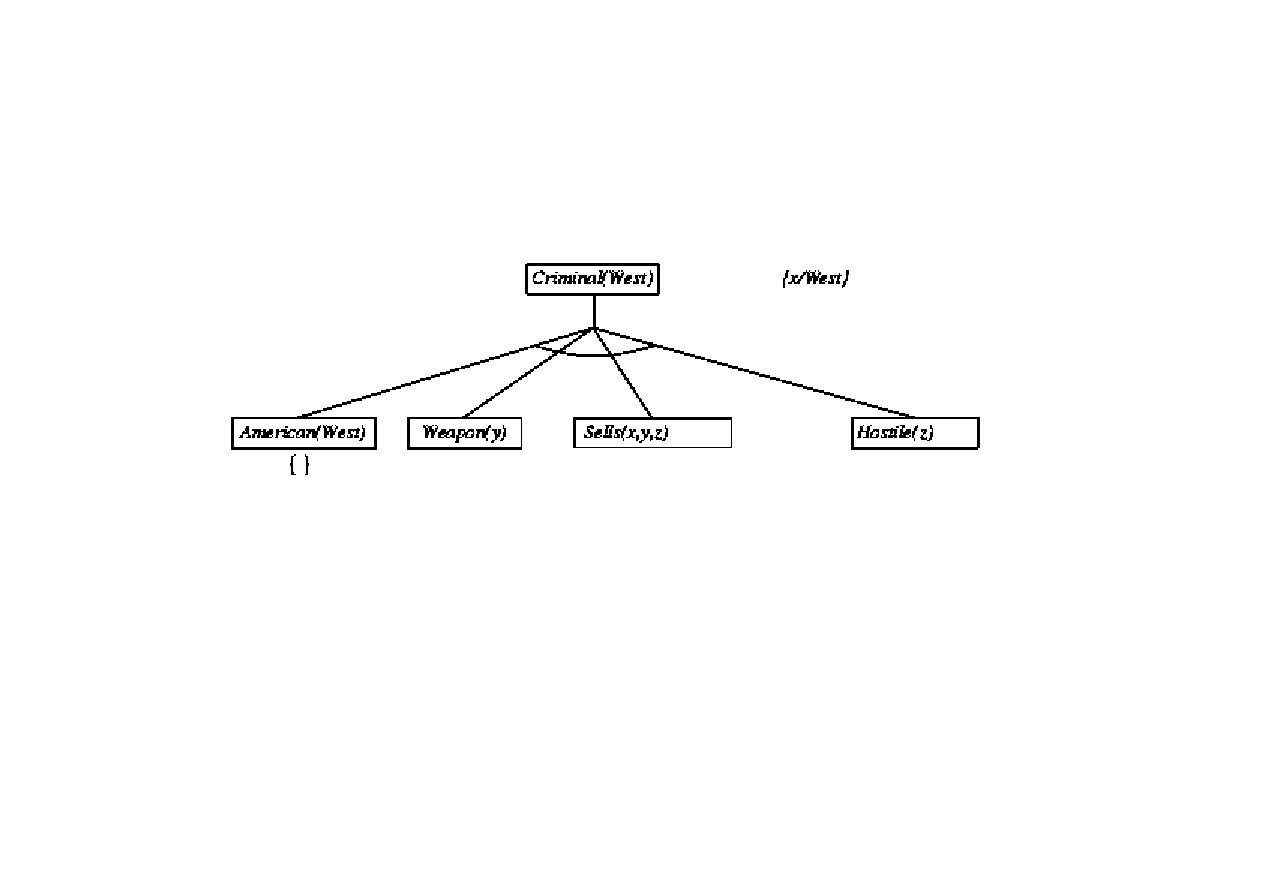
Dowód poprzez wnioskowanie wstecz
9.3. Algorytmy FOL wnioskowania w przód i wstecz
© F.A. Dul 2007
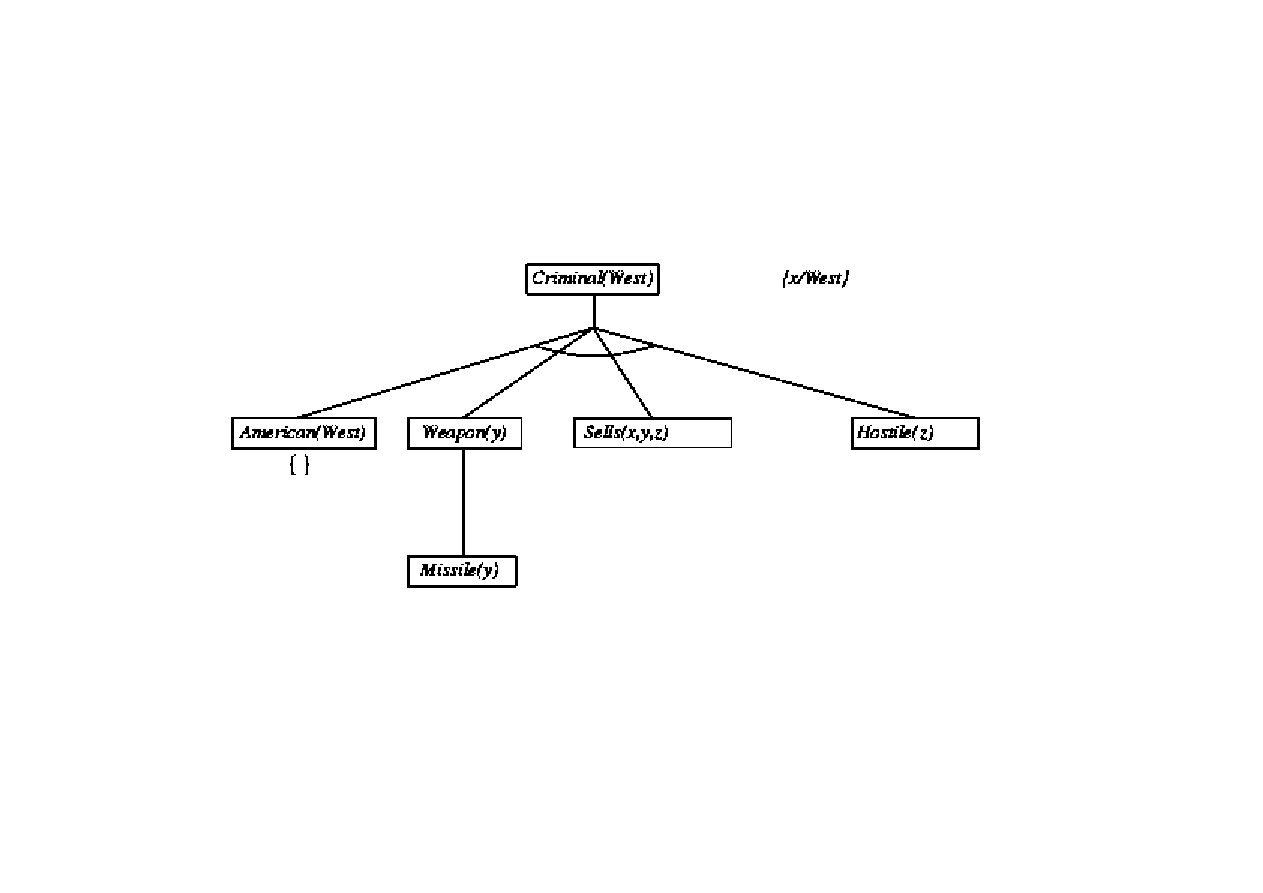
Dowód poprzez wnioskowanie wstecz
9.3. Algorytmy FOL wnioskowania w przód i wstecz
© F.A. Dul 2007
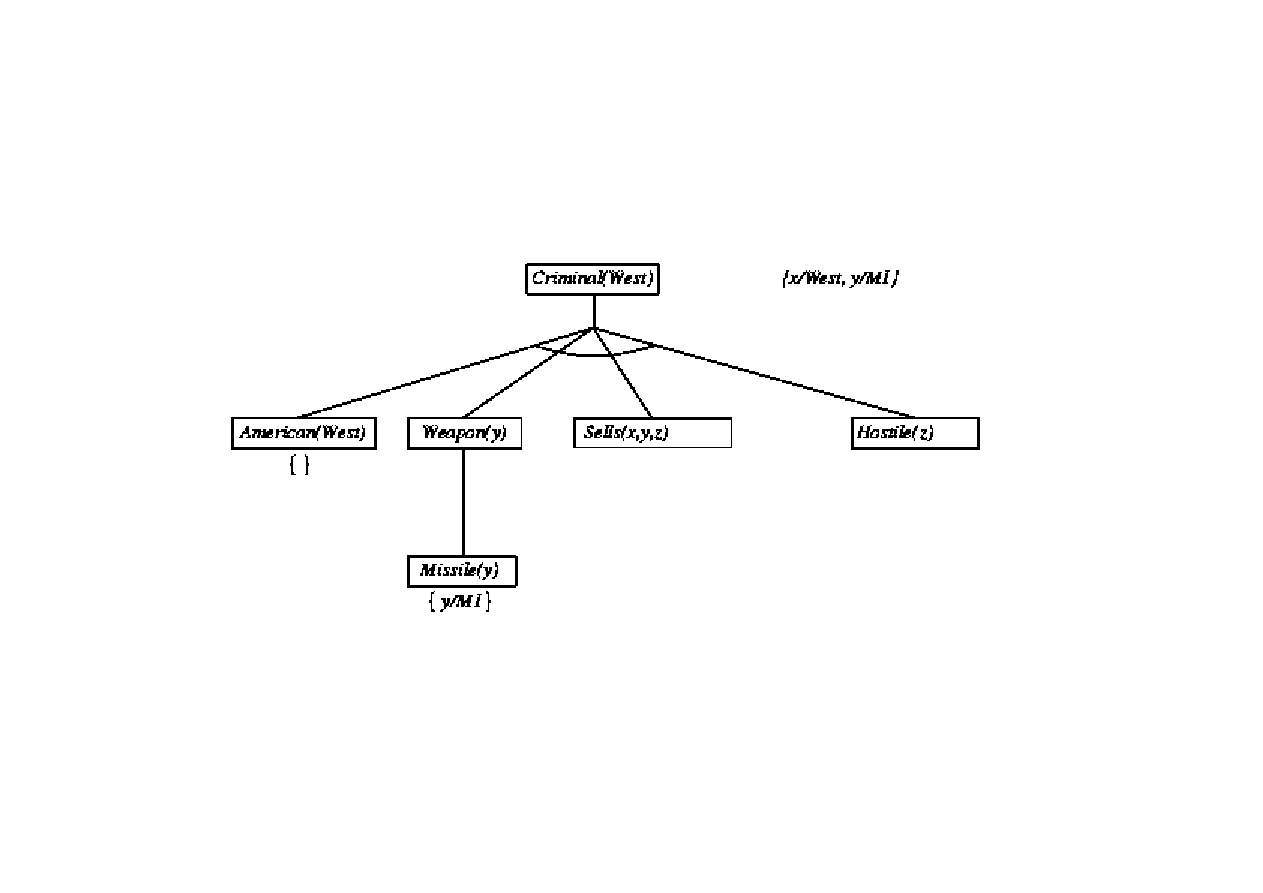
Dowód poprzez wnioskowanie wstecz
9.3. Algorytmy FOL wnioskowania w przód i wstecz
© F.A. Dul 2007
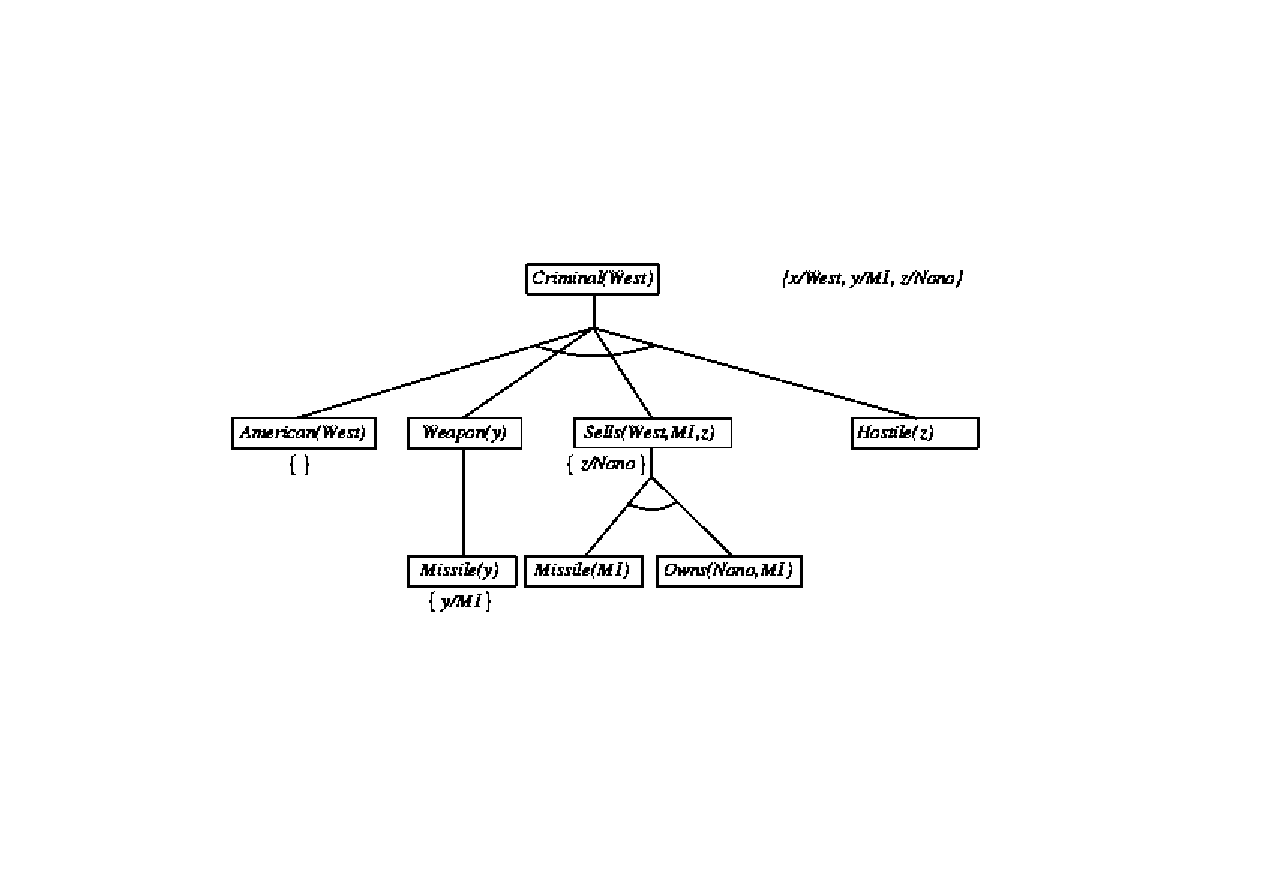
Dowód poprzez wnioskowanie wstecz
9.3. Algorytmy FOL wnioskowania w przód i wstecz
© F.A. Dul 2007
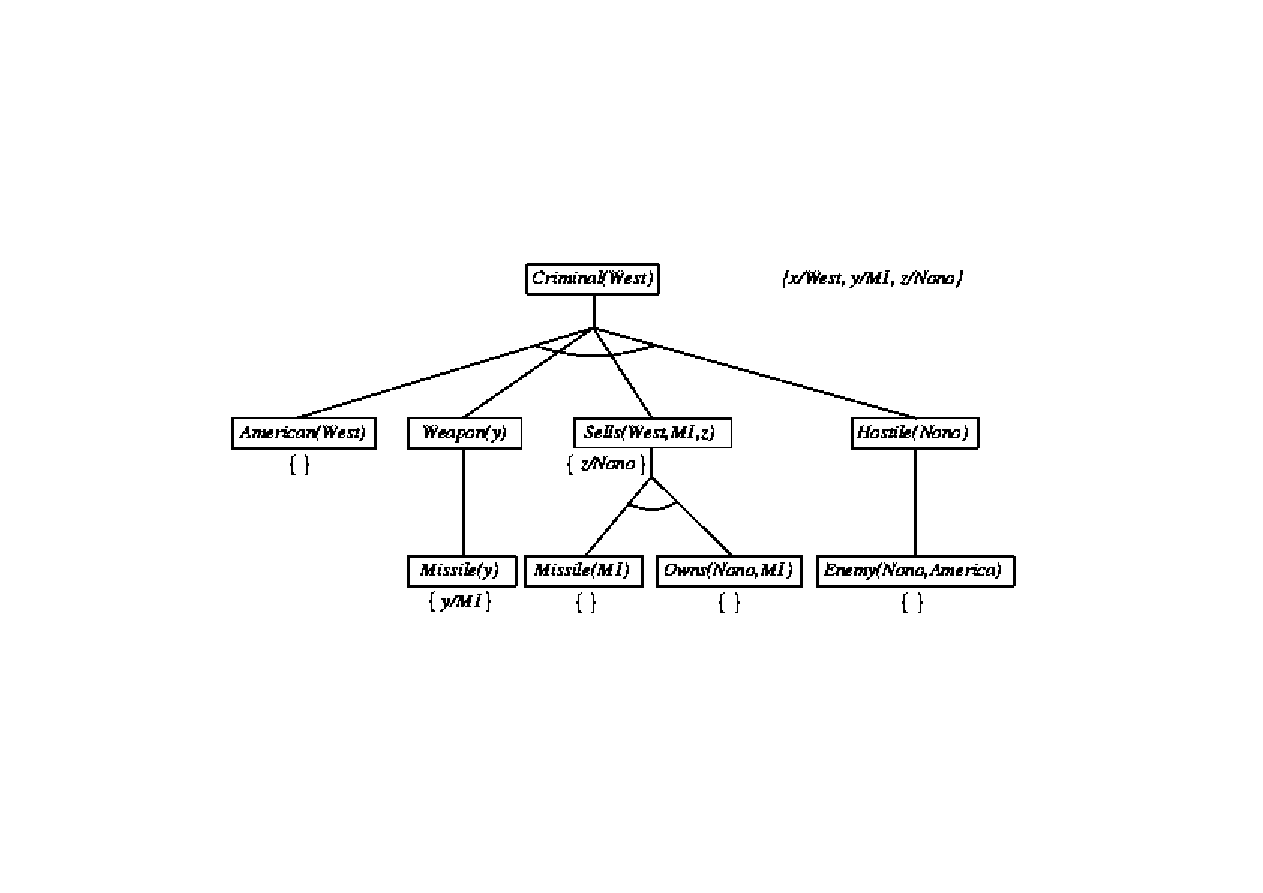
Dowód poprzez wnioskowanie wstecz
9.3. Algorytmy FOL wnioskowania w przód i wstecz
© F.A. Dul 2007

Własno
ś
ci wnioskowania wstecz
9.3. Algorytmy FOL wnioskowania w przód i wstecz
• Przy rekurencyjnym dowodzeniu w gł
ą
b pami
ęć
zale
ż
y
liniowo od długo
ś
ci dowodu.
• Wnioskowanie wstecz jest niezupełne z powodu
mo
ż
liwo
ś
ci zap
ę
tlenia si
ę
algorytmu;
• Mo
ż
na jednak temu zaradzi
ć
poprzez sprawdzenie celu
aktualnego z celami składowanymi na stosie.
• Wnioskowanie wstecz mo
ż
e by
ć
nieefektywne gdy
wielokrotnie sprawdza cele ju
ż
osi
ą
gni
ę
te.
© F.A. Dul 2007
• Wnioskowanie wstecz mo
ż
e by
ć
nieefektywne gdy
wielokrotnie sprawdza cele ju
ż
osi
ą
gni
ę
te.
• Mo
ż
na temu zaradzi
ć
poprzez zapami
ę
tywanie wyników
po
ś
rednich, ale kosztem dodatkowej pami
ę
ci.
• Wnioskowanie wstecz jest szeroko u
ż
ywane
w programowaniu logicznym
.

9.5. Eliminacja (rezolucja)
l
1
∨
···
∨
l
i
∨
···
∨
l
k
, m
1
∨
···
∨
m
k
∨
···
∨
m
n
Subst(
θ
, l
∨
···
∨
l
∨
l
∨
···
∨
l
∨
m
∨
···
∨
m
∨
m
∨
···
∨
m )
Zasada eliminacji pozwala dowodzi
ć
twierdzenia
sformułowane w j
ę
zyku logiki pierwszego rz
ę
du.
Zasada rezolucji umo
ż
liwia tak
ż
e weryfikacj
ę
poprawno
ś
ci
projektów układów elektronicznych oraz dowodzenie
poprawno
ś
ci programów.
Zasada eliminacji dla logiki pierwszego rz
ę
du ma posta
ć
© F.A. Dul 2007
Subst(
θ
, l
1
∨
···
∨
l
i-1
∨
l
i+1
∨
···
∨
l
k
∨
m
1
∨
···
∨
m
j-1
∨
m
j+1
∨
···
∨
m
n
)
gdzie
Unify(l
i
,
¬
m
k
) =
θ
.
Obie klauzule (alternatywy l
j
oraz m
j
) musz
ą
by
ć
standaryzowane, aby nie miały wspólnych zmiennych.
Eliminacja mo
ż
e by
ć
stosowana do bazy FOL przekształconej
do postaci koniunktywnej normalnej (CNF).
Rezolucja mo
ż
e by
ć
zastosowana do udowodnienia zdania
α
poprzez wykazanie,
ż
e ( KB FOL
∧ ¬α
) jest niespełnialne.

9.5. Eliminacja (rezolucja)
Przykład
Dane s
ą
zdania
¬
Bogaty(x)
∨
Nieszcz
ęś
liwy(x)
Bogaty(Jan)
Podstawienie
θ
= { x/Jan }
sprowadza klauzule
¬
Bogaty(x) Bogaty(Jan)
do postaci komplementarnej.
© F.A. Dul 2007
do postaci komplementarnej.
Eliminacja
¬
Bogaty(x)
∨
Nieszcz
ęś
liwy(x) Bogaty(Jan)
Nieszcz
ęś
liwy(Jan)
prowadzi wi
ę
c do wniosku,
ż
e
„Jan jest nieszcz
ęś
liwy”
mimo,
ż
e jest bogaty.

Sprowadzenie zda
ń
FOL do postaci CNF
9.5. Eliminacja (rezolucja)
• Zdanie
“Ka
ż
dy kto kocha wszystkie zwierz
ę
ta jest kochany przez kogo
ś
”.
∀
x [
∀
y Animal(y)
⇒
Loves(x,y) ]
⇒
[
∃
y Loves(y,x) ]
• Eliminacja równowa
ż
no
ś
ci i implikacji
∀
x [
¬∀
y
¬
Animal(y)
∨
Loves(x,y) ]
∨
[
∃
y Loves(y,x) ]
• Reguły negacji kwantyfikatorów,
© F.A. Dul 2007
• Reguły negacji kwantyfikatorów,
¬∀
x p
≡
∃
x
¬
p,
¬∃
x p
≡
∀
x
¬
p
• Przesuni
ę
cie negacji do wn
ę
trza wyra
ż
e
ń
,
∀
x [
∃
y
¬
(
¬
Animal(y)
∨
Loves(x,y)) ]
∨
[
∃
y Loves(y,x) ]
∀
x [
∃
y
¬¬
Animal(y)
∧ ¬
Loves(x,y) ]
∨
[
∃
y Loves(y,x) ]
∀
x [
∃
y Animal(y)
∧ ¬
Loves(x,y) ]
∨
[
∃
y Loves(y,x)]

Sprowadzenie zda
ń
FOL do postaci CNF
9.5. Eliminacja (rezolucja)
• Standaryzacja: ka
ż
dy kwantyfikator musi u
ż
ywa
ć
innej
zmiennej
∀
x [
∃
y Animal(y)
∧ ¬
Loves(x,y) ]
∨
[
∃
z Loves(z,x) ]
• Skolemizacja: ogólna forma podstawienia szczegółowego.
Ka
ż
da zmienna szczegółowa jest zast
ą
piona przez
funkcj
ę
Skolema
zmiennej zewn
ę
trznej kwantyfikatora
ogólnego:
© F.A. Dul 2007
ogólnego:
∀
x
[ Animal(
F(x)
)
∧ ¬
Loves(x,
F(x)
) ]
∨
Loves(
G(x),
x)
• Opuszczenie kwantyfikatora ogólnego
[ Animal(F(x))
∧ ¬
Loves(x,F(x)) ]
∨
Loves(G(x),x)
• Przekształcenie do postaci koniunkcji alternatyw:
[ Animal(F(x))
∨
Loves(G(x),x) ]
∧
[
¬
Loves(x,F(x))
∨
Loves(G(x),x) ]

Dowód rezolucyjny dla kaluzuli Horna
9.5. Eliminacja (rezolucja)
© F.A. Dul 2007

Dowód rezolucyjny dla kaluzuli Horna
9.5. Eliminacja (rezolucja)
{x/West}
© F.A. Dul 2007
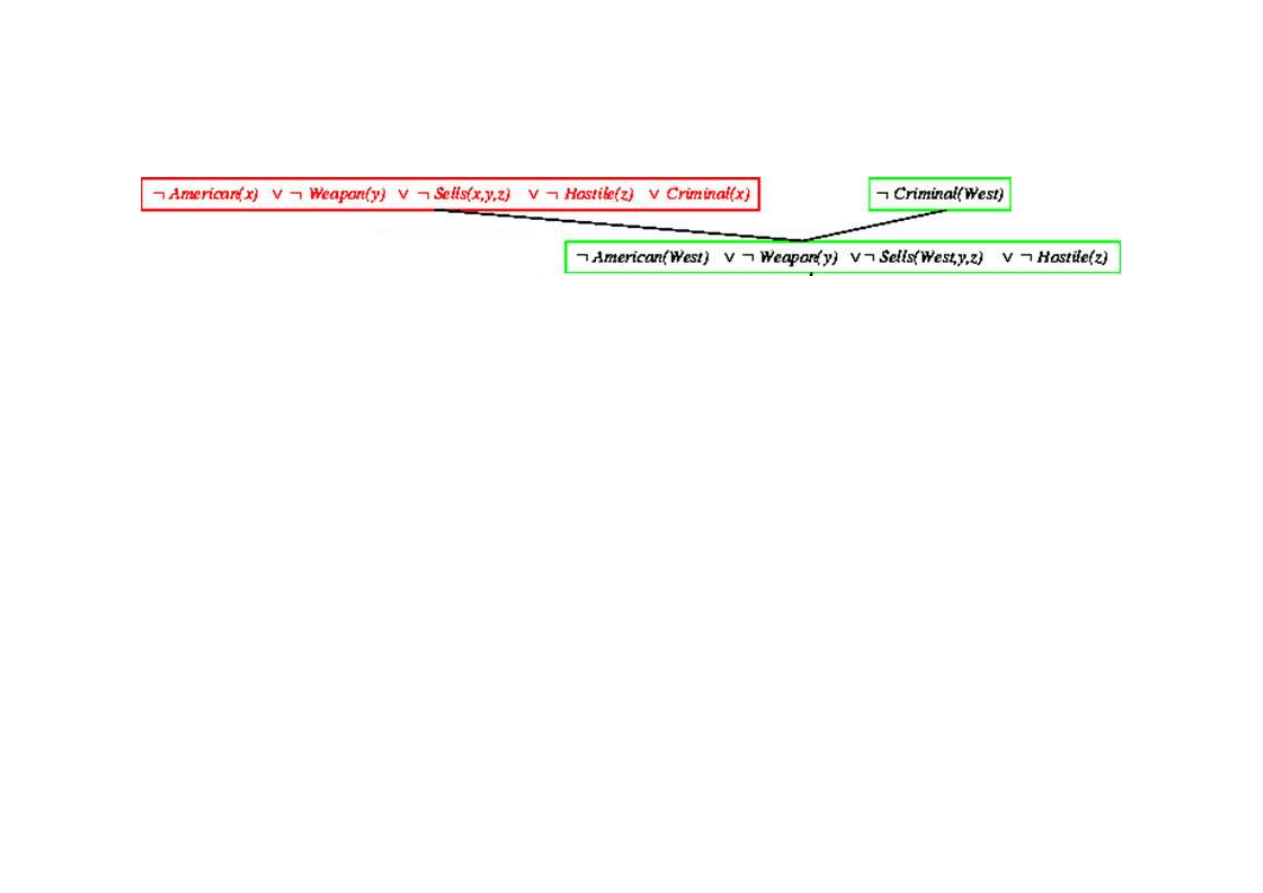
Dowód rezolucyjny dla kaluzuli Horna
9.5. Eliminacja (rezolucja)
{x/West}
© F.A. Dul 2007
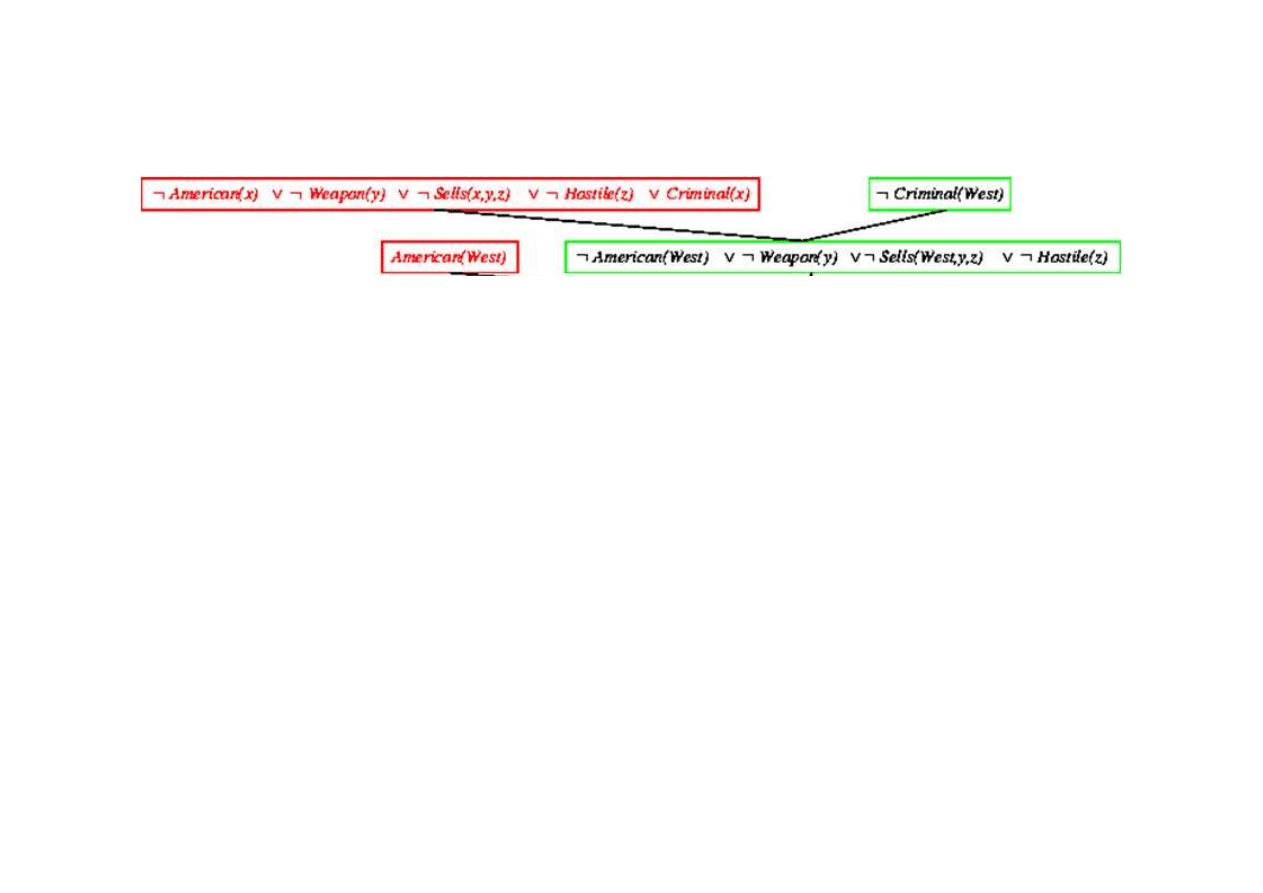
Dowód rezolucyjny dla kaluzuli Horna
9.5. Eliminacja (rezolucja)
{x/West}
© F.A. Dul 2007
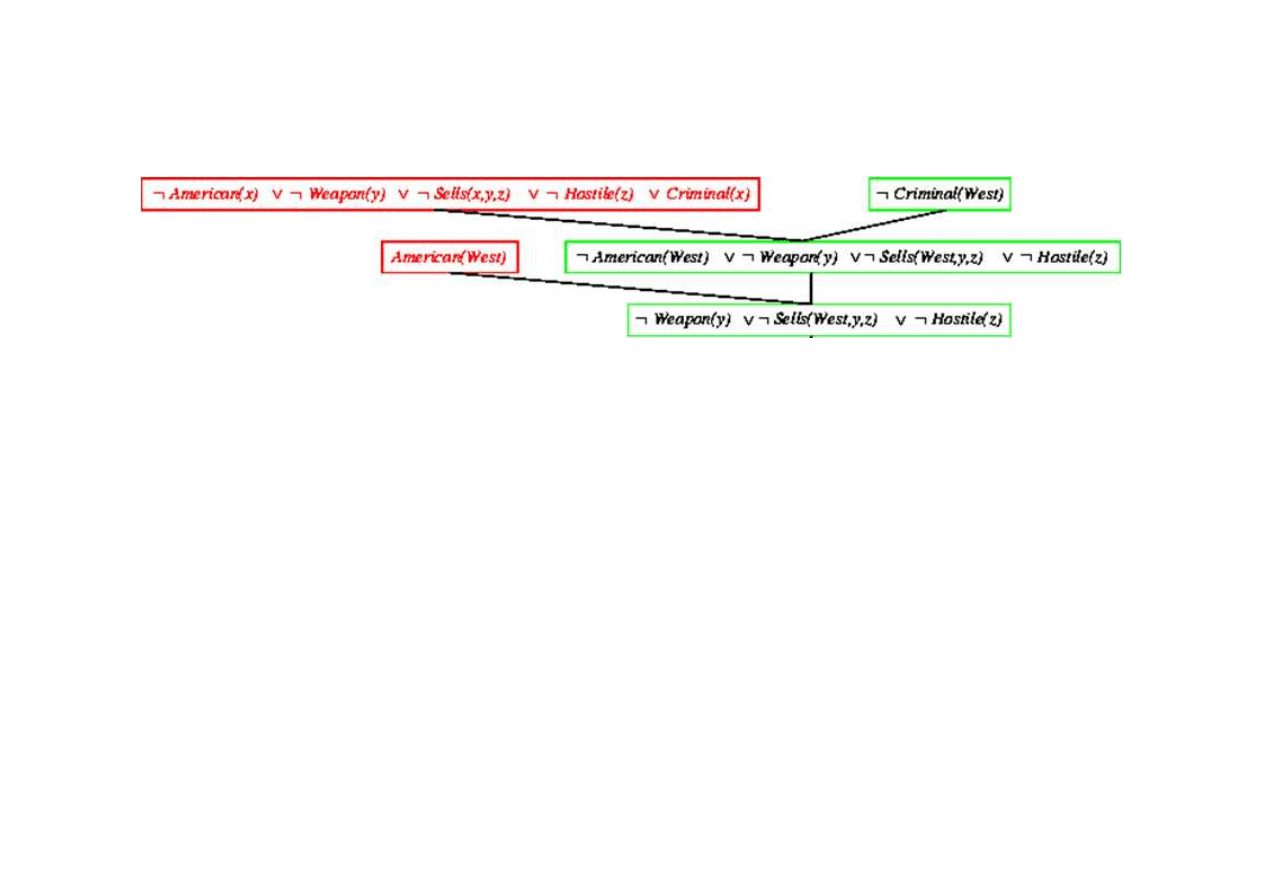
Dowód rezolucyjny dla kaluzuli Horna
9.5. Eliminacja (rezolucja)
{x/West}
© F.A. Dul 2007
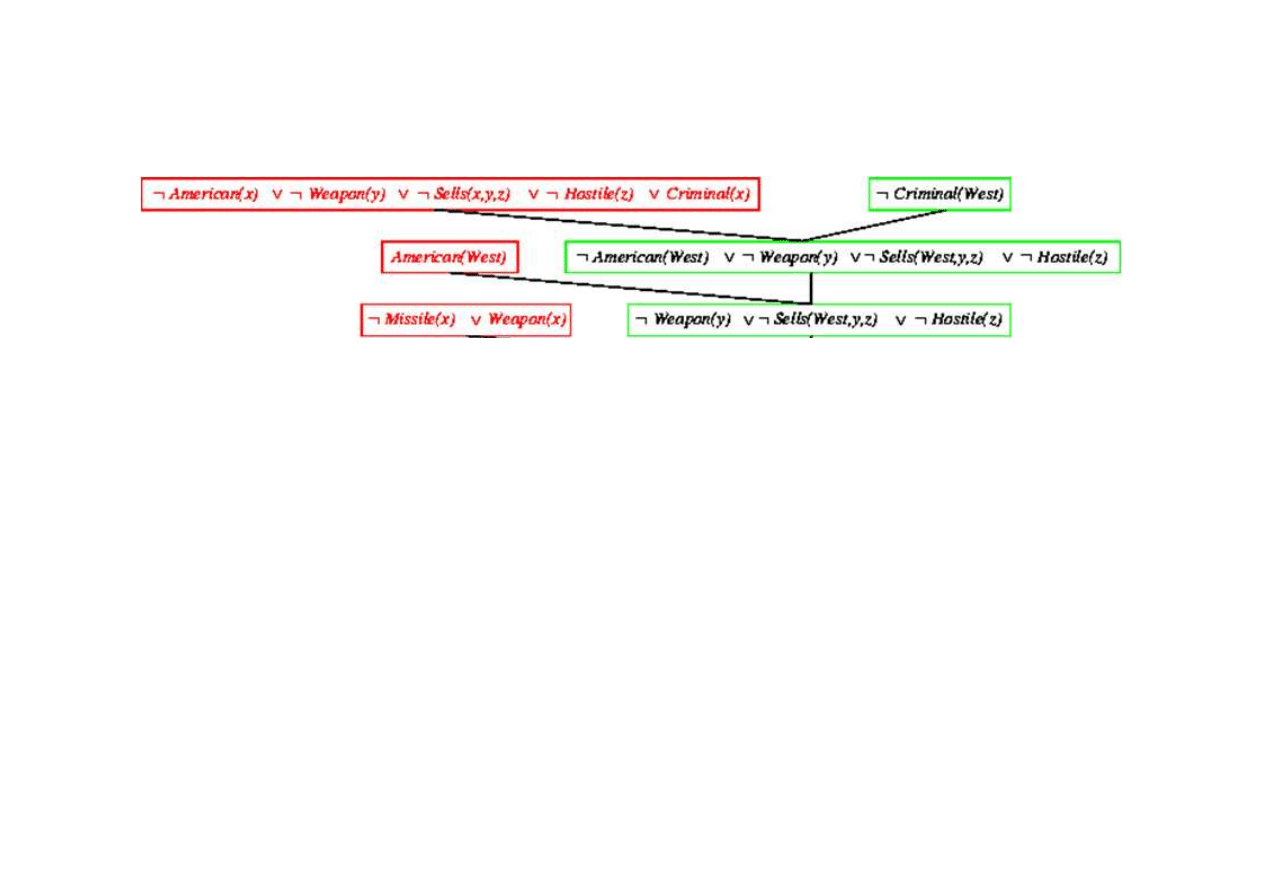
Dowód rezolucyjny dla kaluzuli Horna
9.5. Eliminacja (rezolucja)
{x/West}
{x/y}
© F.A. Dul 2007
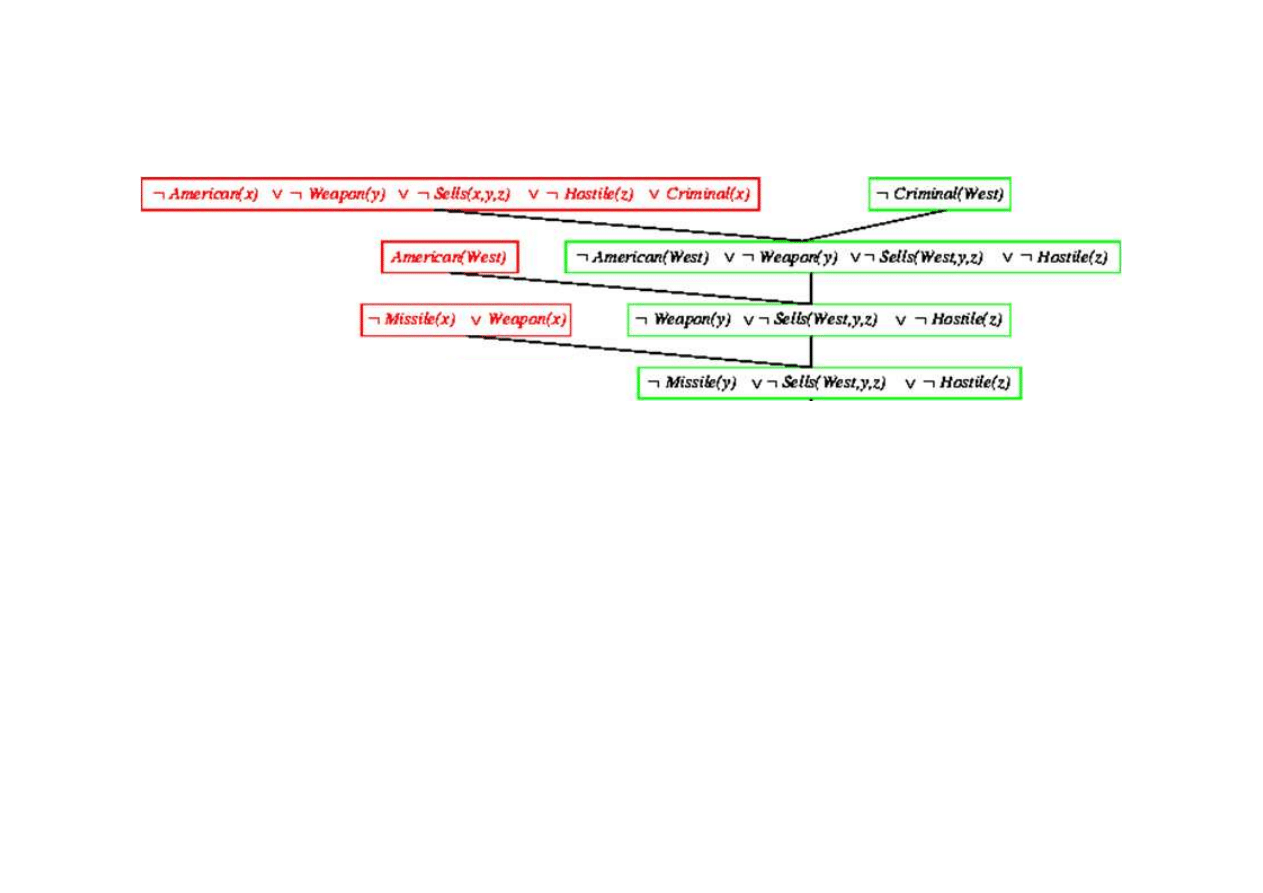
Dowód rezolucyjny dla kaluzuli Horna
9.5. Eliminacja (rezolucja)
{x/West}
{x/y}
© F.A. Dul 2007
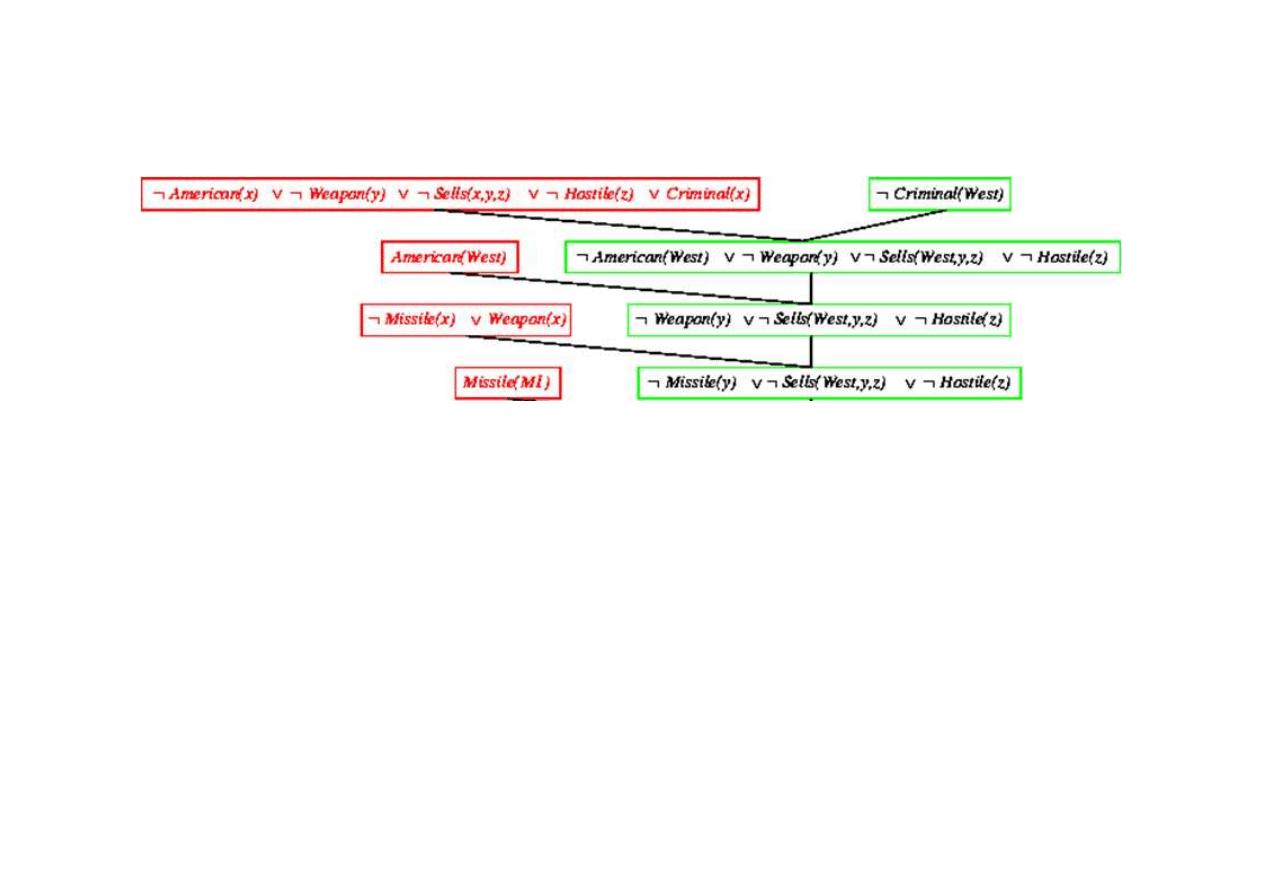
Dowód rezolucyjny dla kaluzuli Horna
9.5. Eliminacja (rezolucja)
{x/West}
{x/y}
{y/M1}
© F.A. Dul 2007
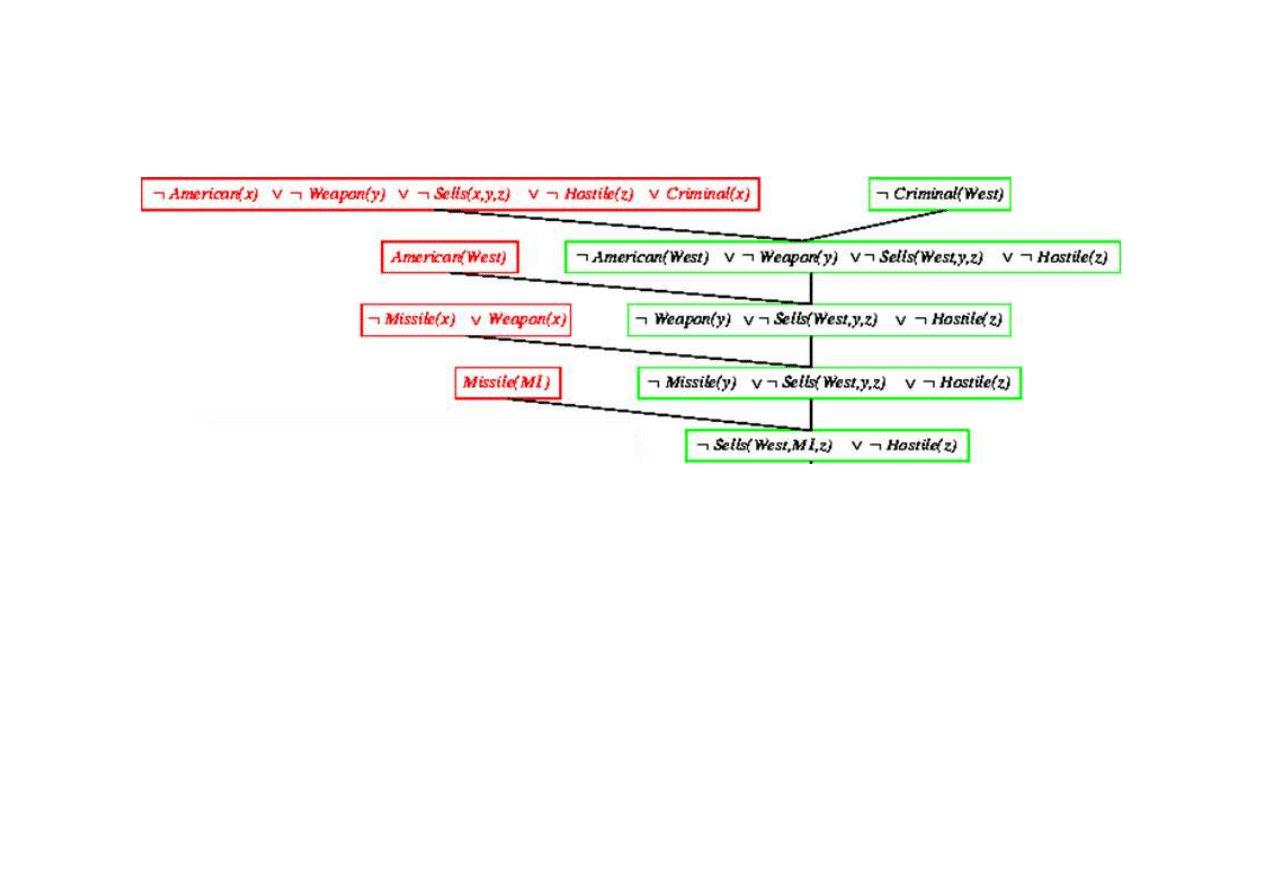
Dowód rezolucyjny dla kaluzuli Horna
9.5. Eliminacja (rezolucja)
{x/West}
{x/y}
{y/M1}
© F.A. Dul 2007
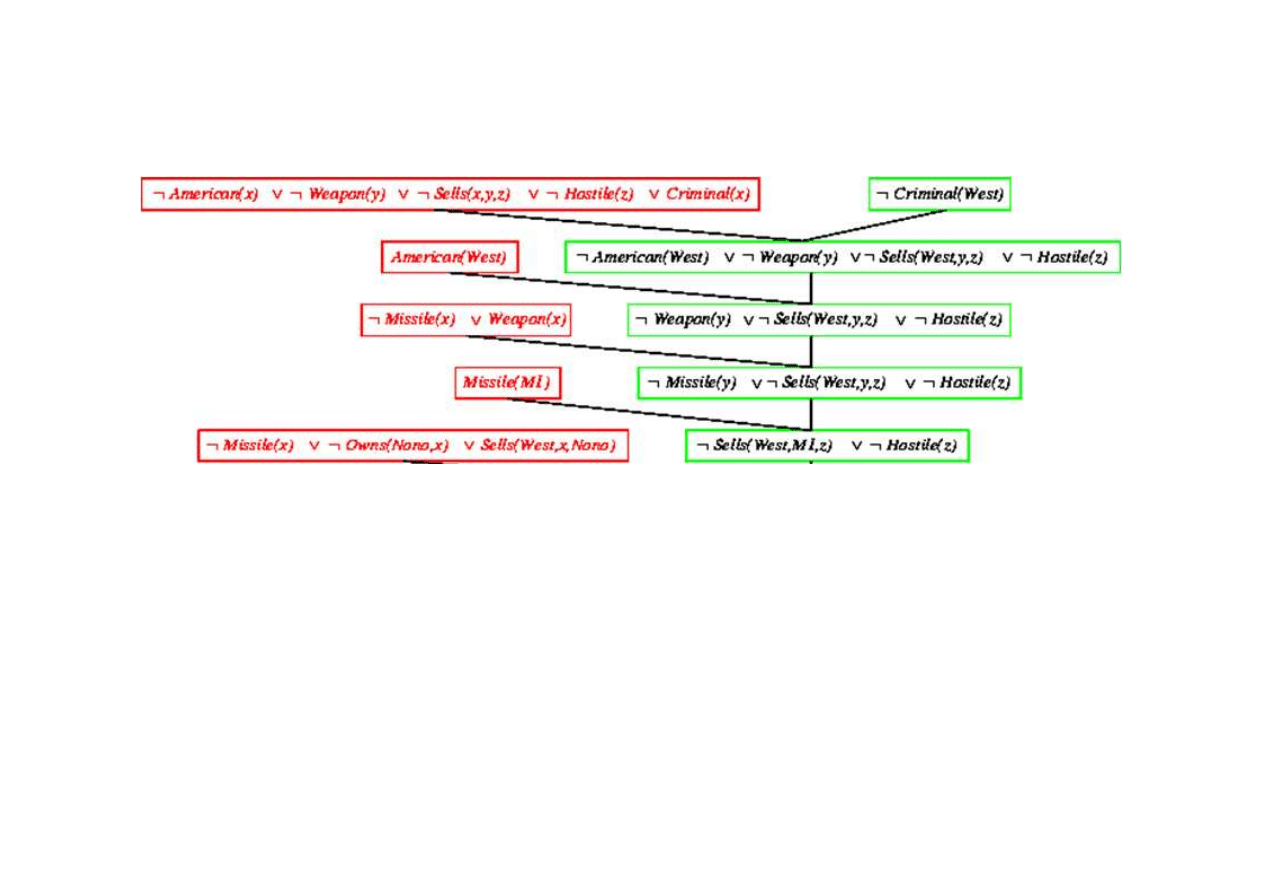
Dowód rezolucyjny dla kaluzuli Horna
9.5. Eliminacja (rezolucja)
{x/West}
{x/y}
{y/M1}
{x/M1}
© F.A. Dul 2007
{x/M1}
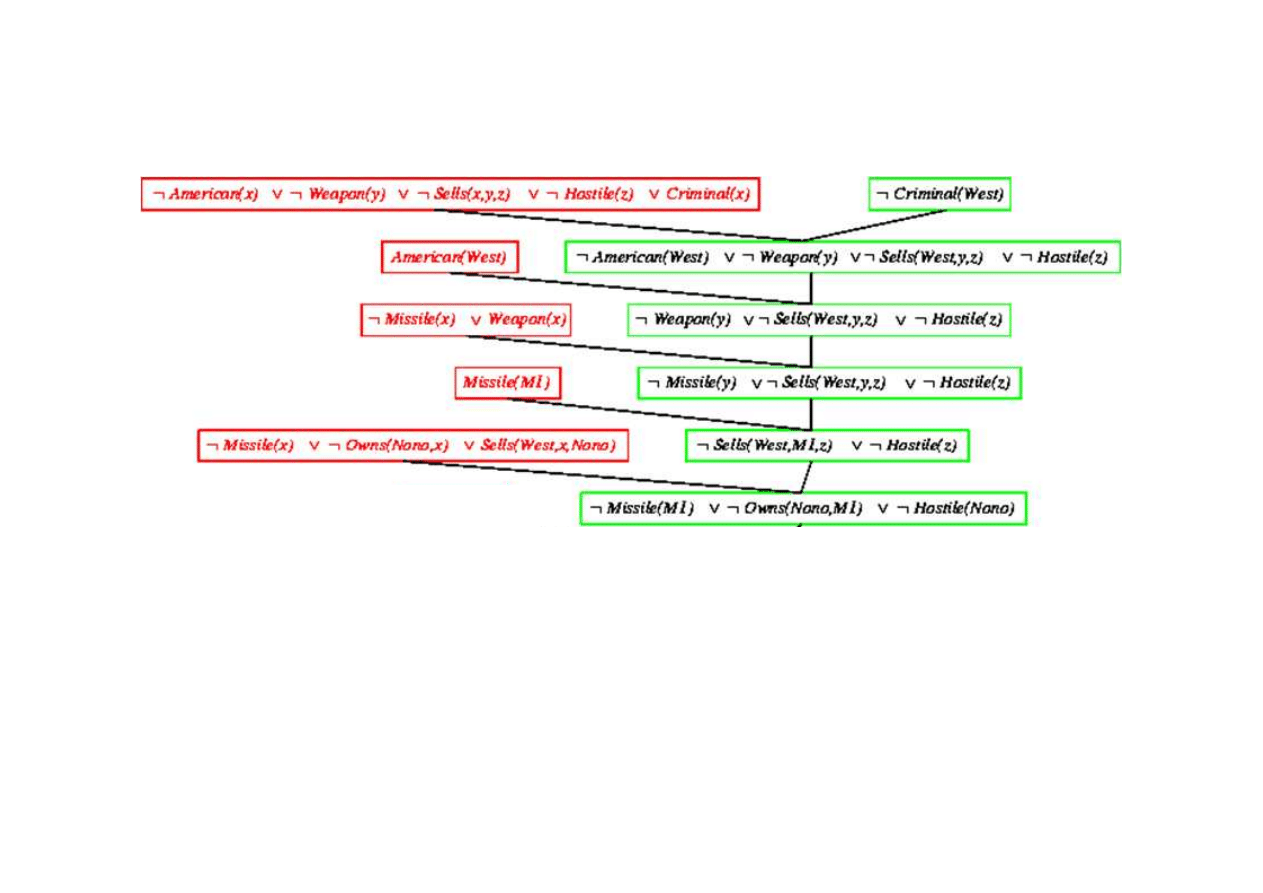
Dowód rezolucyjny dla kaluzuli Horna
9.5. Eliminacja (rezolucja)
{x/West}
{x/y}
{y/M1}
{x/M1}
© F.A. Dul 2007
{x/M1}
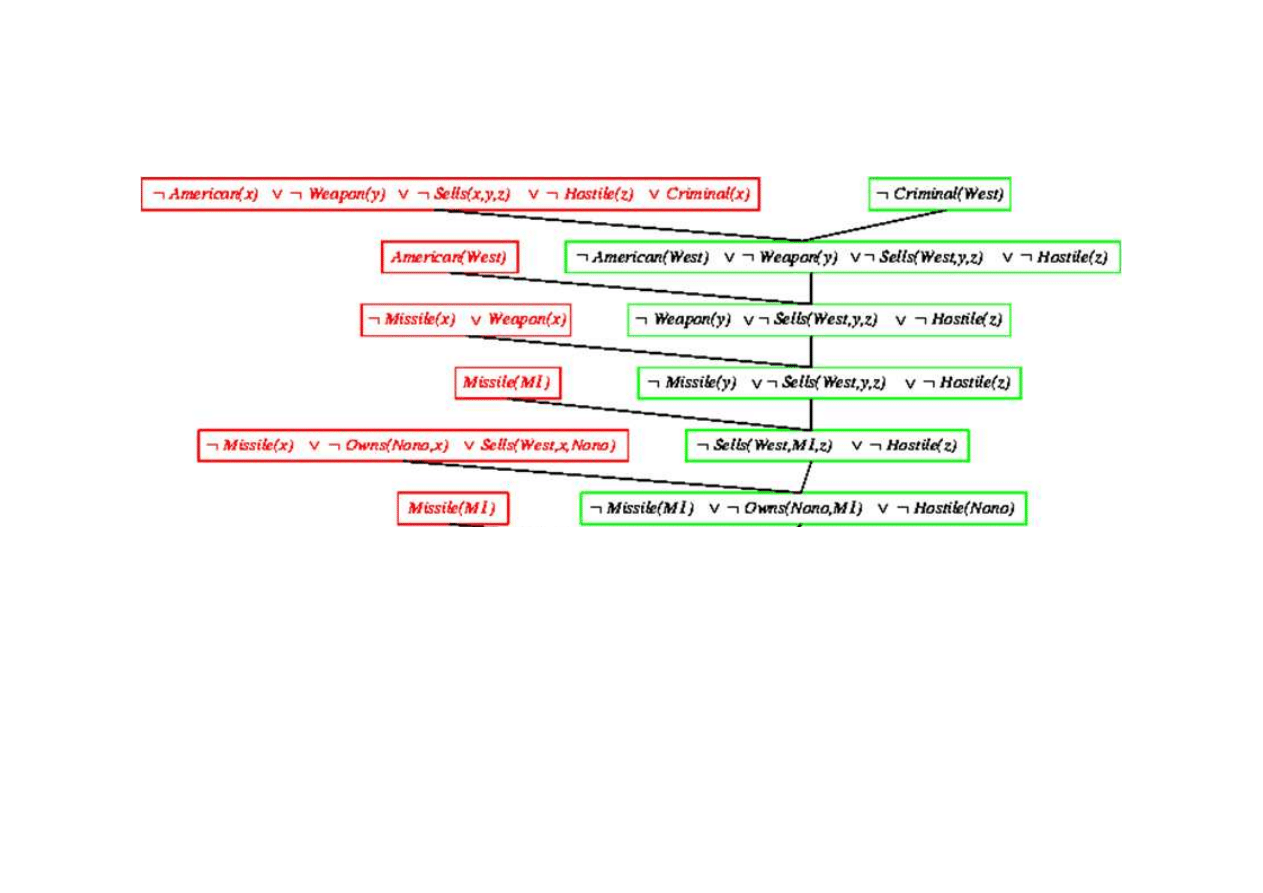
Dowód rezolucyjny dla kaluzuli Horna
9.5. Eliminacja (rezolucja)
{x/West}
{x/y}
{y/M1}
{x/M1}
© F.A. Dul 2007
{x/M1}
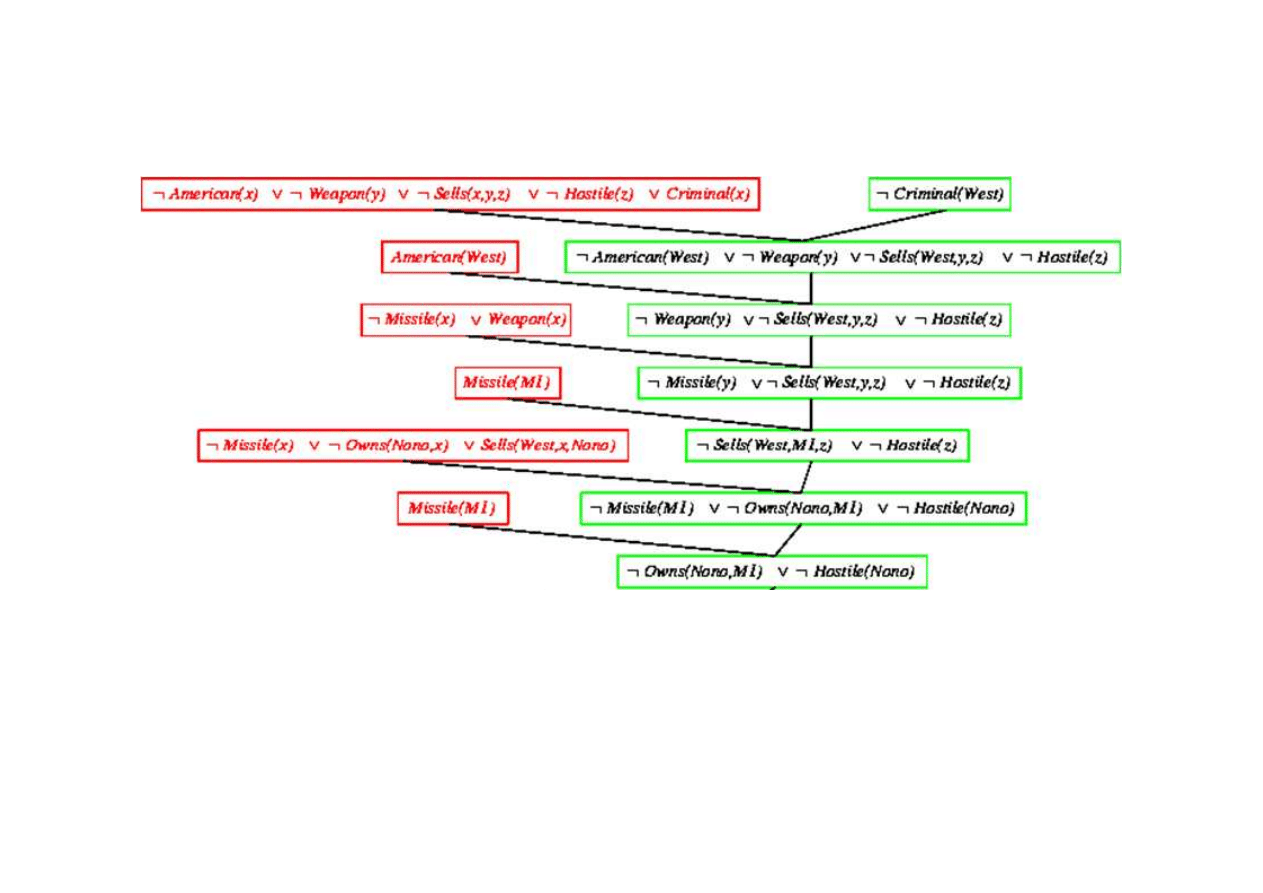
Dowód rezolucyjny dla kaluzuli Horna
9.5. Eliminacja (rezolucja)
{x/West}
{x/y}
{y/M1}
{x/M1}
© F.A. Dul 2007
{x/M1}
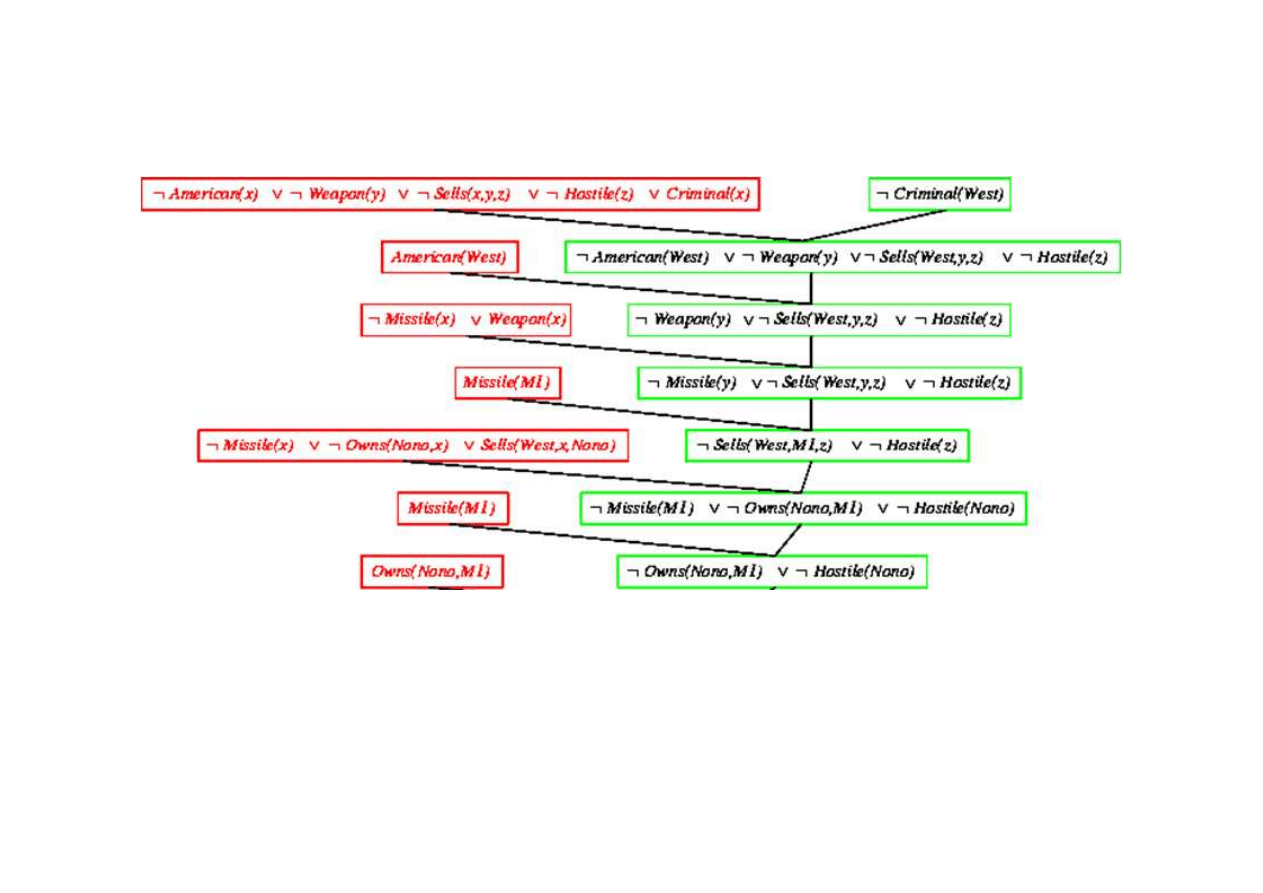
Dowód rezolucyjny dla kaluzuli Horna
9.5. Eliminacja (rezolucja)
{x/West}
{x/y}
{y/M1}
{x/M1}
© F.A. Dul 2007
{x/M1}
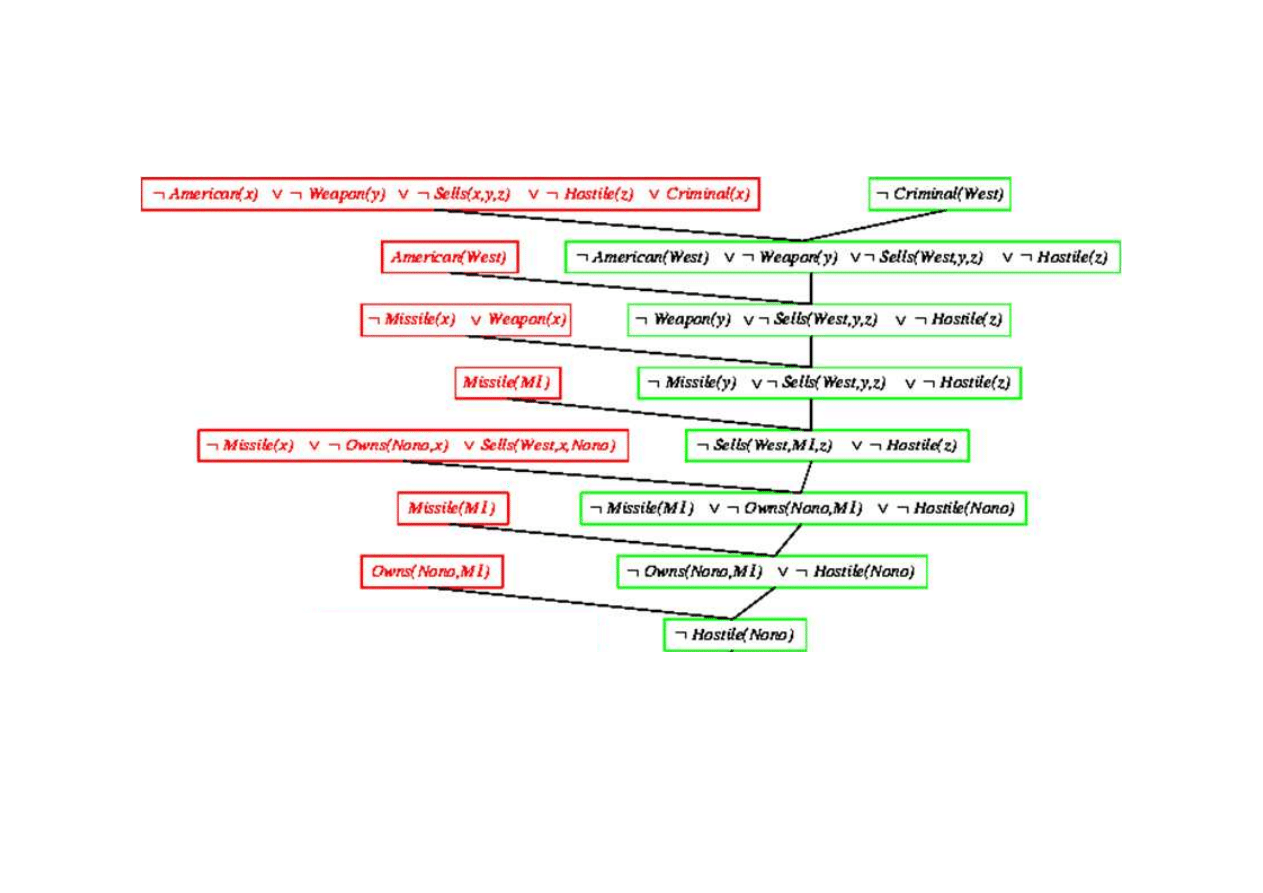
Dowód rezolucyjny dla kaluzuli Horna
9.5. Eliminacja (rezolucja)
{x/West}
{x/y}
{y/M1}
{x/M1}
© F.A. Dul 2007
{x/M1}
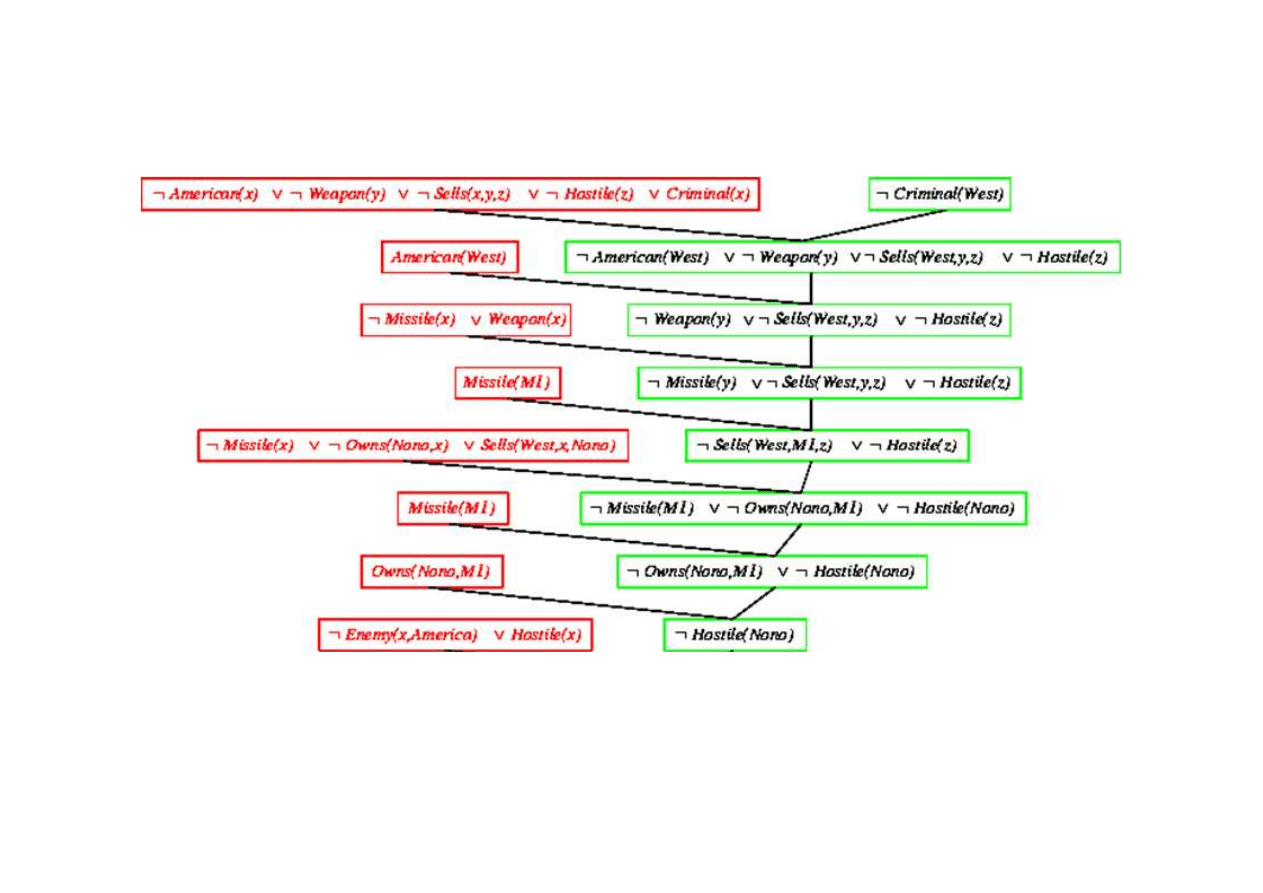
Dowód rezolucyjny dla kaluzuli Horna
9.5. Eliminacja (rezolucja)
{x/West}
{x/y}
{y/M1}
{x/M1}
© F.A. Dul 2007
{x/M1}
{x/Nono}
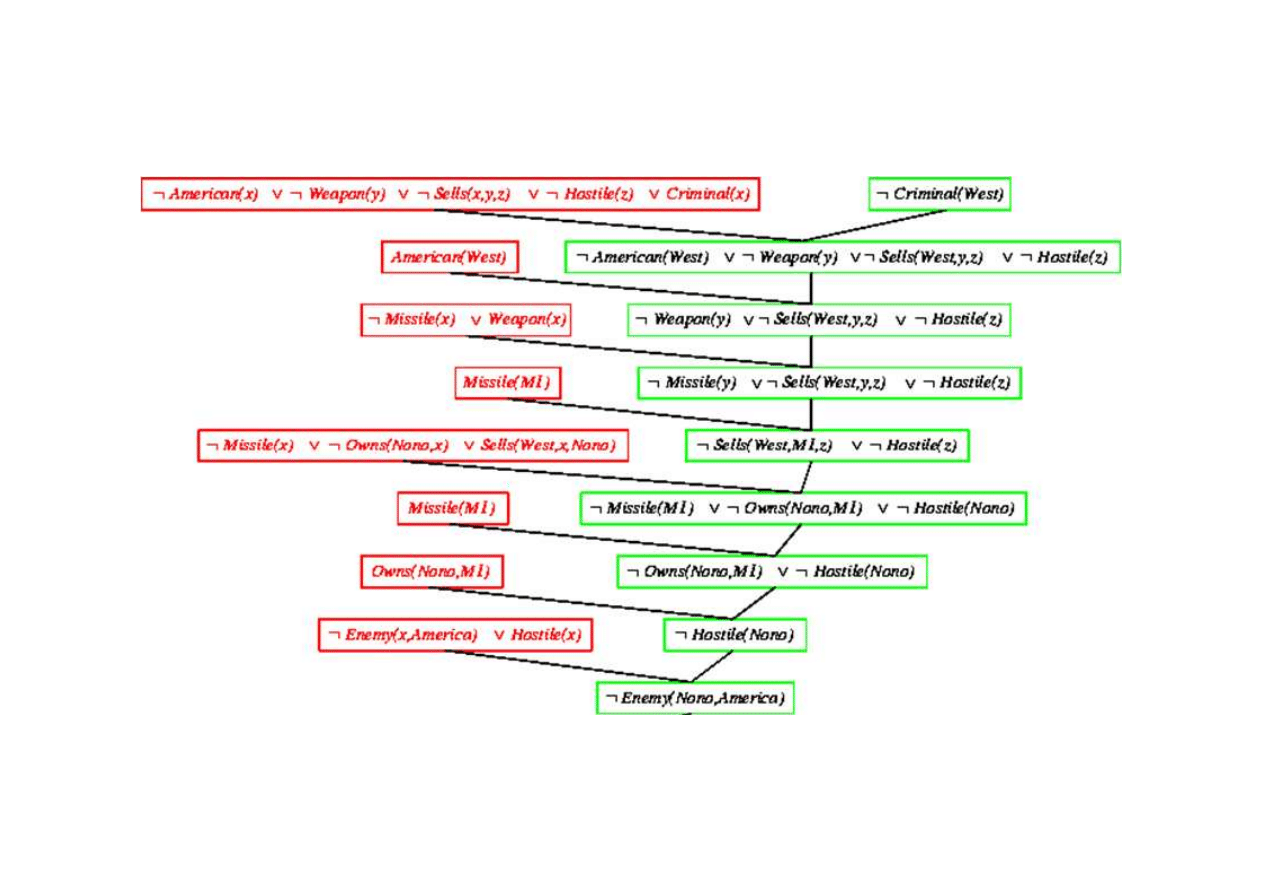
Dowód rezolucyjny dla kaluzuli Horna
9.5. Eliminacja (rezolucja)
{x/West}
{x/y}
{y/M1}
{x/M1}
© F.A. Dul 2007
{x/M1}
{x/Nono}
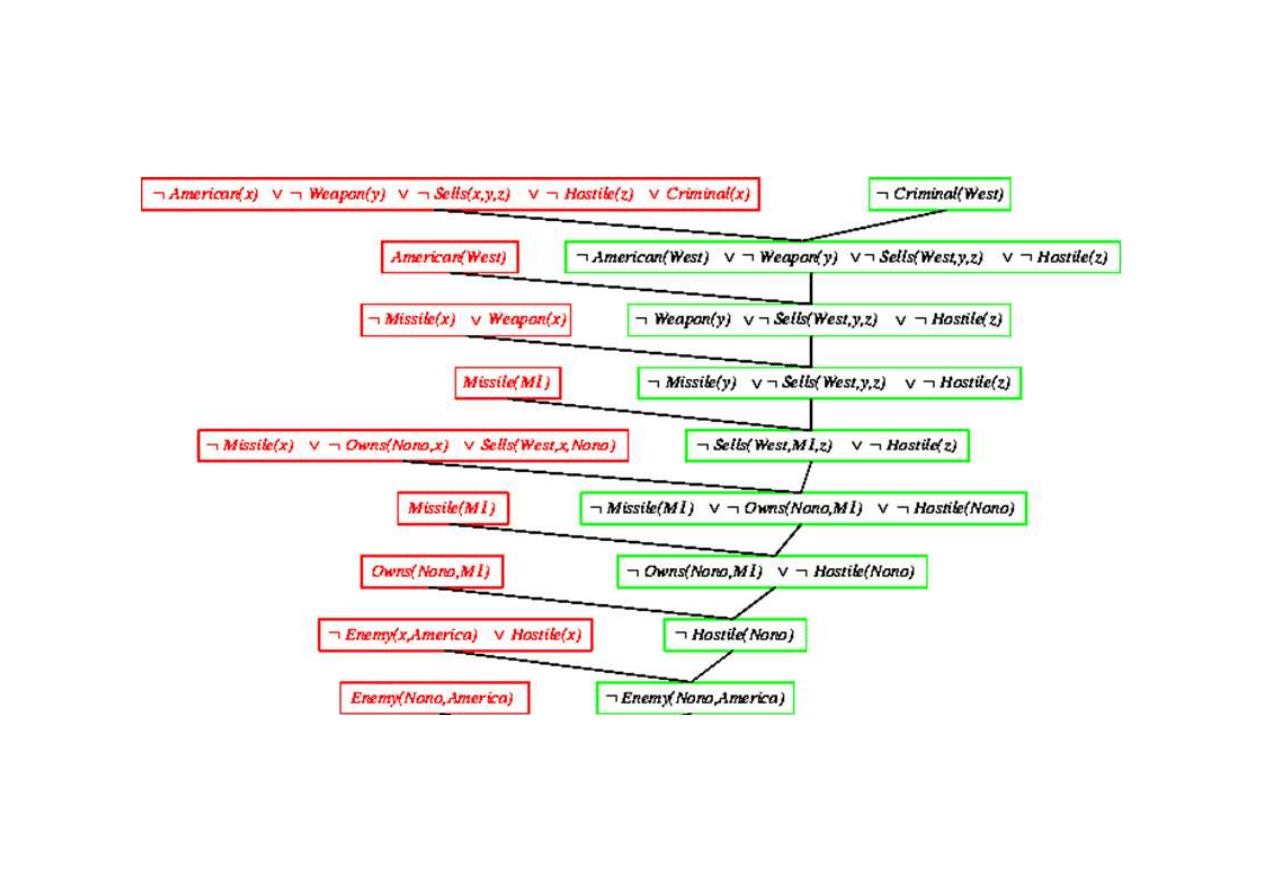
Dowód rezolucyjny dla kaluzuli Horna
9.5. Eliminacja (rezolucja)
{x/West}
{x/y}
{y/M1}
{x/M1}
© F.A. Dul 2007
{x/M1}
{x/Nono}
Dowód rezolucyjny dla kaluzuli Horna
9.5. Eliminacja (rezolucja)
{x/West}
{x/y}
{y/M1}
{x/M1}
© F.A. Dul 2007
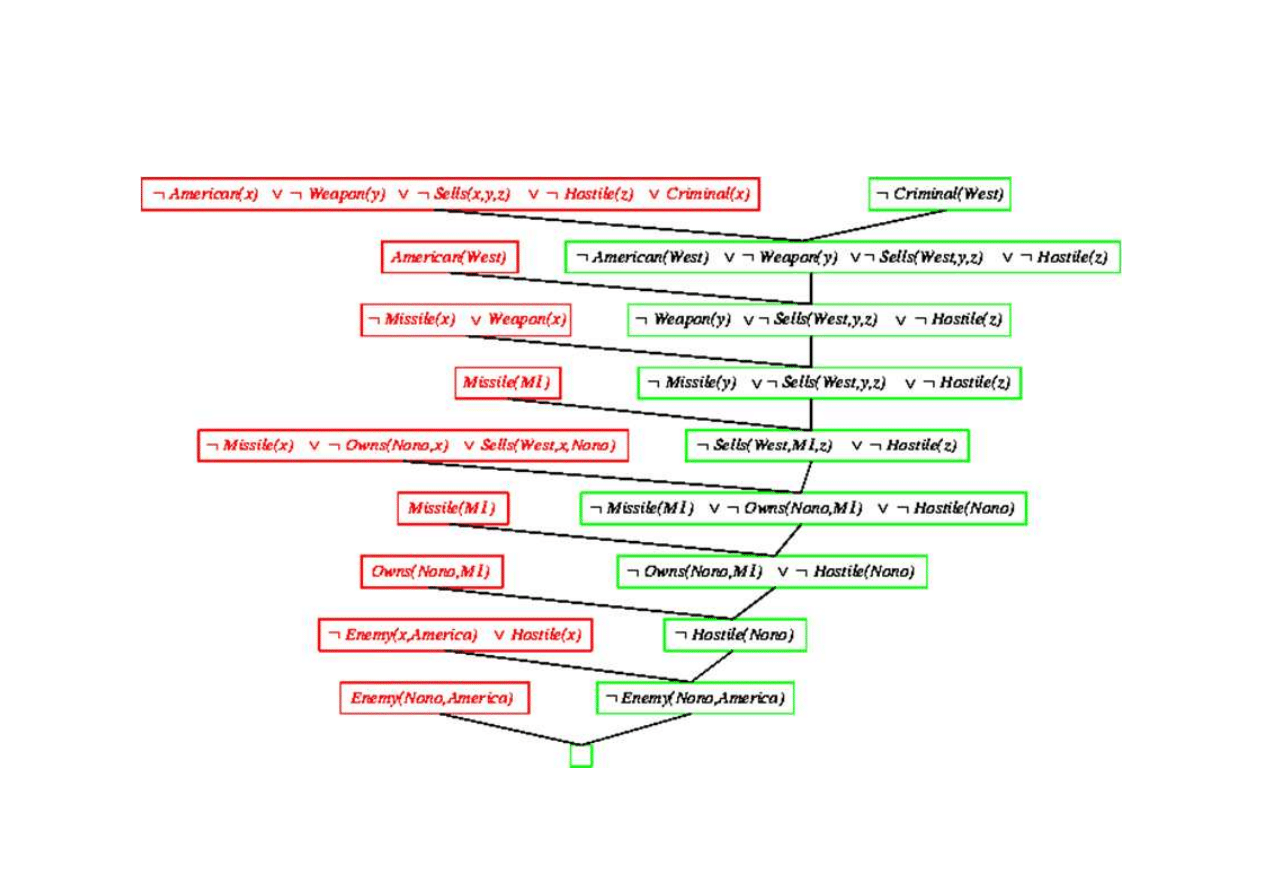
Klauzula pusta - dowiedziono sprzeczno
ś
ci klauzuli
¬
Criminal(West)
{x/M1}
{x/Nono}

Programowanie logiczne vs. proceduralne
9.5. Eliminacja (rezolucja)
Programowanie logiczne
– identyfikacja zadania;
– zebranie informacji;
– kodowanie informacji
w j
ę
zyku logiki bazy
wiedzy;
– kodowanie zadania
Programowanie proceduralne
– identyfikacja zadania;
– zebranie informacji;
– opracowanie algorytmu
rozwi
ą
zania;
– programowanie
algorytmu;
© F.A. Dul 2007
– kodowanie zadania
jako zbioru faktów;
– zadawania pyta
ń
;
– eliminacja błednych
faktów;
algorytmu;
– kodowanie zadania jako
zbioru danych;
– uruchomienie programu
dla zbioru danych;
– eliminacja błedów;
Łatwiej jest analizowa
ć
Stolica(NY,US) ni
ż
x = x+2
Programowanie logiczne: j
ę
zyk PROLOG

Wnioskowanie bezpo
ś
rednie w FOL
Przekształcenie algorytmów wnioskowania w taki
sposób, aby mo
ż
na było prowadzi
ć
wnioskowanie
w bazie FOL pozwala u
ż
y
ć
efektywnych metod
wnioskowania w przód i wstecz, a tak
ż
e algorytmu
eliminacji (rezolucji) dla bazy w postaci Horna.
Przekształcenie algorytmów polega na zastosowaniu
operacji podniesienia i unifikacji oraz wykorzystanie
©
F.A. Dul 2007
operacji podniesienia i unifikacji oraz wykorzystanie
uogólnionej reguły odrywania.
Wnioskowanie przy u
ż
yciu algorytmów
dostosowanych do FOL mo
ż
e by
ć
bardzo efektywne.
Wnioskowanie mo
ż
e by
ć
w pełni automatyczne.
Wnioskowanie automatyczne stwarza mo
ż
liwo
ść
automatycznego dowodzenia twierdze
ń
matematycznych.

9.6. Automatyczne dowodzenie twierdze
ń
Programy dowodzenia twierdze
ń
(
Theorem Provers
,
Automated Reasoners
) umo
ż
liwiaj
ą
dowodzenie twierdze
ń
sformułowanych w j
ę
zyku logiki pierwszego rz
ę
du.
Najbardziej znane programy: O
TTER
, PTTP, O
NTIC
, S
AM
,
A
URA
, EQP, S
PIN.
Idea programu O
TTER
Dane definiuj
ą
ce dowodzony problem:
• Zbiór zda
ń
opisuj
ą
cych problem
(set of support, SOS)
.
• Aksjomaty u
ż
ytkowe
, nie b
ę
d
ą
ce elementami SOS,
© F.A. Dul 2007
• Aksjomaty u
ż
ytkowe
, nie b
ę
d
ą
ce elementami SOS,
opisuj
ą
ce wiedz
ę
ogóln
ą
na temat problemu.
• Zbiór równa
ń
demoduluj
ą
cych (
demodulators
)
okre
ś
laj
ą
cych formy kanoniczne do których przekształcane
s
ą
wszystkie zdania (np. x+0=x: x+0
→
x).
• Zbiór parametrów i klauzul steruj
ą
cych.
Program O
TTER
stosuje rezolucj
ę
do kolejnych zda
ń
zbioru
opisuj
ą
cego SOS wzgl
ę
dem aksjomatów u
ż
ytkowych.
Rezolucja klauzul SOS przebiega w kolejno
ś
ci od najprostszej,
wybieranej heurystycznie za pomoc
ą
algorytmu best-first.

Programy dowodzenia twierdze
ń
pozwoliły uzyska
ć
wiele
wa
ż
nych wyników matematycznych.
• 1969 – program S
AM
udowadnia kilka lematów teorii warstw.
• 1979 – Natarjan Shankar przy u
ż
yciu programu Boyera-
Moora dowodzi po raz pierwszy w sposób
ś
cisły słynne
Twierdzenie Gödla o Niezupełno
ś
ci.
• 1983 – program A
URA
udowadnia twierdzenia z wielu
dziedzin matematyki.
• Program O
TTER
(i jego nowsze wersje: M
ACE
2, EQP) jest
jednym z najlepszych programów dowodzenia twierdze
ń
.
9.6. Automatyczne dowodzenie twierdze
ń
© F.A. Dul 2007
jednym z najlepszych programów dowodzenia twierdze
ń
.
Za pomoc
ą
EQP dowiedziono w roku 1996 słynnej
hipotezy
Robbinsa
(o równowa
ż
no
ś
ci algebry Robbinsa i algebry
boolowskiej), nieudowodnionej od roku 1933, nawet przez
samego
Alfreda Tarskiego*
)
. Dowód uzyskany programem
EQP liczy tylko
17 linijek!
*) Alfred Tarski
(1901-1983) – wybitny polski logik,
wykładowca UW i liceum
ś
eromskiego (do 1939),
oraz uniwersytetów Harvarda, Princeton i Berkeley.
Jako pierwszy sformułował definicj
ę
prawdy.
Uwa
ż
any za najwi
ę
kszego logika po Arystotelesie.

• Za pomoc
ą
programów dowodz
ą
cych udowodniono wiele
twierdze
ń
geometrii algebraicznej, logiki kombinatorycznej,
autodualnych algebr Boolowskich, teorii grup, półgrup
i kwazigrup, teorii krat i kwazikrat, i wielu innych...
• Podejmowane s
ą
nawet próby formalizacji całej matematyki
– projekt QED.
9.6. Automatyczne dowodzenie twierdze
ń
© F.A. Dul 2007

Program dowodz
ą
ce s
ą
te
ż
u
ż
ywane w ró
ż
nych dziedzinach
jako
asystenci
.
Człowiek-ekspert nadzoruje rozwi
ą
zanie problemu wytyczaj
ą
c
kierunki działa
ń
, za
ś
program-asystent rozwi
ą
zuje problemy
szczegółowe.
Innymi zastosowaniami programów dowodz
ą
cych
s
ą
weryfikacja
oraz
synteza
układów elektronicznych
oraz oprogramowania.
• Program A
URA
posłu
ż
ył do weryfikacji 16-bitowego układu
9.6. Automatyczne dowodzenie twierdze
ń
© F.A. Dul 2007
• Program A
URA
posłu
ż
ył do weryfikacji 16-bitowego układu
sumuj
ą
cego (1983).
• Specjalne programy dowodz
ą
ce słu
żą
do weryfikacji
poprawno
ś
ci układów VLSI, np. procesorów CPU.
• Program S
PIN
słu
ż
y do weryfikacji poprawno
ś
ci
oprogramowania.
Za jego pomoc
ą
weryfikowano w NASA oprogramowanie
Remote Agent
steruj
ą
ce lotem sond mi
ę
dzyplanetarnych,
m.in. sondy Deep Space 1 (1999).

Podsumowanie
• Algorytmy wnioskowania w logice pierwszego rz
ę
du
s
ą
wa
ż
nymi narz
ę
dziami sztucznej inteligencji.
• Unifikacja pozwala znacznie zwi
ę
kszy
ć
efektywno
ść
wnioskowania w logice pierwszego rz
ę
du.
• Uogólniona wersja Modus Ponens stanowi efektywn
ą
reguł
ę
wnioskowania w logice pierwszego rz
ę
du.
• Algorytmy wnioskowania w przód i wstecz
s
ą
najwa
ż
niejszymi narz
ę
dziami wnioskowania
© F.A. Dul 2007
s
ą
najwa
ż
niejszymi narz
ę
dziami wnioskowania
automatycznego w logice pierwszego rz
ę
du.
• Uogólnione zasady rezolucji pozwalaj
ą
dowodzi
ć
twierdze
ń
w logice pierwszego rz
ę
du w bazie wiedzy reprezentowanej
w postaci normalnej koniunktywnej.
• Automatyczne dowodzenie twierdze
ń
umo
ż
liwiło
udowodnienie interesuj
ą
cych twierdze
ń
matematycznych.
• Automatyczne dowodzenie twierdze
ń
pomaga tak
ż
e
przy syntezie i weryfikacji oprogramowania.
Wyszukiwarka
Podobne podstrony:
09 Wnioskowanie w logice pierwszego rzędu
09 Karty umiejetnosci pierwszak Nieznany
IS wyklad 14 15 01 09 MDW id 22 Nieznany
ei 2005 09 s004 id 154186 Nieznany
09 Dobieranie materialow odziez Nieznany (2)
PIF2 2007 Wykl 09 Dzienne id 35 Nieznany
09 rany i krwawieniaid 7993 Nieznany (2)
09 pfsc sas gido3vwa6mgy2a3eiib Nieznany (2)
09 Rozroznianie stylow muzyczny Nieznany (2)
cennik 09 2013 id 109720 Nieznany
09 15 id 53452 Nieznany (2)
09 wspolczesne instalacje miesz Nieznany
09 uklad kierowniczy 5MCOQGXUO3 Nieznany (2)
09 Aparat trojosiowy instrukcja Nieznany (2)
Homines2011 09 Walkowiak id 205 Nieznany
09 Utlenianie 2005id 8028 Nieznany (2)
80 Nw 09 Suszarka do bielizny i Nieznany
więcej podobnych podstron