WPROWADZENIE

DO SZTUCZNEJ INTELIGENCJI

POLITECHNIKA WARSZAWSKA

WYDZIAŁ MECHANICZNY ENERGETYKI I LOTNICTWA

MEL

MEL

NS 586

Dr in

ż

. Franciszek Dul

© F.A. Dul 2007

9. WNIOSKOWANIE W LOGICE

PIERWSZEGO RZĘDU

© F.A. Dul 2007

PIERWSZEGO RZĘDU

Wnioskowanie w logice pierwszego rz

ę

du

Poka

ż

emy, w jaki sposób uogólni

ć

algorytmy wnioskowania rachunku
zda

ń

tak, aby wnioskowa

ć

w logice

© F.A. Dul 2007

zda

ń

tak, aby wnioskowa

ć

w logice

pierwszego rz

ę

du.

• Sprowadzenie wnioskowania w logice pierwszego rz

ę

du

do wnioskowania w rachunku zda

ń

• Unifikacja
• Uogólniona reguła odrywania (modus ponens)
• Wnioskowanie w przód i wstecz
• Rezolucja
• Automatyczne dowodzenie twierdze

ń

Plan rozdziału

© F.A. Dul 2007

Jak wnioskowa

ć

z kwantyfikatorami...

W j

ę

zyku logiki pierwszego rz

ę

du mo

ż

na opisa

ć

ś

wiat w sposób

ś

cisły, a zarazem bardzo zwi

ę

zły.

Zwi

ę

zło

ść

opisu osi

ą

ga si

ę

poprzez u

ż

ycie obiektów,

relacji mi

ę

dzy nimi, funkcji oraz

kwantyfikatorów

.

Wyst

ę

powanie kwantyfikatorów uniemo

ż

liwia

jednak prowadzenie wnioskowania w taki sposób,
jak w rachunku zda

ń

.

©

F.A. Dul 2007

jak w rachunku zda

ń

.

Zdania zapisane w j

ę

zyku logiki pierwszego rz

ę

du

musz

ą

wi

ę

c najpierw by

ć

przekształcone do postaci

umo

ż

liwiaj

ą

cej wnioskowanie.

Zdania FOL mo

ż

na przekształci

ć

do postaci

rachunku zda

ń

, albo te

ż

do takich postaci, które

umo

ż

liwiaj

ą

wnioskowanie bezpo

ś

rednie w FOL

za pomoc

ą

przekształconych metod wnioskowania.

9.1. Sprowadzenie wnioskowania logiki pierwszego

rz

ę

du do wnioskowania w rachunku zda

ń

Wnioskowanie w logice pierwszego rz

ę

du mo

ż

e by

ć

sprowadzone do wnioskowania w rachunku zda

ń

.

Idea: nale

ż

y zast

ą

pi

ć

zdania kwantyfikowne przez zbiór zda

ń

bez kwantyfikatorów.

Zbiór zda

ń

zdekwantyfikowanych powinien by

ć

równowa

ż

ny

wyj

ś

ciowemu zbiorowi zda

ń

kwantyfikowanych lub co najmniej

spełnialny.

© F.A. Dul 2007

• Eliminacja kwantyfikatorów ogólnych

Zast

ą

pienie zmiennej przez

symbol podstawowy

(ground term)

• Eliminacja kwantyfikatorów szczegółowych

skolemizacja

spełnialny.

Podstawienie ogólne (universal instantiation, UI)

Ka

ż

de podstawienie do zdania z kwantyfikatorem ogólnym

pewnego wyra

ż

enia za zmienn

ą

kwantyfikowan

ą

wynika

z tego zdania, tj.

∀

v

α

—————————

Subst( {v/g},

α

)

dla ka

ż

dej zmiennej v i ka

ż

dego wyra

ż

enia g.

Subst(

θ

,

α

)

= podstawienie

θ

do

α

.

9.1. Sprowadzenie FOL do PL

© F.A. Dul 2007

Przykład Podstawienie do zdania

∀

x Król(x)

∧

Chciwy(x)

⇒

Zły(x)

wyra

ż

e

ń

: {x/Jan}, {x/Ryszard} i {x/Ojciec(Jan)} daje zdania:

Król(Jan)

∧

Chciwy(Jan)

⇒

Zły(Jan)

Król(Ryszard)

∧

Chciwy(Ryszard)

⇒

Zły(Ryszard)

Król(Ojciec(Jan))

∧

Chciwy(Ojciec(Jan))

⇒

Zły(Ojciec(Jan))

Zdanie z kwantyfikatorem ogólnym jest równowa

ż

ne zbiorowi

zda

ń

z podstawieniami

wszystkich

obiektów z dziedziny.

9.1. Sprowadzenie FOL do PL

Podstawienie szczegółowe (existential instantiation, EI)

Dla ka

ż

dego zdania

α

, zmiennej v i stałej k która

nie wyst

ę

puje

w bazie wiedzy KB zachodzi wynikanie

∃

v

α

—————————

Subst( {v/k},

α

)

Przykład Podstawienie stałej C

1

do zdania

∃

x Korona(x)

∧

NaGłowie(x,Jan)

© F.A. Dul 2007

∃

x Korona(x)

∧

NaGłowie(x,Jan)

daje zdanie

Korona(C1)

∧

NaGłowie(C1,Jan)

Stała C

1

nazywa si

ę

stał

ą

Skolema

, za

ś

procedura jej

podstawienia –

skolemizacj

ą

.

Warunek niewyst

ę

powania w bazie KB stałej Skolema której

chcemy u

ż

y

ć

jest bardzo wa

ż

ny!

Niespełnienie tego warunku powoduje,

ż

e relacja wynikania

zbioru zda

ń

skolemizowanych z bazy KB nie jest spełniona.

9.1. Sprowadzenie FOL do PL

Ró

ż

nice pomi

ę

dzy podstawieniami: ogólnym (UI)

oraz szczegółowym (EI)

• Podstawienie ogólne (UI) mo

ż

e by

ć

wykonane wielokrotnie

w celu

dodania

nowych zda

ń

do bazy wiedzy.

Nowa baza wiedzy KB jest równowa

ż

na logicznie bazie

starej.

• Podstawienie szczegółowe (EI) mo

ż

e by

ć

wykonane

tylko raz

, w celu eliminacji kwantyfikatora szczegółowego.

© F.A. Dul 2007

tylko raz

, w celu eliminacji kwantyfikatora szczegółowego.

Nowa baza wiedzy KB

nie jest

równowa

ż

na logicznie bazie

starej, ale jest spełnialna (tj. prawdziwa dla

pewnych

modeli)

je

ż

eli baza wyj

ś

ciowa była spełnialna.

9.1. Sprowadzenie FOL do PL

Sprowadzenie wnioskowania FOL do wnioskowania

w rachunku zda

ń

Załó

ż

my,

ż

e baza wiedzy KB zawiera nast

ę

puj

ą

ce zdania

i wyra

ż

enia:

Wykonanie

wszystkich

mo

ż

liwych podstawie

ń

, tutaj:

∀

x Król(x)

∧

Chciwy(x)

⇒

Zły(x)

Król(Jan)
Chciwy(Jan)
Brat(Ryszard,Jan)

© F.A. Dul 2007

Król(Jan)

∧

Chciwy(Jan)

⇒

Zły(Jan)

Król(Ryszard)

∧

Chciwy(Ryszard)

⇒

Zły(Ryszard)

Król(Jan)
Chciwy(Jan)
Brat(Ryszard,Jan)

{x/Jan}, {x/Ryszard}

daje w wyniku now

ą

baz

ę

KB:

Nowa baza wiedzy jest ju

ż

czysto

predykatowa

(KB PL)

– nie ma w niej kwantyfikatorów.

Predykatami s

ą

:

Król(Jan), Chciwy(Jan), Zły(Jan),

etc.

9.1. Sprowadzenie FOL do PL

• Ka

ż

da baza wiedzy zapisana w logice pierwszego rz

ę

du

(KB FOL) mo

ż

e by

ć

sprowadzona do bazy predykatowej

(KB PL) w taki sposób,

ż

e wynikanie jest zachowane, tj,

Zdanie wynika z przekształconej bazy KB wtedy
i tylko wtedy, gdy wynika z bazy pierwotnej.

• Zasada: przedstawienie w postaci predykatowej bazy

wiedzy KB PL, zapyta

ń

, rezolucji, odpowiedzi.

• Problem: funkcje generuj

ą

niesko

ń

czone ci

ą

gi wyra

ż

e

ń

, np.

© F.A. Dul 2007

• Problem: funkcje generuj

ą

niesko

ń

czone ci

ą

gi wyra

ż

e

ń

, np.

Ojciec(Ojciec(Ojciec(Jan)))...

Twierdzenie (Turing, Church 1936) Wynikanie w logice
pierwszego rz

ę

du jest

półrozstrzygalne

(semidecidable).

Oznacza to,

ż

e :

istniej

ą

algorytmy

które daj

ą

odpowied

ź

twierdz

ą

c

ą

na ka

ż

de

zdanie wynikaj

ą

ce z bazy KB FOL, ale

nie ma algorytmów

które odpowiadaj

ą

przecz

ą

co na ka

ż

de

zdanie nie wynikaj

ą

ce z bazy KB FOL.

9.1. Sprowadzenie FOL do PL

Problemy ze sprowadzeniem FOL do PL

• Sprowadzenie bazy FOL do postaci predykatowej prowadzi

do utworzenia wielu nieistotnych zda

ń

.

Przykład Z bazy

∀

x Król(x)

∧

Chciwy(x)

⇒

Zły(x)

Król(Jan)

∀

y Chciwy(y)

Brat(Ryszard,Jan)

wynika w sposób oczywisty zdanie

© F.A. Dul 2007

wynika w sposób oczywisty zdanie

Zły(Jan),

ale równie

ż

wiele zda

ń

nieistotnych, np.

Zły(Ryszard).

• Problem liczby podstawie

ń

.

Dla p zda

ń

k-krotnych i n stałych istnieje

p·n

k

podstawie

ń

.

Wnioskowanie w bazie predykatowej

Przekształcenie bazy zapisanej w j

ę

zyku logiki

pierwszego rz

ę

du do bazy predykatowej pozwala

prowadzi

ć

wnioskowanie metodami rachunku zda

ń

.

Jednak takie post

ę

powanie mo

ż

e by

ć

wysoce

nieefektywne, gdy

ż

eliminacja kwantyfikatorów

ogólnych mo

ż

e spowodowa

ć

lawinowy wzrost liczby

zda

ń

w bazie przekształconej.

©

F.A. Dul 2007

zda

ń

w bazie przekształconej.

Lepszym rozwi

ą

zaniem jest

modyfikacja algorytmów

wnioskowania

w taki sposób, aby mo

ż

na było

prowadzi

ć

wnioskowanie bezpo

ś

rednio w bazie FOL.

Osi

ą

ga si

ę

to poprzez zastosowanie operacji

podniesienia i unifikacji oraz wykorzystanie
uogólnionej reguły odrywania i algorytmu eliminacji
(rezolucji).

9.2. Podniesienie i unifikacja

Zamiast przekształca

ć

baz

ę

FOL do postaci PL, mo

ż

na

przedefiniowa

ć

reguły wnioskowania tak, aby były słuszne

dla logiki pierwszego rz

ę

du u

ż

ywaj

ą

cej kwantyfikatorów:

ogólnych i szczegółowych.

Unifikacja

jest to procedura rekurencyjna pozwalaj

ą

ca

sprawdzi

ć

, czy istnieje podstawienie sprowadzaj

ą

ce dwa

wyra

ż

enia do takiej samej postaci.

Unifikacja pozwala cz

ę

sto istotnie zredukowa

ć

liczb

ę

zda

ń

© F.A. Dul 2007

Unifikacja pozwala cz

ę

sto istotnie zredukowa

ć

liczb

ę

zda

ń

zawartych w bazie wiedzy KB.

Podniesienie

(lifting) - wykonanie podstawie

ń

które pozwalaj

ą

prowadzi

ć

wnioskowanie w bazie FOL.

Przykład liftingu - uogólniona reguła odrywania (Generalized
Modus Ponens).

9.2. Podniesienie i unifikacja

Unifikacja

Unifikacja

jest to procedura rekurencyjna pozwalaj

ą

ca

sprawdzi

ć

, czy istnieje podstawienie sprowadzaj

ą

ce dwa

wyra

ż

enia do takiej samej postaci.

Przykłady:

• Kobieta(Anna)

i

M

ęż

czyzna(Jan)

nie unifikuj

ą

si

ę

;

• Kobieta(Anna)

i

Kobieta(Anna)

unifikuj

ą

si

ę

trywialnie;

• Kobieta(Anna)

i

Kobieta(Maria)

nie unifikuj

ą

si

ę

, gdy

ż

maj

ą

© F.A. Dul 2007

• Kobieta(Anna)

i

Kobieta(Maria)

nie unifikuj

ą

si

ę

, gdy

ż

maj

ą

ró

ż

ne argumenty;

• Król(x)

i

Chciwy(x)

oraz

Król(Jan)

i

Chciwy(y).

Podstawienie

α

= { x/Jan, y/Jan }

unifikuje obie pary zda

ń

.

Unifikacja zda

ń

α

,

β

za pomoc

ą

podstawienia

θ

mo

ż

e by

ć

zdefiniowana nast

ę

puj

ą

co

Unify(

α

,

β

) =

θ

je

ż

eli Subst(

θ

,

α

) = Subst(

θ

,

β

)

Unifikacja

p

q

θθθθ

Zna(Jan,x)

Zna(Jan,Maria)

9.2. Podniesienie i unifikacja

Przykłady problemów unifikacji:

© F.A. Dul 2007

Unifikacja

p

q

θθθθ

Zna(Jan,x)

Zna(Jan,Maria)

{x/Maria}

9.2. Podniesienie i unifikacja

Przykłady problemów unifikacji:

© F.A. Dul 2007

Unifikacja

p

q

θθθθ

Zna(Jan,x)

Zna(Jan,Maria)

{x/Maria}

Zna(Jan,x)

Zna(y,OJ)

9.2. Podniesienie i unifikacja

Przykłady problemów unifikacji:

© F.A. Dul 2007

Unifikacja

p

q

θθθθ

Zna(Jan,x)

Zna(Jan,Maria)

{x/Maria}

Zna(Jan,x)

Zna(y,OJ)

{x/OJ,y/Jan}

9.2. Podniesienie i unifikacja

Przykłady problemów unifikacji:

© F.A. Dul 2007

Unifikacja

p

q

θθθθ

Zna(Jan,x)

Zna(Jan,Maria)

{x/Maria}

Zna(Jan,x)

Zna(y,OJ)

{x/OJ,y/Jan}

Zna(Jan,x)

Zna(y,Matka(y))

9.2. Podniesienie i unifikacja

Przykłady problemów unifikacji:

© F.A. Dul 2007

Unifikacja

p

q

θθθθ

Zna(Jan,x)

Zna(Jan,Maria)

{x/Maria}

Zna(Jan,x)

Zna(y,OJ)

{x/OJ,y/Jan}

Zna(Jan,x)

Zna(y,Matka(y))

{y/Jan,x/Matka(Jan)}

9.2. Podniesienie i unifikacja

Przykłady problemów unifikacji:

© F.A. Dul 2007

Unifikacja

p

q

θθθθ

Zna(Jan,x)

Zna(Jan,Maria)

{x/Maria}

Zna(Jan,x)

Zna(y,OJ)

{x/OJ,y/Jan}

Zna(Jan,x)

Zna(y,Matka(y))

{y/Jan,x/Matka(Jan)}

Zna(Jan,x)

Zna(x,OJ)

9.2. Podniesienie i unifikacja

Przykłady problemów unifikacji:

© F.A. Dul 2007

Unifikacja

p

q

θθθθ

Zna(Jan,x)

Zna(Jan,Maria)

{x/Maria}

Zna(Jan,x)

Zna(y,OJ)

{x/OJ,y/Jan}

Zna(Jan,x)

Zna(y,Matka(y))

{y/Jan,x/Matka(Jan)}

Zna(Jan,x)

Zna(x,OJ)

{brak}

9.2. Podniesienie i unifikacja

Przykłady problemów unifikacji:

© F.A. Dul 2007

Nie mo

ż

na podstawi

ć

{x/Jan}

bo otrzymamy

Zna(Jan,Jan)

niezgodne ze

Zna(Jan,OJ)

- wyst

ą

piło nakładanie si

ę

nazw

zmiennych.

Aby usun

ąć

konflikt nazw zast

ę

pujemy zmienn

ą

x w jednym

ze zda

ń

(np. w drugim) inn

ą

zmienn

ą

, np.

z

17

. Otrzymujemy

Zna(Jan,x) , Zna(z

17

,OJ)

Jest to

standaryzacja

która eliminuje konflikty nazw.

Unifikacja

• Aby zunifikowa

ć

Zna(Jan,x)

oraz

Zna(y,z),

mo

ż

na u

ż

y

ć

ró

ż

nych podstawie

ń

(unifikatorów), np.:

α

= { y/Jan, x/z }

→

Zna(Jan,z)

oraz

Zna(Jan,z),

lub

α

= { y/Jan, x/Jan, z/Jan }

→

Zna(Jan,Jan)

oraz

Zna(Jan,Jan)

9.2. Podniesienie i unifikacja

Przykłady problemów unifikacji:

© F.A. Dul 2007

→

Zna(Jan,Jan)

oraz

Zna(Jan,Jan)

• Pierwszy unifikator jest

ogólniejszy

ni

ż

drugi.

• Istnieje jedyny

unifikator najogólniejszy

(most general

unificator, MGU) okre

ś

lony z dokładno

ś

ci

ą

do zmiany

nazw zmiennych.

MGU = { y/Jan, x/z }

Algorytm unifikacji

9.2. Podniesienie i unifikacja

© F.A. Dul 2007

Uogólniona reguła odrywania (Generalized Modus
Ponens)

p

1

', p

2

', … , p

n

', ( p

1

∧

p

2

∧

…

∧

p

n

⇒

q)



Subst(

θ

,q)

gdzie Subst(

θ

,p

i

’) = Subst(

θ

,p

i

) dla ka

ż

dego i.

9.2. Podniesienie i unifikacja

Przykład

p

1

'

oznacza

Król(Jan)

p

1

oznacza

Król(x)

p '

oznacza

Chciwy(y)

p

oznacza

Chciwy(x)

© F.A. Dul 2007

p

2

'

oznacza

Chciwy(y)

p

2

oznacza

Chciwy(x)

θ

oznacza

{x/Jan,y/Jan}

q

oznacza

Zły(x)

Subst(

θ

,q)

oznacza

Zły(Jan)

• Uogólniona reguła odrywania (GMP) jest u

ż

ywana dla

bazy wiedzy zło

ż

onej z

klauzul Horna

(tj. zawieraj

ą

cych

dokładnie jeden

literał niezanegowany)

• Zakłada si

ę

,

ż

e wszystkie zmienne s

ą

kwantyfikowane

ogólnie.

Poprawno

ść

uogólnionej reguły odrywania

p

1

', p

2

', … , p

n

', ( p

1

∧

p

2

∧

…

∧

p

n

⇒

q) l= Subst(

θ

,q)

przy zało

ż

eniu,

ż

e Subst(

θ

,p

i

’) = Subst(

θ

,p

i

) dla ka

ż

dego i.

9.2. Podniesienie i unifikacja

Nale

ż

y wykaza

ć

,

ż

e

Lemat Dla ka

ż

dego zdania p zachodzi p

l=

Subst(

θ

,p)

poprzez podstawienie uniwersalne.

Dowód poprawno

ś

ci GMP (

oznaczenie: Subst(

θ

,p)

≡

p

θ

)

© F.A. Dul 2007

• (p

1

∧

…

∧

p

n

⇒

q)

l=

(p

1

∧

…

∧

p

n

⇒

q)

θ

(z lematu)

• (p

1

∧

…

∧

p

n

⇒

q)

θ

= (p

1

θ ∧

…

∧

p

n

θ

⇒

q

θ

)

• p

1

', …, p

n

'

l=

p

1

'

∧

…

∧

p

n

'

• p

1

'

∧

…

∧

p

n

'

l=

p

1

'

θ ∧

…

∧

p

n

'

θ

(z lematu)

• st

ą

d, i na mocy zwykłej reguły odrywana wynika

p

1

', p

2

', … , p

n

', ( p

1

∧

p

2

∧

…

∧

p

n

⇒

q)

l=

q

θ

Dowód poprawno

ś

ci GMP (

oznaczenie: Subst(

θ

,p)

≡

p

θ

)

9.3. Algorytmy FOL wnioskowania w przód i wstecz

Algorytmy wnioskowania w przód i wstecz dla FOL i logiki
zda

ń

s

ą

identyczne.

Wnioskowanie w przód dla KB FOL

• Zaczynamy od zda

ń

w bazie KB FOL opisuj

ą

cych fakty;

• Stosujemy uogólnion

ą

reguł

ę

odrywania dla FOL

do wyprowadzenia nowych zda

ń

;

• Dodajemy nowe zdania do bazy KB FOL;
• Wnioskowanie ko

ń

czymy, je

ż

eli wyprowadzimy udowadnia-

© F.A. Dul 2007

Wnioskowanie wstecz dla KB FOL

• Zaczynamy od zdania, które jest zapytaniem do KB FOL;
• Stosujemy uogólnion

ą

reguł

ę

odrywania dla FOL

znajduj

ą

c zdania z których wynika udowadniane zdanie;

• Wnioskowanie ko

ń

czymy, je

ż

eli przesłankami zdania

aktualnie dowodzonego b

ę

d

ą

zdania bazy KB FOL

które opisuj

ą

fakty dowiedzione;

• Wnioskowanie ko

ń

czymy, je

ż

eli wyprowadzimy udowadnia-

ne zdanie lub gdy dalsze wnioskowanie nie jest mo

ż

liwe;

Przykład wnioskowania z bazy wiedzy FOL

9.3. Algorytmy FOL wnioskowania w przód i wstecz

• Prawo USA stanowi,

ż

e przest

ę

pstwem jest sprzeda

ż

broni do krajów wrogich.

• Kraj Nono, wróg USA, posiada pewn

ą

liczb

ę

rakiet.

• Wszystkie te rakiety zostały sprzedane Nono przez

niejakiego pułkownika Westa.

• Pułkownik West jest Amerykaninem.

Baza wiedzy KB FOL zawiera nast

ę

puj

ą

ce zdania:

© F.A. Dul 2007

• Pułkownik West jest Amerykaninem.

Dowie

ść

,

ż

e w

ś

wietle prawa ameryka

ń

skiego pułkownik

West jest przest

ę

pc

ą

.

Przykład wnioskowania z bazy wiedzy FOL

9.3. Algorytmy FOL wnioskowania w przód i wstecz

Baza wiedzy w postaci zda

ń

FOL:

... jest przest

ę

pstwem gdy Amerykanin sprzedaje bro

ń

krajom wrogim:

American(x

∧

Sells(x,y,z) )

∧

Weapon(y)

∧

Hostile(z)

⇒

Criminal(x)

Nono … posiada pewn

ą

liczb

ę

rakiet, tj.,

∃

x Owns(Nono,x)

∧

Missile(x)

Owns(Nono,M

1

) i Missile(M

1

)

… wszystkie rakiety zostały sprzedanie Nono prze pułkownika Westa

Missile(x)

∧

Owns(Nono,x)

⇒

Sells(West,x,Nono)

© F.A. Dul 2007

Missile(x)

∧

Owns(Nono,x)

⇒

Sells(West,x,Nono)

Rakiety s

ą

broni

ą

:

Missile(x)

⇒

Weapon(x)

Wróg Ameryki jest wrogiem:

Enemy(x,America)

⇒

Hostile(x)

West jest Amerykaninem …

American(West)

Kraj Nono, wróg Ameryki …

Enemy(Nono,America)

Algorytm wnioskowania w przód

9.3. Algorytmy FOL wnioskowania w przód i wstecz

© F.A. Dul 2007

Dowód poprzez wnioskowanie w przód

9.3. Algorytmy FOL wnioskowania w przód i wstecz

© F.A. Dul 2007

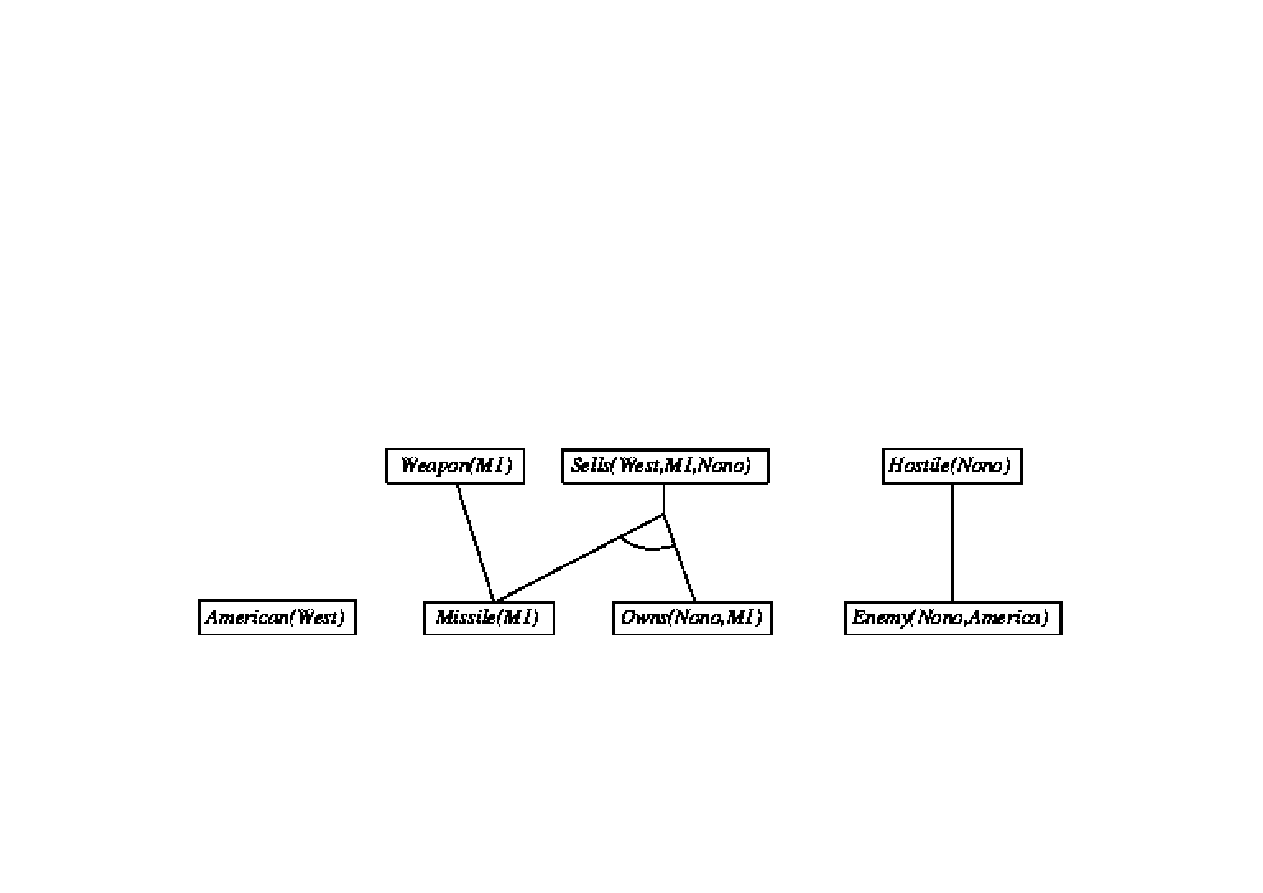
Dowód poprzez wnioskowanie w przód

9.3. Algorytmy FOL wnioskowania w przód i wstecz

© F.A. Dul 2007

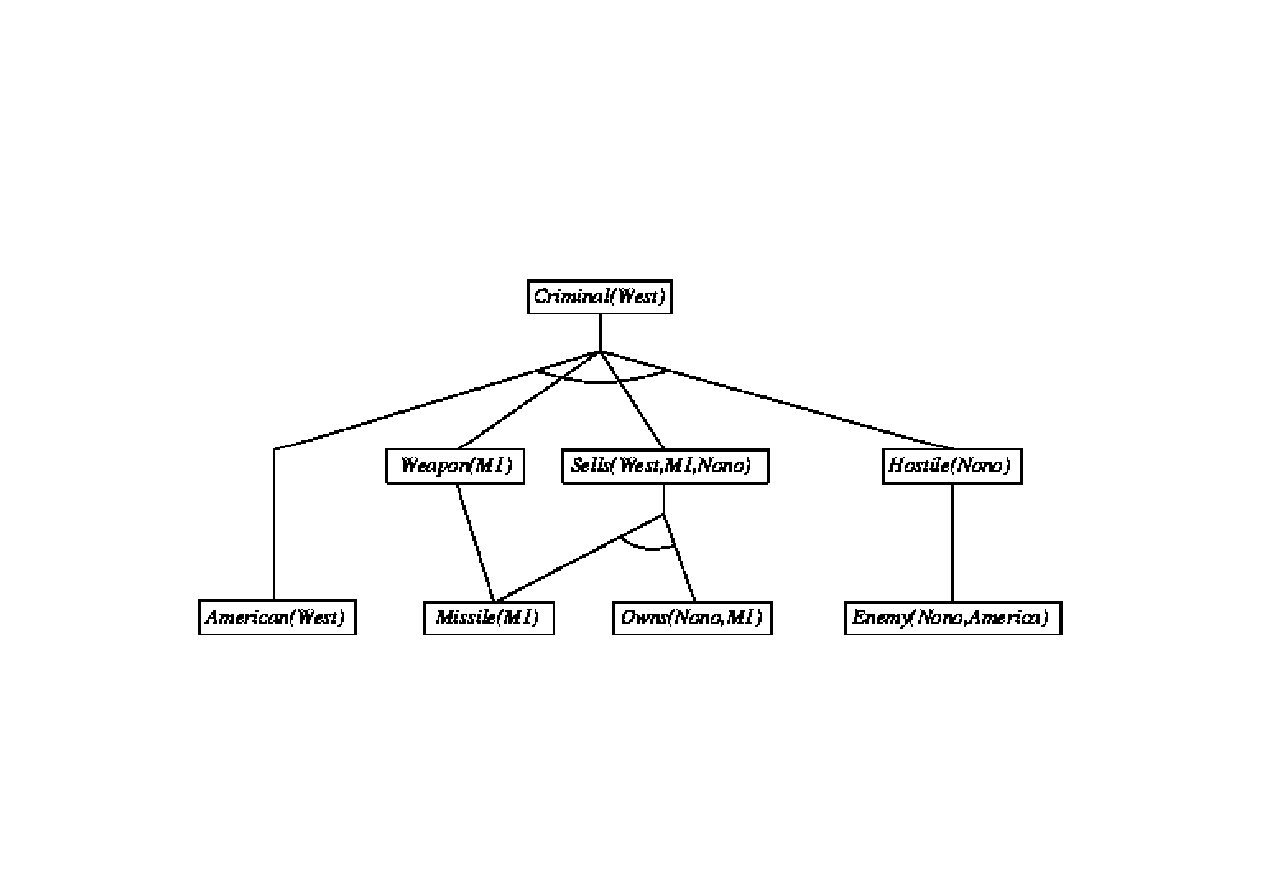
Dowód poprzez wnioskowanie w przód

9.3. Algorytmy FOL wnioskowania w przód i wstecz

© F.A. Dul 2007

Własno

ś

ci wnioskowania w przód

9.3. Algorytmy FOL wnioskowania w przód i wstecz

• Wnioskowanie w przód jest poprawne i zupełne dla bazy

w postaci klauzul Horna pierwszego rz

ę

du.

• Wnioskowanie w przód dla klauzuli Horna pierwszego

rz

ę

du

nie zawieraj

ą

cych funkcji

wymaga sko

ń

czonej

liczby kroków.

• Wnioskowanie w przód w przypadku ogólnym mo

ż

e si

ę

nie zako

ń

czy

ć

je

ż

eli zapytanie nie wynika z bazy FOL.

• Nie mo

ż

na temu zaradzi

ć

; wynikanie z klauzulami Horna

© F.A. Dul 2007

• Nie mo

ż

na temu zaradzi

ć

; wynikanie z klauzulami Horna

pierwszego rz

ę

du jest półrozstrzygalne (patrz twierdzenie

Turinga-Churcha).

Efektywno

ść

wnioskowania w przód

9.3. Algorytmy FOL wnioskowania w przód i wstecz

• Przyrostowe wnioskowanie w przód nie musi

dopasowywa

ć

reguł w k-tym kroku je

ż

eli w kroku k-1

nie została dodana nowa przesłanka.

• Dopasowanie reguł nast

ę

puje wtedy, gdy przesłanka

zawiera nowo dodany literał pozytywny.

• Dopasowanie jest kosztowne.

• Indeksowanie

bazy wiedzy pozwala uzyska

ć

informacje

o znanych faktach kosztem O(1).

© F.A. Dul 2007

• Indeksowanie

bazy wiedzy pozwala uzyska

ć

informacje

o znanych faktach kosztem O(1).

Np. zapytanie Missile(x) zwraca Missile(M

1

).

• Dopasowanie przesłanek do znanych faktów jest

zadaniem NP-hard.

• Wnioskowanie w przód jest szeroko u

ż

ywane

w

dedukcyjnych bazach wiedzy

.

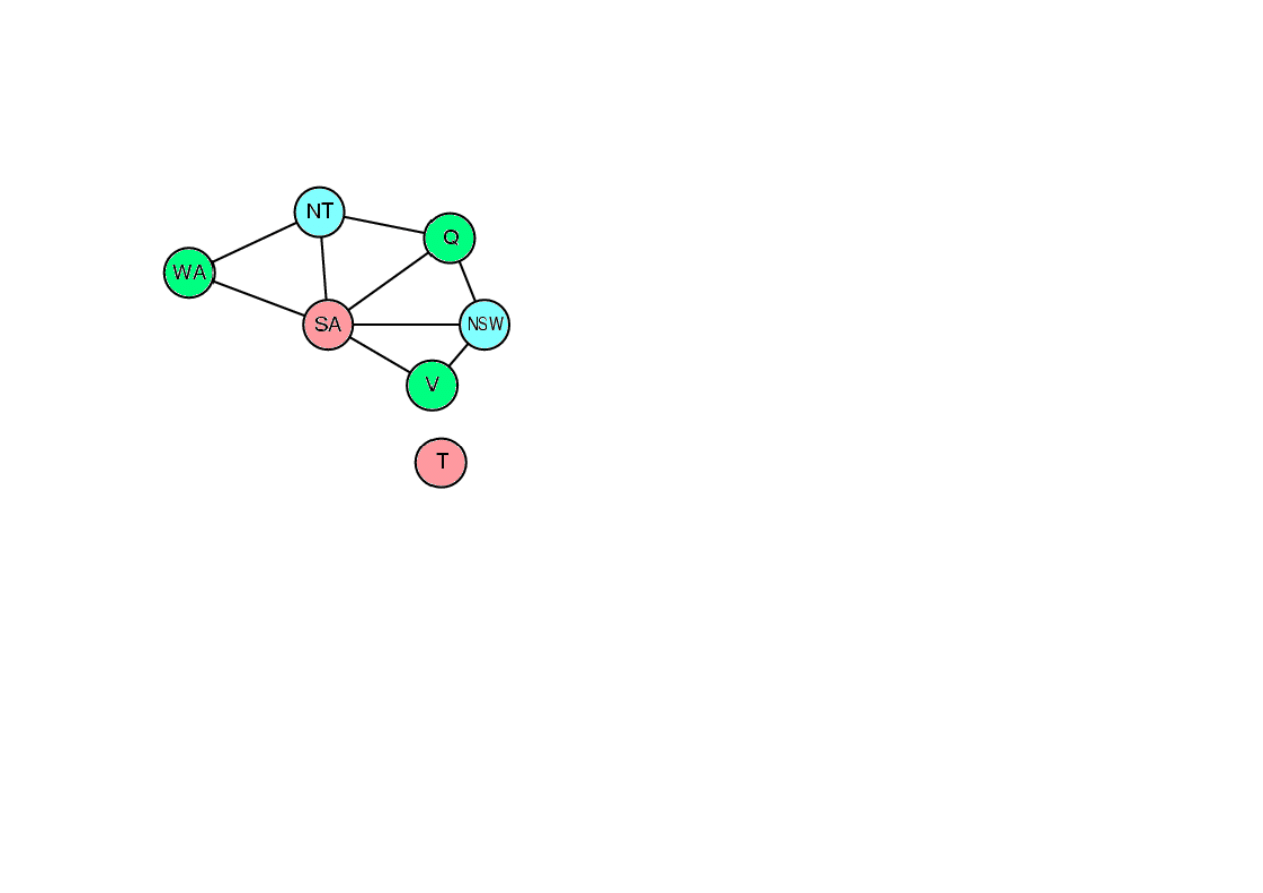
Przykład zadania trudno dopasowalnego

9.3. Algorytmy FOL wnioskowania w przód i wstecz

Diff(wa,nt)

∧

Diff(wa,sa)

∧

Diff(nt,q)

∧

Diff(nt,sa)

∧

Diff(q,nsw)

∧

Diff(q,sa)

∧

Diff(nsw,v)

∧

Diff(nsw,sa)

∧

Diff(v,sa)

⇒

Colorable()

Diff(Red,Blue)

Diff (Red,Green)

Diff(Green,Red) Diff(Green,Blue)

© F.A. Dul 2007

• Colorable()

wynika z bazy wiedzy KB FOL wtedy i tylko

wtedy gdy zadanie poszukiwania z ograniczeniami
(CSP) ma rozwi

ą

zanie.

• Zadanie CSP zawiera zadanie 3SAT jako przypadek

szczególny, zatem dopasowanie jest zadaniem NP-hard.

Diff(Blue,Red)

Diff(Blue,Green)

Algorytm wnioskowania wstecz

9.3. Algorytmy FOL wnioskowania w przód i wstecz

© F.A. Dul 2007

Subst( Compose(

α

1

,

α

2

) , p) = Subst(

α

2

,Subst(

α

1

, p))

Dowód poprzez wnioskowanie wstecz

9.3. Algorytmy FOL wnioskowania w przód i wstecz

© F.A. Dul 2007

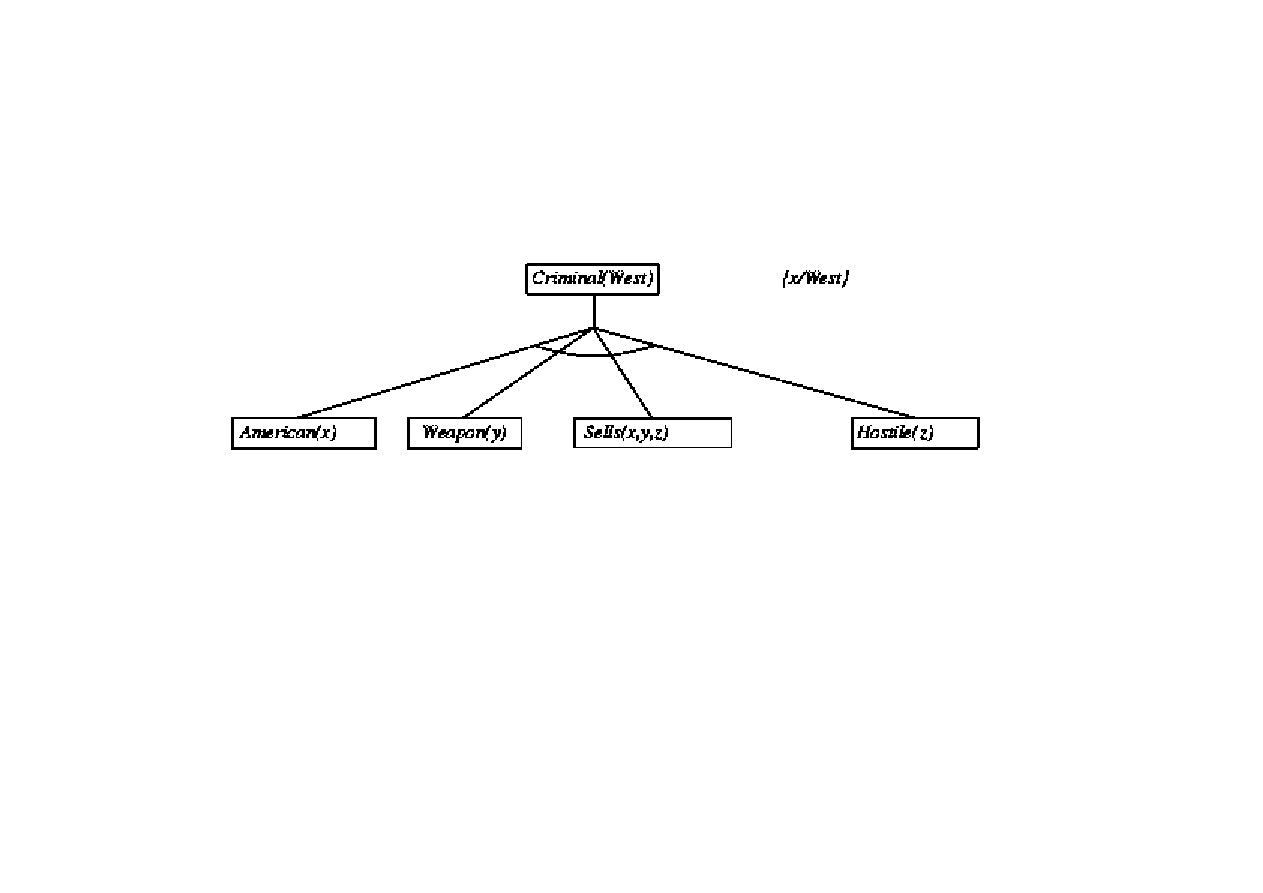
Dowód poprzez wnioskowanie wstecz

9.3. Algorytmy FOL wnioskowania w przód i wstecz

© F.A. Dul 2007

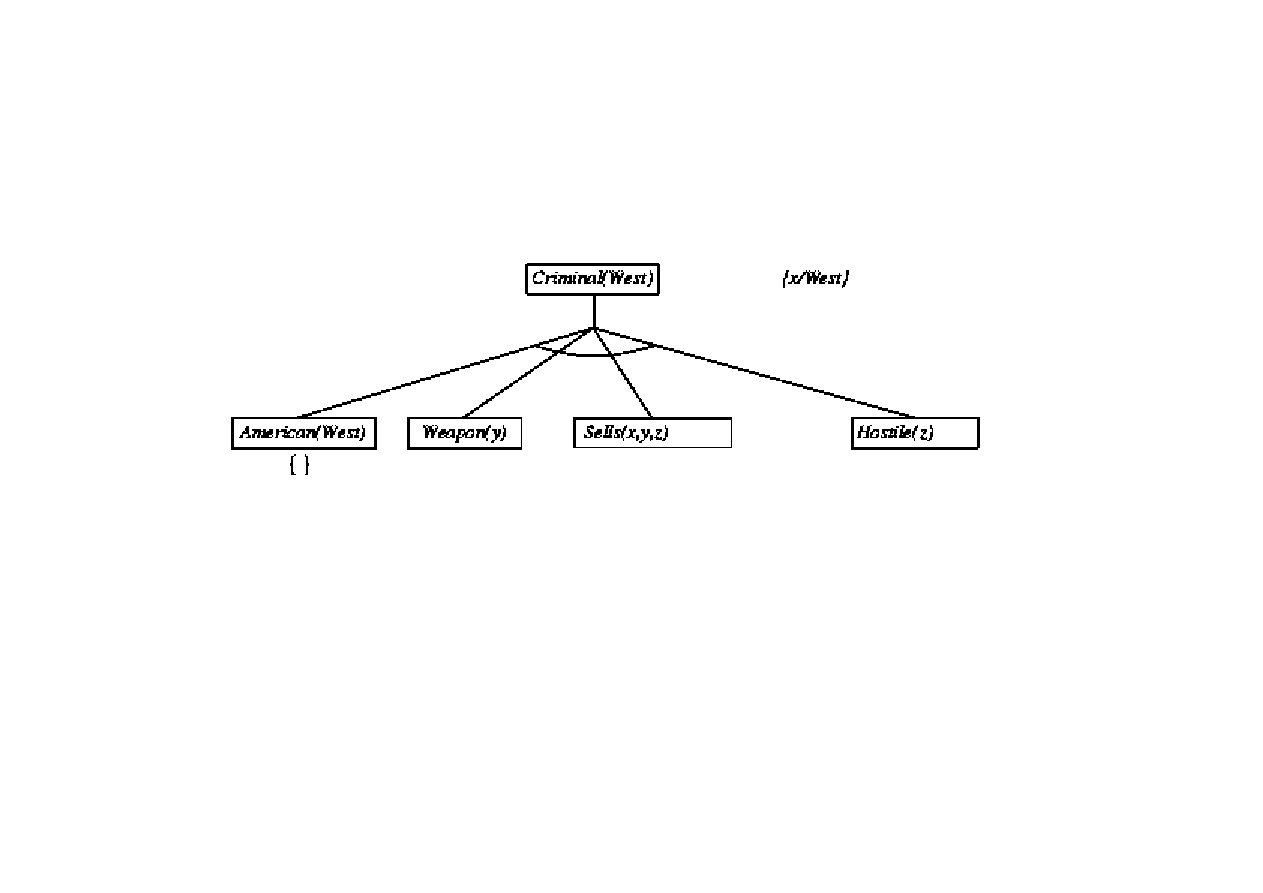
Dowód poprzez wnioskowanie wstecz

9.3. Algorytmy FOL wnioskowania w przód i wstecz

© F.A. Dul 2007

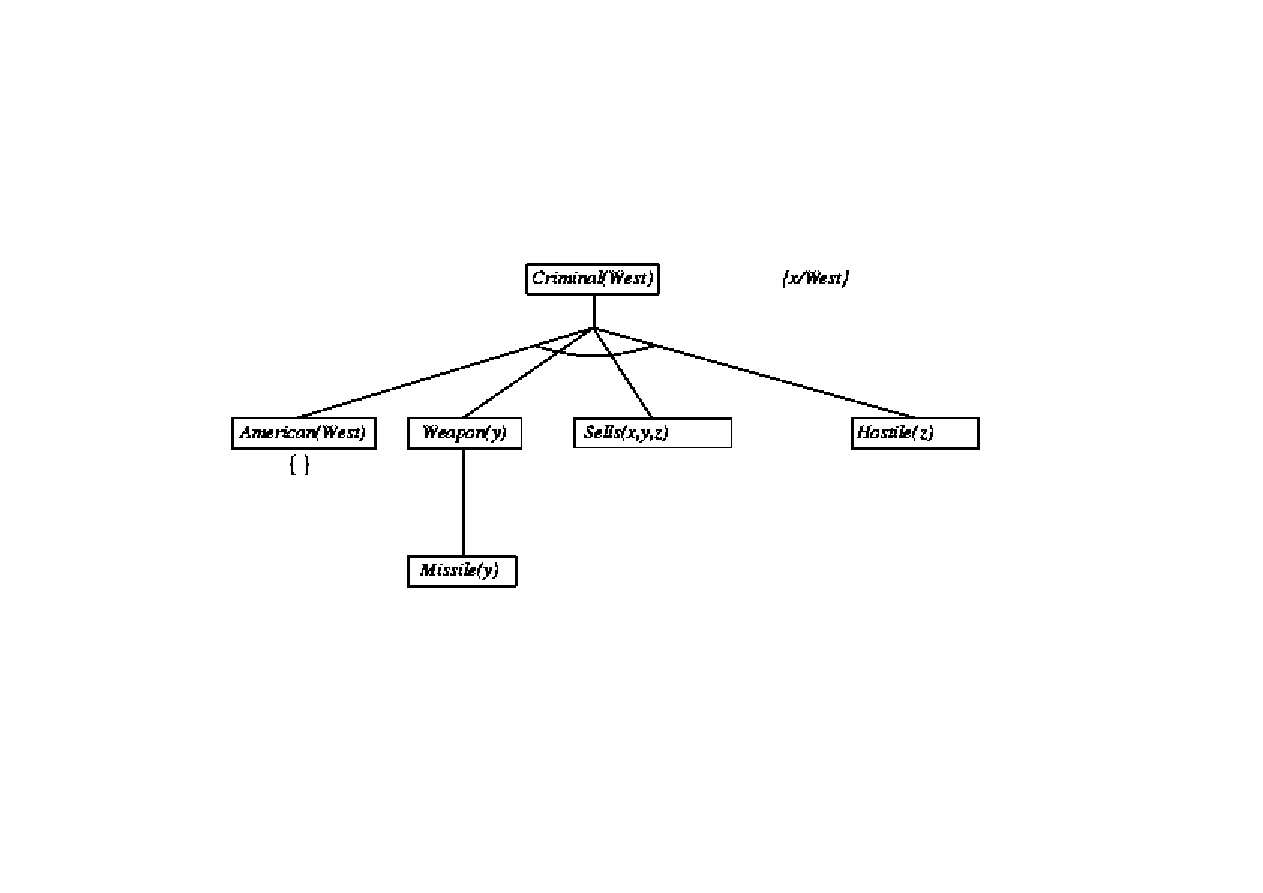
Dowód poprzez wnioskowanie wstecz

9.3. Algorytmy FOL wnioskowania w przód i wstecz

© F.A. Dul 2007

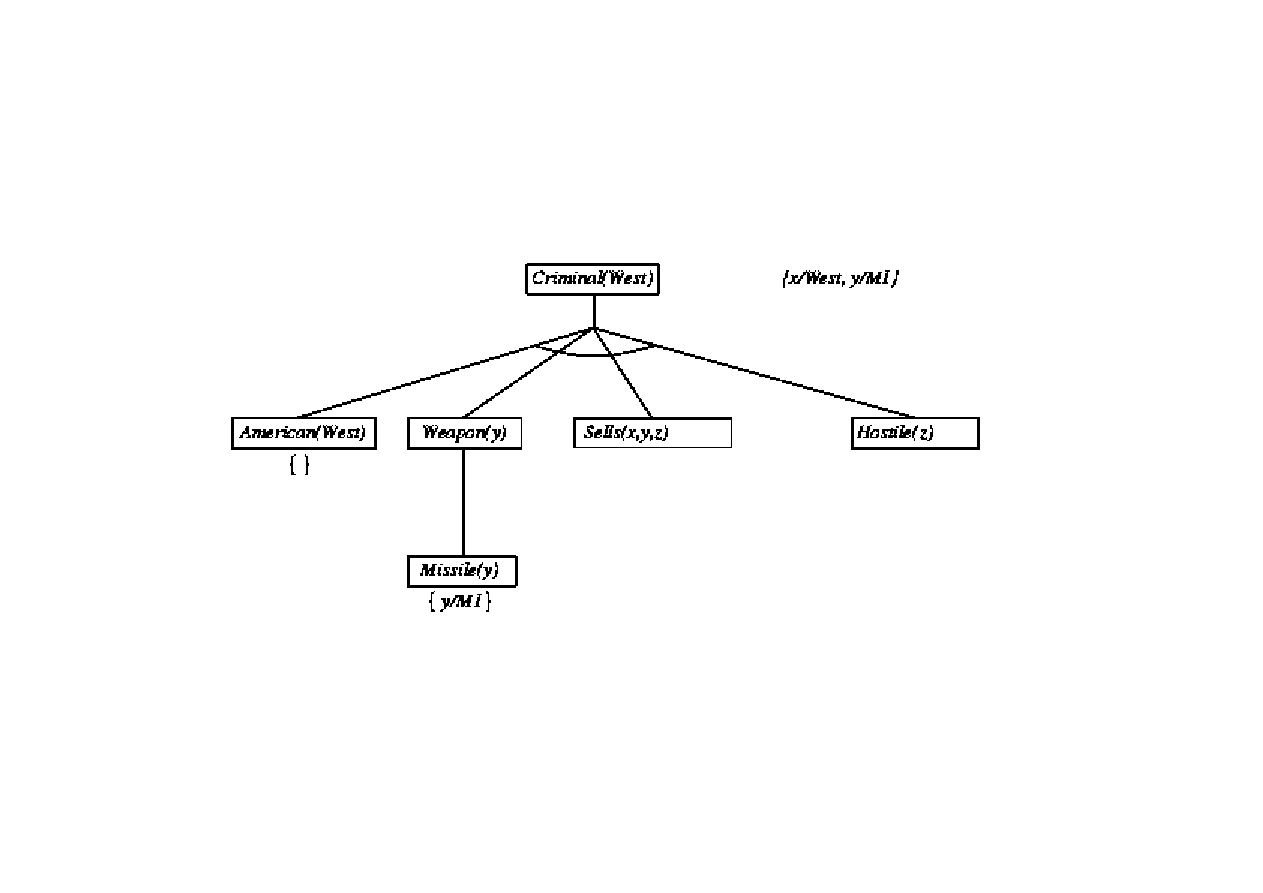
Dowód poprzez wnioskowanie wstecz

9.3. Algorytmy FOL wnioskowania w przód i wstecz

© F.A. Dul 2007

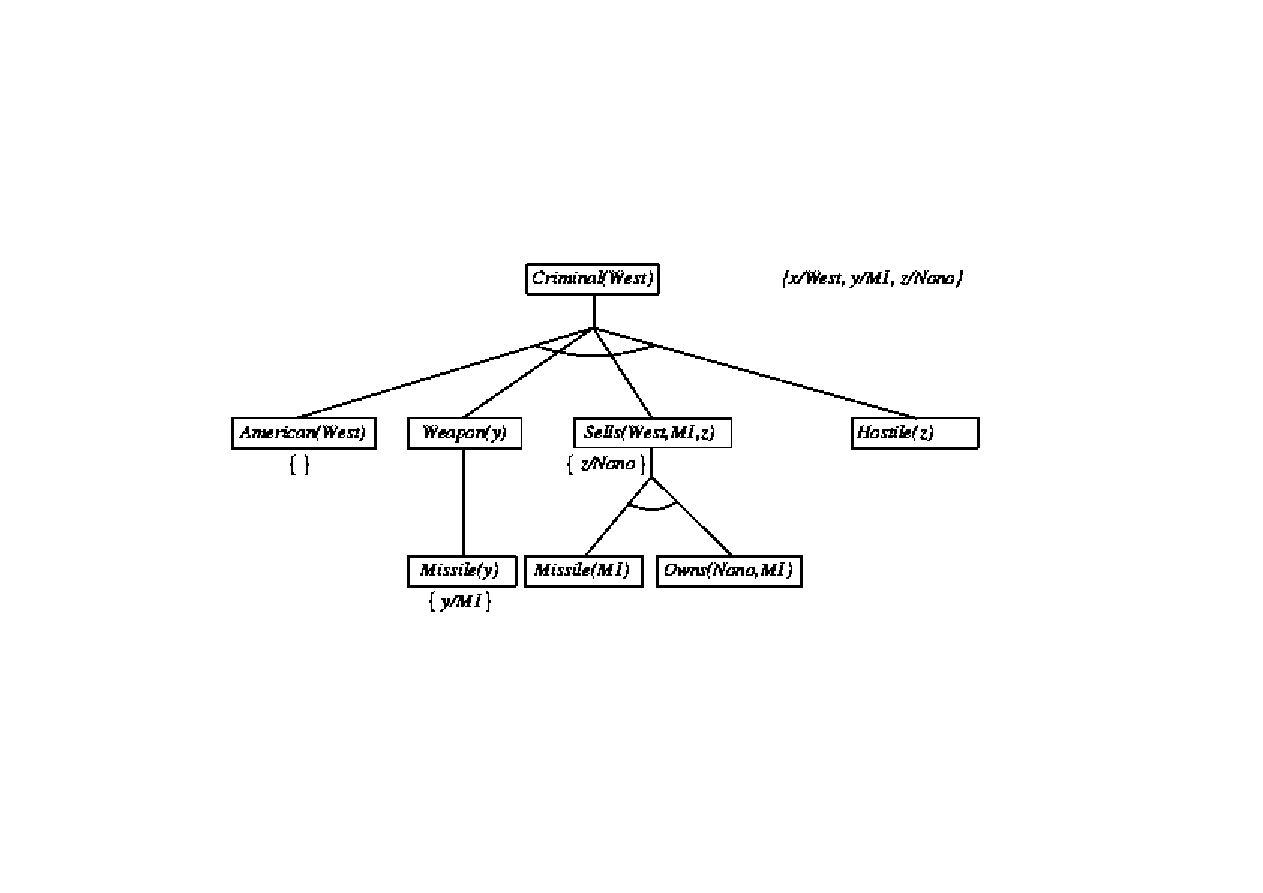
Dowód poprzez wnioskowanie wstecz

9.3. Algorytmy FOL wnioskowania w przód i wstecz

© F.A. Dul 2007

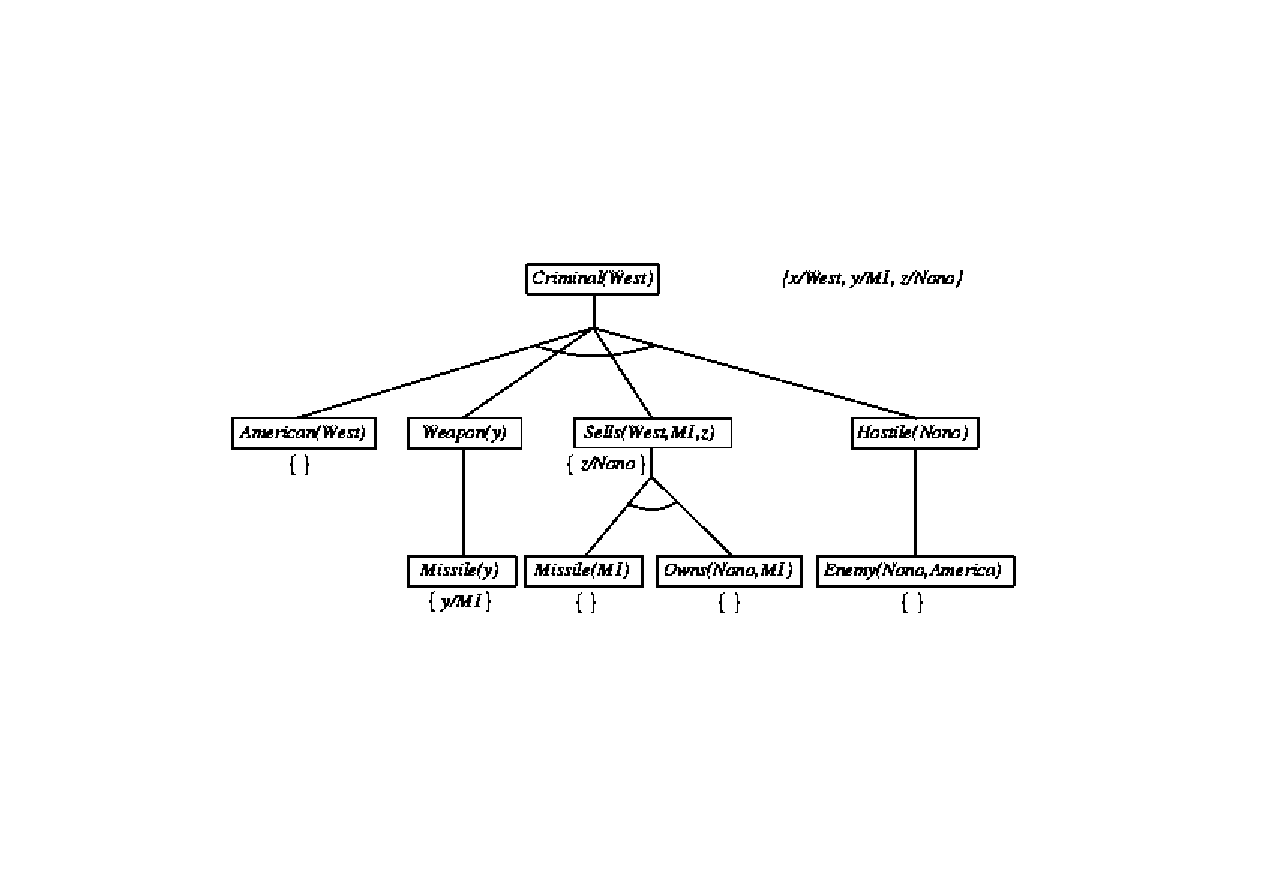
Dowód poprzez wnioskowanie wstecz

9.3. Algorytmy FOL wnioskowania w przód i wstecz

© F.A. Dul 2007

Własno

ś

ci wnioskowania wstecz

9.3. Algorytmy FOL wnioskowania w przód i wstecz

• Przy rekurencyjnym dowodzeniu w gł

ą

b pami

ęć

zale

ż

y

liniowo od długo

ś

ci dowodu.

• Wnioskowanie wstecz jest niezupełne z powodu

mo

ż

liwo

ś

ci zap

ę

tlenia si

ę

algorytmu;

• Mo

ż

na jednak temu zaradzi

ć

poprzez sprawdzenie celu

aktualnego z celami składowanymi na stosie.

• Wnioskowanie wstecz mo

ż

e by

ć

nieefektywne gdy

wielokrotnie sprawdza cele ju

ż

osi

ą

gni

ę

te.

© F.A. Dul 2007

• Wnioskowanie wstecz mo

ż

e by

ć

nieefektywne gdy

wielokrotnie sprawdza cele ju

ż

osi

ą

gni

ę

te.

• Mo

ż

na temu zaradzi

ć

poprzez zapami

ę

tywanie wyników

po

ś

rednich, ale kosztem dodatkowej pami

ę

ci.

• Wnioskowanie wstecz jest szeroko u

ż

ywane

w programowaniu logicznym

.

9.5. Eliminacja (rezolucja)

l

1

∨

···

∨

l

i

∨

···

∨

l

k

, m

1

∨

···

∨

m

k

∨

···

∨

m

n



Subst(

θ

, l

∨

···

∨

l

∨

l

∨

···

∨

l

∨

m

∨

···

∨

m

∨

m

∨

···

∨

m )

Zasada eliminacji pozwala dowodzi

ć

twierdzenia

sformułowane w j

ę

zyku logiki pierwszego rz

ę

du.

Zasada rezolucji umo

ż

liwia tak

ż

e weryfikacj

ę

poprawno

ś

ci

projektów układów elektronicznych oraz dowodzenie
poprawno

ś

ci programów.

Zasada eliminacji dla logiki pierwszego rz

ę

du ma posta

ć

© F.A. Dul 2007



Subst(

θ

, l

1

∨

···

∨

l

i-1

∨

l

i+1

∨

···

∨

l

k

∨

m

1

∨

···

∨

m

j-1

∨

m

j+1

∨

···

∨

m

n

)

gdzie

Unify(l

i

,

¬

m

k

) =

θ

.

Obie klauzule (alternatywy l

j

oraz m

j

) musz

ą

by

ć

standaryzowane, aby nie miały wspólnych zmiennych.

Eliminacja mo

ż

e by

ć

stosowana do bazy FOL przekształconej

do postaci koniunktywnej normalnej (CNF).

Rezolucja mo

ż

e by

ć

zastosowana do udowodnienia zdania

α

poprzez wykazanie,

ż

e ( KB FOL

∧ ¬α

) jest niespełnialne.

9.5. Eliminacja (rezolucja)

Przykład
Dane s

ą

zdania

¬

Bogaty(x)

∨

Nieszcz

ęś

liwy(x)

Bogaty(Jan)

Podstawienie

θ

= { x/Jan }

sprowadza klauzule

¬

Bogaty(x) Bogaty(Jan)

do postaci komplementarnej.

© F.A. Dul 2007

do postaci komplementarnej.

Eliminacja

¬

Bogaty(x)

∨

Nieszcz

ęś

liwy(x) Bogaty(Jan)



Nieszcz

ęś

liwy(Jan)

prowadzi wi

ę

c do wniosku,

ż

e

„Jan jest nieszcz

ęś

liwy”

mimo,

ż

e jest bogaty.

Sprowadzenie zda

ń

FOL do postaci CNF

9.5. Eliminacja (rezolucja)

• Zdanie

“Ka

ż

dy kto kocha wszystkie zwierz

ę

ta jest kochany przez kogo

ś

”.

∀

x [

∀

y Animal(y)

⇒

Loves(x,y) ]

⇒

[

∃

y Loves(y,x) ]

• Eliminacja równowa

ż

no

ś

ci i implikacji

∀

x [

¬∀

y

¬

Animal(y)

∨

Loves(x,y) ]

∨

[

∃

y Loves(y,x) ]

• Reguły negacji kwantyfikatorów,

© F.A. Dul 2007

• Reguły negacji kwantyfikatorów,

¬∀

x p

≡

∃

x

¬

p,

¬∃

x p

≡

∀

x

¬

p

• Przesuni

ę

cie negacji do wn

ę

trza wyra

ż

e

ń

,

∀

x [

∃

y

¬

(

¬

Animal(y)

∨

Loves(x,y)) ]

∨

[

∃

y Loves(y,x) ]

∀

x [

∃

y

¬¬

Animal(y)

∧ ¬

Loves(x,y) ]

∨

[

∃

y Loves(y,x) ]

∀

x [

∃

y Animal(y)

∧ ¬

Loves(x,y) ]

∨

[

∃

y Loves(y,x)]

Sprowadzenie zda

ń

FOL do postaci CNF

9.5. Eliminacja (rezolucja)

• Standaryzacja: ka

ż

dy kwantyfikator musi u

ż

ywa

ć

innej

zmiennej

∀

x [

∃

y Animal(y)

∧ ¬

Loves(x,y) ]

∨

[

∃

z Loves(z,x) ]

• Skolemizacja: ogólna forma podstawienia szczegółowego.

Ka

ż

da zmienna szczegółowa jest zast

ą

piona przez

funkcj

ę

Skolema

zmiennej zewn

ę

trznej kwantyfikatora

ogólnego:

© F.A. Dul 2007

ogólnego:

∀

x

[ Animal(

F(x)

)

∧ ¬

Loves(x,

F(x)

) ]

∨

Loves(

G(x),

x)

• Opuszczenie kwantyfikatora ogólnego

[ Animal(F(x))

∧ ¬

Loves(x,F(x)) ]

∨

Loves(G(x),x)

• Przekształcenie do postaci koniunkcji alternatyw:

[ Animal(F(x))

∨

Loves(G(x),x) ]

∧

[

¬

Loves(x,F(x))

∨

Loves(G(x),x) ]

Dowód rezolucyjny dla kaluzuli Horna

9.5. Eliminacja (rezolucja)

© F.A. Dul 2007

Dowód rezolucyjny dla kaluzuli Horna

9.5. Eliminacja (rezolucja)

{x/West}

© F.A. Dul 2007

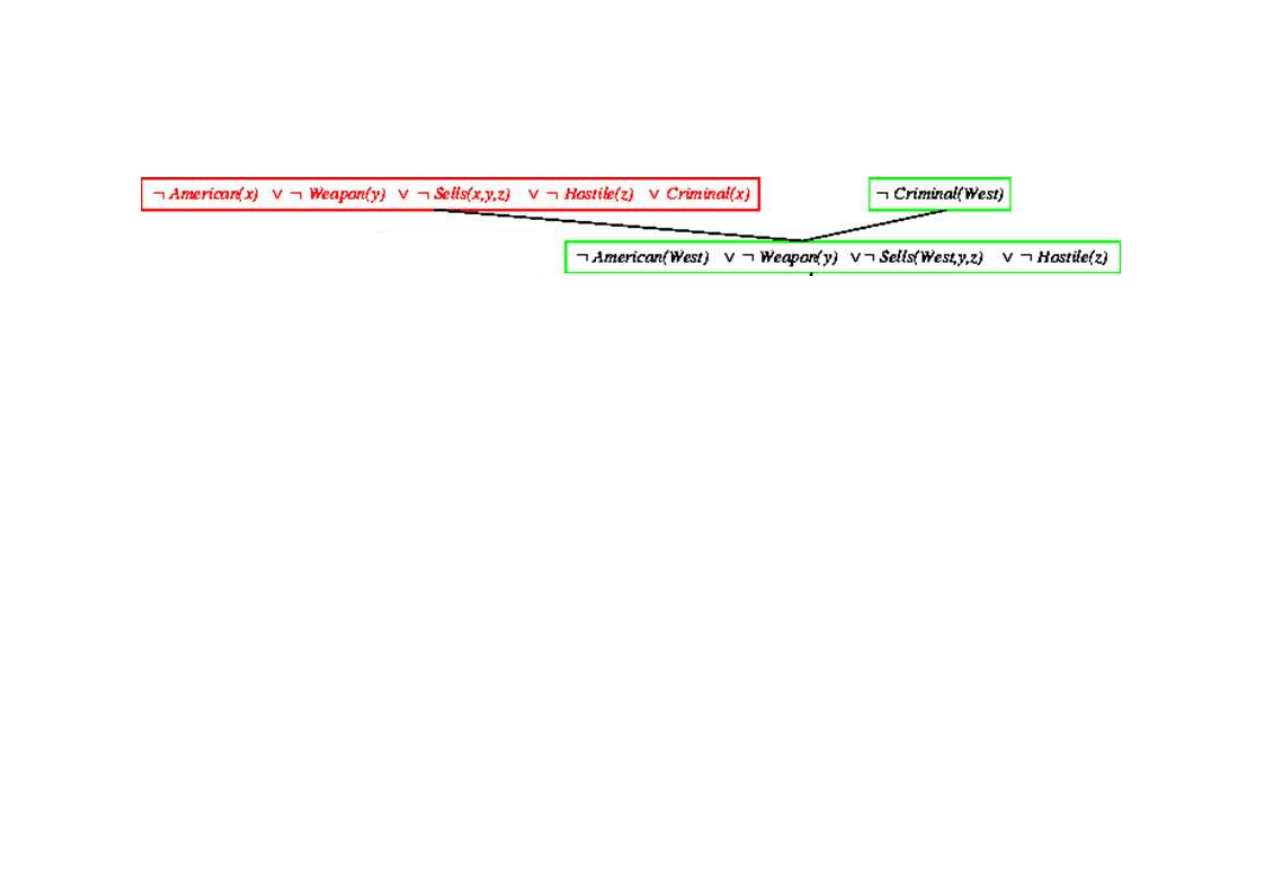
Dowód rezolucyjny dla kaluzuli Horna

9.5. Eliminacja (rezolucja)

{x/West}

© F.A. Dul 2007

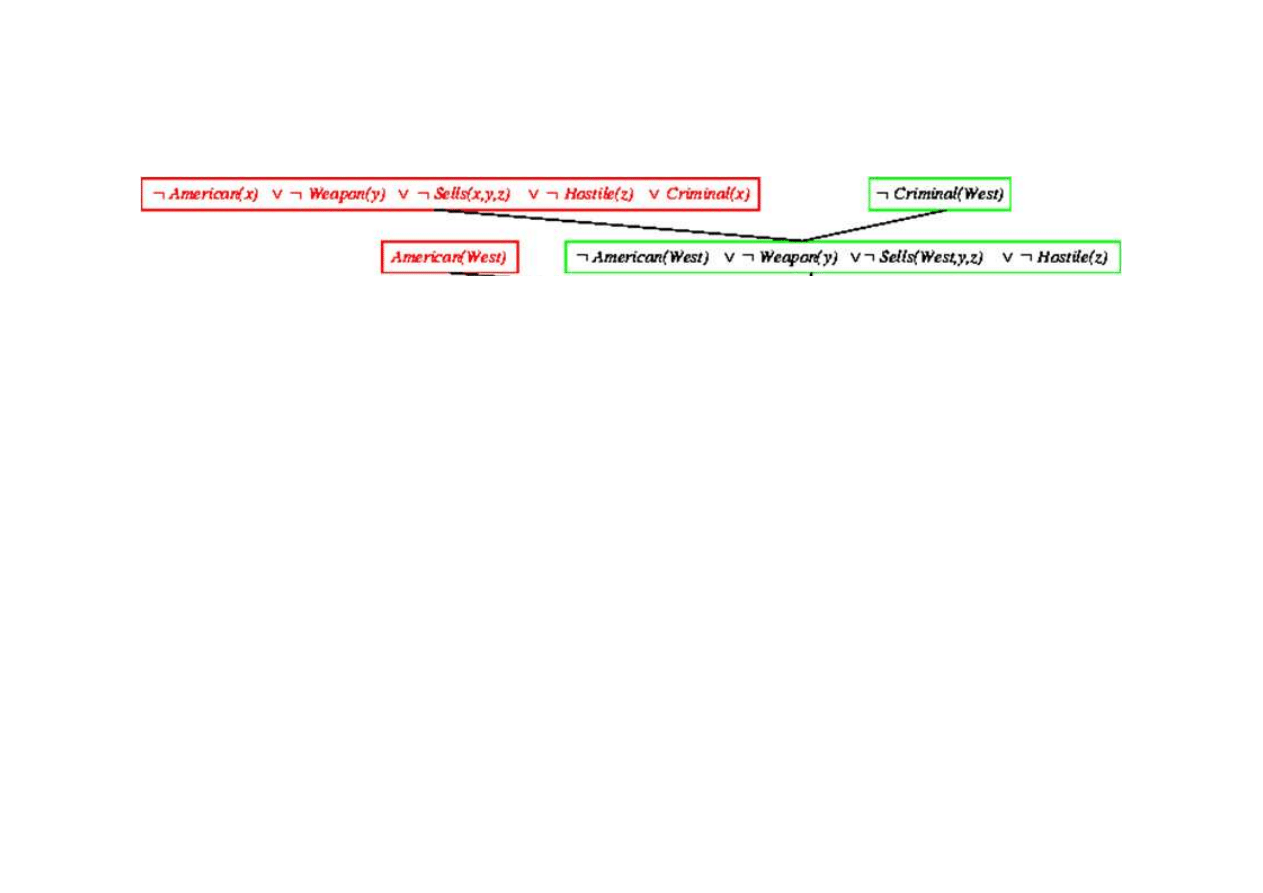
Dowód rezolucyjny dla kaluzuli Horna

9.5. Eliminacja (rezolucja)

{x/West}

© F.A. Dul 2007

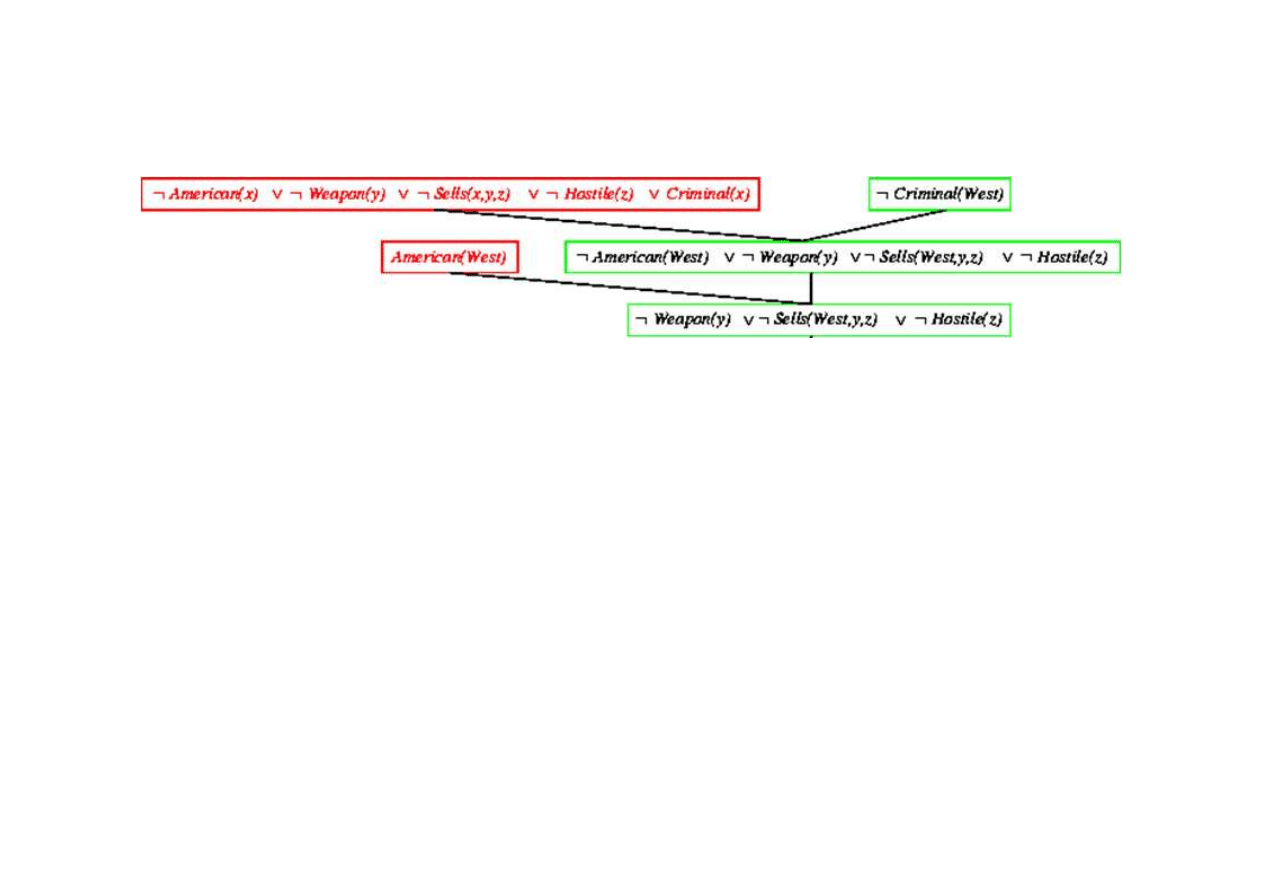
Dowód rezolucyjny dla kaluzuli Horna

9.5. Eliminacja (rezolucja)

{x/West}

© F.A. Dul 2007

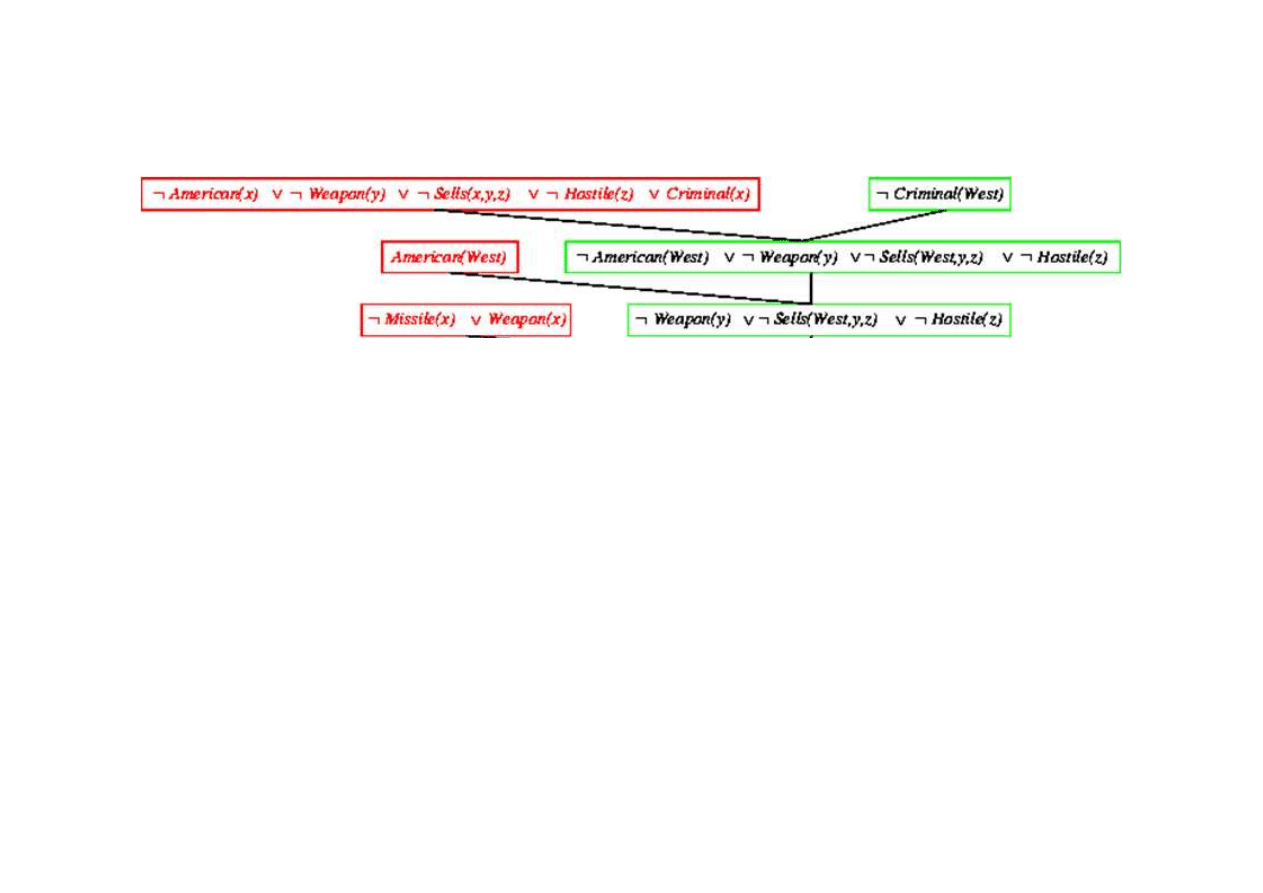
Dowód rezolucyjny dla kaluzuli Horna

9.5. Eliminacja (rezolucja)

{x/West}

{x/y}

© F.A. Dul 2007

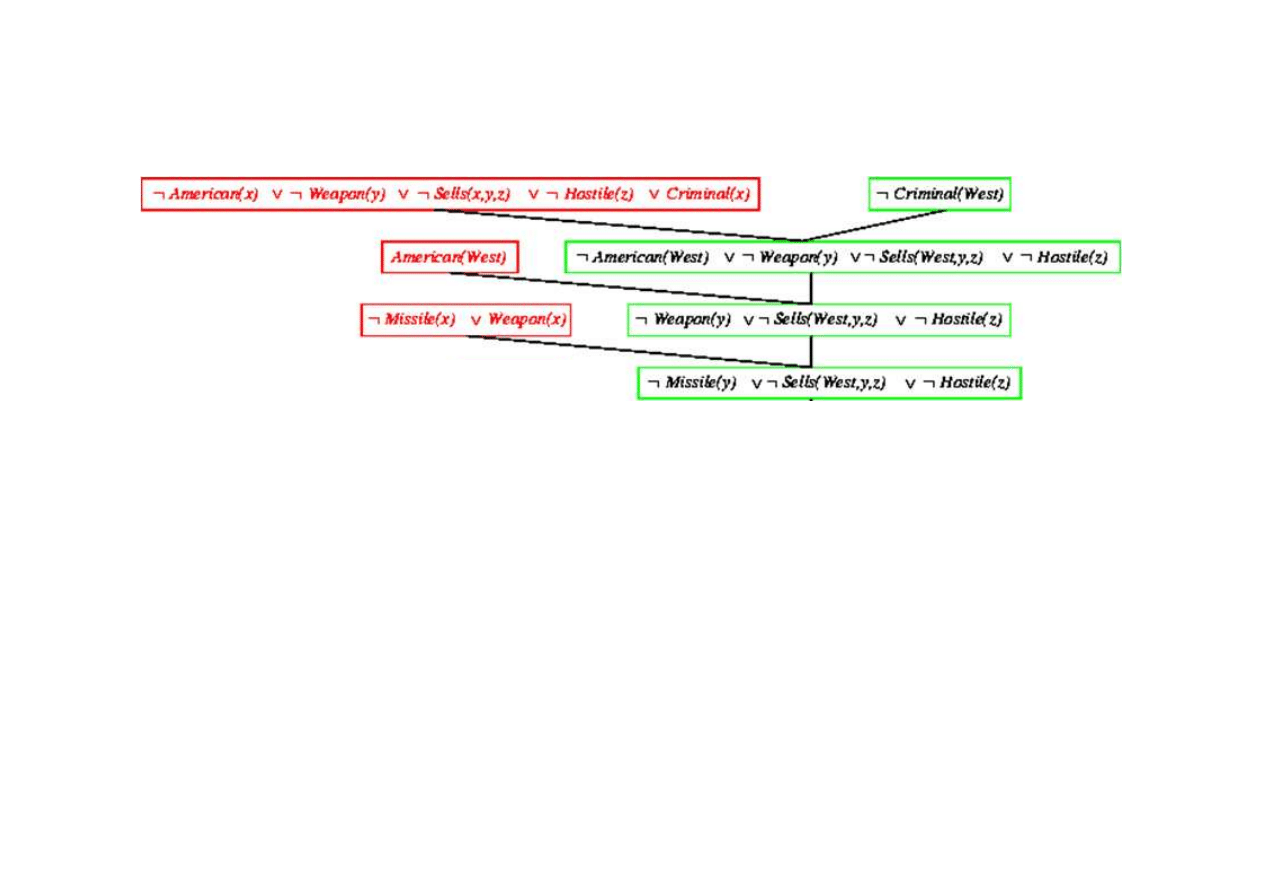
Dowód rezolucyjny dla kaluzuli Horna

9.5. Eliminacja (rezolucja)

{x/West}

{x/y}

© F.A. Dul 2007

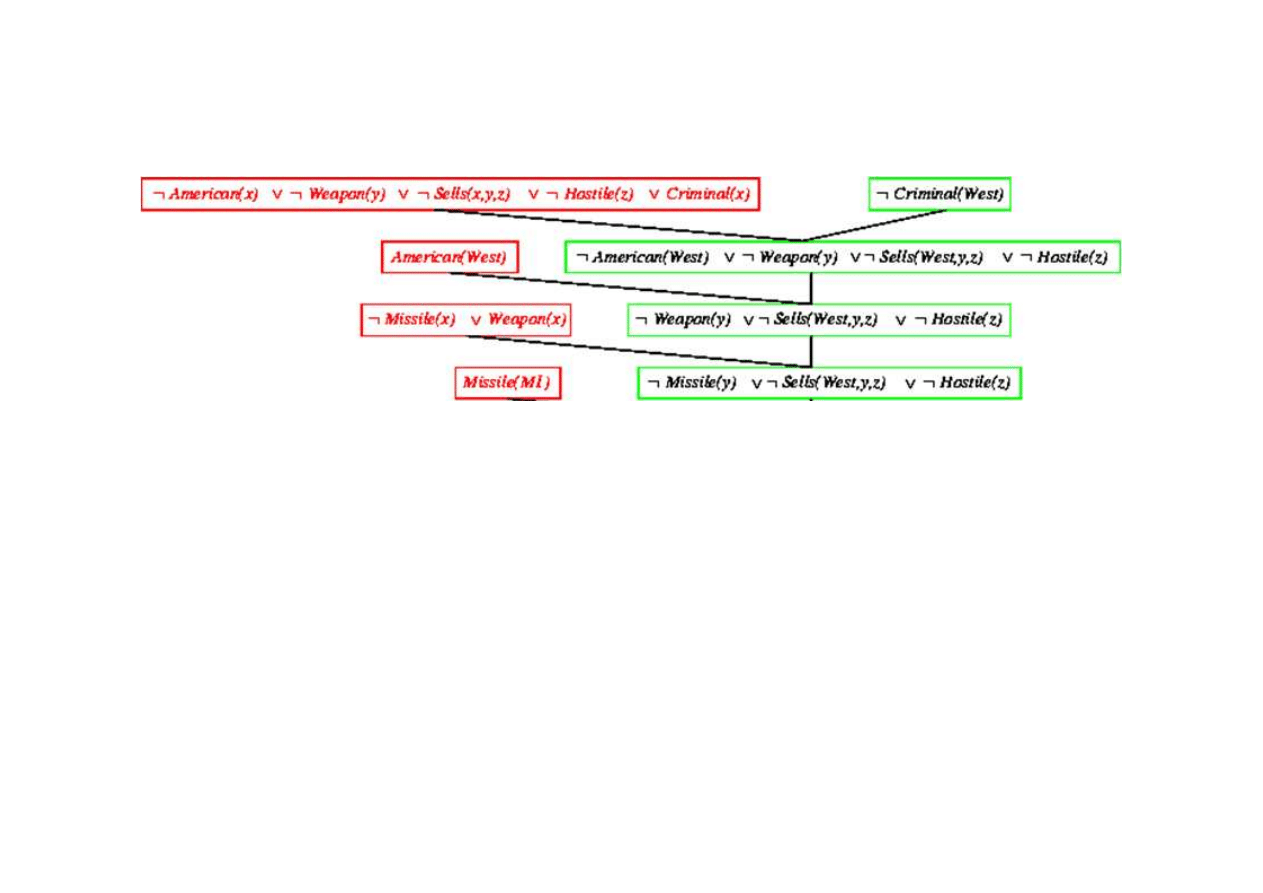
Dowód rezolucyjny dla kaluzuli Horna

9.5. Eliminacja (rezolucja)

{x/West}

{x/y}

{y/M1}

© F.A. Dul 2007

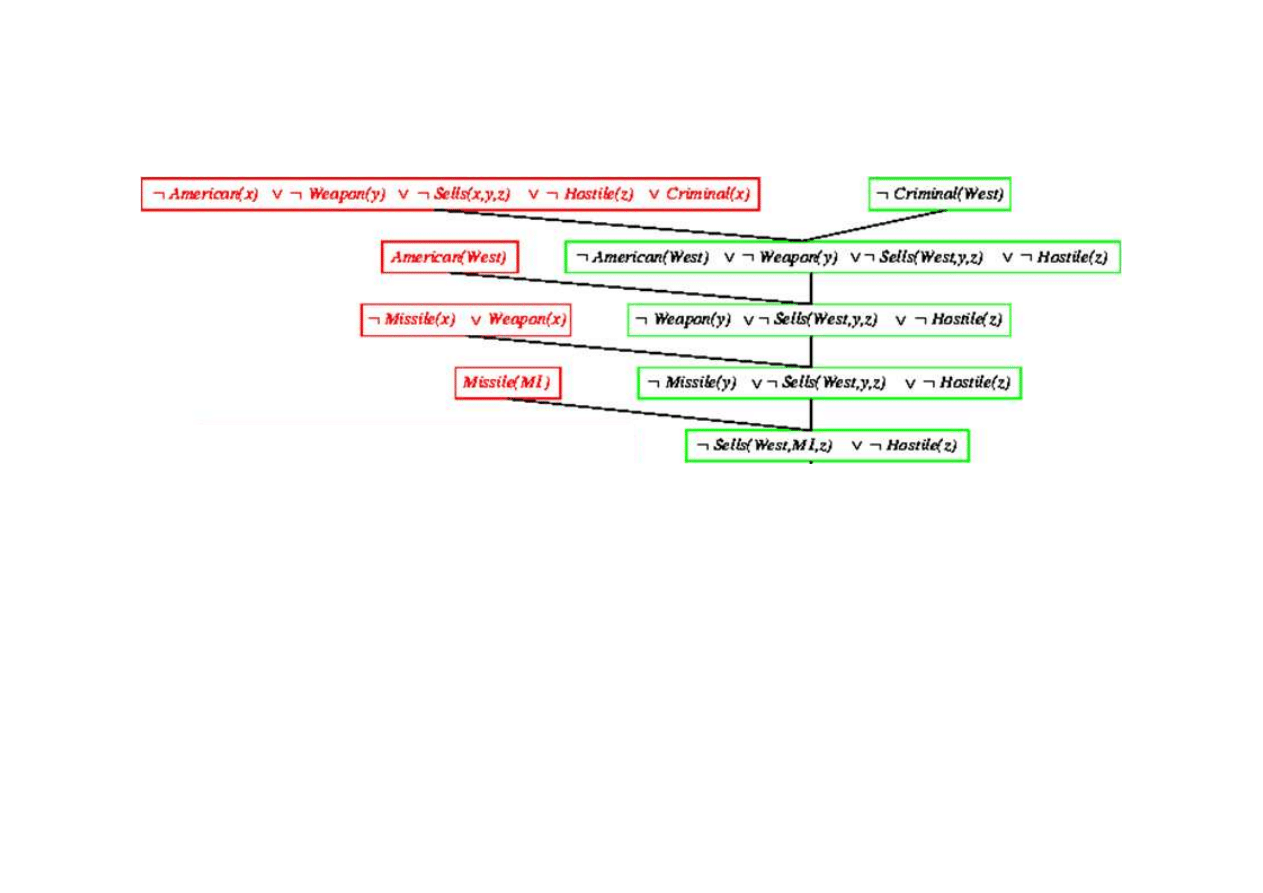
Dowód rezolucyjny dla kaluzuli Horna

9.5. Eliminacja (rezolucja)

{x/West}

{x/y}

{y/M1}

© F.A. Dul 2007

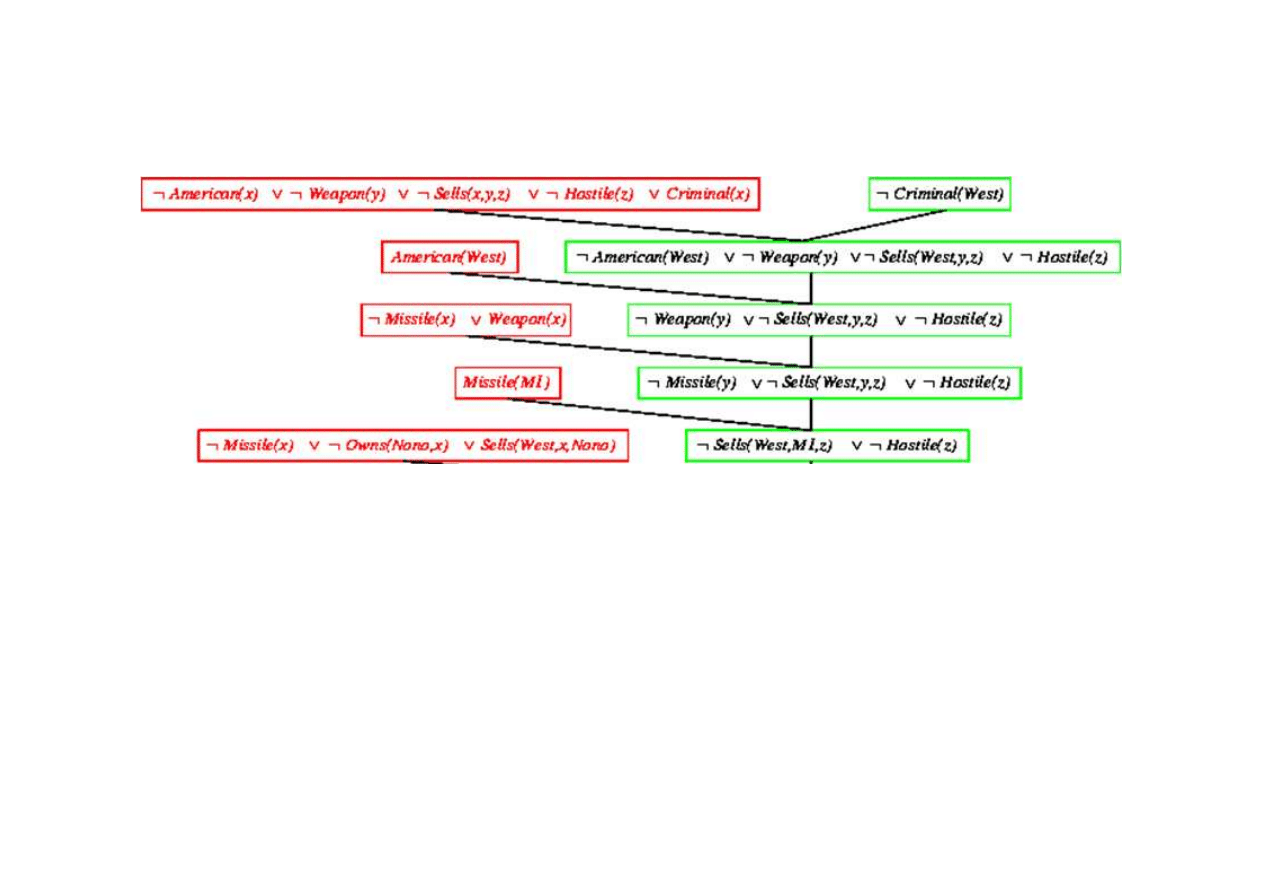
Dowód rezolucyjny dla kaluzuli Horna

9.5. Eliminacja (rezolucja)

{x/West}

{x/y}

{y/M1}

{x/M1}

© F.A. Dul 2007

{x/M1}

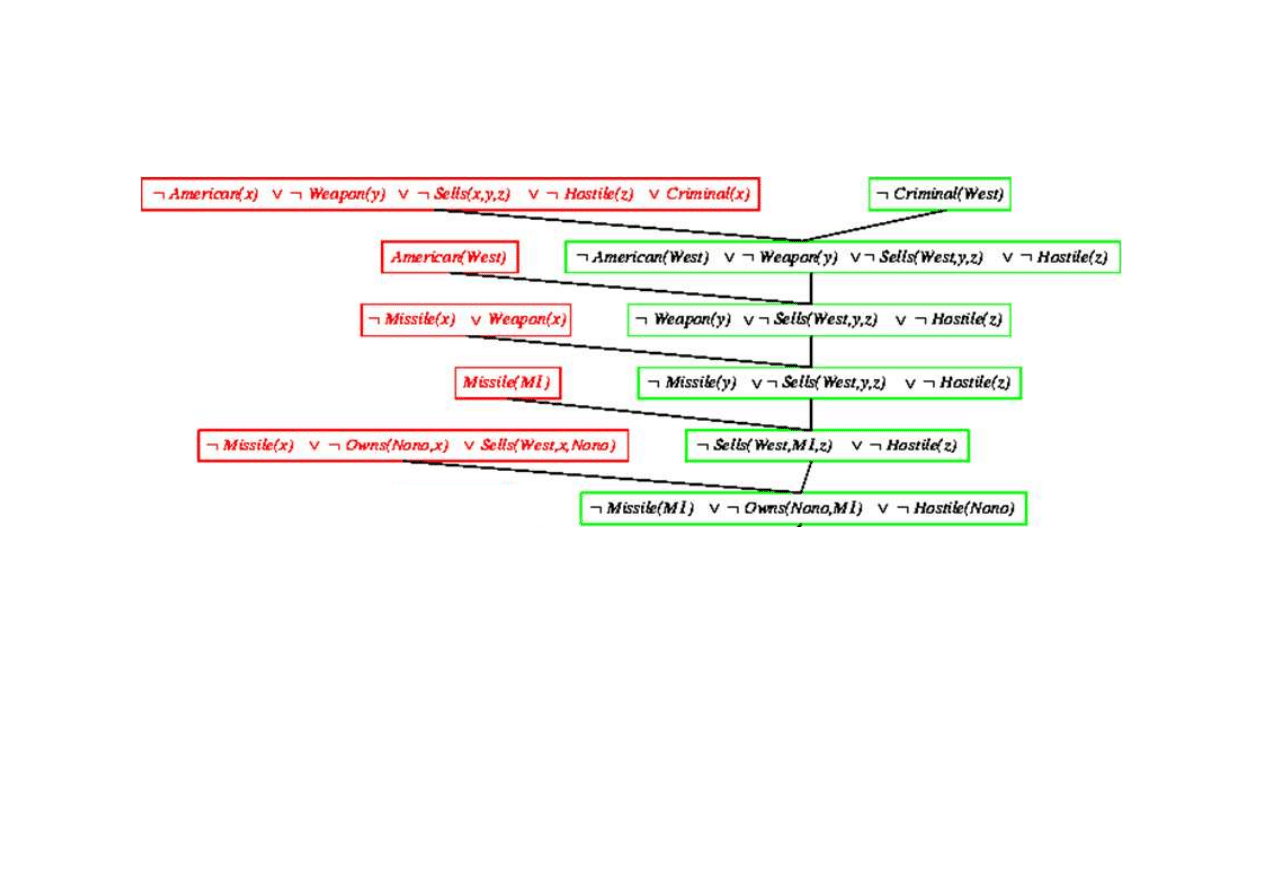
Dowód rezolucyjny dla kaluzuli Horna

9.5. Eliminacja (rezolucja)

{x/West}

{x/y}

{y/M1}

{x/M1}

© F.A. Dul 2007

{x/M1}

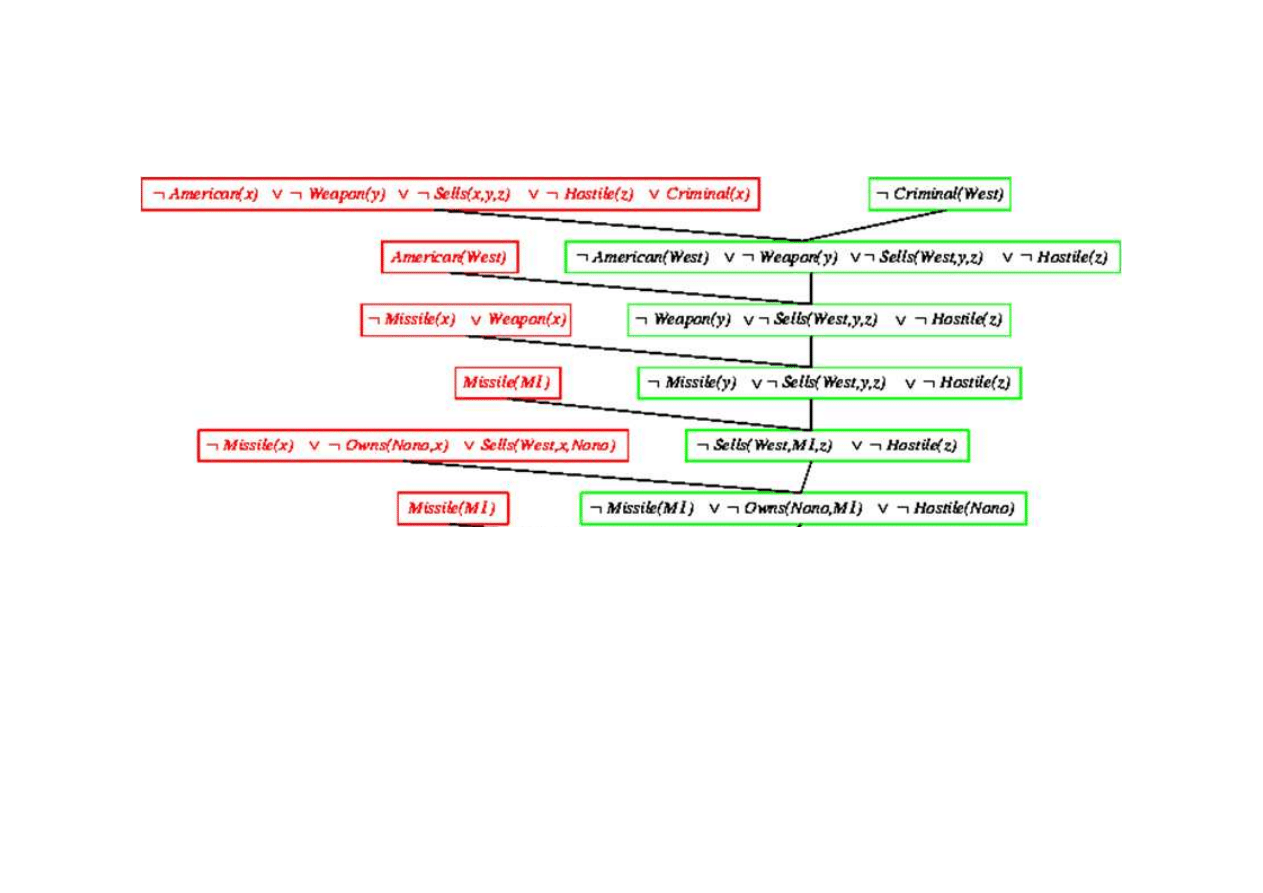
Dowód rezolucyjny dla kaluzuli Horna

9.5. Eliminacja (rezolucja)

{x/West}

{x/y}

{y/M1}

{x/M1}

© F.A. Dul 2007

{x/M1}

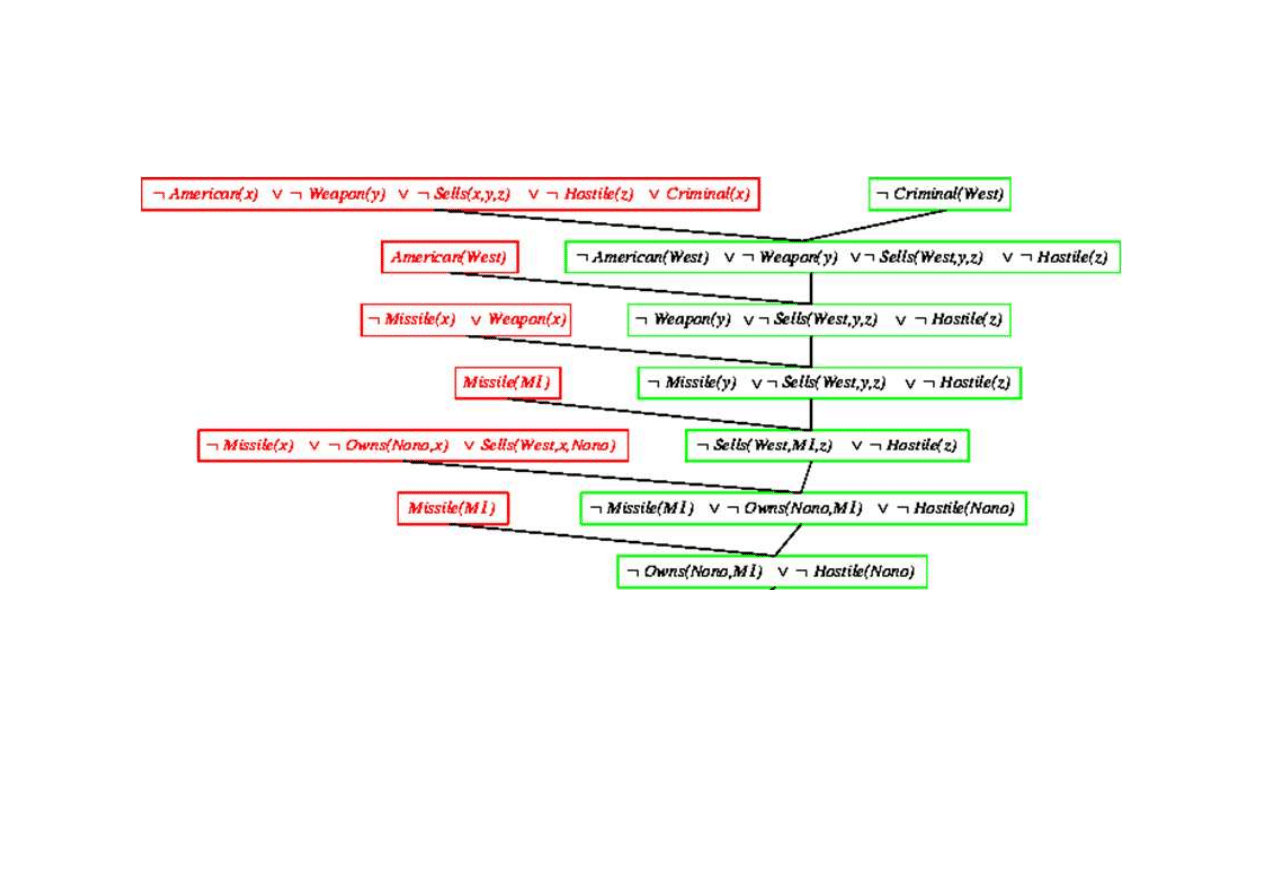
Dowód rezolucyjny dla kaluzuli Horna

9.5. Eliminacja (rezolucja)

{x/West}

{x/y}

{y/M1}

{x/M1}

© F.A. Dul 2007

{x/M1}

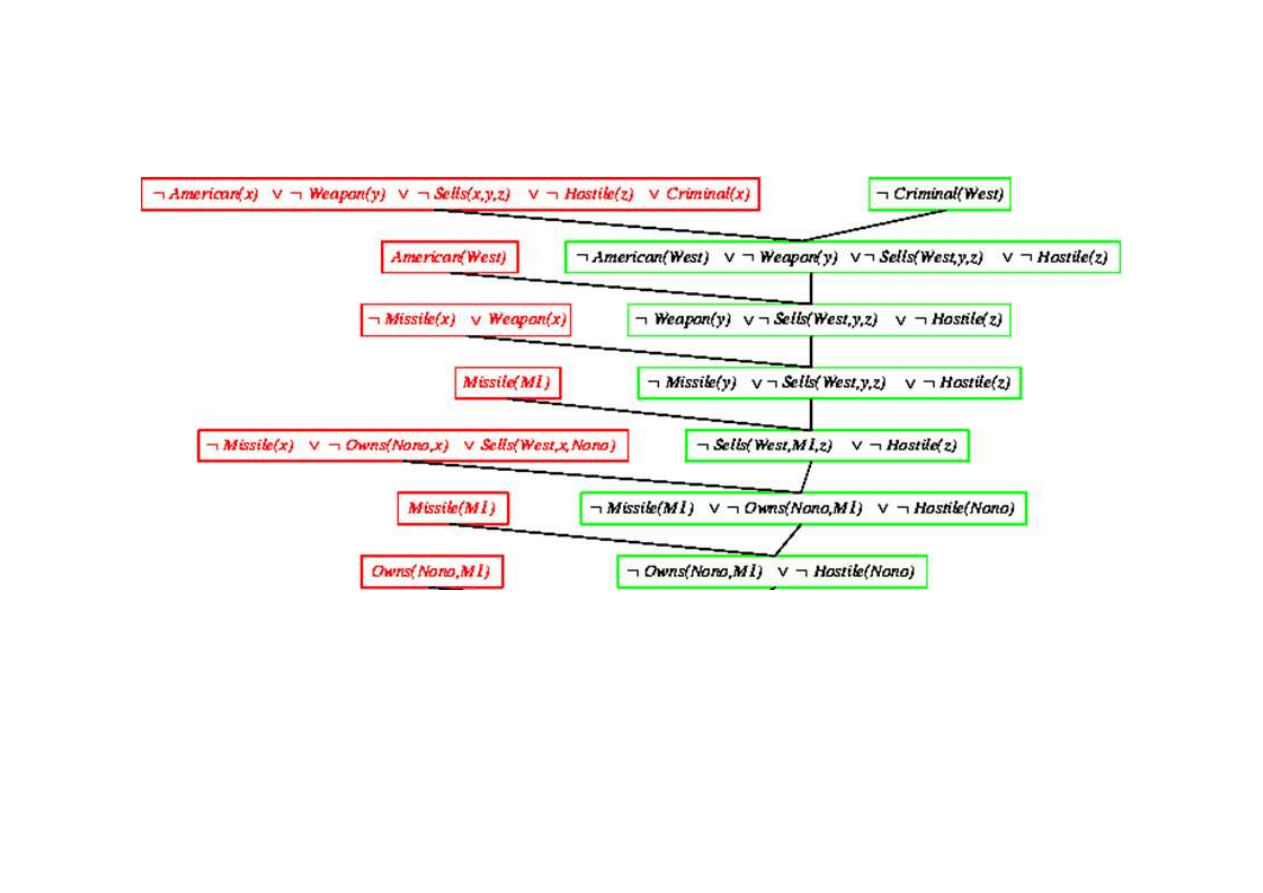
Dowód rezolucyjny dla kaluzuli Horna

9.5. Eliminacja (rezolucja)

{x/West}

{x/y}

{y/M1}

{x/M1}

© F.A. Dul 2007

{x/M1}

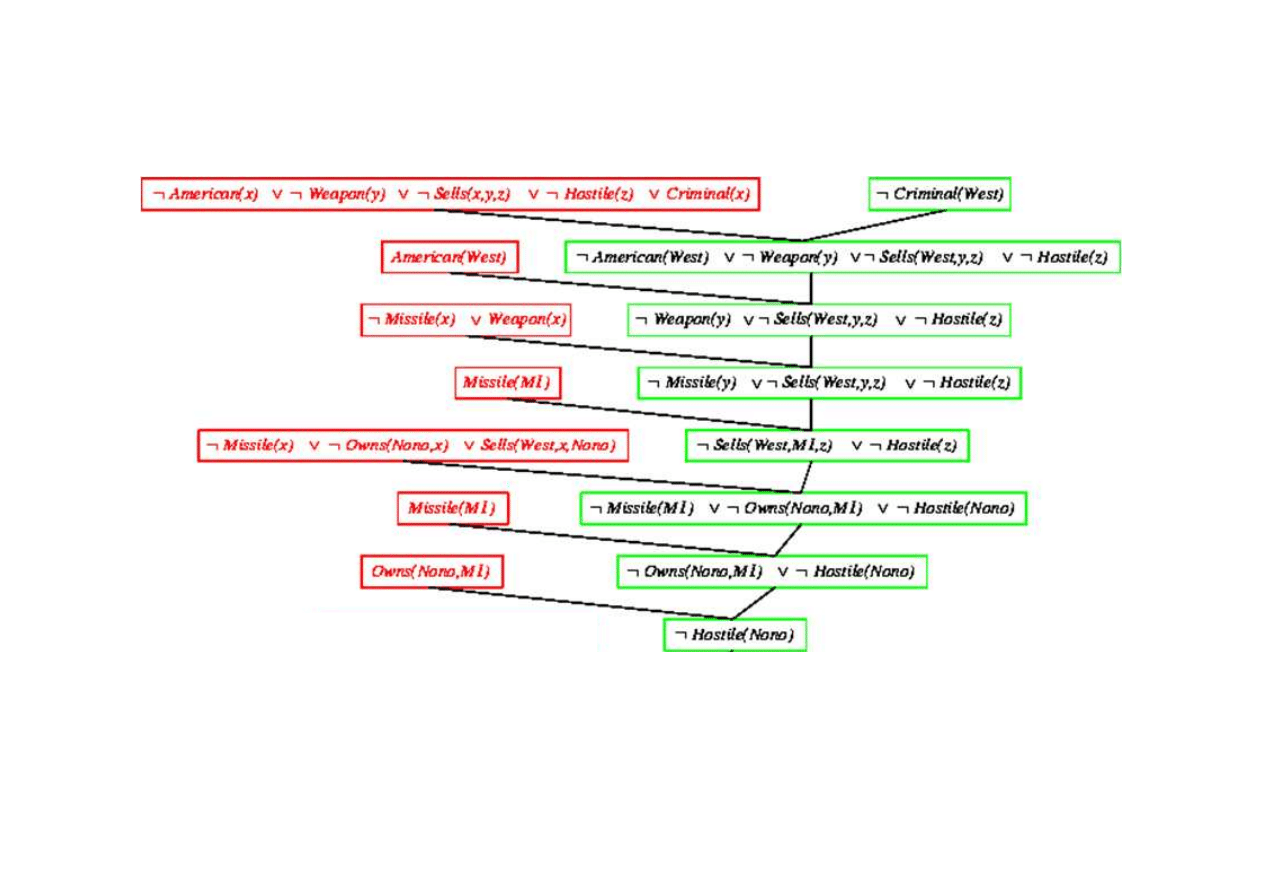
Dowód rezolucyjny dla kaluzuli Horna

9.5. Eliminacja (rezolucja)

{x/West}

{x/y}

{y/M1}

{x/M1}

© F.A. Dul 2007

{x/M1}

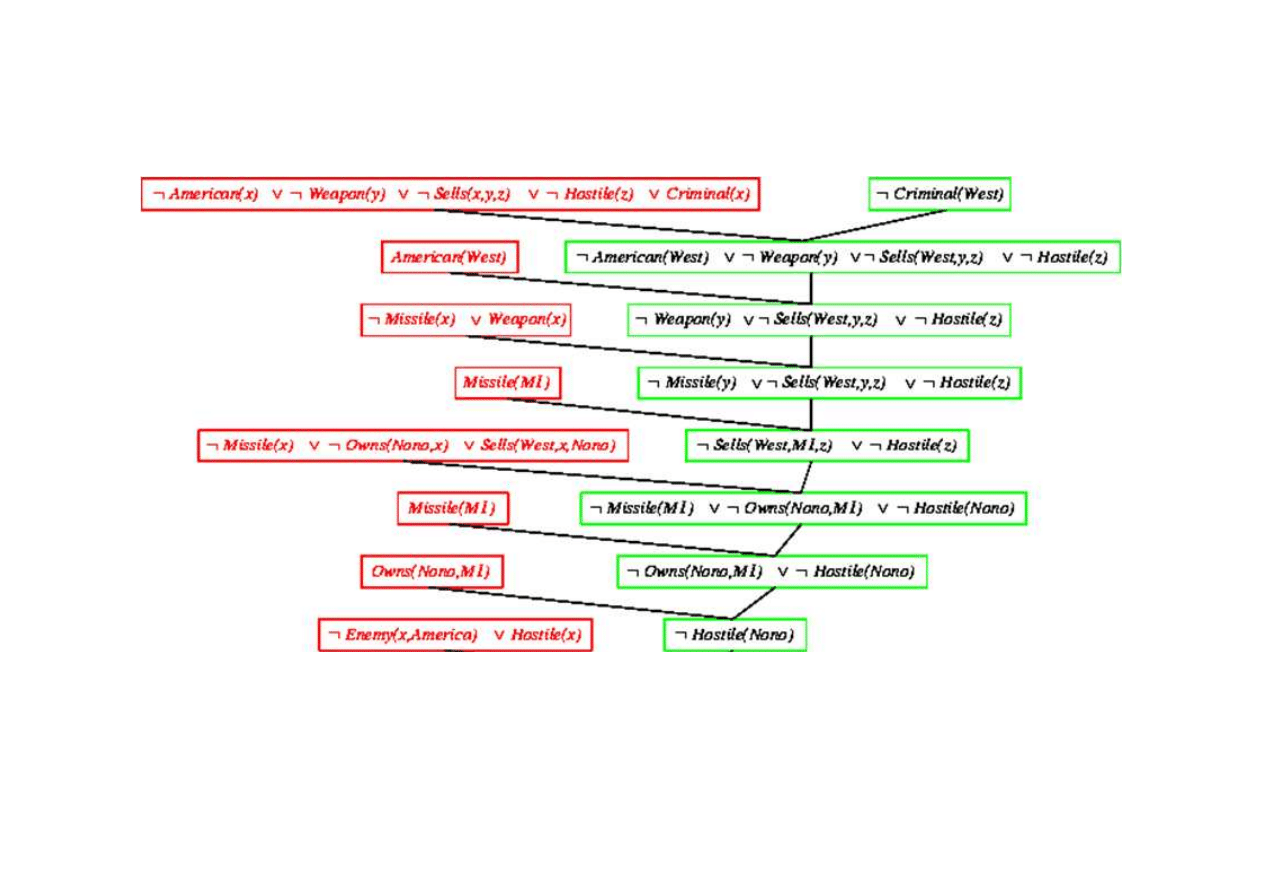
Dowód rezolucyjny dla kaluzuli Horna

9.5. Eliminacja (rezolucja)

{x/West}

{x/y}

{y/M1}

{x/M1}

© F.A. Dul 2007

{x/M1}

{x/Nono}

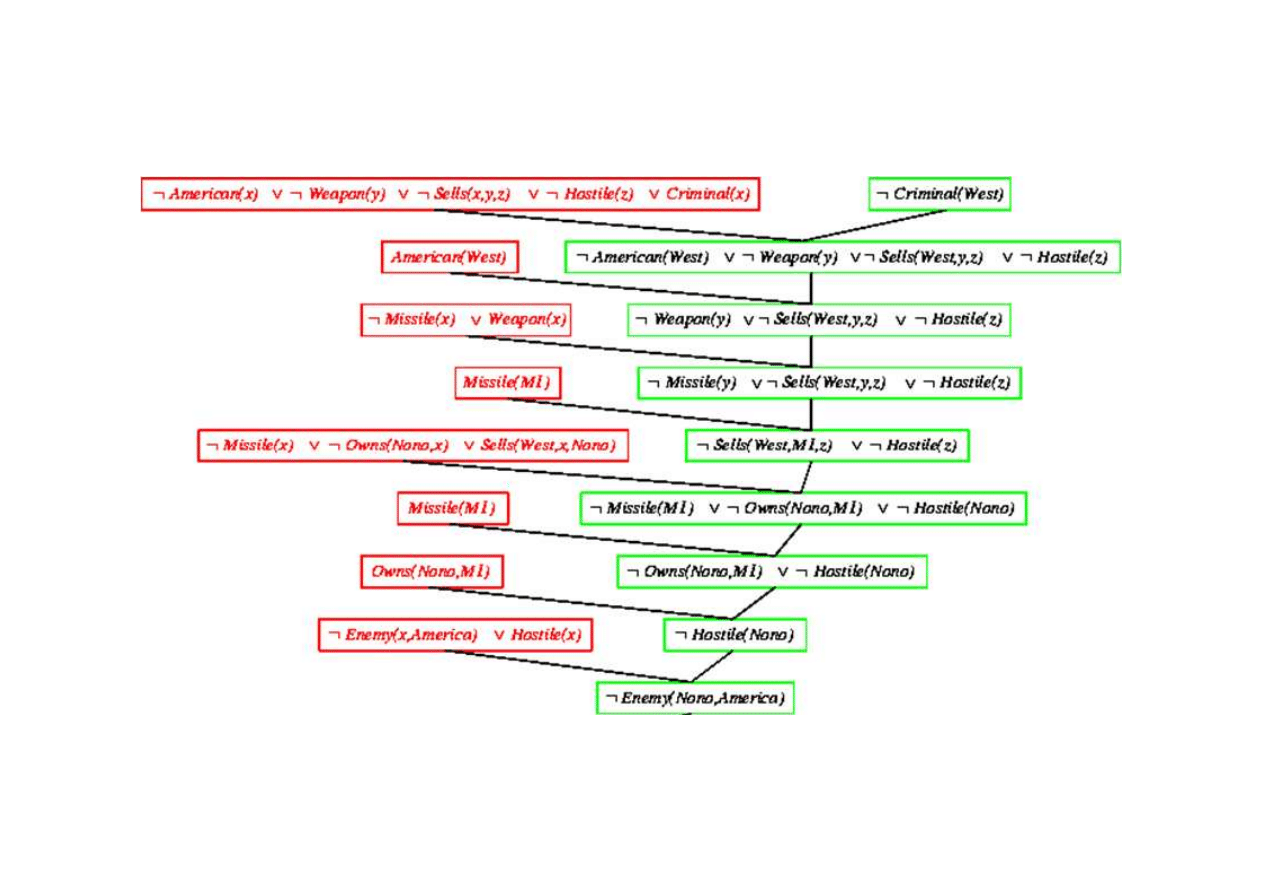
Dowód rezolucyjny dla kaluzuli Horna

9.5. Eliminacja (rezolucja)

{x/West}

{x/y}

{y/M1}

{x/M1}

© F.A. Dul 2007

{x/M1}

{x/Nono}

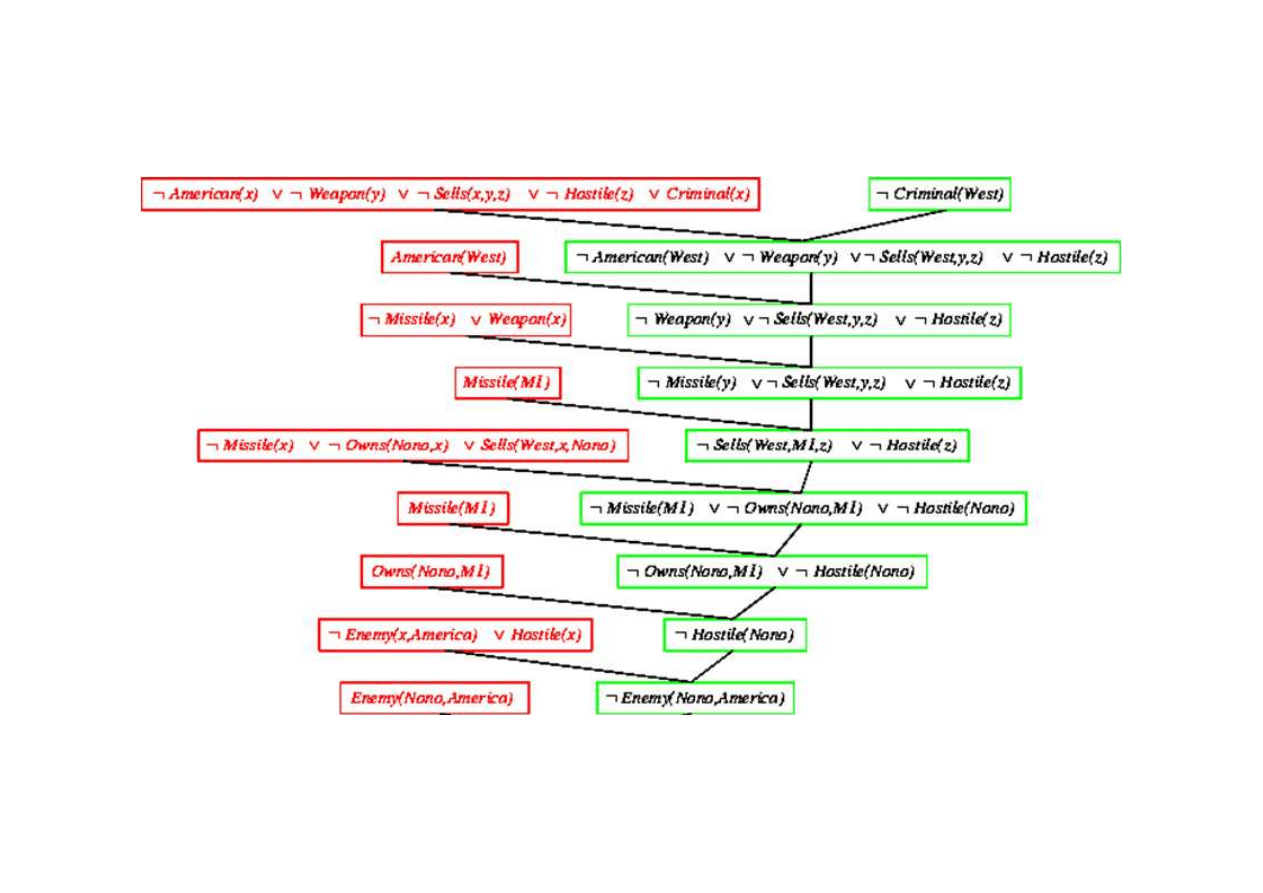
Dowód rezolucyjny dla kaluzuli Horna

9.5. Eliminacja (rezolucja)

{x/West}

{x/y}

{y/M1}

{x/M1}

© F.A. Dul 2007

{x/M1}

{x/Nono}

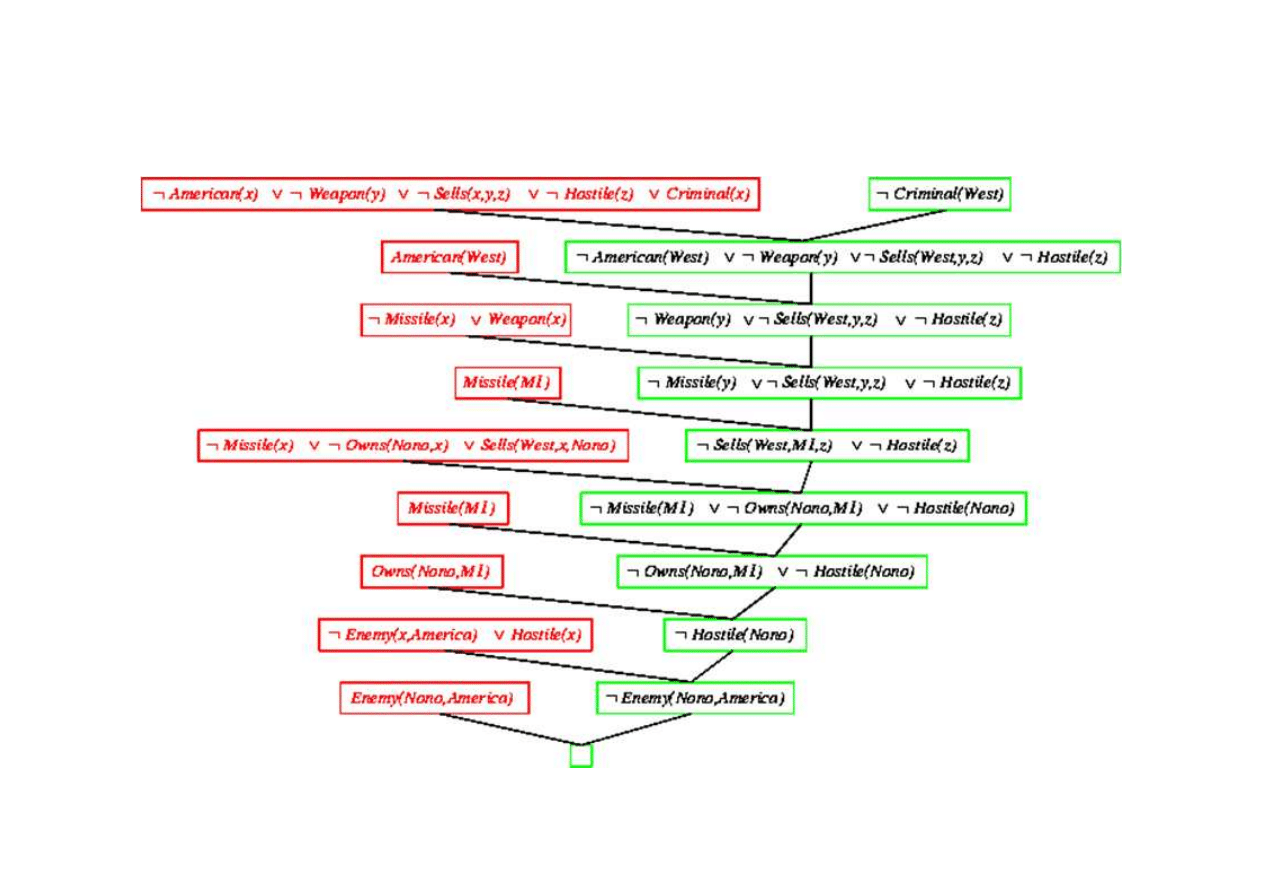
Dowód rezolucyjny dla kaluzuli Horna

9.5. Eliminacja (rezolucja)

{x/West}

{x/y}

{y/M1}

{x/M1}

© F.A. Dul 2007

Klauzula pusta - dowiedziono sprzeczno

ś

ci klauzuli

¬

Criminal(West)

{x/M1}

{x/Nono}

Programowanie logiczne vs. proceduralne

9.5. Eliminacja (rezolucja)

Programowanie logiczne

– identyfikacja zadania;

– zebranie informacji;

– kodowanie informacji

w j

ę

zyku logiki bazy

wiedzy;

– kodowanie zadania

Programowanie proceduralne

– identyfikacja zadania;

– zebranie informacji;

– opracowanie algorytmu

rozwi

ą

zania;

– programowanie

algorytmu;

© F.A. Dul 2007

– kodowanie zadania

jako zbioru faktów;

– zadawania pyta

ń

;

– eliminacja błednych

faktów;

algorytmu;

– kodowanie zadania jako

zbioru danych;

– uruchomienie programu

dla zbioru danych;

– eliminacja błedów;

Łatwiej jest analizowa

ć

Stolica(NY,US) ni

ż

x = x+2

Programowanie logiczne: j

ę

zyk PROLOG

Wnioskowanie bezpo

ś

rednie w FOL

Przekształcenie algorytmów wnioskowania w taki
sposób, aby mo

ż

na było prowadzi

ć

wnioskowanie

w bazie FOL pozwala u

ż

y

ć

efektywnych metod

wnioskowania w przód i wstecz, a tak

ż

e algorytmu

eliminacji (rezolucji) dla bazy w postaci Horna.

Przekształcenie algorytmów polega na zastosowaniu
operacji podniesienia i unifikacji oraz wykorzystanie

©

F.A. Dul 2007

operacji podniesienia i unifikacji oraz wykorzystanie
uogólnionej reguły odrywania.

Wnioskowanie przy u

ż

yciu algorytmów

dostosowanych do FOL mo

ż

e by

ć

bardzo efektywne.

Wnioskowanie mo

ż

e by

ć

w pełni automatyczne.

Wnioskowanie automatyczne stwarza mo

ż

liwo

ść

automatycznego dowodzenia twierdze

ń

matematycznych.

9.6. Automatyczne dowodzenie twierdze

ń

Programy dowodzenia twierdze

ń

(

Theorem Provers

,

Automated Reasoners

) umo

ż

liwiaj

ą

dowodzenie twierdze

ń

sformułowanych w j

ę

zyku logiki pierwszego rz

ę

du.

Najbardziej znane programy: O

TTER

, PTTP, O

NTIC

, S

AM

,

A

URA

, EQP, S

PIN.

Idea programu O

TTER

Dane definiuj

ą

ce dowodzony problem:

• Zbiór zda

ń

opisuj

ą

cych problem

(set of support, SOS)

.

• Aksjomaty u

ż

ytkowe

, nie b

ę

d

ą

ce elementami SOS,

© F.A. Dul 2007

• Aksjomaty u

ż

ytkowe

, nie b

ę

d

ą

ce elementami SOS,

opisuj

ą

ce wiedz

ę

ogóln

ą

na temat problemu.

• Zbiór równa

ń

demoduluj

ą

cych (

demodulators

)

okre

ś

laj

ą

cych formy kanoniczne do których przekształcane

s

ą

wszystkie zdania (np. x+0=x: x+0

→

x).

• Zbiór parametrów i klauzul steruj

ą

cych.

Program O

TTER

stosuje rezolucj

ę

do kolejnych zda

ń

zbioru

opisuj

ą

cego SOS wzgl

ę

dem aksjomatów u

ż

ytkowych.

Rezolucja klauzul SOS przebiega w kolejno

ś

ci od najprostszej,

wybieranej heurystycznie za pomoc

ą

algorytmu best-first.

Programy dowodzenia twierdze

ń

pozwoliły uzyska

ć

wiele

wa

ż

nych wyników matematycznych.

• 1969 – program S

AM

udowadnia kilka lematów teorii warstw.

• 1979 – Natarjan Shankar przy u

ż

yciu programu Boyera-

Moora dowodzi po raz pierwszy w sposób

ś

cisły słynne

Twierdzenie Gödla o Niezupełno

ś

ci.

• 1983 – program A

URA

udowadnia twierdzenia z wielu

dziedzin matematyki.

• Program O

TTER

(i jego nowsze wersje: M

ACE

2, EQP) jest

jednym z najlepszych programów dowodzenia twierdze

ń

.

9.6. Automatyczne dowodzenie twierdze

ń

© F.A. Dul 2007

jednym z najlepszych programów dowodzenia twierdze

ń

.

Za pomoc

ą

EQP dowiedziono w roku 1996 słynnej

hipotezy

Robbinsa

(o równowa

ż

no

ś

ci algebry Robbinsa i algebry

boolowskiej), nieudowodnionej od roku 1933, nawet przez

samego

Alfreda Tarskiego*

)

. Dowód uzyskany programem

EQP liczy tylko

17 linijek!

*) Alfred Tarski

(1901-1983) – wybitny polski logik,

wykładowca UW i liceum

ś

eromskiego (do 1939),

oraz uniwersytetów Harvarda, Princeton i Berkeley.

Jako pierwszy sformułował definicj

ę

prawdy.

Uwa

ż

any za najwi

ę

kszego logika po Arystotelesie.

• Za pomoc

ą

programów dowodz

ą

cych udowodniono wiele

twierdze

ń

geometrii algebraicznej, logiki kombinatorycznej,

autodualnych algebr Boolowskich, teorii grup, półgrup
i kwazigrup, teorii krat i kwazikrat, i wielu innych...

• Podejmowane s

ą

nawet próby formalizacji całej matematyki

– projekt QED.

9.6. Automatyczne dowodzenie twierdze

ń

© F.A. Dul 2007

Program dowodz

ą

ce s

ą

te

ż

u

ż

ywane w ró

ż

nych dziedzinach

jako

asystenci

.

Człowiek-ekspert nadzoruje rozwi

ą

zanie problemu wytyczaj

ą

c

kierunki działa

ń

, za

ś

program-asystent rozwi

ą

zuje problemy

szczegółowe.

Innymi zastosowaniami programów dowodz

ą

cych

s

ą

weryfikacja

oraz

synteza

układów elektronicznych

oraz oprogramowania.

• Program A

URA

posłu

ż

ył do weryfikacji 16-bitowego układu

9.6. Automatyczne dowodzenie twierdze

ń

© F.A. Dul 2007

• Program A

URA

posłu

ż

ył do weryfikacji 16-bitowego układu

sumuj

ą

cego (1983).

• Specjalne programy dowodz

ą

ce słu

żą

do weryfikacji

poprawno

ś

ci układów VLSI, np. procesorów CPU.

• Program S

PIN

słu

ż

y do weryfikacji poprawno

ś

ci

oprogramowania.
Za jego pomoc

ą

weryfikowano w NASA oprogramowanie

Remote Agent

steruj

ą

ce lotem sond mi

ę

dzyplanetarnych,

m.in. sondy Deep Space 1 (1999).

Podsumowanie

• Algorytmy wnioskowania w logice pierwszego rz

ę

du

s

ą

wa

ż

nymi narz

ę

dziami sztucznej inteligencji.

• Unifikacja pozwala znacznie zwi

ę

kszy

ć

efektywno

ść

wnioskowania w logice pierwszego rz

ę

du.

• Uogólniona wersja Modus Ponens stanowi efektywn

ą

reguł

ę

wnioskowania w logice pierwszego rz

ę

du.

• Algorytmy wnioskowania w przód i wstecz

s

ą

najwa

ż

niejszymi narz

ę

dziami wnioskowania

© F.A. Dul 2007

s

ą

najwa

ż

niejszymi narz

ę

dziami wnioskowania

automatycznego w logice pierwszego rz

ę

du.

• Uogólnione zasady rezolucji pozwalaj

ą

dowodzi

ć

twierdze

ń

w logice pierwszego rz

ę

du w bazie wiedzy reprezentowanej

w postaci normalnej koniunktywnej.

• Automatyczne dowodzenie twierdze

ń

umo

ż

liwiło

udowodnienie interesuj

ą

cych twierdze

ń

matematycznych.

• Automatyczne dowodzenie twierdze

ń

pomaga tak

ż

e

przy syntezie i weryfikacji oprogramowania.