Ćwiczenie 2

Potencjometria

Cel ćwiczenia

Celem ćwiczenia jest zapoznanie z metodyką wyznaczania pH roztworów, stałej

dysocjacji słabego elektrolitu, pojemności buforowej oraz sporządzania krzywych

miareczkowania.

Zagadnienia teoretyczne

Współczynnik aktywności jonów w roztworach elektrolitu, siła jonowa, pH roztworów

buforowych, równanie Hendersona - Hasselbacha, pojemność buforowa.

W roztworach rozcieńczonych, z którymi rozpuszczone cząsteczki wzajemnie na

siebie oddziaływują są tak małe, że można je pominąć. Roztwory nieelektrolitów osiągają

doskonały stan rozcieńczenia poniżej stężeń 0,01 mol/dm

3

.

W roztworach elektrolitów nawet przy znacznie mniejszych stężeniach, istotną rolę

odgrywają siły przyciągania elektrostatycznego, zarówno międzyjonowe jak również siły

oddziaływań solwatacyjnych. Stan doskonałego rozcieńczenia w tych wypadkach nie jest

praktycznie osiągany. Roztwory elektrolitów spełniają prawa roztworów doskonałych

wówczas, gdy w miejsce stężenia C wprowadzi się aktywność substancji rozpuszczonej.

a = c

.

f

(9.1)

Współczynnik f nazywamy współczynnikiem aktywności, natomiast c wyraża stężenie

molowe danego elektrolitu. Współczynnik aktywności charakteryzuje stopień ograniczenia

ruchów poszczególnych rodzajów cząsteczek i określa jaką część molowego stężenia stanowi

stężenie aktywne. Jeżeli przyjmiemy, że współczynnik aktywności elektrolitu HX wynosi 0,5

to w 0,1 molowym roztworze stężenie aktywne jest równe a:

a = 0,1 M/dm

3

.

0,5 = 0,05 M/dm

3

.

W silnie rozcieńczonych roztworach elektrolitów (stężenie mniejsze niż 0,01 mol/dm

3

)

współczynnik f zbliża się do 1 i aktywność w przybliżeniu odpowiada stężeniu molowemu

elektrolitu. Tak więc przy obliczaniu pH, jedynie dla roztworów o stężeniu 0,001 mol/dm

3

lub

mniejszych, można korzystać ze wzoru:

pH = -lg [H

+

]

(9.2)

natomiast dla określenia kwasowości roztworów bardziej stężonych w miejsce stężenia we

wzorze 9.2 powinno wprowadzać się wartości aktywności:

p H

a

H

lg

(9.3)

Przybliżoną wartość współczynnika aktywności f można obliczyć jeżeli znana jest siła jonowa

elektrolitów (u)

2

2

2

2

2

1

1

2

1

n

n

z

c

z

c

z

c

u



(9.4)

gdzie: c

1

, ...c

n

są stężeniami molowymi wszystkich jonów w roztworze, a z

1

, ... z

n

to ładunki

tych jonów.

Znając wartości u można wyliczyć współczynnik aktywności f przekształcając wzór:

u

u

z

f

H

1

509

,

0

log

2

(9.5)

Przy obliczaniu pH roztworów buforowych wykorzystuje się równanie Hendersona -

Hasselbacha. Dla roztworu buforowego złożonego ze słabego kwasu i jego soli z mocną

zasadą równanie to przyjmuje postać:

kwasu

soli

a

c

c

pK

pH

log

(9.6)

to samo równanie dla roztworu złożonego ze słabej zasady i jej soli z mocnym kwasem ma

postać:

p H

p K

p K

c

c

w

b

z a s a d y

s o l i

l o g

(9.7)

co pozwala po przekształceniu wzorów 9.6 i 9.7 obliczyć stałe dysocjacji kwasu K

a

lub

zasady K

b

.

Zdolność buforowania jakiegoś roztworu określa pojemność buforowa B wyrażana

jako stosunek liczby dodanych równoważników kwasu lub zasady do wywołanej zmiany pH

w 1 dm

3

roztworu.

n

p H

(9.8)

gdzie: n oznacza liczbę wprowadzonych moli kwasu lub zasady, a pH wywołane zmiany

pH.

Sprzęt:

pehametr,

1 zlewka (250 cm

3

)

6 zlewek (50 cm

3

)

pipeta (25 cm

3

)

pipety (5 i 10 cm

3

pełna i miarowa).

Odczynniki:

H

2

SO

4

roztwory 0,1; 0,01 i 0,001 molowe;

HCl roztwór 0,1 M;

NaOH roztwór 0,1 M;

CH

3

COOH roztwory 0,1 i 0,2 molowe;

CH

3

COONa roztwór 0,2 M;

NH

4

OH roztwór 0,1 M;

NH

4

Cl roztwór 0,1 M.

Wykonanie ćwiczenia

1. Pomiar pH kwasu siarkowego

Przed pomiarami kwasowości roztworów badanych należy dokonać pomiaru pH

wzorcowego roztworu buforowego. Następnie do 3 zlewek nalewamy roztwory kwasu

siarkowego o stężeniach 0,1; 0,01 i 0,001 mol/dm

3

i mierzymy pH. Wyniki zestawiamy w

tabeli 1.

Tabela 1

stężenie roztworu (mol/dm

3

)

0,1

0,01

0,001

pH zmierzone

pH obliczone ze wzoru 9.3

Odpowiedz: jaka może być przyczyna różnic w wartościach pH zmierzonych doświadczalnie

i obliczonych?

2. Wyznaczanie krzywej miareczkowania mocnego kwasu

Do zlewki o poj. 250 cm

3

nalewamy 25 cm

3

0,1 mol/dm

3

HCl. Po zmierzeniu pH

roztworu dodajemy porcjami 0,1 mol/dm

3

NaOH w następujących ilościach: 5; 5; 5; 5; 1; 1;

1; 1; 0,5; 0,5; 0,5; 0,5; 1; 1; 2; 5 i 5 cm

3

mierząc pH roztworu po każdorazowym dodaniu

jednej porcji NaOH. Wyniki zestawić w tabeli 2.

ilość cm

3

0,1 mol/dm

3

NaOH

pH roztworu

3. Wyznaczanie krzywej miareczkowania słabego kwasu mocną zasadą

Do zlewki (250 cm

3

) nalewamy 25 cm

3

0,1 mol/dm

3

CH

3

COOH. Następnie

wprowadzamy odpowiednie ilości 0,1 mol/dm

3

NaOH i wykonujemy pomiary pH jak w

poprzednim przypadku. Uzyskane wyniki przedstawiamy graficznie odkładając na osi

odciętych liczbę cm

3

dodanej zasady, a na osi rzędnych pH roztworu. Po wykreśleniu

krzywych określić pH odpowiadające punktowi równoważnikowemu.

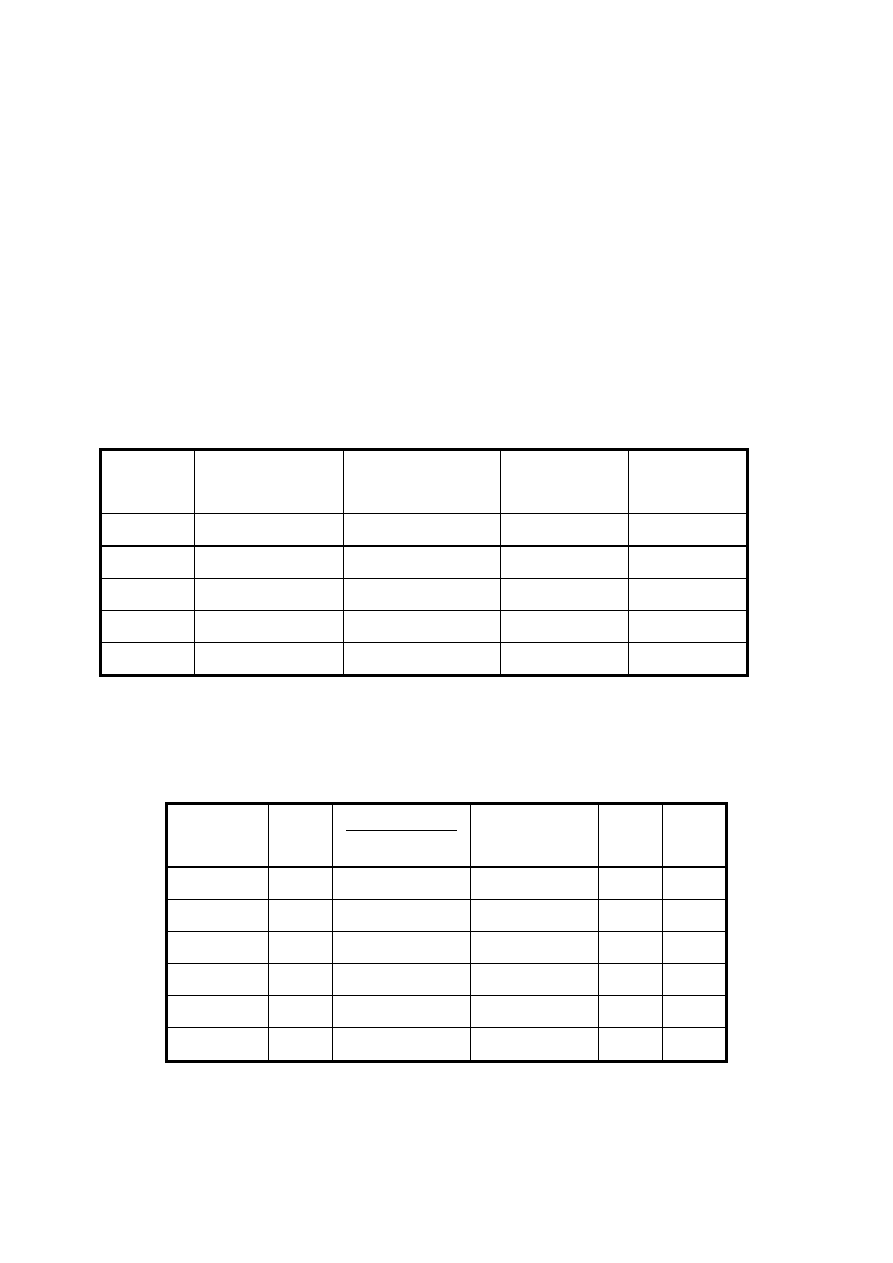
4. Wyznaczanie stałej dysocjacji K słabego kwasu (zasady)

W zlewkach o poj. 50 cm

3

(100 cm

3

) przygotować roztwory buforowe: CH

3

COOH i

CH

3

COONa lub NH

4

OH i NH

4

Cl o składzie podanym w tabeli 3 (jeden bufor do wyboru).

nr zlewki

0,2 M CH

3

COOH

(cm

3

)

0,2 M CH

3

COONa

(cm

3

)

0,1 M NH

4

OH

(cm

3

)

0,1 M NH

4

Cl

(cm

3

)

1

19

1

18

2

2

16

4

15

5

3

11

9

10

10

4

6

14

6

14

5

1

19

2

18

Po wymieszaniu należy zmierzyć pH roztworów (roztwory pozostawić w zlewkach).

Znając wartości pH roztworów, po obliczeniu stężenia kwasu i soli (zasady i soli) można

obliczyć średnie stałe dysocjacji słabego kwasu (zasady). Wyniki przedstawić w tabeli:

nr roztworu

pH

s tę ż e n ie so li

s tę ż e n ie kw a s u

stała dysocjacji

pK

a

pK

aśr.

1

2

3

4

5

6

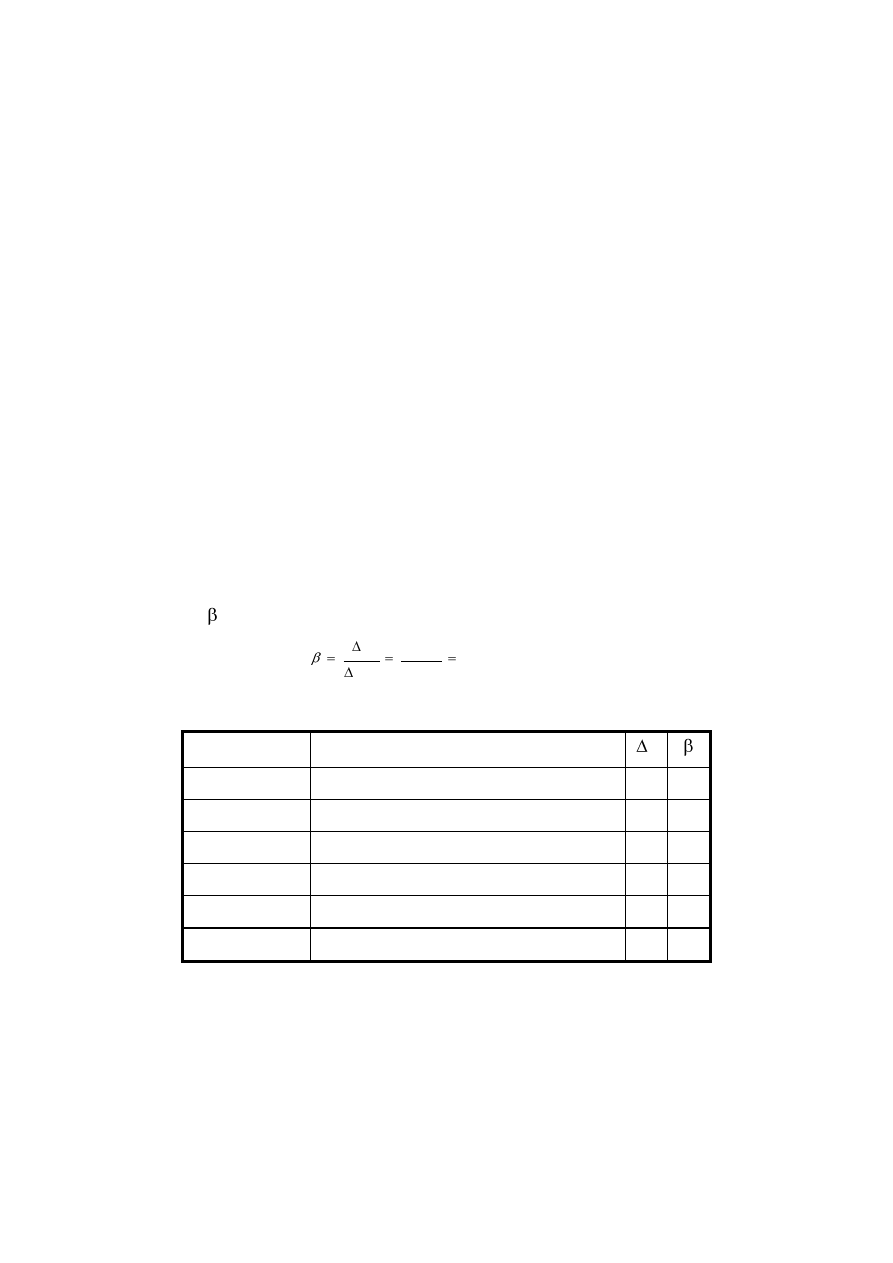
5. Wyznaczanie pojemności buforowej

Do 5 roztworów buforowych z poprzedniego ćwiczenia dodać po 5 cm

3

0,1 mol/dm

3

HCl (NaOH). Zmierzyć pH otrzymanych roztworów. Znając pH roztworu przed

wprowadzeniem HCl (NaOH) i po ich dodaniu można obliczyć pH a następnie pojemność

buforową dla pięciu badanych roztworów.

Przykład obliczeń:

Obliczyć pojemność buforową jeżeli 5 cm

3

0,1 mol/dm

3

HCl zmienia pH 20 cm

3

roztworu buforowego o 0,5 jednostek pH.

1. Ilość moli wprowadzonego kwasu n

n= c

.

V = 0,1 M/dm

3

.

0,005 dm

3

= 0,0005 mol

1. Jeżeli 0,0005 mola kwasu zmieniło pH 0,02 dm

3

buforu to z proporcji można obliczyć jaka

liczba kwasu będzie potrzebna do zmiany pH 1 dm

3

roztworu.

0,0005 M HCl

zmieniło pH

0,02 dm

3

buforu

x

1 dm

3

buforu

x = 0,025 M

3. Obliczamy z zależności 9.8

n

p H

0 0 2 5

0 5

0 0 5

,

,

,

Wyniki podajemy w tabeli

roztwór

pH roztworu po dodaniu kwasu (zasady)

n

1

2

3

4

5

6