Politechnika Cz stochowska 

Wydział In ynierii Mechanicznej i Informatyki 

Kierunek Informatyka 

Specjalno  In ynieria Oprogramowania 

 
 

PRACA MAGISTERSKA 

 

OPRACOWANIE METODY I OPROGRAMOWANIA  

DO WIELOKRYTERIALNEJ I WIELOPOZIOMOWEJ 

OCENY ALTERNATYW W ZAGADNIENIACH 

PODEJMOWANIA DECYZJI 

 

PAWEŁ  FIGAT 

Nr albumu:  24727 
Rok akademicki:  2001/2002 
Promotor:  

Prof. Dr hab. in . Paweł Sewastianow 

Recenzent:

 Prof. Dr hab. in . Roman Wyrzykowski 

Data oddania pracy:                         
Ocena promotora:...................................     Podpis......................................       
Ocena recenzenta:..................................  

Podpis...................................... 

 

 

 

2 

Spis tre ci

 

 

Wst p…. .......................................................................................................................3 
1. 

Cel i zakres pracy...............................................................................................4 

2. 

Problemy oceny alternatyw w warunkach wielokryterialno ci i niepewno ci......6 

3. 

Problem 

budowania 

systemu 

hierarchicznego 

(wielopoziomowego) 

wielokryterialnej oceny alternatyw...................................................................28 

4. 

Opracowanie  metody  i  oprogramowania  wspomagaj cego  wielokryterialn   
i wielopoziomow  ocen  alternatyw.................................................................36 

4.1. Metoda budowania funkcji przynale no ci kryteriów lokalnych........................36 
4.2.  Metoda  i  algorytm  wyliczenia  współczynników  wzgl dnej  wa no ci  kryteriów 
lokalnych na podstawie macierzy parzystych porówna ...........................................40 
4.3. Metoda agregowania kryteriów lokalnych.........................................................44 
4.4. Budowanie hierarchicznego sytemu kryteriów agregowanych...........................46 
4.5. Struktura oprogramowania realizuj cego opracowane metody. .........................50 

5. 

Metoda  oszacowania  alternatyw  przy  rozmytych  współczynnikach  wzgl dnej 
wa no ci kryteriów w warunkach ich oceny przez zespół ekspertów. ...............51 

5.1. Opracowanie metody oszacowania alternatyw na podstawie lokalnych rozmytych 
kryteriów subiektywnych i obiektywnych (cena) oraz ich rozmytych rang. ..............51 
5.2. Przykład zastosowania opracowanej metody  i oprogramowania dla zagadnienia 
optymalizowanego wyboru gatunku stali konstrukcyjnej .........................................53 

Stopnie spójno ci z ocenami lingwistycznymi..................................................63 

5.3. Opisanie struktury klas realizuj cych metod  oszacowania alternatyw. .............69 

6. 

Podsumowanie i kierunki rozwoju....................................................................74 

7. 

Literatura .........................................................................................................75 

Dodatek A - Skrócona dokumentacja programu...........................................................81 
Dodatek B - Najwa niejsze funkcje programu .............................................................83 

 

 

3 

Wst p

 

 

Wiadomo,  e  kwestia  oszacowania  alternatyw  podczas  podejmowania 

do   skomplikowanych  decyzji  jest  nieodzownie  zwi zana  z  ocenami 
subiektywnymi. 

Podejmowanie 

decyzji 

jest 

wszak e 

procesem 

wielokryterialnym, wi c oczywistym staje si  fakt,  e potrzebuje odpowiednich 
narz dzi  matematycznych,  gdy   niepewno   subiektywna  nie  mo e  by  
adekwatnie  przedstawiona  tylko  za  pomoc   podej cia  probabilistycznego. 
Takiego  rodzaju  wieloaspektowy  problem  zawiera  w  sobie  przecie   takie 
problemy  jak  formalizacja  matematyczna  kryteriów  lokalnych  w  warunkach 
niepewno ci,  oceny  współczynników  ich  wzgl dnych  wa no ci,  agregowanie 
kryteriów 

lokalnych 

oraz 

budowanie 

systemów 

hierarchicznych 

(wielopoziomowych) kryteriów agregowanych. 

Nale y  podkre li   fakt,  e ka dy z  tych aspektów,  jest opisany  odr bnie  

w  literaturze  naukowej.  Jednak  cała  zło ono   problemu  jest  w  tym,  

e  niezb dne  jest  zbudowanie  systemu  do   uzasadnionego  z  punktu  widzenia 

naukowego,  syntetyzuj cego  wszystkie  omówione  aspekty  w  zintegrowany 
system  wspomagaj cy  podejmowanie  decyzji.  W  trakcie  budowania  systemu 
niezb dne  jest  u ycie  nowoczesnych  narz dzi  matematycznych  w  tym 
elementów teorii zbiorów rozmytych, teorii mo liwo ci oraz metod optymalizacji 
wielokryterialnej.  Oczywi cie  system  powinien  dostarcza   u ytkownikowi 
mo liwo   w  sposób  elastyczny  formułowa   problemy  w  j zyku  konkretnej 
dziedziny za pomoc  rozwini tego interfejsu.  

 
 

 
 

 

 

4 

 

1.

 Cel i zakres pracy 

 

Celem poni szej pracy jest opracowanie metody oraz stworzenie aplikacji 

pomagaj cej  w  procesach  podejmowania  decyzji  w  warunkach  niepewno ci 
rozmytej.  Na  etapie  analizy  dziedziny  przyj to  nast puj ce  zało enia  w 
zgodno ci, z którymi metoda i oprogramowanie powinny zapewnia : 
 

1. 

Elastyczno   i  uniwersalno   metody.  Metoda  powinna  by  
skuteczna  dla  dowolnego  typu  zadania  podejmowania  decyzji. 
Metoda powinna dawa   mo liwo   wiernego odzwierciedlenia 
rzeczywisto ci  i  pozwala   na  wprowadzenie  wszystkich 
warunków  i  przesłanek  pojawiaj cych  si   podczas  oceny 
alternatyw. 

2. 

Jak najmniejsza utrata informacji. Podczas pierwotnej obróbki 
danych  w  zło onych  problemach  metoda  powinna  zapewnia  
jak  najmniejsz   strat   informacji,  aby  wiarygodno   
do otrzymywanych rezultatów była mo liwie najwi ksza. 

3. 

Prostot   w  obsłudze  aplikacja  z  intuicyjnym  interfejsem 
u ytkownika.  Sposób  wprowadzania  danych  w  programie 
powinien  by   jak  najprostszy,  posiada   mo liwo   dokonania 
szybkich  zmian  w  analizie  danego  problemu,  a  wyniki  łatwe  
do interpretacji  przy wykorzystaniu rozszerzonych graficznych 
mo liwo ci komputera. 

 

W  nast pnym  2  rozdziale  pracy  omówiono  podstawy  teorii,  a  tak e 

najwa niejsze kierunki i metody, które były rozwijane na przestrzeni lat.  

 

 

5 

W  punkcie  3  przedstawiono  główne  problemy  pojawiaj ce  si   podczas 

podejmowania zło onych decyzji.  

W  rozdziale  4  zaprezentowano  sposoby  rozwi zywania  tych  problemów 

na podstawie opracowanej metody przy u yciu stworzonej w tym celu aplikacji.  

W  punkcie  5  przedstawiono  bazow   struktur   aplikacji  opracowanej  na 

podstawie  grupy  metod  opisanych  w  rozdziale  4.  Wszystkie  rozwa anie 
teoretyczne  s   ilustrowane  odpowiednimi  przykładami  praktycznymi  z 
ró norakich dziedzin.  

W  ostatnim  punkcie  6  przedstawi   mo liwe  kierunki  dalszego  rozwoju 

pracy. 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 

 

6 

2.

 Problemy 

oceny 

alternatyw 

w 

warunkach 

wielokryterialno ci i niepewno ci. 

 
Jako   dowolnego  do   skomplikowanego  realnego  obiektu  lub  procesu 

zwi zanego  z  działalno ci   człowieka  z  reguły  charakteryzuje  si   zbiorem 
kryteriów  lokalnych  cz sto  znajduj cych  si   w  stosunkach  antagonistycznych 
miedzy sob , kiedy ulepszenie wzgl dnie

 

jednego z nich powoduje pogorszenie 

innego  i  na  odwrót.  Oprócz  tego  kryteria  lub  ograniczenie  cz sto  formalizuje  
si  na poziomie werbalnym w postaci stwierdze  raczej o charakterze ogólnym 
na przykład stwierdze  o dominowaniu jakiego  parametru w pewnym zakresie. 
Przy zwi kszaniu zło ono ci zadania rola takiego rodzaju informacji jako ciowej 
wzrasta i w wielu przypadkach mo e sta  si  dominuj ca [1]. Jak pokazano w [2] 
je eli  mamy  tylko  dwa  kryteria  w  zadaniu  optymalizacji  niezb dnie  istniej  
faktory  subiektywne  zwi zane  na  przykład  z  ocen   wzgl dnej  wa no ci 
rozpatrywanych  kryteriów.  Nie  ma  w tpliwo ci,  e  takiego  rodzaju  trudno ci 
mog  by  łatwo wyeliminowane za pomoc  uproszczenia formułowania zadania. 
Na przykład mo na sztucznie wyodr bni  jakie  jedno główne kryterium jako ci 
przy  tym  ostatnie  rozpatrywa   jako  ograniczenia  [2].  Inny  sposób  to  u ywanie 
metody kolejnych upustów [2]. Jednak wszystko to powoduje odej cie od istoty 
zadania i wcale nie eliminuje jako ciowo - subiektywne elementy przenosz c je  
z  etapu  formułowania  zadania  do  etapu  analizy  rezultatów.  Dlatego  mo na 
powiedzie ,  e  ródłami niepewno ci w zagadnieniach oceny wielokryterialnych 
jest  niezb dno   rangowania  kryteriów  lokalnych  oraz  niepewno   zwi zana  
z  faktorami  subiektywnymi  na  etapie  ich  formalizacji(opisanie  na  podstawie 
opinii  ekspertów).  Wa no   uwzgl dnienia  informacji  o  charakterze 
jako ciowym 

podkre lana 

jest 

przez 

wielu 

uczonych,  

 

 

7 

co  odzwierciedlone  jest  w  aktywnych  poszukiwaniach  narz dzi  dla  jej 
formalizacji.  

Jak to cz sto zdarza si  w takich sytuacjach sukces był osi gni ty prawie 

jednocze nie  przez  dwóch  autorów.  W  1963  roku  wydrukowano  artykuł 
Harringtona,  w  którym  dla  opisania  kryteriów  lokalnych  i  ograniczenia 
zaproponowano funkcje u yteczno ci. Przyjmuje ona warto ci ci gle wzrastaj ce 
od 0 do 1 przy zmianie odpowiedniego wska nika jako ci z zakresu najgorszych 
warto ci  do  strefy  najlepszych.  Konkretne  formy  funkcji  u yteczno ci 
formułowane  s   przez  osob   podejmuj c   decyzje  na  podstawie  
jej  do wiadczenia  i  subiektywnych  opinii.  Dalej  na  podstawnie  budowania 
lokalnych  funkcji  u yteczno ci  budowane  s   kryteria  jako ci  globalnej, 
maksymalizacja,  którego  zgodnie  z  metod   Harringtona  dostarczała  optimum. 
Metoda  Harringtona  była  najbardziej  popularna  w  dziedzinie  planowania 
eksperymentów  dla  poszukiwania  warunków  optymalnych  [3].  Najwi kszym 
sukcesem  zostały  optymalizacja  procesów  technologii  chemicznej  [4],  obróbki 
materiałów  [5],  w  hutnictwie  [6],  i  w  całym  szeregu  innych  dziedzin.  Warto 
podkre li ,  e  funkcje  u yteczno ci  Harringtona  zarówno  z  punktu  widzenia 
formy  matematycznej  oraz  sensu  merytorycznego  s   prawie  ekwiwalentne 
funkcjom 

przynale no ci 

w 

teorii 

zbiorów 

rozmytych. 

Jednak  

w skutek nieco ograniczonej interpretacji wprowadzonej przez Harringtona, jego 
metoda  nie  stała  si   do   popularna  i  nie  była  dalej  rozwijana.  Dzisiaj  metoda 
Harringtona  jest  wykorzystywana  raczej  jak  pewien  praktyczny  sposób  
w optymalizowanym planowaniu eksperymentów.  

Zupełnie  inny  los  spotkał  metody  formalizacji  rozmytych  charakterystyk 

proponowanych  przez  L.A.Zadeha  [25]  w  dwa  lata  po  artykule  Harringtona. 
Teoria zbiorów rozmytych zwłaszcza jej podstawa konceptualna oraz narz dzie 
matematyczne  dla  operowania  z  obiektami  natury  lingwistycznej  stały  si  
najbardziej efektywnymi  rodkami formułowania zada  oceny wielokryterialnej 

 

 

8 

w  warunkach  niepewno ci  o  charakterze  nie  statystycznym.  Zadania 
wielokryterialne  s   wyj tkowo  rozmaite  pod  wzgl dem  ilo ci  i  jako ci 
dost pnych  informacji,  co  powoduje  ró norako   proponowanych  wariantów  
w  poj ciu  optymalno ci  rezultatów  oszacowania.  Dlatego  te   jak  podkre laj  
autorzy  pracy  [7]  poszukiwanie  uniwersalnych,  niezale nych  od  dodatkowych 
informacji, „rozumnych” decyzji jest działaniem bezowocnym i dlatego dowolne  
z  heurystycznych  podej   rozwi zania  kompromisowego,  które  mo na  spotka   
w literaturze  mo e by  przydatne tylko  dla  ci le okre lonego, w skiego  grona 
zada .  Główne  osi gni cia  i  problemy  z  zakresu  rozmytej,  wielokryterialnej 
optymalizacji  i  podejmowania  decyzji  opisane  s   w  literaturze  o  charakterze 
uogólniaj cym  [8  -10]  i  zasadniczym  [11-13].  W  artykułach  [14-17]  dla 
kreowania  modelu  podejmowania  decyzji  w  warunkach  niepewno ci  u ywano 
podej cie  lingwistyczne  pozwalaj ce  na  formalizowanie  zadania  w  warunkach 
kryteriów  lokalnych  oraz  preferencji  przedstawionych  w  j zyku  naturalnym.  
W  pracach  [18-21]  zagadnienia  rozmytej  optymalizacji  wielokryterialnej 
rozpatrywane  s   przy  u yciu  współczynników  wzgl dnej  wa no ci  kryteriów 
lokalnych.  W  [22,23]  rozwini to  podej cie  na  podstawie  teorii  mo liwo ci 
zbudowanej  przez  L.Zadeha  u ywaj c  teorii  zbiorów  rozmytych,  
w  [24]  rozpatrywano  zagadnienie  wielokryterialnego  podj cia  decyzji  
w warunkach niepewno ci jednocze nie rozmytych oraz probabilistycznych.  

Przeanalizujemy  zasadnicze  osobliwo ci  zada   wielokryterialnych 

warunkach  lokalnych  kryteriach  rozmytych.  W  ramach  ogólnie  przyj tego 
podej cia [7] głównymi elementami formułowania zada  s : 

a.

  Zbiór alternatyw;  

b.

  Zbiór  ogranicze ,  które  nie  zb dnie  jest  uwzgl dni   w  trakcie 

szacowania alternatyw; 

 

 

9 

c.

  Funkcje  przynale no ci  –  przypisuj ce  ka dej  alternatywie 

odpowiednie  warto ci  wynikowe  (pozytywne  lub  negatywne), 
odpowiadaj ce danej alternatywy.  

 

Cech   specyficzn   zada   rozmytych  jest  pewna  symetria  mi dzy 

kryteriami  lokalnymi  i  ograniczeniami,  które  wyeliminuj   ró nice  mi dzy  nimi  
z punktu widzenia ich wpływu na wybór alternatyw [26].  

Dokładniej: 
Niech G – cel rozmyty, C- ograniczenie rozmyte w przestrzeni X, wtedy 

zbiór  rozmyty  D  =  G

∩

  nazywa  si   rozwi zaniem  kompromisowym  

i charakteryzuje si  funkcj  przynale no ci 

µ

D 

(x) = 

µ

G

(x) 

∧

 

µ

C

(x), x 

∈

X.( gdzie 

∧

 

to operacja minimum). 
W przypadku n celów i m ogranicze  mamy: 

 

D = G

1

 

∩

 … 

∩

 G

n

 

∩

 C

1 

∩

…

∩

 C

m

.                            (2.1)

 

 

 

µ

D 

(x) = 

µ

G1

(x)  

∧

 … 

∧

 

µ

C1

(x) 

∧

… 

∧

 

µ

Cm

(x)                                                                   

(2.2)

  

  

Definicja  i  przykład  rozpatrywany  powy ej  pozwalaj   wnioskowa ,  

e  w  odró nieniu  od  metod  tradycyjnych  podej cie  na  podstawie  zbiorów 

rozmytych  nie  przewiduje  zasadniczej  ró nicy  mi dzy  celami  i  ograniczeniami  
w  ocenach  wielokryterialnych  a  najcz ciej  spotykamy  sytuacje,  kiedy  cele 
przedstawione  s   w  przestrzeni  Y  w  odró nieniu  od  przestrzeni  alternatyw  X. 

Jednak  istnieje  odzwierciedlenie  f:  X

→

Y,    t.j.    Y  =  f(X).  U ywanie  reguły 

rozszerzenia  L.Zadeha  pozwala  na  rozpatrywanie  zadania  w  przestrzeni  X 

u ywaj c nast puj cych wzorów 

µ

G

(y) =  

µ

G

(f(x)),     

µ

C

(z) =  

µ

C

(g(x)). 

Wzór  (2.1)  mo na  rozpatrywa   jak  instrukcj   rozmyto  sformułowan  

u ywanie której powoduje dostrze enie celu rozmytego. Ale i w tym przypadku 

 

 

10 

mamy  niepewno   zwi zan   ze  sposobem  realizacji  takiego  rodzaju  instrukcji 
rozmytej.  To  znaczy  mamy  problem  wyboru  alternatyw.  Pewne  sposoby 
rozwi zania  tego  rodzaju  problemów  proponowane  s   w  artykule  [27]. 
Najłatwiejszym  i  powszechnym  sposobem  jest  poszukiwanie  alternatyw 

maksymalizuj cych 

µ

d 

i dlatego realizuj cych  

 

 

{

}

,

(x)

(x),

min

max

(x)

max

C

G

X

x

D

X

x

∈

∈

=

  

 

(2.3)

  

  

gdzie 

µ

G

( ) –koniunkcje wszystkich celów, 

µ

( ) – wszystkich ogranicze  

W  przypadkach,  kiedy  cele  i  ograniczenia  maj   ró n   wa no   

w  [27]  zaproponowano  sformułowa   kryterium  uogólniaj ce  jak  addytywne 
kombinacje  z  wagami  charakteryzuj cymi  wa no   rozpatrywanych  kryteriów 
lokalnych.  

 

 

(x),

)

x

(

b

 

 

(x)

)

x

(

a

(x)

j

i

C

m

1

j

j

G

n

1

i

i

D

=

=

+

=

 

 

(2.4)

  

                                                                        

gdzie   

.

)

x

(

b

 

)

x

(

a

m

1

j

j

n

1

i

i

1

=

+

=

=

 

 
Analogiczne  podej cie  rozwini to  w  pracy  [19].  Wzór  (2.4)  w  istocie 

przekształca  pewne  kryterium  wektorowe  w  kryterium  skalarne  za  pomoc  
kombinacji liniowej komponentu wektorowego funkcji celu. W monografii [28] 
odpowiednie  funkcje  przynale no ci  proponuje  si   formułowa   w  nast puj cy 
sposób 

 
 

 

 

11 

 

 

(x)}.

 )

x

(

b

(x),...,

 )

x

(

b

 

(x),

)

x

(

a

(x),...,

)

x

(

a

min{

(x)

Cm

m

C

G

n

G

D

1

n1

1

1

1

=

 

(2.5)

  

Na  najbardziej  naturalne  i  kompletnie  odzwierciedlaj ce  jako ciowy 

charakter  formułowania  preferencji  wygl da  podej cie  proponowane  przez  
R.Yagera  w  artykule  [21].  Podstaw   tego  podej cia  s   tak  zwane  operacje 
koncentrowania i rozci gania  

W rezultacie kryterium globalne przyjmuje kształt: 

 

 

m

1

n

2

1

b

m

b

1

a

n

a

2

a

1

C

...

C

G

...

G

G

D

=

 

(2.6)

  

                                                                

 
Odpowiednie funkcje przynale no ci b d  miały posta : 

 

 

0.

b

,...,

b

,

a

,...,

a

 

(x)},

(x),

(x),

(x),...,

min{

(x)

m

1

n

1

b

m

C

b

C

a

n

G

a

G

D

m

1

1

n

1

1

>

=

 

(2.7)

  

                 

 

 

.

b

a

m

n

1

n

i

m

j

j

i

1

1

1

=

+

+

=

=

 

(2.8)

  

                                                                                            
 

W  [21]  pokazano,  e  pot gowanie  w  stopniu  wi kszym  od  jedno ci 

wzmacnia  zapotrzebowanie  realizacji  kryterium  lokalnego,  innymi  słowy 
zwi ksza  jego  wa no .  Pot gowanie  w  stopniu  mniejszym  od  jedno ci 
przeciwnie zmniejsza wa no  kryterium lokalnego. Przy tym zachowywane jest 
skalowanie wszystkich funkcji przynale no ci kryteriów lokalnych i ogranicze . 
Podej cie  Yagera  pozwala  na  rangowanie  lokalnych  celów  i  ogranicze   
w  zgodno ci  z  intuicyjnymi  pogl dami  na  przedmiot  zadania  tych  lub  innych 
zapotrzebowa ,  co  dotyczy  stopnia  dostrze enia  ró nych  celów.  Z  innej  strony 

 

 

12 

podej cie  to  pozwala  w  sposób  naturalny  u ywa   operacje  koniunkcji  dla 
agregowania  kryteriów  lokalnych  razem  z  współczynnikami  ich  wzgl dnej 
wa no ci. 

Dla oceny współczynników wzgl dnej wa no ci R.Yager [21] proponuje 

u ywanie  metody  T.Saaty  [29].  Metoda  ta  polega  na  otrzymaniu  wektora  rang  

W na  podstawie równania typu AW = 

λ

max

W, gdzie 

λ

max

 – maksymalne własna 

warto  macierzy kryteriów parzystych porówna  kryteriów lokalnych. 

 
W  [30]  udowodniono,  e  zadanie  znalezienia  wektora  W  mo na 

zredukowa  do problemu minimalizacji funkcjonału 

(

)

2

N

1

i

N

1

j

i

j

ij

A

S

= =

−

=

 

przy ograniczeniu 

=

=

N

1

j

j

1

. 

U ywaj c  du ej  ilo ci  realnych  danych  autorzy  [30]  udowodnili,  e  ich 

podej cie ma cały szereg zalet w porównaniu z metod  proponowan  wcze niej 
przez T.Saaty’ego.  

Przedstawiona  powy ej  analiza  pozwala  s dzi   o  tym,  e  dla  ka dego 

zadania  mo na  u ywa   kilku  wariantów  agregowania  kryteriów  lokalnych  
w  kryterium  globalne.  W  artykule  [31]  przedstawiono  opini ,  

e w rzeczywisto ci mo e istnie  rozmyta skala ocen takiego rodzaju wariantów 

odzwierciedlaj ca pogl dy osoby podejmuj cej decyzje o najlepszym, idealnym 
sposobie formułowania kryterium globalnego.  

Niech  istnieje  X  –  przestrze   alternatyw  i  D

j

(x),  j  =  1,…,M  –  ró ne 

sposoby agregowania kryteriów lokalnych (na przykład, (2.1), (2.3), (2.5). Dalej 

niech 

ν

(D

j

)  –  stopie ,  w  którym  D

j

  odpowiada  zapotrzebowaniem 

 

 

13 

charakteryzuj cym  kryterium  idealne.  Wtedy  w  zgodno ci  z  [31]  kryterium 
idealne mo na przedstawi  w formie pewnego zbioru rozmytego. 

                         

 

( )

=

j

j

D

D

D

  

(2.9)

  

                                                                                            
W gruncie rzeczy w taki sposób abstrakcyjne poj cie idealnego kryterium 

globalnego  okre lone  jest  przez  jego  cechy  w  terminach  rzeczywistych 
dost pnych do zrozumienia. W [31] pokazano, w jaki sposób za pomoc  zbiorów 
rozmytych  typu  2  mo na  przedstawi   D  w  terminach  przestrzeni  alternatyw  X  
a  tak e,  e  dla  znalezienia  najlepszej  alternatywy  mo na  stosowa   wyra enie 
(2.9). 

Podsumowuj c  warto  podkre li , 

e  teoria  zbiorów  rozmytych  

nie  rozwi zuje  w  cało ci  takich  problemów  w  teorii  podejmowania  decyzji  
jak  istnienie  du ej  ilo ci  mo liwych  sformułowa   zada ,  istnienie  niepewno ci 
zwi zanej  z  subiektywnym  charakterem  preferencji  osób  odpowiedzialnych  
za podejmowanie decyzji itd. 

Zastosowanie  teorii  zbiorów  rozmytych  pozwala  konstruowa   bardziej 

nasycone  informacj ,  sensowne  sformułowania  zada   podejmowania  decyzji, 
gdy   w  jawnej  formie  uwzgl dnia  informacj   jako ciowe  przedstawione  
w  sposób  rozmyty.  Jak  wskazuje  N.Mojsiejew  we  wst pie  do  ksi ki  [28],  
do  prac  L.Zadeha  takiego  rodzaju  jako ciowe  informacje  po  prostu  były 
odrzucane  bo  było  nie  jasne  w  jaki  sposób  mo na  je  stosowa   w  formalnych 
schematach  analizy  alternatyw.  Jednak  ju   najprostsze  zadanie  zawieraj ce  co 
najmniej 2 kryteria niezb dnie zawiera w sobie elementy subiektywizmu. 

Dlatego  jednym  z  wa niejszych  problemów  okazało  si   formułowanie 

globalnego  kryterium  jako ci  dla  równowa nych  (równoznacznych)  

 

 

14 

i  nierównowa nych  kryteriów  lokalnych  i  ogranicze .  Charakterystyczn   cech  
wi kszo ci  rzeczywistych  procesów  jest  ci gło   zmiany  parametrów, 
okre laj cych kryterium optymalizacji. 

W  takich  warunkach  przestrze   alternatyw  jest  ju   niesko czona,  

co  z  kolei  powoduje  niemo liwo   stosowania  metod  teorii  podejmowania 
decyzji  bazuj cych  na  analizie  lokalnych  wska ników  jako ci  przy  dyskretnym 
zbiorze mo liwych alternatyw [32]. 

Takie  zadanie zwykle  rozpatruje si   za  pomoc   formułowania  w  ten lub 

inny  sposób  pewnych  agregacji  kryterium  lokalnych  oraz  ogranicze   
w kryterium globalne, ekstremum którego dostarcza poszukiwane optimum.  

W  zgodno ci  z  wynikami  pracy  [33],  procedura  agregacji  nie  mo e  by   

do  ko ca  formalizowana  i  zawsze  zale y  od  specyfiki  zadania,  celów, 
do wiadczenia i intuicji. 

W  artykule  [6]  wykazano,  e  odmienne  warianty  agregacji  kryteriów 

powoduj  bardzo ró ne ko cowe rezultaty, co  wiadczy o dominuj cej wa no ci 
etapu formułowania kryterium globalnego. 

Dlatego,  niezale nie  od  braku  uogólniaj cej  teorii,  warto  rozpatrzy  

pewne  najwa niejsze  w tki  procesu  formułowania  agregowanych  kryteriów, 
przeprowadzi   analiz   najcz ciej  stosowanych  sposobów  budowania 
uogólniaj cego  wska nika  jako ci  przy  opisywaniu  lokalnych  kryteriów  
za pomoc  funkcji przynale no ci. 

Bior c pod uwag  fakt,  e funkcje przynale no ci i funkcje u yteczno ci 

Harringtona,  w  niektórych  zastosowaniach  s   ekwiwalentne  w  dalszym  ci gu 
b dziemy  u ywa   terminu  funkcji  u yteczno ci  jako  najprostszy  
i najwygodniejszy w kontek cie zada  optymalizacji i oceny alternatyw. 

W  [7]  przedstawiono,  e  przy  formułowaniu  zada   wielokryterialnych 

najwa niejsze  s   problemy  porównywania  kryteriów  lokalnych  i  wzgl dnej 

 

 

15 

ocenie  ich  warto ci  w  optimum.  Inaczej  mówi c  najwa niejsze  s   wymagania 
dotycz ce optymalno ci na podstawie, których formułuje si  kryterium globalne.  

W  [34]  rozpatrywano  problem  porównania  w  niezale no ci  od  ró nicy 

mi dzy  kryteriami  i  ograniczeniami,  które  jak  to  było  pokazane  powy ej, 
jednakowo uczestnicz  w formułowaniu kryterium globalnego. 

W ramach tego sposobu opisanie kryteriów, problemy ich porównywania 

rozszerzaj  si  do  prosto i naturalnie, bo stopie  realizacji wymaga  kryterium 
ilo ciowo charakteryzuje si  warto ciami odpowiednich funkcji u yteczno ci. 

Dlatego,  je eli  A  i  B  –  s   kryteriami,  okre lonymi  przez  własne  funkcje 

u yteczno ci   

µ

( ),   

µ

( ), 

∈

,  wtedy  punkt 

1 

w  równym  stopniu  realizuje 

wymagania  kryteriów    i    je eli 

µ

(

1

)  = 

µ

(

1

)  i  punkt 

2

  spełnia  kryterium  

 w wi kszym stopniu ni   , je li 

µ

(

2

) 

>

 

µ

(

2

). 

Sformułowany  sposób  porównywania  kryteriów  lokalnych  jest  podstaw  

do ich agregacji. 

Jako  podstawowe  wymaganie  optymalizacji  w  [34]  wprowadzono 

warunek  obowi zkowego  spełnienia  wszystkich  kryteriów  i  ogranicze   
tj.  w  punkcie  optimum  wszystkie  funkcje  u yteczno ci  powinny  by   powy ej 
zera.  

Dodatkowo istniała potrzeba  eby w punkcie optimum wszystkie kryteria 

ograniczenia były spełnione w mo liwie maksymalnym stopniu.  

Innymi  słowy  niepo dane  jest  eby  warto ci  kryterium  globalnego 

wzrastały przy jednoczesnym ulepszeniu pewnych wska ników jako ci kosztem 
ostatnich  (co  wygl da  dosy   naturalne  zwłaszcza  je eli  wszystkie  kryteria 
lokalne i ograniczenia s  równowa ne). 

W  terminologii  teorii  podejmowania  decyzji  jest  to  ekwiwalentne 

wymaganie przynale no ci punktu optimum do przestrzeni Pareto [35] 

Analiza  sposobów  formułowania  globalnego  kryterium  na  podstawie 

przedstawionych  powy ej  zasad  w  [34]  przeprowadzono  rozpoczynaj c  

 

 

16 

od najprostszego przypadku dwóch równowa nych kryteriów lokalnych. Dla tej 
sytuacji w [34] udowodniono nast puj cy teoremat 1. 

Niech na zbiorze alternatyw X zadane s  równowa ne lokalne kryteria A  

i  B  przedstawione  odpowiednimi  funkcjami  u yteczno ci 

µ

( ), 

µ

( ), 

∈

 

maj cymi  maksima  w  odpowiednich  punktach    i  .  Przy  tym  spełnione  
s  warunki 

 

 

µ

( ) 

>

 

µ

( ), 

 

µ

( ) 

>

 

µ

( )

 

(2.10) 

 
Wtedy w punkcie optimum b dzie otrzymane maksimum funkcji  

 

µ ( ) = min (µ ( ), µ ( )),  ∈       

 

(2.11)

  

   

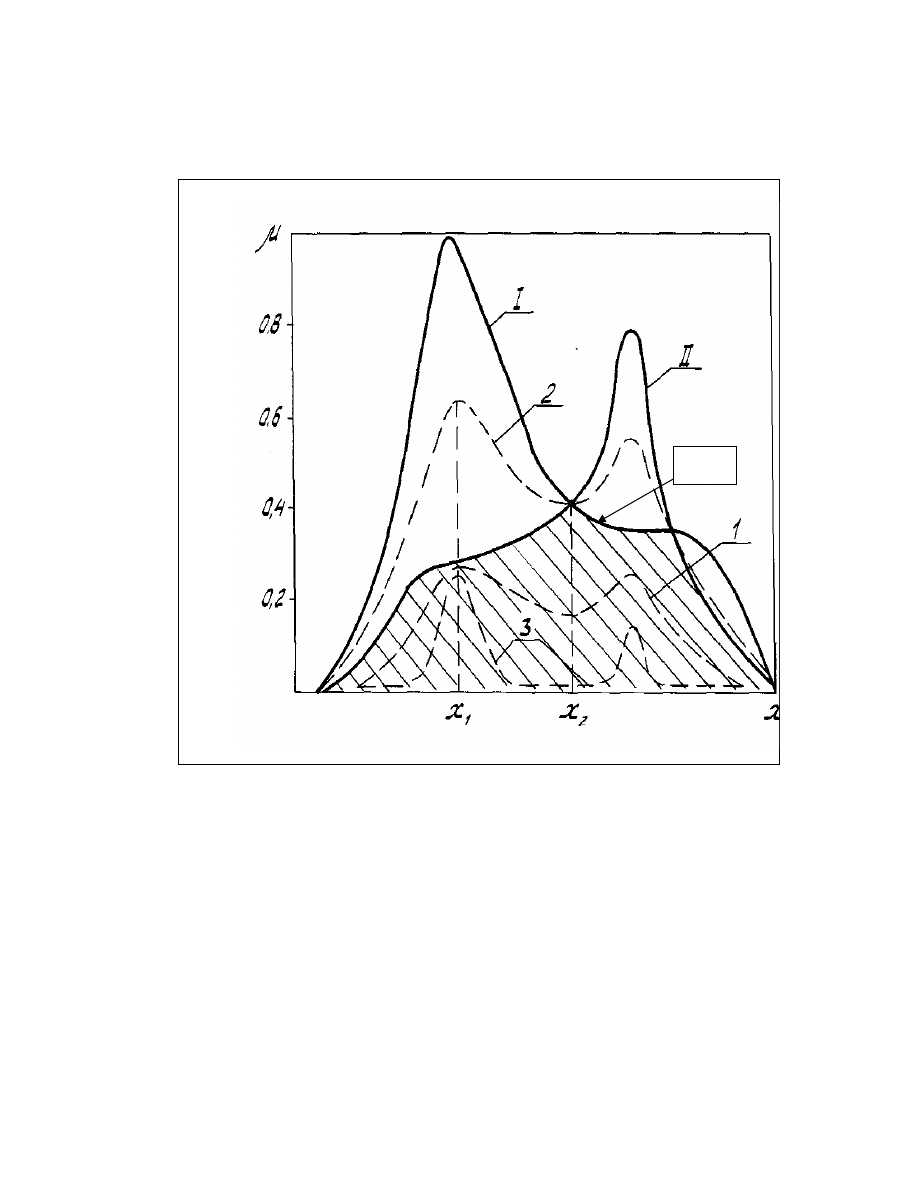
Interpretacja graficzna otrzymanych wyników przedstawiono na 

Rys. 2.1

 

Na  rysunku  jest  widoczne,  e  funkcja 

µ

  ( )  w  postaci  (2.11)  mo e  by  

traktowana  jako  funkcja  przynale no ci  zbioru  C,  kreowanego  przeci ciem 
zbiorów A i B przedstawionych funkcjami przynale no ci (u yteczno ci) 

µ

 ( ), 

µ

 ( ), t.j.   =   

∩

  . 

Przy  tym  w  punkcie  optimum  realizuje  si   maksimum  przeci cia 

kryteriów lokalnych. 

W  zgodno ci  z  warunkami  teorematy  1  obowi zkowe  jest  spełnienie  

obu  nierówno ci  (2.10).  Jednak  funkcje  u yteczno ci  nie  powinny  by   wcale 
skalowane do jednostki. 

Niespełnienie  warunków  (2.10)  mo e  prowadzi   do  sytuacji  kiedy 

maksimum  funkcji 

µ

  ( )  nie  znajduje  si   w  adnym  punkcie  przeci cia 

krzywych 

µ

 ( ), 

µ

 ( ) co pokazane jest na rys 2.2 

   

 

 

17 

 

Rys. 2.1. 

Sposoby agregowania lokalnych kryteriów równowa nych 

 I  - 

µ

 ( );  II - 

µ

 ( );  1 - 

µ

 ( ) = 

µ

 ( )

⋅

 

µ

 ( );  

2  - 

µ

  ( )  =  0.5

µ

 

( ) +0.5 

µ

 ( ); 

3 - 

µ

 ( ) = max (0,  

µ

 ( ) + 

µ

 ( ) – 1);  

x

1

 –punkt optimum dla wariantów 1, 2, 3; 

 

x

2

 – punkt optimum dla przeci cia 

µ

 ( ) = min (

µ

 ( ), 

µ

 ( )). 

µ ( ) 

 

 

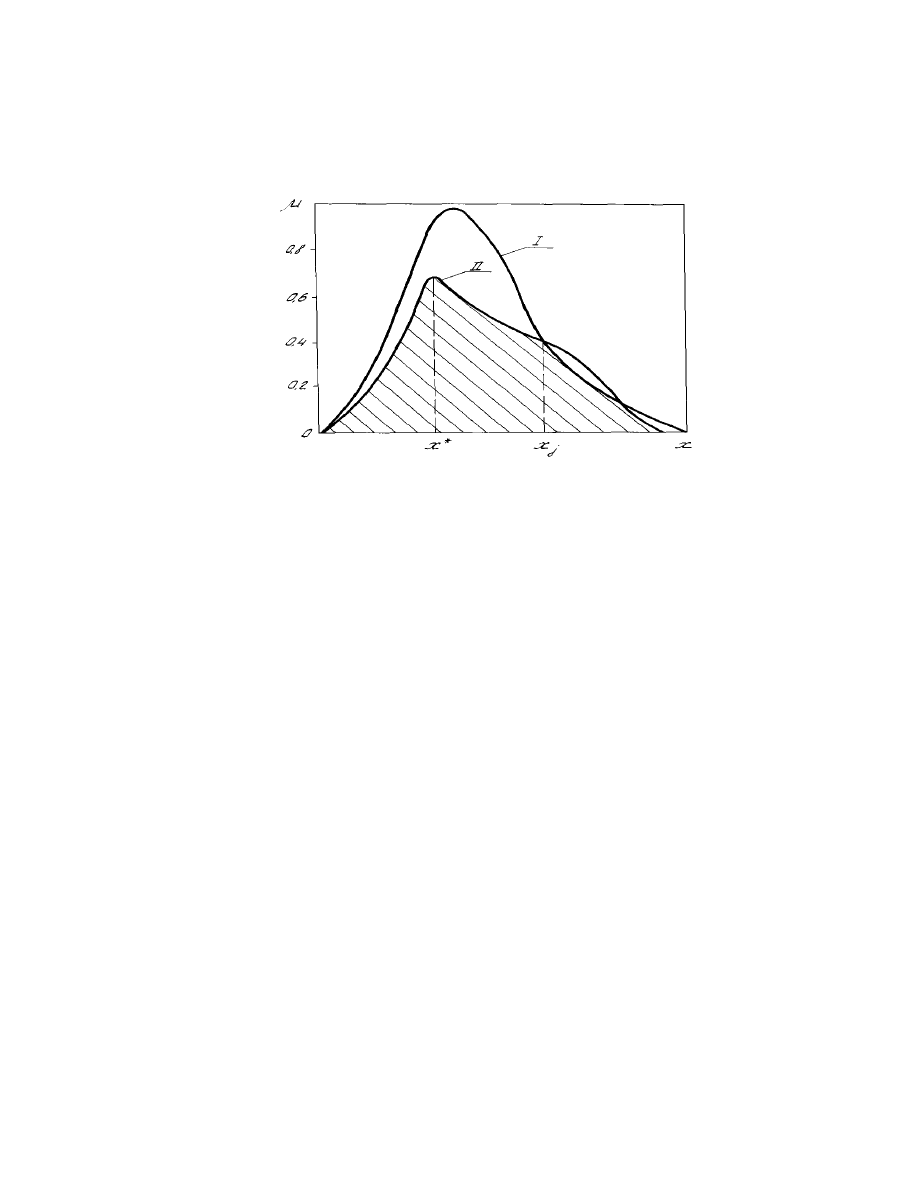
18 

 

Rys. 2.2. Przeci cie kryteriów lokalnych przy niespełnieniu warunków 

(2.10):   I  - 

µ

 ( );   II - 

µ

 ( ). 

W  ostatnim  przypadku  spełnione  jest  tylko  zapotrzebowanie 

maksymalnego spełnienia wymaga  kryteriów lokalnych bez ich równowarto ci 
w  punkcie  optimum.  Takiego  rodzaju  sytuacje  s   typowe  dla  wielu  zada ,  

w których funkcje u yteczno ci otrzymane niebezpo rednie np. 

µ

 ( ) = 

µ

 (f( )), 

mog  zachowywa  si  nie monotonicznie, mie  kilka ekstremów. 

Z udowodnionego w [34] teorematu 1 wynika,  e agregowanie kryteriów 

lokalnych  typu  (2.11)  gwarantuje  spełnienie  wszystkich  sformułowanych 
wymaga  co do optymalno ci rezultatów.  

Warto  podkre li ,  e  w  rozpatrywanym  najprostszym  przypadku  tylko 

agregowanie  (2.11)  zapewnia  otrzymanie  optimum  odpowiadaj cego  tym 
zapotrzebowaniom.  Ostatnie  stwierdzenie  ilustrowane  jest  na  rys  2.1,  gdzie 
widoczne jest,  e najcz ciej u ywane sposoby agregowania kryteriów lokalnych 
dostarczaj  punkty ekstremum w du ej odległo ci od rzeczywistego optimum.  

Rozpatrzmy  jeszcze  jedn   wa n   cech   agregacji  typu  (2.11).  Je eli 

interpretowa  funkcj  

µ

 ( ) jako funkcje przynale no ci zbioru   =   

∩

  , t.j. 

przeci cia  zbiorów  A  i  B  i  traktowa   optimum  jako  punkt  posiadaj cy 

 

 

19 

najwi kszy stopie  przynale no ci do przestrzeni przeci cia kryteriów lokalnych 
wtedy jedynym tylko uzasadnionym sposobem formułowania przeci cia zbiorów 
A  i  B  nale y  uzna   wyra enie  (2.11).  Rzeczywi cie  w  przypadku 

asymptotycznym    =    naturalne  jest  wymaganie   

∩

    =    co  jest 

równoznaczne  z 

µ

  ( )  = 

µ

  ( ),  t.j.  powinna  by   spełniona  zasada 

idempotentno ci

.  

Łatwo  udowodni ,  e  ani  addytywny  ani  multiplikatywny  lub  jaki   inny 

sposób  przeci cia  zbiorów  rozmytych  zawieraj cy  operacje  arytmetyczne  
nie  zachowuje  idempotentno ci  w  zwi zku,  z  czym  sens  ich  u ywania  dla 
agregowani kryteriów lokalnych jest problematyczny w tym samym stopniu jak 
problematyczna jest mo liwo  naturalnej interpretacji nierówno ci   

∩

   

≠

  . 

Wszystko  to  pozwala  wnioskowa ,  e  sposób  agregowania  (2.11)  mo e 

by   przyj ty  jako  najlogiczniejszy  i  uzasadniony  w  przypadku  równowa nych 
kryteriów lokalnych.  

Dalej  w  [34]  rozpatrywany  jest  przypadek  nierównowa nych  kryteriów. 

Przypuszczano,  e  do  nierównowa nych  kryteriów  lokalnych  A  i  B  mo na 

przypisa  odpowiednie współczynniki wzgl dnej wa no ci 

α

 i 

α

.  

Łatwo sprawdzi ,  e najcz ciej u ywane addytywne 

µ

 ( ) = 

α

 

µ

 ( ) +  

α

 

µ

  ( )  oraz  multiplikatywne 

( )

( )

( )

(

)

x

*

x

x

B

A

B

A

C

=

  sposoby  formułowania 

kryterium  globalnego  nie  gwarantuj   poprawnych  rezultatów  zada  

optymalizacji.  Rzeczywi cie  w  przypadku  asymptotycznym 

α

 

= 

α

  oba 

warianty  jak  to  wynika  z  rys  2.1  dostarczaj   maksima  w  odległo ci  od 
rzeczywistego  optimum.  Sposób  agregacji  proponowany  w  [36],  w  naszym 
przypadku ma kształt 

 

µ

 ( ) = min (

α

 

µ

 ( ), 

α

 

µ

 ( ))

 

(2.12) 

,                                                                        

 

 

20 

i przy  

α

 

= 

α

 

= 1 jest równoznaczny ze sposobem (2.11). Jednak taki sposób 

uwzgl dnienia  nierównowa no ci  kryteriów  lokalnych  w  praktyce  mo e 
powodowa  rezultaty absurdalne.  

Rozpatrzmy  sytuacj   szczegółowiej.  Niech  kryteria  A  i  B  spełniaj  

wszystkie  warunki  teorematu  1  z  wyj tkiem  równowa no ci  kryteriów 

lokalnych, na przykład A wa niejsze ni  B sk d naturalnie wynika,  e 

α

 

>

 

α

.

  

I  niech 

0

  punkt  optimum  w  wypadku  równowa no ci  A  i  B.  To  znaczy 

0

 

maksymalizuje funkcj  

µ

 ( ) = min (

µ

 ( ), 

µ

 ( )) i niech 

0

′

- punkt optimum 

dla nierównowa nych A i B maksymalizuj cy 

µ ′

 ( ) = min (

µ ′

 ( ), 

µ ′

( )) = 

min (

α

 

µ

 ( ), 

α

 

µ

 ( )). Wtedy 

0

′

 - jest jednym z pierwiastków równania: 

α

 

µ

 ( ) =  

α

 

µ

 ( ), 

Ostatnie wyra enie mo na przedstawi  w formie: 

 

β

 

µ

 ( ) =   

µ

 ( ),      

β

 = 

α

 

⁄

 

α

 

>

 1

  

(2.13)

  

 
Przypu my,  e 

  < 

,  gdzie 

, 

-  punkty

 

maksimum  funkcji  

µ

  ( )  i 

µ

  ( ).  Wtedy  pod  warunkiem 

µ

  ( )  = 

µ

  ( ), 

∈

,  (2.13),  a  tak e 

uwzgl dniaj c  monotoniczne  zmniejszenie 

µ

  ( )  i  wzrost 

µ

  ( )  na  odcinku  

[  , 

 

],  mo na  wnioskowa ,  e 

0

′

 

>

 

0

.  St d  wynika,  e 

µ

(

0

′

) 

<

 

µ

(

0

′

), 

inaczej  mówi c  kryterium  A  spełnia  si   w  mniejszym  stopniu  ni   B,  co  jest 
sprzeczne  z  pocz tkowym  zało eniem  o  wi kszym  znaczeniu  kryterium  A. 
Udowodnienie teorematu 1 jest ilustrowane na rys 2.3. 

Oczywistym  jest,  e dla  otrzymania  zrozumiałego,  nie  kontrowersyjnego 

rezultatu  za  pomoc   agregacji  typu  (2.12)  nale y  wa niejsze  kryterium 
pomno y   przez  mniejsz   rang .  Jednak  jest  to  sprzeczne  z  intuicyjnymi 
pogl dami  o  rangowaniu  kryteriów  i  bardzo  utrudnia  formalizacj   zadania 
optymalizacji  lub  oceny  alternatyw  przy  du ej  ilo ci  kryteriów  lokalnych.  Inn  

wad   agregacji  (2.12)  jest  nie  skalowalno   funkcji 

µ

( )  na  jednostk   

 

 

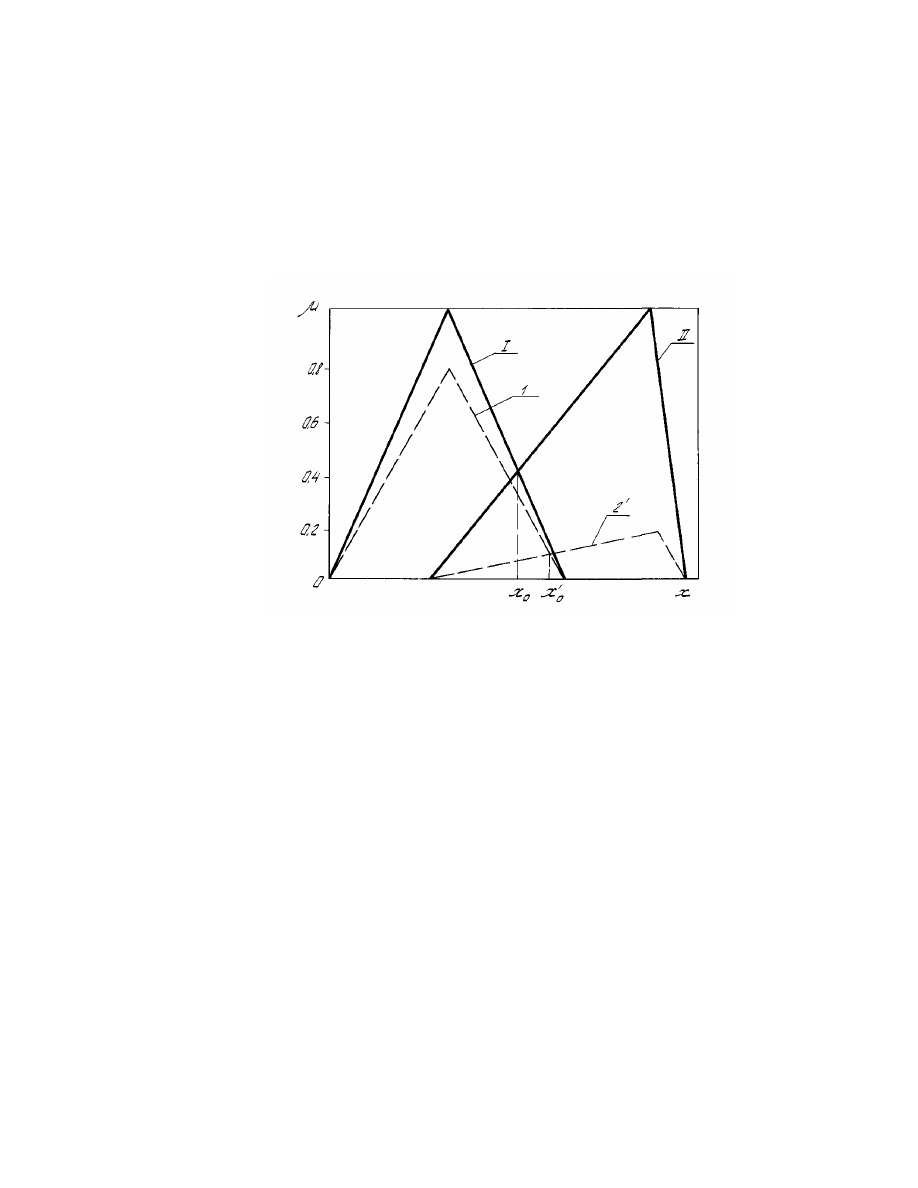
21 

co  uniemo liwia  ocen   ekstremów  lokalnych  z  punktu  widzenia  ich  odległo ci  
od  ekstremum  globalnego.  Warto  podkre li ,  e  w  praktyce  wi kszo   zada  
wielokryterialnych jest jednocze nie zadaniami wieloekstremalnymi. 

 

Rys. 2.3. Agregacja kryteriów rangowanych zgodnie z wyra eniem  

µ

 ( ) = min (

µ ′

 ( ), 

µ ′

( )): 

  I  - 

µ

 ( );   II - 

µ

 ( );    1 - 

µ ′

 ( ) = 0.8

µ

 ( );  

2 - 

µ ′

( ) = 0.2

µ

 ( ); 

Na podstawie, powy szych udowodnie  mo na stwierdzi ,  e naturalnym 

uogólnieniem  wyra enia  (2.11)  w  przypadku  nierównowa nych  kryteriów 
najwi kszym  stopniu  odzwierciedlaj cym  jako ciowy  charakter  zadania 
preferencji  przy  formułowaniu  globalnego  wska nika  jako ci  jest  agregacja 
proponowana w [37]: 

 

 

( )

( )

( )

(

)

x

,

x

min

x

B

A

B

A

'

C

=

 

(2.14)

 

,         

gdzie  (

α

 +  

α

) 

⁄ 2 = 1. 

Oczywiste  jest,  e  w  przypadku  asymptotycznym  tj.  przy 

α

  = 

α

  =  1 

agregacja  (2.14)  jest  równoznaczna  z  (2.11).  Przypu my,  e  kryterium  A  jest 

 

 

22 

wa niejsze od B, tj. 

α

 

>α

. W [37] pokazano,  e w tej sytuacji mamy wi ksze 

wymagania dla spełnienia kryterium A ni  dla B. Przy tym maksymalne warto ci 

kryterium globalnego b d  lokalizowane w punkcie bli szym maksimum 

µ

( ), 

ni  maksimum 

µ

( ) i je li 

0 

– punkt maksimum 

µ

 ( ) = min (

µ

 ( ),  

µ

 ( )), a 

0

′

 - punkt maksimum

µ ′

 ( ), wtedy 

µ

(

0

′

) 

>

 

µ

(

0

).  

Wyra enie  (2.14)  w  sposób  naturalny  uogólnia  si   dla  przypadku  

n lokalnych kryteriów 

 

 

( )

( )

( )

( )

1,

n

1

0,

,...,

,

,

x

...

x

x

x

n

1

i

i

n

2

1

n

2

1

'

C

n

2

1

=

>

∧

∧

∧

=

=

 

 
(2.15) 

  

 

          

gdzie 

∧ - jest operacj  minimum; 

α

1

,…,

α

n

 – współczynnikami wzgl dnej 

wa no ci które mo na otrzyma  na przykład u ywaj c metody [38] na podstawie 
macierzy  parzystych  porówna .  Wa n   po yteczn   cech   agregacji  (2.15)  jest 

fakt zachowania skalowania 

µ ′

 ( ) na jednostk  dlatego  e wszystkie 

µ

1

,…, 

µ

  n

 

te  s  przeskalowane na jednostk . 

Na  postawie  przeprowadzonej  analizy  mo na  stwierdzi ,  e  u ywanie 

strategii opieraj cej si  na wyra eniu (2.15) w zadaniach oceny alternatyw oraz 
optymalizacji  w  przypadku  opisania  kryteriów  lokalnych  za  pomoc   funkcji 
u yteczno ci  (przynale no ci)  jest  najlepszym  rozwi zaniem.  Jak  udowodniono 
jeszcze w pracy [39] strategia optymalizacji, na podstawie operacji minimum tj. 
strategii najpesymistyczniejszej polegaj cej na znalezieniu najlepszej alternatywy 
w ród najgorszych jest podej ciem jedynie gwarantuj cym niezawodne rezultaty 
zgodne z nasz  intuicj .  

W  naszej  sytuacji  znaczy  to,  e  stopnie  spełnienia  kryteriów  lokalnych  

w  punkcie  optimum  s   nie  mniejsze  ni   stopie   spełnienia  najmniej  wa nego 

 

 

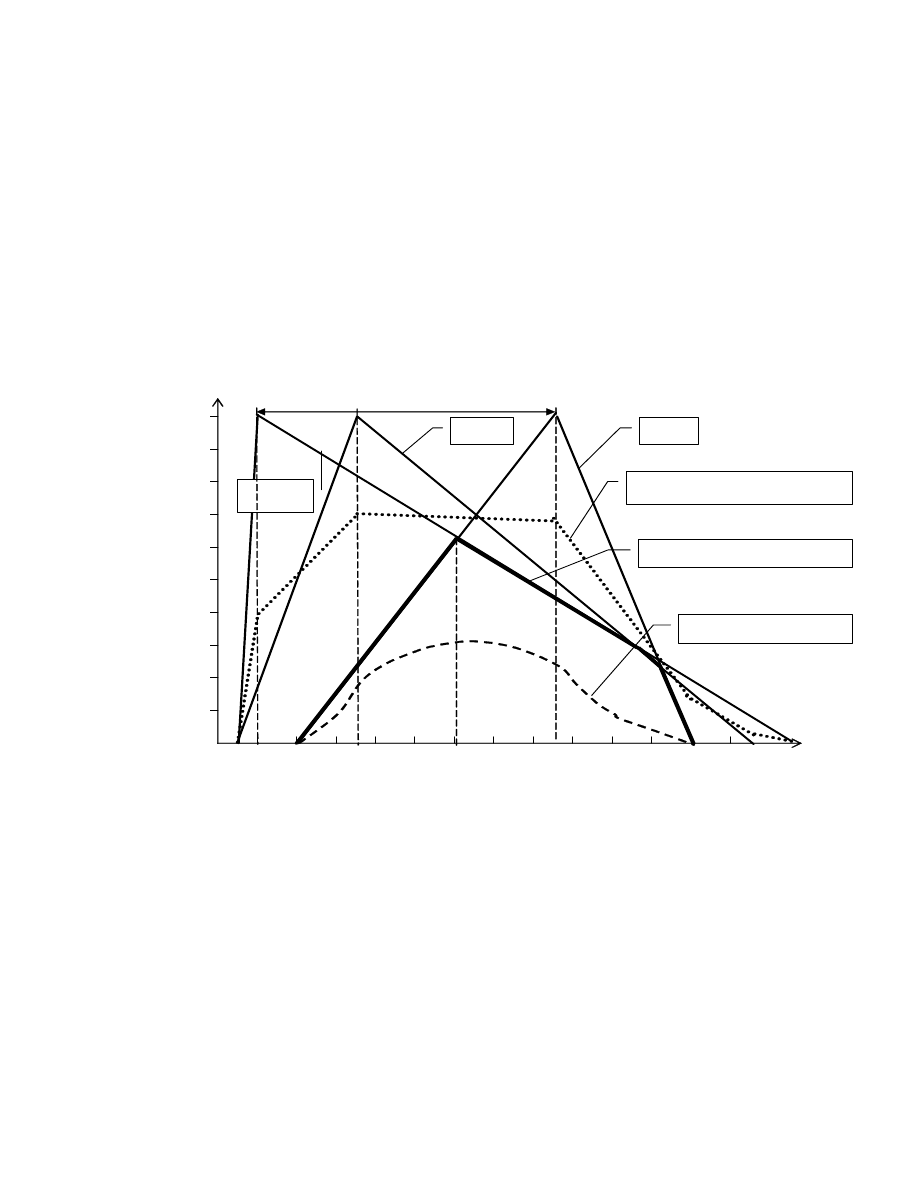
23 

kryterium, przy tym rozwi zanie zadania optymalizacji jest Pareto – optymalne. 
Jednak  w  praktyce  warunki  udowodnionego  w  [34]  teorematu  1  nie  s   zawsze 
spełnione.  Oprócz  tego  udowodniony  teoremat  jest  prawidłowy  wył cznie  
w  przypadku  dwóch  lokalnych  kryteriów.  Zupełnie  inna  sytuacj   mo emy 

spotka  ju  w sytuacji trzech kryteriów lokalnych 

(

µ

A

(x),

µ

B

(x),

µ

C

(x))

. 

 

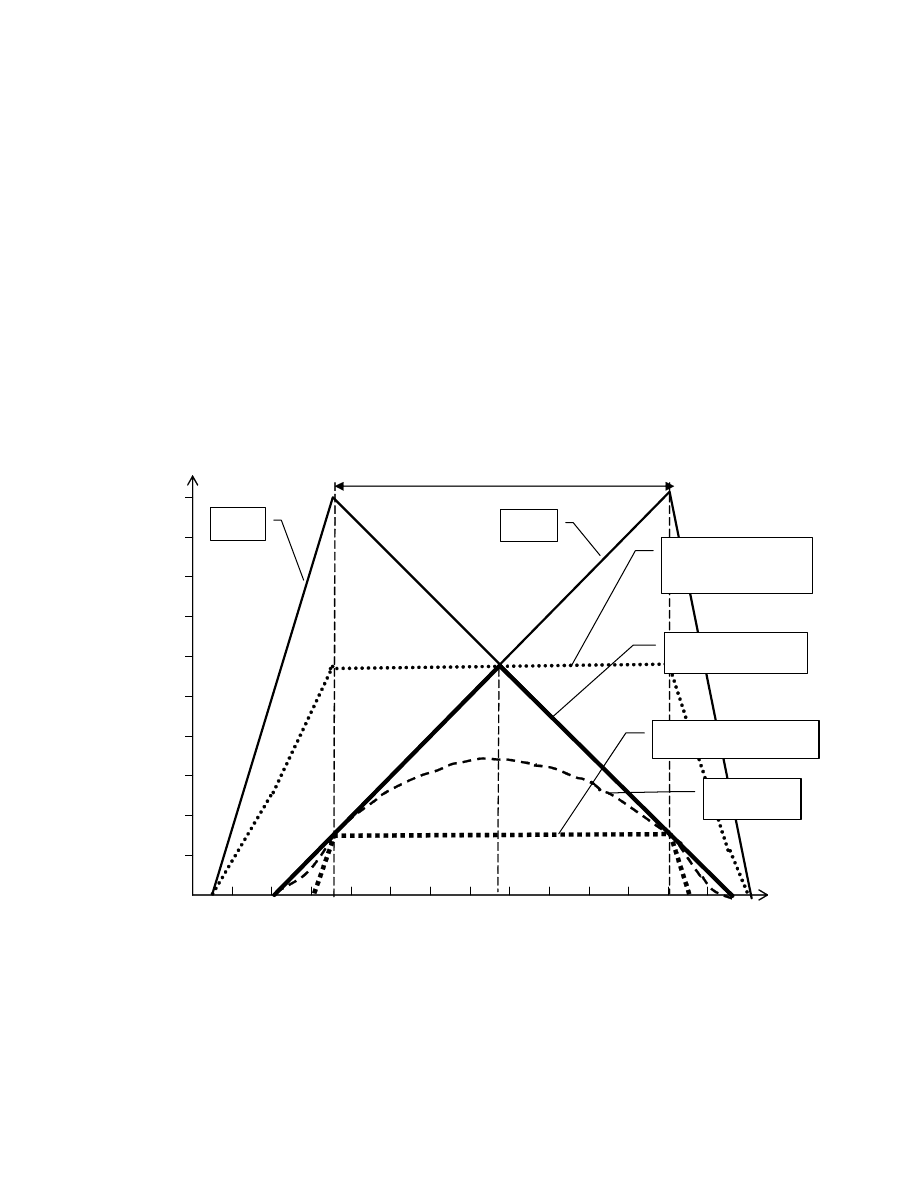
Rys.2.4 Agregacja trzech kryteriów za pomoc  kryteriów: 

addytywnego(1) , maksymalnego pesymizmu(2) i multiplikatywnego(3). 

 

 

µ

(x) 

1.0 

0.9 

0.8 

0.7 

0.6 

0.5 

0.4 

0.3 

0.2 

0.1 

0 

x

4  

µ

B

(x) 

1/3(

µ

A

(x)+

µ

B

(x)+

µ

C

(x))  (1) 

µ

A

(x)

µ

B

(x) 

µ

C

(x) (3) 

Pareto region  

x

3 

x

2  

x 

µ

A

(x) 

µ

(x) 

m in(

µ

A

(x),

µ

B

(x),

µ

C

(x)) (2 ) 

x

1  

 

 

24 

Jak  mo na  zauwa y   na  rysunku  2.4,  przy  równowa nych  trzech 

kryteriach  nie  mo emy  z  cał   pewno ci   przypuszcza ,  e  punkt  x2  jest 
optymalny.  Dzieje  si   tak  gdy   w  całym  Pareto  -  regionie  nie  mamy  takiego 
punktu, w którym przecinaj  si  wszystkie 3 kryteria. W takiej sytuacji mo emy 
stosowa   agregacje  typy  addytywnego.  Nale y  przy  tym  jednak,  zachowa  
pewn   ostro no ,  poniewa   na  przykład  w  sytuacji,  kiedy  oba  kryteria  s   do 
siebie  symetryczne,  agregacja  tego  typu  mo e  prowadzi   do  otrzymania 
niejednoznacznych wyników. Sytuacj  tak  bardzo dobrze odzwierciedla rys 2.5. 

 
Rys 2.5 Porównywanie sposobów agregacji kryteriów 
 

 

µ

(x) 

1.0 

0.9 

0.8 

0.7 

0.6 

0.5 

0.4 

0.3 

0.2 

0.1 

0 

x

1 

µ

A

(x

) 

µ

B

(x) 

µ

A

(x)

µ

B

(x) 

Pareto region 

x

4 

x

2

,x

3 

x 

0.5(

µ

A

(x)+

µ

B

(x)) 

addytywny 

max(0,

µ

A

(x)+

µ

B

(x)-1) 

min(

µ

A

(x),

µ

B

(x)) 

 

 

25 

Jednak nale y podkre li ,  e w wielu sytuacjach najbardziej uzasadniona 

agregacja  typu  (2.15)  po  prostu  nie  odpowiada  do wiadczeniu  i  intuicji  osób 
podejmuj cych decyzj  przy ocenie alternatyw lub optymalizacji[40].  

Dlatego w przypadku skomplikowanych zada  przy du ej ilo ci lokalnych 

kryteriów  i  ogranicze   po  otrzymaniu  gwarantowanych  ocen  na  podstawie 
agregacji  (2.15)  jest  sens  zastosowa   i  inne  addytywne  i  multiplikatywne 
warianty  budowania  kryterium  globalnego.  W  przypadku,  gdy  rezultaty 
otrzymane za pomoc  wszystkich u ywanych sposobów agregacji s  podobne, co 
najmniej  na  poziomie  jako ciowym  utwierdza  nas  to  w  przekonaniu  
o adekwatno ci otrzymanych wyników.  

Osoby 

podejmuj ce 

decyzj  

mog  

mie  

ró ne 

pogl dy,  

co  do  efektywno ci  ró nych  sposobów  agregacji.  Dlatego  powstaje  dodatkowy 
problem  agregowania  wła nie  kryteriów  ju   agregowanych  [41].  
Na  przykład  w  [40]  u ywane  s   do  tego  elementy  teorii  mo liwo ci,  w  [42] 
proponowana jest tak zwana operacja wa onego u rednienia, w [43] rozwija si  
podej cie  na  podstawie  t-skal  Yagera,  w  [44,  45]  metod   hierarchicznego 

agregowania.  Jednak  najbardziej  popularny  jest  dzisiaj  tak  zwany 

γ-  operator  

[46, 47]:  

 

 

( )

1

0

n;

1,2,...,

i

,

i

i

1

1

1

i

i

≤

≤

=

∏ −

−

−

∏

=

 

(2.16)

  

gdzie 

µ

i

 – funkcja przydatno ci lokalnych kryteriów jako ci. 

 
Jasne, 

e  wyra enie  (2.16)  jest  tylko  agregacj   addytywn   

i  multiplikatywn   uogólnionych  kryteriów.  W  [48]  proponowane  s   podobne  
γ- agregacje na podstawie minimum, maksimum oraz kryterium addytywnego: 

 

 

 

26 

 

( ) (

)

n

max

i

i

i

i

or

−

+

=

µ

γ

µ

γ

η

1

  

(2.17)

  

  

 

( ) (

)

n

min

i

i

i

i

and

−

+

=

µ

γ

µ

γ

η

1

  

(2.18)

  

                                                                           

 
Ostatnie  wyra enie  były  u ywane  w  pracy  [50]  w  zagadnieniach 

wielopoziomowego  podejmowania  decyzji.  Jako  najwa niejszy  problem 

stwierdzono brak  cisłych reguł wyboru parametru 

γ. W [49] proponowana jest 

metoda  w  pewnym  stopniu  formalizuj ca  wybór  parametru 

γ,  jednak 

wymagaj ca  od  eksperta  wielkiej  ilo ci  dodatkowych  informacji  przy  tym,  
co  wa niejsze  o  charakterze  ilo ciowym.  Warto  podkre li ,  e  w  wyra eniach 
(2.16)-(2.18)  kryteria  lokalne  rozpatrywane  s   jak  równowa ne.  Istotne  jest,  

e ich, rangowanie za pomoc  np. metody parzystych porówna  przedstawia si  

jako zadanie bardziej skomplikowane i wa niejsze ni  wybór parametru 

γ. 

Oprócz  tego  omówione  powy ej  podej cia  nie  pozwalaj   jednocze nie 

agregowa   wszystkich  trzech  głównych  typów  kryteriów  uogólnionych  
za pomoc  operatorów min oraz addytywnego i multiplikatywnego.  

W  wielu  przypadkach  mo e  by   po yteczna  nast puj ca  procedura 

otrzymania rezultatu kompromisowego [34]. Niech 

µ

1

 ( ), 

µ

2

 ( ), 

µ

3

 ( ) – pewne 

warianty agregacji kryteriów lokalnych np. addytywne, multiplikatywne oraz na 
podstawie  operatora  minimum.  Przypu my,  e  w  rezultacie  maksymalizacji 

ka dej z funkcji 

µ

1

, 

µ

2

   

µ

3

 otrzymano odpowiednie punkty optimum 

1

, 

2

 i 

3

. 

W  wyniku  bada   warto ci  kryteriów  lokalnych  u  osoby  podejmuj cej  decyzj  
formułuje  si   pewne  preferencje,  które  mo na  scharakteryzowa   za  pomoc  
rangowania  wzgl dnego  stopnia  adekwatno ci  otrzymanych 

1

, 

2

  i 

3

,  co  do 

 

 

27 

wymaga   optymalizacji..  Niech  to  rangowanie  zadano  przez  pewne 

współczynniki wzgl dnej wa no ci 

α

1

, 

α

2

, 

α

3 

(które mog  by  jednakowe, kiedy 

przeprowadzenie  rangowania 

1

, 

2

  i 

3

  jest niemo liwe).  Wtedy wprowadzaj c 

skalowane 

na 

1 

funkcje 

µ

1

( ) 

= 

µ

1

( ) 

⁄ 

µ

1

(

1

); 

 

µ

2

( ) = 

µ

2

( ) 

⁄ 

µ

2

(

2

); 

µ

3

( ) = 

µ

3

( ) 

⁄ 

µ

3

(

3

) mo na zbudowa  nowe kryterium 

globalne, które b dziemy nazywa  uogólnionym kompromisowym wska nikiem 
jako ci. 

 

 

( )

( )

( )

( )

=

x

,

x

,

x

min

x

3

2

1

3

2

1

η

 

(2.19)

  

                                                                                 

Oczywi cie punkt globalnego maksimum 

η

( ) b dzie przedstawia  pewne 

kompromisowe  rozwi zanie  zagadnienia  optymalizacji  uwzgl dniaj ce 
mo liwo ci dostrze enia warunków optymalnych za pomoc  ró nych sposobów 
agregacji kryteriów lokalnych. 
 
 
 
 
 
 
 
 
 
 
 
 
 

 

 

28 

3.

 Problem 

budowania 

systemu 

hierarchicznego 

(wielopoziomowego) 

wielokryterialnej 

oceny 

alternatyw. 

 
Wa nym  problemem  podejmowania  decyzji  optymalizowanej  jest  cz sto 

wyst puj ca  hierarchiczno   zagadnie .  Istnieje  wiele  heurystycznych  podej   
do  rozwi zania  tego  problemu  jednak  dzisiaj  faktycznie  standardow   została 
metoda  analizy  hierarchii  (MAH)  T.Saat’ego  [54]  bardzo  popularna  dzi   
w  Stanach  Zjednoczonych,  lecz  maj ca  problemy  wewn trzne,  przez  co  jest  
w stanie ci głego rozwoju [55,56]. 

Istota  metody  polega  na  hierarchicznym  przedstawieniu  elementów 

okre laj cych  sens  rozwi zywanego  problemu.  Metoda  składa  si   
z  dekompozycji  problemu  na  coraz  prostsze  składniki  i  cz ci  a  nast pnie 
obróbce  szeregu  opinii  osoby  podejmuj cej  decyzje  za  pomoc   rozpatrzonej  
w  punkcie  pierwszym  metody  opartej  na  macierzy  parzystych  porówna . 
W  rezultacie  wylicze   na  podstawie  macierzy  oszacuje  si   wzgl dne  stopnie 
wzajemnych  relacji  elementów  rozpatrywanych  hierarchii  oraz  zostanie 
wybierana najlepsza z punktu widzenia sformułowanego celu alternatywa. 

Metoda hierarchii stała si  powszechnie u ywana dla szerokiego zakresu 

problemów  w  tym  dla  planowania  perspektywicznego  oraz  oceny  jako ci 
produkcji. Mo liwo ci metody nie ograniczaj  si  jedynie do analizy sytuacji na 
poziomie  jednego  zakładu  lub  organizacji,  istniej   przykłady  jej  skutecznego 
u ywania  
do rozwi zywania problemów na skale całych pa stw [54]. W skutek osobliwej 
wa no ci metody oraz faktycznego braku literatury w j zyku polskim dotycz cej 
MAH jest sensowne dokładniej opisa  jej podstawowe poj cia.  

 

 

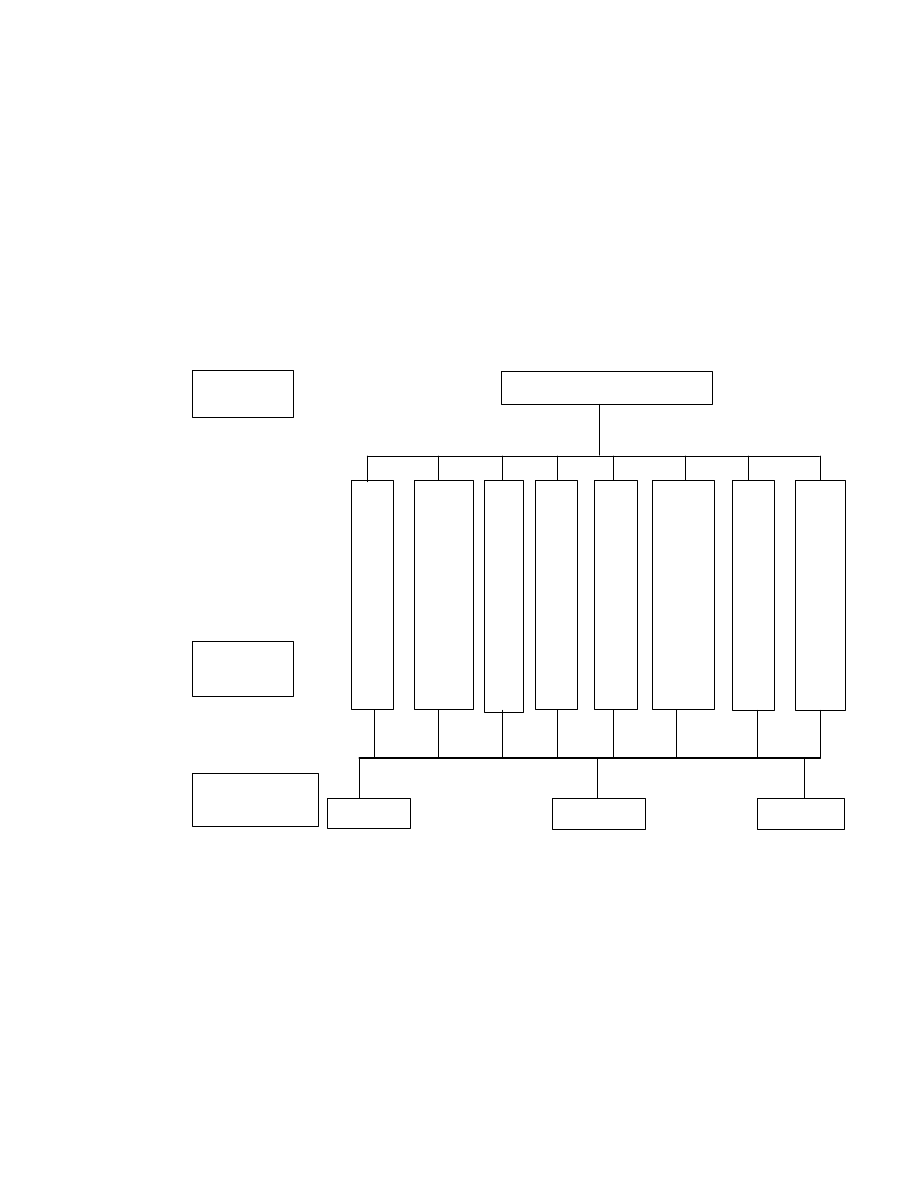
29 

U yjemy  do  tego  do   prostego  przykładu.  Niech  rednio  zamo na 

rodzina  podejmuje  decyzje  o  zakupie  domu.  W  wyniku  dyskusji  udało  si  
wyodr bni   osiem  lokalnych  kryteriów  jako ci  dla  oceny  potrzebnego  rodzinie 
domu.  Zadanie  polega  na  wyborze  jednego  z  trzech  kandyduj cych  domów. 
Pierwszym krokiem jest dekompozycja zadnia w form  hierarchiczn  (rys 3.1). 

 

 
 
 
 
 
       
 
 
 
 
 
 
 
 
 
 

Dom 

W

yg

od

a 

do

ja

zd

u 

K

ra

jo

br

az

 

W

ie

k 

do

m

u 

Po

dw

ór

ko

 

N

ow

oc

ze

sn

o

 w

yp

os

a

en

ia

 

St

an

 o

gó

ln

y 

W

ar

un

ki

 f

in

an

so

w

e 

W

ym

ia

ry

 d

om

u 

Dom   

Dom B 

Dom   

Poziom 1. 

Cel 

Poziom 2. 
Kryteria 

Poziom 3.  
Altrernatywy 

 

Rys.3.1. Hierarchiczna dekompozycja zadania wyboru domu. 

 

Na pierwszym (najwy szym) poziomie znajduje si  ogólny cel - «Dom». 

Na drugim poziomie mamy osiem faktorów (kryteriów lokalnych), u ci laj cych 
cel  i  na  trzecim  najni szym  poziomie  s   trzy  mo liwe  alternatywy  –  domy 
A,B,C, które powinny by  ocenione najpierw pod wzgl dem kryteriów poziomu 

 

 

30 

nr  2,  a  nast pnie  z  punktu  widzenia  ogólnego  agregowanego  celu.  Dalej  
w  zgodno ci  z  MAH,  nast puje  kreowanie  zbiorów  macierzy  parzystych 
porówna   dla  ka dego  ni szego  poziomu  –  po  jednej  macierzy  dla  ka dego 
kryterium.  Przy  tym  elementy  ni szego  poziomu  porównuj   si   nawzajem  
z punktu widzenia spełnienia kryterium na poziomie wy szym.  

W rezultacie otrzymuje si  zbiór kwadratowych macierzy ocen. Parzyste 

porównania  wykonuj   si   w  terminach  dominowania  jednego  elementu 
wzgl dem innego. 

W  podanym  przykładzie  powinno  by   zbudowane  dziewi   macierzy: 

jedna dla drugiego poziomu hierarchii oraz osiem dla poziomu trzeciego 

W tabeli 1.4 przedstawione jest wypełniona macierz elementów drugiego 

poziomu pod wzgl dem kryterium poziomu pierwszego tzn. pod wzgl dem celu. 
Na  przykład przy  odpowiedzi  na proste  pytanie:  „Jaka  jest wa no   wymiarów 
domu wzgl dem wygody dojazdu w odniesieniu do celu ogólnego” członkowie 
rodziny  doszli  do  wniosku,  e  wymiary  s   wyra nie  wa niejsze  i  dlatego  oni 
wpisali  warto   5  w  odpowiedni   kratk   macierzy.  Przy  tym  warto   1/5 
automatycznie wpisuje si  w symetryczn  wzgl dem głównej przek tnej kratk . 
Osiem macierzy parzystych porówna  dla trzeciego poziomu hierarchii tzn. dla 
alternatyw  w  stosunku  do  elementów  2-go  poziomu  zawieraj   parzyste 
porównania  mo liwych  wariantów  wyboru  domu.  Porównuje  si ,  w  jakim 
stopniu  jest  dobry  ten  lub  inny  dom  z  punktu  widzenia  spełnienia  ka dego  
z kryteriów drugiego poziomu. 

W  wyniku  otrzymamy  osiem  macierzy  ocen  o  wymiarach,  3  na  3,  

bo  mamy  osiem  kryteriów  na  drugim  poziomie  i  3  domy,  które  w  sposób 
parzysty porównuj  si  wzgl dem ka dego z kryteriów lokalnych. 

 
 
 

 

 

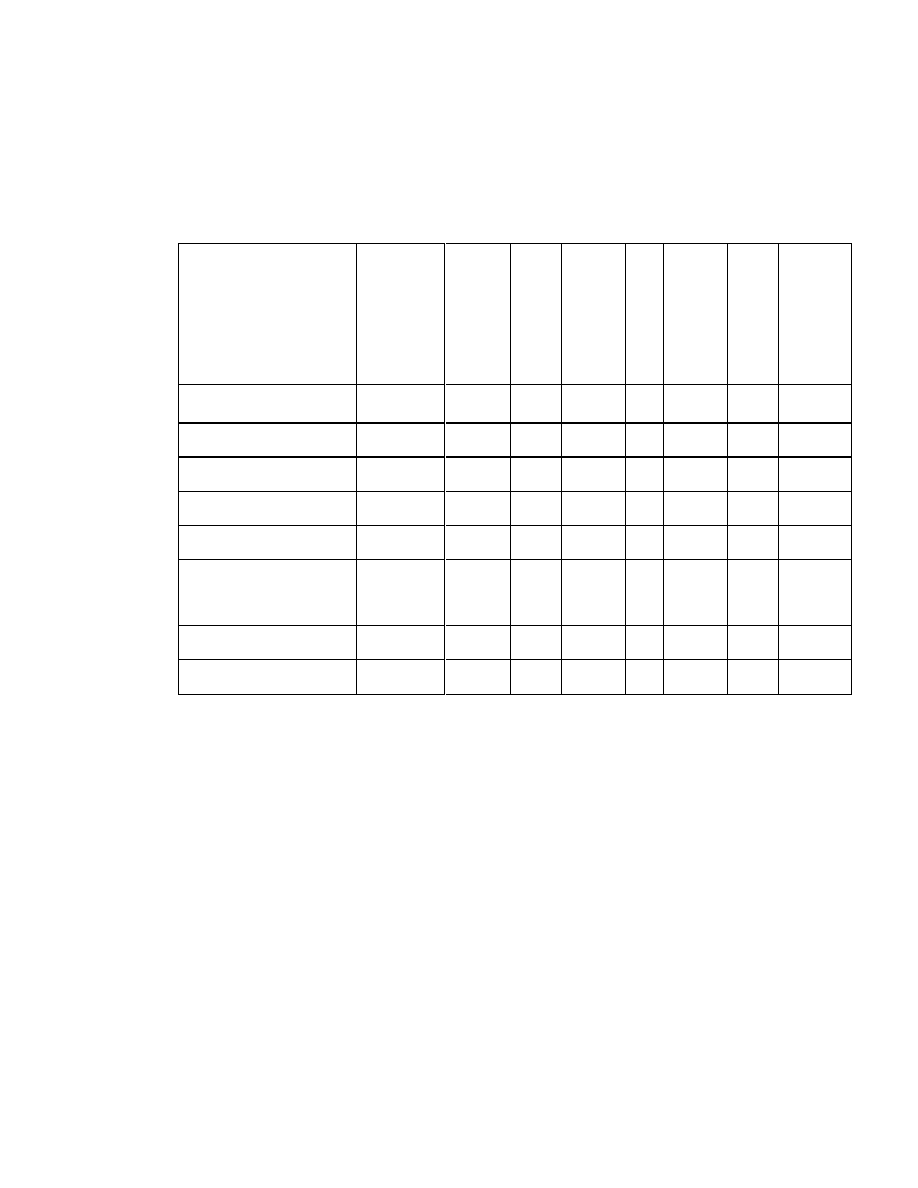
31 

Tabela 1.4 Kupno domu: macierz parzystych porówna  dla drugiego 

poziomu

 

 

W

ym

ia

ry

 d

om

u 

 W

yg

od

a 

do

ja

zd

u 

  Kr

aj

ob

ra

z 

   W

ie

k 

do

m

u 

  Po

dw

ór

ko

 

 

N

ow

oc

ze

sn

o

 

w

yp

os

a

en

ia

 

St

an

 o

gó

ln

y 

  W

ar

un

ki

 

fi

na

ns

ow

e 

Wymiary domu 

1 

5 

3 

7 

6 

6 

1/3 

1/4 

Wygoda dojazdu 

1/5 

1 

1/3 

5 

3 

3 

1/5 

1/7 

Krajobraz 

1/3 

3 

1 

6 

3 

4 

6 

1/5 

Wiek domu 

1/7 

1/5 

1/6 

1 

1/3 

1/4 

1/7 

1/8 

Podwórko 

1/6 

1/3 

1/3 

3 

1 

1/2 

1/5 

1/6 

Nowoczesno  

wyposa enia 

1/6 

1/3 

1/4 

4 

2 

1 

1/5 

1/6 

Stan ogólny 

3 

5 

1/6 

7 

5 

5 

1 

1/2 

Warunki finansowe 

4 

7 

5 

8 

6 

6 

2 

1 

 

Na  nast pnym  etapie  MAH  na  podstawie  ka dej  macierzy  parzystych 

porówna   formuje  si   zbiór  lokalnych  priorytetów  lub  rang,  które  wyra aj  
stosunkowe  wpływy  zbioru  elementów  poziomu  ni szego  na  odpowiadaj ce 
elementy przylegaj cego wy szego poziomu. 

Dla  oszacowania  priorytetów  stosuje  si   nast puj c   metodyk :  niech  

α

i 

>  0,  i  =  1,…,  n  –s   priorytetami  elementów,  wtedy  parzyste  porównanie 

mo na  przedstawi   za  pomoc   macierzy  parzystych  porówna     =  {aij},  
aij = 

α

i

/

α

j

. 

Rzeczywi cie,  mno c  A  z  prawej  strony  przez  wektor  priorytetów  

W  =  (

α

1

, 

α

2

,…, 

α

n

),  otrzymamy  AW=  nW.  St d  wynika,  e  je eli  znana  jest 

 

 

32 

macierz A wtedy znalezienie wektora W b dzie si  sprowadzało do rozwi zania 
systemu liniowych równa  algebraicznych. 

Jednak  w  praktyce  elementy  macierzy  s   ocenami  wzgl dnej  wa no ci 

alternatyw,  które  wybierane  s   ze  skali  wzgl dnej  wa no ci  na  podstawie 
priorytetów subiektywnych przyjmuj ce, dlatego tylko warto ci całkowite lub ich 
odwrotne  warto ci.  Jasne  jest,  e  takiego  rodzaju  macierze  ogólnie  nie  
s   spójne  dlatego  rozwi zanie  otrzymaj   na  podstawie  równania  typu  

AW= 

λ

max

 W, gdzie 

λ

max

 – jest maksymaln  własn  warto ci  macierzy A.   

Dosy   po ytecznym  ubocznym  produktem  teorii  jest  tak  zwany  indeks 

spójno ci (IS) macierzy A, który daje informacj  o stopniu naruszenia liczbowej  

( kardynalnej aij = 

α

i

/

α

j

) i tranzytywnej (porz dkowej) spójno ci.

 Dla ulepszenia 

spójno ci  mo na  proponowa   poszukiwanie  dodatkowej  informacji  i  przegl d 
danych  u ywanych  przy  tworzeniu  skali.  Indeks  spójno ci  w  ka dej  macierzy  
i  dla  hierarchii  ogólnej  mo e  by   otrzymany  w  przybli ony  sposób  za  pomoc  
nast puj cego algorytmu: pierwszym krokiem jest zsumowanie ka dej kolumny, 
nast pnie  sum   pierwszej  kolumny  mno y  si   przez  warto   pierwszego 
elementu normalizowanego wektora priorytetów, sum  nast pnej kolumny przez 
warto  drugiego elementu normalizowanego wektora priorytetów itd.

 

W  nast pnym  kroku  otrzymane  liczby  sumuje  si .  Dzi ki  temu  mo na 

otrzyma  warto  oznaczan  przez 

λ

max

. 

Dla indeksu spójno ci otrzymamy nast puj cy wzór IS = (

λ

max

- n)/(n—1), 

gdzie  n – Ilo  elementów porównywanych. Przy tym dla macierzy odwrotnej 

symetrycznie zawsze spełnia si  nierówno  

λ

max

 

≥

 n. 

Rozwa my  warto ci  IS,  które  były  otrzymane  za  pomoc   losowego 

wyboru ilo ciowych ocen elementów macierzy ze skali 1/9, 1/8, 1/7,...,1,2,...,9 i 
tworzenie macierzy odwrotnie symetrycznej.  

 

 

33 

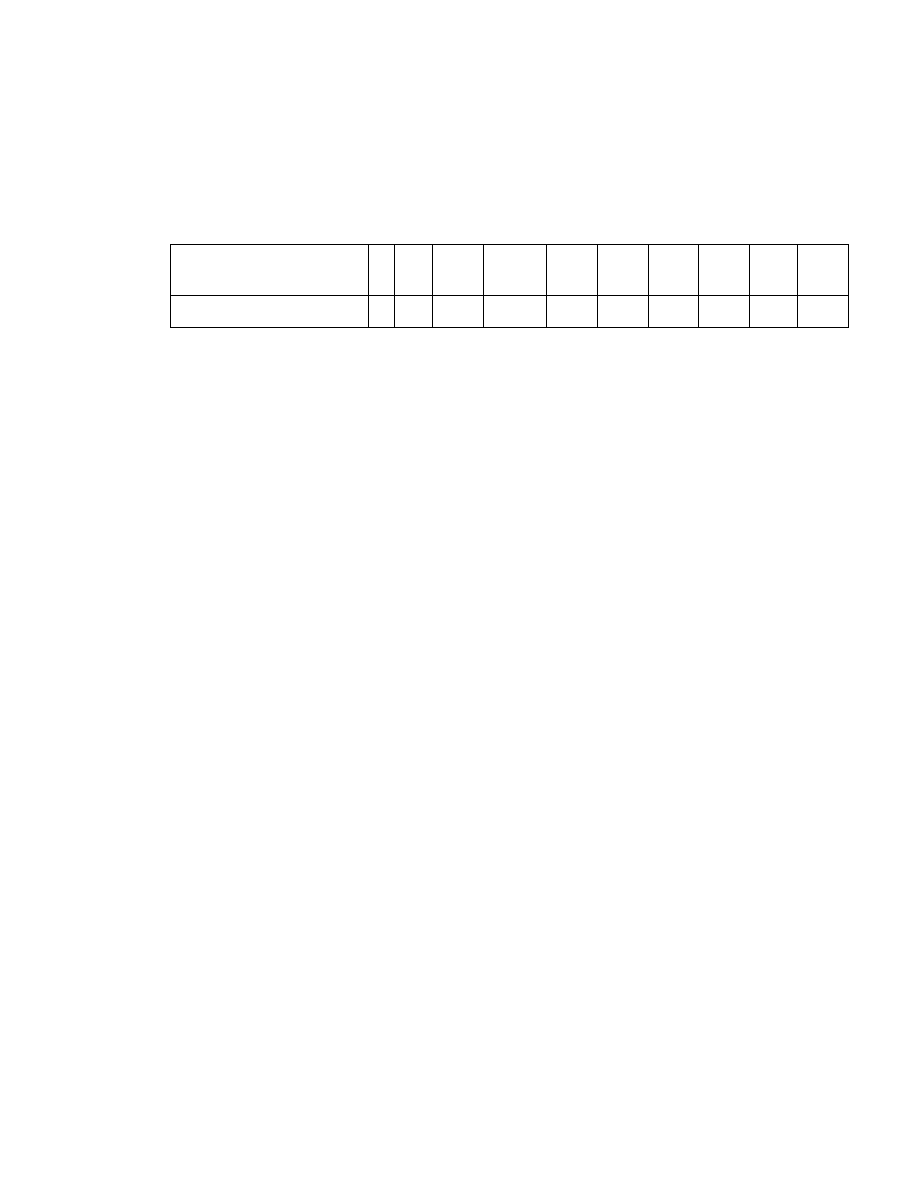
Poni ej przedstawione s  u rednione warto ci IS dla losowych macierzy ró nych 
wymiarów. 

  

Je li,  podzieli   IS  konkretnej  rozpatrywanej  macierzy  parzystych 

porówna   przez  u rednion   warto   IS  odpowiadaj cej  losowej  macierzy 
parzystych porówna  takiego samego wymiaru to otrzymamy wzgl dn  spójno  
(WS).  Warto   WS  powinna  by   około  10%  lub  mniej,  aby  by   wystarczaj ca 
dla u ywania rozpatrywanej macierzy parzystych porówna  w praktyce. 

W niektórych przypadkach dopuszczalna górna granica WS wynosi, około 

20%,  ale  nie  wi cej.  Je eli  WS  przekracza  okre lon   granic   to  uczestnicy 
projektu  oraz  eksperci  powinni  sprawdzi   swoje  oceny  oraz  priorytety.  
W  stosunkowo  du ych  macierzach  (np.  7-9  elementów)  cz sto  trudno  od  razu 
dostrzec wystarczaj co wysoki poziom spójno ci.  

Jednak stopie  spójno ci powinien odpowiada  temu ryzyku, który mamy 

pracuj c  (podejmuj c  decyzj )  u ywaj c  niespójnych  rezultatów.  Np.  przy 
porównywaniu  efektywno ci  leków  potrzebny  jest  bardzo  wysoki  poziom 
spójno ci.  

Rozwa my uogólnienie otrzymanych rezultatów.  
Priorytety  syntezuj   si   rozpoczynaj c  z  drugiego  poziomu  w  dół. 

Priorytety lokalne 

α

k,i,j

 (indeks k – numer poziomu, i – numer elementu na k-tym 

poziomie  
j  –  numer  elementu  na  (k+1)-ym  poziomie)  mno   si   przez  priorytet 
odpowiadaj cego kryterium na powy szym, (k+1)-ym poziomie i sumuj  si  dla 
ka dego  elementu.  Innymi  słowy  wylicza  si   priorytet  globalny  dla  ka dego 
elementu hierarchii w zgodno ci z zasad  addytywno ci:  

Wymiary macierzy 

1  2 

3 

4 

5 

    6     7 

    8 

9 

10 

U rednione warto ci IS 

0  0  0.58  0.90  1.12  1.24  1.32  1.41  1.45  1.49 

 

 

34 

,

j

,

k

J

j

j

,

i,

k

i,

k

1

1

+

=

=

α

α

α

   

k

 

= 1,..., K - 1; i = 1,...,N;                        (3.1) 

gdzie K – ilo  poziomów hierarchii; N – ilo  elementów na k-tym poziomie;  J 
–  ilo   elementów  na  k+1-ym  poziomie  wyst puj cych  jako  kryteria  dla  I 
elementów k-tego poziomu. 

 Otrzymany za pomoc  wzoru (3.1) priorytet globalny elementu nast pnie 

u ywa si  dla wa enia lokalnych priorytetów elementów, porównywanych z nim 
jako z kryterium i lokalizowanych na ni szym poziomie. Procedura ta ci gnie si   
do  najni szego  poziomu,  który  przedstawia  wła nie  wektor  porównywanych 
alternatyw. Otrzymuj c w taki sposób wektor globalnych priorytetów alternatyw 
mo na podejmowa  ko cow  decyzj .  
 

Rozpatrzona MAH posiada dwie powa ne wady: 

1.

  Przy  zmianie  ilo ci  alternatyw  niezb dne  jest  tworzenie  wszystkich 

macierzy  dla  poziomu  alternatyw  od  nowa.  Niestety  przy  tym  nie  jest 
mo liwe skorzystanie z informacji otrzymanej wcze niej, co z kolei zmusza 
do  kompletnego  przeliczenia  wszystkich  kryteriów  dla  wyboru  alternatyw 
od nowa. W przypadku konieczno ci pracy  z du  i szybko zmieniaj cym 
si   zbiorem  alternatyw  (n.p.  analiza  zaproponowanych  ofert  do  du ej 
handlowej firmy) ta wada MAH staje si  krytyczn .  

2.

  Przy  stosowaniu  pierwotnej  informacji  o  alternatywach  w  niezale no ci  

od  tego  czy  miała  ona  charakter  ilo ciowy  czy  jako ciowy  dla  tworzenia 
macierzy  parzystych  porówna   cała  informacja  musi  by   przekształcona  
w  typ  jako ciowe,  wyra aj cy  jako ciowe  oceny  jednej  alternatywy  
w stosunku do drugiej. Strata informacji ilo ciowej w tym wypadku mo e 
powodowa  bł dne, nawet fatalne rezultaty podczas podejmowanej decyzji.  

Na  przykład,  je eli  jeden  dom  kosztuje  $10  ty   a  inny  $10  mln  wtedy  

w  macierzy  parzystych  porówna   w  kratce  odpowiadaj cej  kryterium  kosztu 
najprawdopodobniej  pojawi  si   cyfra  9,  odzwierciedlaj ca  siln   przewag  

 

 

35 

pierwszego domu nad drugim pod wzgl dem ceny. Z innej strony cena domu $10 
mln  dla  przeci tnie  zamo nej  rodziny  jest  nie  tylko  mało  przyjemna,  
ale po prostu nie do rozwa enia.  
  

Jednak przy u ywaniu MAH, przy mniej wi cej po danych warto ciach 

innych  czynników  charakteryzuj cych  jako   domu  (w  praktyce  tak  powinno 
by ,  bo  dom  o  cenie  $10  mln  musi  by   po  ka dym  z  kryteriów  oprócz 
finansowego,  lepszym  od  domu  kosztuj cego  $10  ty )  mo e  okaza   si ,  

e  drugi  dom,  na  który  rodzin   w  ogóle  nie  sta   jest  lepszy  pod  wzgl dem 

kryterium globalnego. Jasne,  e takie wyniki analizy s  po prostu absurdalne.  

 
 
 
 
 
 
 
 
 
 
 
 

 

 

36 

 

4.

 Opracowanie 

metody 

i 

oprogramowania 

wspomagaj cego  wielokryterialn   i  wielopoziomow  
ocen  alternatyw 

4.1. Metoda  budowania  funkcji  przynale no ci  kryteriów 
lokalnych 

Do  oceniania  projektów  trzeba  dysponowa   aparatem  matematycznym  
pozwalaj cym  doprowadzi   wszystkie  charakteryzuj ce  je  ró norakie  kryteria 
lokalne do uniwersalnej skali porównawczej. 

Dlatego  wykorzystujemy  narz dzie  matematyczne  teorii  zbiorów  rozmytych 
[25]. 

Dla  przejrzysto ci  opisania  opracowanej  metody  b dziemy  opiera   si   na  do  
prostym,  ale  konkretnym  przykładzie  porównywania  4  projektów 
inwestycyjnych, 
 z których ka dy jest ucharakteryzowany przez pi tk  kryteriów lokalnych. Przy 
tym w trakcie opisania metody rezultaty po rednie b dziemy ilustrowa  zrzutami 
ekranowymi oprogramowania realizuj cego opracowan  metod . 

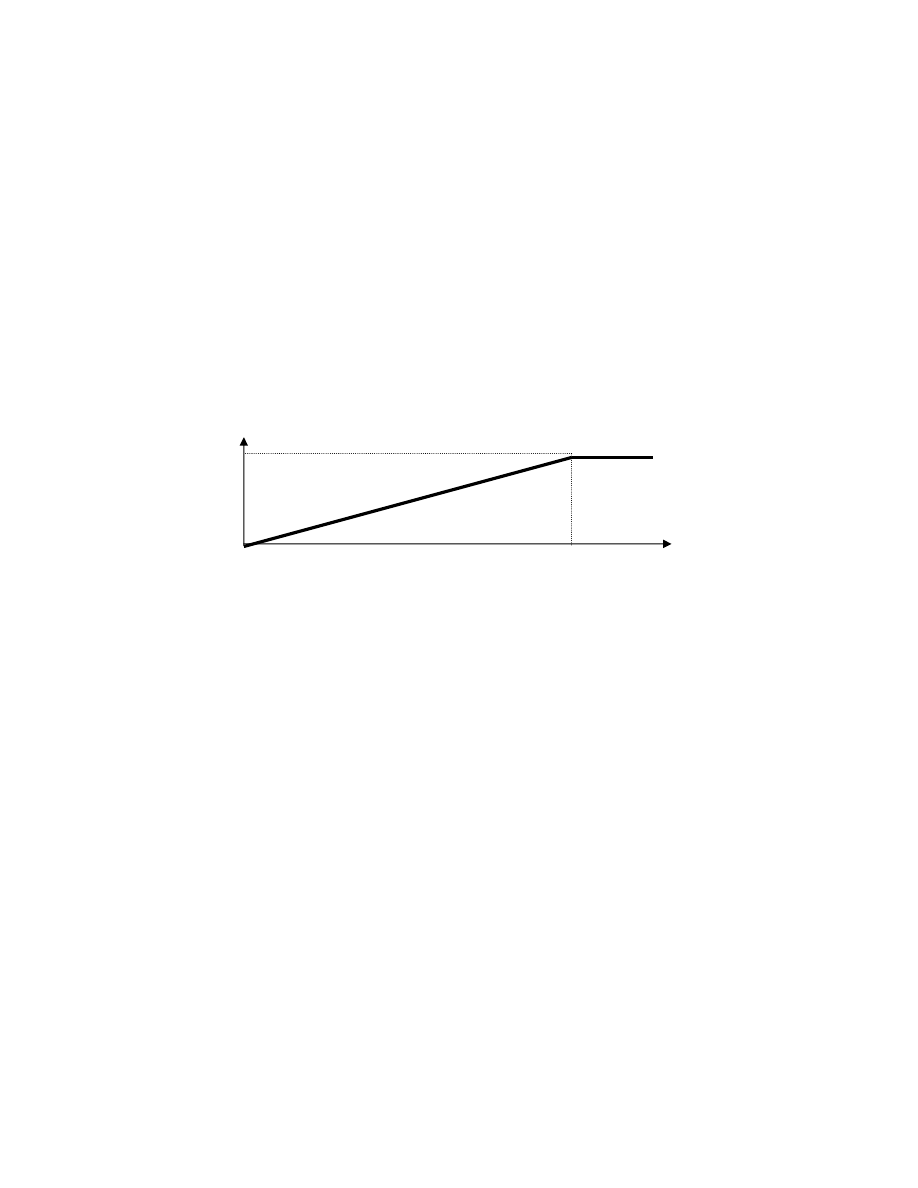
Rozpatrzmy  przykład  takiego  wa nego  wska nika  ilo ciowego  jak  wewn trzna 
stopa zwrotu (IRR). Oczywi cie istnieje jaka  dolna dopuszczalna granica IRR, 
zwykle mniej wi cej równa  redniej bankowej stopie procentowej (r) w pa stwie. 
Jasne te ,  e istnieje do  szeroki zakres r< IRR< IRRm, w którym efektywno  
projektu  ro nie  i  jednocze nie  wzrasta  prawdopodobie stwo  inwestowania. 
Przypuszczamy,  e  przy  IRR>IRRm  efektywno   projektu  pod  wzgl dem 
parametru  IRR  jest  w  takim  stopniu  wysoka,  e  bez  wzgl du  na  inne 

 

 

37 

okoliczno ci  inwestowanie  jest  gwarantowane.  Dla  formalizacji  tego  rodzaju 
opisa   w  ramach  teorii  zbiorów  rozmytych  wykorzystuje  si   aparat  funkcji 
przynale no ci,  który  w  kontek cie  naszego  zadania  wygodniej  nazywa   jako 
funkcje  przydatno ci  (mo liwe  s   i  inne  okre lenie  na  przykład  po yteczno , 
u yteczno   gdy   nie  ma  sztywnie  ustalonego  terminu).  Funkcje  przydatno ci 
zmieniaj   si   od  zera  w  zakresie  niedopuszczalnych  warto ci  parametru  do 
maksymalnej  warto ci  1  w  przedziałach  najlepszych  warto ci  analizowanego 
wska nika  jako ci.  Ogólny  kształt  funkcji  u yteczno ci  dla  naszego  przykładu 
jest  przedstawiony  na  rys.  4.1    (typ  5).  Podkre lamy,  e  liniowy  charakter 
wzrostu funkcji u yteczno ci nie jest dogmatem i najcz ciej wykorzystuje si  w 
wypadkach,  kiedy  dla  ró nych  warto ci  wska nika  jako ci  mo na  powiedzie  
tylko,  e  jeden  z  nich  jest  lepszy,  mo liwie  przydatniejszy  od  drugiego  (ocena 
wył cznie werbalna, jako ciowa). 

W  ten  sam  sposób  mo na  zbudowa   funkcje  u yteczno ci  dla  innych 
wska ników jako ci. Najcz ciej funkcje te maj  kształt rozmytych lub zwykłych 
przedziałów. 

 

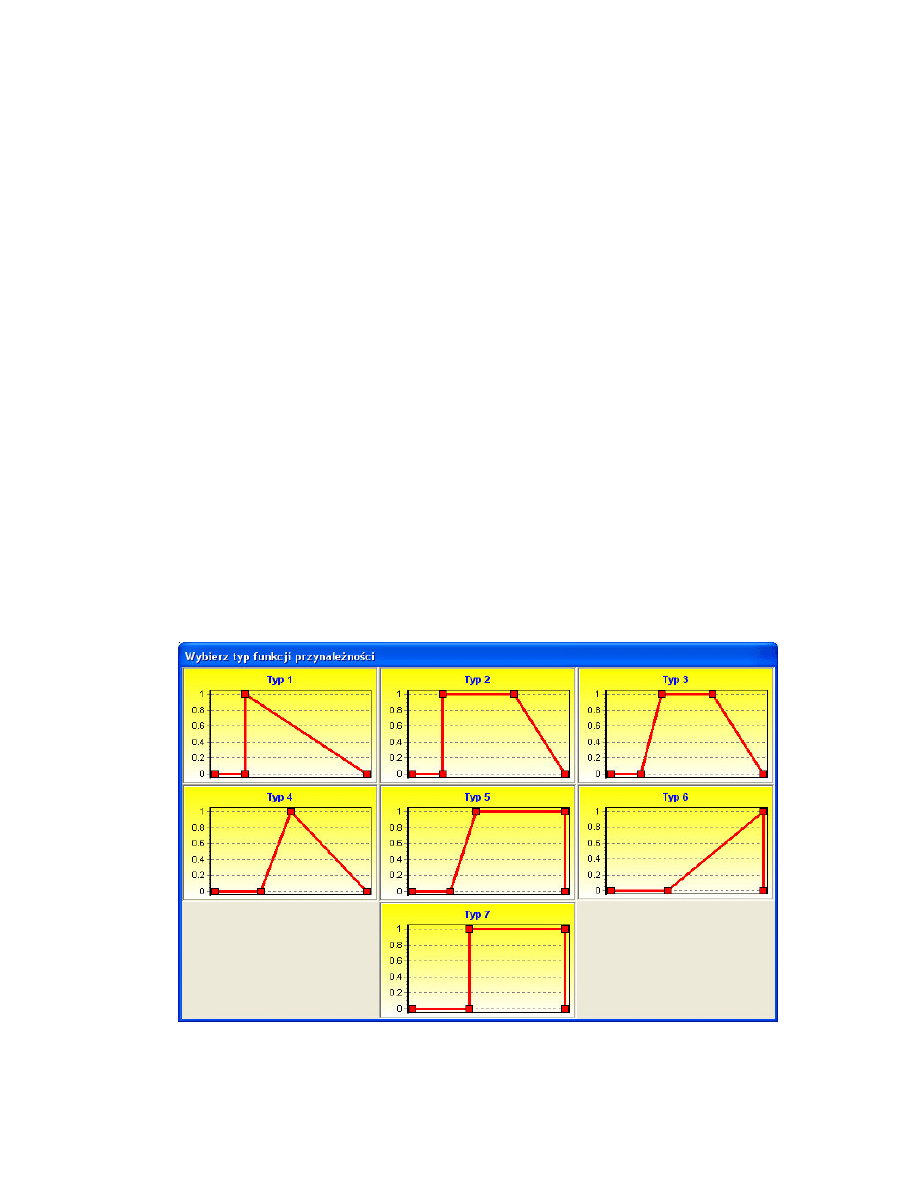
Rys 4.1.Typy funkcji przynale no ci 

 

 

38 

 

Formalizacja  kryteriów  jako ci  przedstawionych  na  poziomie  werbalnym  tak e 
mo e zosta  wykonana za pomoc  funkcji u yteczno ci. Wygodnie jest przy tym 
korzysta  z werbalnych ocen stopni ostro ci lingwistycznych okre le  parametru 
jako ci.  Przykładem  mo e  by   stopie   ostro ci  wska nika  jako ci  ”wpływ  na 
ekologi   regionu”,  który  mo e  by   oszacowany  w  skali  werbalnej:  „nie 
wyra ny”,  „słabo  wyra ny”,  „zdecydowanie  wyra ny”  itd.(ale  nie  wi cej  ni   9 
poziomów o czym wspominałem ju  powy ej). Sposób tworzenia odpowiedniej 
funkcji u yteczno ci przedstawiono na rys. 4.2..  

 

 

 

 

Rys 4.2 Formalizacja kryterium lokalnego przedstawionego za pomoc  opisów 

słownych 

W  rezultacie  wszystkie  ilo ciowe  oraz  jako ciowe  kryteria  przedstawiaj   si   
w  jednej  bez  pomiarowej  skali  funkcji  u yteczno ci.  Mo emy  ju   przej   
do rozpatrzenia przykładu. Przeprowad my ocen  porównawcz  4 projektów pod 
wzgl dem parametrów przedstawionych na rys 4.3. W sytuacji realnej mo e by  
znacznie  wi cej  parametrów.  Jednak  bez  wewn trznej  stopy  zwrotu  (IRR), 
warto ci  zaktualizowanej  netto  przedsi wzi cia  (NPV),rentowno ci  (PI),okresu 
zwrotu (PB) projekty z reguły nie mog  by  oszacowane, gdy  s  to parametry 
najwa niejsze.  Ryzyko  projektu  (R)  jest  powiedzmy  bardzo  skomplikowanie 
agregowane  charakterystyk   w  okre leniu,  której  mog   by   stosowane  tak 
ilo ciowe 

jak  

i jako ciowe oceny ekspertów. Szczegóły w [59].  

 

 0       1       2       3       4        5        6        7        8        9 

0.5 

1 

0 

 

 

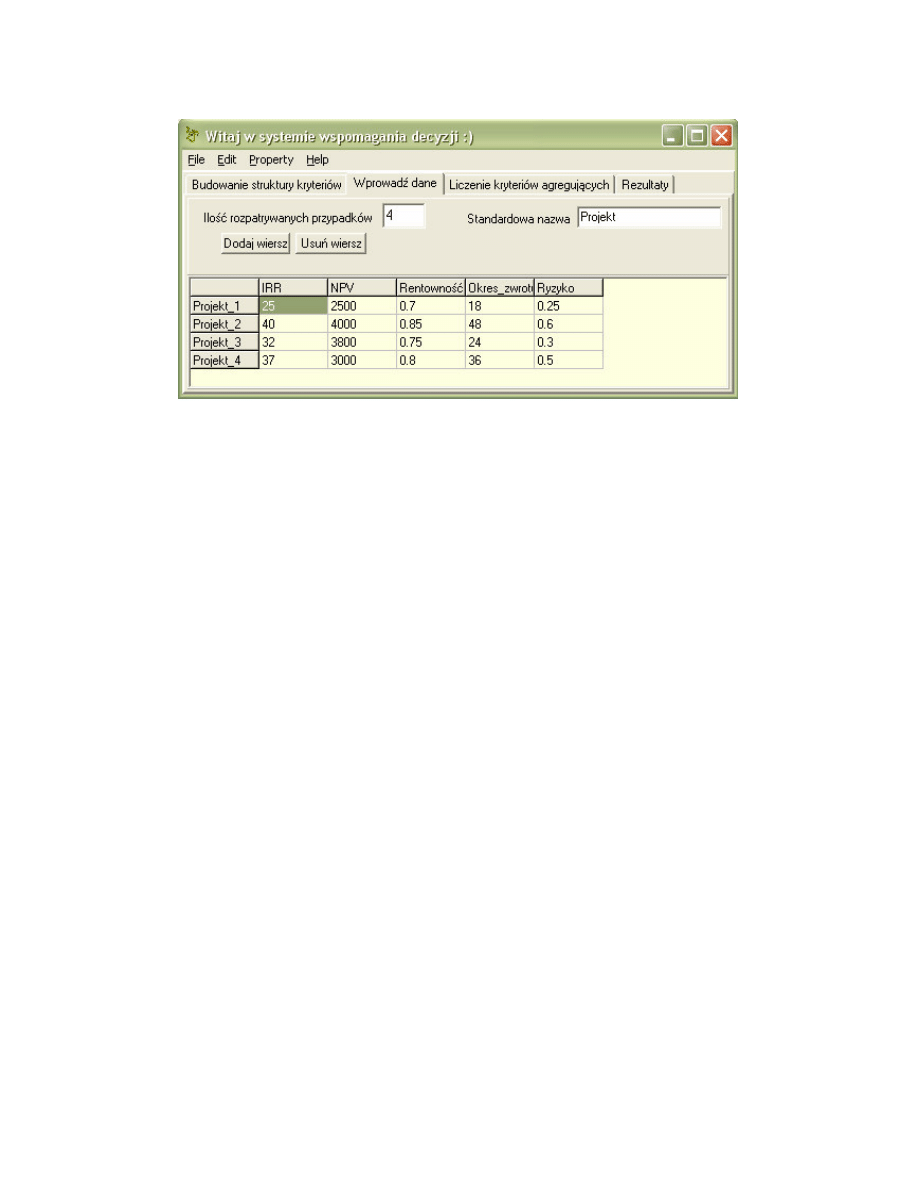
39 

 

rys. 4.3 Dane o czterech projektach, które b dziemy porównywa .  

 

W naszym pro ciutkim przykładzie przypu my,  e w wyniku ryzyko jest w jaki  
sposób ocenione i mo e waha  si  w przedziale od 0 do 1. Warto ci parametrów 
dla  naszego  przykładu  s   przedstawione  w  tabeli  1.  Nast pnym  krokiem  jest 
stworzenie funkcji u yteczno ci.  

W  menu  (rys.4.1)  nale y  wybra   pasuj cy  typ  funkcji  i  zada   warto ci 
odpowiadaj cych punktów kluczowych (x1 – x4). Punkty kluczowe z kolei mog  
by  zadane na podstawie ocen ekspertów, analizy stanu dziedziny, na podstawie 
sztywnych  (na  przykład  bankowych,  pa stwowych)  przepisów  itd.  Poniewa   
w  naszym  przykładzie  nale y  wybra   tylko  lepszy  spo ród  4  projektów,  wi c 
zrobimy  to  pro ciej.  Przykład  najgorsza  warto   NPV  przy  porównaniu 
wszystkich 4 projektów jest równa - 2500, najlepsza – 4000. Dlatego (rys. 4.4) 
definiujemy  x1=2000  (mniej  ni   2500  dlatego  e  nie  chcemy  od  pocz tku 
wyrzuca   projekt  nr.1),  x2=  4000  i  tylko  dla  pewno ci  x3=6000.  Podobnie  w 
sposób interaktywny budujemy pozostałe funkcje u yteczno ci (rys.4.4).  

 

 

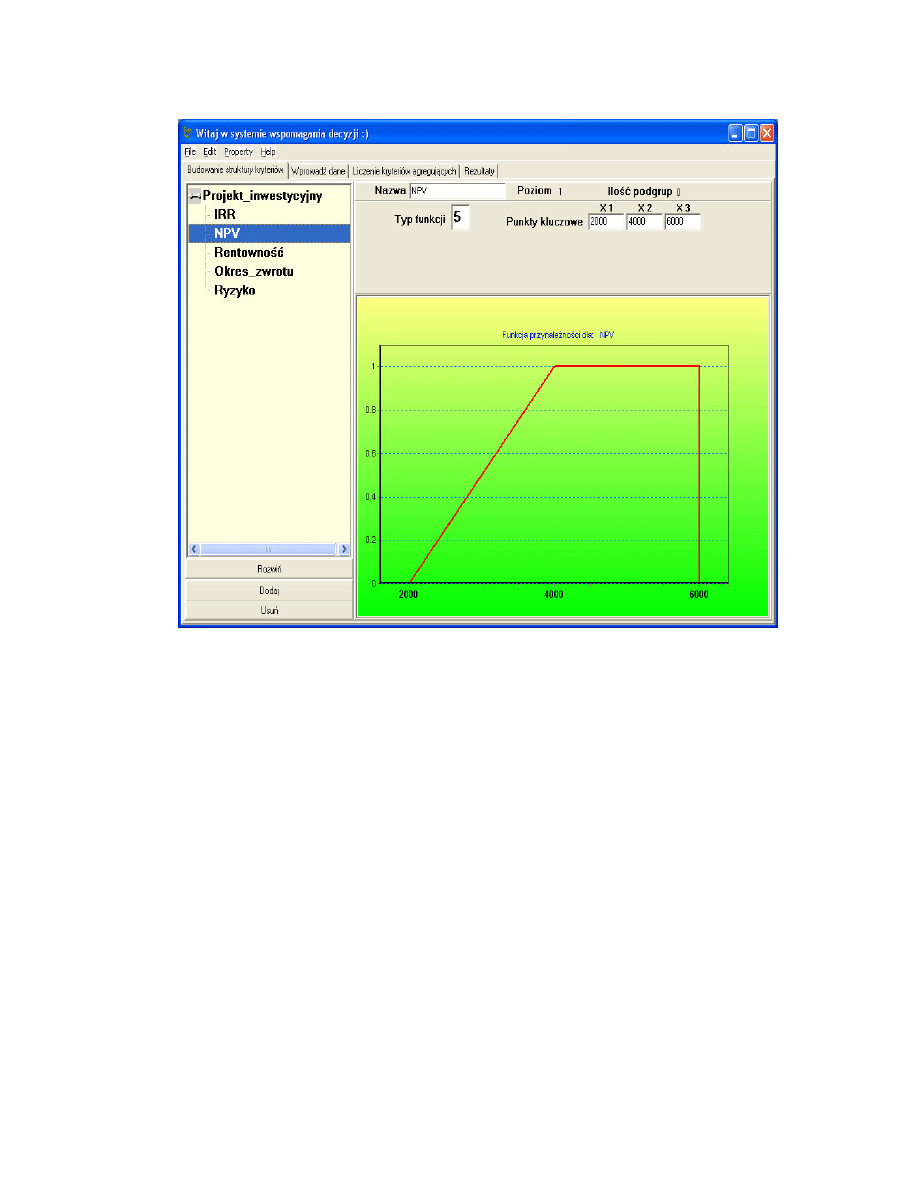
40 

 

rys. 4.4   Budowanie funkcji u yteczno ci 

4.2.Metoda  i  algorytm  wyliczenia  współczynników  wzgl dnej 
wa no ci kryteriów lokalnych na podstawie macierzy parzystych 
porówna . 

Bardzo ci kim problemem metodycznym jest rangowanie du ej ilo ci kryteriów 
na 

podstawie 

opinii 

ekspertów. 

Powy ej 

ju  

wspomniano  

o ograniczonych mo liwo ciach człowieka do ocen sytuacji wielokryterialnych. 
Jednak  przy  porównaniu  dwóch  alternatyw  jest  on  zwykle  w  stanie  w  sposób 
adekwatny  ustali ,  u  której  z  nich  rozpatrywany  wska nik  (wa no )  jest 
silniejszy (lepszy),nawet w niektórych wypadkach w sposób przybli ony oceni  
(werbalnie),  stopie   wyra no ci  tej  ró nicy.  Dlatego  opracowana  metoda 
rangowania 

kryteriów 

zapewnia 

otrzymanie 

ilo ciowych 

warto ci 

 

 

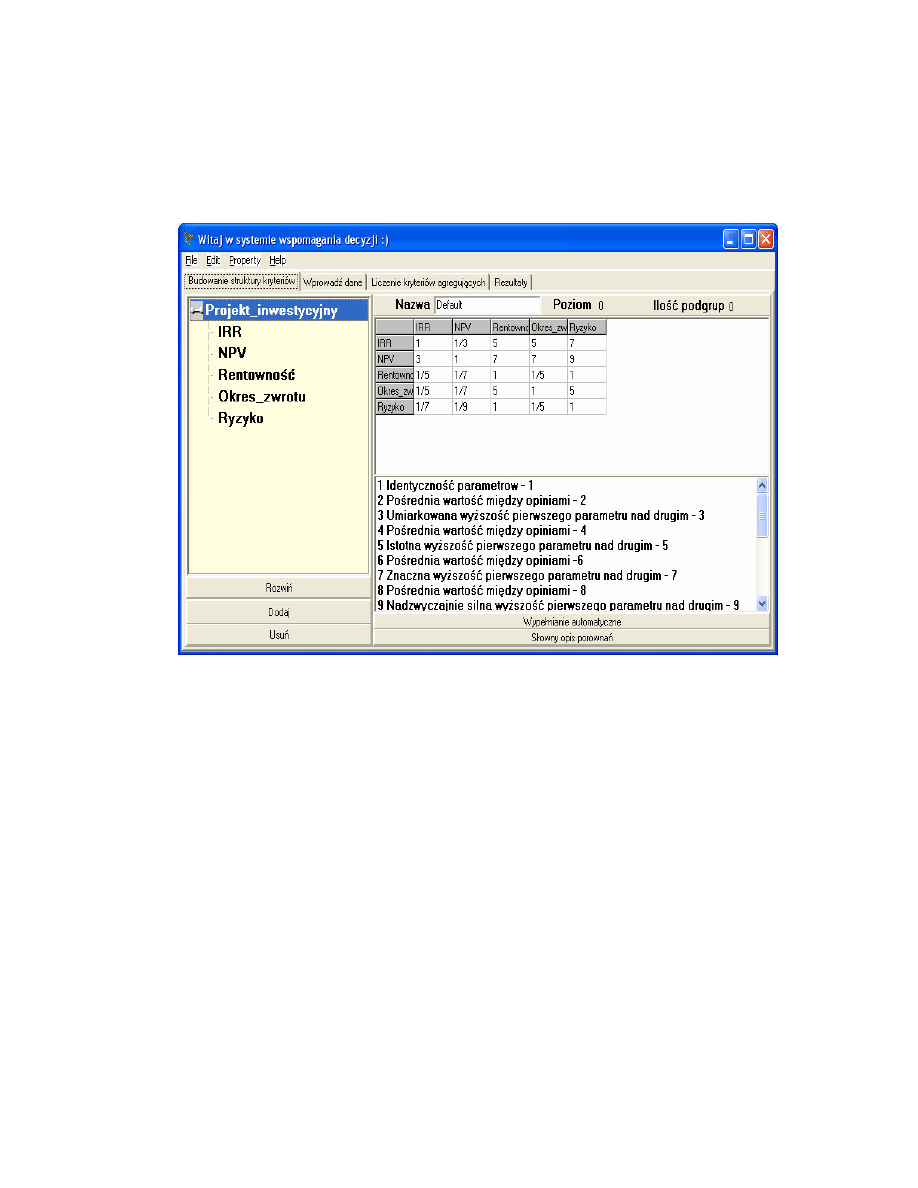
41 

współczynników  wzgl dnej  wa no ci  (rang)  na  podstawie  ich  parzystych 
porówna   w  formie  słownej.  Podstaw   metody  jest  macierz  parzystych 
lingwistycznych porówna , proponowana przez T.Saaty [29]. 

 

Rys 4.5. Wypełnienie macierzy parzystych porówna  i wyliczenie rang. 

Sposób  wypełnienia  tej  macierzy  dla  naszego  przykładu  przedstawiono  na  
rys.  4.5.  Jak  wida   na  nim,  wykorzystuje  si   tylko  9  podstawowych  ocen 
słownych.  Jest  to  nie  przypadkowe  i  zwi zane  z  faktem,  e  w  j zykach 
naturalnych  wi kszo ci  narodów  tak e  wykorzystuje  si   nie  wi cej  ni   9 
lingwistycznych  ocen  wzgl dnej  wa no ci.  Słowne  sformułowania  ocen  mog  
by   inne,  ale  ich  ilo   w  praktyce  jest  stała.  Takie  s   cechy  ludzkiego  umysłu 
[29]. Ocenom werbalnym wzgl dnej wa no ci odpowiadaj  liczby naturalne. Jest 
to oczywiste, gdy  w innym przypadku jakiekolwiek wyliczenie rang byłoby po 
prostu 

nie 

mo liwe. 

Warto 

podkre li ,  

e liczby na rys. 4.5 pokazuje si  wył cznie w celu dydaktycznym. W praktyce 

nie  radzimy  wprost  pokazywa   ekspertom  jakichkolwiek  liczb.  Niech  oceniaj  

 

 

42 

wył cznie  na  podstawie  skali  lingwistycznej.  Chodzi  o  to,  e  je li  proponowa  
grupie  specjalistów  oceni   dobrze  znane  przez  nich  obiekty,  to  wtedy  oceny 
werbalne  zwykle  b d   prawie  takie  same.  Inaczej  by   nie  mo e:  ludzie 
studiowali  na  podstawie  tych  samych  podr czników,  czytaj   te  same  artykuły, 
pracuj  w tej samej dziedzinie. Jednak, je li uda si  zmusi  ich do wykorzystania 
przy ocenianiu liczb (zwykle za do  grube pieni dze: liczb nikt nie lubi) wtedy 

adnego konsensusu ju  nie b dzie [60]. 

Rzecz w tym,  e na „pocz tku było słowo”. Liczby pojawiły si  znacznie pó niej 
przez mikroskopijny w skali historyczny zakres czasu (kilka tysi cleci), ludzie po 
prostu  jeszcze  nie  nauczyli  si   dobrze  z  nich  korzysta .  I  dzi ki  BOGU!!!  Na 
razie, my limy za pomoc  słów a nie liczb i nawet uparcie staramy si  nauczy  
tej sztuki nasze komputery.   

 Ko cowe  rangi  kryteriów  na  podstawie  macierzy  parzystych  porówna   
w  sposób  najlepszy  mo na  otrzyma   za  pomoc   metod  programowania 
nieliniowego [38]. 

Nale y zauwa y  tak e,  e proponowane porównywanie wa no ci kryteriów jest 
du o  bardziej  elastyczne  od  stosowanego  w  przeszło ci  bezpo redniego 
porównywania  projektów.  Wymagało  ono  całkowitej  zmiany  macierzy 
parzystych  porówna   przy  powi kszeniu  grupy  ocenianych  projektów.  W 
naszym  przypadku  rozmiar  macierzy  nie  jest  zale ny  od  ilo ci  ocenianych 
projektów,  ale  od  ilo ci  parametrów  je  opisuj cych.  Dlatego  w  praktyce  przy 
wyra nie okre lonej polityce firmy dotycz cej parametrów oceny inwestycji nie 
zachodzi  potrzeba  cz stej  zmiany  macierzy  parzystych  porówna   a  co  za  tym 
idzie  –  nie  trzeba  cz sto  wykorzystywa   drogiego  czasu  ekspertów  a  sama 
metoda jest łatwiejsza do komputeryzacji i automatyzacji. 
Porównanie 

n

  kryteriów  prowadzi  do  powstania  macierzy  kwadratowej  o 

rozmiarze 

n

, której ka dy element okre la wzgl dn  wa no  dwóch kryteriów. 

Porównania  dokonywane  s ,  wi c  parami,  st d  nazwa  macierzy  –  macierz 
parzystych  porówna .  Nale y  zaznaczy ,  e  ekspert  okre la  jedynie  warto ci 

 

 

43 

powy ej  głównej  przek tnej  –  na  niej  samej  znajduj   si   jednostki 
(odpowiadaj ce  porównaniu  kryterium  z  samym  sob ).  Pozostałe  warto ci 
(poni ej przek tnej) okre la si  zgodnie ze wzorem: 

i

j

j

i

a

a

1

=

. 

  (4.1) 

Je li  przez 

ij

a

oznaczymy  dowolny  element  macierzy  parzystych  porówna   a 

przez 

i

α

 współczynnik wa no ci 

i

-tego kryterium, przy czym 

n

j

i

1

,

=

, to 

j

i

ij

a

α

α

=

. 

(4.2) 

Problem  polega  na  obliczeniu  współczynników  na  podstawie  macierzy 
parzystych porówna . 
Dokonywane jest to według nast puj cej metody:  
Niech  A -  macierz  porówna  parami, a

ij

  - element  macierzy  porówna  parami, 

α

1

, 

α

2

, 

α

3

, 

α

4

  -  szukane  warto ci  współczynników  wzgl dnej  wa no ci,  W== 

(

α

1

, 

α

2

, 

α

3

, 

α

4

) - wektor współczynników wzgl dnej wa no ci.  

Dla ka dego elementu macierzy porówna  parami prawdziwe jest:  

ij

=

α

i

/

α

j

, 

(4.3) 

Po pomno eniu wektora A przez wektor W otrzymamy:  
AW=NW, 

(4.4) 

gdzie N - warto  charakterystyczna macierzy A, wg której mo na wyprowadzi  
wektor  W  współczynników  wzgl dnej  wa no ci 

i

a

  z uwzgl dnieniem  warunku 

normalizacji: 

=

=

n

i

i

k

a

1

1

/

)

(

  

(4.5) 

gdzie: k - liczba kryteriów szczegółowych).  
Poniewa   elementy  macierzy  porówna   parami  nie  s   dokładne,  jako  e 
odzwierciedlaj   subiektywny  pogl d  eksperta,  warto   W  obliczana  jest  jako 
wektor, funkcjonał minimalizuj cy:  

 

 

44 

min

)

(

2

1

1

→

−

=

=

=

j

i

ij

n

j

n

i

a

S

α

α

 

(4.6) 

tzn. warto ci szukane otrzymuje si  przez rozwi zanie zadania optymalizacji:  

min;

)

(

2

1

1

→

−

=

=

=

i

j

ij

n

j

n

i

a

S

α

α

j

i

n

n

i

i

=

=

=

;

1

α

 

(4.7) 

Klasyczn  metod  rozwi zania zadania minimalizacji funkcji wielu zmiennych f 
(x) = f (x

1

, x

2

,… x

n

) przy istnieniu ogranicze , zadanych w formie równo ci g

i

 

(x) = 0, i=1, … k, jest metoda nieokre lonych czynników Lagrange'a.  
Przy  jej  pomocy  powstaje  funkcja  n+k  zmiennych,  nazywana  funkcj  
Lagrange'a:  

=

+

=

k

1

i

i

i

(x)

g

f(x)

)

L(x,

λ

λ

 

(4.8) 

gdzie: i = 1, … k - czynniki nieokre lone 
Tym  sposobem  wyj ciowe  zadanie  umownej  optymalizacji  sprowadza  si   do 
zadania bezwarunkowej minimalizacji funkcji Lagrange'a. I wła nie w ten sposób 
w  ramach  opracowanej  metody  jest  zrealizowane  wyliczenie  współczynników 
wzgl dnej wa no ci kryteriów lokalnych. 

4.3. Metoda agregowania kryteriów lokalnych. 

Mamy  ju   kryteria  szczegółowe  i  ich  rangi.  Dobrze,  e  w  naszym  przykładzie 
mamy  tylko  5  kryteriów,  a  nie  55  jak  mo e  by   w  yciu..  Dla  rozstrzygni cia 
problemu  niezb dne  b dzie  opracowanie  sposobów  agregowania  wszystkich 
ró norodnych informacji w pewne ko cowe ilo ciowe oceny. W wyniku musimy 
otrzyma   jedn   liczb   –  warto   globalnego  wska nika  (kryterium)  jako ci 
projektów.  

Niech: 
µ

1

(x

1

), 

µ

2

(x

2

), ...., 

µ

N

(x

N

) s  funkcjami u yteczno ci (preferencji); 

{x

i

}, i = 1, ..., N s  jako ciowymi i ilo ciowymi parametrami jako ci; 

a

1

, ..., a

N

 s  współczynnikami wzgl dnej wa no ci kryteriów; 

 

 

 

45 

Najcz stszymi  wariantami  formułowania  kryteriów  globalnych  na  podstawie 
kryteriów lokalnych i ich rang s  [3]: 
 

);

)

(

,...

)

(

,

)

(

,

)

(

min(

3

2

1

3

2

1

1

n

n

x

x

x

x

DD

α

α

α

α

µ

µ

µ

µ

=

∏

=

=

N

i

i

i

i

x

DD

1

2

)

(

α

µ

 

=

=

N

i

i

i

i

N

x

DD

1

3

)

(

*

µ

α

 

W wyniku otrzymujemy warto ci kryteriów zawieraj ce si  w przedziale [0,1]  

 

1

,

,

0

3

2

1

≤

≤

DD

DD

DD

 

Istniej   ró ne  opinie  w  odniesieniu  do  porównawczej  skuteczno ci  metod  
w formułowaniu globalnych kryteriów. Warianty DD

2

 i DD

3

 posiadaj  własno ci 

wyrównywania  małych  warto ci  jednego  lokalnego  kryterium  za  pomoc  
zwi kszania innych, co nie jest zawsze po dane. 
Wariant  DD

1

  jest  wolny  od  tych  wad,  ale  prowadzi  do  bardzo  ostrej  oceny 

sytuacji. Dlatego jest czasami nazywany kryterium maksymalnego pesymizmu.  
Udowodnione jest  [34],  e  w  wypadkach  zada   wielokryterialnej  optymalizacji 
najbardziej racjonalnym jest u ycie wariantu DD

1

 

Jednak  praktyka  jest  zawsze  bogatsza  ni   teoria.  Dlatego  w  zadaniach  oceny 
jako ci projektów sensownym jest wykorzystywa  razem trzy wy ej wymienione 
sposoby formułowania kryterium globalnego rys. 4.6. 
Wszystkie  one  gwarantuj   otrzymanie  ilo ciowych  globalnych  ocen  projektów  
w zakresie  od  0 (zdecydowanie  niekorzystny  projekt)  do  1 (projekt –  marzenie 
inwestora). Zgodno  rezultatów otrzymanych za pomoc  kryteriów DD

1

 – DD

3

 

zwi ksza  zaufanie  do  wyników  bada ;  niezgodno   mo e  powodowa   bardzo 
po yteczne  dodatkowe  rozwa ania.  Jasne,  e  im  wy sza  warto   kryterium 

 

 

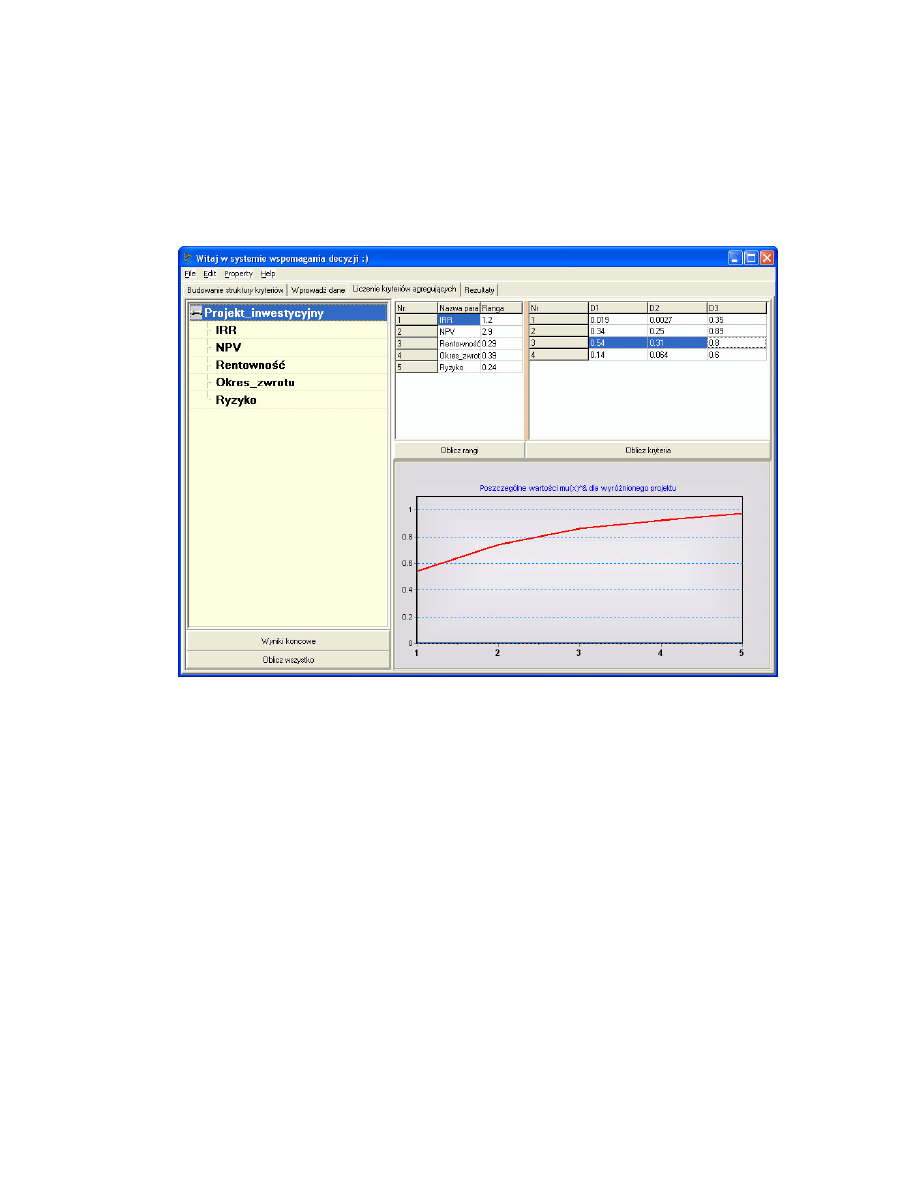
46 

globalnego  tym  lepiej  projekt  analizowany.  Z  rys.  4.6  wynika,  e  w  naszym 
przykładzie  najlepszy  jest  projekt  3.  Wła nie  dla  tego  projektu  otrzymano 
maksymalne  warto ci  kryteriów  globalnych  dla  2  ró nych  sposobów  ich 
formułowania.  

 

rys. 4.6 Wyliczenie kryteriów globalnych 
 
Opracowana  metoda  pozwala  nie  tylko  za  pomoc   jednej  liczby  (ale  na  do  
porz dnej  podstawie  naukowej)  oceni   jako   projektów,  ale  jak  wida   na  rys. 
4.6  ujawni   jaki  wpływ  do  oceny  globalnej  ma  ka de  kryterium  szczegółowe 
razem ze swoj  rang .  

4.4.Budowanie hierarchicznego sytemu kryteriów agregowanych 

Nale y  jednak  podkre li ,  e  w  praktyce  zadania  oceny  jako ci  projektów 
inwestycyjnych  (i  innych),  s   nie  tylko  zadaniami  wielokryterialnymi,  ale  
i wielopoziomowymi (hierarchicznymi).  

 

 

47 

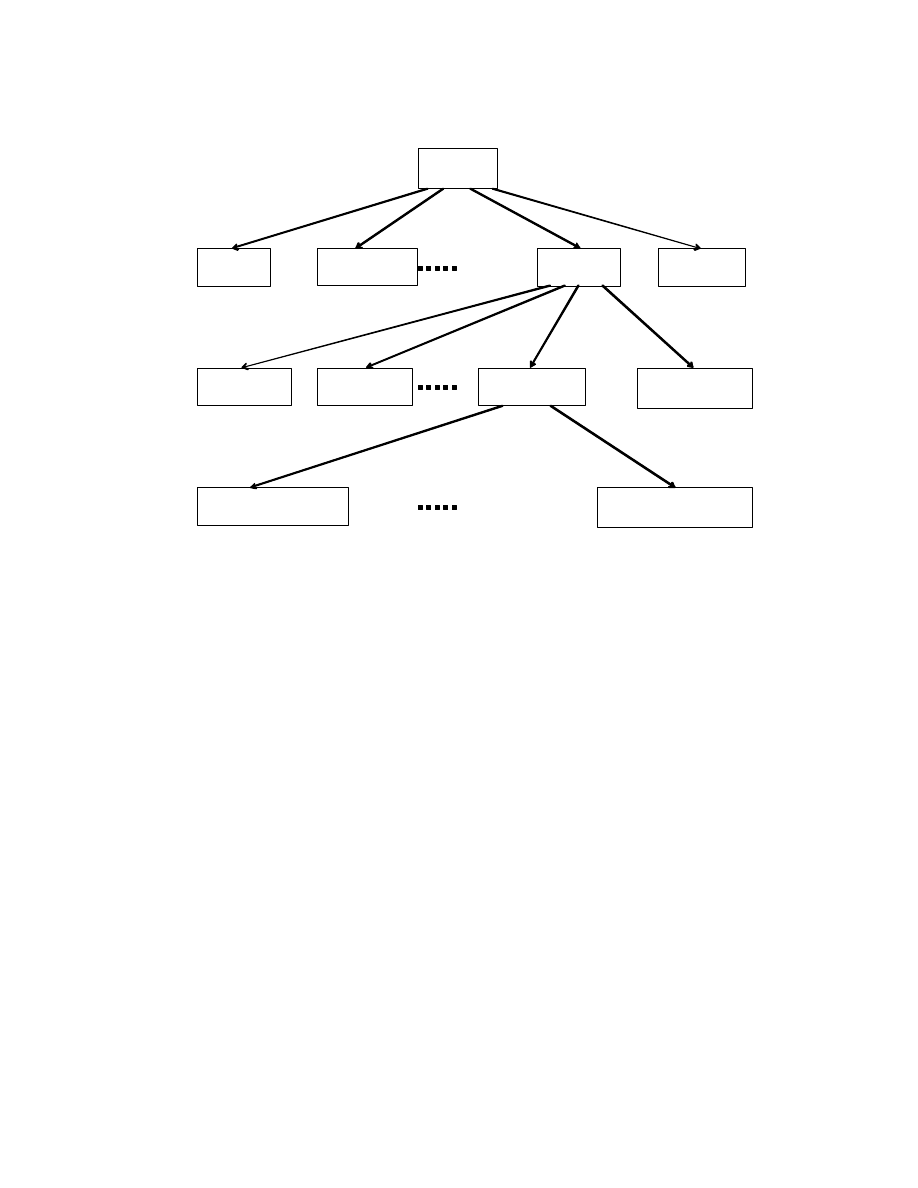
  Opracowana  metoda  pozwala  w  sposób  naturalny  budowa   struktury 
wieloszczeblowe i hierarchiczne, których schemat jest pokazany poni ej. 
Ka de  kryterium  wy szego  rz du  buduje  si   na  podstawie  kryteriów 
szczegółowych  rz du  ni szego  za  pomoc   jednego  ze  sposobów  ich 
agregowania.  Ogólne  wyra enie  matematyczne  do  wyliczenia  kryteriów  na 
poziomach po rednich hierarchii mo e by  przedstawione w nast puj cej formie: 

(

)

1

1

1

1

1

1

1

1

,

,

2

1

,

,

1

,

,

2

1

,

,

1

,

1

,

1

,...,

,

,...,

−

−

−

−

−

−

−

−

−

−

−

−

−

−

=

n

i

n

n

n

i

n

n

n

n

m

i

n

i

n

m

i

n

i

n

i

n

i

n

D

D

f

D

α

α

gdzie 

1

1

−

−

n

i,

n

f

 jest operatorem agregowania kryteriów. 

1

1

,

,

2

−

−

−

n

i

n

m

i

n

D

- to poszczególne kryteria agregowania na odpowiednich poziomach 

hierarchii, a 

1

,

,

1

1

−

−

n

i

n

α

 - odpowiadaj ce im rangi 

 

Jak  to  wynika  ze  sposobu  budowania, 

1

1

−

−

n

i,

n

D

  przyjmuj   warto ci  zawsze 

mi dzy 

0 a 1 . 

Na  najni szym  poziomie  hierarchii  wykorzystane  s   bezpo rednie  funkcje 
przynale no ci 

(u yteczno ci) 

pierwotnych 

kryteriów 

szczegółowych 

okre lanych przez bazowe parametry jako ci. 
 

{ }{ }

(

)

j

j

i

i

i

i

i

i

n

n

n

n

f

D

α

µ

,

2

2

1

2

2

1

,...,

,

,

1

,...

,

,

1

−

−

−

−

=

 

 

48 

 

    

 

1

,

1

−

n

D

 

D

n 

2

1 ,

n

D

−

1

1

−

−

n

i,

n

D

 

1

1

−

−

n

m

,

n

D

1

2

1

,

i,

n

n

D

−

−

 

2

2

1

,

i,

n

n

D

−

−

 

2

1

2

−

−

−

n

n

i

,

i,

n

D

1

1

2

−

−

−

n

i

n

m

,

i,

n

D

1

2

1

3

,

n

n

i

,

i

,

n

D

−

−

−

2

1

2

1

3

−

−

−

−

−

n

i,

n

i

n

n

m

,

i,

i,

n

D

 

Schemat1.Ogólny schemat budowania struktury hierarchicznej

 

 

Rozwi zanie  tych  problemów  w  programie  przedstawia  si   w  nast puj cy 
sposób. Wystarczy najpierw stworzy  „drzewiast  struktur ” dla rozpatrywanego 
przez nas problemy. Nast pnie na ka dym poziomie albo sformalizowa  funkcje 
przynale no ci  (je eli  one  nie  formułuj   si   automatycznie)  i  wypełni  
odpowiednio tablice parzystych porówna . 
 
 
 
 
 
 
 
 
 
 
 

 

 

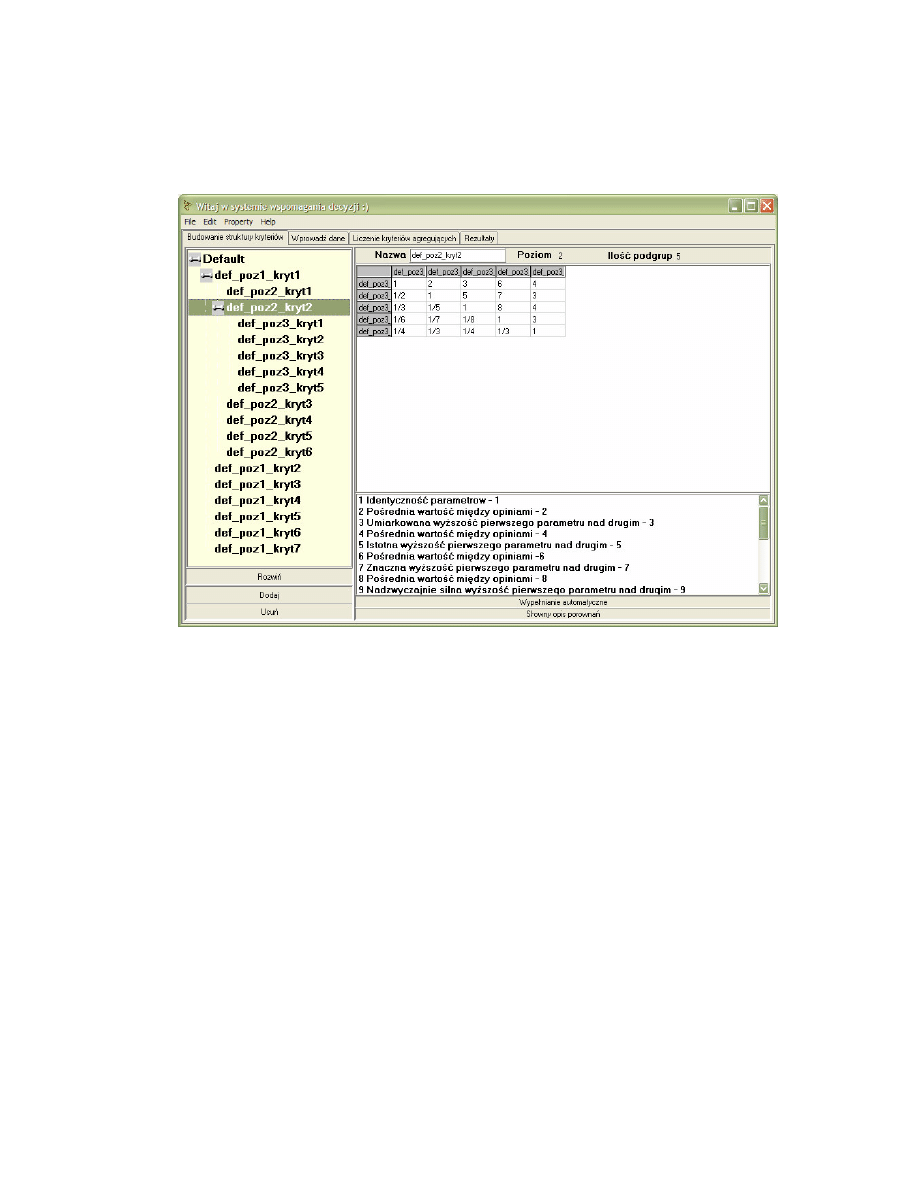
49 

 
Poni ej przedstawiony jest zrzut ekranowy przedstawiaj cy budowanie struktury 
hierarchicznej, gdzie 

def

i,j 

s  kryteriami podrz dnymi w formułowanym zadaniu. 

 

Rys 4.7. Budowa hierarchicznej struktury w zbudowanej aplikacji 
 
      
 
 
 
 
 
 
 
 
 
 
 

 

 

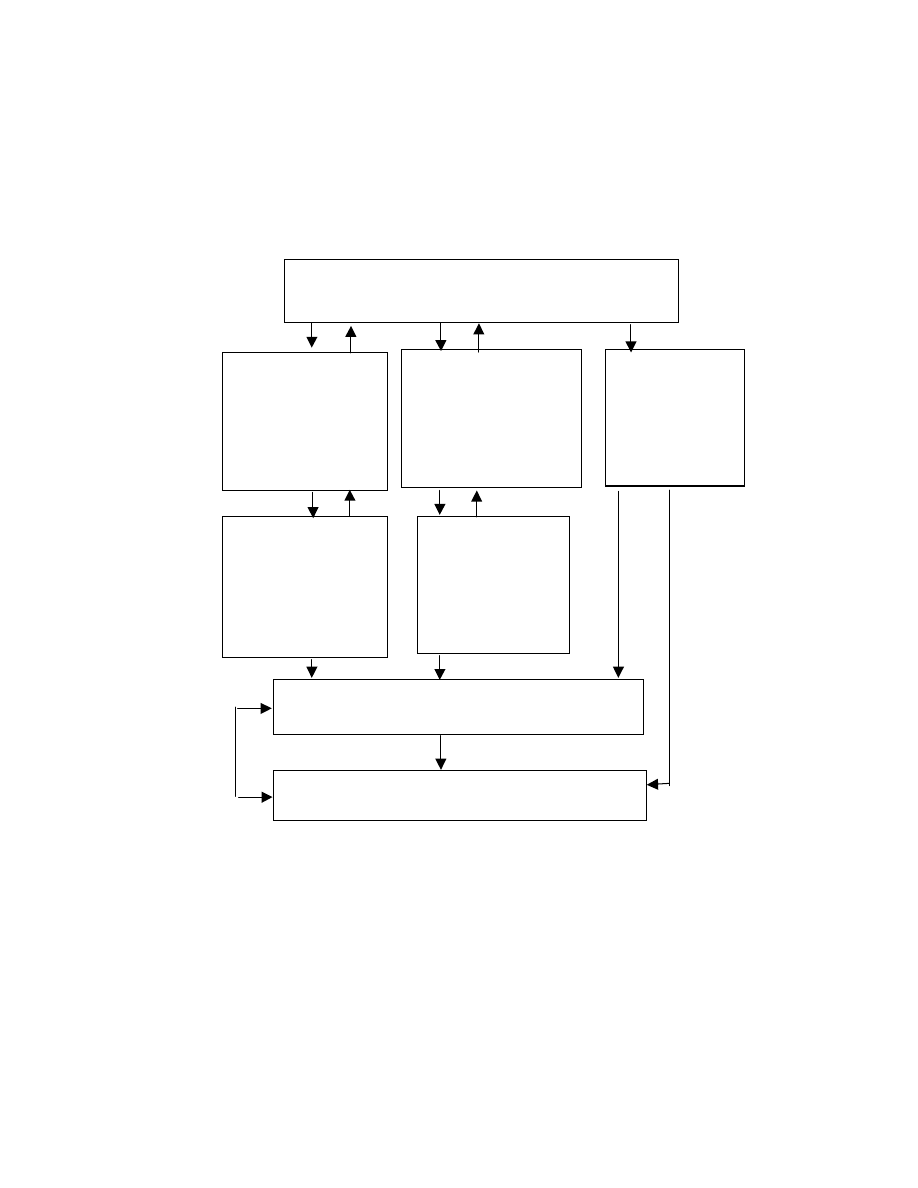
50 

4.5.Struktura oprogramowania realizuj cego opracowane metody. 

Poni ej  przedstawione  ogóln   struktur   oprogramowania  realizuj cego  opracowana  i 
opisan  powy ej metod . 
 

 

Budowanie struktury hierarchicznej kryteriów jako ci 

szczegółowych (interfejs) 

Budowanie funkcji 

u yteczno ci  

kryteriów jako ci 

szczegółowych 

(interfejs) 

  

 

Budowanie macierzy 

parzystych porówna  

kryteriów jako ci 

szczegółowych 

(interfejs) 

Wybór sposobu 

budowania 

kryterium 

jako ci 

globalnego 

(interfejs) 

Budowanie bazy 

danych do 

wyliczenia warto ci 

kryteriów jako ci 

szczegółowych  

Wyliczenie 

współczynników 

wzgl dnej 

wa no ci 

kryteriów jako ci 

szczegółowych  

Wyliczenie kryteriów jako ci globalnych na 

poziomach po rednich hierarchii.  

Wyliczenie uogólniaj cej oceny ilo ciowej po 

wszystkich poziomach hierarchii jako ci  

 

Schemat 4.2 Schemat oprogramowania

 

 
 

 

 

51 

5.

 Metoda  oszacowania  alternatyw  przy  rozmytych 

współczynnikach  wzgl dnej  wa no ci  kryteriów  w 
warunkach ich oceny przez zespół ekspertów. 

5.1.Opracowanie  metody  oszacowania  alternatyw  na  podstawie 
lokalnych  rozmytych  kryteriów  subiektywnych  i  obiektywnych 
(cena) oraz ich rozmytych rang. 

W  pewnych  pracach  [61,62,63]  mo na  zauwa y   problem  szacowania 
alternatyw, gdy cze  kryteriów jest subiektywne, a cz

 obiektywne. Ró nica 

pomi dzy  nimi  jest  dosy   znaczna  i  nie  mo na  ich  porównywa   bezpo rednio. 
Kryteria  subiektywne  (rozmyte)  s   kryteriami  w  wi kszo ci  przypadków 
kształtowanymi  przez  osob   podejmuj c   decyzj   zale y  od  jego  wiedzy  i 
preferencji  w  danej  dziedzinie.  Kryteria  obiektywne  s   kształtowane  przez 
rzeczywisto  i osoba podejmuj ca decyzj  ma nikły lub wcale nie ma na niego 
wpływu. Przykładowo takim kryterium najcz ciej widocznym w literaturze jest 
koszt  danego  produkty  lub  usługi,  która  kształtowana  jest  w  wi kszo ci 
rozpatrywanych przypadków przez wolny rynek.  
W pracy [63] rozpatrywany jest problem lokalizacji siedziby głównej firmy pod 
wzgl dem  mi dzy  innymi  kosztu  inwestycji,  warunków  klimatycznych,  stanu  i 
kwalifikacji  siły  roboczej,  zdolno ci  transportowych,  mo liwo ci  rozwoju, 
dost pno ci  potrzebnych  materiałów,  blisko ci  do  rynku  zbytu  do  kryterium 
obiektywnych zaliczono wła nie kryterium kosztu inwestycji. 
Zaproponowana  przez  autorów  pracy  [63]  metoda  zamiany  kryterium 
obiektywnego na subiektywne opiera si  na nast puj cym podej ciu: 
 
 
 
 

 

 

52 

Najpierw  wprowadzono    podział  wszystkich  kryteriw  lokalnych  na  kryteria 
korzy ci  (B-  benfit)  i  kosztu  (C-cost).  Dalej  autorzy  [63]  u ywali  metod  
normalizacji  tych kryteriów. Przy tym rozpatrywano wył cznie kryteria lokalne 
opisane  przez  trójk ty.  Tak,  je li    a,b,c  to  punkty  kluczowe  trójk tów 
proponowana normalizacja ma nast puj c  posta :  

B

j

c

c

c

b

c

a

r

j

ij

j

ij

j

ij

∈

=

),

,

,

(

*

*

*

~

  

C

j

c

c

c

b

c

a

r

j

ij

j

ij

j

ij

∈

=

−

−

−

),

,

,

(

~

 

B

j

if

c

c

ij

i

j

∈

=

),

(

max

*

 

C

j

if

a

a

ij

i

j

∈

=

−

),

(

min

 

Taka  metoda  normalizacji  zapewnia  nas,  e  zakres  powstałego  w  ten  sposób 
kryterium ma zakres od zera do jedynki.  
Jednak takie podej cie mimo pewnych korzy ci prowadzi do powstania pewnych 
bł dów. Widoczne jest to na poni szym wykresie (wykres 5.1) przedstawiaj cym 
normalizowan   funkcje  kosztu  z  przykładu  wzi tego  [63],  ze  zale no   funkcji 
u yteczno ci  od  konkretnych  kosztów  jest  wyra nie  nieliniowa.  Mo na 
udowodni ,  e przy u ywaniu podej cia [63] takiego rodzaju nieliniowo ci b d  
powtarza   si   w  niezale no ci  o  konkretnych  danych.  Dlatego  w  wi kszo ci 
przypadków  takiego  rodzaju  nieliniowo c  jest  nie  mo liwa  do  uzasadnienia 
nawet  na  poziomie  merytorycznym,  wi c  proponowana  w  [63]  metoda  ma 
wyra n  wad  silnie ograniczaj c   mo liwo ci stosowania jej w praktyce. 

 

 

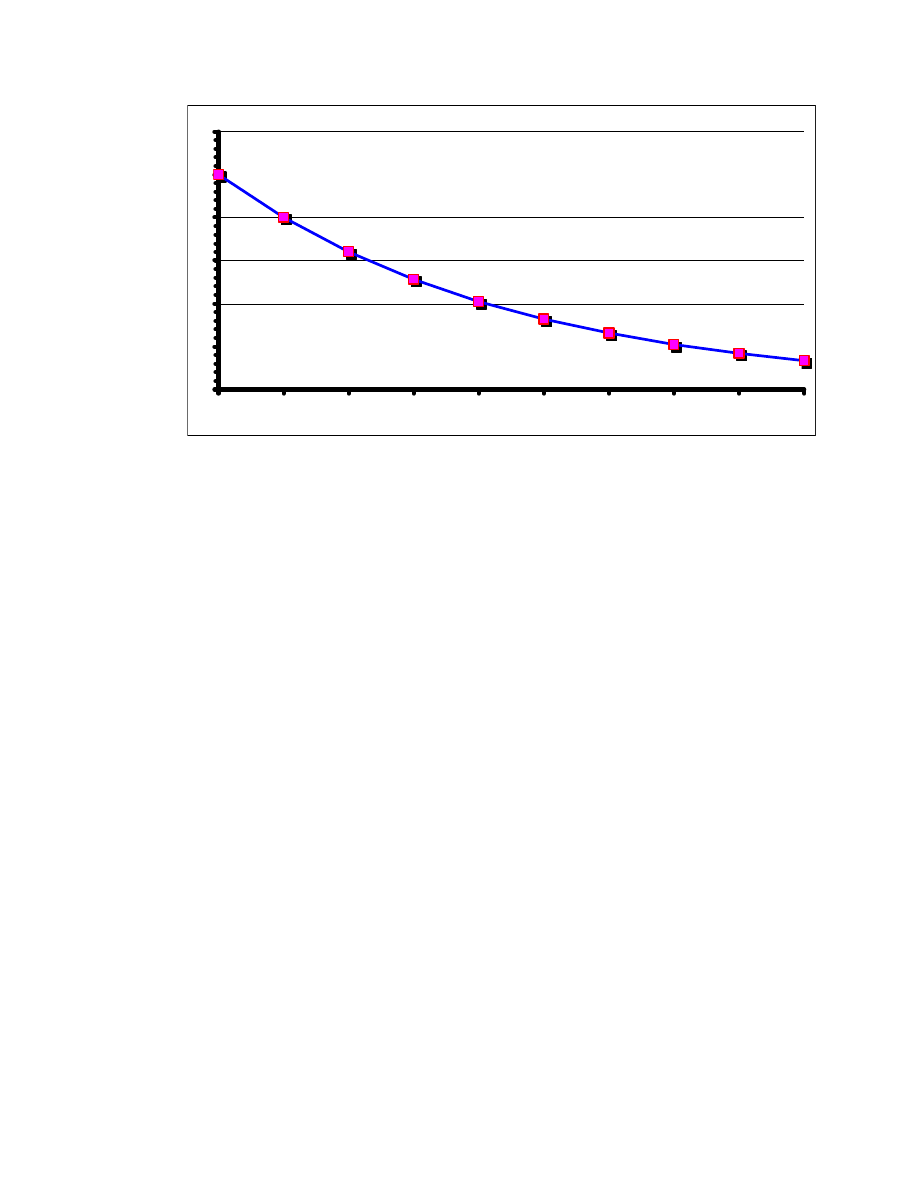
53 

0

1

1

0.9

1

2

0.8

0.8

3

0.7

0.64

4

0.6

0.512

5

0.5

0.4096

6

0.4

0.32768

7

0.3 0.262144

8

0.2 0.209715

9

0.1 0.167772

10

0 0.134218

normalizowna funkcja kosztu

0

0.2

0.4

0.6

0.8

1

1.2

1

2

3

4

5

6

7

8

9

10

Wykres 5.1 Kształt funkcji kosztu po normalizacji według metody z pracy [61] 
 

5.2.Przykład 

zastosowania 

opracowanej 

metody  

i  oprogramowania  dla  zagadnienia  optymalizowanego  wyboru 
gatunku stali konstrukcyjnej 

 
W pracach  [61,62] rozpatrywano problem doboru stali w zale no ci od potrzeb i 
warunków, w których b d  u ywane produkowane z niej wyroby. Oczywiste jest 
przecie ,  e  innej  stali  u yjemy  buduj c  most  kolejowy  a  innej  platform  
wiertnicz   czy  pancerz  czołgu.  Opieraj c  si   na  Ameryka ski  Instytut  elaza  i 
Stali  (AISI)  wyró nijmy  kilka  podstawowych  rodzajów  stali  u ytkowej  V

1

,  A

2

, 

D

2

, 

1

, 

1

,  Taki  wybór  gatunków  stali  dla  oceny  jest  spowodowany  wył cznie 

tym,  e  w  nowoczesnej  literaturze  rozpatrywany  poni ej  przykład  faktycznie 
został  ju   testem  dla  porównywania  efektywno ci  metod  optymalizowanego 
wyboru gatunku stali dla tych lub innych celów.  
 
Aby  mie   mo liwo   skutecznej  oceny  stopnia  przydatno ci  gatunków  stali  do 
wyrobów  b dziemy  potrzebowa   oczywi cie  pewnego  zestawu  kryteriów 

 

 

54 

jako ci. Oczywistym b dzie fakt,  e kryteria te b d  przedstawione w rozmytej 
postaci. 
Chc c skutecznie ocenia  stopie  przydatno ci, u yteczno ci pewnych kryteriów 
jako ci  stali  b dziemy  potrzebowa   odpowiednich  zestawów  ocen 
lingwistycznych,  na  których  b dziemy  si   opierali

.  Jak  ju   wcze niej 

wspomniano  taki  zestaw  słów  powinien  składa   si   maksymalnie  z  9  opisów. 
W  pracy  [62]  pokazano,  e  oceny  lingwistyczne  kryteriów  jako ci  stali  mo na 
przedstawi   za  pomoc   ich  rozmytych  odpowiedników  (Tabela  5.1  
i Tabela 5.2).  
 
Tabela 5.1   

 

 

 

  Tabela 5.2   

 
Liczby w tabelach 5.1 i 5.2 s  punktami kluczowymi u ywanych trapezoidalnych 
funkcji przynale no ci. Zrozumiałe jest,  e ró ne kryteria jako ci stali b d  dla 
osób  podejmuj cych  decyzje  doboru  stali  w  ró nym  stopniu  wa ne.  W  takim 
wypadku  korzystaj c  z  tablicy  parzystych  porówna   mo emy  wyliczy   stopnie 
wa no ci  –  rangi.  Cz sto  bywa  jednak  tak,  e  nie  trzeba  wylicza   wag  dla 
pewnych kryteriów gdy  s  one ju  ogólnie przyj te. Do takich sytuacji dochodzi 
zwykle, gdy problem  nie jest nowy, ale był  ju  nie jednokrotnie rozpatrywany. 
Najcz ciej  jednak  wiarygodne  oceny  wag  nie  s   przedstawiane  za  pomoc  
jednej liczby, ale wła nie za pomoc  rozmytych opisów. Co jest zreszt  zgodne  
z intuicyjnym podej ciem, gdy  jak wiadomo ekspertom rzadko udaje si  doj  
do  porozumienia  wiec  najłatwiej  jest  przedstawi   wagi  wła nie  za  pomoc  
słownych opisów. Jednak do oblicze  potrzebne s  ju  konkretne liczby. Musimy 
wiec dokona  konwersji słownych opisów na ich liczbowe warto ci 

Warto  słowna   Warto ci liczbowe 
Najgorsze (W) 
Słabe (P) 
W porz dku (F) 
Dobre (G) 
Najlepsze (B) 

(0,0,0,0.3) 
(0,0.3,0.3,0.5) 
(0.2,0.5,0.5,0.8) 
(0.5,0.7,0.7,1) 
(0.7,1,1,1) 

Warto  słowna  

Warto ci liczbowe 

Bardzo niski (VL) 
Niskie (L) 

redni (M) 

Wysoki (H) 
Bardzo wysoki (VH) 

(0,0,0,0.3) 
(0,0.3,0.3,0.5) 
(0.2,0.5,0.5,0.8) 
(0.5,0.7,0.7,1) 
(0.7,1,1,1) 

 

 

55 

 

Wagi  wa no ci  dla  kryteriów  wyboru  stali  s   oznaczane  w  nast puj cy 

sposób[62] 
Tabela 5.3   

 

 

 

Tabela 5.4 

Opinie wydane przez jednego eksperta  Opinie wydane przez grup  3 ekspertów 

 
 

 
W  powy szych  tabelach  C

1,..

  C

k 

s   subiektywnymi  i  obiektywnymi  kryteriami 

wyboru, a W

1

…, W

k

 (W

11

…,W

nk 

- n – to liczba ekspertów oznaczonych liter  E) 

s   odpowiadaj cymi  im  warto ciami  opinii  eksperta  lub  ekspertów.  W 
pierwszym przypadku (1 ekspert) opisy słowne zamieniamy na liczby rozmyte na 
podstawie ich rozmytych odpowiedników podanych w tabeli 5.1 i tabeli  5.2. W 
przypadku  drugim  (wi ksza  liczba  ekspertów)  podobnie  musimy  przekształci  
wszystkie słowne opisy na ich rozmyte odpowiedniki, a nast pnie u redniaj c je 
otrzyma   jedna  konkretn   opinie  i  dopiero  je  wykorzystywa   do  dalszych 
oblicze .  

n

W

W

n

j

ij

i

=

=

1

'

 , gdzie 

'

i

W

- oznacza warto  u rednionej w rozmytym sensie wagi 

dla kolejnych kryteriów jako ciowych dla i=1..k, gdzie k – to liczba wszystkich 
kryteriów.W

ij

-  to  wagi  i-tego  kryterium  przedstawionego  przez  n-tego  eksperta 

j=1.. n, gdzie n jest liczb  wszystkich ekspertów podejmuj cych decyzje. 
 

Opinie 

Kryterium 

E

1 

E

2

 

… 

E

n

 

C

1

 

W

11

 

W

21

 

… 

W

n1

 

C

2

 

W

12

 

W

22

 

… 

W

n2

 

C

3

 

W

13

 

W

23

 

… 

W

n3

 

C

4

 

W

14

 

W

24

 

… 

W

n4

 

C

5

 

W

15

 

W

25

 

… 

W

n5

 

... 

… 

… 

… 

… 

C

k-1

 

W

1k

 

W

2k

 

… 

W

nk

 

C

k

 

W

1k-1

  W

2k-1

  …  W

nk-1

 

Kryterium 

Opinie 

C

1

 

W

1

 

C

2

 

W

2

 

C

3

 

W

3

 

C

4

 

W

4

 

C

5

 

W

5

 

… 

…

 

C

k-1

 

W

k-1 

C

k

 

W

k

 

 

 

56 

Przykładowo  wła ciwo ci  (kryteria)  stali,  pod  którymi  mo na  rozpatrywa  
u yteczno   stali  mo emy  podzieli   na  2  kategorie  subiektywne  
i  obiektywne,  przy  tym  oba  typy  mog   by   przedstawiane  za  pomoc   liczb 
rozmytych. 
 
Subiektywne to kolejno: 
1.

 

Wła ciwo ci anty-deformuj ce (C

1

) 

2.

 

Bezpieczne utwardzanie (C

2

) 

3.

 

Twardo  (C

3

) 

4.

 

Odporno  na temperatur  (C

4

) 

5.

 

Odporno  na  cieranie ( cieralno ) (C

5

) 

6.

 

Wła ciwo ci mechaniczne (C

6

) 

Kryterium obiektywnym b dzie w naszym przypadku  
7.

 

Koszt materiału (C

7

) 

 
Kryteria  s   podzielone  w  ten  sposób  gdy   kolejny  raz  nale y  podkre li ,  e 
kryterium  kosztu  jest  ustalany  przez  rynek.  Natomiast  pozostałe  subiektywne 
kryteria zale  tylko i wył cznie od osobistej opinii osoby podejmuj cej decyzj . 
 

 

 

57 

Tabela 5.5 W rozpatrywanym testowym przykładzie[62] tablica wag 

zdefiniowana została przez 3 ekspertów. 

 

 

 
 
 
 
 
 
 
 
 
Podstawiaj c  pod  słowne  opisy  wa no ci  kryteriów  warto ci  z  tabeli  5.1  i 
u ywaj c  metod  arytmetyki  liczb  rozmytych  u redniamy  wagi  i  otrzymamy 
odpowiednie wyniki przedstawione w tabeli 5.6. 
       Tabela 5.6. U rednione warto ci wag 
 
 
 
 

Subiektywne  kryteria  1-6  s   przedstawione  za  pomoc   słownych  opisów,  
a  obiektywne  kryterium  7  (koszt  materiału)  jest  opisane  za  pomoc   rozmytych 
liczb.  Warto  jednak  podkre li ,  e  bezpo rednie  porównywanie  ze  sob  
kryteriów  subiektywnych i  obiektywnych  mo e prowadzi   do  pewnych  bł dów 
w  wyliczeniach.  W  tym  celu  dokonujemy  zamiany  kryterium  obiektywnego  
na  subiektywne.  Aby  nie  prowadzi   do  utraty  cennych  informacji 

Opinie 

Kryterium 

E

1 

E

2

 

E

3

 

C

1

 

H 

H 

VH 

C

2

 

M 

H 

M 

C

3

 

VH 

VH 

H 

C

4

 

H 

H 

M 

C

5

 

M 

M 

M 

C

6

 

H 

H 

VH 

C

7

 

VH 

VH 

VH 

Kryterium 

Opinie liczbowe 

Opinie słowne 

C

1

 

W

1

’=(0.567,0.8,0.8,1) 

H 

C

2

 

W

2

’=(0.3,0.567,0.567,0.867) 

M 

C

3

 

W

3

’=(0.633,0.8,0.8,1) 

H 

C

4

 

W

4

’=(0.4,0.633,0.633,0.933) 

M 

C

5

 

W

5

’=(0.2,0.5,0.5,0.8) 

M 

C

6

 

W

6

’=(0.567,0.8,0.8,1) 

H 

C

7

 

W

7

’=(0.7,1,1,1) 

VH 

 

 

58 

spowodowanych  defuzzyfikacj   danych,  czyli  zamian   liczb  rozmytych  
na rzeczywiste, b dziemy korzysta  wsz dzie z rozmytych przedziałów. 
W  naszym  przykładzie  skorzystamy  z  gatunków  stali  proponowanych  przez 
AISI. S  to kolejno: V

1

, A

2

, D

2

, 

1

, 

1

, 

 
Tabela 5.7 Koszt materiału przedstawiony za pomoc  rozmytych przedziałów 

Numery stali wg AISI 

Koszt materiału za sztuk   

V

1 

(1.5,1.6,1.6,1.7) 

A

2 

(1.8,2.0,2.0,2.2) 

D

2 

(1.0,2.0,2.0,2.2) 

1 

(1.0,1.0,1.0,1.0) 

1

 

(2.5,3.0,3.0,3.5) 

  
Nieco ciekawym mo e wygl da  wprowadzona rozmyto  kosztów materiałów. 
Jednak w rzeczywisto ci takiego rodzaju rozmyte oceny s  rezultatami zwykłych 
bada  marketingowych na podstawie ofert proponowanych przez ró ne firmy.  
Okre lamy  zakres  przydatno ci  parametru.  Jak  widzimy  w  tabeli  5.7  parametr 
zawiera  b dzie si  w granicach od 1 do 3.5 . Nale y tylko ustali , jaki kształt 
funkcji  u yteczno ci  tego  parametru  jest  dla  nas  zadowalaj cy.  Poniewa  
parametrem jest koszt jednostki stali, wi c oczywistym jest,  e im ni sza warto  
tym  lepiej,  mo emy  tak e  przyj ,  e  ka da  cena  powy ej  3,5  jest  dla  nas  nie 
opłacalna, wi c przyjmuje warto  0, a ka da cena poni ej 1 jest dla nas zawsze 
korzystna, wi c przyjmuje warto  1. 
Nast pnie pod tak zdefiniowan  funkcje u yteczno ci (przykładowo na Rys 5.1 
dla  parametru  C

7

  )  dokonujemy  podstawienia  warto ci  kosztu  (z  tabeli  5.6)  

do  funkcji  przydatno ci,  w  ten  sposób  okre laj c  ju   subiektywn   warto  
parametru.  Na  ko cu  nale y  tylko  oceni ,  do  jakiego  rozmytego  opisu  z  tabeli 
5.1  nasz  parametr  b dzie  si   kwalifikował.  Na  rysunku  5.1  widzimy,  

e parametr ten zwiera si  w granicach opisu rozmytego DOBRE (G) .  

 

 

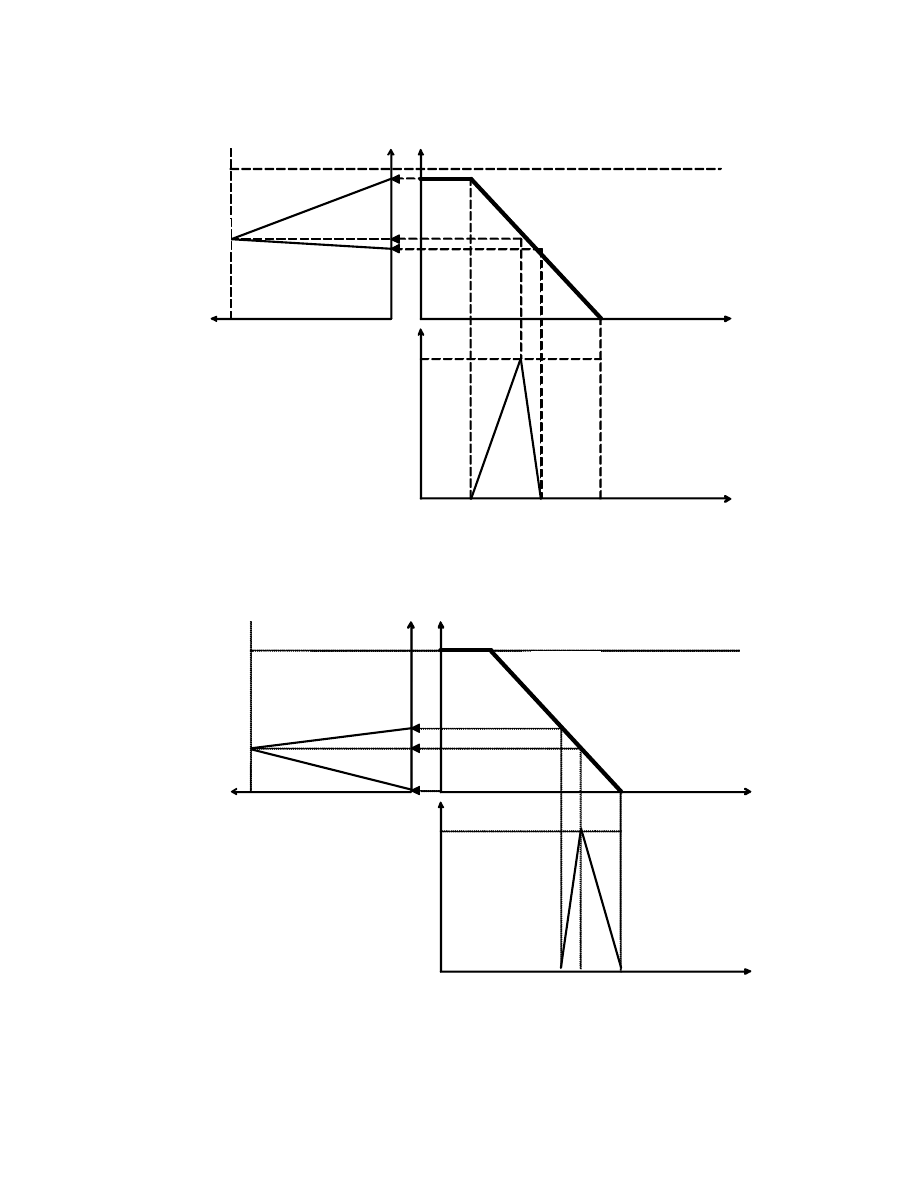
59 

 

 

 ¯ ¯ ¯  

 

 

 

 

 

 

 

 

 

 

 

 

 

0.

52

 

C

7

(D

2

) =(0.52;0.8;0.8;1)= G 

1 

3,5 

 

2 

C

7

(D

2

) 

0 

3,5 

 

2  2,2 

1 

0 

1 

0 

1 

1 

(C

7

) 

0,

6 

Rysunek 5.1 Przekształcenie kryterium jako ci obiektywnego na subiektywny dla 

C

7

(D

2

)

 

 ¯ ¯ ¯  

 

 

 

 

 

 

 

 

 

 

 

 

 

0.

2 

C

7

(

1

) = (0;0.2;0.2;0.4)=P 

3,5 

 

C

7

(

1

) 

0 

3,5 

 

0.

4 

3 

2.5 

0 

1 

0 

1 

1 

(C

7

) 

 Rysunek 5.2 Przekształcenie kryterium jako ci obiektywnego na subiektywny 

dla C

7

(D

2

) 

 

 

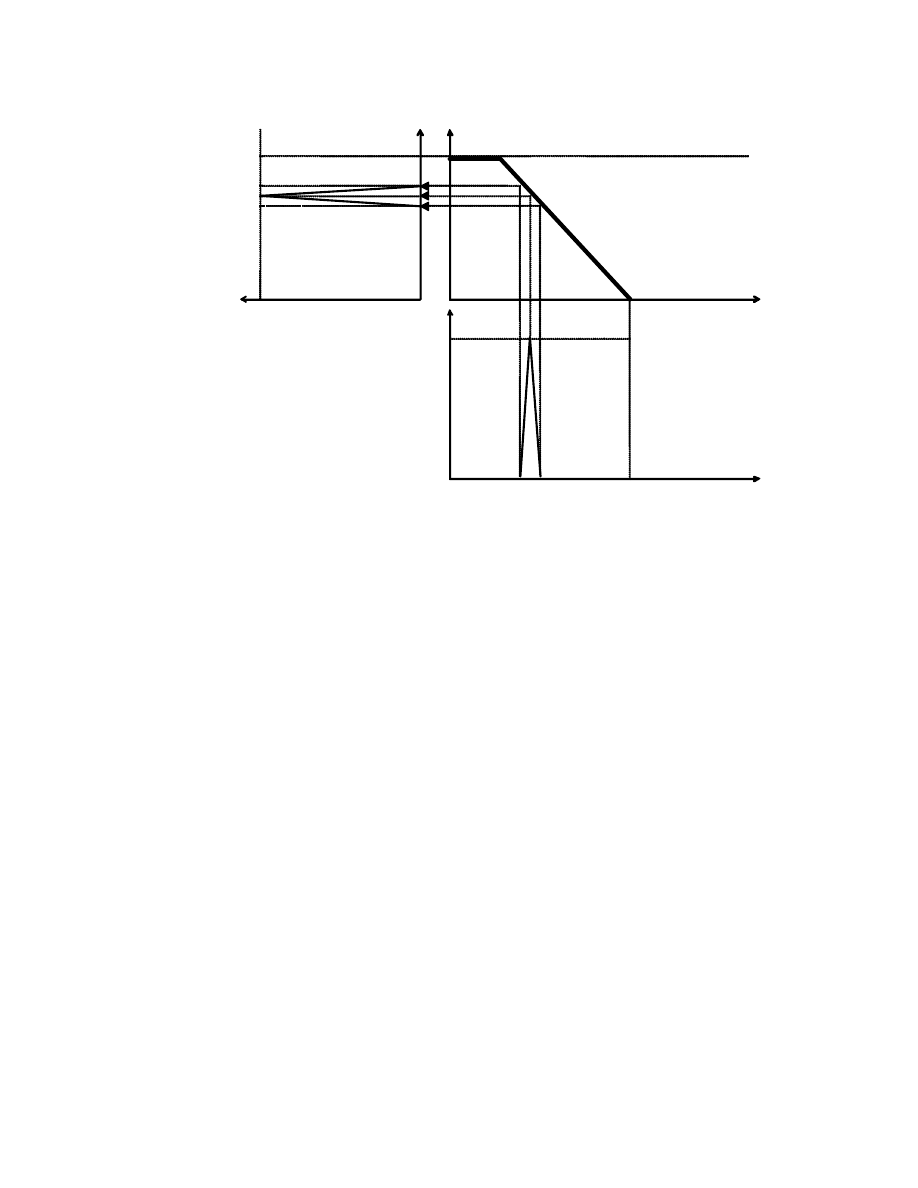
60 

 

 ¯ ¯ ¯  

 

 

 

 

 

 

 

 

 

 

 

 

 

1 

0.

8 

0.

72

 

0.

76

 

C

7

(V

1

) =(0.72;0.76;0.76;0.8)= G 

3,5 

 

C

7

(V

1

) 

0 

3,5 

 

1.6 

1.7 

1.5 

0 

1 

0 

1 

(C

7

) 

 Rysunek 5.3 Przekształcenie kryterium jako ci obiektywnego na subiektywny 

dla C

7

(D

2

) 

Jednak  nie  zawsze  jednoznacznie  wiadomo,  do  jakiej  oceny  ma  zosta  
zakwalifikowany. Dobrze widoczne jest to w ostatnim przypadku (Rysunek 5.3) 
gdzie powstaje zasadnicze pytanie czy otrzymany przedział (0.72;0.76;0.76;0.8) 
jest  równy  słownemu  ocenie  DOBRY(G)  czy  W  PORZ DKU  (F),  gdy  
otrzymany przedział pasuje zarówno do jednego jak i drugiego opisu. Z pomoc  
przychodzi  nam  tu  opracowana  [64]  metoda  porównywania  przedziałów 
rozmytych  z  u yciem  -poziomów.  Dzi ki  niej  mo emy  porówna   otrzymany 
przedział  z  rozmytymi  odpowiednikami  słownych  opisów  z  tabeli  5.1  i  w  ten 
sposób  policzy   prawdopodobie stwo,  e  dany  zbiór  jest  równy  któremu   
z  opisów.  Oczywistym  jest,  e  b dziemy  u ywa   dalej  tego  z  opisów,  którego 
prawdopodobie stwo  równo ci  z  naszym  otrzymanym  przedziałem  jest 
najwi ksze. 
I  tak  prawdopodobie stwo  to  b dziemy  wylicza   za  pomoc   nast puj cego 
wyra enia: 

(

)

(

)

−

=

=

=

=

1

0

n

i

i

i

i

B

A

P

B

A

P

α

α

α

, gdzie n – ilo   -poziomów. 

 

 

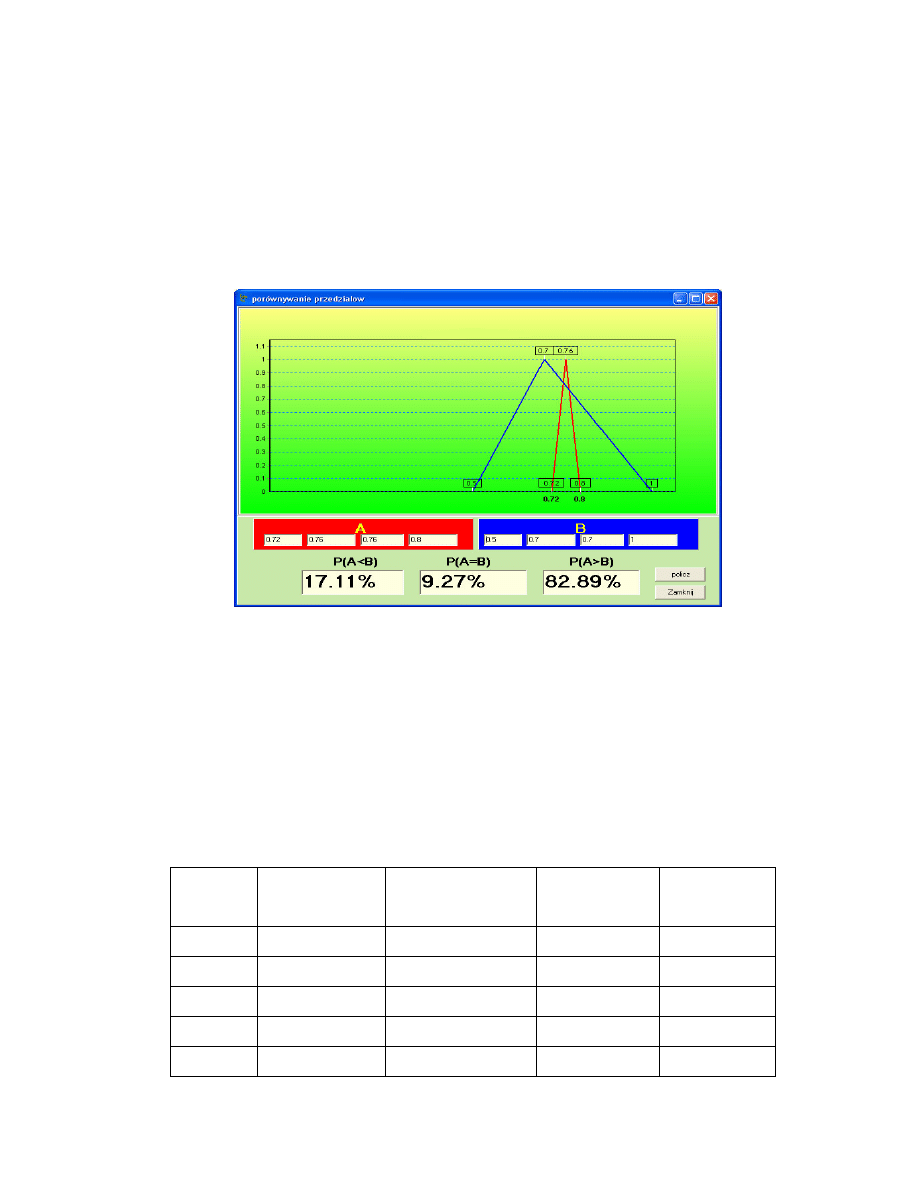
61 

Przykładowo prawdopodobie stwo,  e przedział (0.72;0.76;0.76;0.8) otrzymany 
w  wyniku  przekształcenia  pokazanego  na  Rys  5.5,  b dzie  równy  opisowi 
DOBRY wynosi: 
P( C

7

(D

2

)=DOBRY) = 9.27% 

 

P( C

7

(V

1

)=DOBRY) = 6.31% 

P( C

7

(D

2

)=W PORZ DKU) =0.39% 

P( C

7

(V

1

)=W PORZ DKU) =10.63% 

 

 

Rys.5.5 Porównanie przedziałów C

7

(D

2

) (kolor czerwony) = DOBRY (kolor niebieski) 

  
St d  mo na  by  wysnu   wniosek, 

e  otrzymany  rezultat  mo emy 

 z  wi ksz   pewno ci   zdefiniowa   jako  DOBRY,  i  u ywa   wła nie  jego 
 w dalszych obliczeniach.  
 
Tabela  5.8  Koszt  materiału  przedstawiony  za  pomoc   subiektywnych  opisów 
przy zastosowaniu metody obliczania prawdopodobie stwa równo ci zbiorów 

Numery stali 

wg AISI 

Koszt materiału za 

sztuk  

Koszt po przekształceniu  

Prawdopodobie stwo 

równo ci z opisem 

Koszt według opisów 

słownych 

V

1 

(1.5,1.6,1.6,1.7)  (0.72;0.76;0.76;0.8) 

10,63% 

F 

A

2 

(1.8,2.0,2.0,2.2)  (0,52;0,6;0,6;0.68)  

10,63% 

F 

D

2 

(1.0,2.0,2.0,2.2) 

(0,52;0,8;0,8;1) 

9.27% 

G 

1 

(1.0,1.0,1.0,1.0) 

(1.0,1.0,1.0,1.0) 

16.67% 

VG 

1

 

(2.5,3.0,3.0,3.5) 

(0;0,2;0,2;0,4) 

23.86% 

P 

 

 

62 

 
Poniewa   jak  to  mo na  zauwa y   w  tabeli  5.8  prawdopodobie stwa  równo ci 
zbiorów s  przewa nie bardzo małe (przeci tnie nie przekraczaj  20-30%), wi c 
aby  zwi kszy   wiarygodno   do  wyników  opracowana  została  tak e  inna 
metoda. 
Polega  ona  na  podstawieniu  otrzymanego  zbioru  pod  zbiór  okre laj cy  dana 
ocen  lingwistyczn . W wyniku takiego podstawienia otrzymamy nast pny zbiór 
rozmyty,  który  b dzie  charakteryzował  nam  stopie   spójno ci  z  dan   ocen  
lingwistyczn .  Takie  przekształcenie  wykonujemy  dla  ka dej  oceny 
lingwistycznej,  co  da nam  w  wyniku  pewn   ilo   zbiorów,  które  porównujemy 
ju   w  zdefuzzyfikowanej  postaci.  Defuzzyfikacji  (wyostrzanie)  zbioru 
dokonujemy korzystaj c z prostego przekształcenia: 
 

 

4

4

3

2

1

x

x

x

x

xdef

+

+

+

=

,  gdzie  xdef  oznacza  warto   zdefuzzyfikowan   ,  a  x

i

-  s  

kolejnymi punktami kluczowymi danej funkcji rozmytej [61]. 
 
 Nale y zwróci  uwag ,  e defuzzyfikacja przeprowadzona na tym poziomie nie 
spowoduje  nam  utraty  informacji,  a  jedynie  w  naturalny  sposób  okre la  nam 
stopie  spójno ci z dan  ocen  lingwistyczn , gdy  w ostatnim etapie wybieramy 
t  ocen , której warto  po zdefuzzyfikowaniu b dzie najwi ksza.  
 

 

 

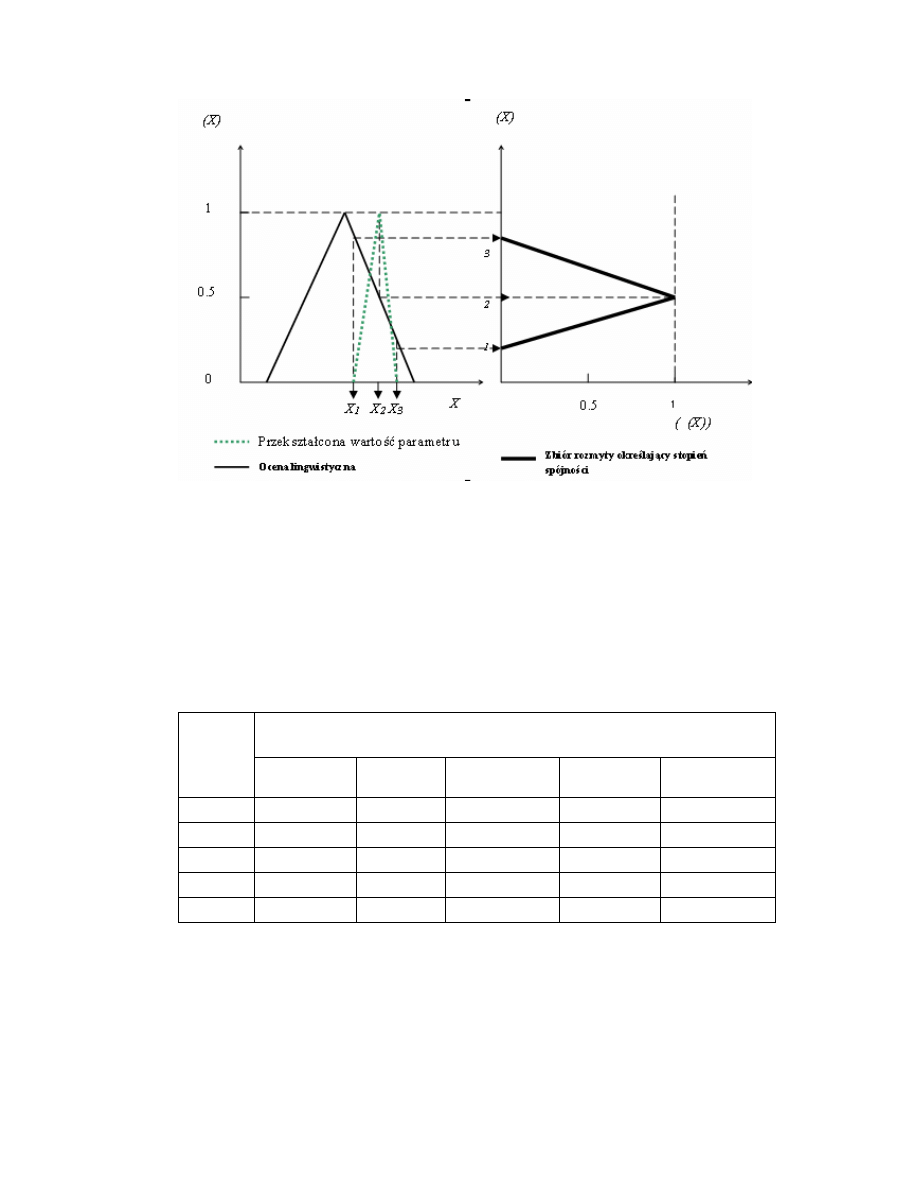
63 

 

Rys 5.9 Podstawienie zbioru rozmytego pod ocen  lingwistyczn   

 
 

Dokonuj c  takiego  przekształcenia  porówna   dla  wszystkich  gatunków  stali 
otrzymamy nast puj ce rezultaty( Tabela 5.8) 
 
Tabela 5.8 Stopnie spójno ci z ocenami ligwistycznymi 

Stopnie spójno ci z ocenami lingwistycznymi 

Numery stali 

wg AISI 

Najgorsze (W) 

(0,0,0,0.3) 

Słabe (P) 

(0,0.3,0.3,0.5) 

W porz dku (F) 
(0.2,0.5,0.5,0.8) 

Dobre (G) 

(0.5,0.7,0.7,1) 

Najlepsze(B) 

(0.7,1,1,1) 

V

1 

0 

0 

(0.266,0,133,0.133,0) 

(0.93,0.8,0.8,0,67) 

(0.02,0.06,0.06,0.1) 

A

2 

0 

0 

(0.93,0.66,0.66,0.4) 

( 0.2,0.1,0.1,0.18)     

0 

D

2 

0 

0 

(0.93,0,0,-0.66) 

(0.2,0.67,0.67,0) 

(-0.18,0.1,0.1,1 ) 

1 

0 

0 

0 

(0,0,0,0) 

(1,1,1,1) 

1

 

(1,0.33,0.33,-0.33) 

(0,0.2,0.2,0.5) 

(-0.2,0,0,0.2) 

0 

0 

 Jak  wida   stopnie  spójno ci  z  ocenami  lingwistycznymi  mog   by  
przedstawione  przez  zwykłe  liczby  oraz  rozmyte.  Dla  unifikacji  rezultatów 
u ywamy  defuzzyfikacji  Po  defuzyfikacji  polegaj cej  na  u rednieniu  warto ci, 
otrzymamy nast puj ce wyniki 
 

 

 

64 

Tabela 5.9 Zdeffuzyfikowane stopnie spójno ci z ocenami ligwistycznymi 

Stopnie spójno ci z ocenami lingwistycznymi 

Numery stali wg AISI oraz w 

nawisach podane otrzymane 

subiektywne przedstawienie 

u ywanych obiektywnych kryteriów 

Najgorsze 

(W)  

Słabe 

(P)  

W porz dku (F)  Dobre (G)   Najlepsze(B)  

V

1  

(0.72;0.76;0.76;0.8)

 

0 

0 

0.133 

0.8 

0.06 

A

2 

 (0,52;0,6;0,6;0.68)

 

0 

0 

0.86 

0.445 

0 

D

2 

 (0,52;0,8;0,8;1)

 

0 

0 

0.23  

0.33 

0.26  

1

  (1.0,1.0,1.0,1.0)

 

0 

0 

0 

0 

1 

1   

(0;0,2;0,2;0,4) 

0.3325  

0.225 

0  

0 

0 

 

Tabela 5.10 Porównanie metod oraz ko cowe rezultaty oceny spójno ci z 
lingwistycznymi ocenami  

Numery stali 

wg AISI 

Koszt materiału za 

sztuk  

Koszt po przekształceniu  

Koszt według opisów 

słownych (metoda I) 

Koszt według opisów 

słownych (metoda II) 

V

1 

(1.5,1.6,1.6,1.7)  (0.72;0.76;0.76;0.8) 

F 

G 

A

2 

(1.8,2.0,2.0,2.2)  (0,52;0,6;0,6;0.68)  

F 

F 

D

2 

(1.0,2.0,2.0,2.2) 

(0,52;0,8;0,8;1) 

G 

G 

1 

(1.0,1.0,1.0,1.0) 

(1.0,1.0,1.0,1.0) 

B 

B 

1

 

(2.5,3.0,3.0,3.5) 

(0;0,2;0,2;0,4) 

P 

W 

 
Pozostałe  stopnie  przydatno ci  kolejnych  gatunków  stali  dla  poszczególnych 
subiektywnych kryteriów zostały oszacowane nast puj co (Tabela 5.9) 

 

Tabela 5.11 Pozostałe stopnie przydatno ci kryteriów jako ci stali konstrukcyjnej 

Numery stali wg AISI 

      

C

1 

C

2 

C

3 

C

4 

C

5 

C

6 

C

7 

V

1 

P 

F 

G 

P 

F 

B 

G 

A

2 

B 

B 

F 

F 

G 

F 

F 

D

2 

B 

B 

F 

F 

G 

P 

G 

1 

F 

G 

G 

F 

F 

F 

B 

1

 

G 

G 

F 

B 

G 

F 

W 

 

 

 

65 

Nast pnym krokiem jest przekształcenie opisów słownych na rozmyte warto ci z 
tabel  5.1, 5.2  co zostało przedstawione  w tabeli  5.12. Nasuwa si  tu  oczywiste 
pytanie,  po  co  przekształca   przekształcane  opisy  kryteriów  obiektywnych  na 
subiektywne  i  dopasowywa   (tylko  z  pewnym  prawdopodobie stwem)do  ich 
słownych  opisów,  a  nast pnie  je  znowu  przekształca   na  ich  rozmyte 
odpowiedniki. Dzieje si  tak, gdy  w wielu problemach wyboru i podejmowania 
zło onych  decyzji  nie  warto  jest  powi ksza   podstawowej  bazy  ocen 
lingwistycznej o kolejne oceny, które cz sto by nam było pó niej rozró nia . 
 
Tabela 5.12 Warto ci kryteriów jako ci stali konstrukcyjnej według ich słownych 
odpowiedników. 

Numery stali wg 

 AISI 

C

1 

C

2 

C

3 

V

1

 

(0,0.3,0.3,0.5)  (0.2,0.5,0.5,0.8)  (0.5,0.7,0.7,1) 

A

2 

(0.7,1,1,1) 

(0.7,1,1,1) 

(0.2,0.5,0.5,0.8) 

D

2 

(0.7,1,1,1) 

(0.7,1,1,1) 

(0.2,0.5,0.5,0.8) 

1

 

(0.2,0.5,0.5,0.8)  (0.5,0.7,0.7,1) 

(0.5,0.7,0.7,1) 

1

 

(0.5,0.7,0.7,1) 

(0.5,0.7,0.7,1)  (0.2,0.5,0.5,0.8) 

 

Numery stali 

wg AISI 

C

4 

C

5 

C

6 

C

7 

V

1

 

(0,0.3,0.3,0.5) 

(0.2,0.5,0.5,0.8) 

(0.7,1,1,1) 

(0.5,0.7,0.7,1) 

A

2 

(0.2,0.5,0.5,0.8) 

(0.5,0.7,0.7,1) 

(0.2,0.5,0.5,0.8) 

(0.2,0.5,0.5,0.8) 

D

2 

(0.2,0.5,0.5,0.8) 

(0.5,0.7,0.7,1) 

(0,0.3,0.3,0.5) 

(0.5,0.7,0.7,1) 

1

 

(0.2,0.5,0.5,0.8) 

(0.2,0.5,0.5,0.8) 

(0.2,0.5,0.5,0.8) 

(0.7,1,1,1) 

1

 

(0.7,1,1,1) 

(0.5,0.7,0.7,1) 

(0.2,0.5,0.5,0.8) 

(0,0.3,0.3,0.5) 

 
B d c  w  posiadaniu  wag  oraz  stopni  przydatno ci  mo emy  przej   
do  agregacji  kryteriów.  Korzystamy  tu  z  metod  agregacji,  przedstawionych  w 
rozdziale  4.3.  Po  obliczeniu  warto ci  wystarczy  tylko  porówna   je  i  wybra   
to najlepsze, z najwi ksz  warto ci . 

 

 

66 

Dla przypomnienia nasze metody agregacji dla gatunku stali V

1

 b d  wygl dały 

nast puj co: 
• 

Maksymalnego pesymizmu: 

}

,...,

,

min{

2

1

1

2

1

1

i

w

i

w

w

V

C

C

C

D

=

 

• Addytywny 

N

C

W

D

N

i

i

i

V

=

=

1

2

1

 

• Multiplikatywny: 

∏

=

=

N

i

W

i

V

i

C

D

1

3

1

 

Korzystaj c z opracowanych i zaimplementowanych operacjach matematycznych 
na 

zbiorach 

rozmytych 

obliczono 

zagregowane 

kryteria.  

Na  przykład  dla  metody  maksymalnego  pesymizmu  powinni my  wykona  
nast puj c  operacje: 

;

.7,1)

(0.5,0.7,0

 ,

)

(0.7,1,1,1

,

.5,0.8)

(0.2,0.5,0

,

,0.5)

(0,0.3,0.3

,

.7,1)

(0.5,0.7,0

,

.5,0.8)

(0.2,0.5,0

,

,0.3,0.5)

min((0,0.3

)

(0.7,1,1,1

,0.8,1

(0.567,0.8

.5,0.8)

(0.2,0.5,0

33)

,0.633,0.9

(0.4,0.633

,0.8,1)

(0.633,0.8

67)

,0.567,0,8

(0.3,0.567

0.8,1

0.567,0.8,

1

1

 )

==

)

)

(

V

D

 
Jasne,  e  pot gowanie  przedziału  rozmytego  w  stopniu  przedziału  rozmytego 
daje  rezultat  tak e  w  postaci  przedziału  rozmytego.    St d  wynika  niezb dno  
wykonania  operacji  znalezienia  minimalnego  przedziału  rozmytego  z 
powy szego  wyra enia.  Do  tego  u ywano  metody  porównywania  liczb 
rozmytych  [64] . 
 

Poni ej  przedstawiono  rezultaty  otrzymane  za  pomoc   metody 

maksymalnego pesymizmu  
 
 
 

 

 

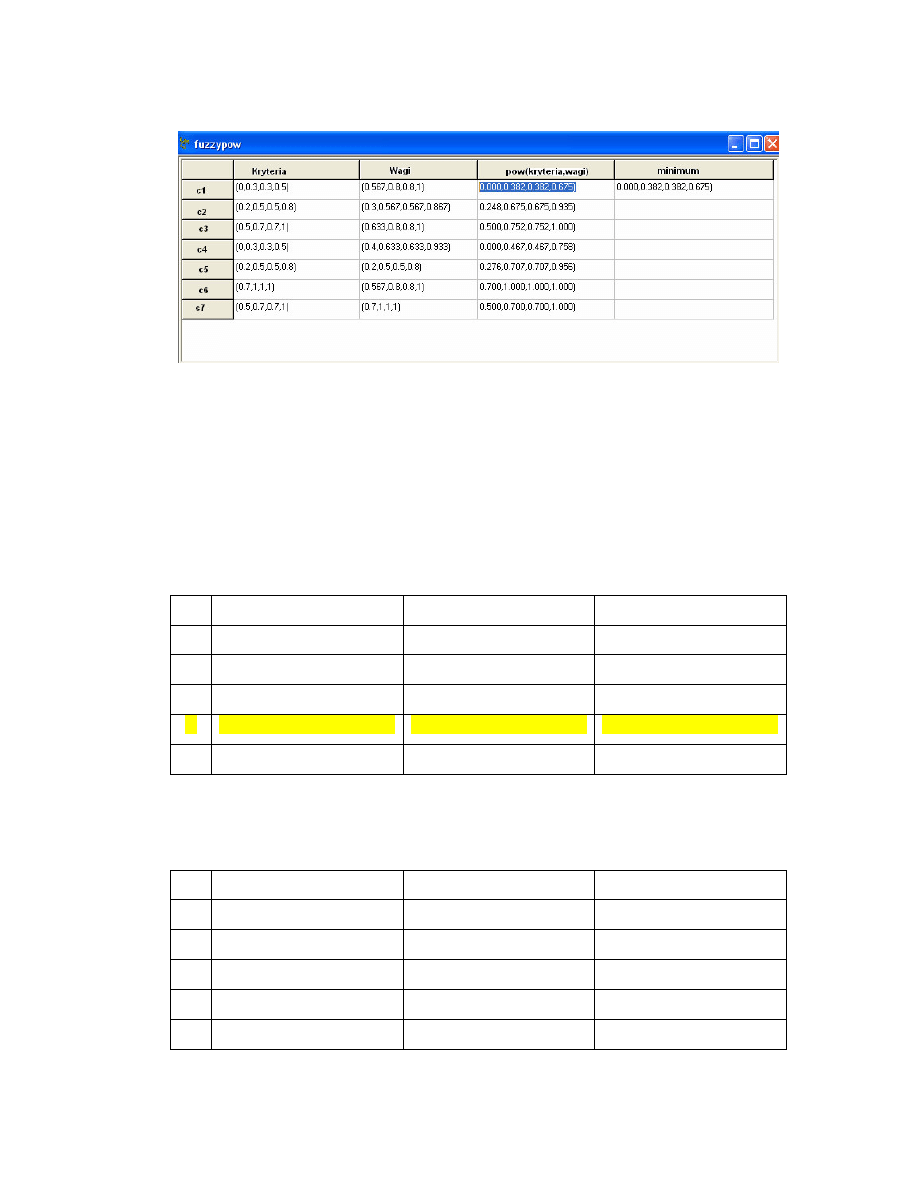
67 

Tabela 5.13 Przykład wyliczenia kryterium maksymalnego pesymizmu dla V

1

 

 

 
 

W  tabeli  5.14  i  5.15  przedstawiono  ko cowe  rezultaty  oceny  gatunków 

stali  otrzymane  na  podstawie  wszystkich  trzech  sposobów  agregowania 
kryteriów lokalnych. 
 
Tabela  5.14    Rezultaty  zagregowanych  kryteriów  dla  kolejnych  gatunków  stali 
konstrukcyjnej. 

 

DD

1 

DD

2 

DD

3 

V

1 

(0.000,0.382,0.382,0.675)  (0.020,0.106,0.106,0.186)  (0.000,0.191,0.191,0.577) 

A

2 

(0.200,0.500,0.500,0.855)  (0.077,0.186,0.186,0.257)  (0.140,0.500,0.500,0.855) 

D

2 

(0.000,0.382,0.382,0.675)  (0.107,0.214,0.214,0.286)  (0.350,0.700,0.700,1.000) 

1 

(0.200,0.574,0.574,0.881)  (0.086,0.200,0.200,0.257)  (0.140,0.574,0.574,0.881) 

1

  (0.000,0.300,0.300,0.616)  (0.040,0.123,0.123,0.214)  (0.000,0.226,0.226,0.616) 

 
Tabela  5.15    Rezultaty  zagregowanych  kryteriów  dla  kolejnych  gatunków  stali 
konstrukcyjnej przedstawione za pomoc  ocen lingwistycznych. 

 

DD

1 

DD

2 

DD

3 

V

1 

P 

W 

P 

A

2 

F 

W 

F 

D

2 

P 

W 

G 

1 

F 

W 

F 

1

 

P 

 W 

P 

 

 

 

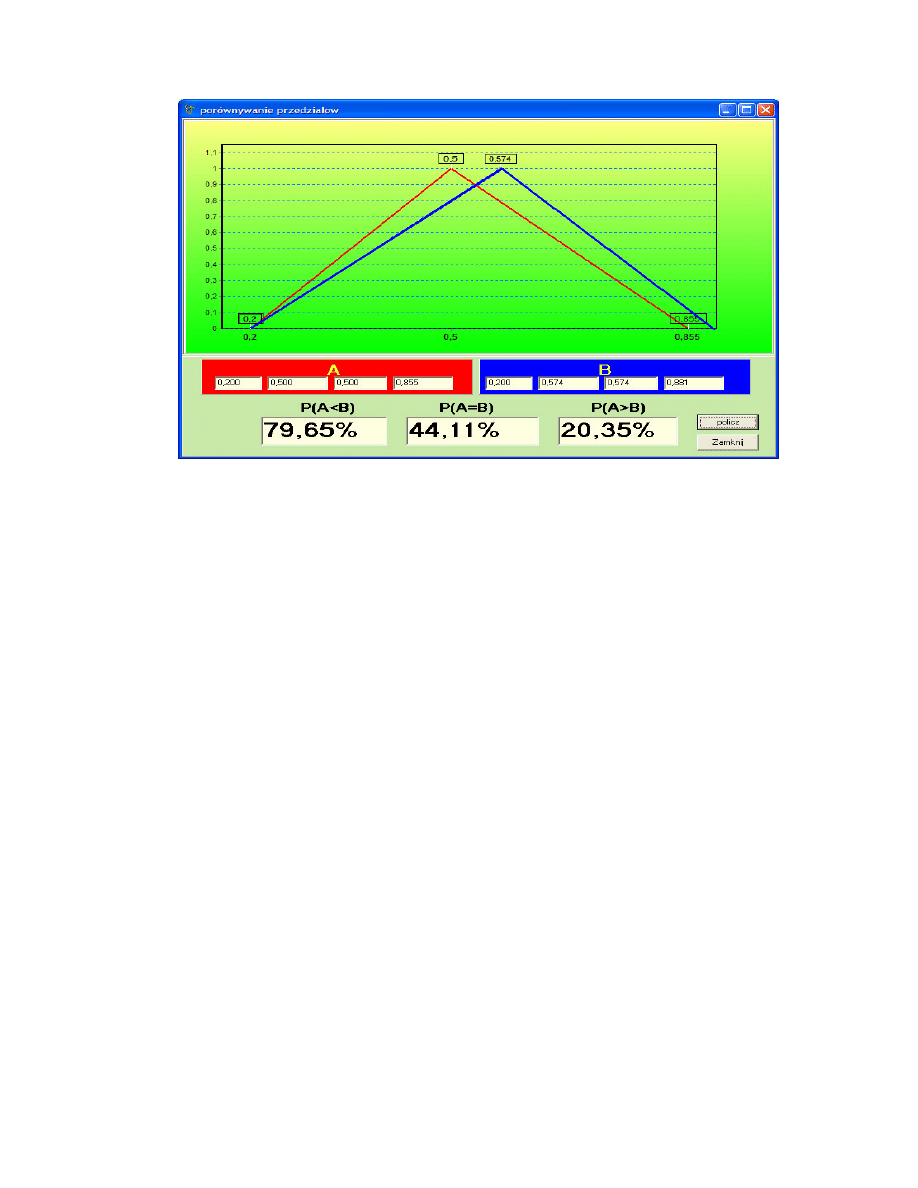
68 

 

rys 5.6 Porównanie ko cowe 

2

2

A

D

(A)oraz 

2

y

1

D

(B), których rezultaty były bliskie 

według agregacji maksymalnego pesymizmu 

 

Jak  widzimy  najwi ksz   ocen   osi gn ła  stal 

1

  gdy   dla  DD

1

  i  dla  DD

3

  

osi gn ła najwi ksz  warto , ale z punktu widzenia agregacji DD

2

 najlepsza jest 

stal  D

2

.  Jednak  w  rozdziale  pokazano  e  rezultatom  agregacji  DD

2 

  (sposób 

addytywny)  nie mo na zawsze ufa . Dlatego w naszym wypadku stal 

1

 mo na 

uzna  za najlepsz . Dla zilustrowania procedury wyboru (podejmowania decyzji) 
na  rysunku  5.6  pokazane  zostało  z  jakim  prawdopodobie stwem  (z  jakim 
prawdopodobie stwem) stal A

2

 (która tak e  ma wysokie noty) jest  mniejsza od 

1.

 

Jak  to  mo na  zauwa y   opracowana  metoda  pozwala  w  skuteczny  sposób 
ocenia  i wspomaga  podejmowanie decyzji nie tylko w dziedzinie wyboru stali, 
ale wsz dzie tam gdzie mamy do czynienia z problemem podejmowania decyzji 
przez grup  ekspertów  

 

 

 

 

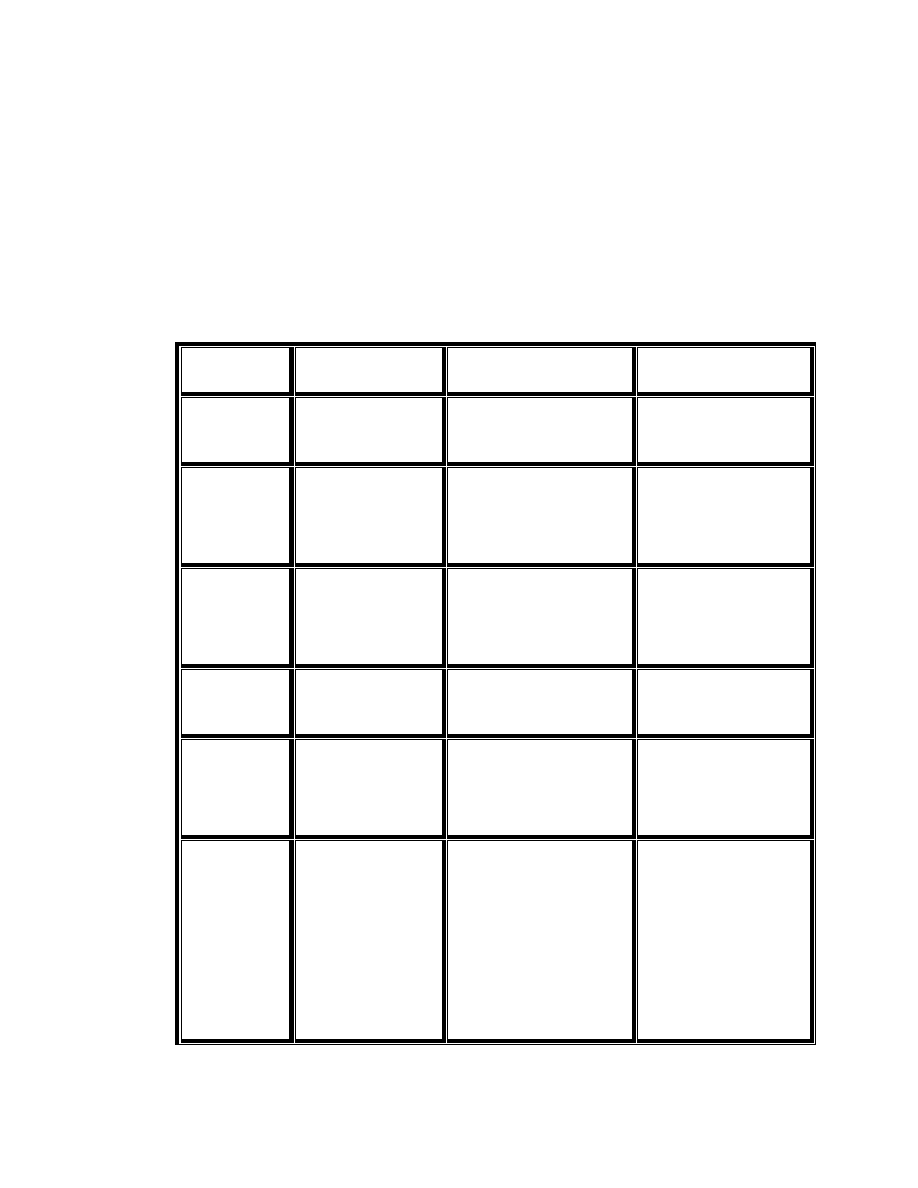
69 

5.3.Opisanie  struktury  klas  realizuj cych  metod   oszacowania 
alternatyw. 

 

Aby  opisa   struktur   chce  najpierw  przybli y   troch   działanie  samego 
programu.  Poni ej  przedstawiam  tabele,  która  opisuje  kluczowe  zachowania 
systemu..   
Etap1. Identyfikacja zachowa  systemu 

Kto 

Działanie 

Kogo ,Czego ? 

Rezultat 

Menu 

rysuje 

si  

Gotowo  
przyjmowania polece  

U ytkownik 

da 

odczytywania 

hierarchii 

Parametry wszystkich 
kryteriów zostaj  
odczytane z dysku 

U ytkownik 

da budowania 

od nowa 

hierarchii 

Wyczyszczona zostaje 
dotychczasowa 
struktura 

Menu 

oferuje 

dialog 

Budowa nowej 
hierarchii 

Menu 

oferuje 

hierarchie 

Umo liwia to wybór 
konkretnego 
kryterium 

U ytkownik  wybiera  

kryterium 

Do tego kryterium 
b dzie si  od tej pory 
zwracał 

 

 

70 

Menu 

oferuje 

parametry funkcji 
przynale no ci, macierz 
parzystych porówna  
dla wybranego 
kryterium 

Umo liwia zmian  
ilo ci, zestawu 
parametrów, macierzy 
parzystych porówna , 
nazw, wyliczenie 
rang. 

U ytkownik 

da zapisu 

wszystkich 
parametrów 

kryteriów hierarchii 

Wszystkie parametry: 
ich ilo , nazwy, 
macierze p.p. zostaj  
zapami tane na dysku. 

U ytkownik 

da zapisu cz ci 

parametrów 

Wybranego kryterium 

Dla wybranego 
kryterium wszystkie 
parametry: ich ilo , 
nazwy, macierze p.p. 
zostaj  zapami tane 
na dysku. 

Menu 

oferuje 

hierarchie 

Umo liwia to dodanie, 
albo usuwanie 
kryteriów 

U ytkownik 

da wyboru 

pliku danych 

Odczytanie danych z 
pliku 

Uzytkownik 

da wyliczenia 

Rang – 
współczynników 
wzgl dnej wa no ci 

Na ekranie zostana 
podane rangi dla 
ka dego z kryteriów 
na danym poziomie 

U ytkownik 

da wyliczenia 

Warto ci kryteriów 
globalnych 

Na ekranie b d  
podane D1,D2,D3 dla 
wszystkich kryteriów 

 

 

 

71 

Etap2. Identyfikacja klas obiektów 
 
Klasa: 

Menu 

Obowi zki:  

1.

  Pokazanie si  na ekranie po starcie programu 

2.

  Umo liwienie odczytania struktury hierarchii z dysku 

3.

  Umo liwienie budowania struktury hierarchii od nowa 

4.

  Umo liwienie zmiany hierarchii  

5.

  Umo liwienie zapisu zmian na dysku 

6.

  Umo liwienie odczytania danych z pliku 

7.

  Polecenie wyliczenia warto ci rang na dowolnym poziomie 

8.

  Polecenie  wyliczenia  warto ci  kryteriów  globalnych  na  dowolnym 

poziomie 

9.

  Przedstawienie wyników w postaci liczbowej i graficznej 

Współpracownicy: 
   Hierarchia 
 
Klasa: 

Hierarchia 

 

Obowi zki: 

1.

  Umo liwienie okre lenia, które z kryteriów chcemy zmieni  albo usun  

2.

  Umo liwienie zmiany w konkretnym kryterium 

3.

  Zapis zmian w kryterium na dysk 

4.

  Wyliczenie warto ci rang 

5.

  Wyliczenie warto ci kryteriów globalnych  

6.

  Wy wietlenie  na  ekran  DD

1

,DD

2

,DD

3

  dla  wszystkich  kryteriów 

globalnych 

 
Widoczne własno ci:  

-

  ilo  podpoziomów  

-

  macierz  parzystych  porówna   (tylko  dla  kryteriów  agreguj cych  pewne 

kryteria stoj ce na ni szym poziomie) 

 

 

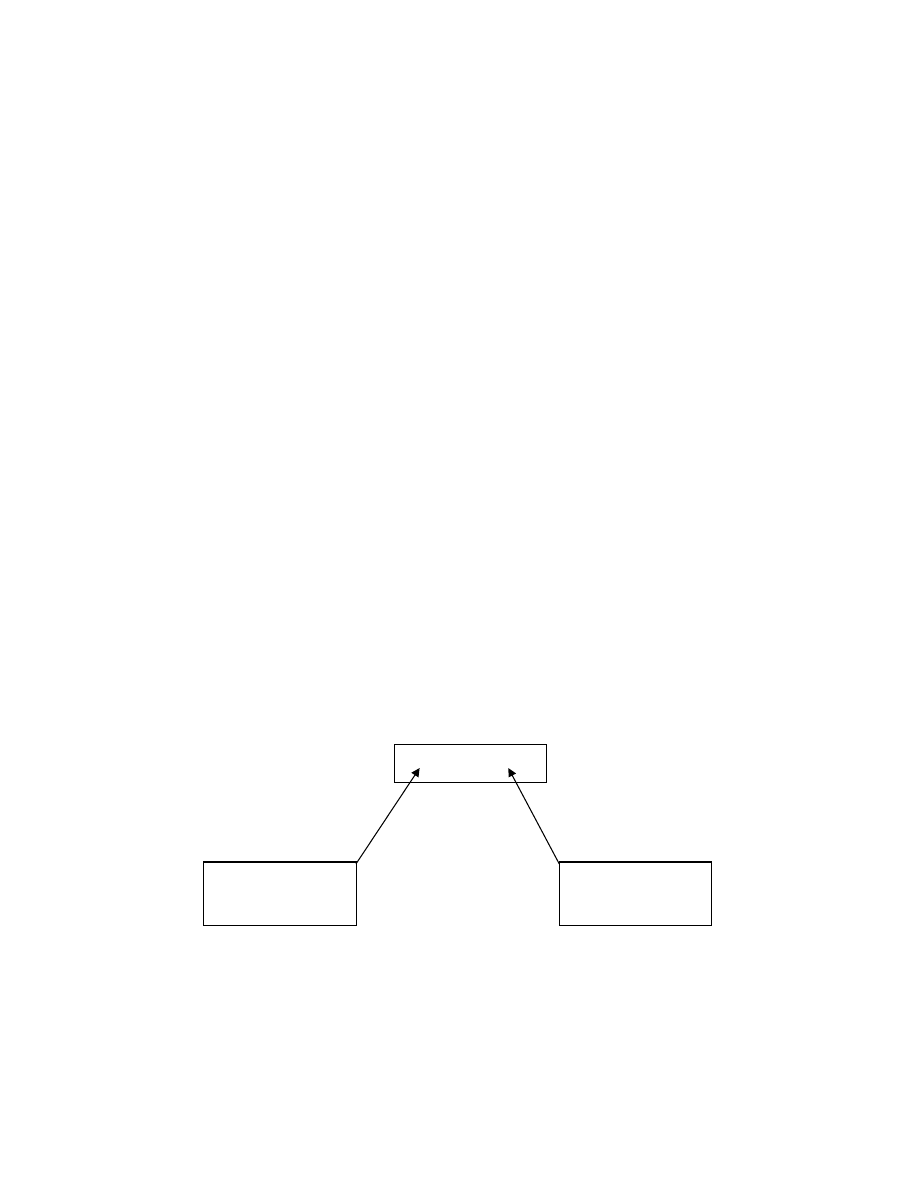
72 

-

  rangi 

-

  globalne kryteria 

 
 
Klasa: 

Kryterium 

 
Obowi zki: 

1.

  Umo liwienie  zmiany  ilo ci,  nazw,  funkcji  przynale no ci,  macierzy 

parzystych porówna , wyliczenie rang i globalnych kryteriów. 

 
Współpracownicy: hierarchia 
 
Widoczne własno ci: 

-

  nazwy, 

-

  punkty kluczowe funkcji przynale no ci 

-

  typ funkcji przynale no ci 

 
 
 
Etap3. Usystematyzowanie klas obiektów 
 
 
 
 
 
 
 
 
 
Hierarchia składa si  z kryteriów, 
klasa kryterium mo e by  klas  składow  klasy hierarchia 

       Kryterium 

     Kryterium 
ni szego poziomu 

     Kryterium 
wy szego poziomu 

 

 

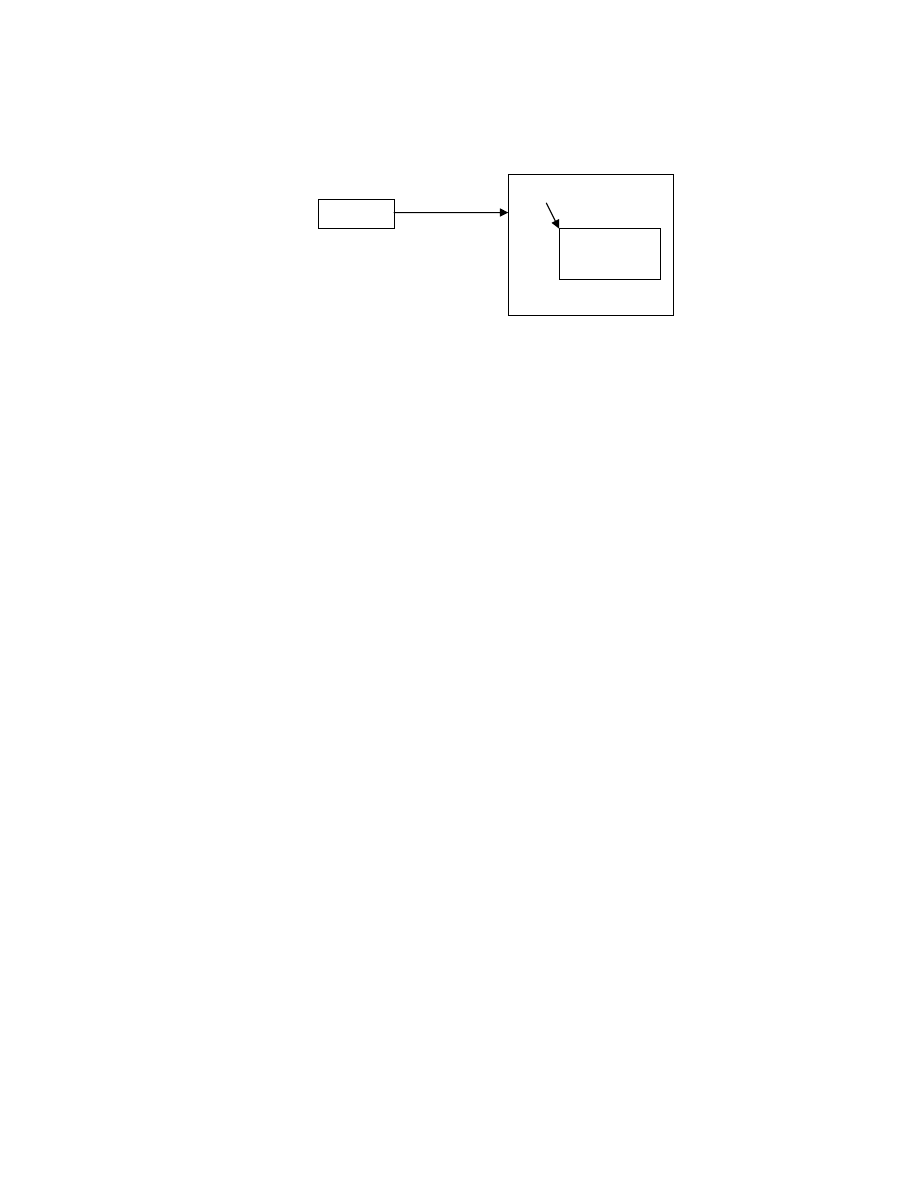
73 

 
Etap4.Okre lenie wzajemnych zale no ci klas 
 
Graf współpracy 
 
 
 
Spis relacji 
 
Menu: 

-

 Zleca hierarchii narysowanie si  na ekranie 

-

 Zleca hierarchii zapisanie jej struktury i parametrów na dysku 

-

 Zleca hierarchii odczytania z dysku jej struktury i parametrów 

-

 Zleca  hierarchii  wstawienie  konkretnego  kryterium  w  wybrane  miejsce  

w strukturze 

-

 Zleca hierarchii usuni cie konkretnego kryterium z jej struktury 

-

 Zleca hierarchii usuni cie wszystkich kryteriów 

 

Hierarchia: 

-

 Dowiaduje si  o zapisanej na dysku strukturze 

-

 Zleca kryterium by odczytał z dysku warto  swoich parametrów 

-

 Zleca  kryterium  podrz dnym  by  zapisała  na  dysku  warto   swoich 

parametrów 

-

 Wybranemu  kryterium  zleca  rysowanie  na  ekranie  funkcji  przynale no ci  i 

je eli  ma  kryterium  ni szego  poziomu  to  wy wietla  macierz  parzystych 
porówna  

-

 Zleca kryterium by powiedział, kim jest, zidentyfikował si  

Hierarchia 

Menu 

Kryterium 

 

 

74 

6.

 Podsumowanie i kierunki rozwoju 

 
 

Niew tpliwie  podejmowanie  decyzji  jest  dziedzin   bardzo  szerok   

i rozwijaj c   si  w obecnych  czasach,  która jednocze nie korzysta  z rozwi za  
pojawiaj cych  si   w  innych  gał ziach  nauki.  Chocia   jest  wokół  nich  du o 
kontrowersji, zwi zanych z podstawowymi zasadami i poj ciami to jak pokazano 
za pomoc  praktycznych przykładów nie ma  adnej w tpliwo ci nad ich u yciem 
w tak sformułowanych zadaniach podejmowania decyzji, a proponowana metoda 
gwarantuje wła nie du y zakres mo liwo ci w formalizowaniu i rozwi zywaniu 
zada .  
 

Lista problemów jednak nie ko czy si  tylko na tych, których rozwi zanie 

dokonano  w  niniejszej  pracy.  Kolejne  problemy  to  mi dzy  innymi 
rozwi zywanie  zada   z  rozmyt   tablic   parzystych  porówna   nie  za  pomoc  
u redniania, ale przy u yciu zbiorów rozmytych typu II. Podobne zastosowanie 
tych  zbiorów  b dzie  uzasadnione  w  momencie  wprowadzenia  danych 
wej ciowych o alternatywach przez grup  ekspertów, którzy jak wiadomo rzadko 
si  ze sob  zgadzaj . Inny problem pojawia si  tak e przy zastosowaniu zbiorów 
rozmytych  drugiego  stopnia  w  trakcie  formalizowania  kryteriów  lokalnych. 
Cz

  z  tych  problemów  zostało  ju   teoretycznie  rozwi zane  a  praktyczne 

rozwi zania w programie s  na zaawansowanym etapie implementacji. 
 
 

 

 

75 

 

7.

 Literatura 

 
 

1.

 

    . . 

 

 

     !"

 

# $ %

&

 

#

&

  //'#. 

-   / ()) 

&

 

% $

*

.   . 1980.  +6.   . 14 - 33

.           

2.

 

, %-

  .. .  ) % $

 

# , *

:  /$

, 

# , &

, 

$ % 0 1

. –  .: (   , 1980. – 208 

  

3.

  $% #  2.3., 

#

  .. .,  4#

*

  2. .  3%

#

 

5

#

  #  

 

%- &

   %

*

. –  .: (   , 1976. – 

279  . 

4.

  6 # 7

  '. . 

# &

 

/,

  #   # /# !

  # ,  #&   

% 0

  % 

1

 

&

  %

# &

 

# %

: 

# 8

.  $ . 

… 

$

. 

.    . –  . – 1969. – 20  . 

5.

  6 ,   3.4. 

 

$&

 

% $

1

  # 9 : 0  

# 

. –  .: 

7

#

, 1974. – 231  . 

6.

  (

 ;. .,  #/  <.=. >

/, 1

  # ,

 

% 0

 

%%

 

$

  %

#

1

 5

#

. –  .: 

7

#

, 1980. – 

304  .

 

  

7.

 

%

  ?.@., 

*

  ..A.  B 7

1

: 

# 1

, 

8 # , 1

, 

$ % #

. –  .: B $     1/-, 1981. – 328  . 

8.

  Dubois  D.,  Prade  H.  Fuzzy  sets  and  systems.  Theory  and  applications.  – 

New York: Asad. Press, 1980. XVIII. – 344 p. 

9.

  Tanaka  Hideo,  Asai  Kiyaii.  Fuzzy  linear  programming  based  on  fuzzy 

functions //Bull. Univ. Osaka Prefect. – 1980. – Vol. 29. – + 2. – P. 113 – 
125. 

10.

 ( 0 *,  6. 3#

 

#

 

    # !%

   # %

1

. –  .: 

#

, 1981. – 180  . 

  

 

 

76 

11.

 = #

  .(. 

% /

 # 7

*

   

# 1

 

 

9

 // 

$&

 

 

&

  # 1 1 # 7

*

. 

$&

   

$ %

 

% /

  # 7

*

.  – 

B 0

, 1981. -  . 5 – 10. 

12.

 Negoita  C.  The  carrent  interest  in  fuzzy  optimization  //Fuzzy  Sets  and 

Systems. – 1981. -  Vol. 6. -  + 3. - P. 261 – 269. 

13.

 Hannan E. Linear programming with multiple fuzzy goals //Fuzzy Sets and 

Systems. – 1981. -  Vol. 6. - + 3. - P. 235 – 489. 

14.

 

 = #

  .(.,  3

  . .  >$   %   /$  

0 #

# %- *

 

/,

  #   % 0

  /$

  # #   //

$&

   

$ %

   # %

1

   

# %1

. – B 0, 1979. -  . 56 – 61. 

15.

 =% 7   

.;.,  C

#

  D.).  3# 1   # 7

*

 

 

 

% 0

0

  # $

%

1

 

  ,

&

  $

&

    # #  

//)/.  ( 

B

.  '

1

  ! #

. –  1981.  -  + 5. –  . 212  – 

217. 

16.

 = #

  .(.,  6 #

  4. . 

0

*

  $ $   

#

E

 

$ % *

  # 1 1  # 7

*

      %

1

 

# $ %

  //

$&

 

# 1 1

 # 7

*

     %

1

 

# $ %

. – B 0, 1980. -  + 7. - 

. 4 – 11. 

17.

 Tong R., Bonissone P. A linguistic approach to decision-making with fuzzy 

sets //IEEE Trans. Syst. Mang. and Cybern. – 1980. – Vol. 10. – + 11. – P. 
716 – 723. 

18.

 

 </

 

. .  A $  

# *

 

/,

 

 

 

588 ,

 

9

 

#

#

  //

 

$&

 

/,

     # %

1

    % 9 &  

. – 6 %

, 1981. -  . 

38 – 51. 

19.

 Ramesh J. A procedure for multiple-aspect decision making using fuzzy sets 

//Int. J. Syst. Sci. – 1977. – Vol. 8. – + 1. – P. 1 – 7. 

20.

 Yager R. Fuzzy decision making including unequal objectives //Fuzzy Sets 

and Systems. 1978. - Vol. 1. - + 2. - P. 87 – 95. 

21.

 Yager R. Multiple objective decision-making using fuzzy sets //Int. J. Man-

Mach. Sfud. – 1979. - Vol. 9. – + 4. – P. 375 – 382.

  

 

 

77 

22.

 = #

 

.(.,  6#  ! #0  >. . 

% /

  # 7

*

 

#

 

&! #

 

% 0

  !"

  //

$&

  # 1 1  # 7

*

      %

1

 

# $ %

. – B 0, 1980. + 7. -  . 126 – 134.  

23.

 Hagg C. Possibility and cost in decision analysis // Fuzzy Sets and Syst. – 

1978. – Vol. 1. – + 2. – P. 81 – 86.

 

24.

 Yager R. Fuzzy Sets, probabilistics and decision //J. Cybern. – 1980. - V. 

10. -  + 1 - 3. - P.1 - 18. 

25.

 Zadeh L.A. Fuzzy  Sets //Information and  Control.- 1965. V.  8. - P. 338  - 

353. 

26.

 Bellman R., Zadeh L Decision-making in fuzzy environment //Management 

Science. - 1970. - V. 17. - P. 141 - 164.   

27.

 Zadeh L.A. Fuzzy algorithms //Inf.Contr. - 1968. - V. 12. - P. 94 - 102

.  

28.

 >#%

*

  . . 3# !% &  # 1 1 # 7

*

  #  

*

 

$ *

 

8 # ,

. –  .: (   , 1981. – 208  . 

29.

 Saaty  T.  Scaling  Method  for  Priorities  in  Hierarchical  Structures  //J.  of 

Mathematical Psychology. – 1977. – Vol. 15. – + 3. – P. 234 – 281.  

30.

 Chu  A.,  Kalaba  R.,  Springarn  R.  A  Comparison  pf  Two  Methods  for 

Determining  the  weights  of  Belonging  to  Fuzzy  Sets  //J.  of  Optimization 
theory and applications. – 1979. – Vol. 27. – + 4. – P. 531 – 538.  

31.

 Yager R. Fuzzy subsets of type II in decisions //J. Cybern. - 1980 - V. 10. -   

+

 1 - 3. - P. 137 - 159.  

32.

 3 $

*

 

. .,  ( 0   .D.  3 #   - 

%- &

  # 7

1

 

0 #

# %- &

 /$ . –  .: (   , 1982. – 256  .  

33.

 

  (.(. 

  /$

 

0

 

% /

.  – 

.: 

(  

, 1981. – 488  . 

34.

 

-1

  3. .,  ' 

 (. . 

0 #

# %- 1

  $

8

, 1

 

 

/, 1

 

% 0

  # ,

. – 

: (      

, 

1990. – 224  .  

35.

  %   ?.@., 

*

  ..A.  B 7

1

: 

# 1

, 

8 # , 1

, 

$ % #

. –  .: B $     1/-, 1981. – 328  . 

 

 

78 

36.

 Zimmermann  H.J.  Fuzzy  Sets,  Decision-Making  and  Expert  Systems.  – 

Dordrecht: Kluver Academic Publ., 1987. – 352 p.  

37.

 Yager R. Multiple objective decision-making using fuzzy sets //Int. J. Man-

Mach. Sfud. – 1979. - Vol. 9. – + 4. – P. 375 – 382.  

38.

 Chu  A.,  Kalaba  R.,  Springarn  R.  A  Comparison  pf  Two  Methods  for 

Determining  the  weights  of  Belonging  to  Fuzzy  Sets  //J.  of  Optimization 
theory and applications. – 1979. – Vol. 27. – + 4. – P. 531 – 538.  

39.

 4 # * #  2.=. 

$

   

# E

 

% $

1

 

# , *

.  – 

.: 

(  

, 1971. – 220  .

  

40.

 Dubois  D.,  Koenig  J.L.  Social  choice  axioms  for  fuzzy  set  aggregation 

//Fuzzy Sets and Systems. – 1991. - V. 43. - P. 257 – 274. 

41.

 Roubens M. Fuzzy sets and decision analysis //Fuzzy Sets and Systems. – 

1997. - V. 90. - P. 199-206.

 

42.

 Yager  R.R.  On  ordered  weighted  averaging  aggregation  operators  in 

multicriteria  decision  making  //IEEE  Trans.  Systems  Man  and  Cybern.  – 
1988. - V. 18. - + 1.- P. 183 – 190.

  

43.

 Hauke W. Using Yager’s t-norms for aggregation of fuzzy intervals //Fuzzy 

Sets and Systems. – 1999. - V. 101. - P. 59 – 65.

  

44.

 Dyckhoff  H.  Basic  concepts  for  theory  of  evaluation:  hierarchical 

aggregation via autodistributive connectives in fuzzy set theory //European 
J. Operation Research. –1985. - V. 20. - B. 221-233.

  

45.

 Migdalas A., Pardalos P.M. Editorial: hierarchical and bilevel programming 

//J. Global Optimization. – 1996. - V. 8. - + 3. - P. 209 – 215. 

46.

 Zimmerman H.J., Zysno P.  Latent  connectives in human decision making 

//Fuzzy Sets and Systems. – 1980. - V. 4. - P. 37 - 51. 

47.

 Zimmerman  H.J.,  Zysno  P.    Decision  and  evaluations  by  hierarchical 

aggregation of information //Fuzzy Sets and Systems. – 1983. -  V.104. - P. 
243 – 260. 

48.

 Mitra  G.  Mathematical  Models  for  Decision  Support.  –Berlin:  Springer, 

1988. 

 

 

79 

49.

 Choi  D.-Y.,  Oh  K.-W.  Asa  and  its  application  to  multi-criteria  decision 

making //Fuzzy Sets and Systems. – 2000. - V. 114. - P. 89 - 102. 

50.

 Shih  H.-S.  Lee  E.S.  Compensatory  fuzzy  multiple  level  decision  making 

//Fuzzy Sets and Systems. – 2000. -  V. 114. - P. 71 – 87.

 

51.

 Ursu V. Metode de imbunatire’a calitatii lingorior /V. Ursu, P. Murariu, T. 

Popescu //Cecetari metalgice. – 1981. – Vol. – 22. – P. 32 – 41. 

52.

 Fisher  K.M.  The  effect  of  fluid  flow  on  the  solidification  of  industrial 

casting ingots //Physic-Chemical Hydrodynamics. – 1981. - Vol. 2. – + 4. –  
P. 331 – 332. 

53.

 ( 0  %   B.).  >

&

 

  0 # 0 &   # $.  –  .:  (   , 

1978. – 336  . 

54.

     . 4 $# $

 

0 8 / &

 

. –  .: 

#

, 1971.– 536  . 

55.

  L.C.Leung  ,  D.Cao  „On  consistency  and  ranking  of  alternatives  In  fuzzy 

AHP”    European Journal of Operation Research volume 124 ,issue 1, 01-
July-2000 European Journal of Operation Research vol 124. (1) pp. 102-113 

56.

  L.C.Leung  ,  D.Cao  “On  the  efficacy  of  modeling  multi-attribute  decision 

problems using AHP and Sinarchy”.  
European Journal of Operation Researchvol 132 (1)pp 39-49] 

57.

 Chen-Tung  Chen.”  A  fuzzy  approach  to  selsect  the  location  of  the 

distribution  center”  Departamnet  of  Information  Management.  Da-Yeh 
University, april 1998 

58.

 Sevastianov,  V.I.  Valkovsky,  D.P.  Sevastianov,  D.V.  Stepanov.  The 

methods  and  software  for  financial  an  economic  analysis  in  conditions  of 
fuzzy and probabilistic  uncertainty// Proc. of the Fifth International Conf. 
Computer Data  Analysis and Modeling .1998.- Minsk. Vol. 2.,  P. 93-98 

59.

 Dymova L.,Sevastjanov D., Sevastjanov P. Application of fuzzy sets theory 

methods  for  the  evaluation  of  investment  efficiency  parameters//  Fuzzy 
economic review. 2000, Vol. V, N 1, P. 34-48 . 

60.

    Zollo  G.,  Iandoli  L.,  Cannavacciuolo  A.  The  performance  requirements 

analysis with fuzzy logic// Fuzzy economic review. 1999, Vol. IV, N 1, P. 
35-69.     

 

 

80 

61.

   Shyi-Ming  Chen.,  A  new  method  for  tool  steel  materials  selection  under 

fuzzy environment / Fuzzy sets and systems, 1998. 

62.

 Mao-Jiun  J  Wanga  and  Tien-Chien  Chang.,  Tool  steel  materials  selection 

under fuzzy environment //Fuzzy sets and systems, 1995. 

63.

 Chen-Tung  Chen.  A  fuzzy  approach  to  select  the  location  of  distribution 

center //Fuzzy sets and systems, 1998. 

64.

 Paweł Róg. „The method of Intervals Ordering Based on the Probibalistic 

Approach” //Computer Science. 2001, Vol I, N 1, P. 103-108 

 
Własne publikacje63 
1.

  „Komputerowy  system  wspomagania  decyzji  przy  wyborze  projektów 

inwestycyjnych”//  Informatyka  Teoretyczna  i  stosowana  Rocznik  1  Nr  1 
2001 L.Dymowa, A.Zenkowa, P. Figat 

2.

   „Metoda i oprogramowanie do oceny wielokryterialnej i wielopoziomowej 

decyzji w warunkach niepewno ci rozmytej” (streszczenie) III Krajowa 
konferencja: Metody i systemy komputerowe w badaniach naukowych 
projektowaniu in ynierskim”Kraków 19-21 listopad 2001 

3.

  Informatyka 2- „Investment project quality comparison” 

4.

  Polskie towarzystwo informatyczne Szczyrk 2002 “System wspomagania 

decyzji na podstawie wiedzy rozmytej” L. Dymowa, P.Figat, 
P.Sevastianow, A. Zenkowa 

5.

  Zakopane 2002 „Methodology and application comparison for managing 

fuzzy subsets of different type In financial decision making” 

 
 
 
 
 

 

 

81 

 

Dodatek A - Skrócona dokumentacja programu 

 
 

      

Witamy Pa stwa w systemie wspomagania decyzji. 

 
Nasz  system  pozwala  w  szybki  i  sprawny  sposób  agregowa   kryteria  zarówno 
ilo ciowe jak i jako ciowe w jedno uogólnione kryterium globalne na podstawie, 
którego mo emy podj  decyzje. Rozwi zuje takie problemy optymalizacji, jak 
wielokryterialno  i wielopoziomowo  zada .  
 
A oto kolejno , w jakiej powinni my działa , aby poprawnie rozwi za  problem 
podj cia decyzji: 
 

1)

  Utworzenie drzewa kryterialnego 

a)

 

Podanie nazw dla ka dego kryterium i podkryterium 

b)

 

Ustalenie  typu  funkcji  przynale no ci.  Dla  ka dego  kryterium 
szczegółowego (takiego, które nie ma podgrup) ustalamy jeden z 7 
typów funkcji przynale no ci, które mo emy podejrze  naciskaj c 
na pole edycyjne prawym guzikiem myszy. 

c)

 

Wprowadzenie  punktów  kluczowych  dla  ka dej  funkcji 
przynale no ci.  W  zale no ci  od  typu  funkcji  okre lamy 
szczegółowe warto ci punktów kluczowych ka dej  funkcji. W ten 
sposób ostatecznie formalizuj c dane kryterium. 

 

2)

  Wprowadzenie danych  

  W tym oknie wprowadzamy dane dla rozpatrywanych przypadków. 
Mo emy  ustali   standardow  nazw  dla  naszych  przypadków (w  zale no ci 
do  oceny,  czego  jest  nasz  program  wykorzystywany  -  jedni  ocenia   b d  
marki  samochodów  a  drudzy  skomplikowane  projekty  inwestycyjne). 

 

 

82 

Mo emy  zapisa   utworzony  zestaw  danych  do  pliku  lub  sczyta   te  dane  z 
pliku  utworzonego  wcze niej.  Oczywi cie  liczba  przypadków,  które 
porównujemy  jest  dowolna  i  mo e  by   zmieniana  dla  w  trakcie  oblicze   w 
dowolny sposób.  

 

 

3)

  Obliczenie kryterium globalnego. 

Mo emy  obliczy   kryteria  na  dowolnym  poziomie  (przycisk 

oblicz 

kryterium)  lub  od  razu  policzy   kryterium  globalne  (przycisk  oblicz 
wszystko) 
Nast pnie  naciskaj c  na  dowolny  rz d  w  tabeli  z  wynikami  mo emy 
zobaczy , jaki przebieg miały funkcje agreguj ce poszczególnych projektów 
(porównywanych  przypadków).  Naciskaj c  przycisk 

Wyniki  ko cowe 

(dokonujemy  automatycznych  oblicze   na  całym  drzewie  kryterialnym) 
mo emy zorientowa  si , który z rozpatrywanych przypadków jest najlepszy 
pod  wzgl dem  1  z  trzech  sposobów  agregowania  (  maksymalnego 
pesymizmu, multiplikatywnego, addytywnego)  

 

 

83 

Dodatek B - Najwa niejsze funkcje programu 

Poniewa   zamieszczenie  całego  kodu  byłoby  niemo liwo ci   gdy   w  tym 

momencie  w  podstawowej  wersji  zajmuje  on  około  4000  linii  kodu, 

zamieszczam  wiec  poni ej  zestaw  kluczowych  funkcji,  na  których  opiera  si  

cz

 wylicze . 

 

 

1. Funkcja wyliczaj ca rangi – współczynniki wzgl dnej wa no ci 

 

double* TCriterion::frang() 
{ 
TCriterion* foc=this; 
int i,j,ii; 

int liczba=foc->get_sgc();//liczba kryteriow podrzednych 

int c=liczba; 

double y=2; 

double **b; 
b=new 

double*[liczba+1]; 

for (int i = 0; i < liczba+1; i++) /// b 
  b[i] = new 

double[liczba+1]; 

double *m; 
m=new 

double[liczba+1];             //m 

  

double *rang; 
rang=new 

double[liczba]; 

double *r;                            //r i rangi 
r=new 

double[liczba+1]; 

for(i=0; i<liczba; i++) 
  { 
  m[i]=0; 
    

for(j=0; j<liczba; j++) 

       b[i][j]=-foc->getElem(i,j)-foc->getElem(j,i); 
    b[i][i]=c-1; 
    

for(j=0; j<liczba; j++) 

      

if(i!=j) 

       b[i][i]+=pow(foc->getElem(i,j),y);//element do kwadratu 
   }                                      

for(i=0; i<liczba; i++) 
  { 
   b[liczba][i]=1; 
   b[i][liczba]=1; 
  } 
 m[liczba]=1; 
 b[liczba][liczba]=0; 

for(i=0; i<liczba; i++)  
{ 
 

for(j=i+1; j<liczba+1; j++) 

 { 
  y=b[j][i]/b[i][i]; 
  m[j]-=y*m[i]; 
    

for(ii=i+1; ii<liczba+1; ii++) 

     b[j][ii]-=y*b[i][ii]; 
 } 
} 
for(i=liczba; i>-1; i--)     
{ 

 

 

84 

 y=0; 
 

for(j=i+1; j<liczba+1; j++) 

    y+=b[i][j]*r[j]; 
    r[i]=(m[i]-y)/b[i][i]; 
} 

for(i=0; i<liczba; i++) 
  rang[i]=r[i]*liczba;   
 

for (int i = 0; i < liczba;  i++) 

   

delete[] b[i]; 

 

delete[] b; 

 

delete []r; //zwalnianie pamieci 

 

delete[]m; 

 
 

return rang; 

} 

 

 

 

2. 

Wylicza  warto

  funkcji  przynale no ci  dla  zadanego  parametru 

wej ciowego

  

 

////////////////////////////////////////////////////////////////////// 

double TCriterion::fmu(double y)  
 { 
 

double* x; 

 

int ilosc= getNumberOfPoints() ; 

 x=new 

double[ilosc] ; 

 

for(int i=0;i<ilosc;i++) 

 x[i]= get_pk(i); 
 

double b; 

 

if( get_tof()==1) 

   { 
     

if((y>=x[0])&&(y<=x[1])) 

        b=(x[1]-y)/(x[1]-x[0]); 
     

if(y<x[0]) 

         b=0; 
     

if(y>x[1]) 

         b=0; 
   } 
 

if( get_tof()==2) 

   { 
 
     

if((y>=x[0])&&(y<x[1])) 

     b=1; 
          

if(y<x[0]) b=0; 

 

        

if((y>=x[1])&&(y<=x[2])) b=(x[2]-y)/(x[2]-x[1]); 

 

        

if(y>x[2]) b=0; 

   } 
   

if( get_tof()==3) 

   { 
           

if(y<x[0]) b=0; 

          

if((y>=x[0])&&(y<x[1])) b=(y-x[0])/(x[1]-x[0]); 

 

        

if((y>=x[1])&&(y<=x[2])) b=1; 

 

        

if((y>x[2])&&(y<=x[3])) b=(x[3]-y)/(x[3]-x[2]); 

 

        

if(y>x[3]) b=0; 

   } 
   

if( get_tof()==4) 

   { 
            

if(y<x[0]) b=0; 

 

        

if(y>x[2]) b=0; 

 

        

if((y>=x[0])&&(y<=x[1])) b=(y-x[0])/(x[1]-x[0]); 

 

 

85 

 

        

if((y>x[1])&&(y<=x[2])) b=(x[2]-y)/(x[2]-x[1]); 

   } 
   

if( get_tof()==5) 

   { 
     

if(y<x[0]) 

      b=0; 
       

if((y>=x[0])&&(y<x[1])) 

        b=(y-x[0])/(x[1]-x[0]); 
 

  

if((y>=x[1])&&(y<=x[2])) 

           b=1; 
 

      

if(y>x[2]) 

              b=0; 
   } 
   

if( get_tof()==6) 

   { 
     

if(y<x[0]) 

      b=0; 
       

if((y>=x[0])&&(y<=x[1])) 

        b=(y-x[0])/(x[1]-x[0]); 
          

if(y>x[1]) 

          b=0; 
   } 
   

if( get_tof()==7) 

   { 
      

if(y<x[0]) b=0; 

       

if((y>=x[0])&&(y<=x[1])) b=1; 

        

if(y>x[1]) b=0; 

   } 
  

delete []x; 

 

return(b); 

} 

////////////////////////////////////////////////////////////////////// 

 

 

3. 

Wyliczenie  kryterium  D1,D2  lub  D3

-  parametr  wej ciowe  to  

które  -  które  kryterium  i  proj  -  okre laj cy  numer  szacowanej 
alternatywy. Jako wynik zwracana jest nam warto

 kryterium  

 
 

double TCriterion::Dglob(int ktore,int proj)     //kryterium globalne 
{ 
  

double  d=0 ; 

  

if(this->get_done()==true) 

    { 
     

if(ktore==1) 

//maksymalnego pesymizmu

 

       { 
        d=2; 
        

for(int j=0; j<sgc; j++) 

          { 
           

if(this->get_k(j).get_sgc()==0) 

             { 
              

if(d>=pow(this->getMu(j,proj),this->getRang(j))) 

                d=pow(this->getMu(j,proj),this->getRang(j)); 
             } 
           

else 

             { 
             this->setMu(j,proj,this->get_k(j).Dglob(1,proj)); 
             

if(d>=pow(this->get_k(j).Dglob(1,proj),this->getRang(j))) 

                d=pow(this->get_k(j).Dglob(1,proj),this->getRang(j)); 
             } 
          } 

 

 

86 

         

return d; 

      } 
  

if(ktore==2) 

// mltiplikatywne

 

    { 
     

double d=1; 

     

for(int j=0; j<sgc; j++) 

       

if(this->get_k(j).get_sgc()==0) 

         d*=pow(this->getMu(j,proj),this->getRang(j)) ; 
       

else 

         { 
          this->setMu(j,proj,this->get_k(j).Dglob(2,proj)); 
          d*=pow(this->get_k(j).Dglob(2,proj),this->getRang(j)) ; 
         } 
       

return d; 

    } 
  

if(ktore==3) 

//addytywne

 

    { 
     

double d=0; 

     

for(int j=0; j<sgc; j++) 

       

if(this->get_k(j).get_sgc()==0) 

         d+=this->getMu(j,proj)*this->getRang(j); 
       

else 

         { 
          this->setMu(j,proj,this->get_k(j).Dglob(3,proj)); 
          d+=this->get_k(j).Dglob(3,proj)*this->getRang(j); 
         } 
         

return d/=(double)sgc; 

    } 
  } 
 

return d; 

}