Gliwice 2003

Zadanie brzegowe

Rozdział 1

Zadanie brzegowe

1.1

Równanie Poissona i Laplace’a

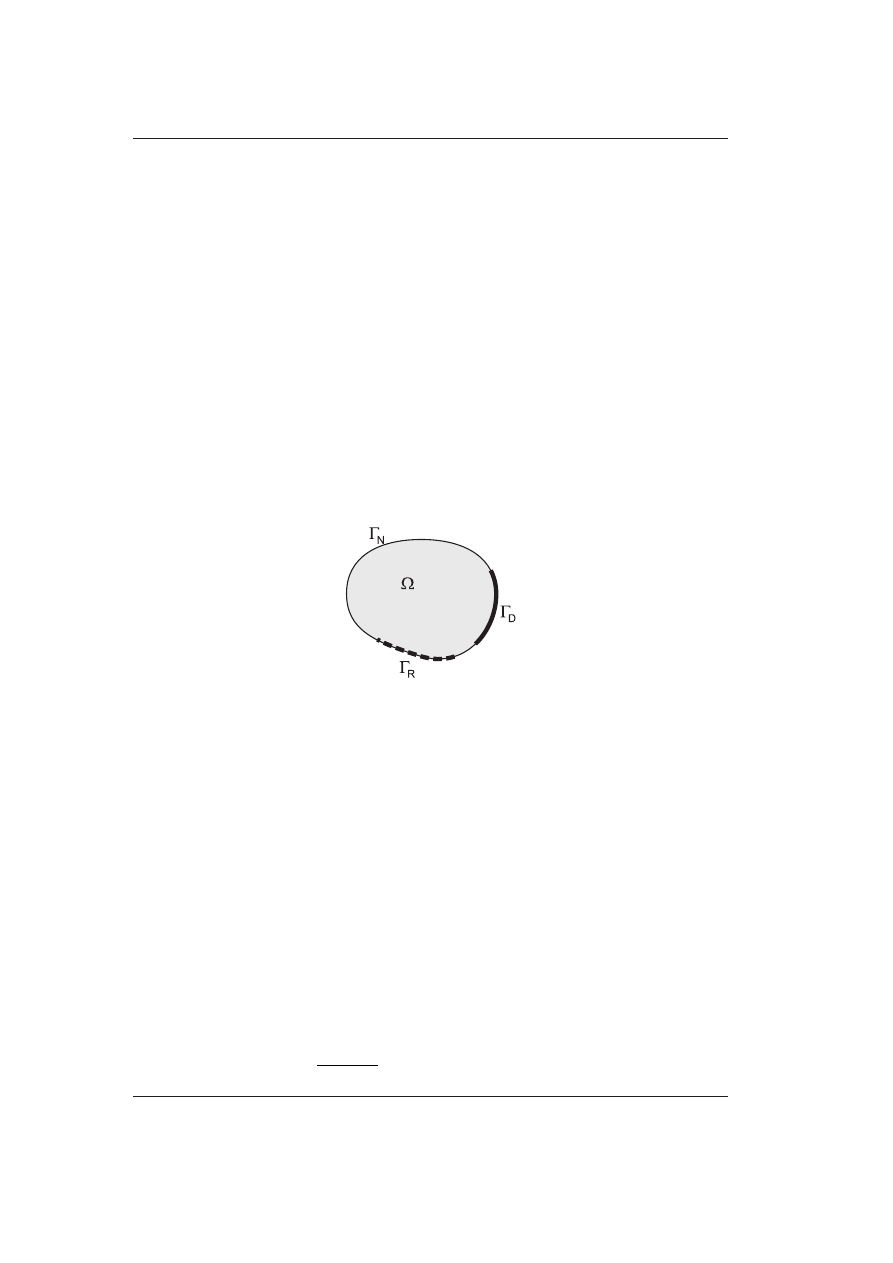
Rysunek 1.1: Rozważane ciało

Rozważmy ciało Ω o brzegu Γ = ∂Ω. Rozkład potencjału u w ciele okre-

ślony jest równaniem Poissona:

k∇

2

u = −f

(1.1)

gdzie f jest funkcją źródła, k współczynnikiem. W przypadku gdy rozpatru-
jemy ciało dwuwymiarowe (2D), wartość potencjału w ciele możemy zapisać
jako u(x, y). Równanie 1.1 uzupełniamy warunkami brzegowymi. Warunek
pierwszego rodzaju (Dirichleta, istotny):

u(x, y) = ˆ

u(x, y); (x, y) ∈ Γ

D

(1.2)

gdzie ˆ

u(x, y) jest pewną znaną wartością. Warunek drugiego rodzaju (Neu-

manna, naturalny):

∂u(x, y)

∂n

= ˆ

q(x, y); (x, y) ∈ Γ

N

(1.3)

1

1.1 Równanie Poissona i Laplace’a

Rysunek 1.2: Wektor normalny i styczny do brzegu

gdzie n jest wektorem normalnym do brzegu (rys. 1.1), a ˆ

q(x, y) jest znaną

wartością pochodnej potencjału w kierunku normalnym do brzegu. Warunek
trzeciego rodzaju (Robina):

∂u(x, y)

∂n

= −h (u (x, y) − u

∞

(x, y)) ; (x, y) ∈ Γ

R

(1.4)

gdzie h jest współczynnikiem wnikania, u

∞

jest stałą wartością potencjału.

W przypadku gdy funkcja f w równaniu 1.1 jest równa zeru, otrzymujemy

równanie Laplacea:

k∇

2

u = 0

(1.5)

Za pomocą równań Poissona oraz Laplacea można modelować wiele zja-

wisk fizycznych m.in. zagadnienia przepływu ciepła, skręcanie pręta o stałym
przekroju, zjawiska elektrostatyczne, magnetostatyczne, laminarny przepływ
cieczy.

W przypadku rozważania przepływu ciepła, potencjał u odpowiada tem-

peraturze T , pochodna potencjału - strumieniowi ciepła q, współczynnik k -
przewodności cieplnej λ, a funkcja f - funkcji źródła ciepła Q.

2

1.2 Równanie przepływu ciepła dla ciał jednowymiarowych

1.2

Równanie przepływu ciepła dla ciał jedno-
wymiarowych

a)

, b)

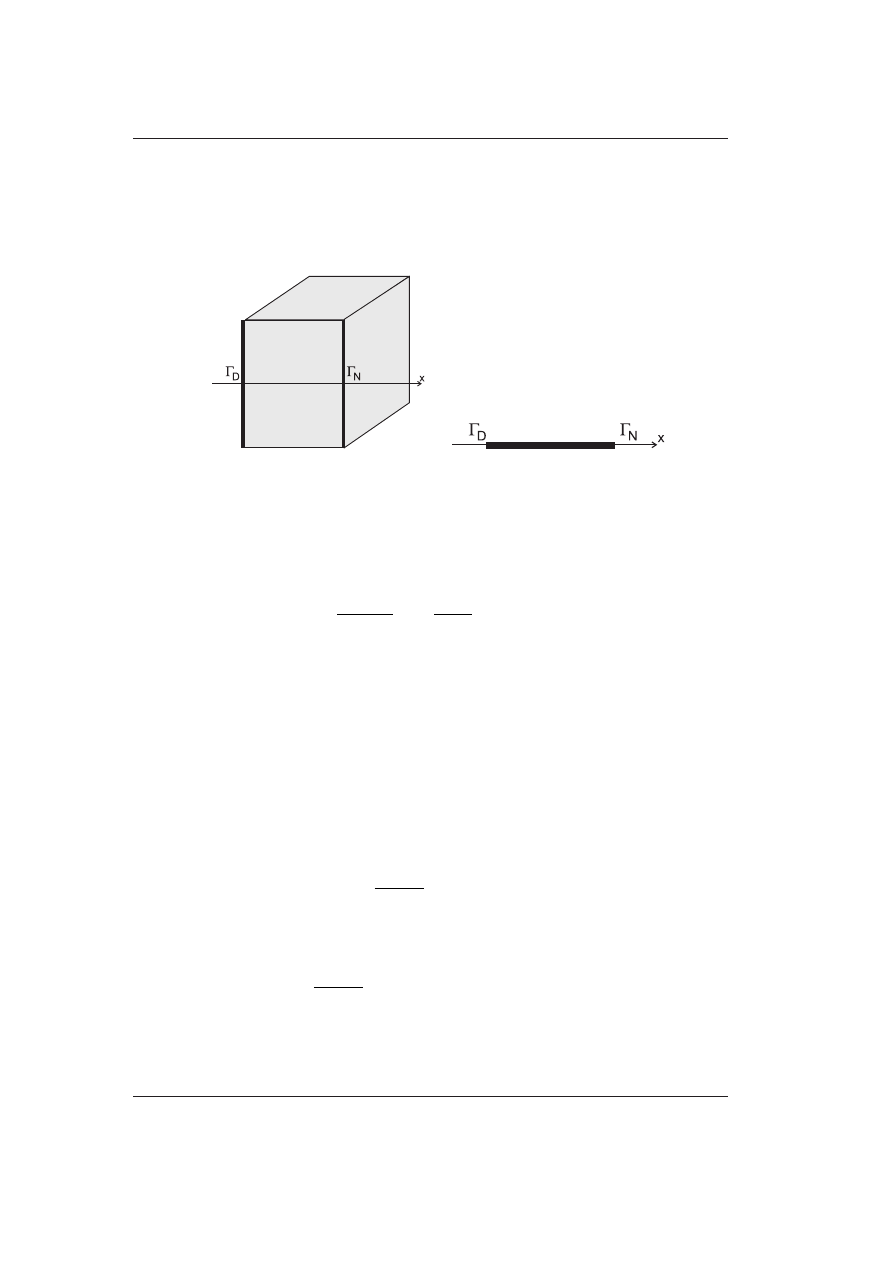
Rysunek 1.3: Jednowymiarowy przepływ ciepła: a) ciało 3D, b) model 1D

Dla ciała jednowymiarowego równanie przepływu ciepła jest określone rów-

naniem Poissona postaci:

d

2

T (x)

d x

2

= −

Q(x)

λ

; x ∈ Ω

(1.6)

gdzie T (x) jest wartością temperatury w punkcie o współrzędnej x, Q(x)

jest wartością źródła ciepła w punkcie x, a λ jest przewodnością cieplną ma-
teriału, z którego wykonano ciało.

Powyższe równanie musi być uzupełnione warunkami brzegowymi. Warun-

kiem brzegowym pierwszego rodzaju (Dirichleta) jest warunek postaci:

T (x) = ˆ

T (x); x ∈ Γ

D

(1.7)

gdzie ˆ

T (x) jest pewną znaną wartością, Γ = ∂Ω jest brzegiem ciała. Warunek

drugiego rodzaju (Neumanna) jest postaci:

q(x) =

d T (x)

d x

= ˆ

q(x); x ∈ Γ

N

(1.8)

gdzie ˆ

q(x) jest znanym strumieniem ciepła. Warunek trzeciego rodzaju (Ro-

bina):

q(x) =

d T (x)

d x

= −h (T (x) − T

∞

(x)) ; x ∈ Γ

R

(1.9)

gdzie h jest współczynnikiem wnikania, T

∞

jest stałą wartością temperatury.

Warunek ten wiąże ze sobą wartość strumienia ciepła na brzegu oraz wartość
temperatury. Warunek taki spotykamy gdy ciało styka się z innym medium,

3

1.2 Równanie przepływu ciepła dla ciał jednowymiarowych

np. jest chłodzone cieczą o temperaturze T

∞

. Współczynnik wnikania h de-

terminuje jak "mocno"wpływa temperatura medium na temperaturę w rozpa-
trywanym ciele.

Równanie przepływu ciepła możemy zapisać jako:

L(u) = f

(1.10)

gdzie u jest funkcją temperatur T , f funkcją źródła ciepła Q, a L jest opera-
torem różniczkowym postaci:

L =

d

2

d x

2

(1.11)

4

Metody odchyłek ważonych w rozwiązywaniu różniczkowych równań cząstkowych

Rozdział 2

Metody odchyłek ważonych w
rozwiązywaniu różniczkowych
równań cząstkowych

2.1

Wstęp

Rozważmy równanie różniczkowe postaci:

L(u) = f ; u ∈ Ω

(2.1)

gdzie: L – operator różniczkowy, f – funkcja o znanym rozkładzie, u –

funkcja o poszukiwanym rozkładzie

Równanie 2.1 uzupełnione jest warunkami brzegowymi

u = ˆ

u; u ∈ Γ

(2.2)

∂u
∂n

= ˆ

q; u ∈ Γ

(2.3)

gdzie ˆ

u oraz ˆ

q są funkcjami o znanych wartościach, n jest wektorem normalnym

do brzegu.

Równanie 2.1 możemy zapisać w postaci:

L(u) − f = 0

(2.4)

Jeżeli rozkład funkcji u będzie aproksymowany rozkładem przybliżonym ˜

u

spełniającym warunki brzegowe:

˜

u =

n

X

j=1

c

j

φ

j

(2.5)

5

2.1 Wstęp

gdzie φ

j

są funkcjami aproksymującymi, a c

j

parametrami tych funkcji

to równanie 2.4 przyjmuje postać:

L(˜

u) − f 6= 0

(2.6)

Równanie to nie można przyrównać do zera ze względu na obecność rozwią-

zanie przybliżone, które nie musi spełniać równania różniczkowego 2.1. W celu
określenia odchyłki spowodowanej zastosowaniem rozwiązania przybliżonego,
wprowadza się oznaczenie tej odchyłki nazwanej również residuum, resztą, błę-
dem, R.

R = L(˜

u) − f

(2.7)

Na podstawie równania 2.6 można zapisać:

R 6= 0

(2.8)

W celu dobrania optymalnego rozwiązania równania różniczkowego, przyj-

mujemy funkcje wagowe w

i

takie aby odchyłka zaniknęła w sposób całkowy na

obszarze poszukiwanego rozwiązania:

Z

Ω

Rw

i

dΩ = 0; i = 1..n

(2.9)

Wagi w

i

są funkcjami liniowo niezależnymi.

Po uwzględnieniu równania 2.7 otrzymujemy:

Z

Ω

[L(˜

u) − f ]w

i

dΩ = 0; i = 1..n

(2.10)

Metody, które pozwalają określić wartości funkcji u stosując powyższe rów-

nanie nazywamy metodami odchyłki ważonej. W zależności od postaci funkcji
aproksymujących φ

i

oraz funkcji wag w

i

, mamy doczynienie z jedną z odmian

metody odchyłki ważnej:

•

Galerkina-Petrova - w przypadku gdy funkcje aproksymujące różnią się
od funkcji wagowych φ

i

6= w

i

,

•

Bubnova-Galerkina - gdy funkcje aproksymujące i wagowe mają taką
samą postać φ

i

= w

i

,

•

najmniejszych kwadratów - gdy funkcje wag są postaci w

i

=

∂R

c

i

,

•

kollokacji - gdy funkcja wag jest postaci w

i

(x) = δ(x − x

i

), gdzie x

i

jest

punktem kollokacji,

6

2.2 Metoda Galerkina-Petrova

•

podobszarów - gdy obszar Ω dzielimy na kilka podobszarów Ω

i

i funkcje

wag okreslone są jako w

i

(x) =

½

1

gdyx ∈ Ω

i

0 wprzeciwnymprzypadku

.

2.2

Metoda Galerkina-Petrova

W metodzie Galerkina-Petrova funkcje aproksymujące różnią się od funkcji

wagowych φ

i

6= w

i

.

Przykład.
Rozważmy jednowymiarowy przepływ ciepła w ciele o długości 1 opisany

równaniem:

d

2

T (x)

d x

2

= −

q(x)

λ

; x ∈ Ω

(2.11)

z warunkami brzegowymi

T (0) = 0

(2.12)

T (1) = 0

(2.13)

funkcja źródła ma postać

q(x) = 2

(2.14)

a przewodność cieplna λ = 1.

Funkcję aproksymującą przyjmiemy:

T (x) = c

1

x(1 − x) + c

2

x

2

(1 − x)

(2.15)

czyli

φ

1

= x(1 − x); φ

2

= x

2

(1 − x)

(2.16)

Funkcje aproksymujące spełniają warunki brzegowe zadania. Funkcje wag
przyjmujemy postaci:

w

1

= 1; w

2

= x

(2.17)

Odchyłka rozwiązania przybliżonego wyrażona jest wzorem:

R =

d

2

T (x)

d x

2

+

q(x)

λ

(2.18)

czyli

R =

∂

2

T (x)

∂x

2

+ 2 = 2(c

2

− c

1

) − 6c

2

x + 2

(2.19)

7

2.3 Metoda Bubnova-Galerkina

Stosując metodę odchyłek ważonych otrzymujemy układ równań

1

Z

0

[2(c

2

− c

1

) − 6c

2

x + 2] d x = 0

1

Z

0

[2(c

2

− c

1

) − 6c

2

x + 2]x d x = 0

(2.20)

Rozwiązanie powyższego układu równań prowadzi do

c

1

= 1

c

2

= 0

(2.21)

czyli otrzymujemy rozwiązanie zadania postaci:

T (x) = x(1 − x)

(2.22)

2.3

Metoda Bubnova-Galerkina

W metodzie Bubnova-Galerkina przyjmuje się funkcje wag w

i

takie same

jak funkcje aproksymujące φ

i

. Ważne jest aby funkcje aproksymujące φ

i

speł-

niały warunki brzegowe zadania.

Przykład.
Rozważmy jednowymiarowy przepływ ciepła w ciele o długości 1 opisany

równaniem:

d

2

T (x)

d x

2

= −

q(x)

λ

; x ∈ Ω

(2.23)

z warunkami brzegowymi

T (0) = 0

(2.24)

T (1) = 0

(2.25)

funkcja źródła ma postać

q(x) = 2

(2.26)

a przewodność cieplna λ = 1.

Funkcję aproksymującą przyjmiemy:

T (x) = c

1

x(1 − x) + c

2

x

2

(1 − x)

(2.27)

czyli

φ

1

= x(1 − x); φ

2

= x

2

(1 − x)

(2.28)

8

2.4 Metoda najmniejszych kwadratów

Funkcje aproksymujące spełniają warunki brzegowe zadania. Funkcje wag
przyjmujemy takiej samej postaci jak funkcje aproksymujące

w

1

= x(1 − x); w

2

= x

2

(1 − x)

(2.29)

Odchyłka rozwiązania przybliżonego wyrażona jest wzorem:

R =

d

2

T (x)

d x

2

+

q(x)

λ

(2.30)

czyli

R =

d

2

T (x)

d x

2

+ 2 = 2(c

2

− c

1

) − 6c

2

x + 2

(2.31)

Stosując metodę odchyłek ważonych otrzymujemy układ równań

1

Z

0

[2(c

2

− c

1

) − 6c

2

x + 2]x(1 − x) d x = 0

1

Z

0

[2(c

2

− c

1

) − 6c

2

x + 2]x

2

(1 − x) d x = 0

(2.32)

Rozwiązanie powyższego układu równań prowadzi do

c

1

= 1

c

2

= 0

(2.33)

czyli otrzymujemy rozwiązanie zadania postaci:

T (x) = x(1 − x)

(2.34)

2.4

Metoda najmniejszych kwadratów

W metodzie najmniejszych kwadratów przyjmuje się funkcje wag w

i

po-

staci:

w

i

=

∂R

c

i

(2.35)

W przypadku gdy rozpatrujemy równanie liniowe z operatorem różniczkowym
dodatnio określonym, rozwiązanie otrzymane metodą najmniejszych kwadra-
tów jest takie samo jak w metodzie Bubnova-Galerkina.

Przykład

9

2.5 Metoda kollokacji

Rozpatrując zadanie przykładowe takie jak w metodzie Bobnova-Galerkina,

dla równania reszt (przykład dla metody Bubnova-Galerkina):

R = 2(c

2

− c

1

) − 6c

2

x + 2

(2.36)

otrzymujemy wagi postaci

w

1

= −2; w

2

= 2 − 6x

(2.37)

Stosując metodę odchyłek ważonych otrzymujemy układ równań

1

Z

0

[2(c

2

− c

1

) − 6c

2

x + 2](−2) d x = 0

1

Z

0

[2(c

2

− c

1

) − 6c

2

x + 2](2 − 6x) d x = 0

(2.38)

Rozwiązanie powyższego układu równań prowadzi do

c

1

= 1

c

2

= 0

(2.39)

czyli otrzymujemy rozwiązanie zadania postaci:

T (x) = x(1 − x)

(2.40)

2.5

Metoda kollokacji

Metoda ta jest odmianą metody Petrova-Galerkina, funkcje aproksymujące

są różne od funkcji wag. W metodzie kollokacji funkcje wag są postaci w

i

(x) =

δ(x − x

i

), gdzie x

i

jest punktem kollokacji, a δ jest deltą Diraca. Cechą delty

Diraca jest przyjmowanie dwu wartości:

δ(a) =

½

a = 0 ∞
a 6= 0

0

(2.41)

Liczba punktów kollokacji zależy od liczby parametrów funkcji aproksymującej.

Przykład
Rozwiążemy zadanie jednowymiarowego przepływu ciepła, takie samo jak

w metodzie Bubnova-Galerkina.

Funkcję aproksymującą przyjmiemy w postaci:

T (x) = c

0

+ c

1

x + c

2

x

2

+ c

3

x

3

(2.42)

10

2.5 Metoda kollokacji

czyli

φ

0

= 1; φ

1

= x; φ

2

= x

2

; φ

3

= x

3

(2.43)

Funkcje aproksymujące spełniają warunki brzegowe zadania, więc:

c

0

= 0

c

1

+ c

2

+ c

3

= 0

(2.44)

stąd:

c

3

= −c

1

− c

2

(2.45)

czyli

T (x) = c

1

x + c

2

x

2

− (c

1

+ c

2

)x

3

(2.46)

Ponieważ funkcja aproksymująca jest dwuparametrowa, przyjmujemy dwa
punkty kollokacji: x

1

=

1
3

i x

2

=

2
3

.

Funkcje wag przyjmujemy postaci:

w

1

= δ(x − x

1

)

w

2

= δ(x − x

2

)

(2.47)

Odchyłka rozwiązania przybliżonego wyrażona jest wzorem:

R =

∂

2

T (x)

∂x

2

+ 2 = 2c

2

− 6(c

1

+ c

2

)x + 2

(2.48)

Stosując metodę odchyłek ważonych otrzymujemy układ równań

1

Z

0

[2c

2

− 6(c

1

+ c

2

)x + 2]δ(x − x

1

) d x = 0

1

Z

0

[2c

2

− 6(c

1

+ c

2

)x + 2]δ(x − x

2

) d x = 0

(2.49)

Wykorzystujemy własność:

∞

Z

−∞

f (x)δ(x − x

i

) d x =

x

i

+a

Z

x

i

−a

f (x)δ(x − x

i

) d x = f (x

i

)

(2.50)

Równanie 2.30 otrzymujemy w postaci:

2c

2

− 6(c

1

+ c

2

)x + 2 = 0; x =

1
3

2c

2

− 6(c

1

+ c

2

)x + 2 = 0; x =

2
3

(2.51)

11

2.6 Metoda podobszarów

Rozwiązanie powyższego układu równań prowadzi do

c

1

= 1

c

2

= −1

(2.52)

czyli otrzymujemy rozwiązanie zadania postaci:

T (x) = x − x

2

= x(1 − x)

(2.53)

2.6

Metoda podobszarów

Metoda ta jest odmianą metody Petrova-Galerkina. Obszar zadania dzieli

się na podobszary. Funkcje wag przyjmują postać:

w

i

(x) =

½

1

gdyx ∈ Ω

i

0 wprzeciwnymprzypadku

(2.54)

W metodzie tej minimalizowane błędy mogą przyjmować wartości ujemne i do-
datnie w wyniku czego, sumaryczny błąd może być mniejszy od sumy wartości
bezwzględnych poszczególnych błędów.

Przykład
Rozważmy przykład przedstawiony w metodzie Bubnova-Galerkina. Funk-

cję aproksymującą przyjmiemy w postaci:

T (x) = c

1

x(1 − x) + c

2

x

2

(1 − x)

(2.55)

czyli

φ

1

= x(1 − x); φ

2

= x

2

(1 − x)

(2.56)

Odchyłka rozwiązania przybliżonego wyrażona jest wzorem:

R =

d

2

T (x)

d x

2

+ 2 = 2(c

2

− c

1

) − 6c

2

x + 2

(2.57)

Ponieważ funkcje wag przyjmują wartość różną od zera tylko dla x należą-
cych do podobszaru, stosując metodę odchyłek ważonych otrzymujemy układ
równań:

0.5

Z

0

[2(c

2

− c

1

) − 6c

2

x + 2]1 d x +

1

Z

0.5

[2(c

2

− c

1

) − 6c

2

x + 2]0 d x = 0

0.5

Z

0

[2(c

2

− c

1

) − 6c

2

x + 2]0 d x +

1

Z

0.5

[2(c

2

− c

1

) − 6c

2

x + 2]1 d x = 0

(2.58)

12

2.6 Metoda podobszarów

czyli

0.5

Z

0

[2(c

2

− c

1

) − 6c

2

x + 2] d x = 0

1

Z

0.5

[2(c

2

− c

1

) − 6c

2

x + 2] d x = 0

(2.59)

Rozwiązanie powyższego układu równań prowadzi do

c

1

= 1

c

2

= 0

(2.60)

czyli otrzymujemy rozwiązanie zadania postaci:

T (x) = x(1 − x)

(2.61)

13

Metoda Rayleigh’a-Ritz’a

Rozdział 3

Metoda Rayleigh’a-Ritz’a

Metoda Rayleigh’a-Ritz’a pozwala na określenie współczynników równania

aproksymującego rozwiązanie dokładne cząstkowych równań różniczkowych.
Działanie tej metody polega na minimaliza funckjonału reprezentującego ener-
gię cząstkowego równania różniczkowego. W przypadku równania:

L(u) = f

(3.1)

funkcjonał I(u) możemy zapisać w postaci:

I(u) =

1
2

Z

Ω

(L(u)u) dΩ −

Z

Ω

f u dΩ

(3.2)

Jeśli równanie aproksymujące zapiszemy w postaci:

˜

u =

n

X

j=1

c

j

φ

j

(3.3)

gdzie ˜

u jest przybliżonym rozwiązaniem, c

j

współczynnikami równania aprok-

symującego, a φ

j

są funkcjami aproksymującymi. Funkcjonał możemy wyrazić

z użyciem funckji aproksymującej:

I(˜

u) =

1
2

Z

Ω

(L(˜

u)˜

u) dΩ −

Z

Ω

f ˜

u dΩ

(3.4)

Warunkiem koniczecznym znalezienia optimum powyższego funkcjonału zależ-
nego od wartości c

j

jest przyrównanie cząstkowych pochodnych po każdym z

parametrów c

j

do zera:

∂I

∂c

1

= 0,

∂I

∂c

2

= 0, ...,

∂I

∂c

n

= 0,

(3.5)

14

Przykład
Rozważmy jednowymiarowy przepływ ciepła opisany równaniem:

∂

2

T (x)

∂x

2

= −

q(x)

λ

; x ∈ Ω

(3.6)

z warunkami brzegowymi

T (0) = 0

(3.7)

T (1) = 0

(3.8)

funkcja źródła ma postać

q(x) = 2

(3.9)

a przewodność cieplna λ = 1.

Funkcję aproksymującą przyjmiemy:

˜

T (x) = c

1

x(1 − x) + c

2

x

2

(1 − x)

(3.10)

czyli

φ

1

= x(1 − x); φ

2

= x

2

(1 − x)

(3.11)

Funkcje aproksymujące spełniają warunki brzegowe zadania oraz warunek cią-
głości drugiej pochodnej wzgledem zmiennej x.

Funkcjonał metody Rayleigh’a-Ritz’a zapiszemy w postaci:

I( ˜

T ) =

1
2

Z

1

0

d

2

˜

T (x)

d x

2

˜

T (x) +

Z

1

0

q(x)

λ

˜

T (x) d x

(3.12)

po podstawieniu ˜

T (x) otrzymamy:

I(c

1

, c

2

) =

1
3

c

1

+

1
6

c

2

−

1

15

c

2

2

−

1
6

c

1

c

2

1
6

c

2

1

(3.13)

Przyrównując pochodzne funkcjonału po współczynnika równania aproksy-

mującego c

j

do zera, otrzymujemy układ dwóch równań:

∂I(c

1

, c

2

)

∂c

1

= 0;

1
3

−

1
6

c

2

−

1
3

c

1

= 0

∂I(c

1

, c

2

)

∂c

2

= 0;

1
6

−

2

15

c

2

−

1
6

c

1

= 0

(3.14)

Rozwiązanie powyższego układu równań prowadzi do

c

1

= 1

c

2

= 0

(3.15)

czyli otrzymujemy rozwiązanie zadania postaci:

˜

T (x) = x(1 − x)

(3.16)

15

Sformułowanie słabe

Rozdział 4

Sformułowanie słabe

Rozwiązywanie zadań brzegowych za pomocą medod Rayleigh’a-Ritz’a oraz

reszt ważonych wymaga stosowania równań aproksymujących, o stopniu róż-
niczkowalności równym stopniowi równania różniczkowego. W celu obniże-
nia wymogu różniczkowalności równań aproksymujących stosuje się całkowanie
przez części. W wyniku tego przekształcenia uzyskujemy sformułowanie słabe
cząstkowego równania różniczkowego, w którym warunek stopnia różniczko-
walności funkcji został obniżony.

4.1

Całkowanie przez części

Rozważmy różniczkowalne funkcje u,v,w będące zależne od współrzędnej

x. Całkowanie przez części równania różniczkowego możemy zapisać jako:

Z

b

a

w

d v

d x

d x =

Z

b

a

w d v = −

Z

b

a

v d w + [wv]

b

a

=

= −

Z

b

a

v

d w

d x

d x + w(b)v(b) − w(a)v(a)

(4.1)

W przypadku równania różniczkowego drugiego stopnia oznaczając:

v ≡

d u
d x

(4.2)

możemy zapisać:

Z

b

a

w

d

2

u

d x

2

d x = −

Z

b

a

v

d w

d x

d x + w(b)v(b) − w(a)v(a) =

= −

Z

b

a

d u
d x

d w

d x

d x + w(b)

d u
d x

(b) − w(a)

d u
d x

(a)

(4.3)

16

4.1 Całkowanie przez części

W przypadku ciał wielowymiarowych używamy tożsamości Greena wyni-

kającej z twierdzenia Gaussa-Ostrogradskiego-Greena, dla funkcji G(x, y) oraz
w(x, y) możemy zapisać:

−

Z

Ω

(∇

2

G)w d x d y =

Z

Ω

∇w · ∇G d x d y −

I

Γ

∂G

∂n

w d s

(4.4)

gdzie n jest wektorem normalnym do brzegu Γ.

Przykład

Rozważmy jednowymiarowy przepływ ciepła opisany równaniem:

∂

2

T (x)

∂x

2

= −

q(x)

λ

; x ∈ Ω

(4.5)

z warunkami brzegowymi

T (0) = 0

(4.6)

T (1) = 0

(4.7)

funkcja źródła ma postać

q(x) = 2

(4.8)

a przewodność cieplna λ = 1.

Zadanie rozwiążemy metodą Reileigh’a-Ritz’a z użyciem sformułowania sła-

bego. Funkcjonał energetyczny możemy zapisać jako:

I( ˜

T ) =

1
2

Z

1

0

d

2

˜

T (x)

d x

2

˜

T (x) +

Z

1

0

q(x)

λ

˜

T (x) d x

(4.9)

Sformułowanie słabe dla pierwszej całki ma postać:

Z

1

0

d

2

˜

T (x)

d x

2

˜

T (x) =

Z

1

0

(

d ˜

T (x)

d x

d ˜

T (x)

d x

) d x + ˜

T (1)

d ˜

T (x)

d x

(1) − ˜

T (0)

d ˜

T (x)

d x

(0) =

Z

1

0

(

d ˜

T (x)

d x

)

2

d x

(4.10)

17

4.1 Całkowanie przez części

Uzyskujemy równanie energetyczne postaci:

I( ˜

T ) =

1
2

Z

1

0

(

d ˜

T (x)

d x

)

2

d x +

Z

1

0

q(x)

λ

˜

T (x) d x

(4.11)

18

Metoda elementów skończonych

Rozdział 5

Metoda elementów skończonych

Stosowanie metod Releigh’a-Ritz’a oraz reszta ważonych jest skompliko-

wane, szczególnie w przypadku ciał o skomplikowanej geometrii. Opracowanie
efektywnego algorytmu komputerowego w oparciu o te metody jest również
skomplikowane.

Metoda elementów skończonych opiera się na podziale obszaru rozpatry-

wanego ciała na proste elementy skończone. Dla poszczególnych elementów
tworzone są cząstkowe równania różniczkowe. Kolejny krok polega na do-
borze współczynników równania aproksymującego rozwiązanie dokładne dla
elementu. Zazwyczaj przyjmuje się funkcje aproksymujące w postraci wie-
lomianów. Równanie aproksymujące musi spełniać tylko naturalne warunki
brzegowe. Po podstawieniu równania aproksymującego do cząstkowych rów-
nań różniczkowych i wykorzystaniu jednej z metod reszt ważonych lub me-
tody Reileigh’a-Ritz’a otrzymujemy macierzowe równanie dla pojedynczego
elementu (macierze lokalne). Następnie tworzymy macierz globalną w pro-
cesie agregacji, uwzględniając połączenia pomiędzy elementami (wspólne wę-
zły), macierze lokalne elementów oraz ciągłość zmiennych oraz ich pochodnych.
Uwzględniamy warunki brzegwe zadania. Otrzymujemy poszukiwane wartości
zmiennych w węzłach po rozwiązaniu układu równań.

Ponieważ w metodzie elementów skończonych stosuje się zazwyczaj nie-

wielką ilość typów elementów, wyznaczanie macierzy lokalnych można w bar-
dzo prosty sposób zautomatyzować. Również proces agregacji macierzy global-
nej i rozwiązanie układu równań może zostać zautomatyzowany. Za pomocą
metody elementów skończonych można modelować ciała o skomplikowanej geo-
metrii. Ze względu na powyższe cechy metoda elementów skończonych znalazła
szerokie zastosowanie w symulacjach z użyciem komputerów.

Przykład
Rozważmy przepływ ciepła w ciele jednowymiarowym.

19