
1. CIĄGI LICZBOWE
1.1. Definicja ciągu i ciągu liczbowego
Definicja 1.1.
• Ciągiem nieskończonym nazywamy każdą funkcję określoną na zbiorze liczb naturalnych.
• Jeśli funkcja a jest ciągiem, to wartości tej funkcji nazywamy wyrazami ciągu i oznaczamy
przez
a
n
def
= a(n),
n
∈ N.
• Ciąg o wyrazach a
n
zapisujemy symbolem
(a
n
) lub a
1
, a
2
, . . . ,
zaś zbiór wartości tego ciągu oznaczamy przez
{a
n
}
n
∈N
.
Ciągi, których wszystkie wyrazy są liczbami nazywamy ciągami liczbowymi (np. ciągi liczbowe
o wyrazach rzeczywistych, ciągi liczbowe o wyrazach zespolonych).
Ciągi, których wszystkie wyrazy są funkcjami nazywamy ciągami funkcyjnymi.
1.2. Własności ciągów liczbowych o wyrazach
rzeczywistych: monotoniczność, ograniczo-
ność, zbieżność.
Definicja 1.2.
• Ciąg (a
n
) jest rosnący
def
⇔
V
n
∈N
a
n+1
> a
n
.
• Ciąg (a
n
) jest niemalejący
def
⇔
V
n
∈N
a
n+1
a
n
.
• Ciąg (a
n
) jest malejący
def
⇔
V
n
∈N
a
n+1
< a
n
.
• Ciąg (a
n
) jest nierosnący
def
⇔
V
n
∈N
a
n+1
¬ a
n
.
Twierdzenie 1.3.
Jeśli a
n
> 0 dla n
∈ N, to
ciąg (a
n
) jest rosnący
⇔
V
n
∈N
a
n+1
a
n
> 1.
Ćwiczenie 1.4. Sformułować analogiczne własności dla ciągu niemalejącego, malejącego i nierosną-
cego.
Definicja 1.5.
• Ciąg (a
n
) jest ograniczony z dołu
def
⇔
W
m
∈R
V
n
∈N
a
n
m.
• Ciąg (a
n
) jest ograniczony z góry
def
⇔
W
M
∈R
V
n
∈N
a
n
¬ M.
1

1. CIĄGI LICZBOWE
2
• Ciąg (a
n
) jest ograniczony
def
⇔ (a
n
) jest ograniczony z dołu i z góry.
Ćwiczenie 1.6. Zbadać własności ciągów o wyrazach ogólnych:
a) a
n
=
√
n;
c) a
n
=
(
−1)
n
n
−1
;
b) a
n
= (
−3)
n
;
d) a
n
=
1
n
2
+ 1
.
Definicja 1.7.
Ciąg liczbowy (a
n
) jest zbieżny do a
∈ R, gdy
V
ε>0
W
K
∈N
V
n
K
|a
n
− a| < ε,
czyli
V
ε>0
W
K
∈N
V
n
K
a
− ε < a
n
< a + ε.
Liczbę a nazywamy granicą właściwą ciągu (a
n
) i zapisujemy
lim
n
→∞
a
n
= a lub a
n
→ a.
Przykład 1.8. Wykazać, że zachodzą równości:
a) lim
n
→∞
1
n
= 0;
b) lim
n
→∞
1
n
3
= 0.
Definicja 1.9.
• Mówimy, że ciąg (a
n
) jest rozbieżny do +
∞ i zapisujemy
lim
n
→∞
a
n
= +
∞,
gdy
V
ε>0
W
K
∈N
V
n
K
a
n
> ε.
• Mówimy, że ciąg (a
n
) jest rozbieżny do
−∞ i zapisujemy
lim
n
→∞
a
n
=
−∞),
gdy
V
ε>0
W
K
∈N
V
n
K
a
n
<
−ε.
• Mówimy, że ciąg (a
n
) jest rozbieżny, gdy nie posiada granicy (właściwej lub niewłaściwej).
Przykład 1.10. Wykazać, że lim
n
→∞
n
2
= +
∞.
Twierdzenie 1.11.
Każdy ciąg posiada conajwyżej jedną granicę (właściwą lub niewłaściwą).
Ćwiczenie 1.12. Wykazać, że:
a) lim
n
→∞
a
n
=
±∞ ⇒ lim
n
→∞
1
a
n
= 0;
{
1
±∞
= 0
}
1. CIĄGI LICZBOWE
3
b) lim
n
→∞
a
n
= 0
⇒ lim
n
→∞
1
a
n
=
(
+
∞, gdy a
n
> 0 dla prawie wszystkich n
∈ N,
−∞, gdy a
n
< 0 dla prawie wszystkich n
∈ N.
{
1
0
+
= +
∞}
{
1
0
−
=
−∞}
Ćwiczenie 1.13. Wykazać, że
a) lim
n
→∞
q
n
=
nie istnieje dla q
¬ −1,
0
dla q
∈ (−1; 1),
1
dla q = 1,
+
∞
dla q > 1.
b) lim
n
→∞
n
α
=
0
dla α < 0,
1
dla α = 0,
+
∞ dla α > 0.
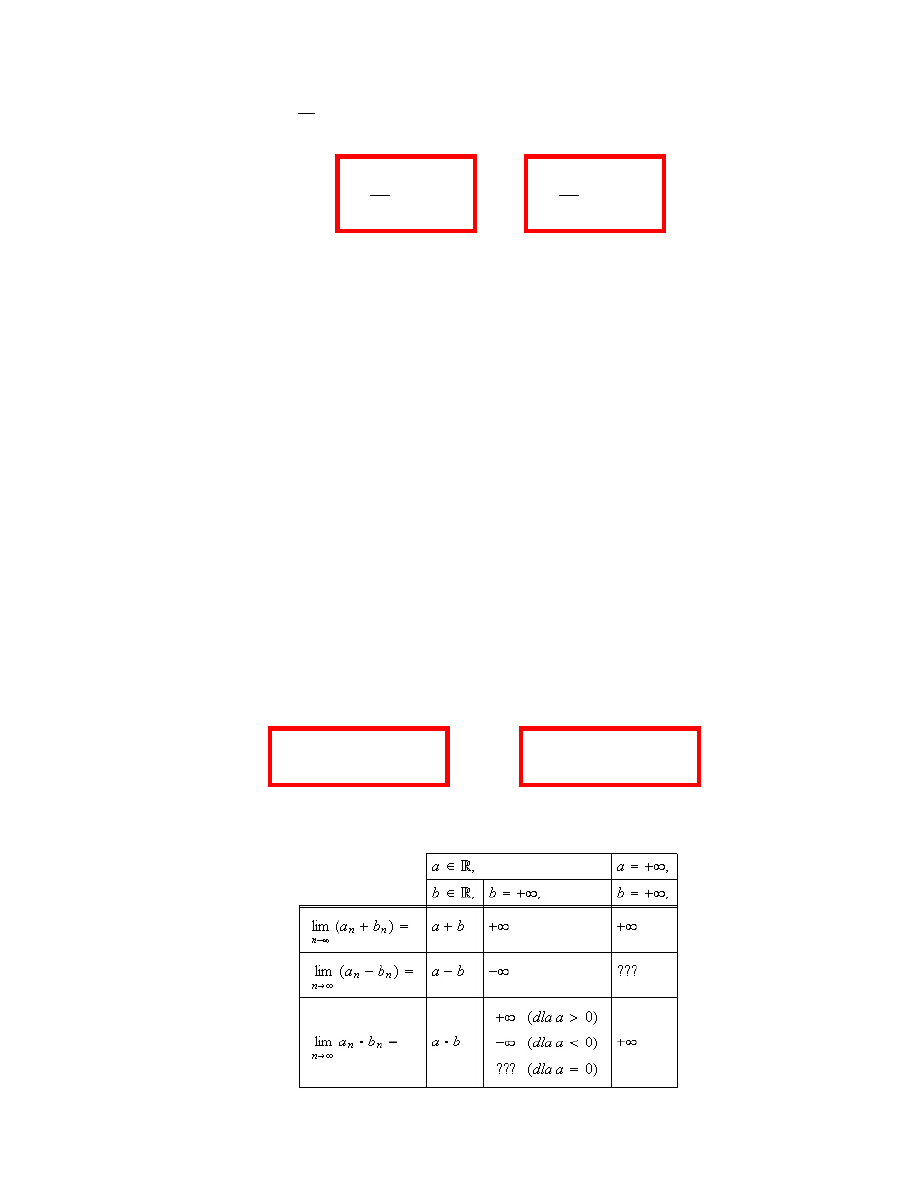
1.3. Arytmetyka granic
Twierdzenie 1.14.
Jeśli lim
n
→∞
a
n
= a oraz c
6= 0, to
lim
n
→∞
c
· a
n
=
(
c
· a, gdy a ∈ R,
±∞, gdy a = ±∞.
W szczególności dla c > 0 mamy
{c · (+∞) = +∞}
oraz
{c · (−∞) = −∞}
Twierdzenie 1.15.
Jeśli lim
n
→∞
a
n
= a oraz
lim
n
→∞
b
n
= b, to

1. CIĄGI LICZBOWE
4
Twierdzenie 1.16.
Jeśli lim
n
→∞
a
n
= a,
lim
n
→∞
b
n
= b oraz b
n
6= 0 dla n ∈ N, to
Twierdzenie 1.17.
Jeśli lim
n
→∞
a
n
= a,
lim
n
→∞
b
n
= b oraz b
n
0 dla n ∈ N, to
Symbole nieoznaczone:
∞ − ∞ 0 · ∞
∞
∞
0
0
0
0
∞
0
1
∞
1.4.
Twierdzenia
o
ciągach
zbieżnych
i roz-
bieżnych
Definicja 1.18.
Podciągiem ciągu (a
n
) nazywamy każdy ciąg (a
k
n
), gdzie (k
n
) jest dowolnym ro-
snącym ciągiem liczb naturalnych.
Np. Podciągami ciągu (a
n
) są ciągi:
a
1
, a
3
, a
5
, . . .
a
2
, a
4
, a
6
, . . .
a
3
, a
4
, a
5
, . . .
(a
2n
−1
)
∞
n=1
(a
2n
)
n
∈N
(a
n
)
n
3
Twierdzenie 1.19.
Każdy podciąg ciągu zbieżnego jest zbieżny i ma tę samą granicę, co dany ciąg.
Przykład 1.20. Wykazać, że nie istnieją granice:
a) lim
n
→∞
(
−1)
n
;
b) lim
n
→∞
cos
nπ
2
.
Twierdzenie 1.21.
Jeśli ciąg liczbowy jest zbieżny, to jest ograniczony.
Uwaga 1.22. Twierdzenie odwrotne do Tw.1.21 nie jest prawdziwe.
Twierdzenie 1.23 (Bolzano-Weierstrassa).
Jeśli ciąg liczbowy jest ograniczony, to istnieje pod-
ciąg zbieżny. Jeśli ciąg liczbowy jest nieograniczony, to posiada podciąg rozbieżny do
−∞ lub +∞.

1. CIĄGI LICZBOWE
5
Twierdzenie 1.24.
Jeśli ciąg liczbowy jest ograniczony i monotoniczny, to jest zbieżny.
Lemat 1.25. Jeśli ciągi (a
n
), (b
n
) są zbieżne oraz
W
K
∈N
V
n
K
a
n
¬ b
n
,
to lim
n
→∞
a
n
¬ lim
n
→∞
b
n
.
Twierdzenie 1.26 (o trzech ciągach).
Załóżmy,że
(
∗)
W
K
∈N
V
n
K
a
n
¬ b
n
¬ c
n
,
1) Jeśli lim
n
→∞
a
n
= lim
n
→∞
c
n
= a, to istnieje granica ciągu (b
n
), przy czym lim
n
→∞
b
n
= a.
2) Jeśli lim
n
→∞
a
n
= +
∞, to lim
n
→∞
b
n
= +
∞.
3) Jeśli lim
n
→∞
c
n
=
−∞, to lim
n
→∞
b
n
=
−∞.
1.5. Zbieżność pewnych ciągów specjalnych.
Liczba
e.
Twierdzenie 1.27.
1) lim
n
→∞
n
√
n = 1.
2) lim
n
→∞
n
√
a = 1.
3) Jeśli a
n
0 dla każdego n ∈ N oraz lim
n
→∞
a
n
= a > 0, to lim
n
→∞
n
√
a
n
= 1.
Uwaga 1.28. Tw. 1.27 3) nie zachodzi w przypadku, gdy a = +
∞ lub a = 0.
Twierdzenie 1.29.
Ciąg a
n
= (1 +
1
n
)
n
dla n
∈ N jest ograniczony i monotoniczny.
Definicja 1.30.
Liczbą e nazywamy granicę ciągu (1 +
1
n
)
n
, n
∈ N.
Twierdzenie 1.31.
a)
∗
lim
n
→∞
n
X
k=0
1
k!
= e.
b) Liczba e jest liczbą niewymierną.
e = 2, 7182818284 . . .
Twierdzenie 1.32.
Jeśli a
n
6= 0 dla każdego n ∈ N oraz lim
n
→∞
a
n
=
±∞, to lim
n
→∞
(1 +
1
a
n
)
a
n
= e.
Definicja 1.33.
Logarytm o podstawie równej e nazywamy logarytmem naturalnym i oznaczamy
symbolem ln.
ln x
def
= log
a
x dla x > 0

1. CIĄGI LICZBOWE
6
1.6. Zbiory ograniczone na prostej. Kresy górny
i dolny.
Definicja 1.34.
Niech E
⊂ R, E 6= ∅.
• Liczbę M
0
∈ E taką, że
∧
x
∈E
x
¬ M
0
nazywamy elementem największym w zbiorze E i oznaczamy przez max E.
• Liczbę m
0
∈ E taką, że
∧
x
∈E
x
m
0
nazywamy elementem najmniejszym w zbiorze E i oznaczamy przez min E.
Definicja 1.35.
Niech E
⊂ R, E 6= ∅.
• Zbiór E jest ograniczony z góry, gdy
∨
M
∈R
∧
x
∈E
x
¬ M.
Lczbę M nazywamy ograniczeniem górnym zbioru E.
• Zbiór E jest ograniczony z dołu, gdy
∨
m
∈R
∧
x
∈E
x
m.
Liczbę m nazywamy ograniczeniem dolnym zbioru E.
• Zbiór E jest ograniczony, gdy zbiór E jest ograniczony z góry i z dołu.
Definicja 1.36.
Niech E
⊂ R, E 6= ∅.
• Jeśli zbiór E jest ograniczony z góry, to liczbę M ∈ R taką, że
(1)
∧
x
∈E
x
¬ M,
(2)
∧
M
1
<M
∨
x
∈E
x > M
1
nazywamy kresem górnym zbioru E i oznaczamy przez sup E.
(Liczba sup E jest najmniejszym ograniczeniem górnym zbioru E.)
W przypadku gdy E nie jest ograniczony z góry przyjmujemy sup E = +
∞.
• Jeśli zbiór E jest ograniczony z dołu, liczbę m ∈ R taką, że
(1)
∧
x
∈E
x
m,
(2)
∧
m
1
>m
∨
x
∈E
x < m
1
nazywamy kresem dolnym zbioru E i oznaczamy przez inf E.
(Liczba inf E jest największym ograniczeniem dolnym zbioru E.)
W przypadku gdy E nie jest ograniczony z dołu przyjmujemy inf E =
−∞.
Twierdzenie 1.37.
Każdy niepusty zbiór E
⊂ R posiada kresy górny i dolny, które należą do zbioru
R
.

1. CIĄGI LICZBOWE
7
Twierdzenie 1.38.
a) Jeśli ciąg (a
n
) jest niemalejący, to
sup
{a
n
: n
∈ N} = lim
n
→∞
a
n
,
inf
{a
n
: n
∈ N} = a
1
.
b) Jeśli ciąg (a
n
) jest nierosnący, to
sup
{a
n
: n
∈ N} = a
1
,
inf
{a
n
: n
∈ N} = lim
n
→∞
a
n
.
Document Outline
- 1. CIAGI LICZBOWE
- 1.1. Definicja ciagu i ciagu liczbowego
- 1.2. Wlasnosci ciagów liczbowych o wyrazach rzeczywistych: monotonicznosc, ograniczonosc, zbieznosc.
- 1.3. Arytmetyka granic
- 1.4. Twierdzenia o ciagach zbieznych i rozbieznych
- 1.5. Zbieznosc pewnych ciagów specjalnych. Liczba e.
- 1.6. Zbiory ograniczone na prostej. Kresy górny i dolny.
Wyszukiwarka
Podobne podstrony:
2007 AMI wyklad print4 id 55147 Nieznany (2)
analiza czestotliwosciowa id 59 Nieznany (2)
Analiza ekon 08 w2 id 60028 Nieznany
AiSD Wyklad4 dzienne id 53497 Nieznany (2)
analiza sem 2 lista nr5 id 6134 Nieznany (2)
3 Wyklad OiSE id 33284 Nieznany
or wyklad 4b id 339029 Nieznany
analiza swot (10 stron) id 6157 Nieznany
Materialy do wykladu nr 5 id 28 Nieznany
analiza pomoc naukowa cz1 id 61 Nieznany (2)
Finanse Wyklady FiR id 172193 Nieznany
mesmeb r1 id 293404 Nieznany
AiSD Wyklad9 dzienne id 53501 Nieznany
Folie wyklad2 Krakow id 286699 Nieznany
OP wyklad nr 3 id 335762 Nieznany
prc wyklad zagad 5 id 388963 Nieznany
hydrologia wyklad 06 id 207845 Nieznany
więcej podobnych podstron