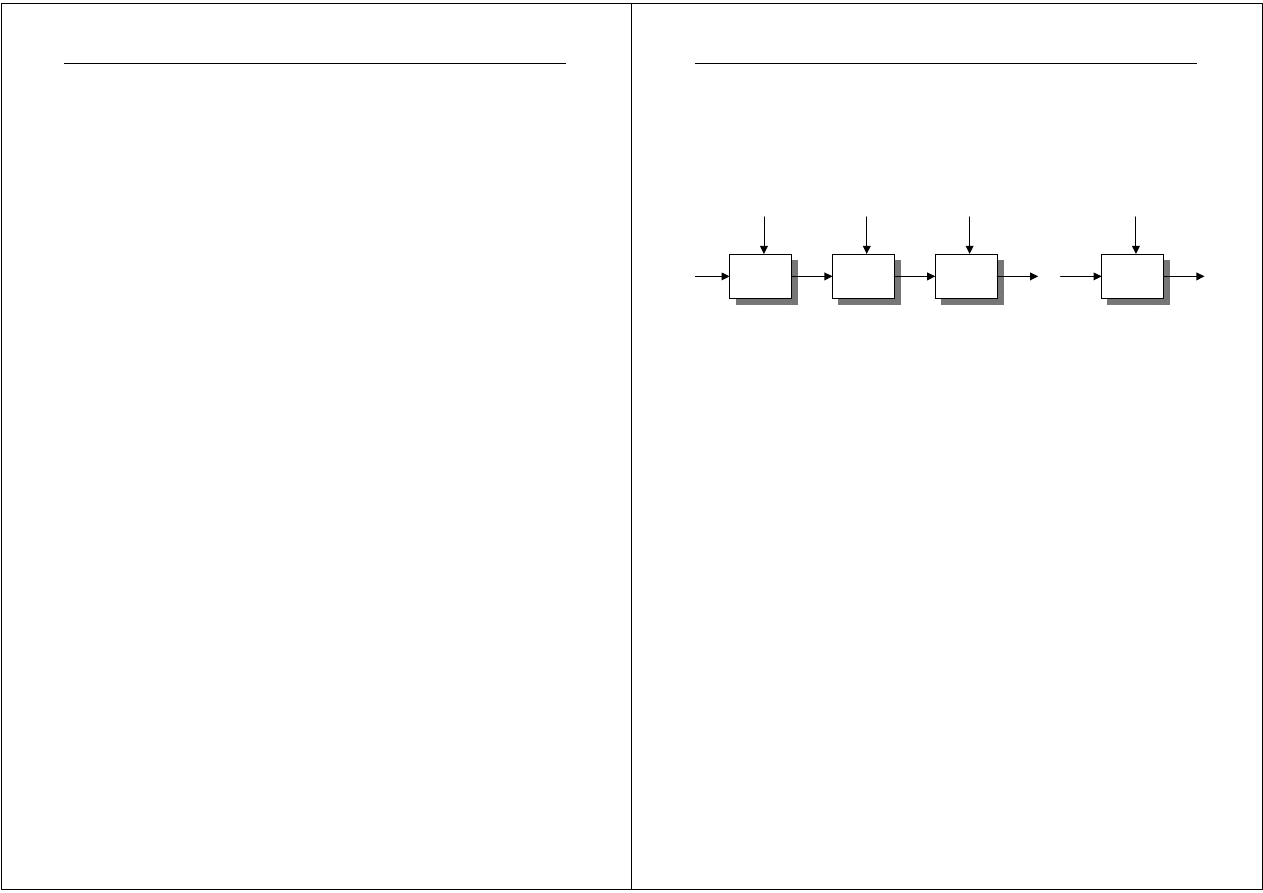
Badania operacyjne

dr inż. W. Zalewski

41

PROGRAMOWANIE DYNAMICZNE

Metody programowania dynamicznego polegają na zmianie zadań

optymalizacyjnych z N zmiennymi decyzyjnymi w N zadań z jedną

zmienną decyzyjna, przy czym zadania te są powiązane ze sobą określoną

zależnością rekurencyjną. Operacja taka jest możliwa tylko w przypadku,

gdy funkcja celu jest funkcją separowalną (daje się wyrazić jako

kompozycja funkcji jednej zmiennej).

Programowanie dynamiczne jest pewnym podejściem do

optymalizacji wieloetapowych procesów decyzyjnych.

Rozpatrzmy dowolny proces, którego przebieg można podzielić na

N etapów. W dowolnym etapie tego procesu możemy wyróżnić

następujące elementy:

⇒

stan wejściowy procesu do danego etapu – jest to stan jaki osiągnął

proces w wyniku realizacji etapu poprzedniego;

⇒

decyzję podejmowaną na danym etapie;

⇒

stan wyjściowy procesu z danego etapu – stan ten zależy od stanu

wejściowego oraz podjętej decyzji na danym etapie.

Stan

procesu

można opisać za pomocą jednego lub kilku parametrów

zwanych zmiennymi stanu. W dalszym ciągu będziemy rozpatrywać

procesy decyzyjne z jedną zmienną stanu s. Decyzje podejmowane

w kolejnych etapach będziemy opisywać za pomocą zmiennych

decyzyjnych x

1

, x

2

, ..., x

n

.

Badania operacyjne

dr inż. W. Zalewski

42

Ogólny schemat wieloetapowego procesu decyzyjnego przedstawia

rysunek poniżej.

W procedurze programowania dynamicznego wykorzystujemy dwie

własności, które umożliwiają podejmowanie decyzji w procesie

n-etapowym:

⇒

Wartość funkcji celu w zadaniu n-etapowym jest sumą wartości

uzyskanych w poszczególnych etapach, a wartość uzyskana w j-tym

etapie zależy od stanu w etapie poprzednim oraz od decyzji podjętej

w j-tym etapie. Nie zależy natomiast od tego, jaką drogą system doszedł

do stanu j-1. (Własność Markowa).

⇒

Aby ciąg decyzji (x

1

*

, x

2

*

, ..., x

N

*

) był optymalną strategią w procesie

N-etapowym. potrzeba, by ciąg decyzji (x

2

*

, x

3

*

, ..., x

N

*

) był optymalną

strategią w procesie (N-1)-etapowym wynikającym z podjęcia

w pierwszym etapie decyzji x

1

*

.

x

1

x

2

x

3

x

N

s

0

s

1

s

2

s

3

s

N-1

s

N

HACKED BY VIPER :)

Badania operacyjne

dr inż. W. Zalewski

43

Ogólny schemat programowania dynamicznego

Rozważmy N-etapowy dyskretny proces decyzyjny dla i = 1, 2, ..., N-1, N.

Oznaczmy:

s

0

– zadany stan początkowy procesu,

s

1

, s

2

, ..., s

N

– stany dla poszczególnych etapów,

x

1

, x

2

, ..., x

N

– decyzje w poszczególnych etapach,

Z

1

(s

0

, x

1

) –

wartość funkcji celu uzyskana w pierwszym etapie przy

zadanym stanie początkowym;

analogicznie:

Z

2

(s

1

, x

2

), Z

3

(s

2

, x

3

), ..., Z

N-1

(s

N-2

, x

N-1

), Z

N

(s

N-1

, x

N

) – wartości funkcji

w kolejnych etapach 2, 3, ..., N.

Zachodzi

również:

Z(s

0

, X) = Z

1

(s

0

, x

1

) + Z

2

(s

1

, x

2

) + Z

3

(s

2

, x

3

) + ... + Z

N-1

(s

N-2

, x

N-1

) +

+

Z

N

(s

N-1

, x

N

)

Należy wyznaczyć optymalną strategię (ciąg decyzji): X

*

= (x

1

*

, x

2

*

,

..., x

N

*

) taką, aby uzyskać max(min) Z(s

0

, X) przy ograniczeniach X

⊂

Ω

,

gdzie

Ω

oznacza obszar określenia zadania wyjściowego.

Aby

rozwiązać to zadanie dokonuje się dekompozycji, otrzymując

rodzinę zadań, tzn.

Ω

N

,

Ω

N-1,N

, ...,

Ω

1, 2, ..., N

≡

Ω

.

Niech

F

1

(s

N-1

) oznacza warunkowo optymalną wartość funkcji celu

w pierwszym etapie, tj.:

( )

( ) (

)

N

1

N

N

x

1

N

1

x

,

s

Z

min

max

s

F

N

N

−

Ω

∈

−

=

Badania operacyjne

dr inż. W. Zalewski

44

Oznaczając przez F

2

(s

N-2

), F

3

(s

N-3

), ..., F

K

(s

N-K

), ..., F

N

(s

0

) warunkowo

optymalne wartości funkcji celu w kolejnych etapach aż do N-tego,

otrzymamy:

F

2

(s

N-2

) = max(min) [Z

N-1

(s

N-2

, x

N-1

) + Z

N

(s

N-1

, x

N

)] =

= max(min)[Z

N-1

(s

N-2

, x

N-1

) + F

1

(s

N-1

)

Analogicznie:

(

)

( )

(

)

( )

[

]

1

N

1

1

N

2

N

1

N

x

2

N

2

s

F

x

,

s

Z

min

max

s

F

N

,

1

N

1

N

−

−

−

−

Ω

∈

−

+

=

−

−

( )

( )

(

) ( )

[

]

2

N

2

2

N

3

N

2

N

x

3

N

3

s

F

x

,

s

Z

min

max

s

F

N

,

1

N

,

2

N

2

N

−

−

−

−

Ω

∈

−

+

=

−

−

−

..............................................................................

dla k-tego etapu:

( )

( )

( )

( )

(

)

( )

(

)

[

]

1

k

N

1

k

1

k

N

k

N

1

k

N

k

N

k

s

F

x

,

s

Z

min

max

s

F

+

−

−

+

−

−

+

−

−

+

=

dla N-tego etapu:

( )

( ) (

)

( )

[

]

1

1

N

1

0

1

x

0

N

s

F

x

,

s

Z

min

max

s

F

1

−

Ω

∈

+

=

Z

równań powyższych wynika, że maksymalna wartość funkcji

z N-etapowego procesu decyzyjnego jest równa maksimum ze względu na

pierwszą decyzję, przy założeniu stanu początkowego oraz maksymalnej

wartości funkcji dla procesu (N-1)-etapowego.

Powyższy ciąg równań funkcyjnych wyraża zasadę optymalności,

która umożliwia uzyskanie najpierw warunkowo optymalnego rozwiązania

dla N-tego etapu, następnie dla N-1, N-2, ..., aż do etapu pierwszego.

HACKED BY VIPER :)

Badania operacyjne

dr inż. W. Zalewski

45

ANALIZA SIECIOWA

Model sieciowy przedsięwzięcia

Przedsięwzięcie – wyodrębniony zbiór czynności powiązanych ze

sobą sposobem wykonania (technologią).

Technologię nazywamy strukturą, a odwzorowanie przedsięwzięcia

projektem, który przedstawiamy w postaci sieci czynności.

Definicja 1.

Sieć czynności to graf spójny antycykliczny, który ma jeden
wierzchołek początkowy i jeden wierzchołek końcowy. Łuki sieci
reprezentują czynności, wierzchołki zdarzenia w projekcie.

Konstrukcja sieci czynności

W

trakcie

wykreślania powinny być przestrzegane zasady:

! zdarzenie początkowe nie ma czynności poprzedzających,

! zdarzenie końcowe nie ma czynności następujących,

! dwa kolejne zdarzenia mogą być połączone tylko jedną czynnością,

!

wszystkie zdarzenia w sieci, z wyjątkiem początkowego lub

końcowego, powinny być początkiem i końcem co najmniej jednej

czynności.

Można wyróżnić następujące etapy konstruowania sieci:

! ustalenie listy czynności,

! ustalenie zdarzenia początkowego i końcowego,

! określenie kolejności wykonywania czynności,

! numerowanie wierzchołków.

Badania operacyjne

dr inż. W. Zalewski

46

Analiza sieci z funkcją czasu

Definicja 2.

Czasem realizacji projektu określonym przez czas trwania czynności

będziemy nazywali czas t*:

( )

k

S

s

*

s

t

max

t

k

∈

=

Definicja 3.

Ścieżką krytyczną w sieci czynności (critical path method – CPM)

nazywamy ścieżkę pełną , dla której czas trwania jest najdłuższy.

Definicja 4.

Najwcześniejszy możliwy termin zaistnienia zdarzenia określony jest

następującym wzorem:

{

}

ij

0
i

i

0

j

t

t

max

t

+

=

, i < j

gdzie t

i

0

oznacza najwcześniejszy możliwy termin wystąpienia i-tego

zdarzenia bezpośrednio poprzedzającego wydarzenie j-te.

Definicja 5.

Najpóźniejszy dopuszczalny termin zaistnienia zdarzenia i-tego, t

i

1

określony jest wzorem:

{

}

ij

1

j

j

1

i

t

t

min

t

−

=

,

i < j

gdzie t

j

1

oznacza najpóźniejszy dopuszczalny termin zaistnienia j-tego

zdarzenia, następującego po i-tym zdarzeniu.

Najwcześniejszy i najpóźniejszy termin zdarzenia końcowego są

sobie równe (zdarzenie to nie ma następnika).

HACKED BY VIPER :)

Badania operacyjne

dr inż. W. Zalewski

47

Definicja 6.

Luz

czasowy

L

i

dowolnego zdarzenia i-tego określamy jako:

0
i

1

i

i

t

t

L

−

=

.

Wskazuje on, o ile może opóźnić się termin zaistnienia zdarzenia bez

wpływu na termin zakończenia realizacji projektu.

Charakterystyki czasowe czynności

Dla

każdej czynności <i, j> wyróżnia się cztery terminy związane

z czasem realizacji.

Definicja 7.

Najwcześniejszy możliwy termin rozpoczęcia czynności <i, j>

wyznacza najwcześniejszy możliwy termin zajścia zdarzenia

początkowego tej czynności.

Definicja 8.

Najpóźniejszy dopuszczalny termin rozpoczęcia czynności określony

jest przez różnicę t

j

1

– t

ij

.

Definicja 9.

Najwcześniejszy możliwy termin zakończenia czynności <i, j>

wyrażony jest przez sumę t

i

0

+ t

ij

.

Definicja 10.

Najpóźniejszy dopuszczalny termin zakończenia czynności <i, j>

określa najpóźniejszy termin zajścia zdarzenia końcowego tej czynności.

Badania operacyjne

dr inż. W. Zalewski

48

Dla

każdej czynności można wyznaczyć rezerwy czasu wykonania,

zwane zapasami czasu.
Wyróżnia się cztery rodzaje zapasów:

! zapas całkowity,
! zapas swobodny,
! zapas warunkowy,
! zapas niezależny.

Definicja 11.

Zapas

całkowity Z

c

określony jest przez równanie:

Z

c

= t

j

1

– t

i

0

– t

ij

.

Stanowi on rezerwę czasu, który może być wykorzystany dodatkowo na
wykonanie czynności bez wpływu na termin realizacji projektu.

Definicja 12.

Zapas swobodny Z

s

określony jest przez równanie:

Z

s

= t

j

0

– t

i

0

– t

ij

.

Nie wpływa na zapasy związane z czynnościami należącymi do danej
ścieżki.

Definicja 13.

Zapas

warunkowy

Z

w

określony jest przez równanie:

Z

w

= t

j

1

– t

i

1

– t

ij

.

Rezerwa czasu może być wykorzystana bez zmniejszenia zapasów
poprzednich, określonych dla danej ścieżki.

Definicja 14.

Zapas

niezależny Z

n

określony jest przez równanie:

Z

n

= t

j

0

– t

i

1

– t

ij

.

Wykorzystanie tej rezerwy nie ma wpływu na zapas jakiejkolwiek innej
czynności.

HACKED BY VIPER :)