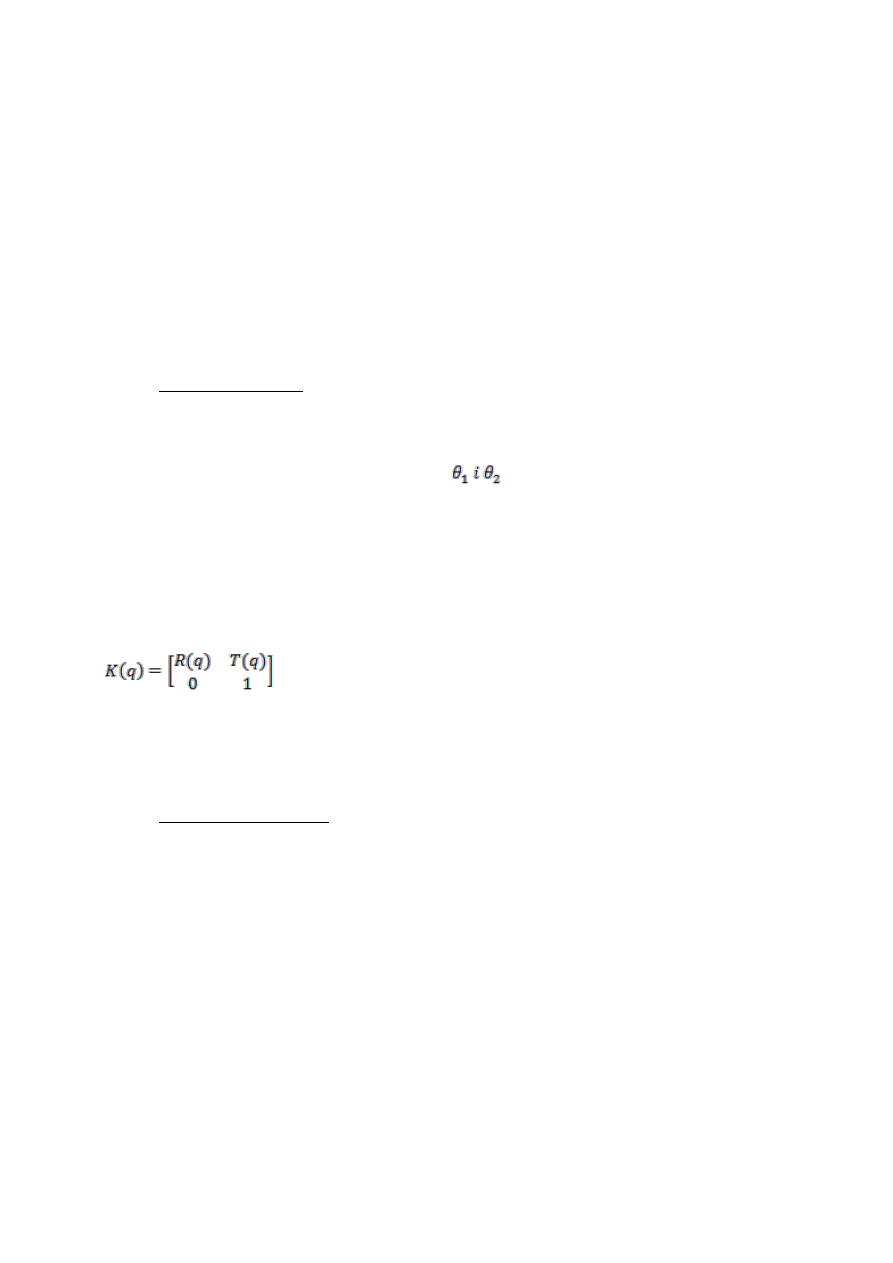
Zadania, metody i algorytmy robotyki

Def. ROBOT – jest programowalnym wielofunkcyjnym manipulatorem zaprojektowanym do
przemieszczania materiałów, części, narzędzi lub specjalizowanych urządzeo poprzez różne
programowalne ruchy w celu realizacji różnorodnych zadao

(oficjalna definicja przyjęta przez RIA(Robot institute of America))

Zadania:



Kinematyka prosta

Problem: Opisanie pozycji efektora (narzędzia) we wspólnym układzie współrzędnych.
Najczęściej manipulator osczytuje swoją pozycję za pomocą czujników wewnętrznych,
mierzących wartości zmiennych przegubowych

.

Zadanie: polega na wyrażeniu położenia efektora manipulatora w zależności od
współrzędnych wewnętrznych.

Przyjmuje się stały układ, zwany układem odniesienia albo bazowym.

Kinematyka manipulatora ma postad:

gdzie wektor T(q) określa położenie efektora wyrażone w bazowym układzie współrzędnych,
natomiast macierz R(q) określa jego orientację w przestrzeni również wyrażoną w bazowym
układzie współrzędnych.



Kinematyka odwrotna

Problem: Jest to podstawowe zadanie programowania i sterowania ruchu manipulatora, gdy
trzeba znaleźd jak poszczególne współrzędne konfiguracyjne powinny zmieniad się w czasie
w celu realizacji pożądanego ruchu członu roboczego.

Zadanie: polega na wyznaczeniu wszystkich możliwych zbiorów wartości przemieszczeo
kątowych i liniowych (współrzędnych konfiguracyjnych) w połączeniach ruchowych, które
umożliwią manipulatorowi osiągnięcie zadanych pozycji lub orientacji członu roboczego
chwytaka lub narzędzia. Mając dane pozycję i orientację należy obliczyd wszystkie możliwe
zbiory współrzędnych konfiguracyjnych tak, aby osiagnac pożadaną pozycję i orientację.

Jest to zadanie trudniejsze do prostego zadania kinematyki ze wzgledu na wielokrotnośd
rozwiązao i ich nieliniowośd.

W ogólności rozwiązanie nie jest jednoznaczne



Dynamika prosta

Problem: Manipulator robota jest przede wszystkim urządzeniem pozycjonującym. Jeżeli
chcemy sterpwad pozycją, to musimy znad właściwości dynamiczne manipulatora, żeby
wiedzied jak dużą siłę należy wywrzed w celu spowodowania ruchu.

Zadanie: W zadaniu prostym dynamiki dany jest punkty trajektorii ruchu, prędkości oraz
przyspieszenia, a wyznacza się wektory sił i momentów napędowych u(t). Takie zadanie
występuje przy sterowaniu ruchem manipulatora.

Wzór na dynamikę uzyskuje się z równao Eulera-Lagrange`a oraz równao Hamiltona.
Przyjmuje on postad:

, gdzie:

- to położenie, prędkośd oraz przyspieszenie,

- macierz bezwładności,

- macierz sił odśrodkowych i Coriolisa,

- macierz grawitacji,

- macierz tarcia,

F + u - siły działające na układ.

Znajomośd modelu dynamiki jest ważna przy sterowaniu manipulatorem, bo możemy
stosowad lepsze algorytmy (np. Obiczanego momentu albo dysypatywne)



Dynamika odwrotna

Zadanie: polega na wyznaczeniu ruchu manipulatora będącego pod działaniem sił i
momentów napędowych, tzn. dany jest wektor u(t), a należy wyznaczyd położenie, prędkości
i przyspieszenia.

Inne ważne pojęcia



Reprezentacja Denavita-Hartenberga

Możliwe jest dokonanie obliczeo nie przestrzegając tej konwencji, jednak w celu
uproszczenia równao oraz w celu kreowania uniwersalnego języka często do opisu
kinematyki wykorzystuje się tę notację. Podstawowe założenia to: robot posiada n członów
ponumerowanych od 0 do n, zaczynając od podstawy robota, którą oznaczono jako człon 0.
Przeguby są ponumerowane od 1..n, przy czym przegub i łączy człon i-1 z członem i. Zmienna
przegubowa dla przegubu 1 jest oznaczona przez qi. W przypadku przegubu obrotowego qi
reprezentuje kąt, natomiast w przypadku przegubu pryzmatycznego jest to przemieszczenie.
Z każdym członem w sposób sztywny doczepia się układ współrzędnych. W podstawie
dołącza się układ bazowy oznaczony numerem 0. Następnie są wybierane układy od 1..n w
sposób taki iż układ i jest na sztywno związany z członem i. Oznacza to, iż przy ruchu robota
współrzędne każdego punktu członu i pozostają niezmienne. Dokonano założenia, że Ai jest
macierzą przekształcenia jednorodnego, które transformuje współrzędne punktu z układu i
do układu i-1. Macierz Ai nie posiada stałych wartości, lecz zmienia się wraz ze zmianą
konfiguracji robota w przestrzeni. Dokonując założenia, że wszystkie przeguby są obrotowe
lub pryzmatyczne oznacza to, iż Ai jest funkcją tylko jednej zmiennej qi.

Taka konwencja powoduje, iż każde jednorodne przekształcenie Ai jest reprezentowane
przez cztery przekształcenia podstawowe:

- kinematyka manipulatora



Jakobian analityczny

Jakobinem analitycznym manipulatora nazywamy macierz Jacobiego:

 

 

q

x

k

q

J









reprezentacji kinematyki manipulatora we współrzędnych: k R

n

→ R

m

, y=k(q) Jakobian

analityczny można traktowad jako przekształcenie prędkości zmian współrzędnych

przegubowych w prędkośd zmian współrzędnych zadaniowych, przy zadanej konfiguracji
manipulatora,

 

q

q

J

y









.

Postad jakobianu analitycznego zależy od wyboru układu współrzędnych (parametryzacji)
dokonanego w celu zdefiniowania odwzorowania k.



Jakobian manipulatora

Jakobian manipulatora jest to macierz przekształcenia prędkości ruchu w przegubach w
prędkośd liniową i prędkośd kątową w przestrzeni efektora względem układu podstawowego
tj.:























q

q

J

T

m

s

)

(



.

Jakobian manipulatora wyraża się jako:























n

m

n

i

m

i

m

m

m

q

q

J

q

q

J

q

q

J

q

q

J

q

q

J

)

(

...

)

(

...

)

(

)

(

)

(

2

2

1

1

Zatem:











)

(

),...,

(

),

(

)

(

q

J

q

J

q

J

q

J

m

n

m

m

m

2

1

.

Aby wyliczyd

)

(q

J

m

i

zatrzymujemy q

k

dla k≠i (

0



k

q

) i analizujemy ruch efektora

będący efektem ruchu w i-tym przegubie dla























1

0

1

0

1

0

1

0

i

i

i

T

R

A

.

Jeżeli i-ty przegub jest obrotowy, to:





























1

3

0

1

0

0

1

3

0

i

k

i

n

i

k

m

i

R

T

T

R

q

J

)

(

)

(

.

Jeżeli i-ty przegub jest przesuwny, to:



















0

1

3

0

i

k

m

i

R

q

J

)

(

.

Ponadto istnieje związek między jakobianem manipulatora a jakobianem analitycznym. Dla
y=(kartezjaoskie,KKM) mamy:

)

(

)

(

q

J

M

I

q

J

KKM

m





















0

0

3

gdzie:









































s

c

s

c

c

c

s

M

KKM

0

1

0

0

.



Osobliwości

Konfiguracje osobliwe to takie wartości współrzędnych wewnętrznych manipulatora
robotycznego, przy których układ zaczyna się zachowywad w inny sposób niż przewidziano.
Przykładowo efektor robota może znaleźd się w takim położeniu, w którym pozostanie
pomimo ruchów silników.

Aby otrzymad zbiór konfiguracji osobliwych należy policzyd wyznacznik macierzy J (patrz
algorytm Jakobianowy). Wynik przyrównujemy do 0 i wyznaczamy wartości współrzędnych
wewnętrznych, przy których spełnione jest to równanie.

Cechy konfiguracji osobliwych:

1. Zmieniona liczba rozwiazao zadania odwrotnego kinematyki.

2. Nie działa algorytm Jakobianowy.

3. Zbiór konfiguracji jest "mały" (miary 0).

4. Możliwy jest ruch przegubów nie powodujący ruchu efektora.

5. Istnieją siły działające na efektor, które nie wymagają równoważenia.

Ad2. W tym przypadku wymagana jest odwracalnośd macierzy J, a w konfiguracji osobliwej
wyznacznik macierzy J wynosi 0.

Ad5. Podczas przenoszenia większych ciężarów cecha ta jest przydatna, i niekiedy specjalnie
wprowadza się manipulator w stan "osobliwy". Podobna sytuacja ma miejsce przy zawodach
w podnoszeniu sztangi, gdzie zawodnicy odpowiednio zginają i prostują ramiona.



KKM, kąty eulera (parametryzacja)

Kąty Eulera — układ trzech kątów, za pomocą których można jednoznacznie określid
wzajemną orientację dwu kartezjaoskich układów współrzędnych

Poszczególne kąty Eulera (

) parametryzują powyższe trzy obroty; definiujemy je zatem

następująco:

— kąt obrotu wokół Z

ψ - kąt obrotu wokół X

θ — kąt obrotu wokół Z

KKM – kąty

oznaczające obroty odpowiednio wokół osi Z,Y i X.

Określone są na zbiorze

Roboty mobilne



Kinematyka robota mobilnego

Kinematyka robota mobilnego jest scharakteryzowana przez układ sterowania,
liniowy z uwagi na sterowania postaci

(11)

gdzie

,

, m = n − l, a n jest liczba stopni swobody układu, natomiast l jest

liczba niezaleznych graniczen nieholonomicznych układu. Załózmy, ze dla kazdego stanu
poczatkowego q0 i zadanego sterowania u(·) istnieje trajektoria

q(t) =

(q0, u(·)),(12)

które stanowi poczatkowemu q0 układu i sterowaniu u(·) przyporzadkowuje
stan układu w chwili t e [0, T]. Dla t = 0 mamy zawsze

(q0, u(·)) = q0. Przy ustalonym

stanie poczatkowym i zmieniajacym sie sterowaniu u(·) odwzorowanie (12) opisuje stany
osiagalne w układzie sterowania (11) ze stanu q0 w chwili t. Jezeli dla kazdego q0 zbiór
stanów osiagalnych w chwili t obejmuje cała przestrzen stanu Rn, to układ (11) jest układem
osiagalnym, a jako ze dla układów tej postaci osiagalnosc pociaga za soba sterowalnosc to
układ (11) równiez sterowalny.

Kinematyka robota mobilnego



Ograniczenia holonomiczne, nieholonomiczne

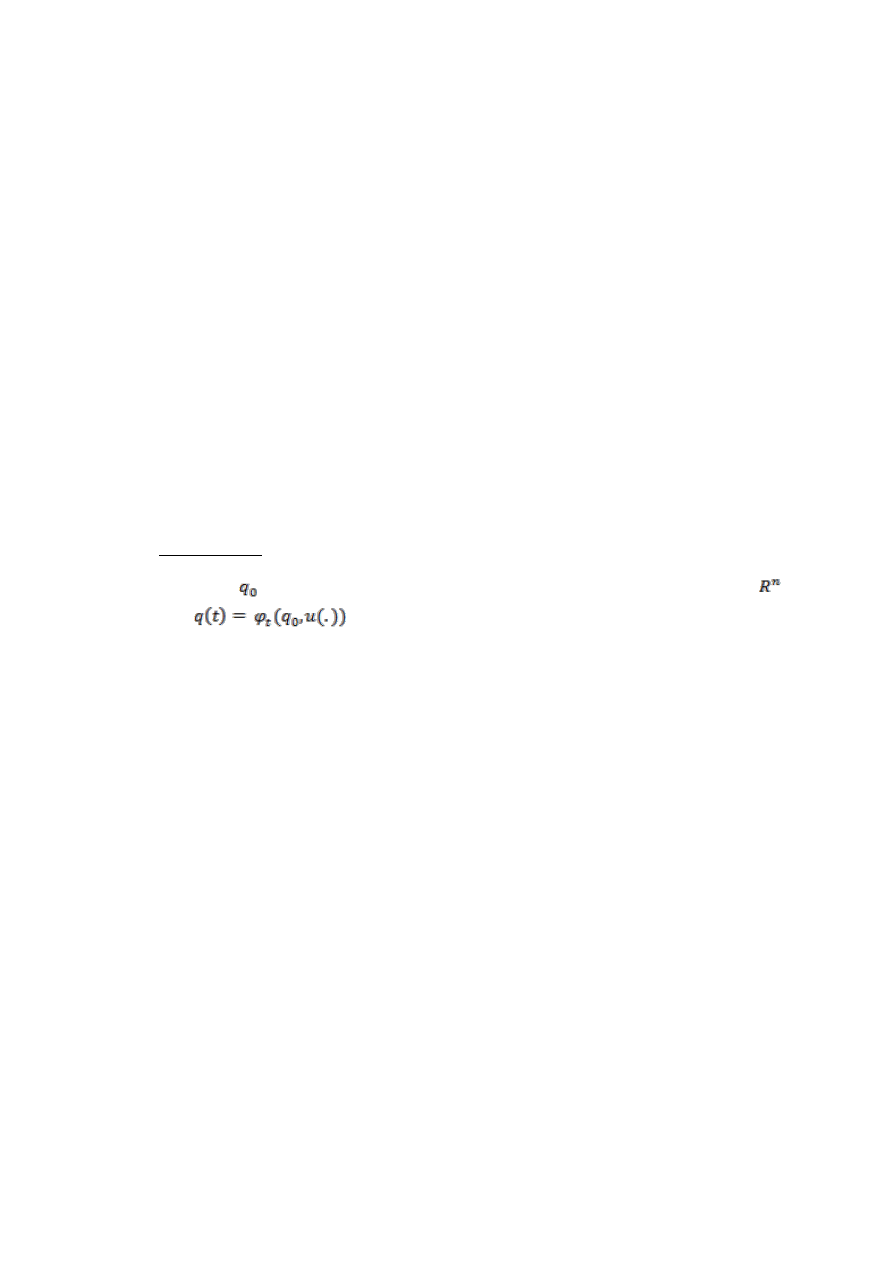
Holonomicznośd jest to pojęcie nierozerwalnie związane z robotami mobilnymi oraz
ograniczeniami Pfaffa i opisuje ograniczenia ruchu jakim podlega robot. Razem z nim
występuje przeciwstawne pojęcie nieholonomicznośd. Robot jest holonomiczny, jeśli może
zmienid kierunek swojego ruchu (swoją orientację) w miejscu.

Jednymi z ograniczeo nakładanymi na ruch robota, są ograniczenia dotyczące przestrzeni, w
której robot może się poruszad. Nie można przejechad przez ścianę, ani wbid się w podłogę.
Ograniczenia takie dotyczą robotów holonomicznych. Innymi ograniczeniami są ograniczenia
dotyczące sposobu realizacji ruchu. Opisują one po jakich prostych i krzywych może poruszad
się robot, który posiada określoną orientację. Ograniczenia te nazywane są ograniczeniami
nieholonomicznymi i dotyczą większości klas robotów mobilnych.

Najprostszym przykładem robota nieholonomicznego jest samochód. Podczas parkowania
należy wykonad serię manewrów, aby ustawid się równolegle do krawężnika.

Holonomicznośd (nieholonomicznośd) wpływa na sposób wyznaczania trasy.



Sterowalnośd

Jeżeli dla każdego

, zbiór stanów osiągalnych, w chwili t obejmuje całą przestrzeo stanu

,

układ układ

nazywamy sterowalnym w chwili t