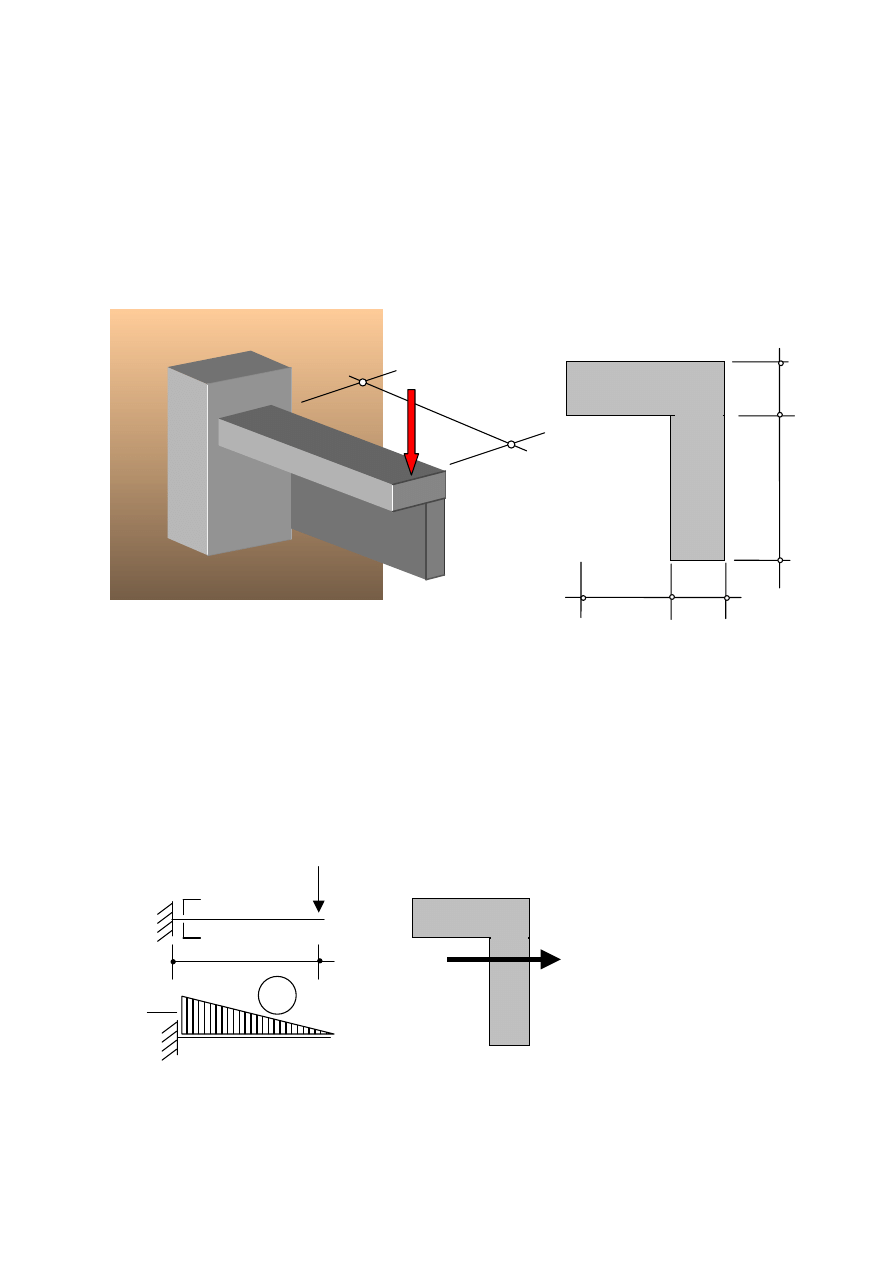
Przykład 3.2. Zginanie ukośne. Układ współrzędnych (0xy)

Wyznacz rozkład naprężenia normalnego w przekroju podporowym belki wspornikowej o
długości L obciążonej na końcu swobodnym pionową siłą P. Wymiary przekroju
poprzecznego belki podane są na rysunku zamieszczonym poniżej.
Oblicz naprężenia przyjmując następujące wartości liczbowe:
P=20kN, L=200cm, a=1cm

P

L

Przekrój poprzeczny

6a

2a

2a

4a

Rozwiązanie
Obliczmy moment gnący i charakterystyki przekroju. Przekonamy się czy wektor momentu
gnącego pokrywa się z jedną z głównych osi momentów bezwładności przekroju.
Przed przystąpieniem do obliczeń warto przez chwilę zastanowić się nad zadaniem.
Przyglądając się kształtowi przekroju poprzecznego łatwo możemy przewidzieć, że osie
główne są ustawione skośnie. Ponieważ wektor momentu jest poziomy (prostopadły do siły
P) przewidujemy, że mamy odczynienia ze zginaniem ukośnym.

Wyznaczmy wektor momentu gnącego w utwierdzeniu.
M=L P=PL=4000[kNcm]

PL

α -α

α

α

M

M

L

P

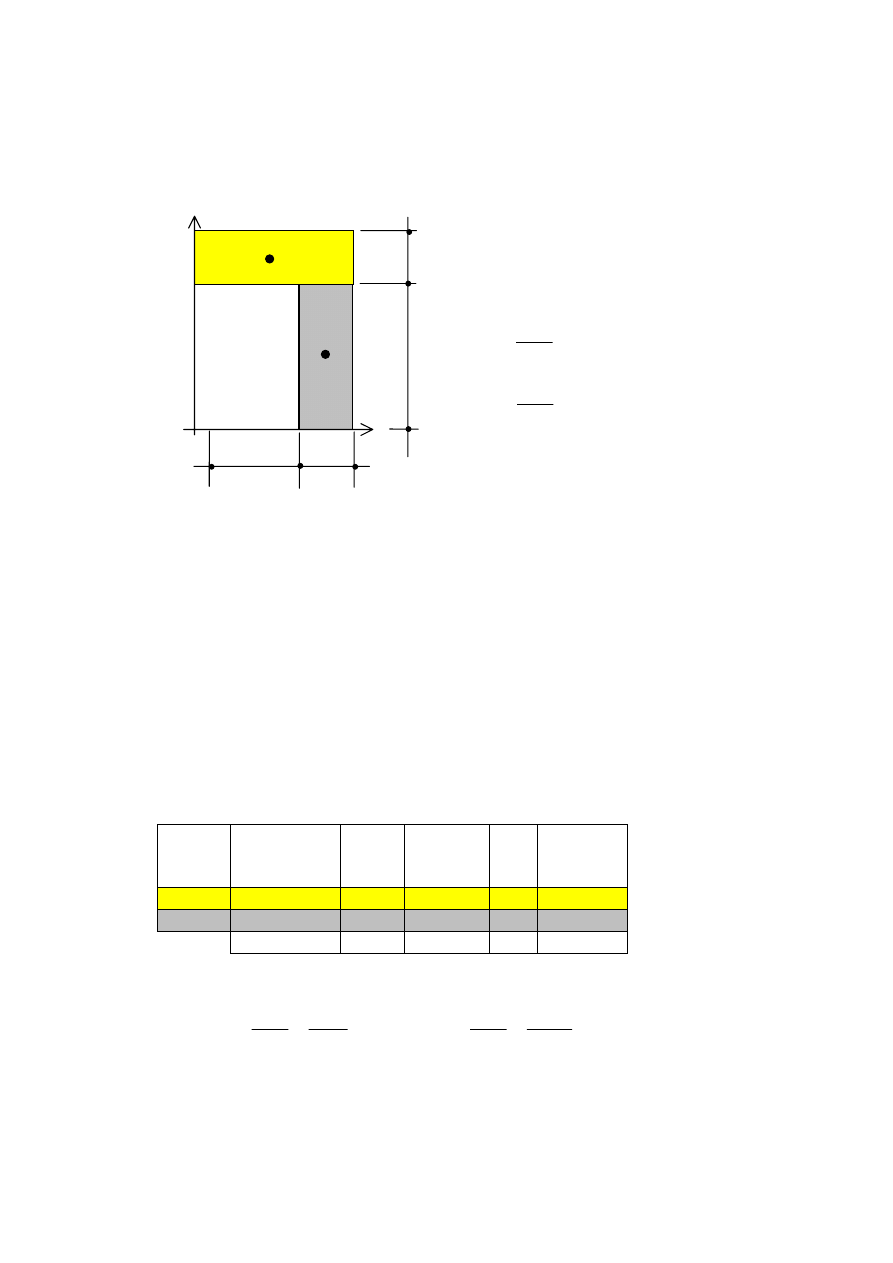
Obliczmy momenty bezwładności przekroju poprzecznego.

Podzielimy figurę na dwa prostokąty, wyznaczymy środek ciężkości i wartość momentów
bezwładności względem osi centralnych.

y

x

II

I

6a

2a

2a

4a

Współrzędne środka ciężkości
wyznaczamy ze wzorów:

i

i

yi

i

c

F

S

x

Σ

Σ

=

,

i

i

xi

i

c

F

S

y

Σ

Σ

=

.

F

i

-oznacza pole powierzchni i-tej figury, na które podzielono cały przekrój.

i

i

yi

x

F

S

=

- jest momentem statycznym i-tej figury, na które podzielono cały przekrój

względem osi y. Moment statyczny względem osi y równy jest iloczynowi pola
powierzchni tej figury przez współrzędną jej środka ciężkości x

i

.

i

i

xi

y

F

S

=

- jest momentem statycznym i-tej figury, na które podzielono cały przekrój

względem osi x. Moment statyczny względem osi x równy jest iloczynowi pola
powierzchni tej figury przez współrzędną jej środka ciężkości y

i

.

Obliczenia możemy szybko przeprowadzić wykorzystując arkusz kalkulacyjny.

nr figury

F

pole

powierzchni

x

Sy

moment

statyczny

y

Sx

moment

statyczny

I

12 [a2]

3 [a]

36 [a3] 7 [a]

84 [a3]

II

12 [a2]

5 [a]

60 [a3] 3 [a]

36 [a3]

24

[a2]

4 [a]

96 [a3]

5 [a]

120 [a3]

a

a

a

F

S

x

i

i

yi

i

c

4

24

96

2

3

=

=

Σ

Σ

=

a

a

a

F

S

y

i

i

xi

i

c

5

24

120

2

3

=

=

Σ

Σ

=

2

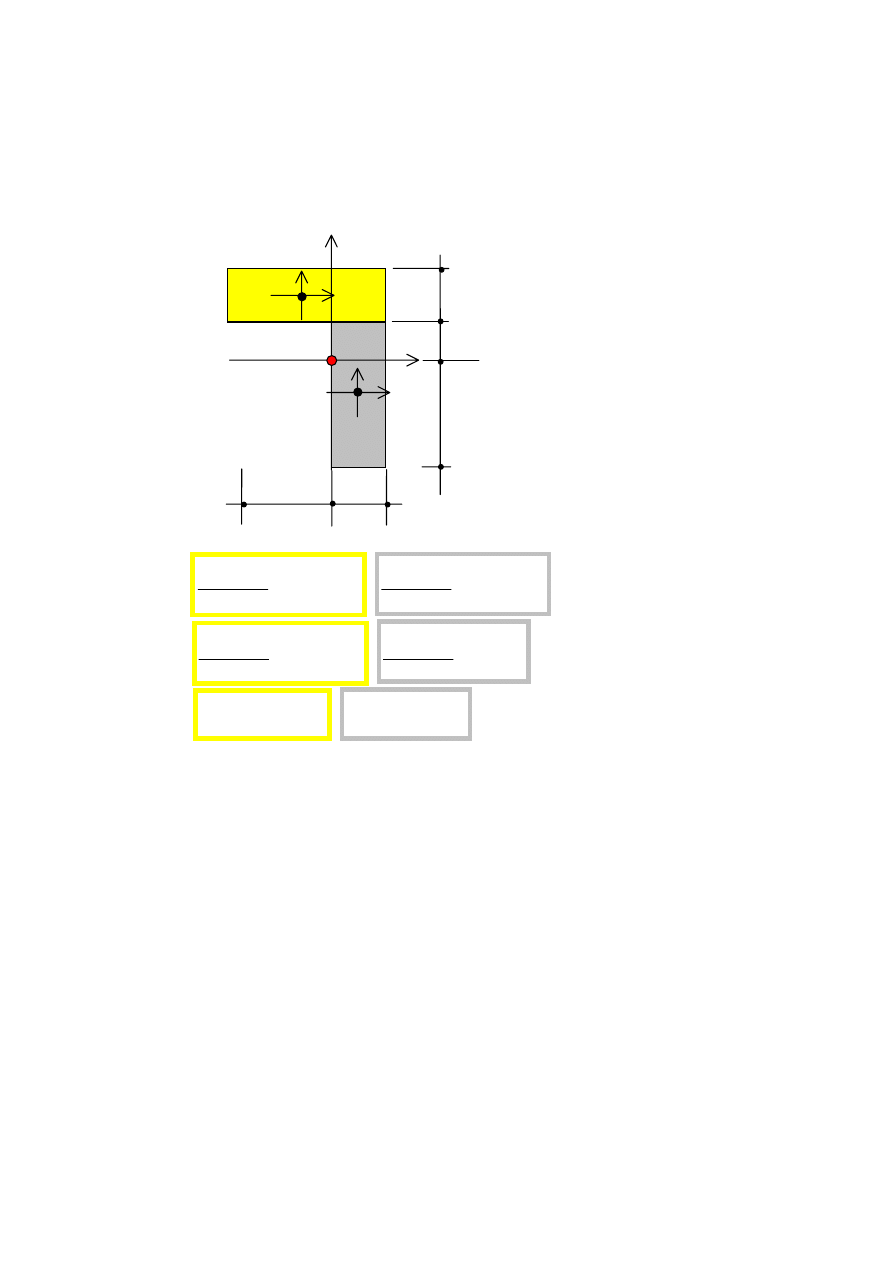
Obliczmy teraz korzystając ze wzorów Steinera wartości momentów bezwładności względem
osi centralnych x i y .Niech osie x

1

i y

1

oznaczają osie centralne dla poszczególnych figur, na

które podzielono cały przekrój.

x

1

y

1

x

1

y

1

1a

y

x

II

I

5a

2a

2a

4a

4

2

3

2

3

136

12

)

2

(

12

)

6

(

2

12

)

2

(

12

)

2

(

6

a

a

a

a

a

a

a

a

a

I

x

=

⋅

+

⋅

+

⋅

+

⋅

=

4

2

3

2

3

64

12

12

)

2

(

6

12

)

(

12

)

6

(

2

a

a

a

a

a

a

a

a

a

I

y

=

⋅

+

⋅

+

⋅

−

+

⋅

=

4

48

12

)

2

(

0

12

)

(

2

0

a

a

a

a

a

a

a

I

xy

−

=

⋅

⋅

−

+

+

⋅

−

⋅

+

=

Dalszą część zadania możemy rozwiązać na dwa sposoby.

Można wyznaczyć osie główne centralne, znaleźć współrzędne wektora momentu

gnącego w osiach głównych centralnych i wykorzystać wzór na naprężenia przy zginaniu dla
osi głównych centralnych.

Drugi sposób polega na wykorzystaniu wzoru na naprężenia przy zginaniu

wyprowadzonego dla osi centralnych.

Metoda druga jest krótsza, ale daje mniej możliwości sprawdzenia poprawności

naszego rozwiązania.

Rozwiązując metodą pierwszą znamy ustawienie osi głównych i możemy sprawdzić

czy wyznaczona przez nas oś obojętna dla zginania ukośnego jest odchylona od kierunku
wektora momentu w stronę osi głównej względem, której moment bezwładności jest
mniejszy.
Przedstawmy więc obydwa rozwiązania.

3

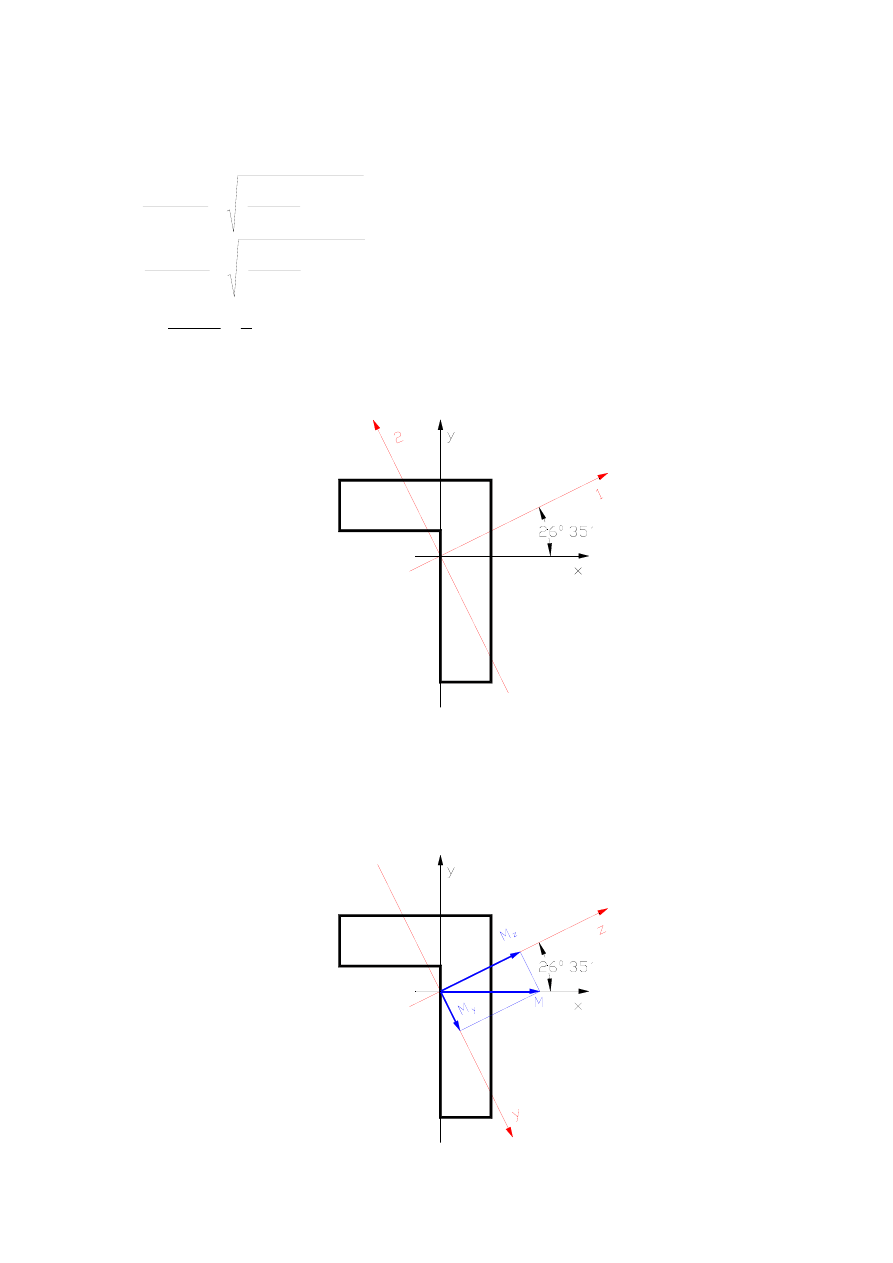
Metoda I – rozwiązanie w osiach głównych centralnych.

Wyznaczmy osie główne centralne i główne centralne momenty bezwładności.

4

2

2

1

160

2

2

)

(

a

I

I

I

I

I

I

xy

y

x

y

x

=

+













−

+

+

=

4

2

2

2

40

2

2

)

(

a

I

I

I

I

I

I

xy

y

x

y

x

=

+













−

−

+

=

3

4

2

2

tg

=

−

−

=

y

x

xy

I

I

I

β

,

,

'

]

[

2

/

4636

.

0

rad

n

π

β

⋅

+

=

45

35

26

0

0

n

+

=

β

Ponieważ moment dewiacyjny I

xy

ma wartość ujemną, więc oś główna, względem której

moment bezwładności osiąga maksimum przechodzi przez pierwszą ćwiartkę układu (0xy).

Zmieńmy układ osi na taki, jaki tradycyjnie stosuje się w zadaniach na zginanie belek.
Zamiast układu (012) wprowadzimy układ (0yz).
Zapiszmy momenty bezwładności względem osi nowego układu:

I

z

= I

1

= 160a

4

I

y

= I

2

= 40a

4

4

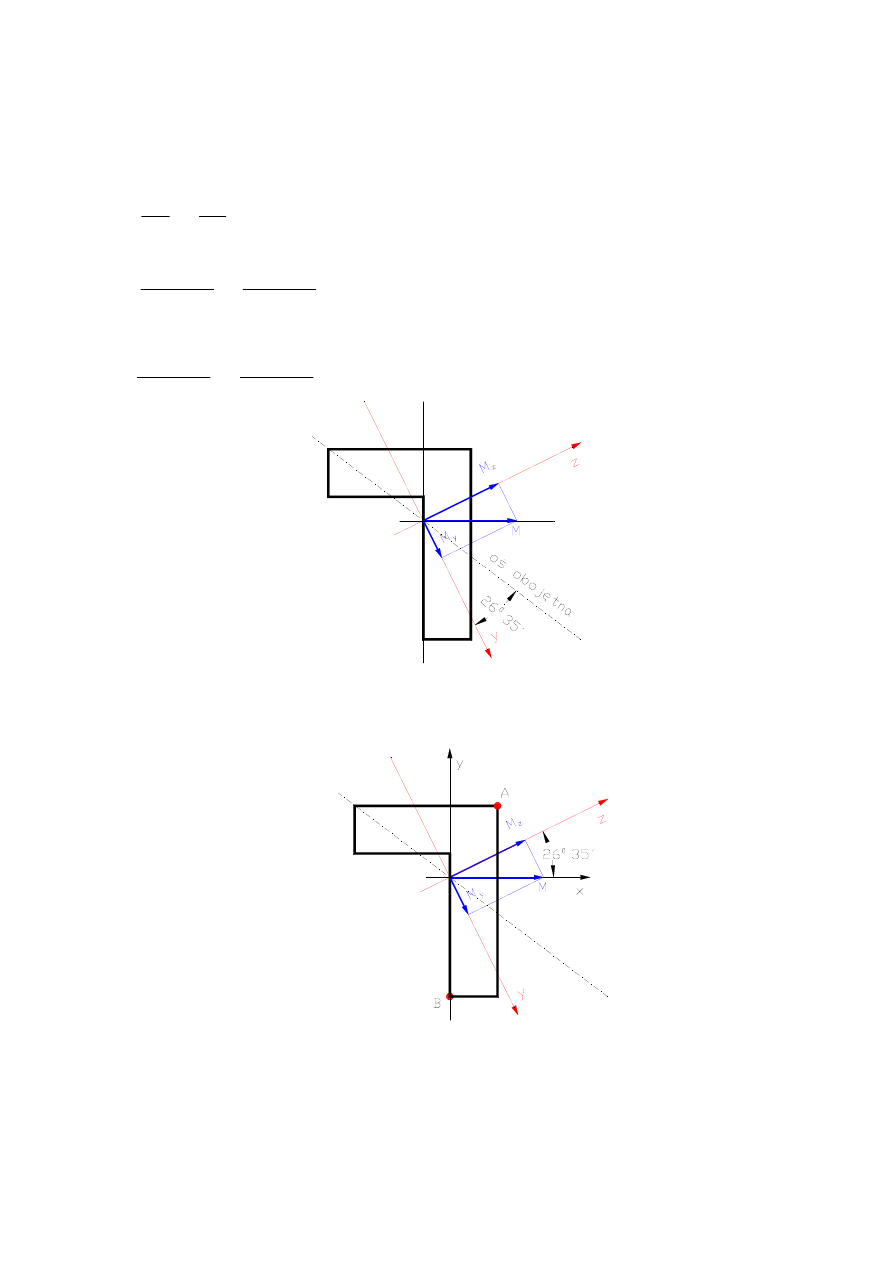
Obliczmy współrzędne momentu gnącego w układzie (0yz).

M

y

=M sin(26

0

35’)=0.4472 M

M

z

=M cos(26

0

35’)=0.8944 M

Rozkład naprężenia normalnego od zginania wyznaczymy ze wzoru:

y

I

M

z

I

M

z

z

y

y

−

=

σ

Podstawiając wartości M=PL i I

y

=40a

4

, I

z

=160a

4

otrzymujemy:

y

a

PL

z

a

PL

4

4

160

8944

.

0

40

4472

.

0

−

=

σ

Równanie osi obojętnej (zbioru punktów przekroju dla których naprężenie równe jest zeru)
otrzymujemy podstawiając za σ wartość zero.

y

a

PL

z

a

PL

4

4

160

8944

.

0

40

4472

.

0

0

−

=

⇒

y

z

⋅

= 5

.

0

Wyznaczmy naprężenia w punktach położonych najdalej od osi obojętnej.
Oznaczmy te punkty literami A i B i wyznaczmy współrzędne tych punktów w osiach
głównych centralnych

(0yz)

Zapiszemy współrzędne punktów w osiach (0xy) i dokonamy transformacji układu przez
obrót o kąt α=26

o

35’.

5

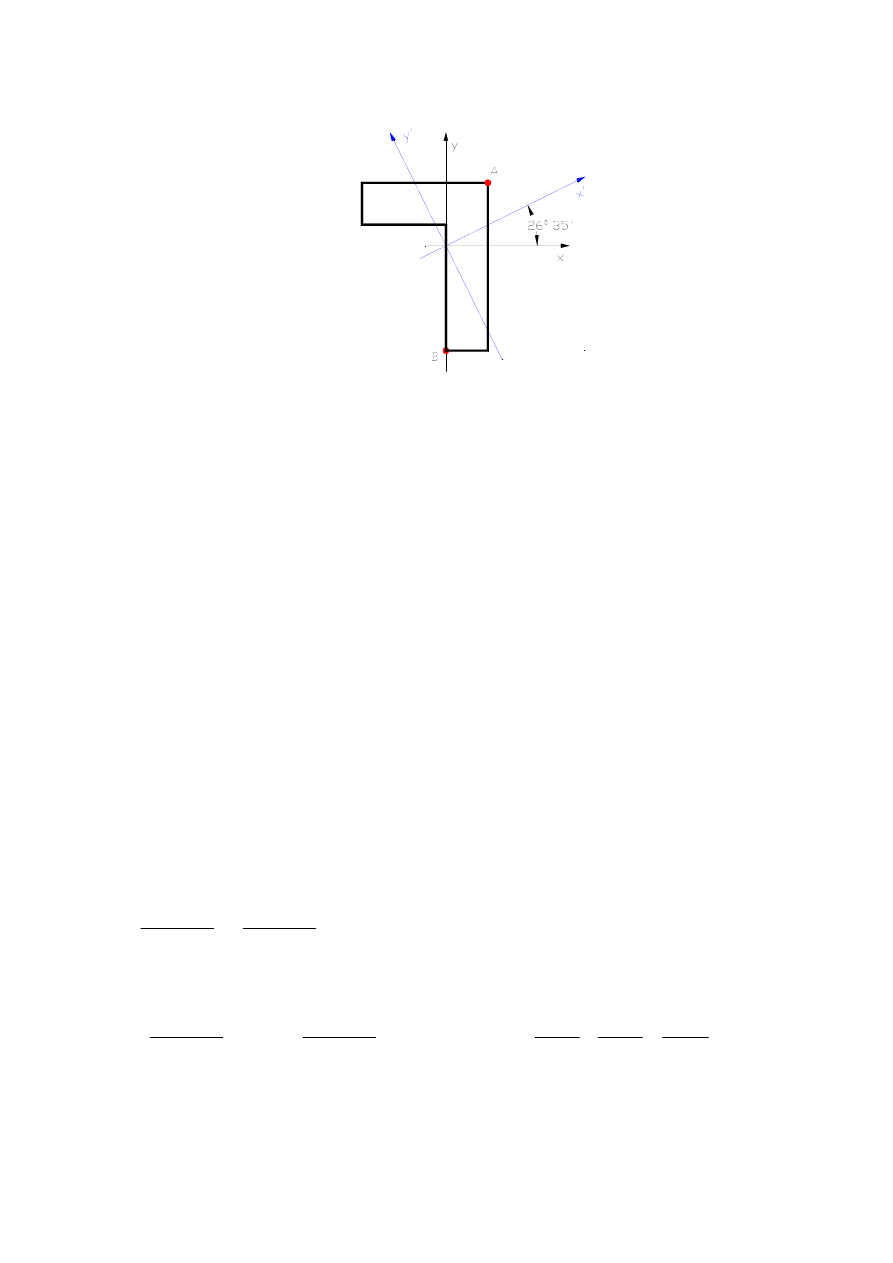
α

α

sin

cos

,

⋅

+

⋅

=

y

x

x

α

α

cos

sin

,

⋅

+

⋅

−

=

y

x

y

podstawiając dla punktu A x=2a, y=3a
i dla punktu B x=0, y=-5a otrzymamy odpowiednio współrzędne punktów A i B w układzie z
prymami.
Dla punktu A:

α

α

sin

3

cos

2

,

⋅

+

⋅

=

a

a

x

⇒

a

x

1305

.

3

,

=

α

α

cos

3

sin

2

,

⋅

+

⋅

−

=

a

a

y

⇒

a

y

7889

.

1

,

=

Dla punktu B:

α

α

sin

)

5

(

cos

0

,

⋅

−

+

⋅

=

a

a

x

⇒

a

x

2361

.

2

,

−

=

α

α

cos

)

5

(

sin

0

,

⋅

−

+

⋅

−

=

a

a

y

⇒

a

y

4721

.

4

,

−

=

Wróćmy do układu (0yz), w którym wyznaczaliśmy naprężenie od zginania.
Współrzędne punktów A i B w tym układzie wynoszą:
Dla punktu A:

y=-y’= -1.7889a
z=x’= 3.1305a

Dla punktu B:

y=-y’= 4.4721a
z=x’= -2.2361a

Podstawmy teraz wyznaczone współrzędne punktów A i B do wyprowadzonego wcześniej
równania na naprężenie normalne przy zginaniu:

y

a

PL

z

a

PL

4

4

160

8944

.

0

40

4472

.

0

−

=

σ

Dla punktu A:

y= -1.7889a
z= 3.1305a

)

7889

.

1

(

160

8944

.

0

1305

.

3

40

4472

.

0

4

4

a

a

PL

a

a

PL

A

−

−

=

σ

⇒

3

3

3

160

2

.

7

160

6

.

1

40

4

.

1

a

PL

a

PL

a

PL

A

=

+

=

σ

,

dla PL=4000 [kNcm], a=1 [cm] otrzymamy:

σ

.

]

[

8

.

1

]

/

[

180

2

GPa

cm

kN

A

⋅

=

⋅

=

Dla punktu B:

y=-y’= 4.4721a

6

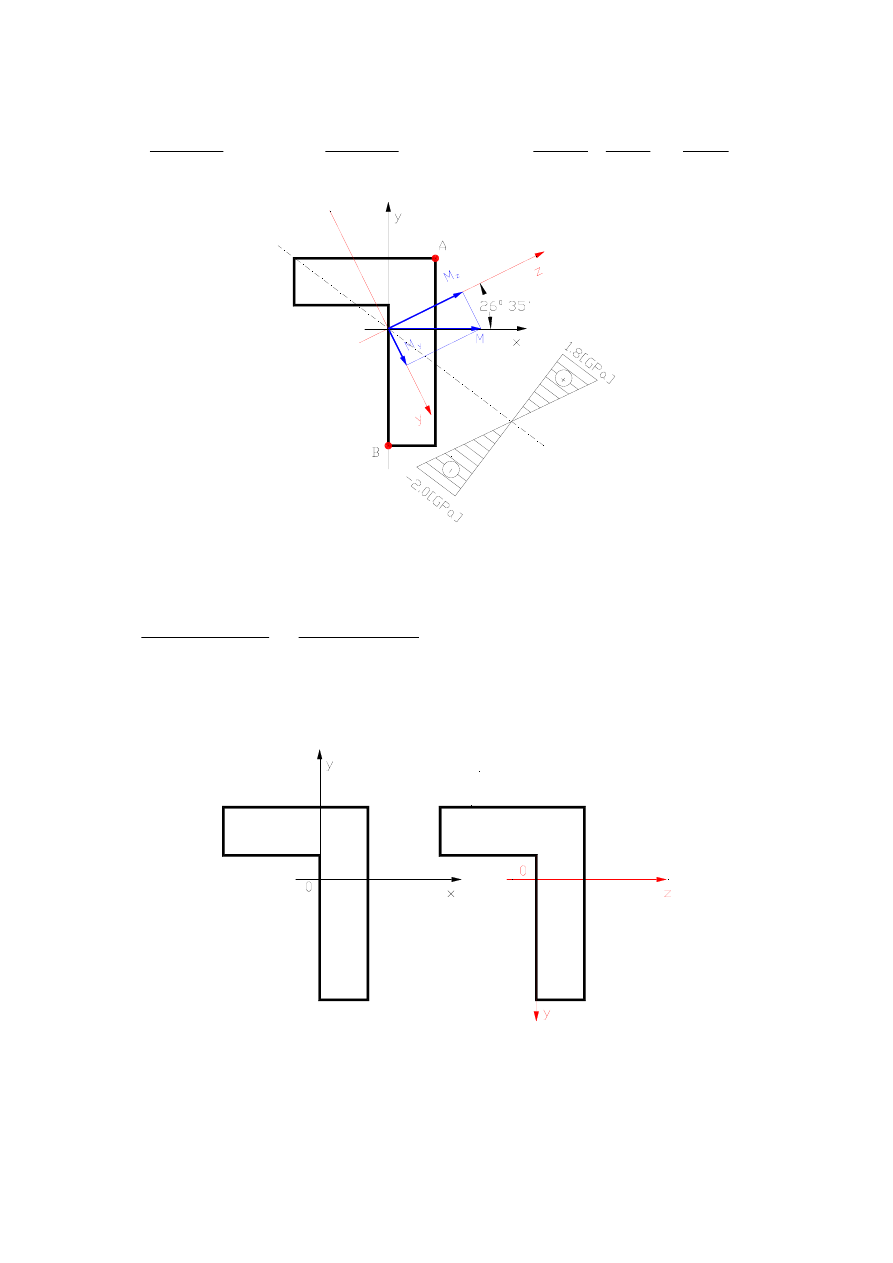
z=x’= -2.2361a

a

a

PL

a

a

PL

B

4721

.

4

160

8944

.

0

)

2361

.

2

(

40

4472

.

0

4

4

−

−

=

σ

⇒

3

3

3

160

8

160

4

40

)

1

(

a

PL

a

PL

a

PL

B

−

−

=

−

−

=

σ

dla PL=4000 [kNcm], a=1 [cm] otrzymamy:

σ

.

]

[

0

.

2

]

/

[

200

2

GPa

cm

kN

B

⋅

−

=

⋅

−

=

Metoda II – rozwiązanie w osiach centralnych.

Rozkład naprężenia normalnego od zginania zapisany dla układu centralnego wyraża wzór:

y

I

I

I

J

M

I

M

z

I

I

I

I

M

I

M

yz

y

z

yz

y

y

z

yz

y

z

z

y

yz

z

2

2

−

⋅

⋅

+

−

−

⋅

⋅

+

⋅

=

σ

Przejdźmy z układu (0xy), w którym szukaliśmy momentów bezwładności przekroju
poprzecznego do układu

(0yz)

w którym wyprowadzony był wzór na naprężenia normalne od

zginania

4

136 a

I

x

⋅

=

4

136 a

I

z

⋅

=

4

64 a

I

y

⋅

=

4

64 a

I

y

⋅

=

4

48 a

I

xy

⋅

−

=

4

48 a

I

yz

⋅

=

7

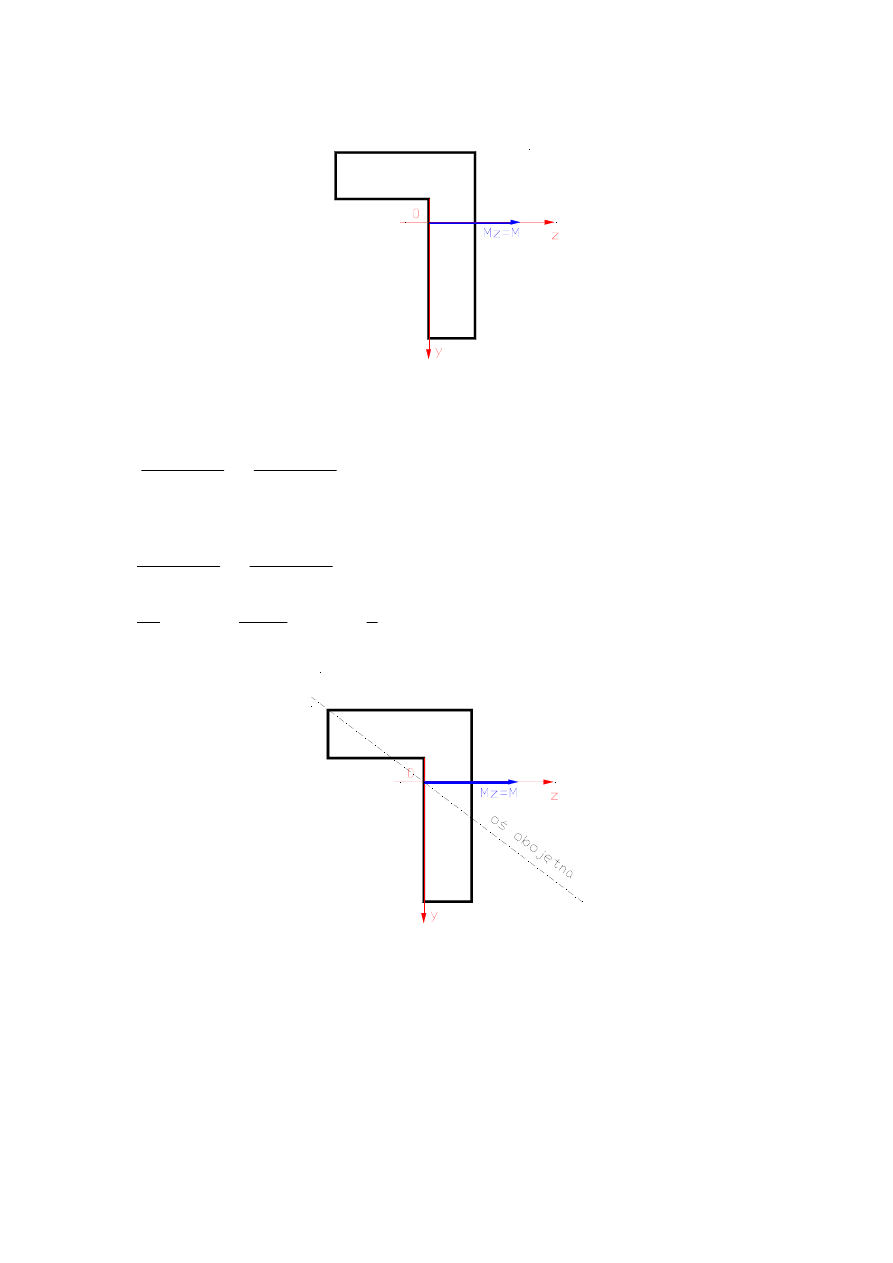
Zauważymy, że naszym zadaniu wektor momentu gnącego pokrywa się z osią z.

Wartości składowych momentu wynoszą więc:

M

z

= PL,

M

y

= 0.

Wzór na naprężenia normalne od zginania upraszcza się do postaci:

y

I

I

I

I

M

z

I

I

I

I

M

yz

y

z

y

z

yz

y

z

yz

z

2

2

−

⋅

−

−

⋅

⋅

=

σ

Równanie osi obojętnej otrzymujemy podstawiając za σ wartość zero.

y

I

I

I

I

M

z

I

I

I

I

M

yz

y

z

y

z

yz

y

z

yz

z

2

2

0

−

⋅

−

−

⋅

⋅

=

⇒

y

I

z

I

y

yz

⋅

−

=

0

y

I

I

z

yz

y

=

⇒

y

a

a

z

4

4

48

64

⋅

⋅

=

⇒

y

z

3

4

=

Wyznaczmy naprężenia w punktach położonych najdalej od osi obojętnej.
Oznaczmy te punkty literami A i B i wyznaczmy współrzędne tych punktów w osiach
centralnych

(0yz)

.

8

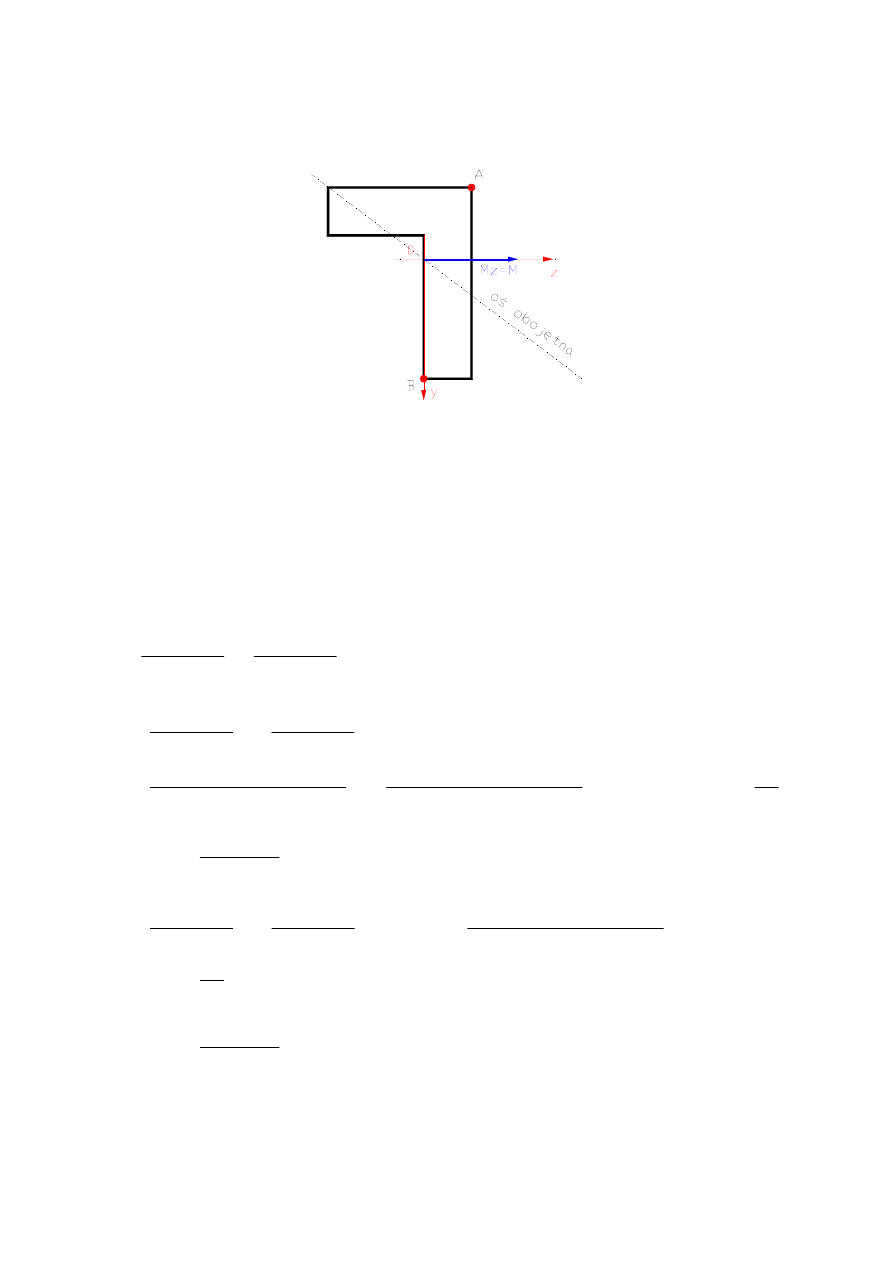
Współrzędne punktów A i B wynoszą:
Punktu A

y

A

= -3a,

z

A

= 2a

Punktu B

y

B

= 5a,

z

B

= 0

Podstawmy teraz współrzędne punktów A i B i wartości momentów bezwładności do
wyprowadzonego wcześniej równania na naprężenie normalne przy zginaniu. Otrzymamy
naprężenia normalne w punktach leżących najdalej od osi obojętnej.

y

I

I

I

I

M

z

I

I

I

I

M

yz

y

z

y

z

yz

y

z

yz

z

2

2

−

⋅

−

−

⋅

⋅

=

σ

dla punktu A

A

yz

y

z

y

z

A

yz

y

z

yz

z

A

y

I

I

I

I

M

z

I

I

I

I

M

2

2

−

⋅

−

−

⋅

⋅

=

σ

⇒

)

3

(

)

48

(

64

64

2

)

48

(

64

136

48

2

4

4

4

4

2

4

4

4

4

a

a

a

a

a

PL

a

a

a

a

a

PL

A

−

⋅

−

⋅

⋅

⋅

⋅

⋅

−

⋅

−

⋅

⋅

⋅

⋅

⋅

=

σ

136

⇒

3

045

.

0

a

PL

A

⋅

=

σ

Po podstawieniu wartości liczbowych dla P i L otrzymujemy:

3

4000

045

.

0

cm

kNcm

A

⋅

=

σ

σ

⇒

]

[

8

.

1

]

/

[

180

2

GPa

cm

kN

A

⋅

=

⋅

=

i dla punktu B

B

yz

y

z

y

z

B

yz

y

z

yz

z

B

y

I

I

I

I

M

z

I

I

I

I

M

2

2

−

⋅

−

−

⋅

⋅

=

σ

⇒

)

5

(

)

48

(

64

136

64

2

4

4

4

4

a

a

a

a

a

PL

B

⋅

−

⋅

⋅

⋅

⋅

⋅

−

=

σ

⇒

3

05

.

0

a

PL

B

⋅

−

=

σ

Po podstawieniu wartości liczbowych dla P i L otrzymujemy:

3

4000

05

.

0

cm

kNcm

B

⋅

−

=

σ

σ

⇒

]

[

0

.

2

]

/

[

200

2

GPa

cm

kN

B

⋅

=

⋅

−

=

9