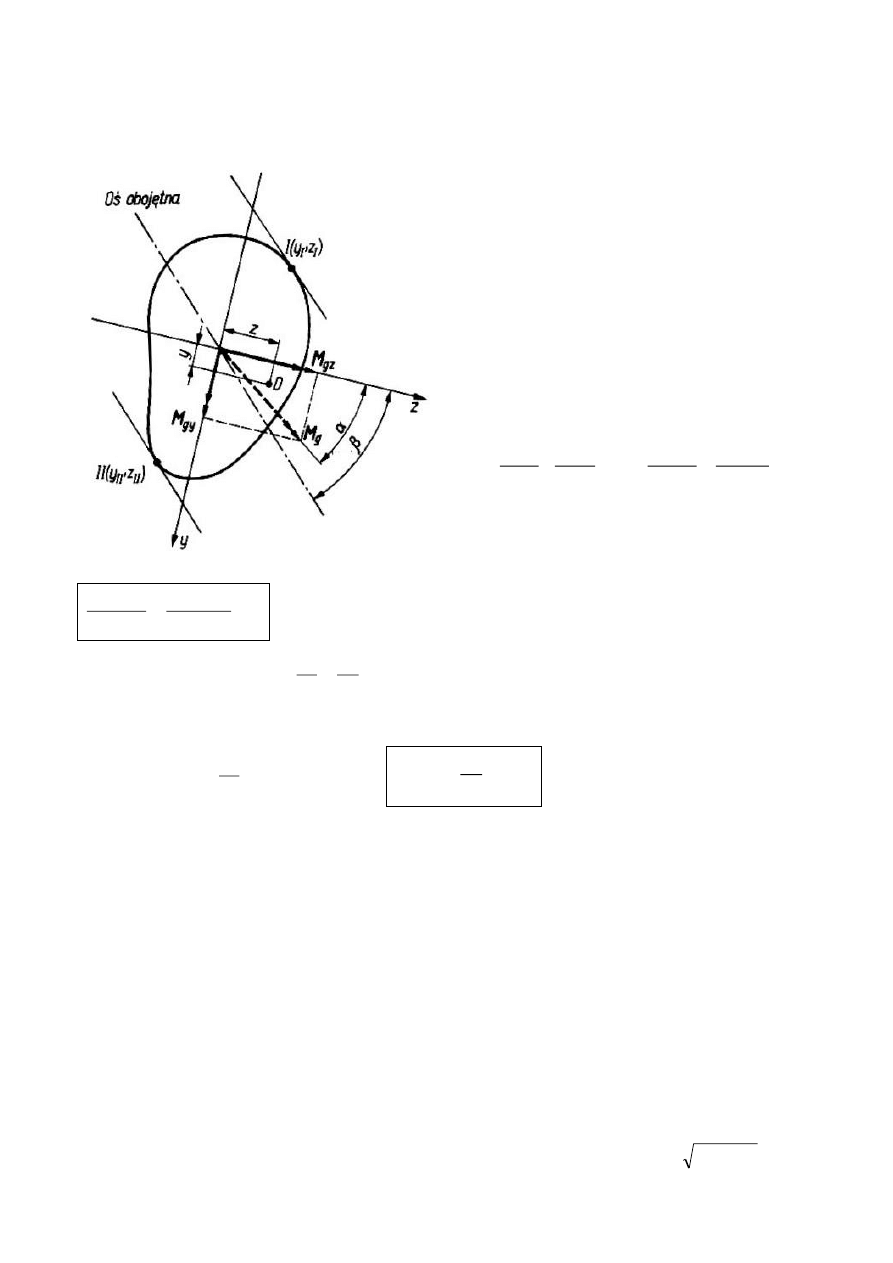
ZGINANIE UKOŚNE (ZŁOŻONE)

Zginanie ukośne – gdy kierunek wektora momentu gnącego nie pokrywa się z kierunkiem

jednej z głównych osi bezwładności przekroju.

z, y

– główne centralne osie bezwładności

M

g

– moment gnący i jego składowe:

M

gy

= M

g

sin



,

M

gz

= M

g

cos



Naprężenia w dowolnym punkcie D(y,z)
wyznaczymy jako superpozycję naprężeń
wywołanych dwoma zginaniami prostymi.

W przyjętym układzie osi i zwrocie moment



=



+

























z

y

g

z

gz

y

gy

J

y

J

z

M

J

y

M

J

z

M







cos

sin

Przyrównując naprężenie do zera (



=0),

otrzymamy

równanie osi obojętnej przekroju.

0

cos

sin

0

0





z

y

J

y

J

z





gdzie y

o

, z

o

-

współrzędne dowolnego punktu na osi obojętnej.

Po przekształceniu



tg

J

J

z

y

y

z



0

0

Niech



określa położenie osi obojętnej względem osi z

wówczas



tg

z

y



0

0

i





tg

J

J

tg

y

z





położenie osi obojętnej nie zależy od wartości M

g

, a tylko od kierunku jego wektora i

stosunku dwóch głównych momentów bezwładności,



kierunek osi obojętnej w zginaniu ukośnym nie pokrywa się z kierunkiem wektora
momentu głównego,



naprężenia maksymalne wystąpią w punktach najbardziej odległych od osi obojętnej,



zginanie ukośne nie występuje w przypadku takich przekrojów jak np. kołowy czy
kwadratowy co wynika z równości J

z

= J

y

.

Przemieszczenia belki ukośnie określimy za pomocą superpozycji:

jeżeli w płaszczyźnie xy ugięcie określimy z EJ

z

y



= - M

gz

a w płaszczyźnie xz

z EJ

y

z



= - M

gy

to ugięcie wypadkowe będzie sumą geometryczną:

2

2

z

y

f





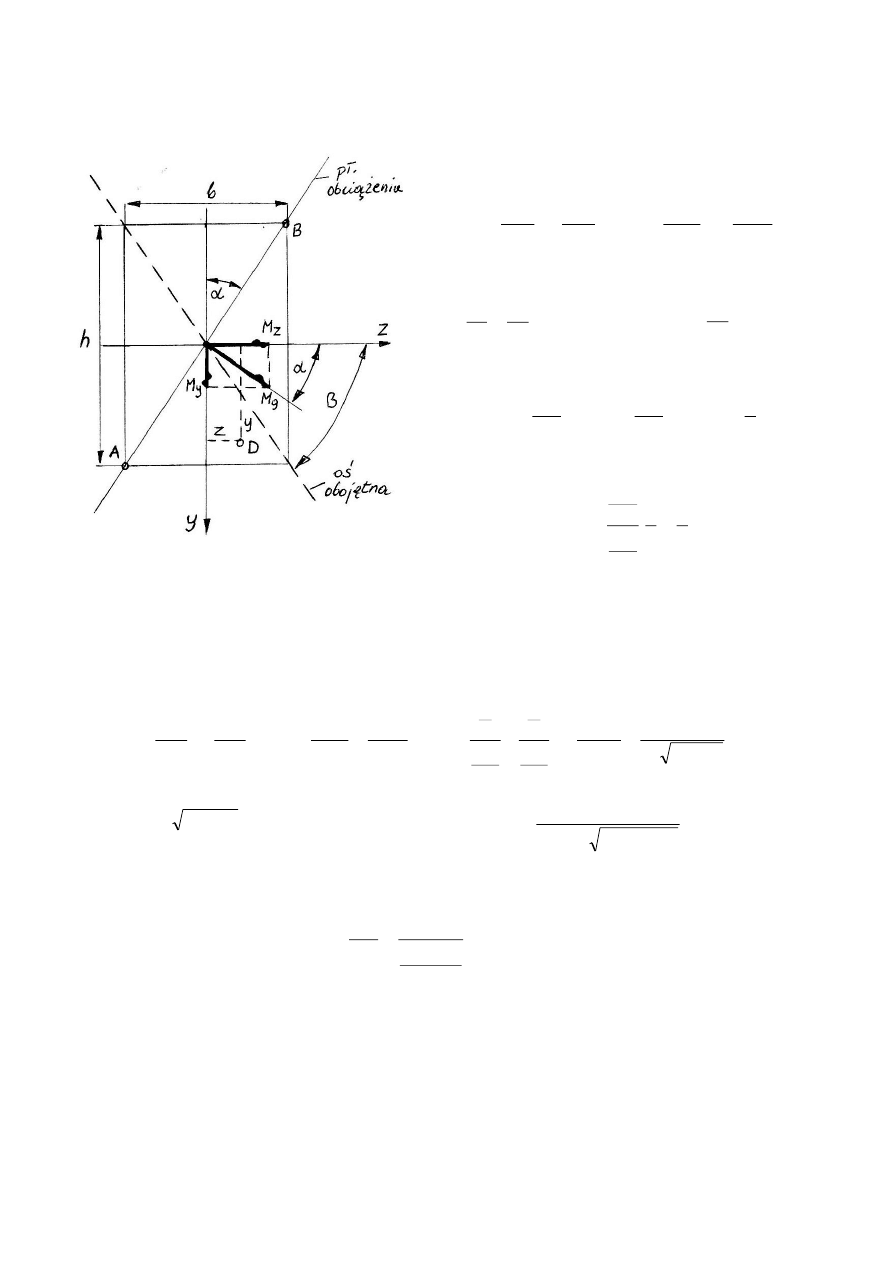
Przykład.

Na belkę o przekroju prostokątnym b=10 cm, h=20 cm działa M

g

=30 kNm.

Płaszczyzna działania momentu przechodzi przez przekątną AB. Znaleźć położenie
osi obojętnej zginania i obliczyć największe naprężenia

.

Całkowite naprężenie w dowolnym punkcie D:























y

J

z

J

M

y

J

M

z

J

M

z

y

g

z

gz

y

gy

D







cos

sin

równanie osi obojętnej:



tg

J

J

z

y

y

z



0

0







tg

J

J

tg

y

z



Wyznaczmy potrzebne wielkości:

h

b

tg

bh

J

hb

J

z

y









12

12

3

3

stąd

b

h

h

b

bh

hb

tg





12

12

3

3



-

osią obojętną jest druga przekątna prostokąta

Maksymalne naprężenia występują w punktach najbardziej oddalonych od osi obojętnej
czyli w punktach A i B.



























































2

2

2

2

max

12

12

6

6

cos

sin

h

b

bh

M

bhd

M

bh

d

b

hb

d

h

M

W

W

M

y

J

M

z

J

M

g

g

g

z

y

g

z

gz

y

gy







gdzie

2

2

h

b

d





– długość przekątnej,

 

Pa

6

2

2

3

10

5

,

80

2

,

0

1

,

0

2

,

0

1

,

0

12

10

30















W przypadku zginania prostego (płaszczyzna obciążenia przechodzi przez xy:

 

Pa

W

M

z

g

6

2

3

max

10

45

6

2

,

0

1

,

0

10

30













