„Co to jest geniusz? Gen i

już.”

Hugo Steinhaus

UKŁAD WSPÓŁRZĘDNYCH.

Układy współrzędnych zostały stworzone po
to, by móc w dokładny sposób określić
położenie ciała fizycznego czy po prostu
punktu. Oprócz układów współrzędnych
kojarzonych bezpośrednio z matematyką
takich jak oś liczbowa, kartezjański układ
współrzędnych

na

płaszczyźnie

i

w

przestrzeni istnieje wiele innych układów, np.
szerokość

i

długość

geograficzna,

numerowane pola na planszy do gry w szachy
czy nawet w popularne „statki” itp.

UKŁAD WSPÓŁRZĘDNYCH.

KARTEZJAŃSKICH.

Prostokątny układ współrzędnych to

dwie wzajemnie prostopadłe osie liczbowe

o wspólnym punkcie (0, 0) zwanym

początkiem układu współrzędnych

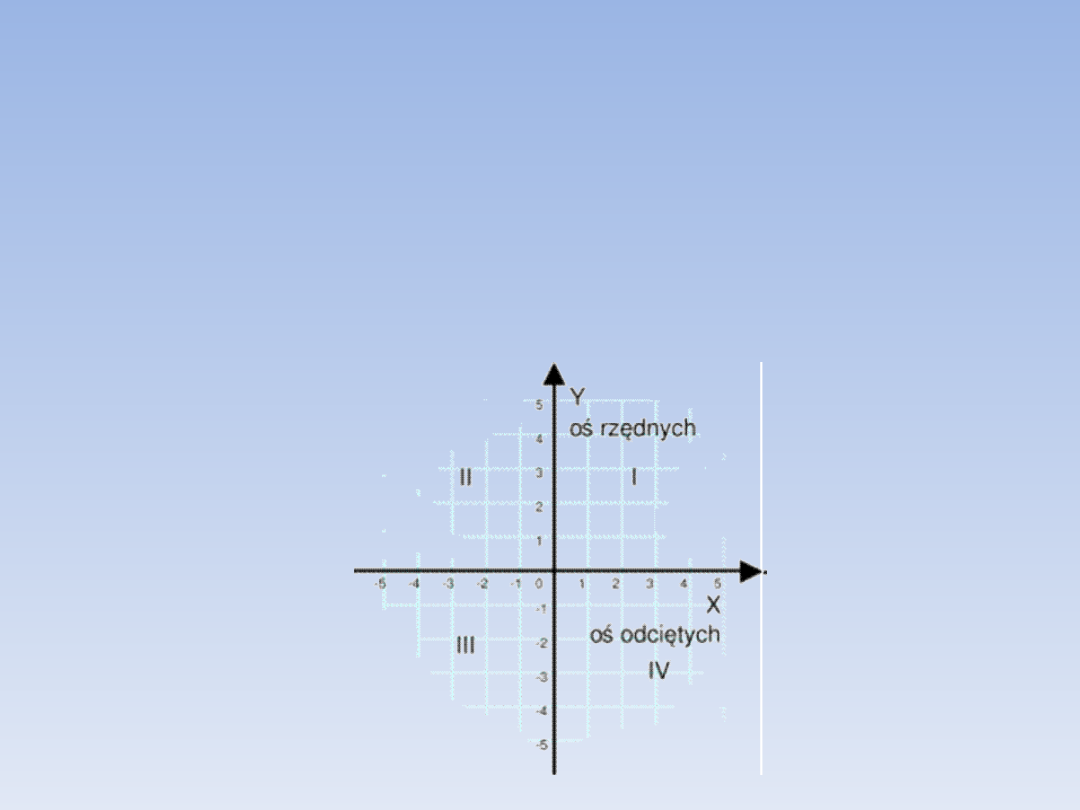
UKŁAD WSPÓŁRZĘDNYCH.

KARTEZJAŃSKICH.

Oś poziomą (OX) nazywamy osią odciętych,
natomiast oś pionową (OY) – osią rzędnych.
Osie układu dzielą płaszczyznę na cztery
części –ćwiartki układu.

WSPÓŁRZĘDNE.

Położenie

każdego

punktu w układzie
współrzędnych
można określi za
pomocą
współrzędnych.
Zawszę

jako

pierwszą podajemy
współrzędną
odczytywaną na osi
X, a jako drugą tę,
którą

odczytujemy

na osi Y.

P = (x,

y)

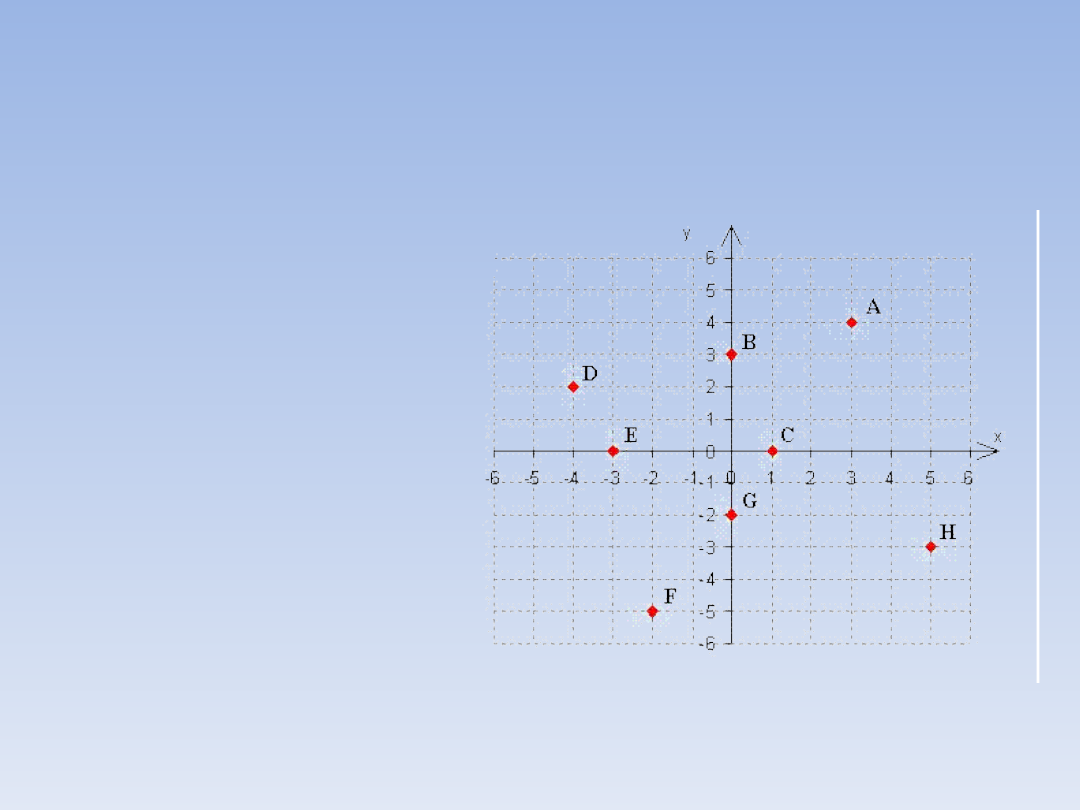
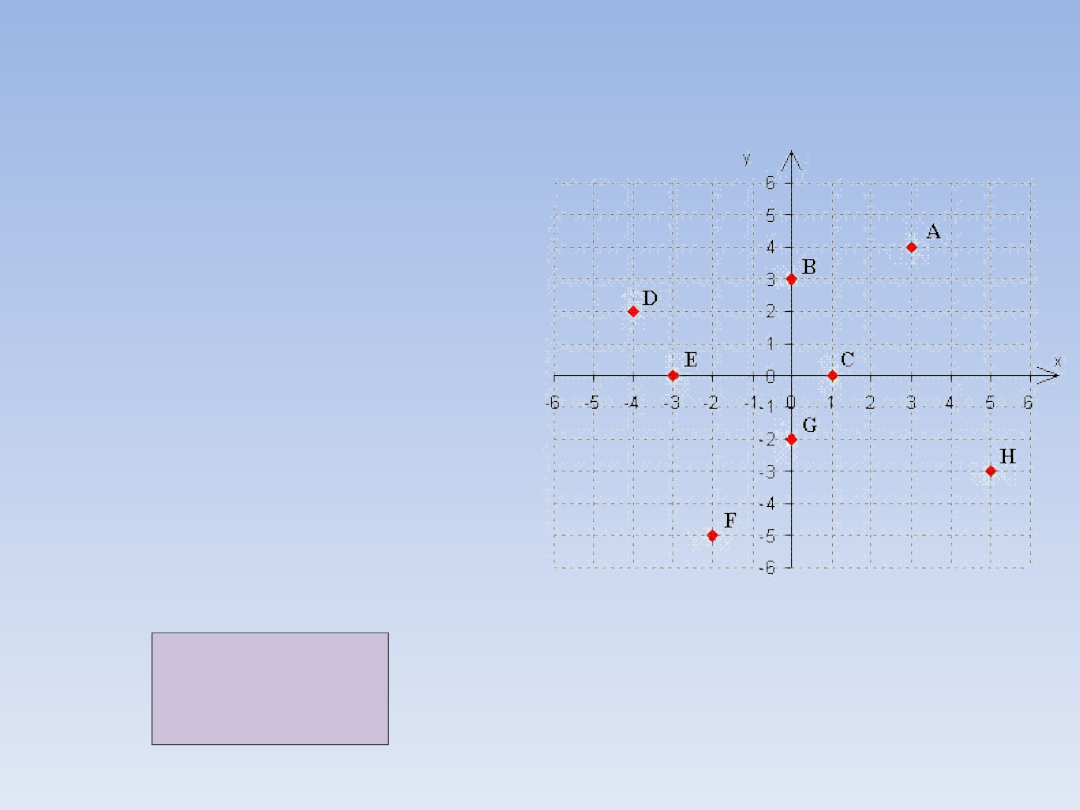
WSPÓŁRZĘDNE.

Na

układzie

zamieszczonym
obok zaznaczono
punkty

o

następujących
współrzędnych:
A = (3, 4)
B = (0, 3)
C = (1, 0)
D = (-4, 2)
E = (-3, 0)
F = (-2, -5)
G = (0, -2)
H = (5, -3)

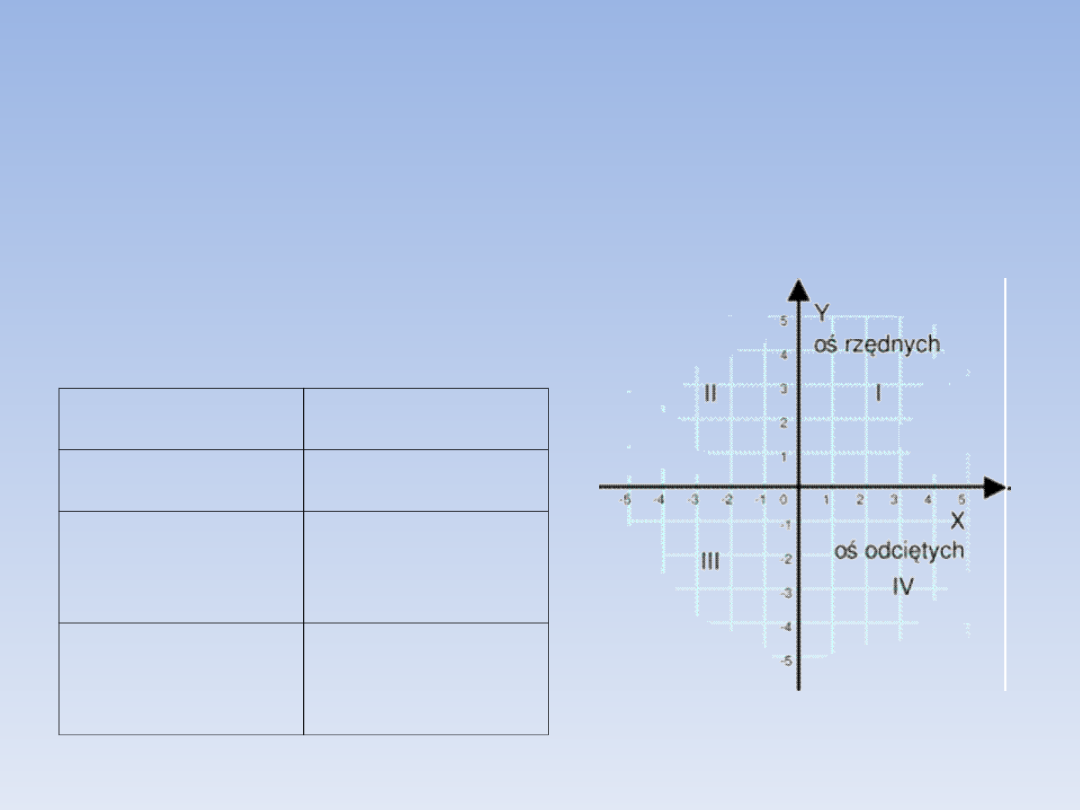
WSPÓŁRZĘDNE.

Znak współrzędnych pozwala określić w
której ćwiarce układu znajduje się punkt:

(+, +)

I ćwiartka

(-, +)

II ćwiartka

(-, -)

III

ćwiartka

(+, -)

IV

ćwiartka

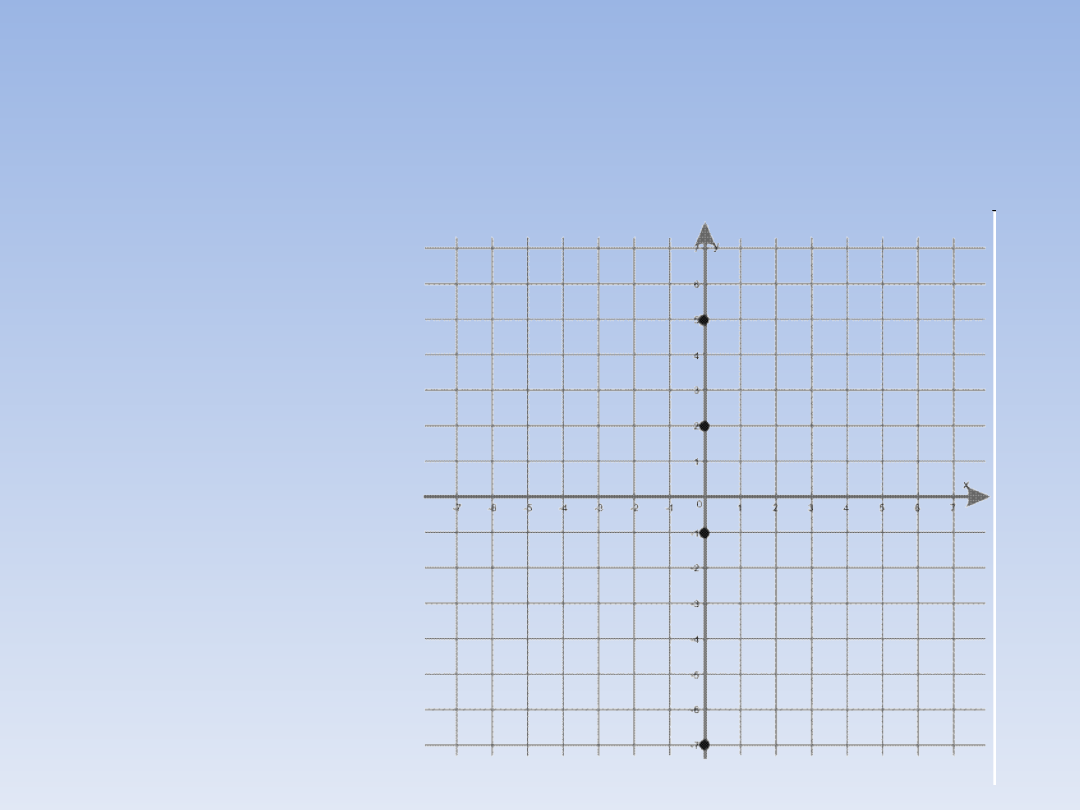
WSPÓŁRZĘDNE.

Punkty, których pierwsza współrzędna jest
równa zero, leżą na osi OY.

Np.:
(0, 5)
(0, 2)
(0,
-1)
(0,
-7)

WSPÓŁRZĘDNE.

Punkty, których druga współrzędna jest
równa zero, leżą na osi OX.

Np.:
(-5,
0)
(-4,
0)
(2, 0)
(5, 0)

WSPÓŁRZĘDNE.

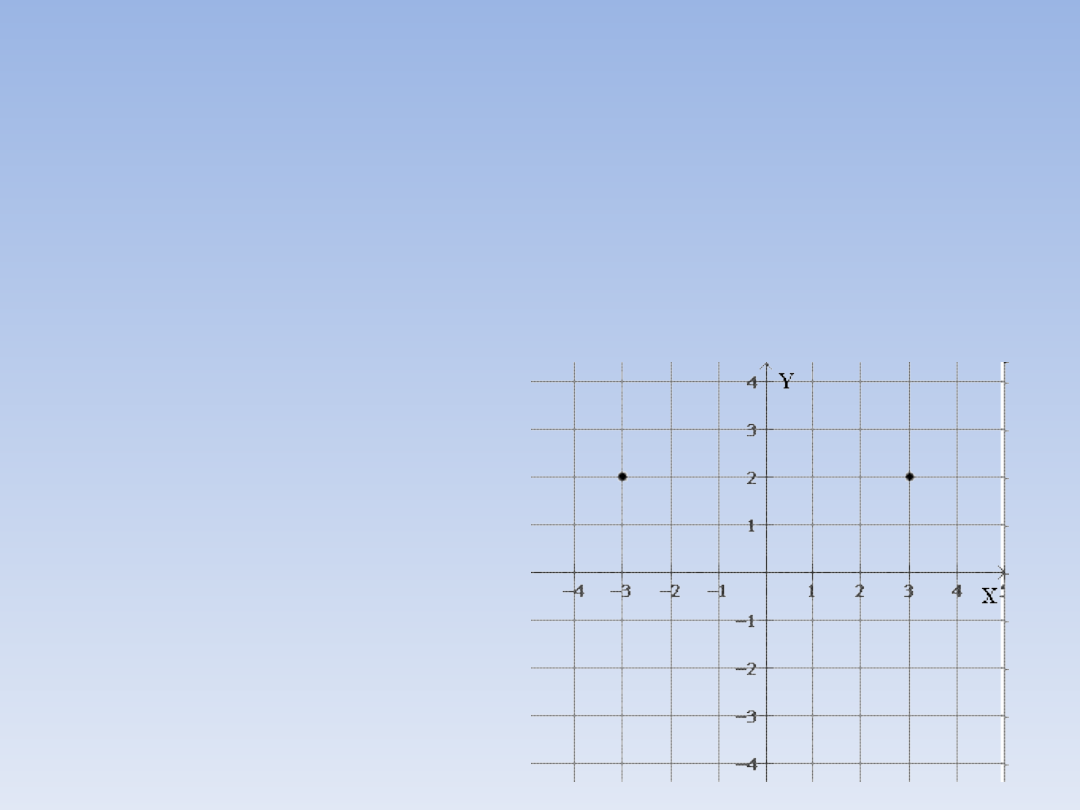
Punkty, których pierwsze współrzędne są
liczbami przeciwnymi a drugie są takie same
leżą w takiej samej odległości od osi OY po
przeciwnych jej stronach (są do siebie
symetryczne względem osi OY)

Np.: (-3, 2) i (3, 2)

WSPÓŁRZĘDNE.

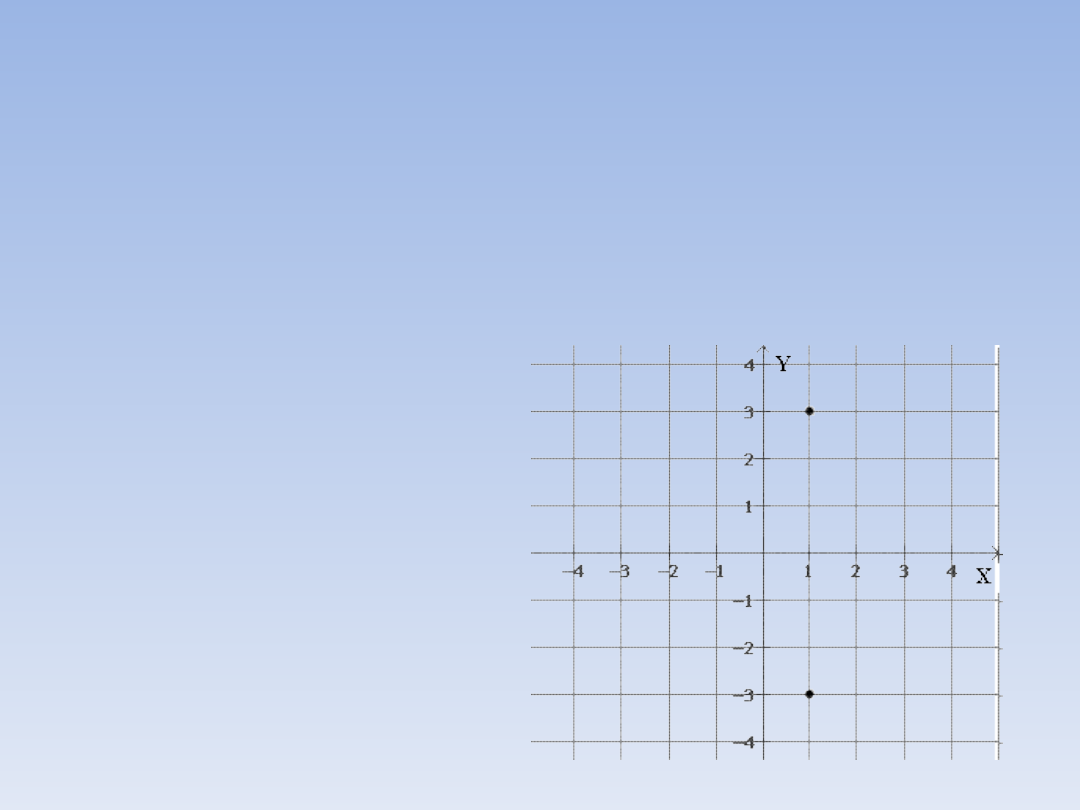
Punkty, których drugie współrzędne są
liczbami przeciwnymi a pierwsze są takie
same leżą w takiej samej odległości od osi
OX po przeciwnych jej stronach (są do siebie
symetryczne względem osi OX)

Np.: (1, 3) i (1, -3)

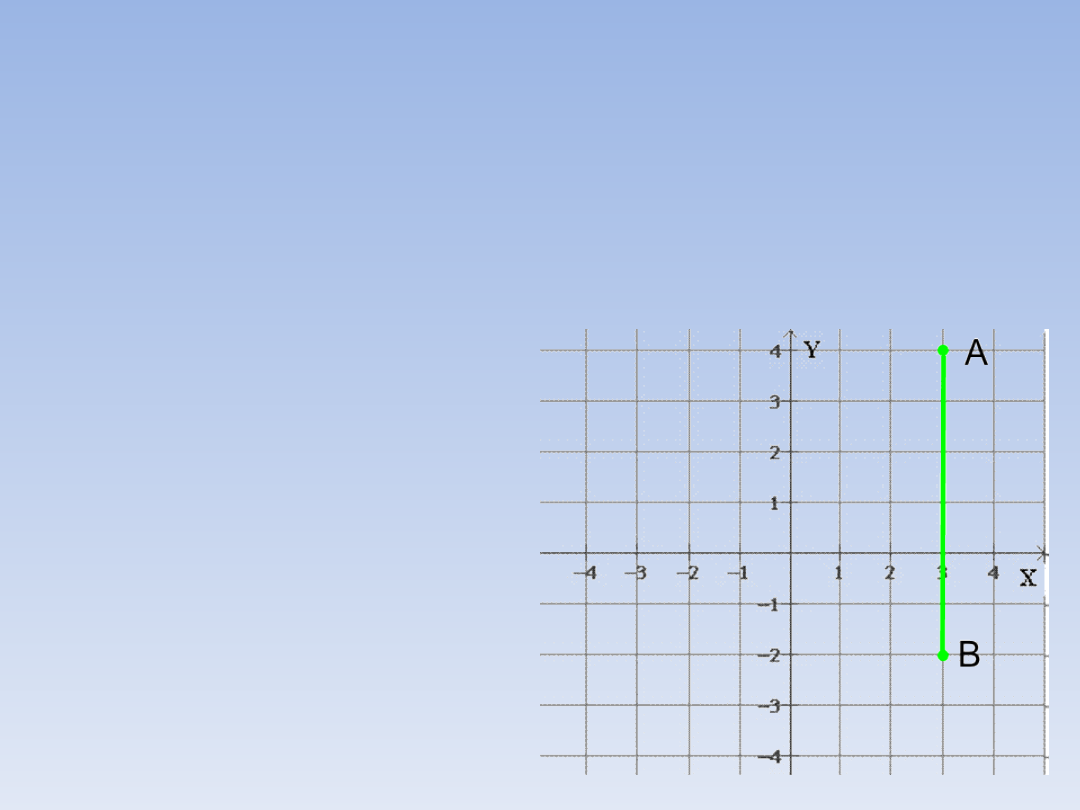
WSPÓŁRZĘDNE.

Odcinki, których końce mają takie same
pierwsze współrzędne są równoległe do osi
OY. Aby policzyć ich długość wystarczy
obliczyć

wartość

bezwzględną

różnicy

drugich współrzędnych.

Np.: A = (3, 4) i B = (3, -2)
|AB| = |4 – (-2)| = |6| = 6

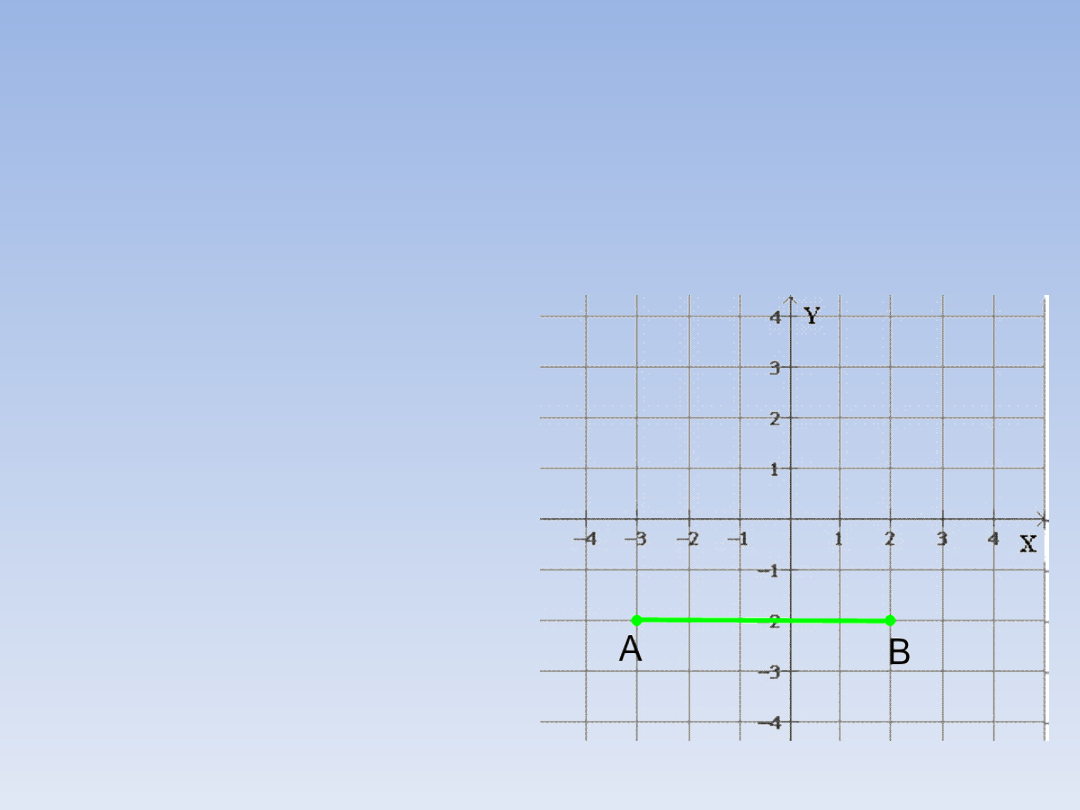
WSPÓŁRZĘDNE.

Odcinki, których końce mają takie same
drugie współrzędne są równoległe do osi OX.
Aby policzyć ich długość wystarczy obliczyć
wartość bezwzględną różnicy pierwszych
współrzędnych.

Np.: A = (-3, -2) i B = (2, -2)
|AB| = |-3 – 2| = |-5| = 5

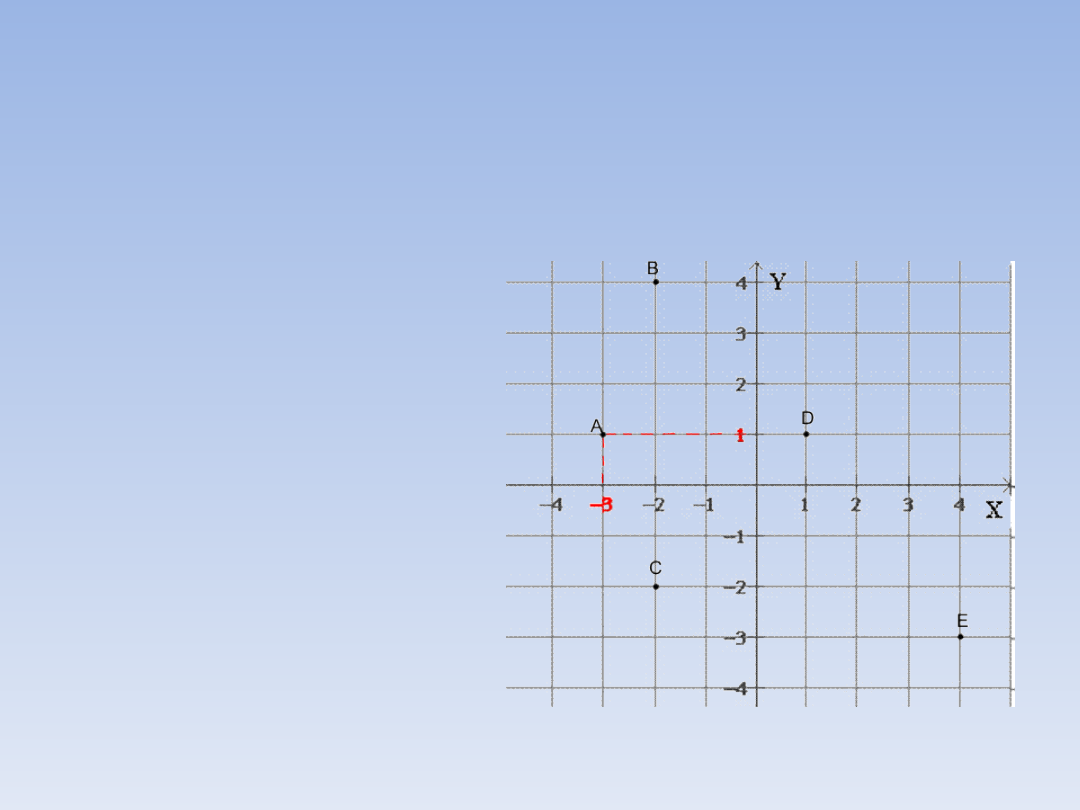
PRZYKŁADOWE ZADANIA.

Zadanie 1.
Odczytaj z rysunku współrzędne punktów.

Przy punkcie A
zaznaczyliśmy
sposób
odczytywania
współrzędnych.
Mamy więc:
A = (-3, 1)
B = (-2, 4)
C = (-2, -2)
D = (1, 1)
E = (4, -3)

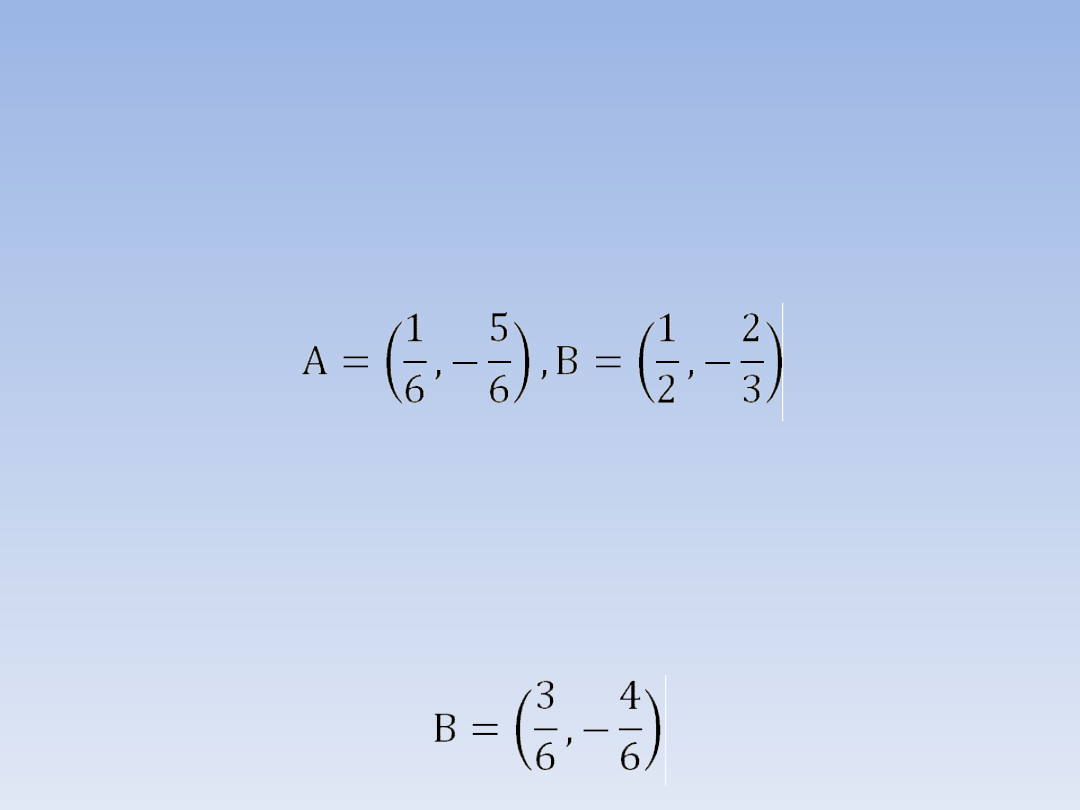
PRZYKŁADOWE ZADANIA.

Zadanie 2.
Narysuj

układ

współrzędnych,

dobierz

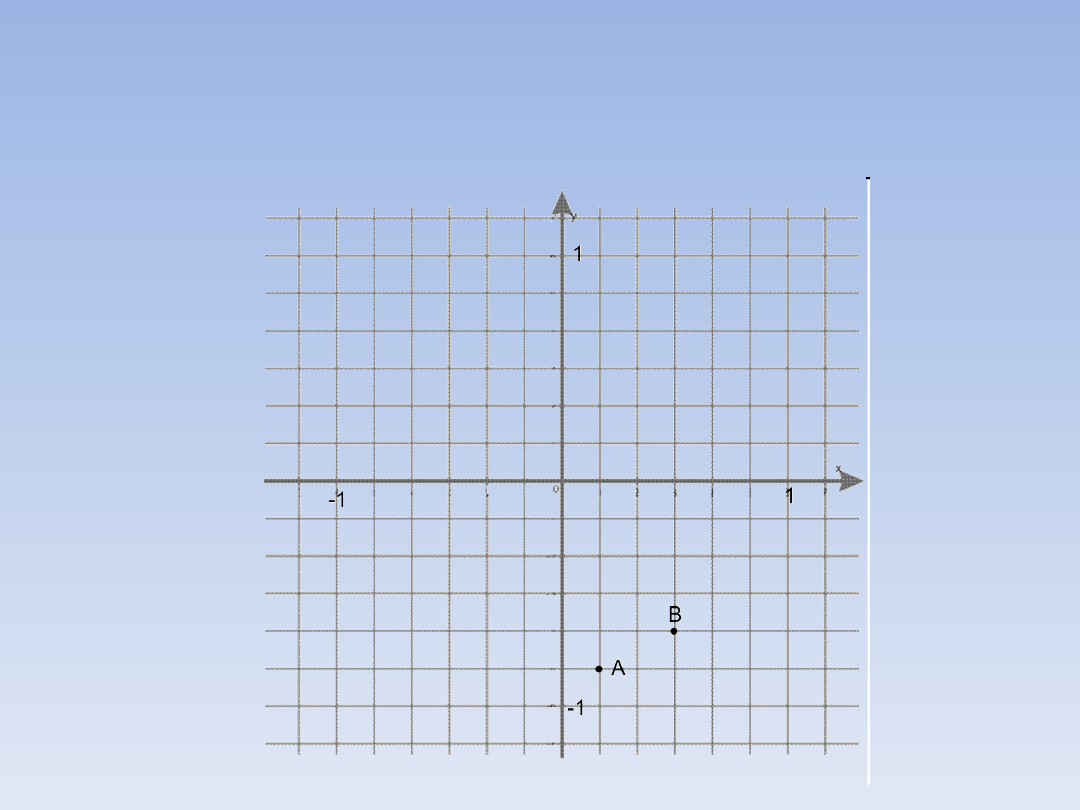
odpowiednią jednostkę i zaznacz punkty:

Żeby w łatwy sposób zaznaczyć podane
punkty, należy obrać jednostkę, która będzie
się składała z 6 mniejszych części, np. 1 na
układzie

to

6

kratek

w

zeszycie.

Współrzędne punktu B łatwo sprowadzić do
postaci z mianownikiem 6:

PRZYKŁADOWE ZADANIA.

Zadanie 2 – ciąg dalszy.

PRZYKŁADOWE ZADANIA.

Zadanie 3.
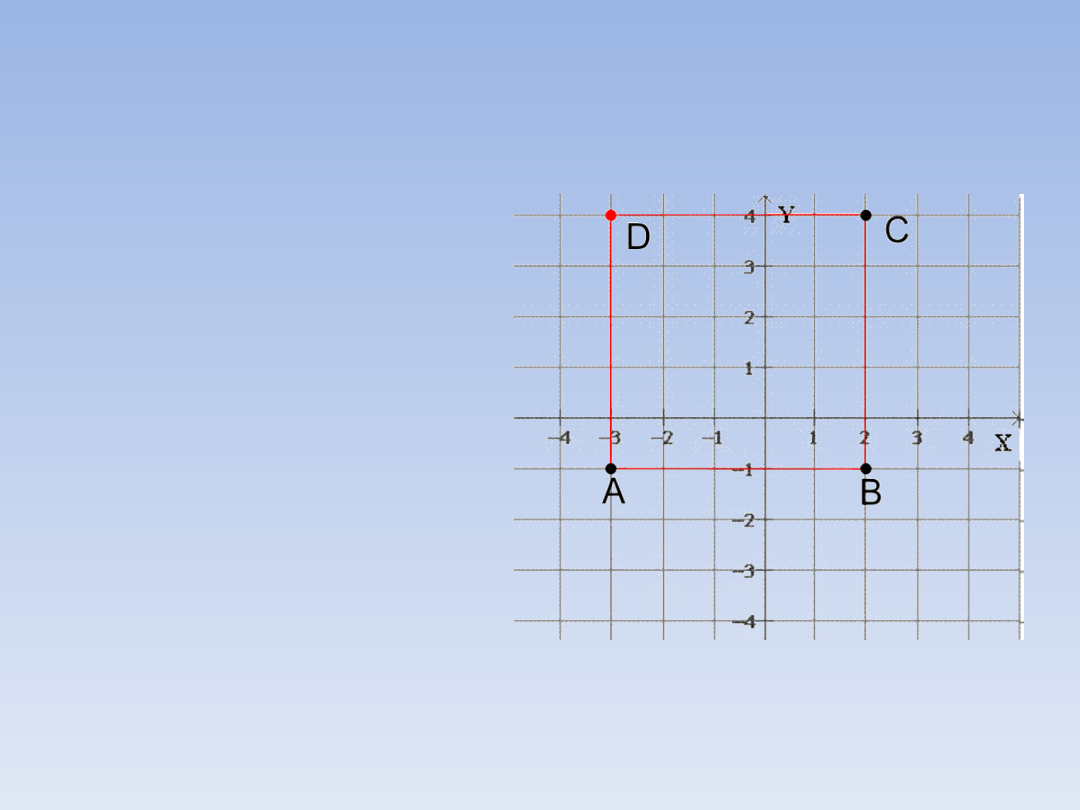
Punkty A, B i C są wierzchołkami prostokąta.
Podaj współrzędne czwartego wierzchołka.

A = (-3, -1), B = (2, -1), C = (2, 4)

Najłatwiej jest zaznaczyć te punkty w
układzie

współrzędnych,

dorysować

brakujący

punkt

i

odczytać

jego

współrzędne.

PRZYKŁADOWE ZADANIA.

Zadanie 3 – ciąg dalszy.

Z rysunku wynika,
że

współrzędne

czwartego
wierzchołka D = (-
3, 4).

PRZYKŁADOWE ZADANIA.

Zadanie 4.
Określ, w której ćwiartce układu leżą punkty:
A = (45, 78) ; B = (-257, 1209) ; C = (123,
-4) ;
D = (- 26; -65) ; E = (345; -243) ; F = (500;
321) ;
G = (-43; 56) ; H = (23; 89)

Wystarczy spojrzeć na znaki współrzędnych i
skorzystać z tabeli z planszy 7.

(+, +)

I

ćwiartka

A; F; H

(-, +)

II

ćwiartka

B; G

(-, -)

III

ćwiartka

D

(+, -)

IV

ćwiartka

C; E

PRZYKŁADOWE ZADANIA.

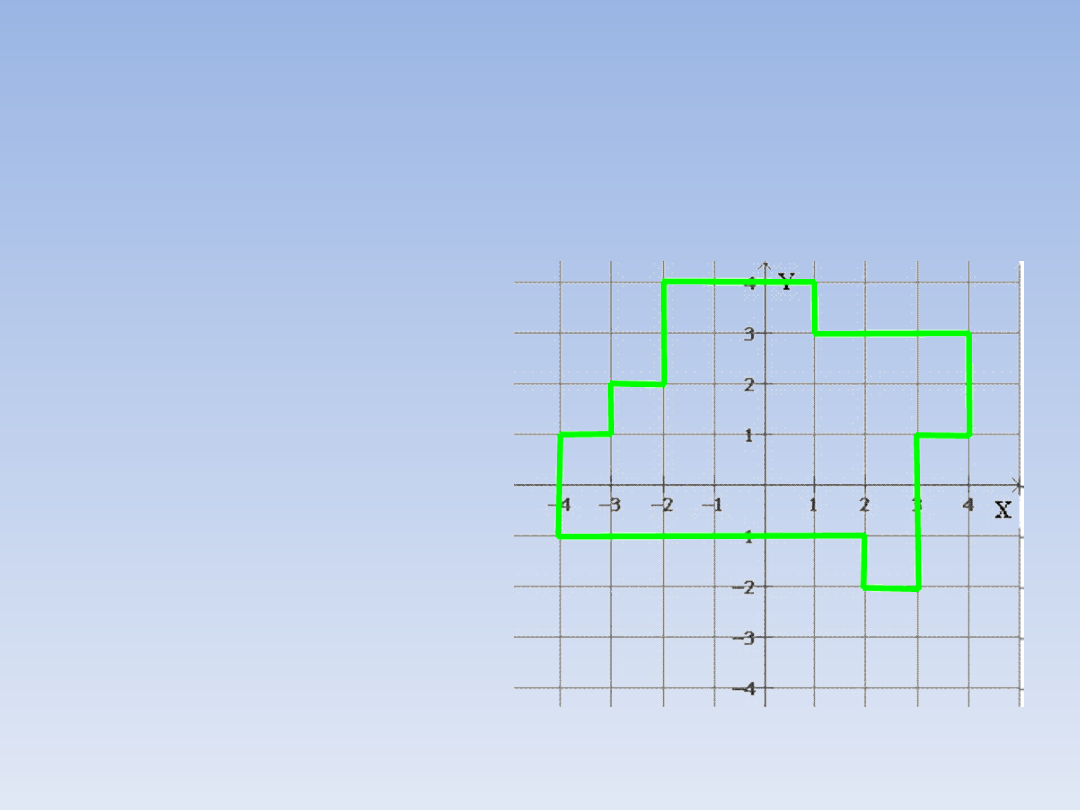
Zadanie 5.
Oblicz obwód narysowanego wielokąta.

Jedna kratka na
rysunku
odpowiada
odcinkowi
jednostkowemu (o
długości

1),

wystarczy

więc

policzyć ile kratek
zajmuje każdy z
boków wielokąta a
następnie dodać je
do siebie.
Ob = 28.

PRZYKŁADOWE ZADANIA.

Zadanie 5.
Oblicz długość odcinków o podanych
końcach bez rysowania ich.

a)A = (-6, 3) ; B = (10, 3)
Drugie współrzędne tych punktów są takie
same, więc aby obliczyć długość tego
odcinka wystarczy podać odległość między
pierwszymi współrzędnymi:
|AB| = |-6 – 10| = |-16| = 16

b) C = (2, -9) ; D = (2, 8)
|CD| = |-9 – 8| = |-17| = 17