Wektory w przestrzeni

trójwymiarowej

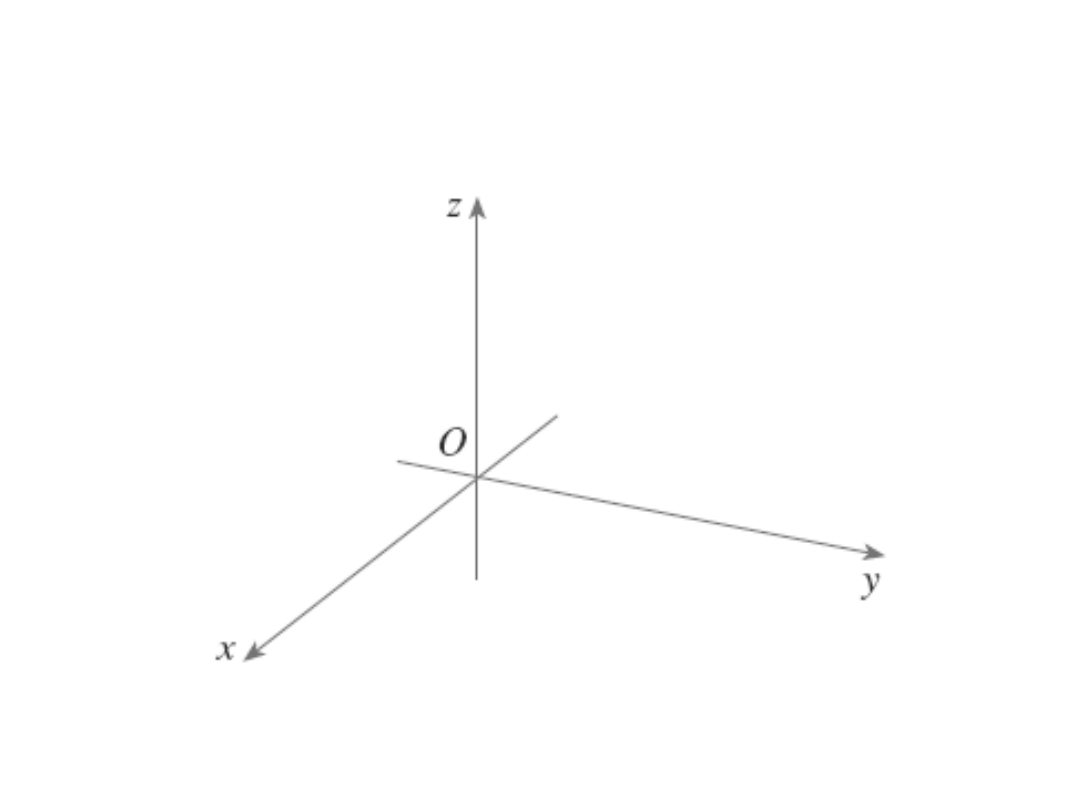
Układ współrzędnych w R

3

Osie współrzędnych

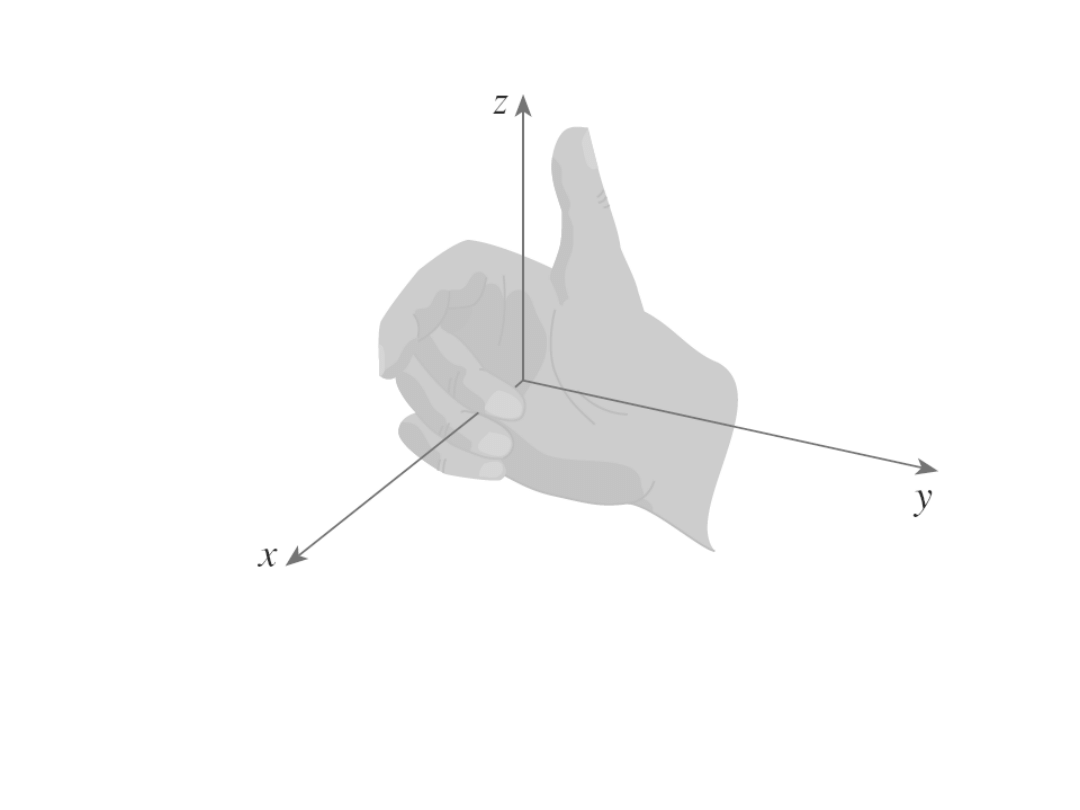
Reguła prawej ręki – układ prawoskrętny

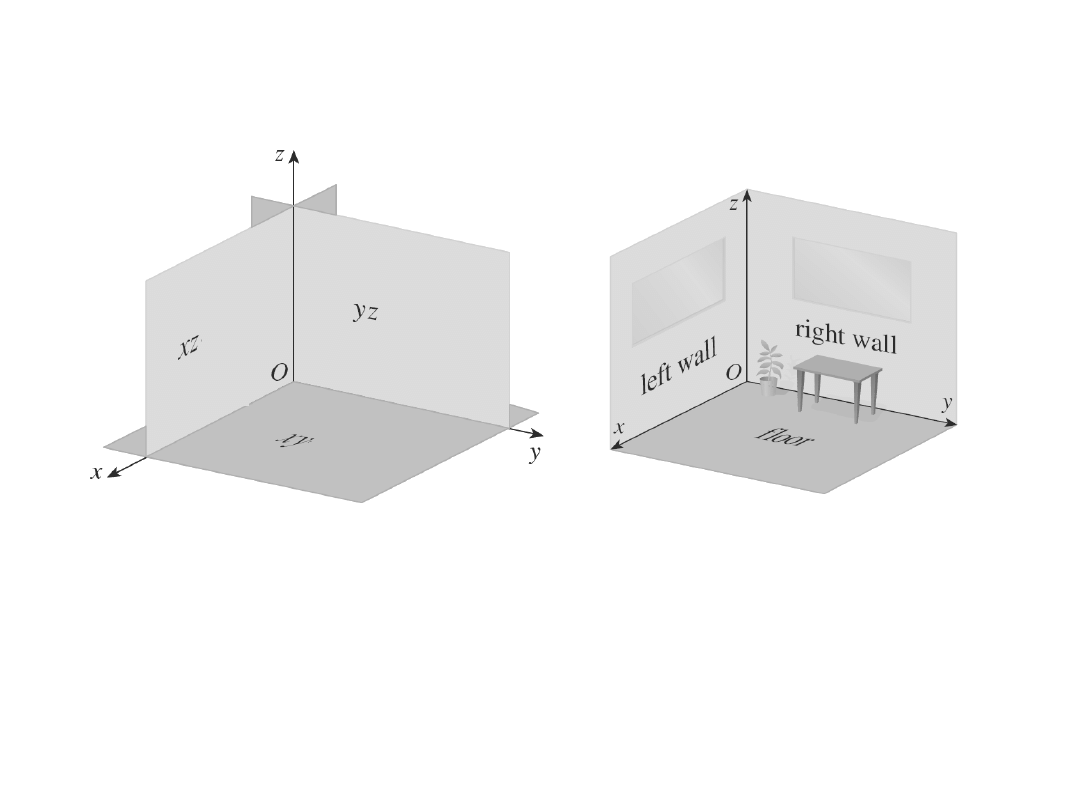
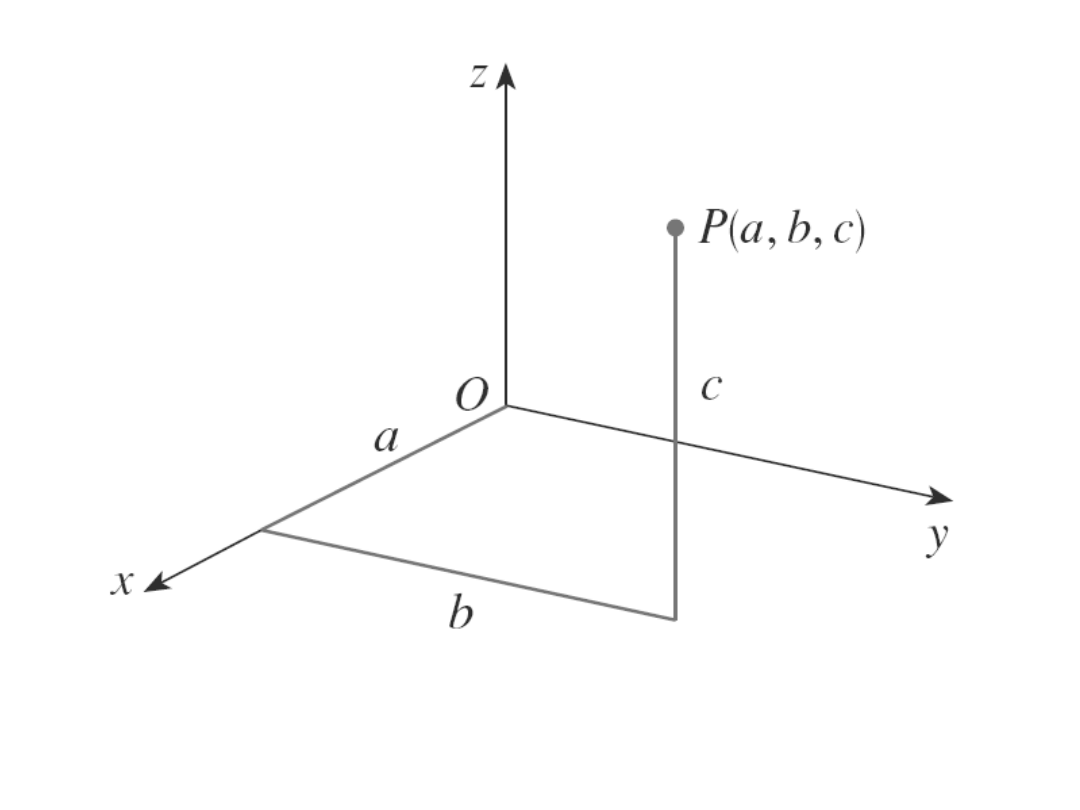
Współrzędne punktu P (a,b,c)

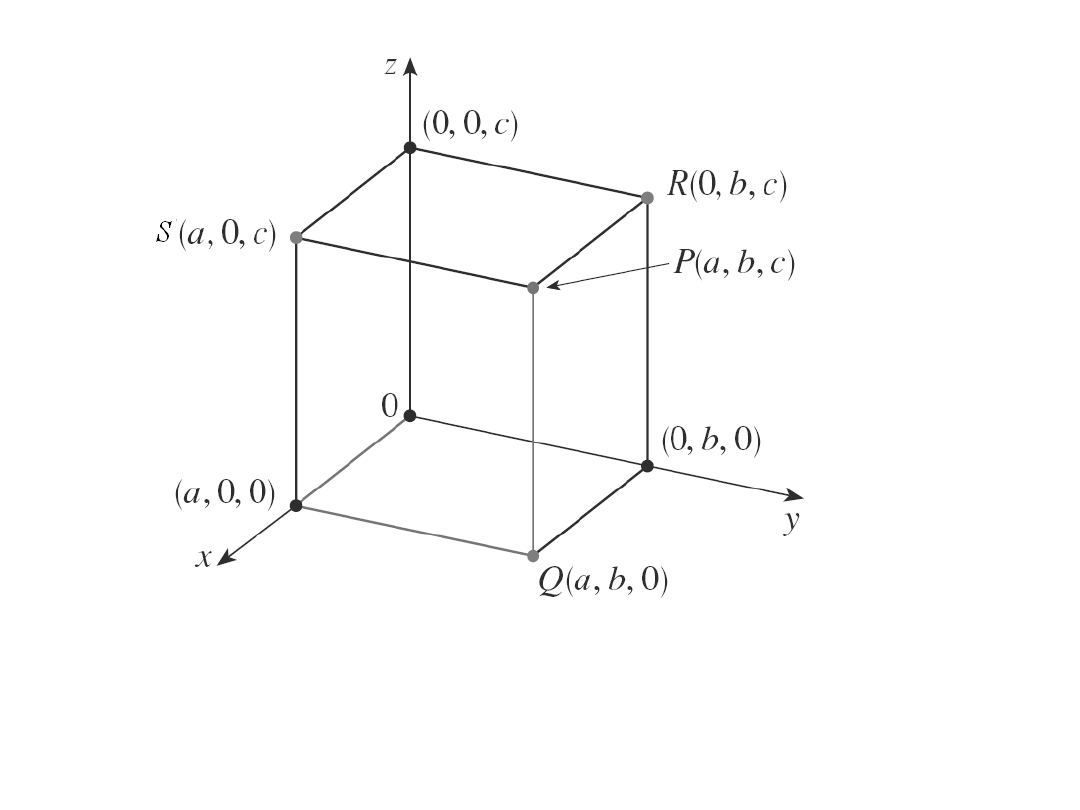
Iloczyn kartezjański





R

R

R

R









z

y

x

z

y

x

,

,

:

)

,

,

,

(

Współrzędne prostokątne

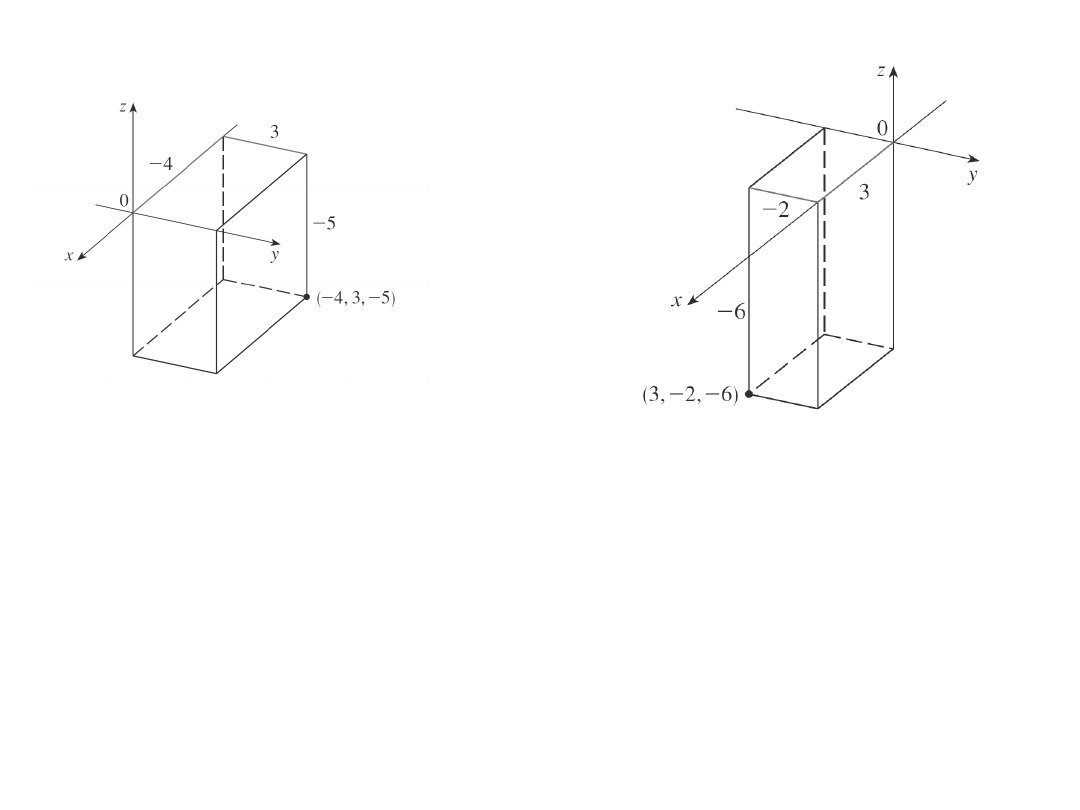
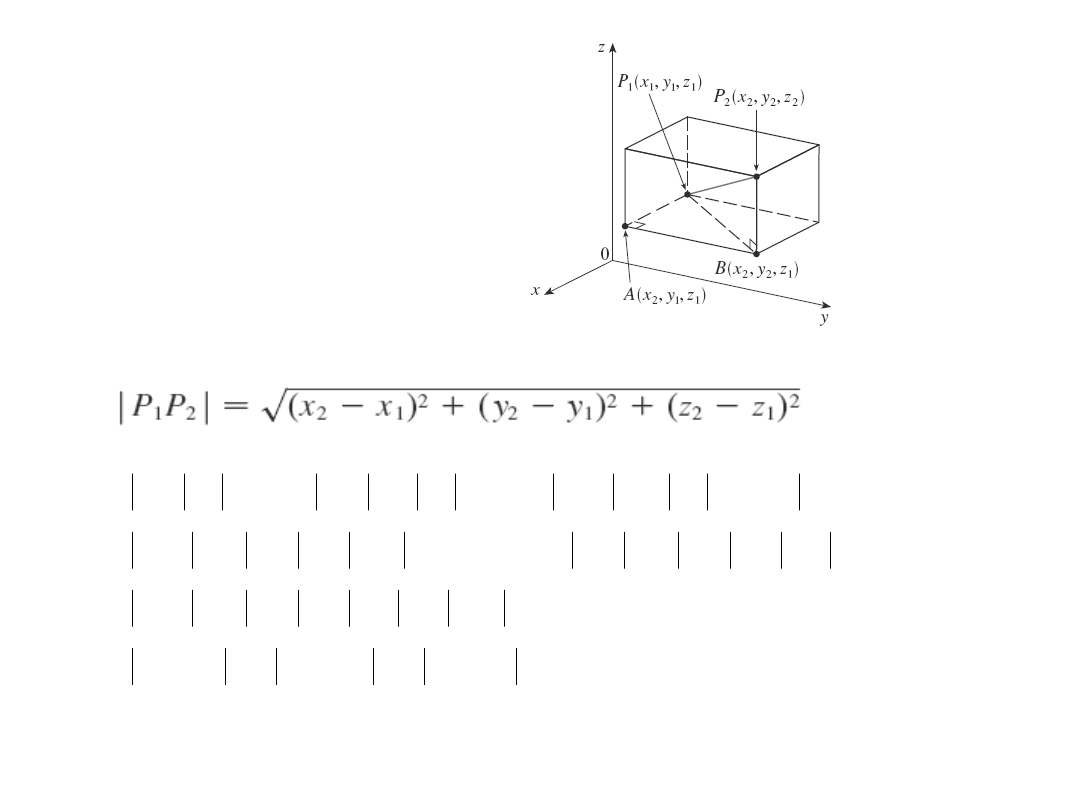
Odległość w R

3



 

 



2

1

2

2

1

2

2

1

2

2

1

2

2

1

2

2

1

2

2

2

2

2

1

2

2

1

2

2

1

2

1

2

2

2

1

2

2

1

1

2

2

1

2

1

2

1

z

z

y

y

x

x

z

z

y

y

x

x

BP

AB

A

P

P

P

AB

A

P

B

P

BP

B

P

P

P

z

z

BP

y

y

AB

x

x

A

P



















































Przykład
Znajdź odległość pomiędzy punktami P(2,-1,7) i Q(1,-3,5) .





3

4

4

1

)

7

5

(

)

1

3

(

2

1

2

2

2























PQ

Przykład
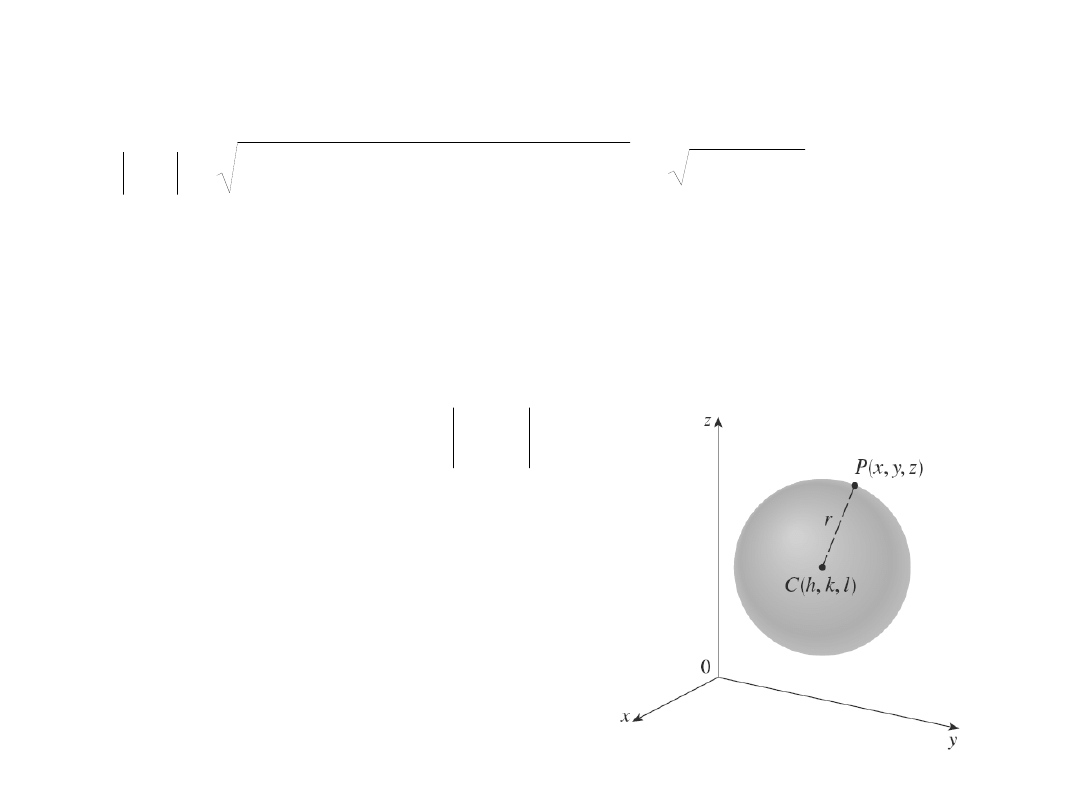
Znajdź równanie sfery o środku w punkcie C(h,k,l) i promieniu r .





r

PQ

z

y

x

P

r

C

S





:

)

,

,

(

)

,

(

2

2

2

2

)

(

)

(

)

(

r

l

z

k

y

h

x













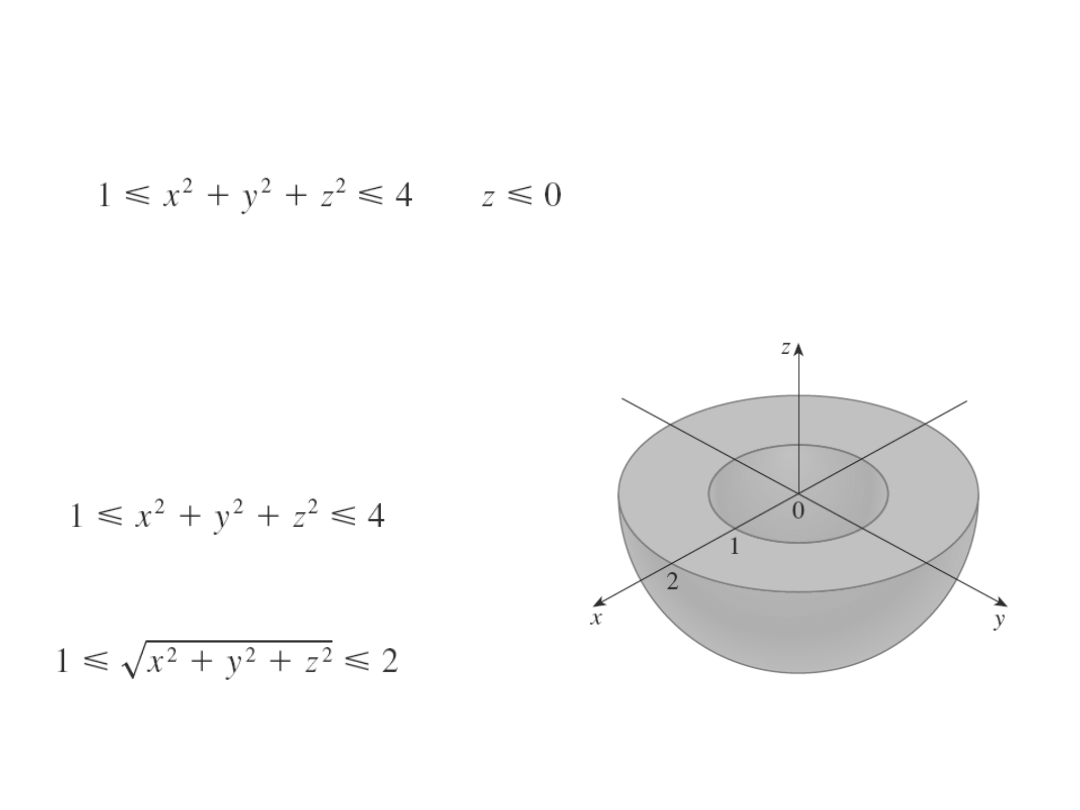
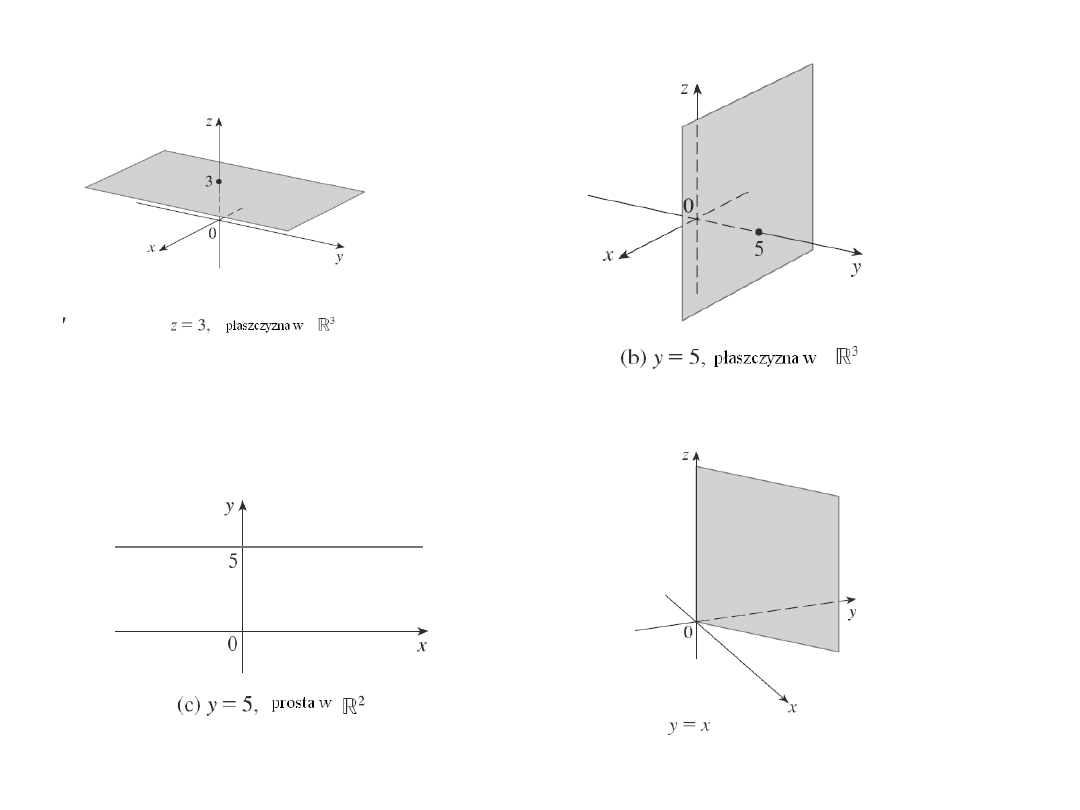
Przykład

Jak wygląda obszar dany równaniami:

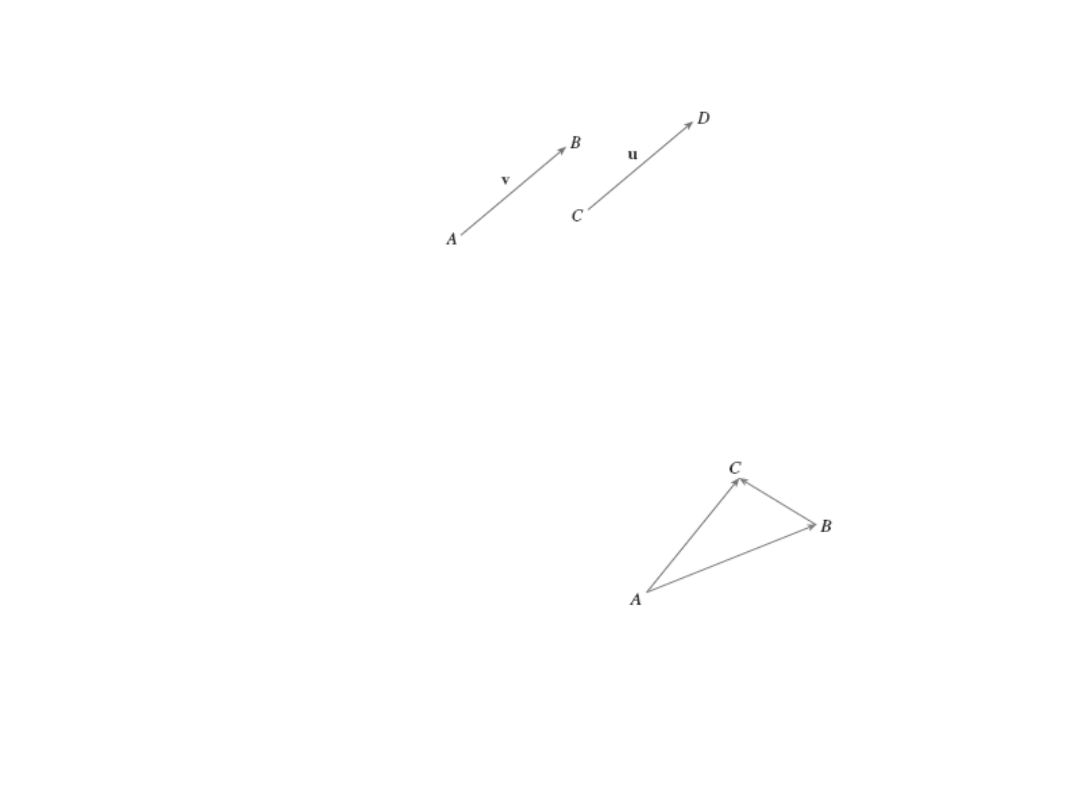
Wektory

Składanie wektorów

AB





v

CD





u

BC

AB

AC











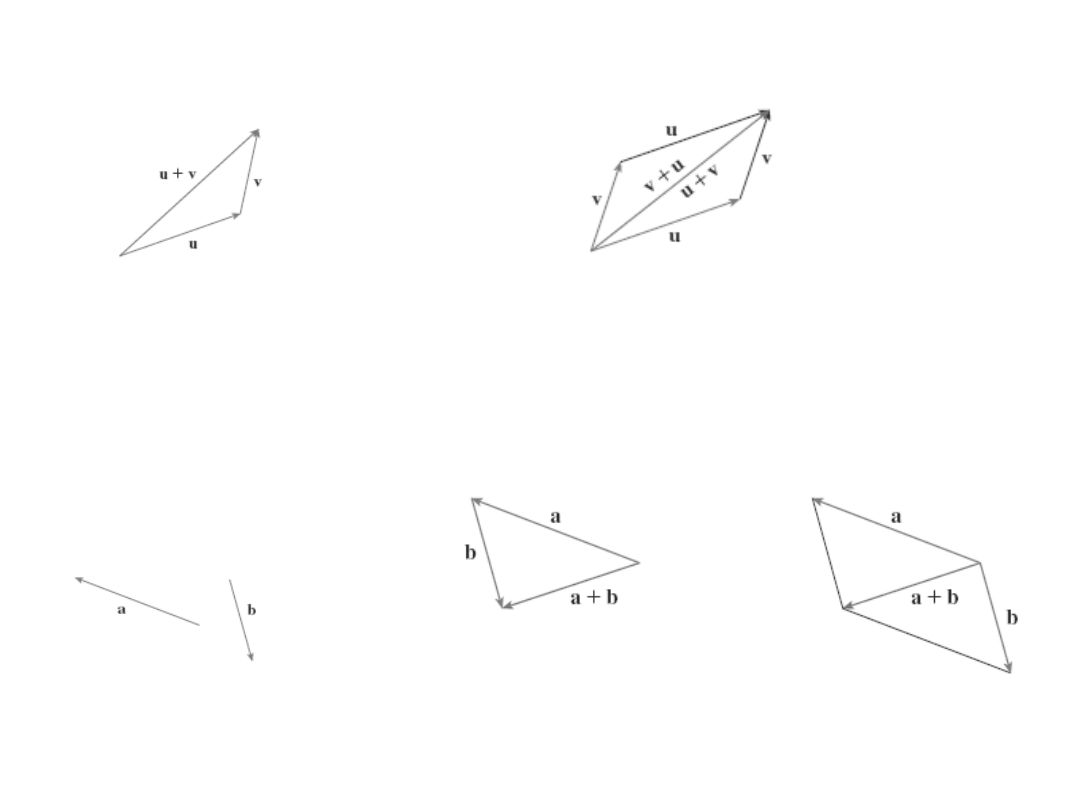
Reguła
równoległoboku

Suma wektorów

Przykład Znajdź
sumę
wektorów
a i b

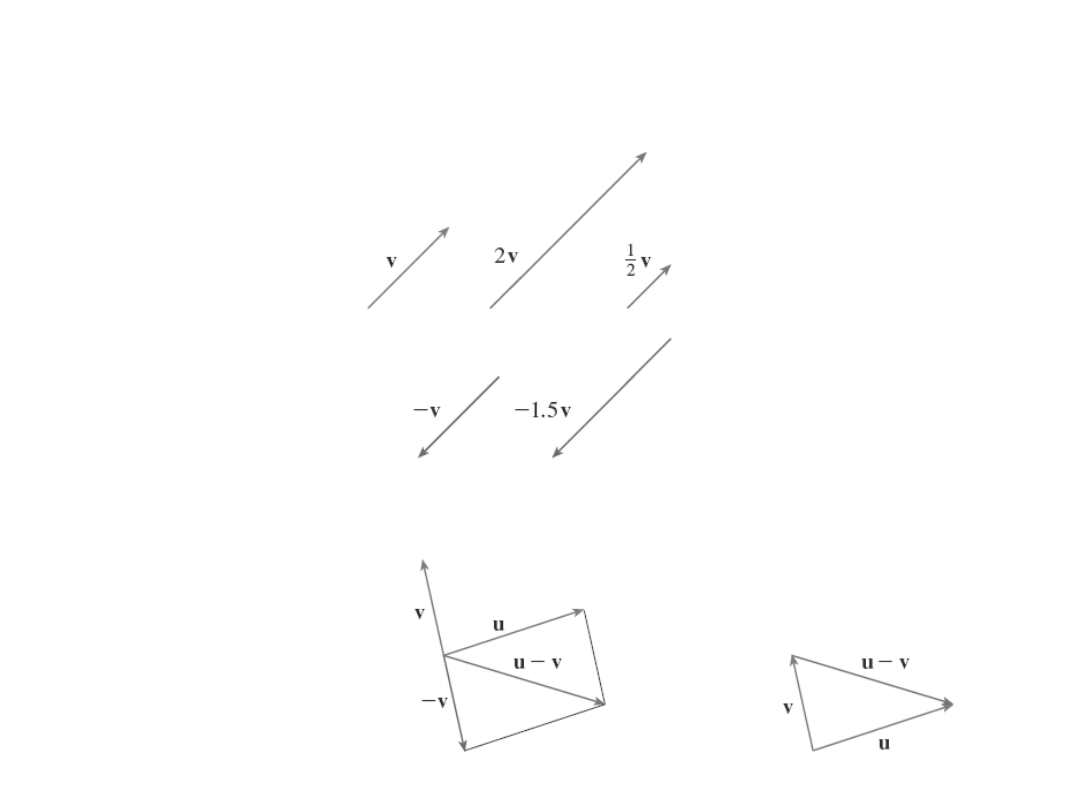
Mnożenie wektora przez

liczbę

)

( v

u

v

u









Różnica wektorów

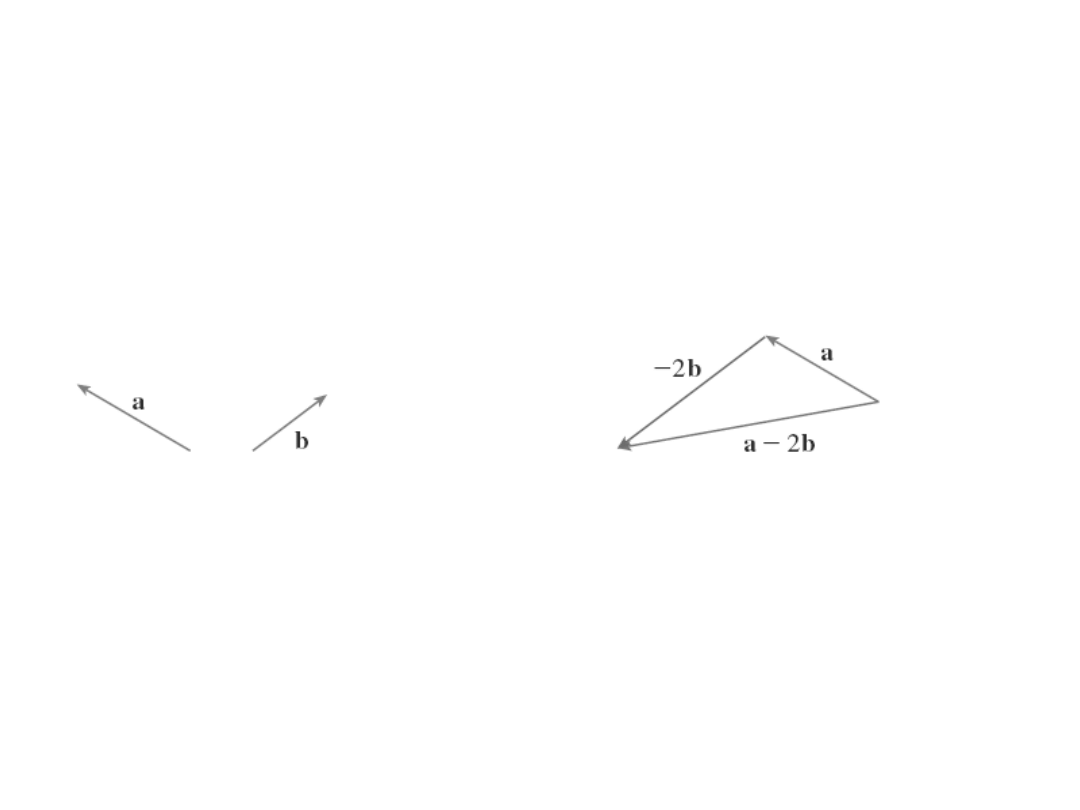
b

a 2



Przykład

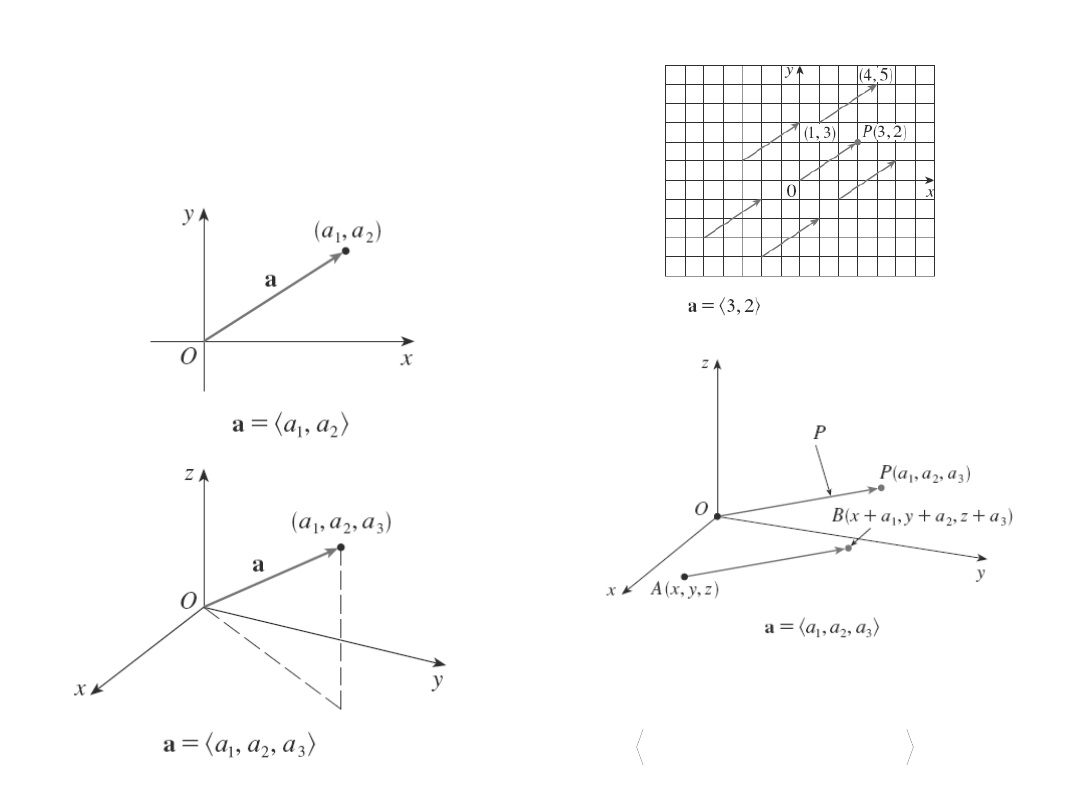
Współrzędne

wektora

1

2

1

2

1

2

2

2

2

1

1

1

,

,

)

,

,

(

)

,

,

(

z

z

y

y

x

x

z

y

x

B

z

y

x

A

AB













a

a

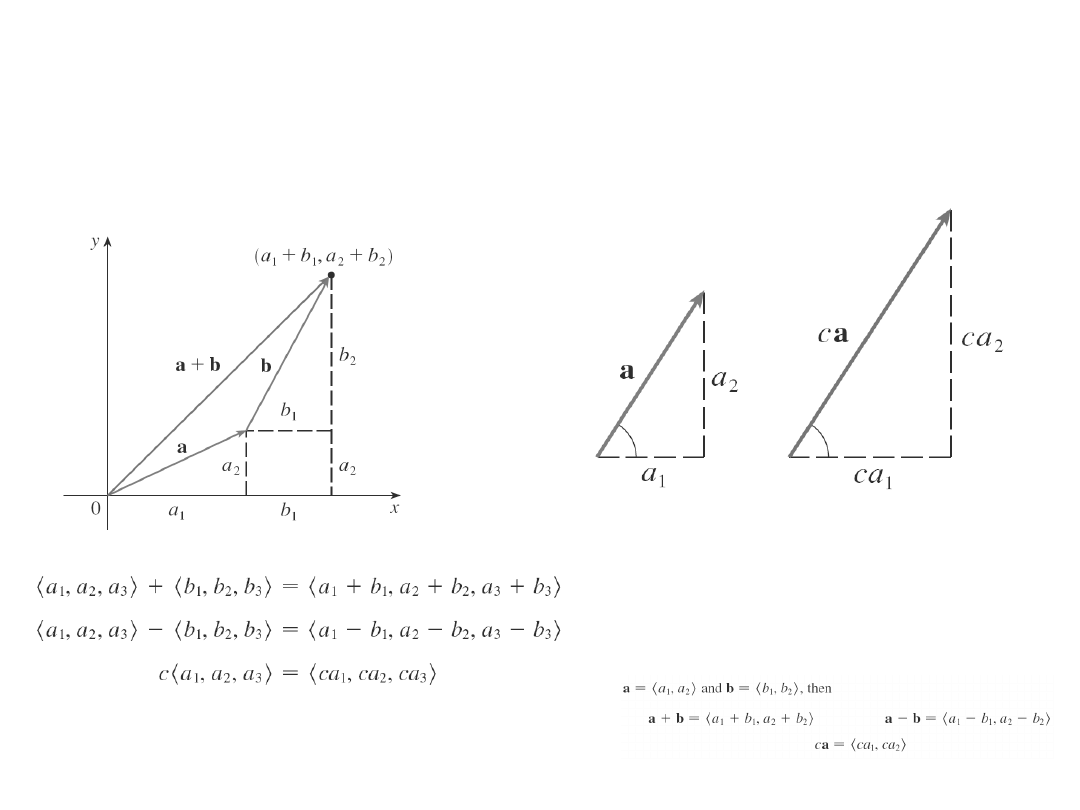
Dodawanie wektorów

– dodawanie
współrzędnych

Mnożenie przez liczbę

Długość
wektora

2

3

2

2

2

1

a

a

a







a

3

2

1

,

,

a

a

a



a

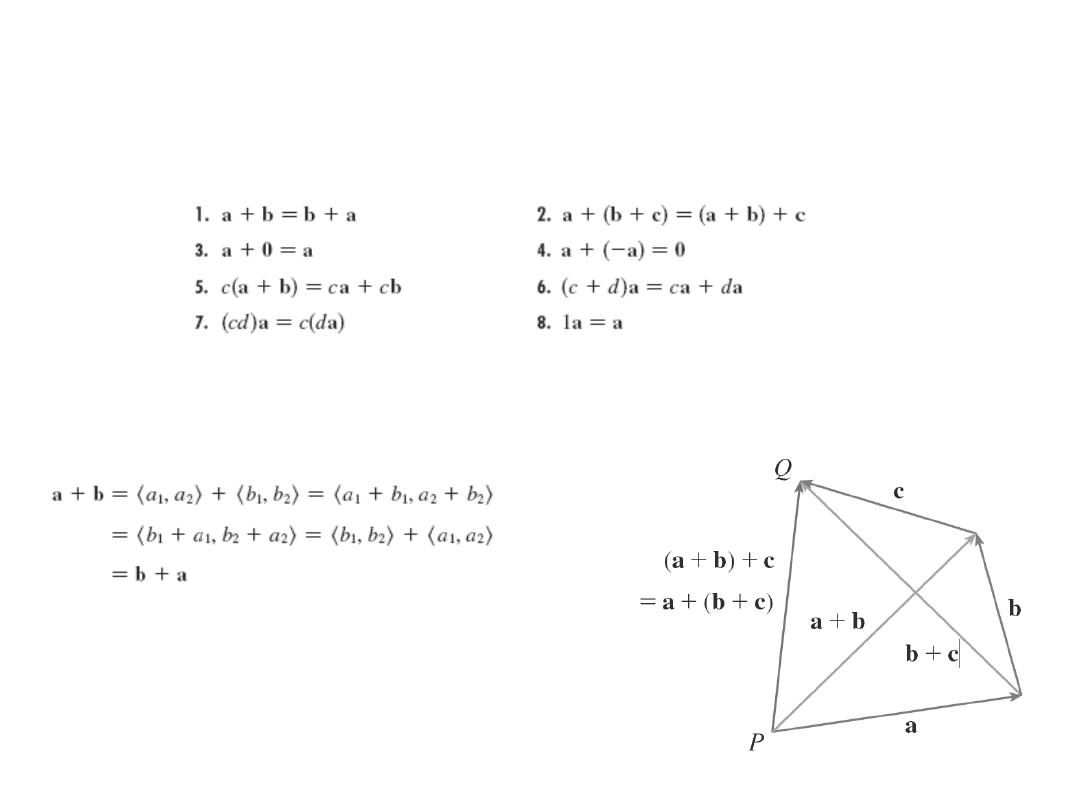
Własności wektorów

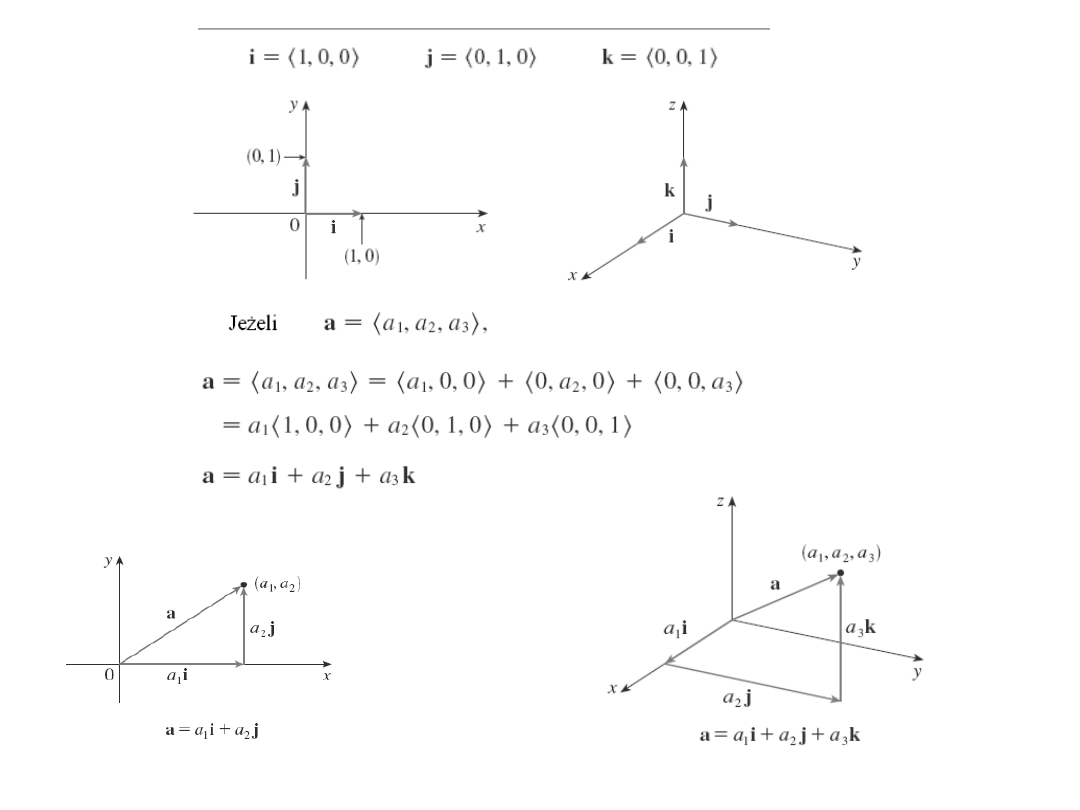
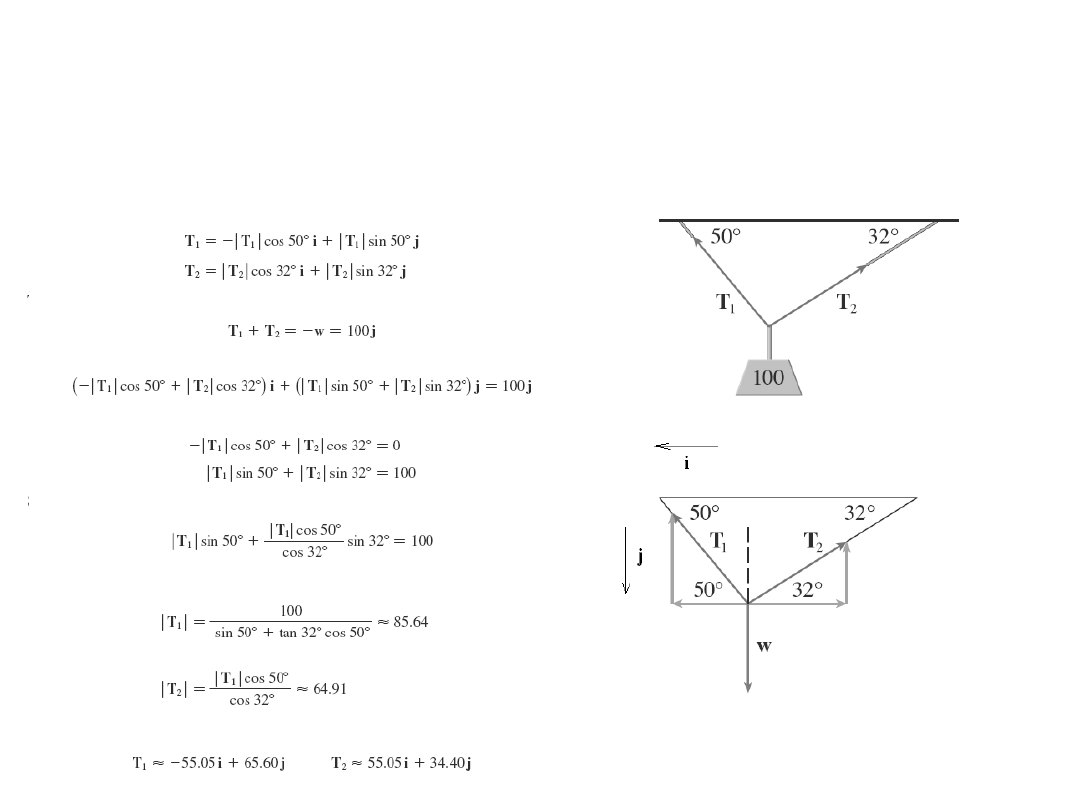
Przykład
 
Ciężar 100 kg wisi sobie na dwóch drutach.
(rys ). Znajdź, siły T

1

, T

2

.

 

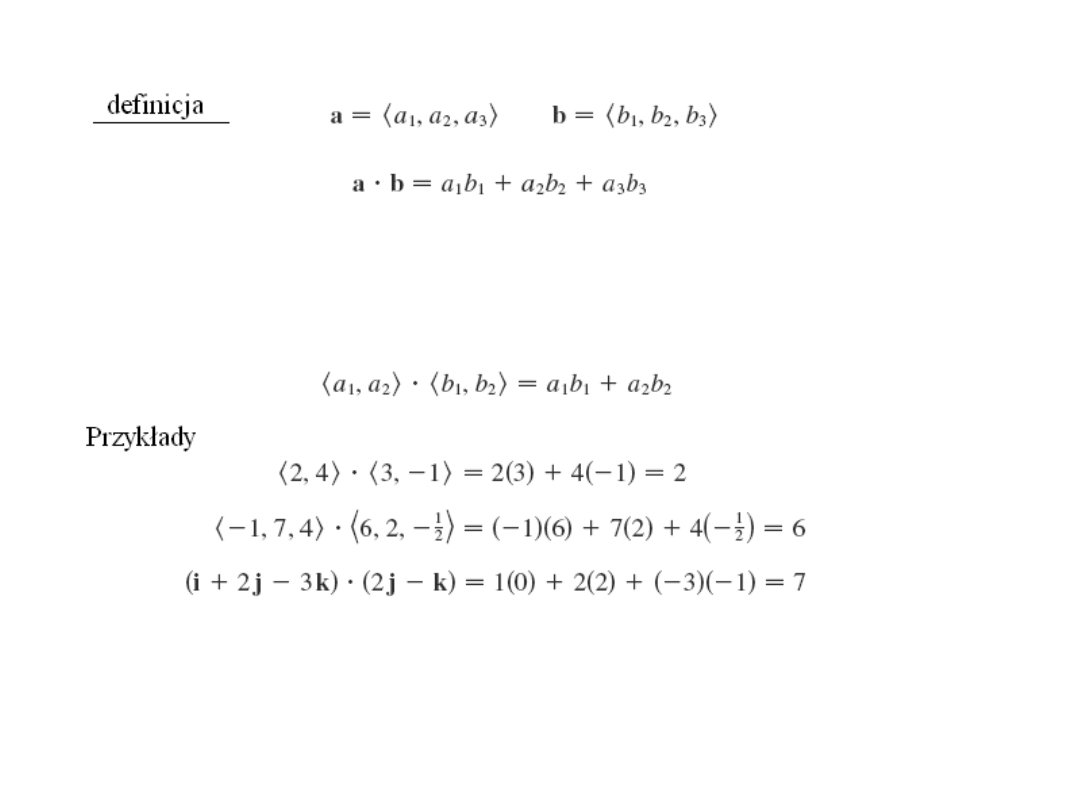
Iloczyn skalarny

Własności iloczynu

skalarnego

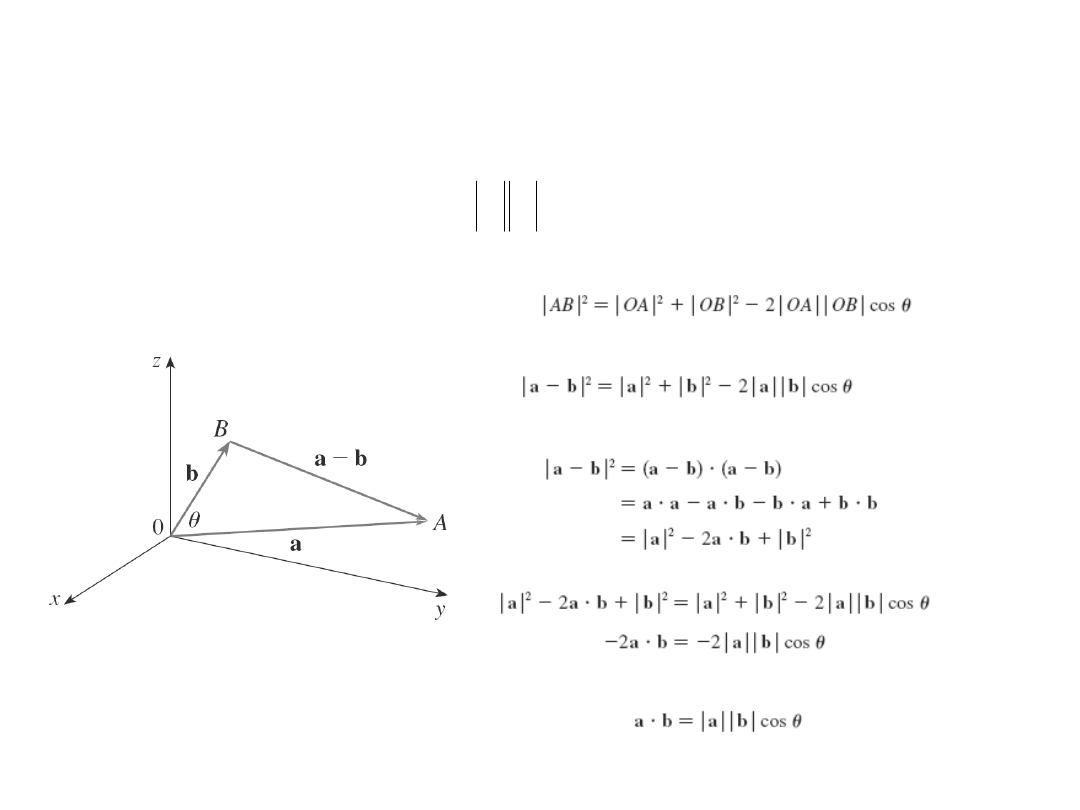
Twierdzenie

Niech  oznacza kąt pomiędzy wektorami a i b .



cos

b

a

b

a 



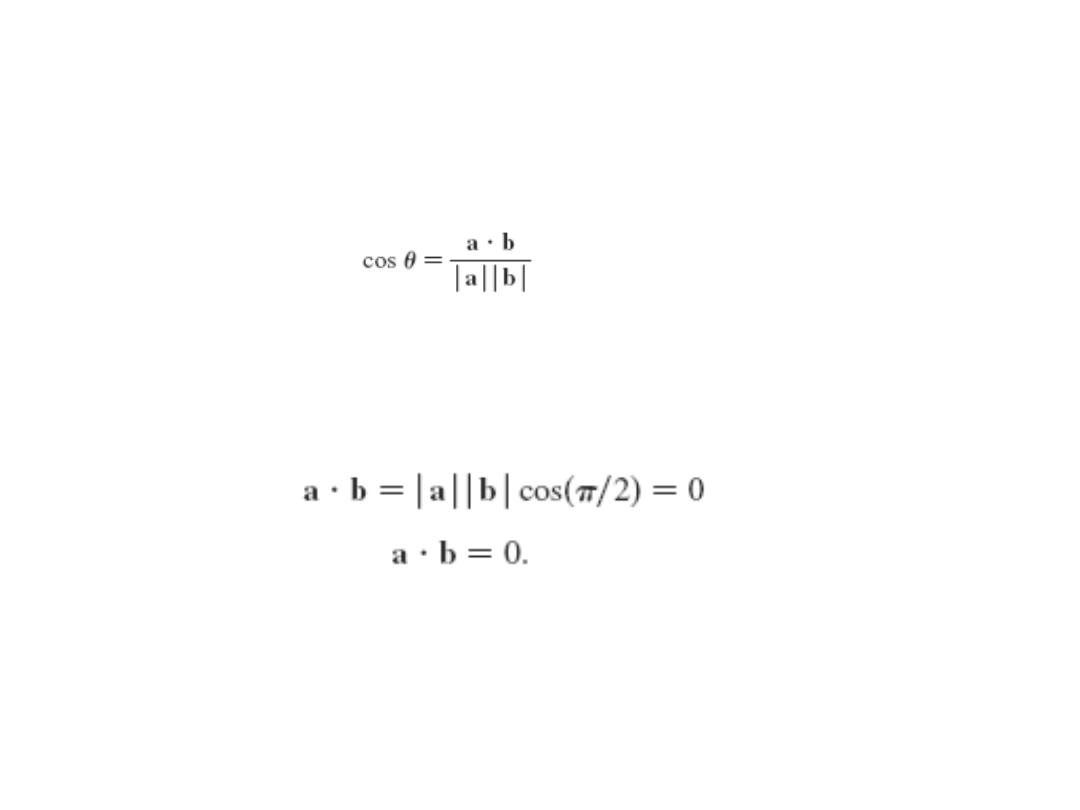
Kąt między wektorami niezerowymi

Wektory ortogonalne

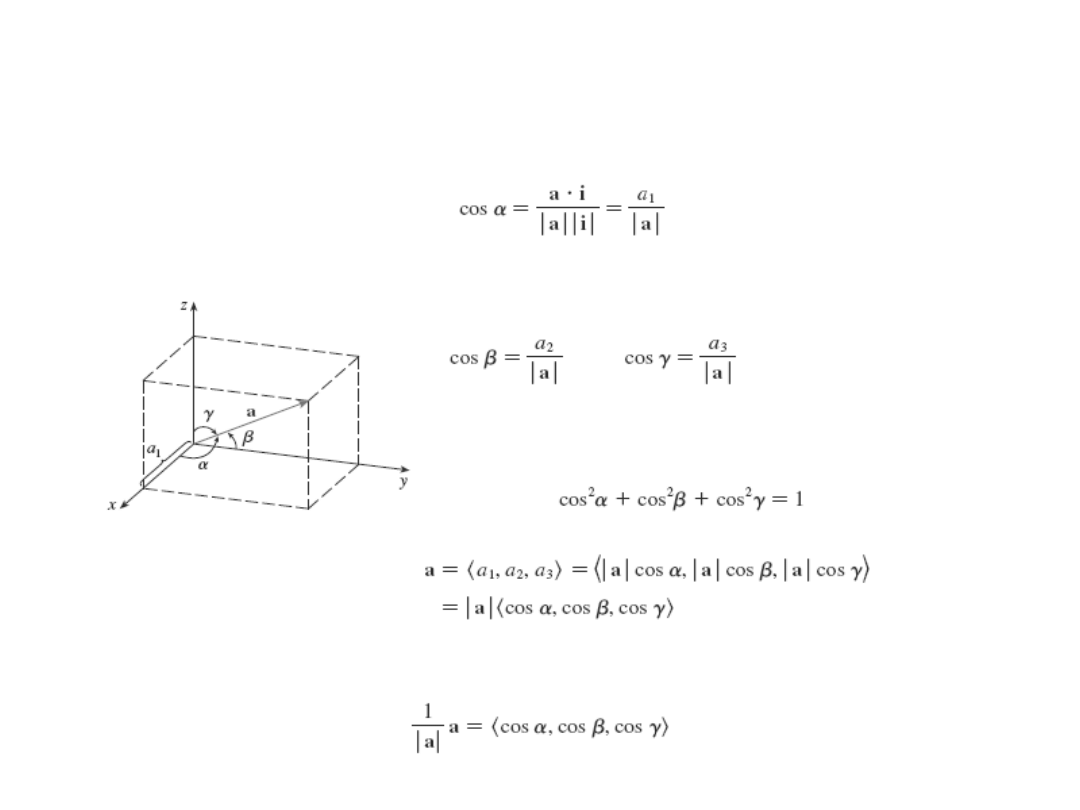
Cosinusy kierunkowe

 

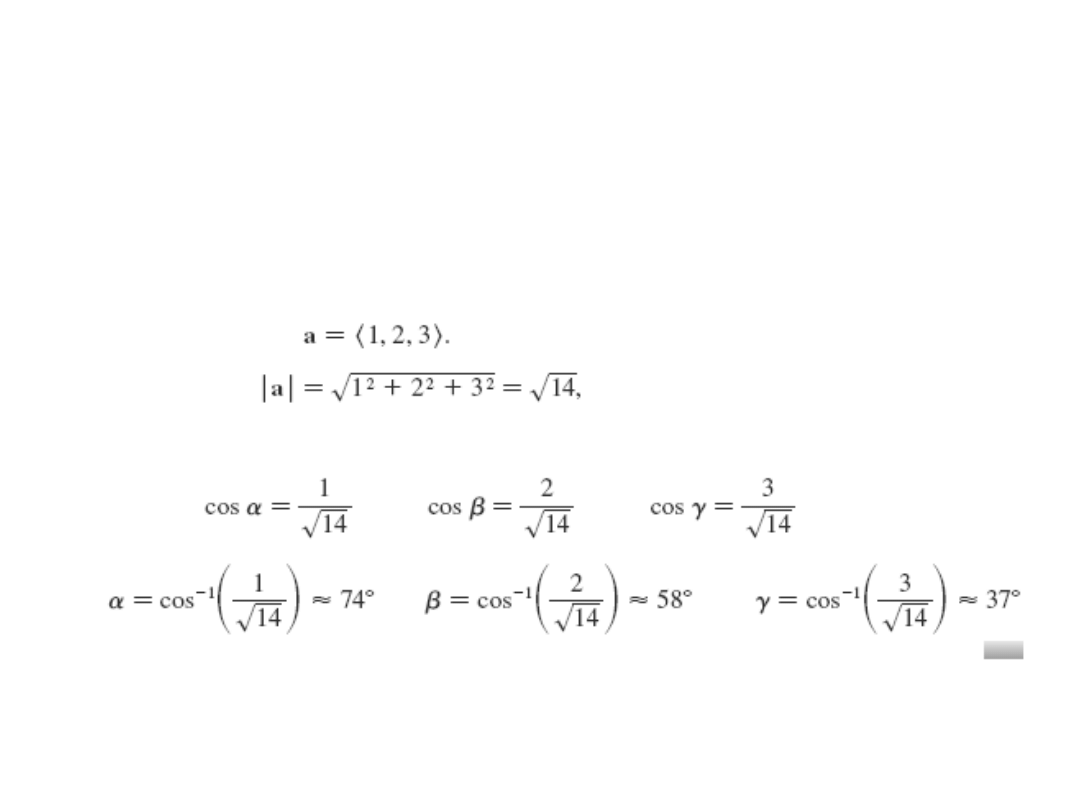
Przykład.

Oblicz cosinusy kierunkowe wektora a

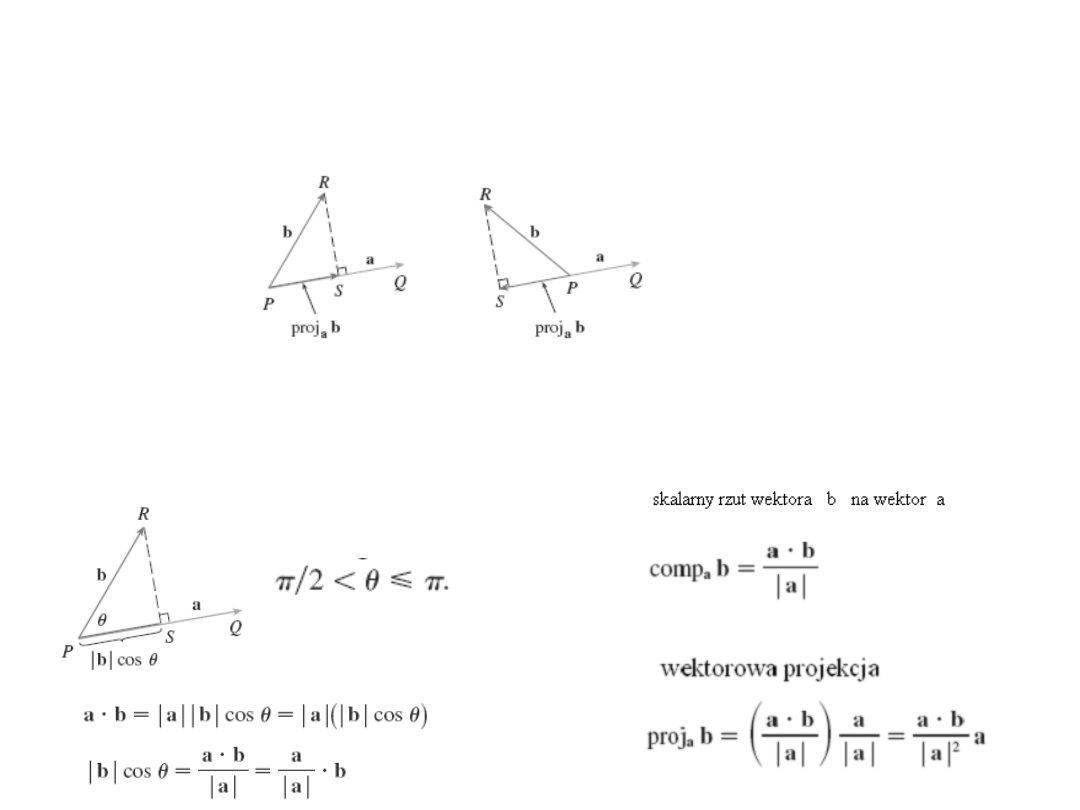
Projekcja – rzut wektora na kierunek

Skalarna projekcja wektora b na wektor a
( składowa b wzdłuż a).

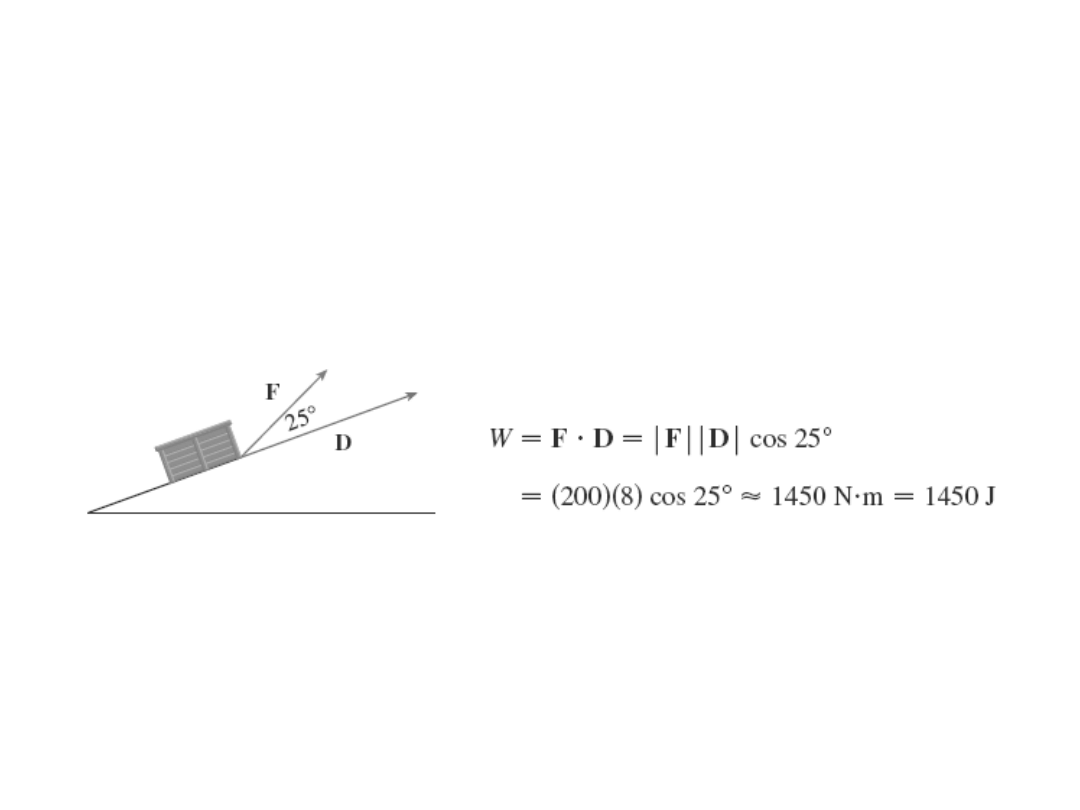
Przykład
Oblicz pracę wykonaną przez siłę
200N działającą na długości 8 m
pod kątem 25

o

 

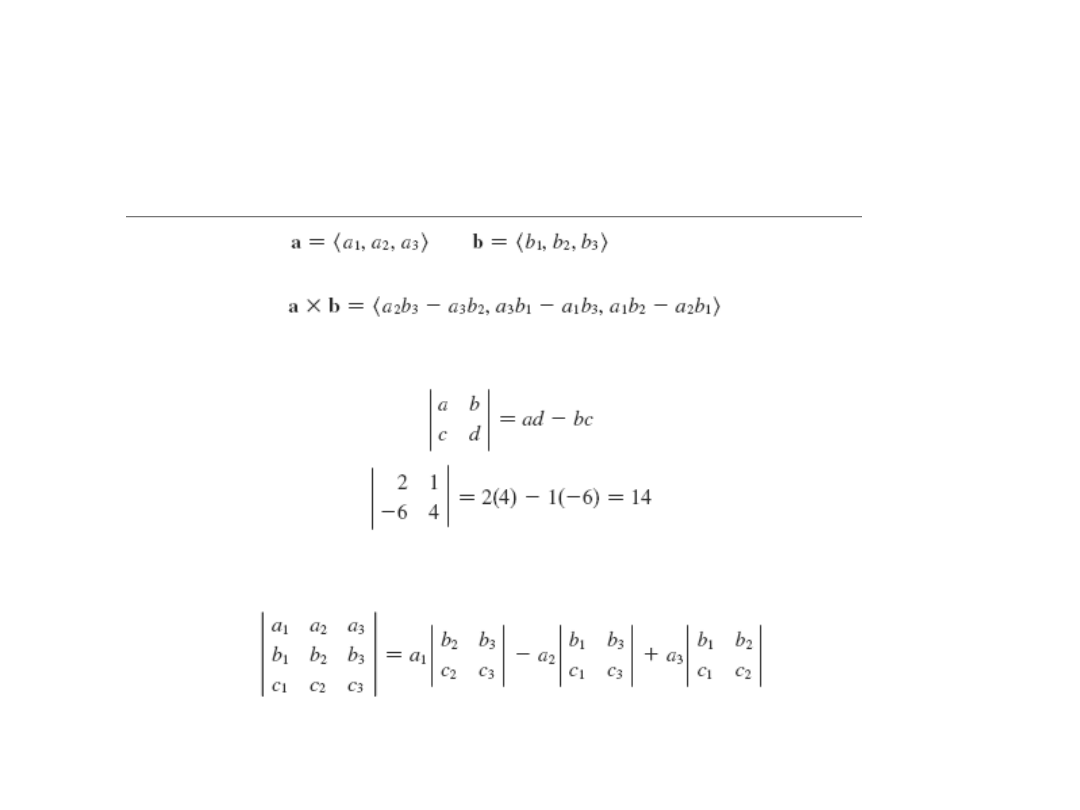
Iloczyn wektorowy

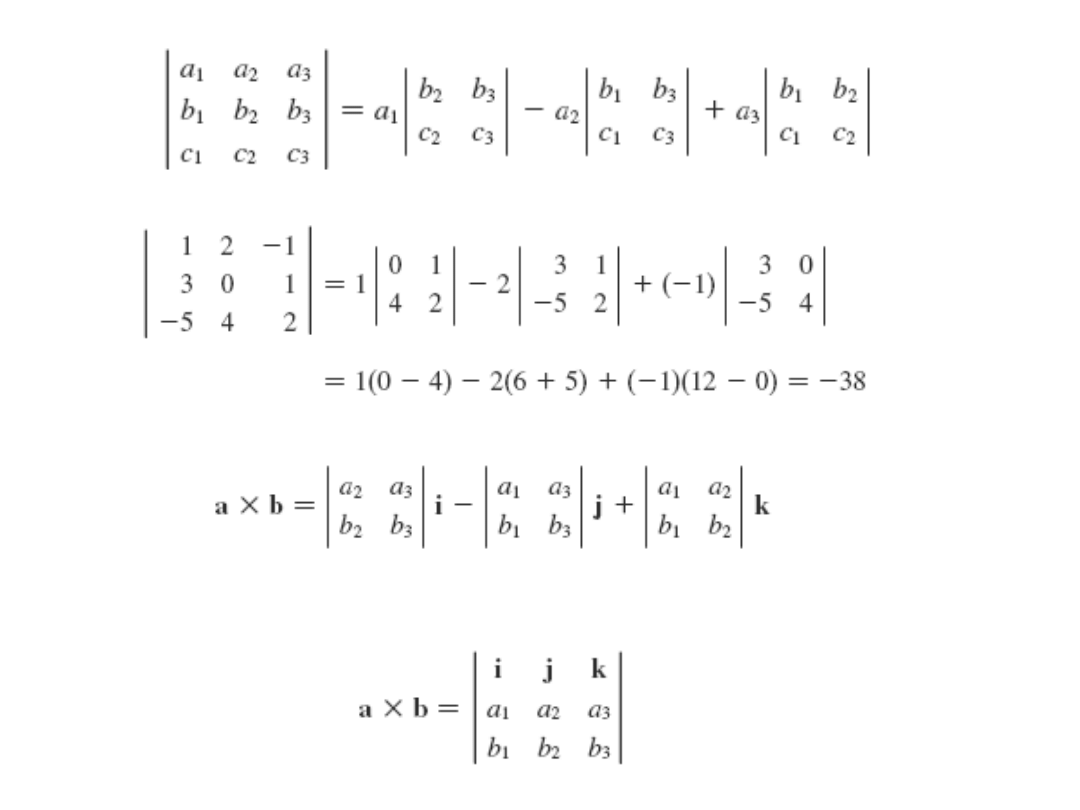
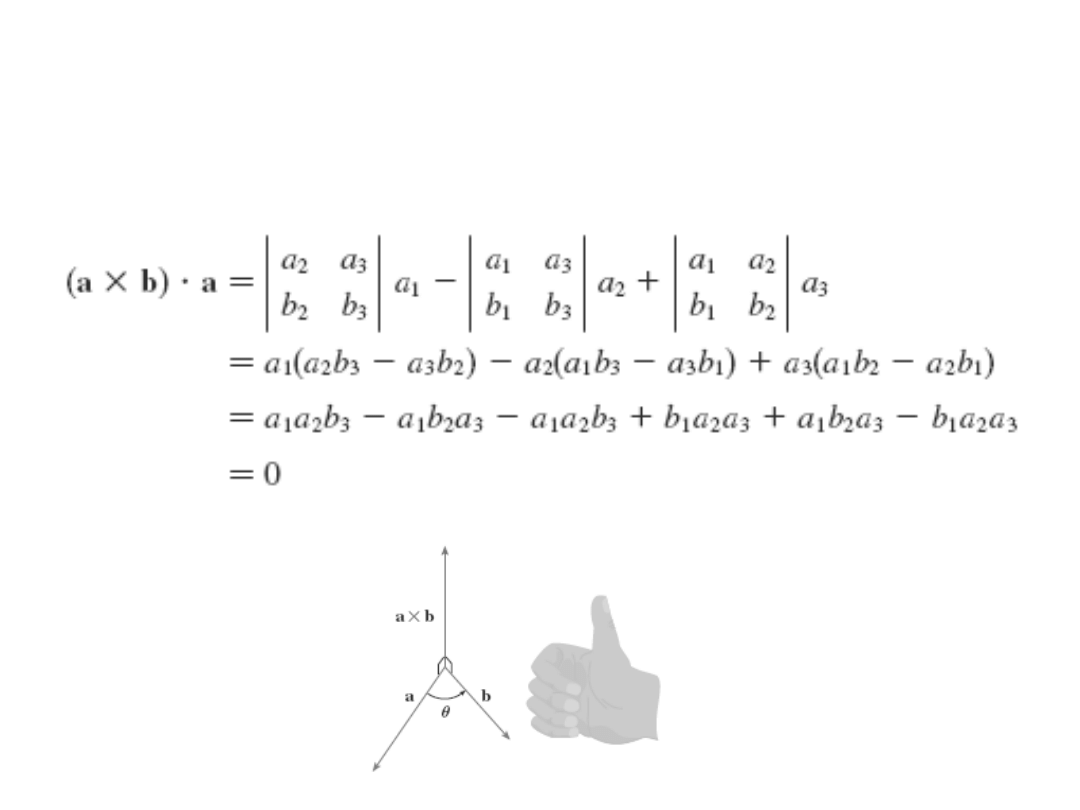
Twierdzenie
Wektor jest ortogonalny do a
i b
 

b

a

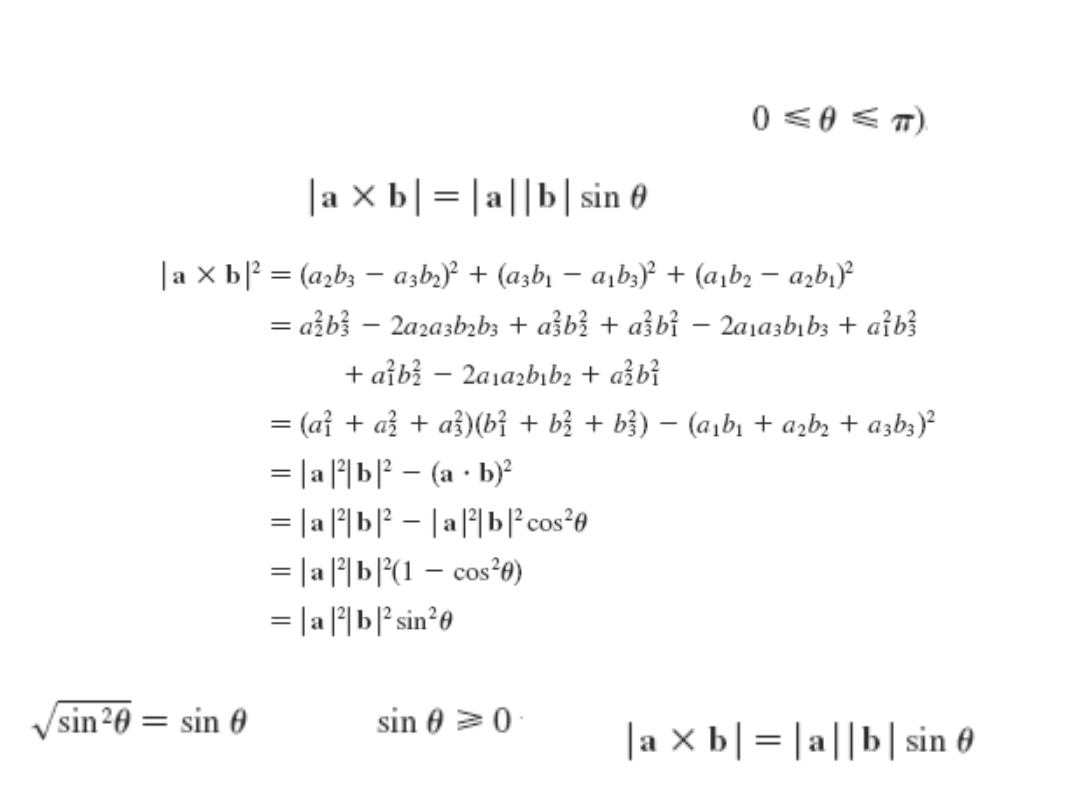
Twierdzenie 

Niech



oznacza kąt pomiędzy wektorami a i b

.

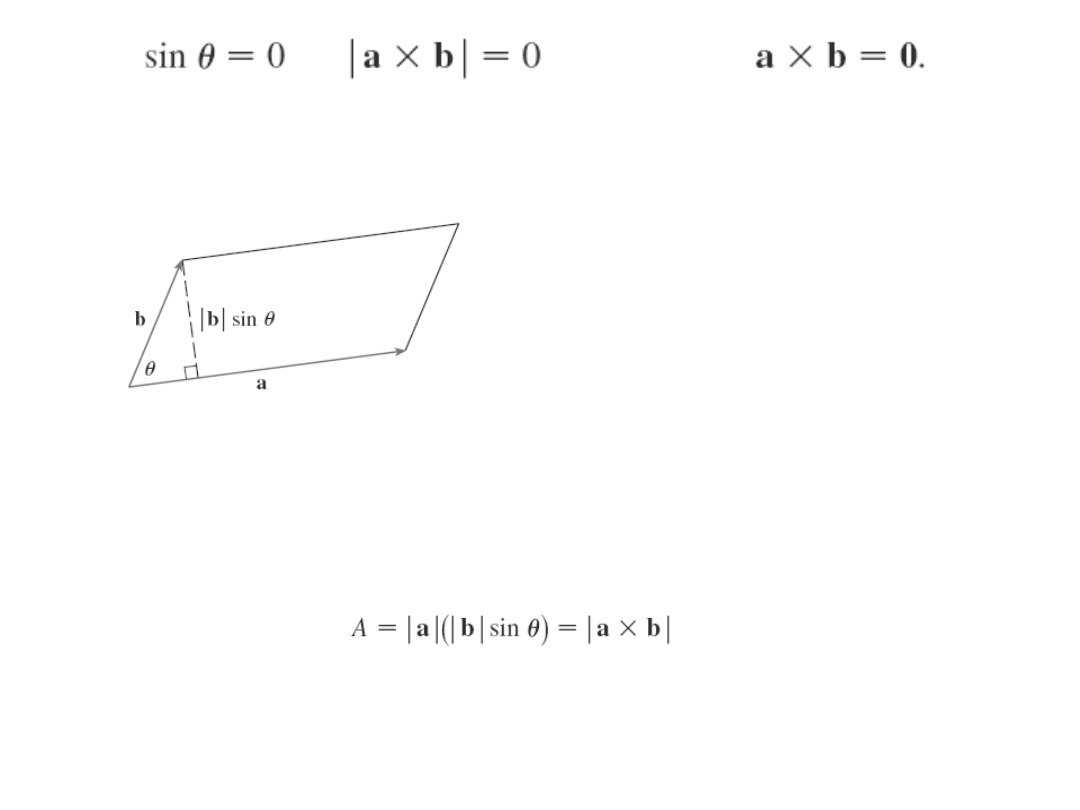
Pole równoległoboku którego boki są
odpowiedni wektorami a b jest równe: