
1
WYKŁAD 3:
CHARAKTERYSTYKI LINIOWYCH UKŁADÓW DYNAMICZNYCH W
DZIEDZINIE CZASU I CZĘSTOTLIWOŚCI
PODSTAWOWE CZŁONY DYNAMICZNE
1 Opis układu dynamicznego w dziedzinie czasu:
1.1 Odpowiedź impulsowa:
g t
L G s
( )
[ ( )]
=
−
1
:
- odpowiedź na pobudzenie deltą Diraca
δ
( )
t przy zerowych warunkach początkowych,
- własności delty Diraca
δ
( )
t :
δ
( )
t
t
t
=
∞
=
≠
dla
dla
0
0
0
,
δ
( )
t t
−∞
∞
∫
=
d
1,
f t
t t
f
( ) ( )
( )
δ
−∞
∞
∫
=
d
0 , L
t
[ ( )]
δ
=
1.
1.2 Odpowiedź skokowa:
h t
L G s s
( )
[ ( ) / ]
=
−
1
:
- odpowiedź na pobudzenie jednostkową funkcją skokową (jedynką Haeviside'a)
1( )
t
przy zerowych warunkach początkowych,
-
własności jedynki Haeviside'a
1( )
t :
1( )
t
t
t
=
<
≥
0
0
1
0
dla
dla
, 1( )
( )
t
t
=
−∞
∫
δ τ τ
d , L t
s
[ ( )]
/
1
=
1 .
1.3 Związki z modelem ( , , , )
A b c d w przestrzeni stanu:
-
rozważamy (dla uproszczenia) układ skalarny (SISO - Single Input Single Output):
)
(
)
(
)
(
t
u
t
t
b
Ax
x
+
=
&
(równanie stanu),
y t
t
du t
( )
( )
( )
=
+
c x
T
(równanie obserwacji),
-
x( )
t
R
n
∈
, u t y t
R
( ), ( )
∈
,
∀
t
,
- A
∈
×
R
n n
,
b c
,
∈
R
n
,
d R
∈
,
-
g t
t
d
( )
=
+
c
b
T
( )
Φ
gdzie
Φ
( )
s
s
=
−
−
(
)
I
A
1
,
[
]
[
]
Φ
Φ
( )
( )
t
L
s
L
s
t
=
=
−
=
−
−
−
1
1
1
(
)
exp(
)
I
A
A
,
I
macierz jednostkowa,
- h t
d t
( )
( )
=
+
∫
c
b
T
( )d
Φ τ τ
τ
0
1
,
-
G s
L g t
s
d
s
d
( )
[ ( )]
(
)
=
=
−
+ =
+
−
c
I
A
b
c
b
T
T
( )
1
Φ
,
-
H s
L h t
G s s
s
s d s
s
s d s
( )
[ ( )]
( ) /
(
)
/
/
/
/
=
=
=
−
+
=
+
−
c
I
A
b
c
b
T
T
( )
1
Φ
.

2
2 Opis układu dynamicznego w dziedzinie częstotliwości:
2.1 Charakterystyki częstotliwościowe (
ω ∈
+
R
):
G s
X
jY
M
e
s j
j
( )
( )
( ),
( )
,
( )
=
=
+
⋅
ω
ϕ ω
ω
ω
ω
X
( )
ω −
część rzeczywista
,
Y
( )
ω −
część urojona
,
M
( )
ω −
charakterystyka amplitudowa
(moduł),
ϕ ω
( )
−
charakterystyka fazowa
(faza),
M
X
Y
( )
( )
( )
ω
ω
ω
=
+
2
2
,
ϕ ω
ω
ω
( ) arctan
( )
( )
=
Y
X
,
X
M
( )
( ) cos ( )
ω
ω
ϕ ω
=
⋅
,
Y
M
( )
( ) sin ( )
ω
ω
ϕ ω
=
⋅
,
X
G s
s j
( ) Re[ ( )
]
ω
ω
=
=
,
Y
G s
s j
( ) Im[ ( )
]
ω
ω
=
=
2.2 Reprezentacje:
- reprezentacja funkcji M( )
ω
w układzie kartezjański z osiami (log,dB)
oraz funkcji
ϕ ω
( ) w układzie kartezjański z osiami (log,deg)
to
charakterystyki Bodego
(odpowiednio: amplitudowa oraz fazowa),
- reprezentacja funkcji
M
e
j
( )
( )
ω
ϕ ω
⋅
w układzie biegunowym z osiami ( X
Y
( ), ( )
ω
ω
)
to
charakterystyka amplitudowo-fazowa
(hodograf).
3 Podstawowe człony dynamiczne
u t
( )
G s
( )
y t
( )
U s
( )
Y s
( )
Y s
G s U s
( )
( )
( )
=
⋅
,
G s
( )
−
transmitancja podstawowego (prototypowego) członu dynamicznego.
3.1 Człon proporcjonalny:
G s
k
( )
=
,
H s
k s
( )
/
=
,
g t
k
t
( )
( )
= ⋅δ
,
h t
k
t
( )
( )
= ⋅
1
,
X
k
( )
ω =
,
Y
( )
ω =
0 ,
M
k
( )
ω =
,
ϕ ω
( )
=
0
o
.
3.2 Człon całkujący:
G s
k s
( )
/
=
,
H s
k s
( )
/
=
2
,
k
>
0
g t
k
t
( )
( )
= ⋅
1
,
h t
k t
t
( )
( )
= ⋅ ⋅
1
,
X
( )
ω =
0 ,
Y
k
( )
/
ω
ω
= −
,
M
k
( )
/
ω
ω
=
,
ϕ ω
( )
= −
90
o
.
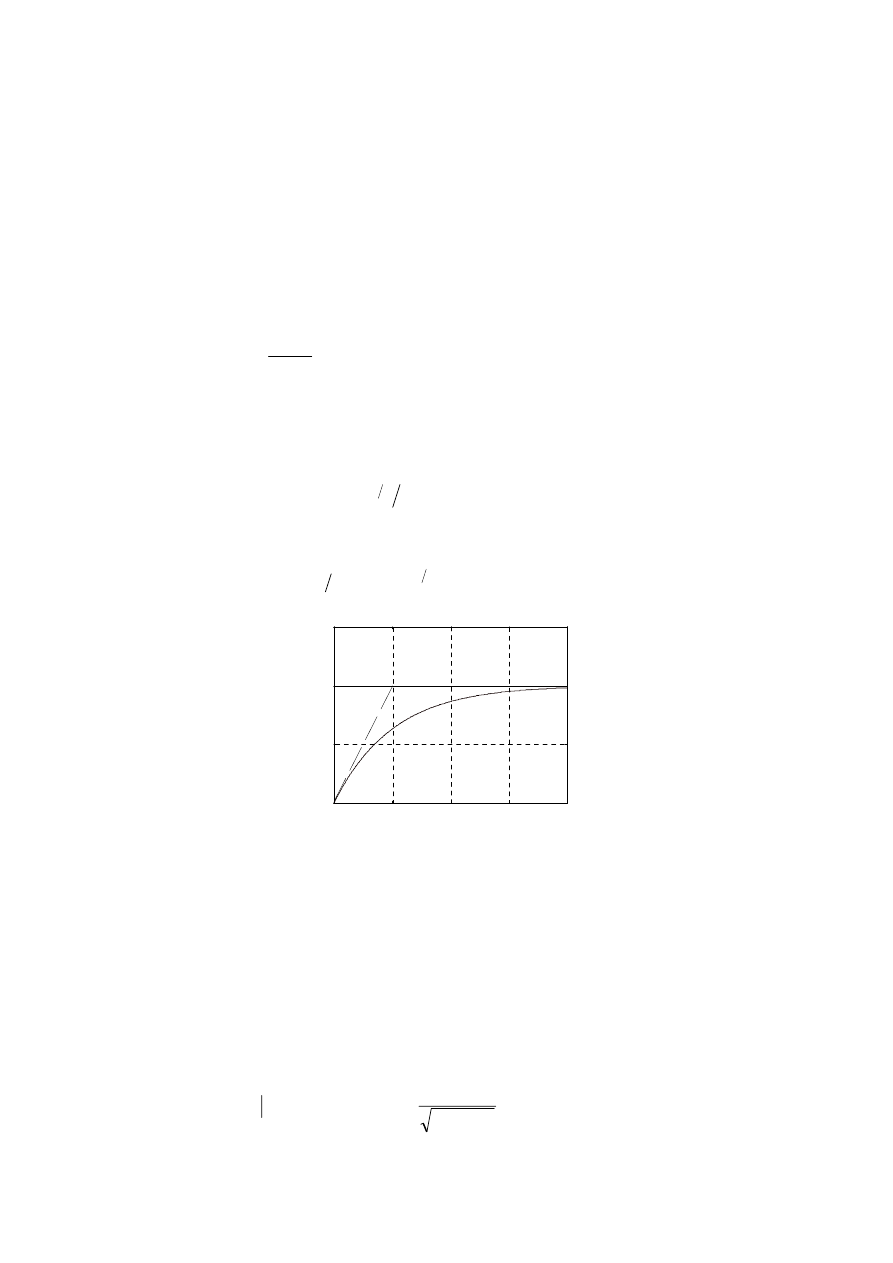
3
Model w przestrzeni stanu (założono: x t
y t
( )
( )
=
oraz
)
(
)
(
t
u
k
t
y
⋅
=
&
):
[ ]
A
=
0
,
[ ]
b
=
k
,
[ ]
c
=
1
,
[ ]
d
=
0
.
3.3 Człon różniczkujący:
G s
k s
( )
= ⋅
,
H s
k
( )
=
,
k
>
0
,
)
(
)
(
t
k
t
g
δ
&
⋅
=
, h t
k
t
( )
( )
= ⋅
1
,
X
( )
ω =
0 ,
Y
k
( )
ω
ω
= ⋅
,
M
k
( )
ω
ω
= ⋅
,
ϕ ω
( )
=
90
o
.
3.4 Człon inercyjny:
G s
k
sT
( )
=
+
1
,
(1)
k - wzmocnienie statyczne,
T - stałą czasową.
Odpowiedź impulsowa:
[ ]
g t
L G s
ke
T
t
t T
( )
( )
( )
=
=
⋅
−
−
1
1
.
Odpowiedź skokowa:
[
]
h t
L G s s
k
e
t
t T
( )
( )
(
) ( )
=
=
−
⋅
−
−
1
1
1
.
0
1
2
3
4
0
0.5
1
1.5
h ( )
t
t/T
Rys. 3.1. Znormalizowana odpowiedź skokowa członu dynamicznego pierwszego rzędu
(k
=
1).
Czas ustalania T
s
∆
odpowiedzi skokowej h t
( ) , definiowany jako
{
}
T
t h t
k
s
∆
∆
=
=
−
: ( )
(
)
1
, 0
1
< ≤
∆
,
wynosi
T
T
s
∆
∆
= − ⋅
ln .
Widmowa charakterystyka członu (1):
G s
M
e
k
T
e
s j
j
j
T
( )
( )
( )
arctan
=
− ⋅
=
=
+
ω
ϕ ω
ω
ω
ω
1
2 2
.
(2)
4
0
1
2
3
4
5
0
0.5
1
1.5
( )
M
ω
0.707
ω
3dB
ω
T
a)
0
1
2
3
4
5
-90
-60
0
o
-30
o
o
o
( )
ϕ ω
b)
ω
T
ω
3dB
-45
o
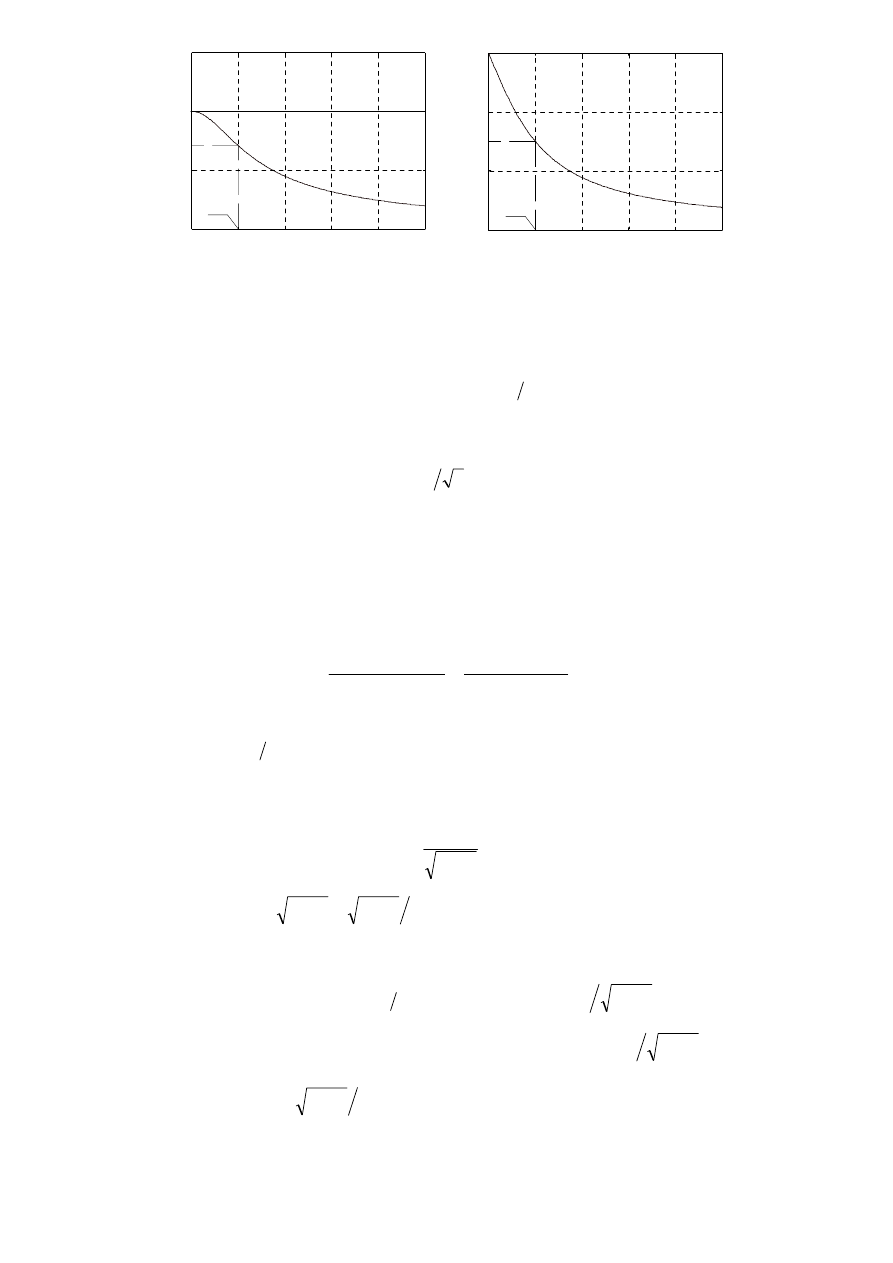
Rys. 3.2. Znormalizowane częstotliwościowe charakterystyki członu inercyjnego (k
=
1).
Pulsacja trzydecybelowego pasma przenoszenia członu (1) wynosi
ω
3
1
dB
T
=
,
czemu odpowiadają następujące wartości charakterystyki amplitudowej oraz
fazowej tego członu:
M(
)
ω
3
1 2
dB
=
oraz
ϕ ω
(
)
3
45
dB
o
= −
.
Model w przestrzeni stanu (założono: )
(
)
(
)
(
t
u
k
t
y
t
y
T
⋅
=
+
&
oraz y t
x t
( )
( )
=
):
[
]
A
= −
1/
T
,
[ ]
b
=
k T
/
,
[ ]
c
=
1
,
[ ]
d
=
0
.
3.5 Człon oscylacyjny:
G s
s s
s
s
n
n
n
( )
=
+
+
=
+
+
ω
ω
ζω
ζτ τ
2
2
2
2 2
2
1
1 2
, 0
1
< <
ζ
,
(3)
ζ
- współczynnik tłumienia,
ω
τ
n
=
1 jest pulsacją naturalną (pulsacją dragań nietłumionych),
Odpowiedź impulsowa:
[ ]
g t
L G s
e
t
t
n
t
n
( )
( )
sin
( )
=
=
−
⋅
−
−
1
2
0
1
ω
ζ
ω
ζω
1
,
(4)
ω
ω
ζ
ζ τ
0
2
2
1
1
=
−
=
−
n
- pulsacja drgań tłumionych.
Odpowiedź skokowa:
[
]
(
)
h t
L G s s
e
t
t
e
t
t
t
n
n
t
t
( )
( )
sin
( )
cos
sin
( ),
=
= −
+
−
⋅
=
= −
+
−
⋅
−
−
−
1
0
2
0
0
2
1
1
1
1
ζω
ζω
ω
α
ζ
ω
ζ
ω
ζ
1
1
(5)
α
ζ ζ
=
−
arc tan 1
2
.
5
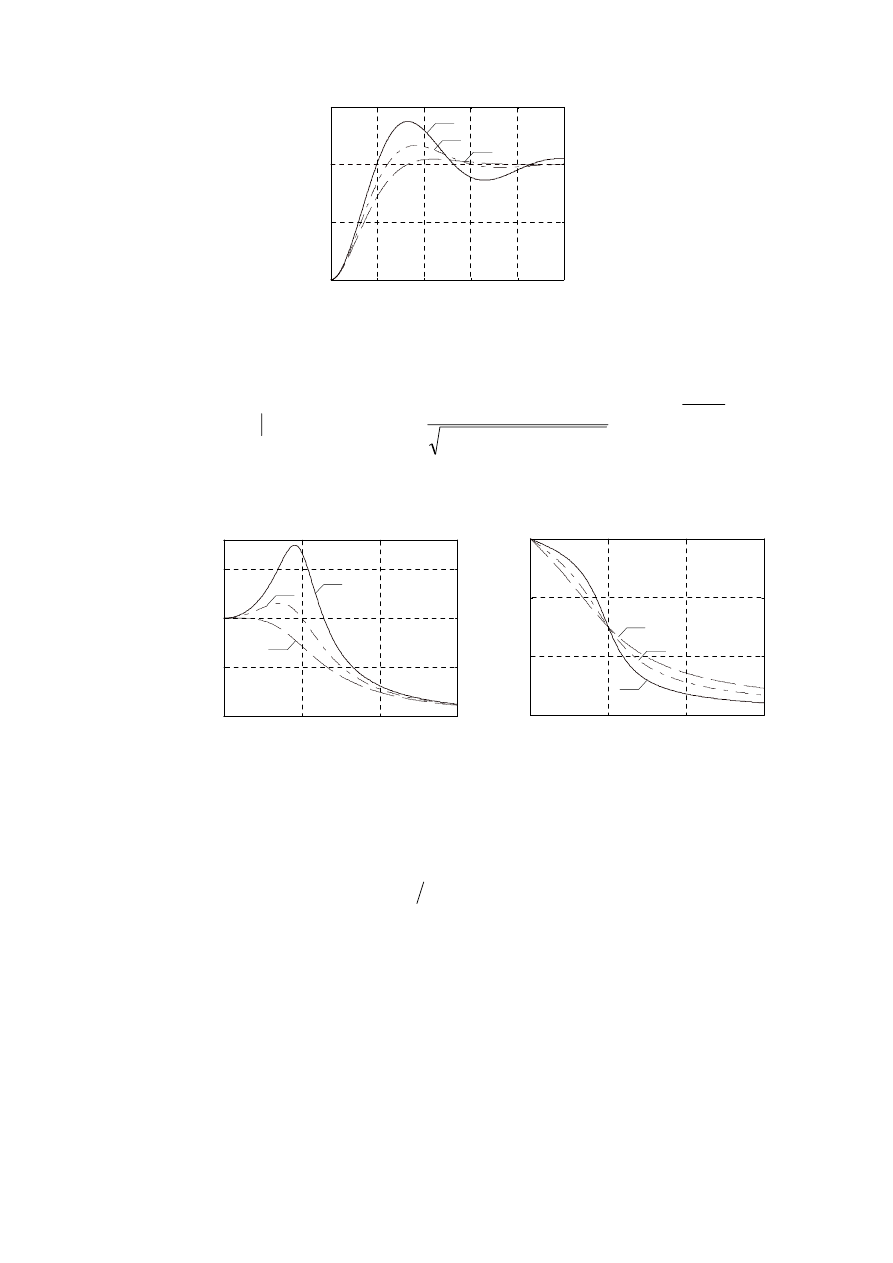
Przykładowe znormalizowane przebiegi odpowiedzi skokowych dla różnych
wartości współczynnika tłumienia
ξ
pokazano na rys. 3.3.
0
2
4
6
8
10
0
0.5
1
1.5
ζ
=
h( )
t
0.3
0.5
0.7
t/T
Rys. 3.3. Znormalizowane odpowiedzi skokowe członu oscylacyjnego.
Widmowa charakterystyka członu oscylacyjnego (3):
G s
M
e
e
s j
j
n
n
n
j
n
n
( )
( )
(
)
(
)
( )
arctan
=
− ⋅
−
=
⋅
=
−
+
⋅
ω
ϕ ω
ζω ω
ω ω
ω
ω
ω
ω
ζω ω
2
2
2 2
2
2
2
2
2
. (6)
Przykładowe znormalizowane przebiegi funkcji
M ( )
ω
oraz
ϕ ω
( )
dla różnych
wartości współczynnika tłumienia
ζ
pokazano na rys. 3.4.
0
1
2
3
0
0.5
1
1.5
ζ
=
0.3
0.5
0.7
ω
T
a)
( )
M
ω
0
1
2
3
ζ
=
0.5
0.7
0.3
0
o
-60
-120
o
-180
o
( )
ϕ ω
ω
T
b)
o
Rys. 3.4. Znormalizowane częstotliwościowe charakterystyki członu
oscylacyjnego.
Dla odpowiedzi skokowej
h t
( )
definiuje się wskaźniki (por. rys. 3.5):
- przeregulowanie
(
)
κ =
− ∞
∞ ⋅
h
h
h
max
( )
( ) 100%
, gdzie
h
h t
t
max
max ( )
=
≥
0
,
- czas osiągnięcia maksimum (czas piku, czas maksimum)
{
}
T
t h t
h
κ
=
=
: ( )
max
,
- czas ustalania dla strefy kontrolnej 2
∆
{
}
T
t h t
h
h
s
t
∆
∆
=
− ∞ = ⋅ ∞
≥
arg max : | ( )
( )|
( )
0
.
Odpowiednie wskaźniki definiuje się także dla amplitudowej charakterystyki
M ( )
ω
rozważanego członu dynamicznego (por. rys. 3.6):
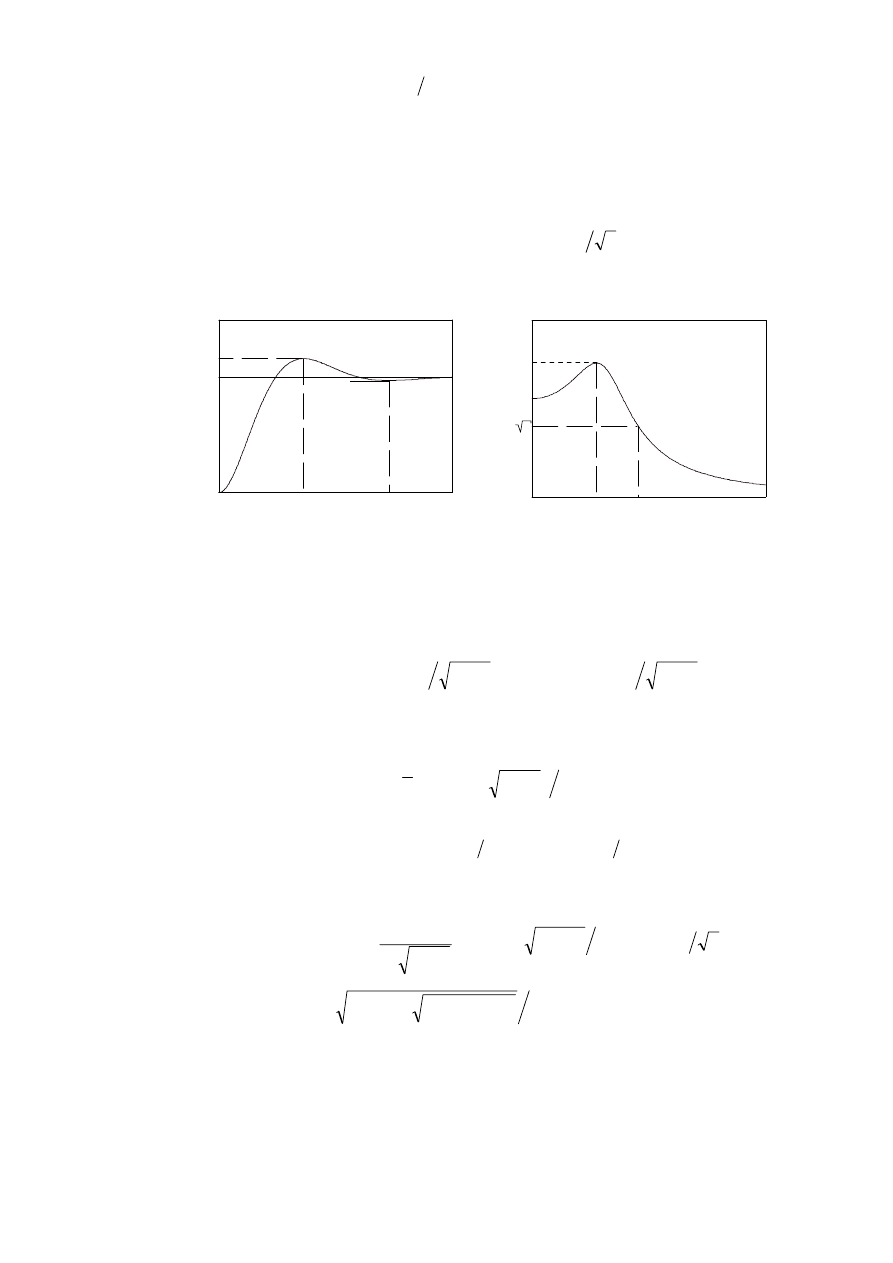
6
- wskaźnik oscylacyjności
M
M
M
r
=
max
( )
0 , gdzie M
M
max
max
( )
=
≥
ω
ω
0
,
- pulsacja rezonansowa
{
}
ω
ω
ω
r
M
M
=
=
:
( )
max
,
- trzydecybelowe pasmo przenoszenia
{
}
ω
ω
ω
3
3
0
2
dB
dB
=
=
:
(
)
( )
M
M
.
0
0
h ( )
t
t
h ( )
∞
h
max
∆
∆
T
κ
T
s
0
( )
M
ω
ω
M
r
ω
r
2
)
(
M 0
/
ω
3dB
0
)
(
M 0
Rys. 3.5. Definicja wskaźników
dotyczących odpowiedzi
sokowej.
Rys. 3.6. Definicja wskaźników
dotyczących charakterystyki amplitudowej.
Przeregulowanie
κ
oraz czas maksimum T
κ
zależą w następujący sposób od
parametrów
ζ
, 0
1
< <
ζ
, oraz
τ
transmitancji (3):
κ
ζπ
ζ
=
−
−
exp
1
2
oraz T
κ
πτ
ζ
=
−
1
2
.
(7)
Czas ustalania T
s
∆
jest nieciągłą funkcją współczynnika tłumienia
ζ
, dla której
można podać następującą ciągłą funkcję majoryzującą
T
T
s
s
∆
∆
∆
≤
=
−
| ln(
)|
τ
ζ
ζ
1
2
, 0
1
< <
ζ
.
Dla
∆ =
0 02
.
i
∆ =
0 05
.
oraz przy dostatecznie małych wartościach
ζ
obowiązują oszacowania: T
s2%
4
≅ τ ζ
oraz T
s5%
3
≅ τ ζ
. Wskaźniki M
r
,
ω
r
oraz
ω
3dB
, opisujące amplitudową charakterystykę
M ( )
ω
członu (3), związane
są z parametrami
ζ
oraz
τ
tego członu następującymi formułami:
M
r
=
−
1
2 1
2
ζ
ζ
,
ω
ζ τ
r
=
−
1 2
2
,
0
1 2
< <
ζ
, (8)
ω
ζ
ζ
τ
3
2
2 2
1 2
1 2
1
dB
=
−
+
−
+
(
)
.
(9)
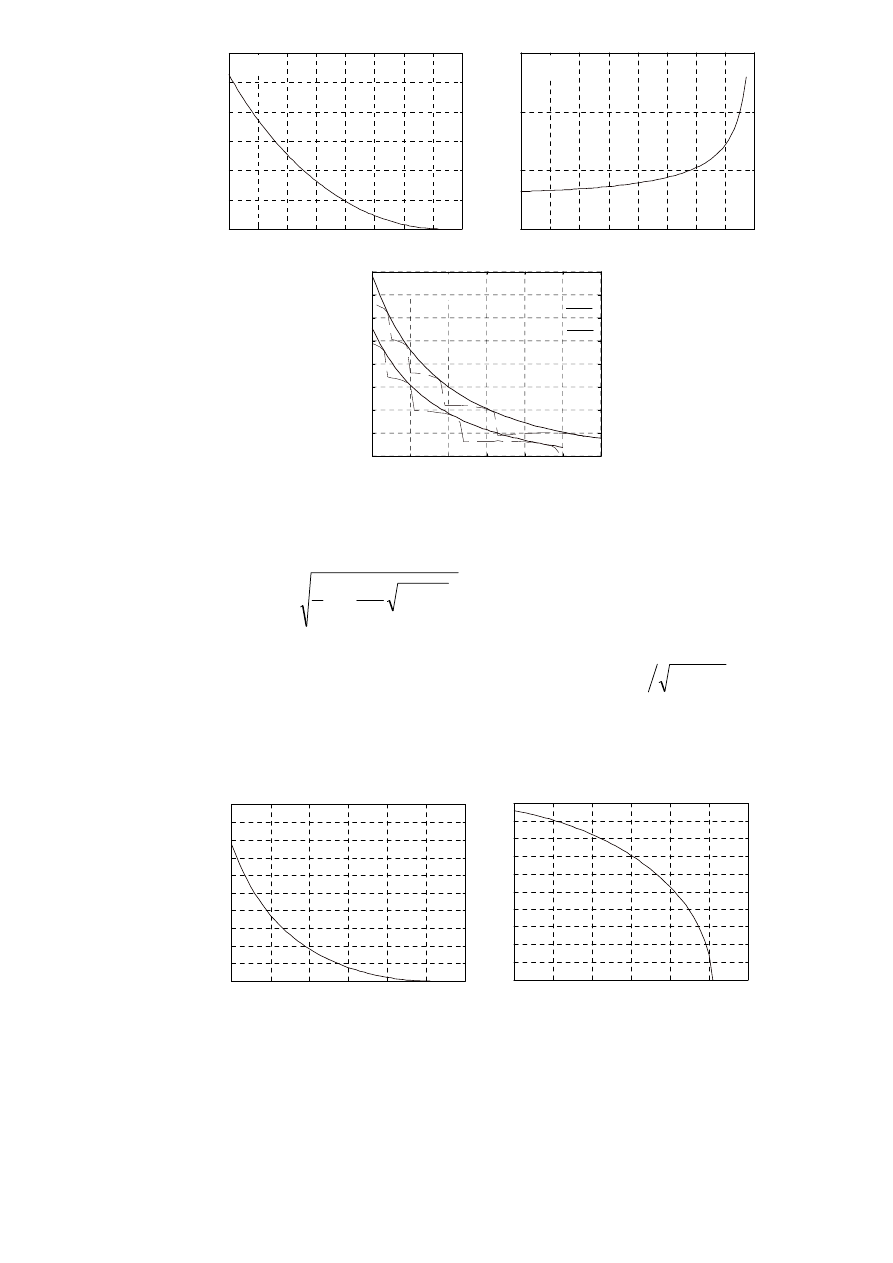
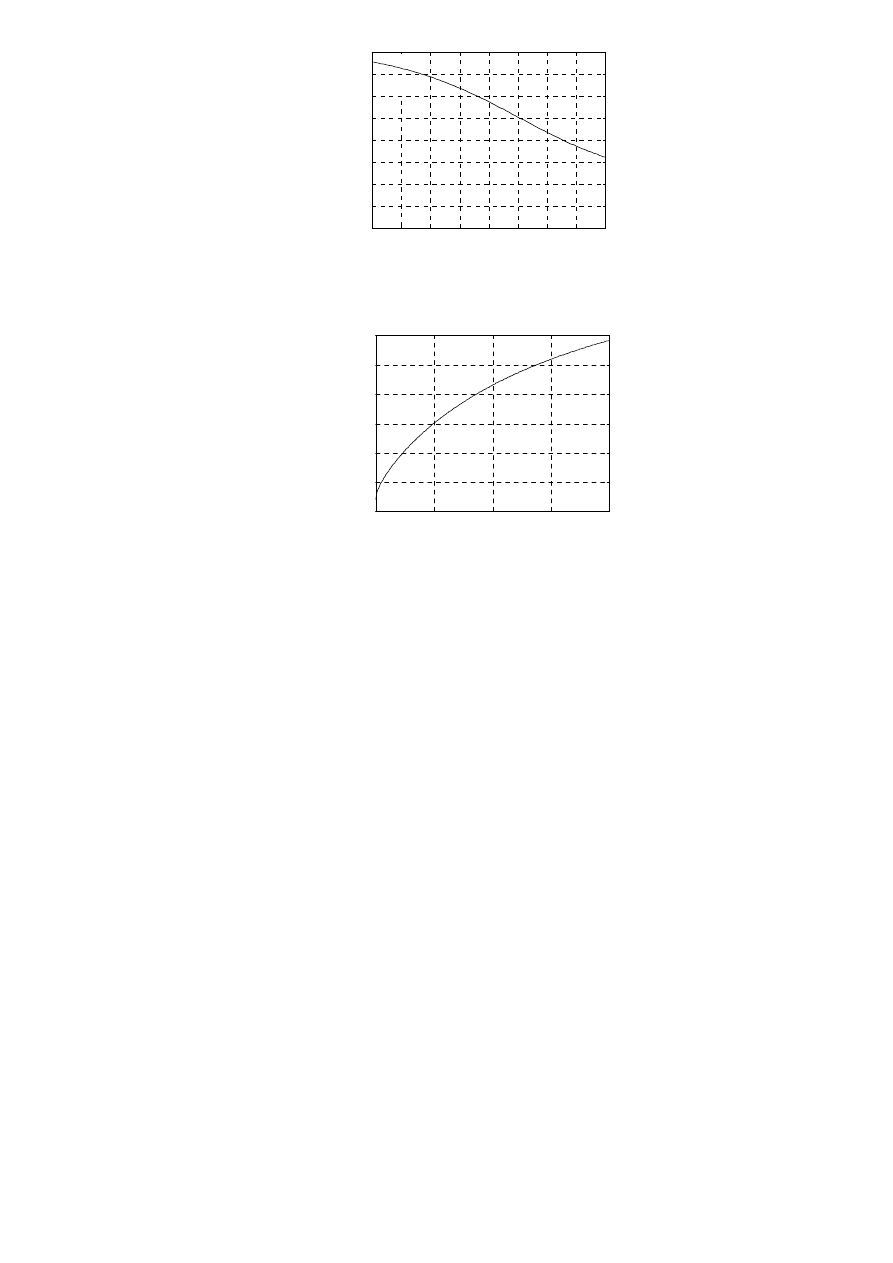
Wykresy rozważanych wskaźników przedstawiono na rys. 37 (wskaźniki
dotyczące odpowiedzi skokowej) oraz na rys. 3.8 (wskaźniki dotyczące
charakterystyki amplitudowej).
7
0.2
0.4
0.6
0.8
1
0
20
40
60
ζ
κ
[%]
a)
0.2
0.4
0.6
0.8
1
0
5
10
15
ζ
b)
T
κ
τ
/
0.2
0.4
0.6
0.8
4
8
12
16
20
ζ
∆
=
2%
5%
T
∆
s
τ
/
c)
_
T
∆
s
τ
/
T
∆
s
τ
/
_
T
∆
s
τ
/
Rys. 3.7. Wskaźniki odpowiedzi skokowej członu oscylacyjnego.
Ze wzoru (8) wynika, iż
ζ =
−
−
1
2
1
1
1
2
M
M
r
r
, M
r
≥
1.
(10)
Korzystając ze wzoru (7) wyznaczyć można zależność przeregulowania
κ
od
wskaźnika oscylacyjności M
r
. Zachodzi ponadto
ζ
κ
π
κ
=
+
|ln |
|
2
2
,
κ >
0,
zatem na podstawie wzoru (8) można określić relację odwrotną, pozwalającą na
wyrażenie wartości wskaźnika oscylacyjności M
r
w zależności od
przeregulowania
κ
. Opisany jednoznaczny związek między wskaźnikami M
r
oraz
κ
ilustruje wykres dany na rys. 3.9.
0.2
0.4
0.6
0.8
1
1.4
1.8
2.2
2.6
3
ζ
M
r
a)
0.2
0.4
0.6
0.8
0
0.2
0.4
0.6
0.8
1
ζ
b)
ω
r
τ
8
0.2
0.4
0.6
0.8
1
0
0.4
0.8
1.2
1.6
ζ
ω
3dB
τ
c)
Rys. 3.8. Wskaźniki charakterystyki amplitudowej członu oscylacyjnego.
1
1.5
2
2.5
3
0
20
40
60
M
r
κ
[%]
Rys. 3.9. Związek między wskaźnikiem oscylacyjności a przeregulowaniem
odpowiedzi skokowej członu oscylacyjnego.
Model w przestrzeni stanu:
)
(
0
)
(
)
(
2
1
0
)
(
)
(
2
2
1
2
2
1
t
u
k
t
x
t
x
t
x
t
x
n
n
n
+
−
−
=
ω
ζω
ω
&
&
,
[ ]
[ ]
y t
x t
x t
u t
( )
( )
( )
( )
=
+
1 0
0
1
2
.

9
4. Transmitancja operatorowa jako model. Wyznaczanie charakterystyk czasowych na
podstawie transmitancji operatorowej
Przykład 1 (Odpowiedzi czasowe)
Oblicz odpowiedź impulsową oraz skokową modelu o transmitancji operatorowej
G s
s
s
s
s
s
( )
=
+
+
+
+
+
(
) / (
)
24 30
8
24 26
9
2
2
3
.
Rozwiązanie
Ponieważ rozważana transmitancja jest transmitancją o jednokrotnych biegunach - zachodzi
bowiem
G s
s
s
s
s
s
L s M s
( )
=
+
+
+
+
+
=
(
) / (
)(
)(
)]
( ) /
( )
24 30
8
2
3
4
2
- odpowiedź impulsową
obliczyć można w następujący sposób:
g t
L s
M s
e
L s
M s
e
L s
M s
e
t
s
t
s
t
s
t
( )
( )
( )
( )
( )
( )
( )
,
2
3
4
=
′
⋅
+
′
⋅
+
′
⋅
≥
=−
−
=−
−
=−
−
2
3
4
0
,
(1)
gdzie
′
=
=
+
+
M s
M s
s
s
s
( ) d ( ) d
26 18
3
2
. Wynika stąd, iż
g t
e
e
e
t
t
t
( )
6
2
3
4
= −
−
+
−
−
−
2
16
,
t
≥
0. Odpowiedź skokową obliczamy analogicznie ze wzoru
h t
L s
M s
L s
sM s
e
L s
sM s
e
L s
sM s
e
s
s
t
s
t
s
t
( )
( )
( )
( )
( )
( )
( )
( )
( )
2
3
4
=
+
′
⋅
+
′
⋅
+
′
⋅
=
=−
−
=−
−
=−
−
0
2
3
4
, t
≥
0, (2)
skąd ostatecznie otrzymujemy
h t
t
t
t
t
( )
e
2e
e
,
2
3
4
= +
+
−
≥
−
−
−
1
4
0
.
Przykład 2 (Oryginał)
Znajdź oryginał transformaty
F s
s
s
( )
1 3s
1
= + +
+
(
) / (
)
2
3
.
Rozwiązanie
Przedstawiając F s
( ) w postaci
F s
A
s
A
s
A
s
( )
=
+ +
+
+
+
1
2
2
3
3
1
1
1
/ (
)
/ (
)
/ (
)
, otrzymujemy
A
s
A
s
A
s s
1
2
3
2
1 3
(
)
(
)
1
1
2
+
+
+ +
= + +
. A zatem A
1
1
=
, 2
3
1
2
A
A
+
=
, A
A
A
1
2
3
1
+
+
=
, skąd
wynika, iż
A
1
1
=
,
A
2
1
=
oraz A
3
1
= −
. Korzystając ze wzoru
L
s
t
n
e
n
n
t
−
−
−
− +
=
− ⋅
1
1
1
[(
) ]
/ (
)!
α
α
, n
≥
1, t
≥
0, otrzymujemy
f t
t
t
e
t
( )
1
0
= + −
⋅
−
(
.
)
5
2
, t
≥
0.
Przykład 3 (Odpowiedź impulsowa)
Znajdź odpowiedź impulsową oraz skokową modelu danego transmitancją operatorową
G s
s
s
s
s
s
s
s
s
s
( )
45 20
7
15 11
5
45 20
7
3
2
1
2
=
+
+
+
+
+
=
+
+
+
+ +
2
2
3
2
2
(
)[
(
) ]
.
(1)
Rozwiązanie
Rozkładając (1) na ułamki proste, otrzymujemy
G s
s
s
s
( )
5
2
=
+ + +
+ +
6 3
2
1
2
/ (
) (
) / [
(
) ]
.
Odpowiedź impulsowa ma zatem postać
g t
e
t
t e
t
t
( )
cos2
sin
3
=
+
+
⋅
−
−
6
2
2
(
)
, t
≥
0. Z kolei,
rozkładając na ułamki proste transformatę odpowiedzi skokowej H s
G s s
( )
( )
=
/ , stwierdzamy,
iż
H s
s
s
s
s
( )
=
−
+ − +
+ +
3
2 3
1
2
1
2
2
/
/ (
) (
) / [
(
) ]
. Odpowiedź skokowa ma zatem postać:
h t
e
e
t
t
t
( )
cos2
3
= −
−
⋅
−
−
3 2
, t
≥
0.

10
5. Układy pierwszego rzędu
Przykład 4 (Całkowanie+sprzężenie zwrotne)
Obiekt dynamiczny całkujący o operatorowej transmitancji
G s
k
s
p
p
( )
=
/
objęto pętlą
proporcjonalnego ujemnego sprzężenia zwrotnego poprzez kanał o wzmocnieniu
k
f
.
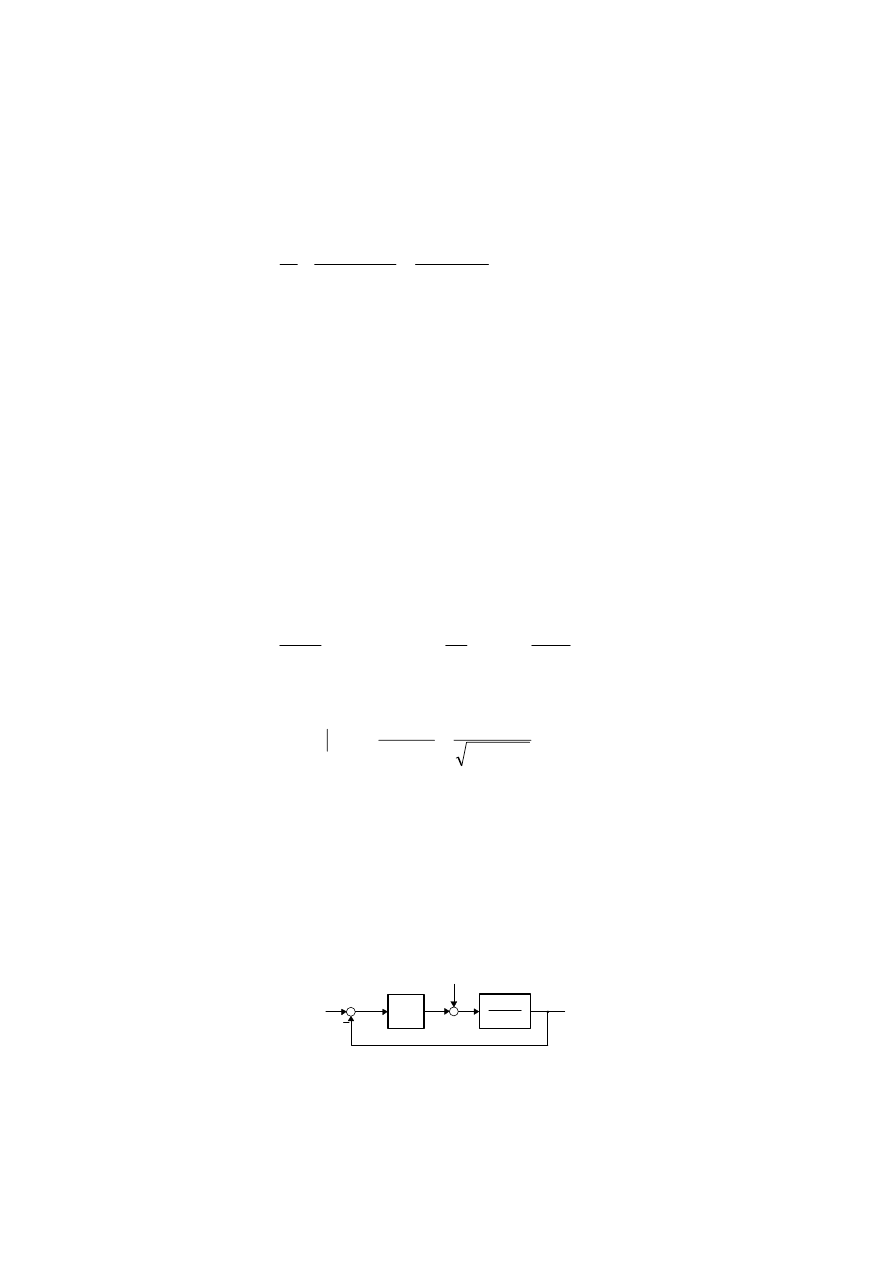
Wyznacz operatorową transmitancję otrzymanego układu zamkniętego (rys. 3.10), wyrażając
ją za pomocą statycznego wzmocnienia
k
i stałej czasowej T . Zakładając, że do wejścia
rozpatrywanego układu przyłożono sygnały: a - jednostkowego skoku położeniowego oraz b -
jednostkowego skoku prędkościowego, podaj przebieg odpowiedzi na każde z tych pobudzeń,
a następnie, definiując uchyb e t
( ) jako różnicę pomiędzy wejściem i wyjściem rozpatrywanego
układu, znajdź wartość końcową tego uchybu, wyrażając ją jako funkcję wyróżnionych wyżej
parametrów
k
i T .
c t
( )
k
s
p
r t
( )
k
f
Rys. 3.10. Strukturalny schemat układu dynamicznego
Rozwiązanie
Operatorowa transmitancja rozpatrywanego układu wyraża się wzorem
G s
k
s
k k
s
k
s k k
p
p f
p
p f
( )
=
+
=
+
/
/
1
.
(1)
Zapisując (1) w postaci
G s
k
Ts
( )
=
+
1
,
(2)
gdzie: k oznacza statyczne wzmocnienie układu zamkniętego, zaś T jest stałą czasową tego
układu, mamy
k
k
f
=
1/
oraz
T
k k
p f
=
1/ (
)
. Dla wejściowego sygnału r t
( ) w postaci
jednostkowego skoku odpowiedź układu (1) opisana jest wzorem
c t
L G s R s
L
k
s
Ts
k
e
t
t T
( )
( ) ( )
( )
=
=
+
=
−
⋅
−
−
−
1
1
1
1
[
]
(
)
(
)
/
1
.
(3)
Zauważmy, że wzmocnienie obiektu
k
p
nie wpływa na końcową wartość tej odpowiedzi. Dla
sygnału wejściowego w postaci jednostkowego skoku prędkościowego, otrzymujemy
c t
L G s R s
L
k
s
Ts
k t T
Te
t
t T
( )
( ) ( )
( )
=
=
+
=
−
+
⋅
−
−
−
1
1
2
1
[
]
(
)
[(
)
]
/
1
.
(4)
Wyznaczmy teraz końcową wartość uchybu e t
r t
c t
( )
=
−
( )
( ) w każdym z rozważanych wyżej
przypadków. W pierwszym przypadku - dla wejścia w postaci jednostkowego skoku
położeniowego - końcowa wartość uchybu jest wartością skończoną; wartość tę możemy
obliczyć na podstawie danej transformaty uchybu. Mamy
E s
s
k
s
Ts
k sT
s
Ts
( )
= −
+
= − +
+
1
1
1
1
(
)
(
)
.
(5)
11
Otrzymujemy zatem e
sE s
k
s
( )
( )
∞ =
= −
→
lim
0
1
. Rozpatrywany układ nie wprowadza uchybu
końcowego tylko wtedy, gdy
k
=
1
. W drugim przypadku, dla wejściowego sygnału w postaci
jednostkowego skoku prędkościowego zachodzi
e t
t k t T
Te
t
k t kT kTe
t
t T
t T
( )
( )
( )
= −
−
+
⋅
=
−
+
−
⋅
−
−
[(
)
]
[(
)
]
/
/
1
1
1
.
(6)
Jak widać, jeżeli
k
≠
1
, uchyb e t
( ) narasta nieograniczenie w miarę upływu czasu. Natomiast,
w przypadku, w którym
k
=
1
, wartość końcowa e( )
∞
uchybu e t
( ) istnieje. Korzystając z
twierdzenia o wartości końcowej oryginału, obliczamy najpierw
E s
s
T
s s
T
s s
T
( )
=
−
+
=
+
1
1
1
1
1
2
2
/
(
/ )
(
/ )
,
(7)
a następnie e
sE s
T
s
( )
( )
∞ =
=
→
lim
0
.
Przykład 5 (Całkowanie+ sprzężenie)
Obiekt dynamiczny całkujący o operatorowej transmitancji
G s
k
s
p
p
( )
=
/
objęto pętlą
proporcjonalnego ujemnego sprzężenia zwrotnego poprzez kanał o wzmocnieniu
k
f
(rys. 3.10
z
Przykładu 4). Wyznacz widmową transmitancję G j
(
)
ω
układu zamkniętego. Zbadaj
zależność trzydecybelowego pasma przenoszenia tego układu
ω
3dB
od
k
f
. Niech
ω
3
1
10
dB
rad s
=
⋅
−
, zaś dla
ω
ω
=
01
3
.
dB
zachodzi | (
)|
dB
dB
G j
ω
≈
20
. Oszacuj na tej podstawie
wartości parametrów
k
p
oraz
k
f
.
Rozwiązanie
Operatorowa transmitancja rozważanego układu zamkniętego dana jest wzorem
G s
k
Ts
( )
=
+
1
, gdzie
k
k
f
=
1
,
T
k k
p f
=
1
.
(8)
A zatem widmowa transmitancja tego układu ma postać
G j
G s
k
j T
k
T
e
s j
j
T
(
)
( )
arctg (
ω
ω
ω
ω
ω
=
=
+
=
+
=
−
1
1
2 2
)
.
(9)
Z wyrażenia opisującego moduł tej transmitancji wynika, że pasmo przenoszenia równa się
ω
3
1
dB
=
/ T , a zatem na podstawie wzoru (8) otrzymujemy
ω
3dB
=
k k
p f
. Wynika stąd, iż jest
to wielkość proporcjonalna do wzmocnienia kanału sprzężenia zwrotnego. Z kolei, ze wzoru
wzoru (9) wynika, iż dla
ω
ω
=
01
3
.
dB
można przyjąć, że |
|
G j
k
(
)
ω ≈
. Dla założonych danych
liczbowych otrzymujemy zatem
k
k
f
=
≈
1
01
/
.
, a następnie
k
k
p
f
=
≈
ω
3
100
dB
/
.
Przykład 6 (Człon inercyjny)
Obiekt sterowania, będący członem inercyjnym pierwszego rzędu, sterowany jest za pomocą
proporcjonalnego sterownika w układzie, którego schemat przedstawia się jak na rys. 3.11.
c t
( )
k
r t
( )
d t
( )
+
s
1 +
1
Rys. 3.11. Strukturalny schemat układu sterowania
Zakładając, iż r t
t
( )
,
=
∀
0
, oraz przyjmując, że do sygnału sterującego obiektem dodaje się
zakłócenie d t
t
( )
( )
= δ
, zbadaj wpływ tego zakłócenia na wielkość sterowaną c t
( ) .

12
Rozwiązanie
Zapiszmy zakłóceniową transmitancję rozważanego układu zamkniętego. Mamy
C s
D s
k
s
( )
( )
=
+ +
1
1
(
)
.
(10)
Dla założonego zakłócenia D s
L
t
( )
( )
=
=
[
]
δ
1 wyznaczamy transformatę wielkości sterowanej
C s
k
s
( )
=
+ +
1
1
(
)
,
(11)
a następnie, po obliczeniu odwrotnej transformaty Laplace'a, otrzymujemy
c t
e
t
k t
( )
( )
(
)
=
⋅
− +
1
1
.
Widzimy zatem, iż powiększając wzmocnienie
k
sterownika, powodujemy zwiększenie
szybkości zaniku zakłóceniowej odpowiedzi impulsowej tego układu.
Wyszukiwarka
Podobne podstrony:
Anatomia czlowieka Uklad krazenia id 62632
ES lab uklad zaplonowy id 16347 Nieznany
Charakterystyki liniowe, f
47 UKLAD HORMONALNY id 39006
7 UKLAD CHLONNY id 44983 Nieznany
Chemia IV Uklad okresowy id 112318
karta charakterystykiI MPREGNAT DO DREWNA id 231833
liniowe zastosowania wo id 2687 Nieznany
Karta Charakterystyki Rozcienczalnik Nitro lPPG id 23
instrukcja uklad cyfrowy id 217 Nieznany
fizjologia uklad krwionosny id Nieznany
Fizyka ciekawostki uklad sloneczny id
Anatomia czlowieka Uklad krazenia id 62632
charakterystyka id 110667 Nieznany
więcej podobnych podstron