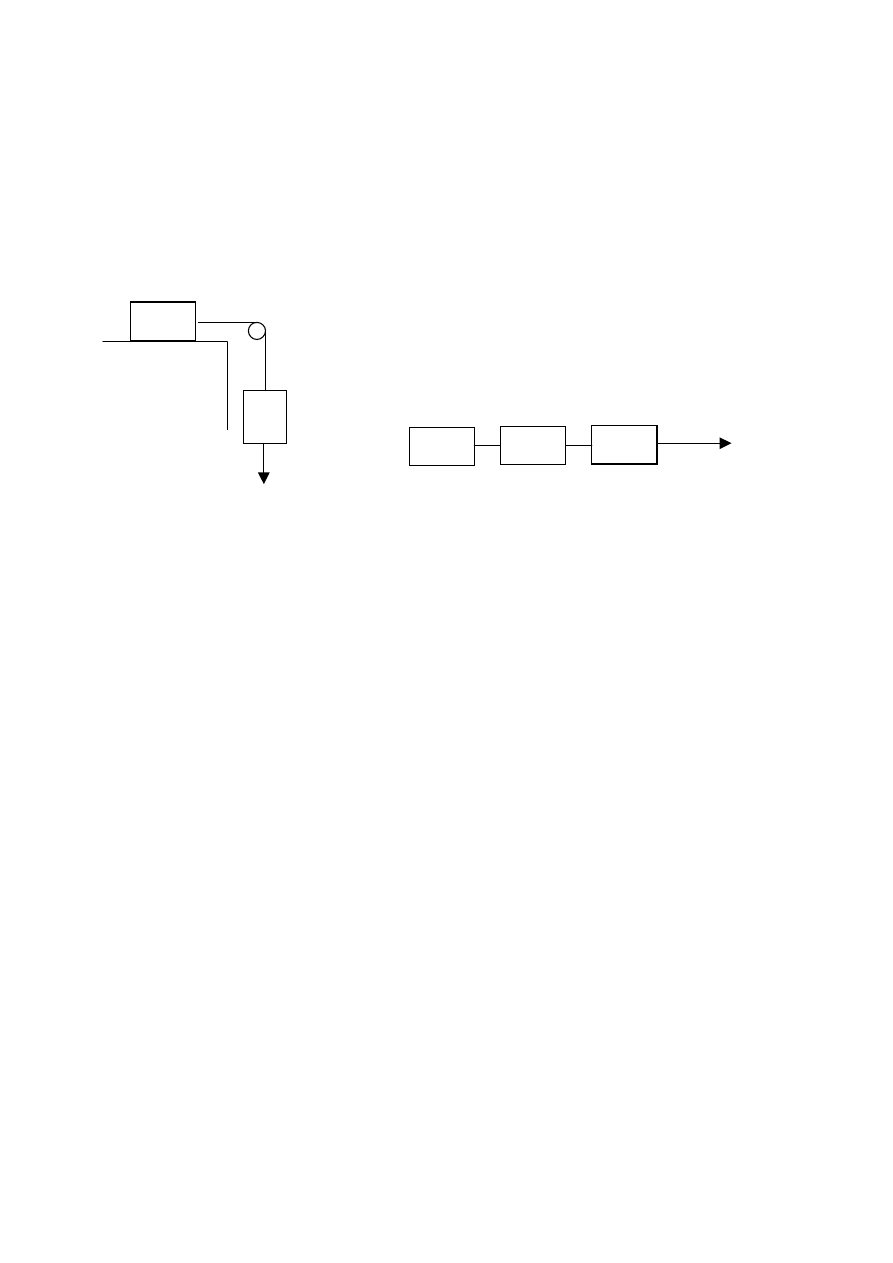
Zadania na ćwiczenia 3


1. Przypomnieć sobie siły tarcia (kinematyczne, statyczne)

2. Rozpatrzyć ruch po równi pochyłej bez tarcia i z tarciem

3. Dla układów mas z rysunków poniżej znaleźć przyspieszenia i naprężenia nici

4. Jednorodny giętki łańcuch o długości l i liniowej gęstości masy

λ

jest przewieszony

przez mały idealny bloczek. Znaleźć przyspieszenie łańcucha w funkcji długości x
zwisającej z jednej strony bloczka.

5. Na poziomej powierzchni stołu spoczywa jednorodny łańcuch, przy czym jeden jego

koniec zwisa ze stołu. Znaleźć współczynnik tarcia, jeżeli wiadomo, że łańcuch zaczyna
zsuwać się ze stołu, gdy długość jego zwisającej części jest równa [ 1/5] całej długości
łańcucha.

6. Na spadające swobodnie ciało działa siła oporu powietrza F

oporu

=-kv (v – prędkość, k –

współczynnik proporcjonalności). Napisać równanie ruchu (II zasadę dynamiki).
Pokazać, że ciało osiąga prędkość graniczną v

g

= mg/k. Sprawdzić przez podstawienie do

równania ruchu, że prędkość zmienia się zgodnie ze wzorem:

)

1

(

/ m

kt

g

e

v

v

−

−

=

Wykonać wykres v(t). Spróbować policzyć drogę w funkcji czasu.

7. Obliczyć maksymalną szybkość jaką uzyska kula o promieniu 8 cm i masie 1 kg,

spadająca swobodnie, jeśli siła oporu powietrza dana jest wzorem: R=k

σ

v

2

, gdzie v -

prędkość ciała,

σ

- powierzchnia przekroju ciała w płaszczyźnie prostopadłej do kierunku

ruchu, k - współczynnik zależny od kształtu poruszającego się obiektu. Dla kuli k =
0,024 Ns

2

m

−

4

.

8. Dwie nieruchome łodzie znajdujące się na jeziorze połączone są długim sznurem.

Człowiek znajdujący się na pierwszej łodzi ciągnie sznur działając siłą F = 50 N. Oblicz
prędkość względną obu łodzi po czasie t = 4 s działania siły. Ciężar pierwszej łodzi wraz
z człowiekiem wynosi Q

1

= 2000 N, a ciężar drugiej łodzi Q

2

= 800 N. Opory ruchu

można pominąć.

m

1

m

1

m

1

m

2

m

3

F

F=m

1

g