1

Wielkości skalarne, wektorowe i tensorowe w fizyce

.

Wielkości fizyczne występujące w mechanice i innych działach fizyki można podzielić na skalary i wektory. Aby

określić wielkość skalarną, wystarczy podać tylko jedną liczbę. Wielkościami takimi są masa, czas, temperatura,
objętość i inne.

Do określenia wielkości wektorowej nie wystarcza podanie jednej liczby. Przykładem takiej wielkości jest siła. Aby

ją określić, należy podać wartość, kierunek w przestrzeni oraz zwrot. W ogólnym przypadku aby określić wektor,
należy znać:

a) wartość bezwzględną wektora, zwaną modułem,
b) kierunek, czyli prostą, na której leży wektor (linię działania),
c) zwrot,
d) punkt przyłożenia.

Nie wszystkie wielkości wektorowe wymagają dla swego określenia podania wszystkich wymienionych cech. Z tego
punktu widzenia rozróżniamy: wektory zaczepione, wektory przesuwne lub ślizgające się oraz wektory swobodne.
Wektory zaczepione wymagają do ich określenia podania wszystkich czterech cech. Wektorów takich nie można
przemieszczać ani przesuwać.

Wektory przesuwne są określone za pomocą modułu, zwrotu oraz linii działania. Takie wektory mogą być jedynie
przesuwane wzdłuż prostych, na których leżą.

Wektory swobodne są określone przez moduł, zwrot oraz kierunek równoległy do ich linii działania. Oznacza to, że
wektor swobodny można dowolnie przemieszczać, równolegle do kierunku jego działania.

Działania na wektorach

Dodawanie wektorów

Żeby dodać dwa wektory, gdy znamy ich współrzędne, należy dodać odpowiednie współrzędne - x-owe do

x-owych, a y-owe do y-owych (ew. z-owe do z-owych).

Na płaszczyźnie

(w

x

, w

y

) + (u

x

, u

y

) = (w

x

+u

x

, w

y

+u

y

)

W przestrzeni

(w

x

, w

y

, w

z

) + (u

x

, u

y

, u

z

) =(w

x

+u

x

, w

y

+u

y

, w

z

+ u

z

)

W odróżnieniu od dodawania liczb całkowitych wektor-suma wcale nie musi być dłuższy od któregoś z
wektorów wyjściowych, a często bywa krótszy.
Suma dwóch wektorów może być też wektorem zerowym (mimo, że wektory wyjściowe miały długości
różne od zera)
Zachodzi to w dwóch przypadkach:
- oba sumowane wektory są zerowe
- dodawane wektory są przeciwne - tzn. mają ten sam kierunek i wartość, ale przeciwne zwroty.

Odejmowanie wektorów

Żeby odjąć dwa wektory, gdy znamy ich współrzędne, należy odjąć odpowiednie współrzędne - x-owe od x-
owych, a y-owe od y-owych (ew. z-owe od z-owych).

2

Na płaszczyźnie

(w

x

, w

y

) - (u

x

, u

y

) =

(w

x

- u

x

, w

y

- u

y

)

W przestrzeni

(w

x

, w

y

, w

z

) - (u

x

, u

y

, u

z

) =

(w

x

- u

x

, w

y

- u

y

, w

z

- u

z

)

Wektor-różnica wcale nie musi być krótszy od pierwszego z wektorów wyjściowych. Może być dłuższy.

Różnica dwóch wektorów jest równa zero (jest wektorem zerowym) w dwóch przypadkach:

1. oba odejmowane wektory są zerowe
2. odejmowane wektory są równe - tzn. mają ten sam kierunek, zwrot i wartość.

Mnożenie wektora przez liczbę

Tak samo dzielenie przez liczbę.

otrzymujemy nowy wektor

Aby wektor podzielić przez liczbę, mnożymy go przez odwrotność tej liczby

powstaje wektor a razy dłuższy od wektora wyjściowego.
Zwrot wektora wynikowego jest:
- taki sam jak wyjściowy, gdy a jest dodatnie
- przeciwny do wyjściowego, gdy a jest ujemne

Wynik może być równy zero (będzie tzw. wektorem zerowym) gdy:
- wektor wyjściowy jest równy zero, lub
- liczba a jest równa zero

Mnożenie skalarne wektorów

otrzymujemy skalar

Powstaje liczba (skalar) o wartości równej iloczynowi wartości obu wektorów razy kosinus kąta między nimi
zawartego.

3

Lub inaczej:
Iloczyn skalarny jest równy iloczynowi długości jednego wektora mnożonego przez długość rzutu drugiego
wektora na kierunek wyznaczony przez pierwszy wektor.

Iloczyn skalarny stanie się równy Zero, gdy którykolwiek z wektorów wyjściowych jest zerowy, lub
wektory są do siebie prostopadłe.

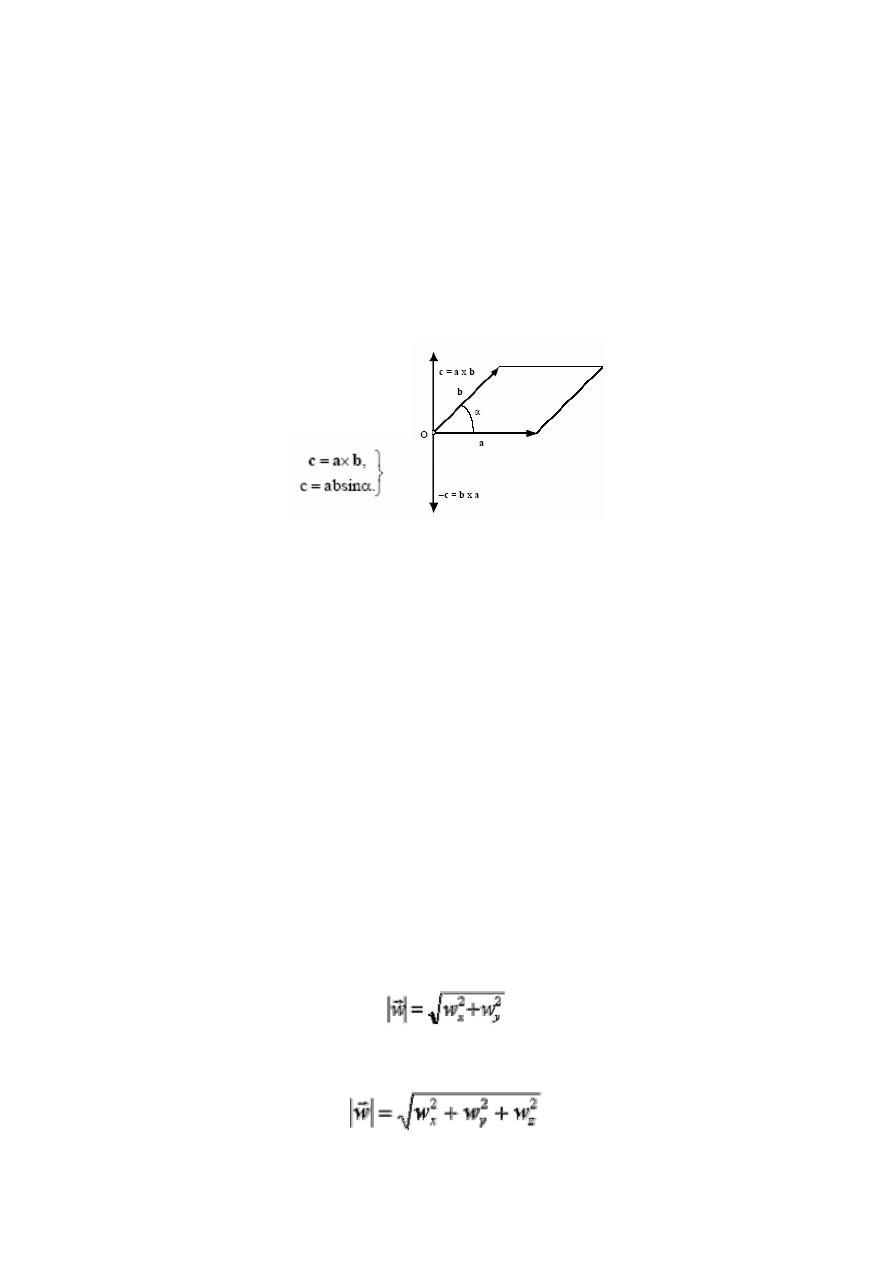
Iloczyn wektorowy

(stosuje się wyłącznie do wektorów w trzech wymiarach)

Iloczynem wektorowym a x b dwóch wektorów a i b nazywamy wektor c prostopadły do płaszczyzny
utworzonej przez te wektory, którego moduł jest równy iloczynowi modułów tych wektorów pomnożonemu
przez sinus kąta zawartego między nimi

otrzymujemy nowy wektor prostopadły do obu wektorów wyjściowych.

Długość (wartość) tego wektora wynosi: c= |a| |b| sinα.

- wartość wektora wynikowego jest równa iloczynowi wartości obu wektorów wyjściowych razy sinus kąta
między nimi zawartego (ma to sens tylko w trzech wymiarach);
- kierunek wektora wynikowego jest prostopadły do płaszczyzny wyznaczonej przez wektory wyjściowe;
- zwrot ustalamy w oparciu o regułę śruby prawoskrętnej

Interpretacja iloczynu wektorowego 2:
Wartość iloczynu wektorowego jest równa iloczynowi długości pierwszego wektora przez długość rzutu
drugiego wektora na kierunek prostopadły do pierwszego wektora.

Wektor zerowy otrzymamy, gdy jeden z wektorów wyjściowych jest zerowy, lub gdy wyjściowe wektory są
równoległe.

Znajdowanie wartości

(długości) wektora gdy znamy jego współrzędne

Długość wektora na płaszczyźnie obliczamy stosując twierdzenie Pitagorasa.

Żeby obliczyć wartość wektora trójwymiarowego trzeba zastosować to twierdzenie dwa razy.

4

Długość wektora jest równa zero tylko wtedy, gdy wszystkie współrzędne wektora są równe zero.

Tensory

W każdej przestrzeni tensorowej istnieje wiele typów tensorów. Przyrównywać do siebie można tylko
tensory tego samego typu.

•

Każdy skalar jest tensorem

•

Każdy tensor można pomnożyć przez skalar otrzymując tensor tego samego typu

•

Dwa tensory tego samego typu można dodać, otrzymując tensor tego samego typu

•

Dwa tensory tego samego typu można odjąć, otrzymując tensor tego samego typu

•

Dla dwóch tensorów dowolnych typów można obliczyć iloczyn zewnętrzny, otrzymując tensor
innego typu

•

Tensor odpowiedniego typu można poddać kontrakcji, otrzymując tensor innego typu

•

Łącząc działania mnożenia zewnętrzego i kontrakcji można dla dwóch tensorów obliczyć iloczyn
wewnętrzny otrzymując tensor innego typu; czasem również nazywa się to działanie kontrakcją

•

Odpowiedni (różniczkowalny) tensor dowolnego typu można poddać różniczkowaniu otrzymując
tensor innego typu zwany pochodną kowariantną tego tensora

•

Łącząc działania różniczkowania i kontrakcji na różne sposoby można zdefiniować działania
dywergencji i rotacji

•

Tensor odpowiedniego typu można transponować, otrzymując tensor tego samego typu

Niektóre szczególne przypadki działań mają specjalne nazwy.

•

Pochodną kowariantną skalara nazywamy gradientem

•

Iloczyn wewnętrzny dwóch wektorów nazywamy iloczynem skalarnym

•

Dodawanie tensora do jego transpozycji nazywamy symetryzacją

•

Odejmowanie tensora od jego transpozycji nazywamy antysymetryzacją

•

Kontrakcja tensora mieszanego drugiego rzędu nazywa się obliczaniem śladu

Oznaczenia

Tensory oznacza się zwykle dużymi i małymi literami alfabetu łacińskiego, czasem z dodatkowymi
akcentami, jak kreski, kropki i gwiazdki. Przy literach tych stoją rozmaite indeksy, których ilość, pozycja i
alfabet zależą od typu tensora. Skalary nie mają żadnych indeksów. Najczęściej spotyka się następujące
oznaczenia:

•

Indeksy kontrawariantne - małe litery greckie od μ wzwyż stojące u góry: T

μ

(UWAGA: to nie jest

potęgowanie)

•

Indeksy kowariantne - małe litery greckie od μ wzwyż stojące u dołu: T

ν

•

Indeksy spinorowe - małe litery łacińskie od a wzwyż, stojące u góry lub u dołu T

b

Jeden tensor może mieć wiele indeksów:

Dodawanie tensorów oznacza się znakiem +; indeksy tensorów muszą się zgadzać

Odejmowanie znakiem -; indeksy tensorów muszą się zgadzać

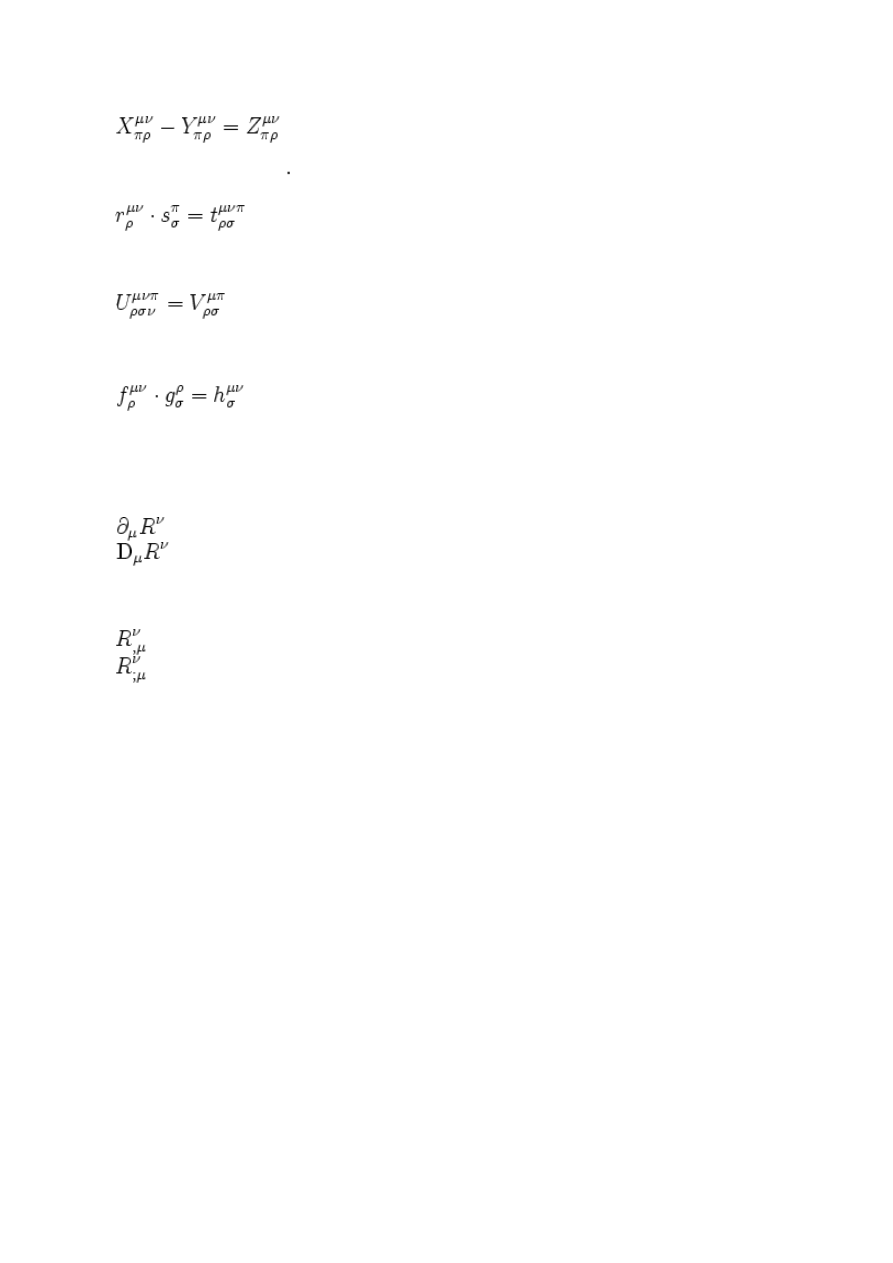
5

Mnożenie zewnętrzne znakiem , który można pominąć; indeksy tensorów nie mogą się powtarzać

Kontrakcję zapisuje się przez powtórzenie tego samego indeksu u góry i u dołu

(powtórzył się symbol ν)

Mnożenie wewnętrzne to połączenie mnożenia zewnętrznego i kontrakcji

(powtórzył się symbol ρ)

Zwróć uwagę na podobieństwo zapisu kontrakcji i iloczynu wewnętrznego do konwencji sumacyjnej.

Różniczkowanie oznacza się na różne sposoby: albo przez zapis "operatorowy":

albo "indeksowy" z użyciem przecinka lub średnika

Transpozycję zapisuje się jako przestawienie indeksów tego samego typu:

M

μν

= N

νμ

Przykłady tensorów w fizyce

Przykłady tensorów w fizyce:

•

skalary: temperatura, masa, energia, gęstość, liczba cząstek i wiele innych,

•

wektory: prędkość, siła, wektor położenia, przyspieszenie i wiele innych,

•

tensory drugiego rzędu: tensor pola elektromagnetycznego, tensor odkształcenia, tensor naprężenia w
ciele stałym itp.,

•

spinory: spin elektronu, spiny fermionów.