
2013-11-22
Podstawy automatyki -
ćwiczenia
1
Rozwiązywanie równań
różniczkowych metodą
przekształcenia Laplace’a

2013-11-22
Podstawy automatyki -
ćwiczenia
2
Przekształcenie Laplace’a - ważniejsze wiadomości
- Przekształcenie Laplace’a:
0
)
(
)
(
dt
e
t
f
t
f
s
F
st
- Odwrotne przekształcenie Laplace’a :
)
(
)
(
1
s
F
t
f

2013-11-22
Podstawy automatyki -
ćwiczenia
3
Przekształcenie Laplace’a - ważniejsze wiadomości
- Odwrotne przekształcenie Laplace’a (cd):
)
(
)
(
1
s
F
t
f
0
1
1
1
1
0
1
1
1
1
...
...
)
(
)
(
)
(
a
s
a
s
a
s
a
b
s
b
s
b
s
b
s
M
s
L
s
F
n
n
n
n
m
m
m
m
2013-11-22
Podstawy automatyki -
ćwiczenia
4
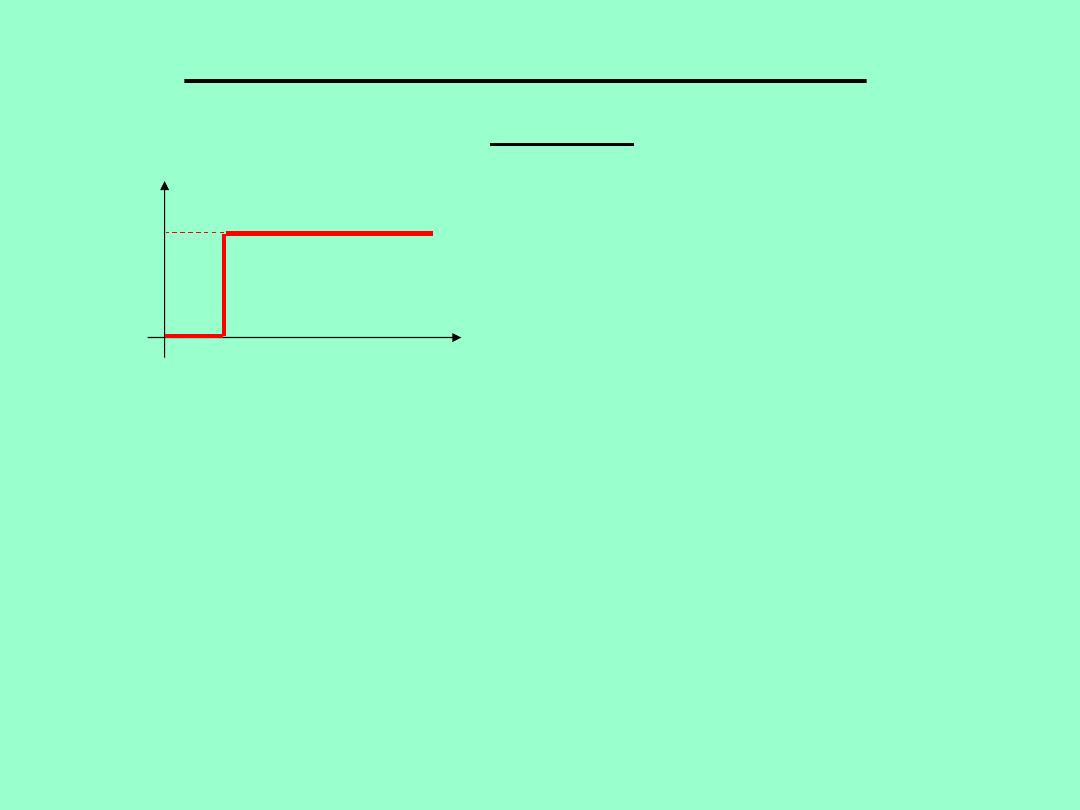
Wyznaczyć transformatę funkcji Heviside’a – 1/2
y(t) =
1
(t)
dt
t
e
st
0
)
(
1
y(t)
t
t
0
0
1
0
0
dla
1
dla
0
t
t
t
t
t
y
2013-11-22
Podstawy automatyki -
ćwiczenia
5
Wyznaczyć transformatę funkcji Heviside’a – 2/2
dt
r
st
r
e
0
lim
r
st
r
e
s
0
1
lim
s
e
s
sr
r
1
lim
1
s
t
1
)
(
1

2013-11-22
Podstawy automatyki -
ćwiczenia
6

2013-11-22
Podstawy automatyki -
ćwiczenia
7
Rozwiązywanie równań różniczkowych (1):
• dokonujemy przekształcenia Laplace’a równania
różniczkowego;
• doprowadzamy Y(s) do postaci dogodnej do
skorzystania z tablic;
)
(
)
(
1
s
F
t
y
• za pomocą tablic wyznaczamy funkcję w dziedzinie
czasu (oryginał)
• wyznaczamy:
)
(
)
(
)
(
s
M
s
L
s
Y

2013-11-22
Podstawy automatyki -
ćwiczenia
8
Rozwiązywanie równań różniczkowych
(wybrane twierdzenia rachunku operatorowego):
0
0
2
2
2
x
x
s
s
X
s
dt
x
d
0
x
s
sX
dt
x
d
Przekształcenie Laplace’a dla:
- zapisu 2 - pochodnej:
- zapisu 1 - pochodnej:

2013-11-22
Podstawy automatyki -
ćwiczenia
9
Rozwiązywanie równań różniczkowych
(wybrane twierdzenia rachunku operatorowego):
t
s
s
s
n
k
k
k
e
s
M
s
L
t
y
1
)
(
)
(
)
(
)
(
)
(
)
(
s
M
s
L
s
Y
Twierdzenie Laplace’a (o rozkładzie 1 ):
- gdy
- to
ds
s
M
d
s
M
)
(
)
(
S
k
– pierwiastki równania M(s)

2013-11-22
Podstawy automatyki -
ćwiczenia
10
Rozwiązywanie równań różniczkowych
(wybrane twierdzenia rachunku operatorowego):
t
s
s
s
n
k
k
k
e
s
M
s
s
L
M
L
t
y
1
)
(
)
(
)
0
(
)
0
(
)
(
Twierdzenie Laplace’a (o rozkładzie 2 ):
- gdy
)
(
)
(
)
(
s
M
s
s
L
s
Y
- to
ds
s
M
d
s
M
)
(
)
(
S
k
– pierwiastki równania M(s)

2013-11-22
Podstawy automatyki -
ćwiczenia
11
Rozwiązać równanie różniczkowe1/5:
0
)
(
6
)
(
5
)
(
t
y
t
y
t
y
b
y
a
y
pocz
war
)
0
(
)
0
(
.
.
- Dokonując α-transformacji otrzymujemy:
0
)
(
6
)
0
(
)
(
5
)
0
(
)
0
(
)
(
2
s
Y
y
s
sY
y
sy
s
Y
s
- Stąd wynika, że:
2
5
6
5
)
(
s
s
s
a
b
a
s
Y
- Co z kolei daje:
)
3
)(
2
(
5
)
(
s
s
s
a
b
a
s
Y

2013-11-22
Podstawy automatyki -
ćwiczenia
12
Rozwiązać równanie różniczkowe 2/5:
- Bieguny otrzymanej transformaty Y(s) są biegunami pojedynczymi,
więc należy je rozłożyć na ułamki proste:
s
B
s
A
s
s
s
a
b
a
s
Y
3
2
)
3
)(
2
(
5
)
(
- Po obliczeniu:
)
2
(
3
b
a
B
b
a
A
- Więc:
s
b
a
s
b
a
s
s
s
a
b
a
s
Y
3
2
2
3
)
3
)(
2
(
5
)
(

2013-11-22
Podstawy automatyki -
ćwiczenia
13
Rozwiązać równanie różniczkowe 3/5:
- Rozwiązanie w dziedzinie czasu wyznaczamy dokonując
odwrotnej transformacji Laplace’a:
s
b
a
s
b
a
s
Y
t
y
3
2
2
3
)
(
)
(
1
1
1
s
b
a
s
b
a
t
y
3
1
2
2
1
)
3
(
)
(
1
1
- Więc ostatecznie:
0
2
3
)
(
3
2
t
e
b
a
e
b
a
t
y
t
t

2013-11-22
Podstawy automatyki -
ćwiczenia
14
Rozwiązać równanie różniczkowe 4/5:
- sprawdźmy wynik korzystając z tw. o rozkładzie:
2
5
6
5
)
(
)
(
)
(
s
s
s
a
b
a
s
M
s
L
s
Y
t
s
s
s
n
k
k
k
e
s
M
s
L
t
y
1
)
(
)
(
)
(
2013-11-22
Podstawy automatyki -
ćwiczenia
15
Rozwiązać równanie różniczkowe 5/5
- Więc ostatecznie:
0
2
3
)
(
3
2
t
e
b
a
e
b
a
t
y
t
t
s
ds
s
M
d
s
M
2
5
)
(
)
(
t
s
t
s
e
s
M
s
L
e
s
M
s
L
t
y
3
3
2
2
)
(
)
(
)
(
)
(
)
(
- Pochodna mianownika:
- Zgodnie ze wzorem:

2013-11-22
Podstawy automatyki -
ćwiczenia
16

2013-11-22
Podstawy automatyki -
ćwiczenia
17

2013-11-22
Podstawy automatyki -
ćwiczenia
18
Znajdowanie współczynników rozkładu na ułamki proste:
b
s
D
a
s
C
s
B
As
s
b
s
a
s
s
e
s
X
2
2
)
(
1. doprowadzić sumy prawej strony do wspólnego mianownika
a
s
s
D
b
s
s
C
b
s
a
s
B
As
s
e
2
2
2. przyrównać wyrazy o tych samych potęgach wielomianu w obu licznikach
3. rozwiązać otrzymany układ równań wyznaczając A, B, C, D
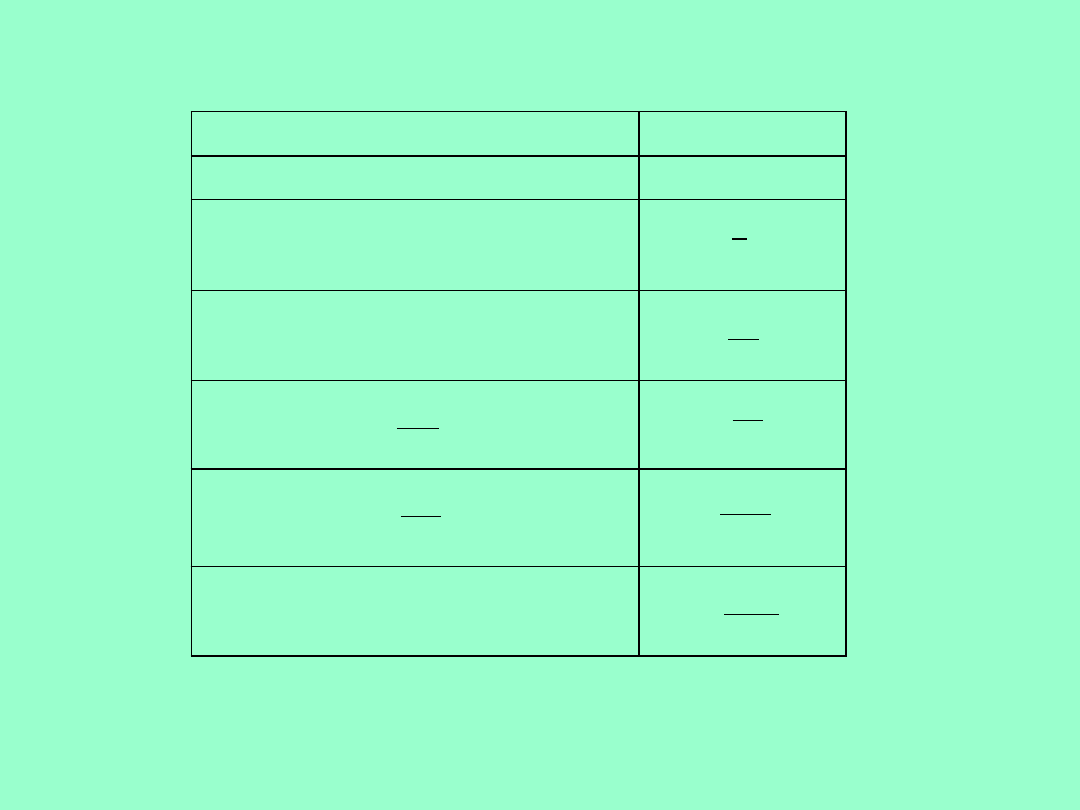
19
Transformaty Laplace’a niektórych funkcji
Funkcja f(t)
Transformata F(s)
1
1(t)
kt
)
(t
s
1
2
s
k
2
2
kt
3
s
k
!
n
kt
n
1
n
s
k
at
ke
a
s
k

20
a
t
e
a
k
1
as
k
t
sin
2
2
s
t
cos
2
2
s
s
t
e
at
sin
2
2
)
(
a
s
t
e
at
cos
2
2
)
(
a
s
a
s
a
t
e
1
)
1
(
1
as
s

21
a
t
te
a
2
1
2
)
1
(
1
as
b
a
e
e
b
t
a
t
)
1
)(
1
(
1
bs
as
a
t
e
t
a
a
)
(
1
3
2
)
1
(
as
s
)
(
b
a
ab
be
ae
a
t
b
t
)
1
)(
1
(
bs
as
s
a
t
e
a
b
1
1
)
1
(
1
as
s
bs

22
a
b
be
ae
b
t
a
t
1
)
1
)(
1
(
1
bs
as
s
)
1
(
a
t
e
a
t
)
1
(
1
2
as
s
)
(
t
e
k
n
t
n
n
2
2
1
sin
1
2
2
2
2
n
n
n
s
s
k
)
(
)
(
t
t
e
k
n
n
t
n
2
2
2
1
sin
1
1
cos
1
)
(
2
2
2
2
n
n
n
s
s
s
k
t
a
b
e
a
b
ad
c
t
a
b
de
t
a
t
a
4
sin
4
2
4
cos
2
2
2
2
2
b
as
s
c
ds
2
Wyszukiwarka
Podobne podstrony:
Cwiczenie nr 8 Teksty id 99954
Cwiczenia nr 2 RPiS id 124688 Nieznany
cwiczenie 3 leki przeciwdepresyjne id 12532
cwiczenie 1b inkscape id 125205 Nieznany
Cwiczenie 8 Komponent Radiobutton id 99753
Kropki cwiczenie na kreatywnosc id 250
Cwiczenie 4 opis i zagadnienia id 99493
Logika rozwiazania zadan id 272023
Cwiczenie nr 15 id 125710 Nieznany
WDT koło z ćwiczeń rozwiązania(1)
Zobowiązanie podatkowe ćwiczenie z rozwiązaniem
Cwiczenie 5 opis i zagadnienia id 99566
Cwiczenie HP1 instrukcja id 125650
Cwiczenie 16 omowienie id 125188
Cwiczenia i kontrola magii id 9 Nieznany
Cwiczenia nr 6 RPiS id 124693 Nieznany
Cwiczenia Access Podstawy 3 id Nieznany
więcej podobnych podstron