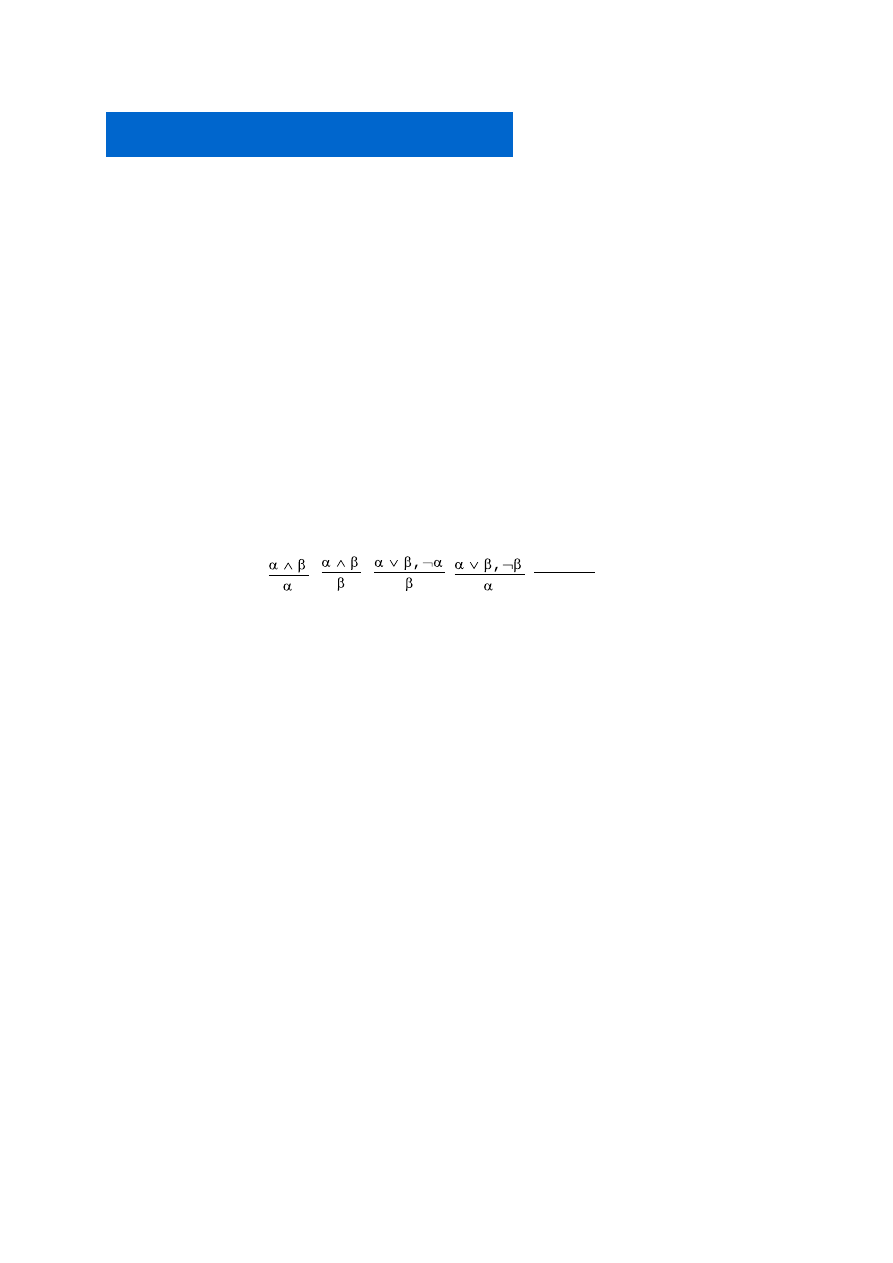
Przykład 1
Rozważmy formułę ¬(p ∧ ¬q) ⇒ q oraz zbiór formuł X = {p, ¬q}. Rozważmy wszystkie wartościowania
v, w których są prawdziwe wszystkie formuły (zmienne) ze zbioru X. Mamy wartościowanie
v(p) = 1 i v(q) = 0. Mamy wtedy w(¬(p ∧ ¬q) ⇒ q) = 1. Zatem formuła ¬(p ∧ ¬q) ⇒ q wynika ze zbioru
X = {p, ¬q}.

Przykład 2
Rozważmy formułę (p ⇒ q) ⇒ ¬q oraz zbiór formuł X = {¬p, q}. Rozważmy wszystkie wartościowania
v, w których są prawdziwe wszystkie formuły (zmienne) ze zbioru X. Mamy wartościowanie v(p) = 0
i v(q) = 1. Mamy wtedy w((p ⇒ q) ⇒ ¬q) = 0. Zatem formuła (p ⇒ q) ⇒ ¬q nie wynika ze zbioru
X = {¬p, q}.

Przykład 3

Weźmy zbiór reguł ℜ = {

,

,

,

, α, α ⇒ β

β

} oraz zbiór formuł

X = {(¬p ∨ q) ∧ ¬q, ¬p ⇒ s}.

Rozważmy następujący ciąg formuł:
1. ϕ

1

= (¬p ∨ q) ∧ ¬q (formuła ze zbioru X).

2. ϕ

2

= ¬p ⇒

s (formuła ze zbioru X).

3. ϕ

3

= ¬p ∨ q (formuła wyprowadzona z formuły ϕ

1

za pomocą reguły

EK).

4. ϕ

4

= ¬q (formuła wyprowadzona z formuły ϕ

1

za pomocą reguły

EK).

5. ϕ

5

= ¬p (formuła wyprowadzona z formuły ϕ

3

oraz ϕ

4

za pomocą reguły

EA).

6. ϕ

6

= s (formuła wyprowadzona z formuły ϕ

2

oraz ϕ

5

za pomocą reguły

EI).

Powyższy ciąg spełnia definicję dowodu wprost formuły s na gruncie ℜ oraz X.

Przykład 4
Wykażemy, że: p ∨ (q ⇒ r), ¬p ∧ s, r ∧ s ⇒ t, q ∧ u ׀−

DN

q ⇒ (u ∧ t).

Wypisujemy kolejno założenia — (Z):
1. ϕ

1

= p ∨ (q ⇒ r) (Z).

2. ϕ

2

= ¬p ∧ s (Z).

3. ϕ

3

= r ∧ s ⇒ t (Z).

4. ϕ

4

= q ∧ u (Z).

Formuły ϕ

5

– ϕ

8

wyprowadzamy z formuł ϕ

2

, ϕ

4

w myśl reguły

EK:

5. ϕ

5

= ¬p (2,

EK).

6. ϕ

6

= s (2,

EK).

7. ϕ

7

= q (4,

EK).

8. ϕ

8

= u (4,

EK).

Przykłady

Stosujemy teraz regułę

EA do formuł ϕ

1

i ϕ

5

:

9. ϕ

9

= q ⇒ r (1, 5,

EA).

Teraz

EI do ϕ

7

i ϕ

9

:

10. ϕ

10

= r (7, 9,

EI).

DK do ϕ

6

i ϕ

10

:

11. ϕ

11

= r ∧ s (6, 10,

DK).

EI do ϕ

11

i ϕ

3

:

12. ϕ

12

= t (11, 3,

EI).

DK do ϕ

8

i ϕ

12

:

13. ϕ

13

= u ∧ t (8, 12,

DK).

DIN do ϕ

13

:

14. ϕ

14

= q ⇒ (u ∧ t) (13,

DIN), co kończy dowód.

Przykład 5
Wykażemy nie wprost wynikanie z poprzedniego przykładu:
p ∨ (q ⇒ r), ¬p ∧ s, r ∧ s ⇒ t, q ∧ u ׀−

DN

q ⇒ (u ∧ t).

Wypisujemy kolejno założenia — (Z):
1. p ∨ (q ⇒ r) (Z).
2. ¬p ∧ s (Z).
3. r ∧ s ⇒ t (Z).
4. q ∧ u (Z).
Dopisujemy założenie nie wprost:
5. ¬(q ⇒ (u ∧ t)) (ZN).
Stosujemy regułę

NI:

6. q ∧ ¬(u ∧ t) (5,

NI).

Następnie

EK:

7. q (6,

EK).

8. ¬(u ∧ t) (6,

EK).

I kolejno:
9. ¬u ∨ ¬t (8,

NK).

10. u (4,

EK).

11. ¬¬u (10,

PN).

12. ¬t (11, 9,

EA).

13. ¬p (2,

EK).

14. q ⇒ r (1, 13,

EA).

15. r (7, 14,

EI).

16. s (2,

EK).

17. r ∧ s (15, 16,

DK).

18. t (17, 3,

EI).

19. ⊥ (12, 18,

DS), co kończy dowód.

Przykład 6
Wykażemy nie wprost, że: ¬p ∨ q, ¬(s ⇒ q), s ⇒ t ׀−

DN

¬(p ∨ ¬t).

Wypisujemy kolejno założenia — (Z):
1. ¬p ∨ q (Z).
2. ¬(s ⇒ q) (Z).
3. s ⇒ t (Z).
Zakładamy nie wprost:
4. ¬¬(p ∨ ¬t) (ZN).
Z reguły

PN i ϕ

4

wyprowadzamy:

5. p ∨ ¬t (4,

PN).

I kolejno stosujemy do odpowiednich formuł reguły

NI, EK, EA, EI oraz DS:

6. s ∧ ¬q (2,

NI).

7. s (6,

EK).

8. ¬q (6,

EK).

9. ¬p (1, 8,

EA).

10. ¬t (5, 9,

EA).

11. t (3, 7,

EI).

12. ⊥ (10,11,

DS), co kończy dowód nie wprost.