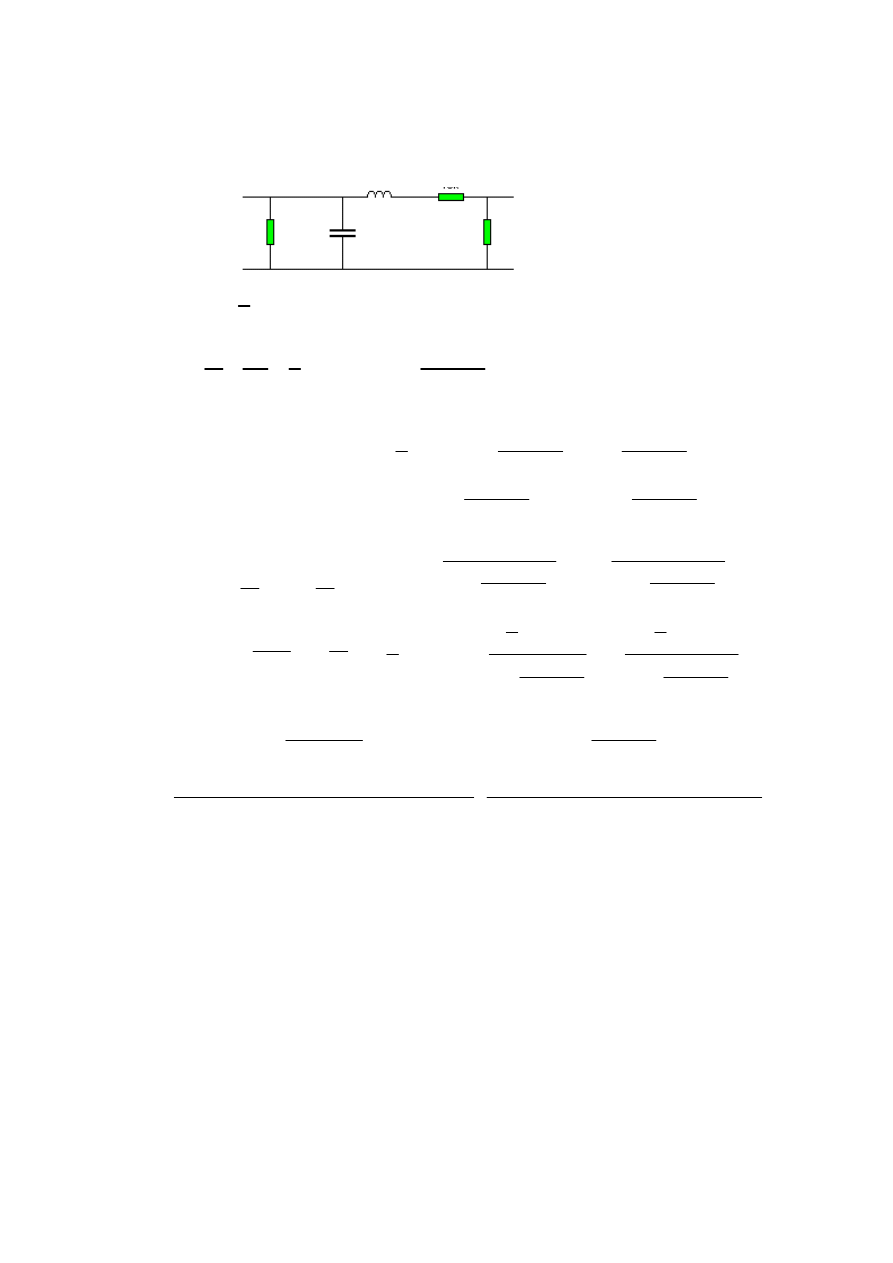
zadanie 1
L R
R
C
R
Y
1
1
R
jωC
+
=
Y
2
R
=
1
Y
3
1
jωL
1
R
+
=
solve Y
3
,
jωL
R
R
jωL
+
(
)
⋅
→
y
Y
1
Y
3
+
Y
3
−
Y
3
−
Y
2
Y
3
+
=
1
R
jωC
+
jωL
R
R
jωL
+
(
)
⋅
+
jωL
−
R
R
jωL
+
(
)
⋅
jωL
−
R
R
jωL
+
(
)
⋅
R
jωL
R
R
jωL
+
(
)
⋅
+
=
a
1
Y
2
Y
3
+
Y
1
Y
2
+
Y
1
Y
2
Y
3
+
1
Y
3
1
Y
1
Y
3
+
=
1
R
jωL
R
R
jωL
+
(
)
⋅
+
1
R
jωC
+
R
+
1
R
jωC
+
R
jωL
R
R
jωL
+
(
)
⋅
+
1
jωL
R
R
jωL
+
(
)
⋅
1
1
R
jωC
+
jωL
R
R
jωL
+
(
)
⋅
+
=
a
2 jωL
⋅
R
+
(
)
jωL
2 jωL
⋅
2 jωC
⋅
jωL
⋅
R
⋅
+
jωL R
2
⋅
+
R
+
jωC R
2
⋅
+
(
)
jωL R
⋅
R
jωL
+
(
)
jωL R
⋅
jωL R
2
⋅
R
+
jωL
+
jωC R
2
⋅
+
jωC jωL
⋅
R
⋅
+
(
)
jωL R
2
⋅
=
Wyszukiwarka
Podobne podstrony:
Mathcad zadanie12
Mathcad zadanie 3
Mathcad zadanie 11
Mathcad zadanie 8
Mathcad zadanie 6
Mathcad zadanie 4
Mathcad zadanie 13
Mathcad zadanie 10
Mathcad zadanie 14
Projekt mathcad zadanie
Mathcad zadanie 3
Mathcad zadanie 9
Zadania 1 Mathcad, Elektrotechnika PCZ, Mathcad
mathcad, Podstawy Informatyki - zadania z programu Mathcad
więcej podobnych podstron