Podstawy Teorii Obwodów

PPOM

2013

Model obwodowy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
Klasyfikacja obwodów . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Założenia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Opis obwodów. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

Topologia obwodu. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

Rodzaje elementów obwodów . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Konwencje oznaczeń elementów obwodów . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
Liniowość . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

Elementy bierne

10

Opór . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
Pojemność . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
Indukcyjność . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14

Elementy czynne

16

Idealne źródła niezależne . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17

Podstawowe prawa obwodowe

18

Prawa Kirchhoffa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
Równoważność źródeł rzeczywistych . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
Zasada superpozycji . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
Twierdzenie o źródle zastępczym . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
Przykład 4.2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
Przykład 4.3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24

1

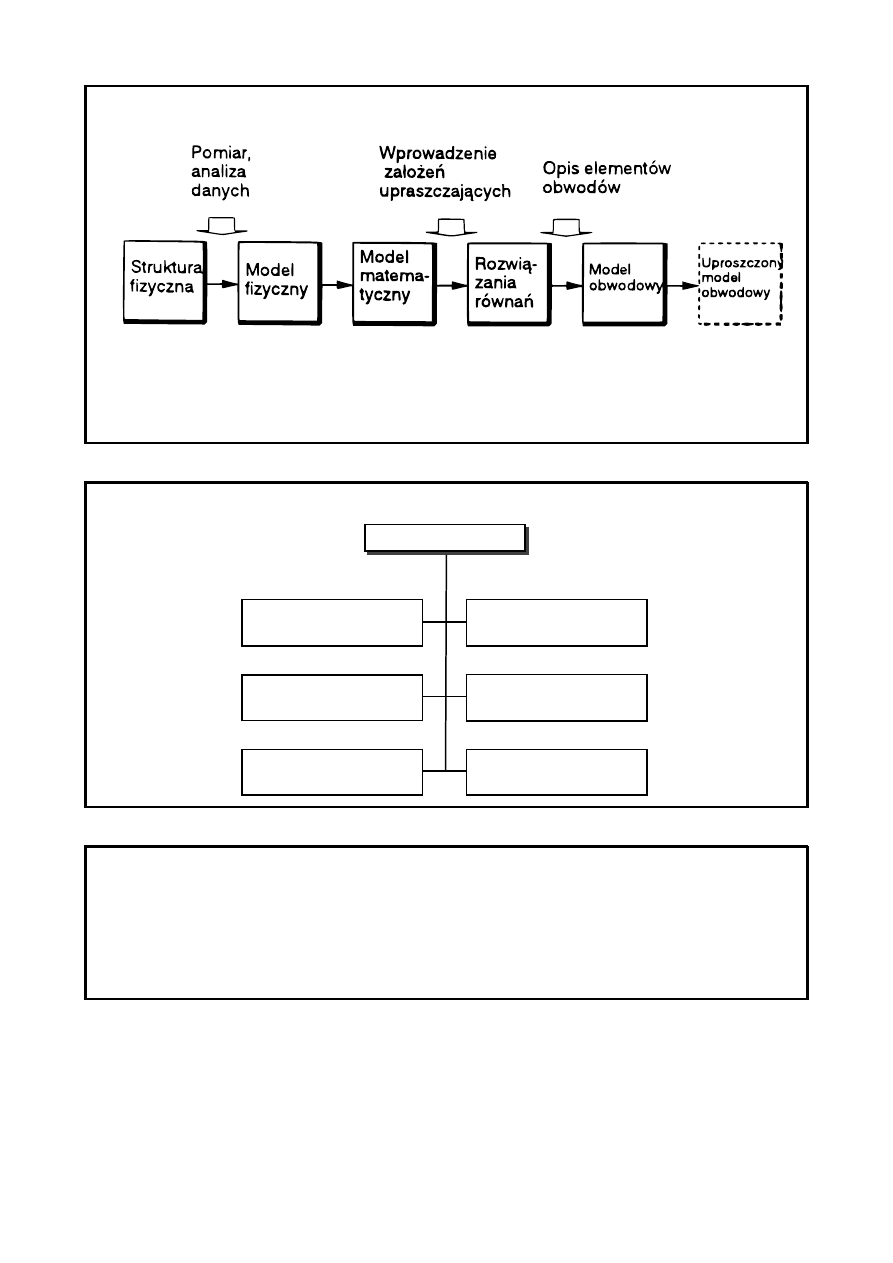
Obwody elektryczne jako modele przyrządów i struktur fizycznych

podzespoły,
przyrządy,
zjawiska

elektrody-
namika,
f

izyka ciała

stałego

równania
Maxwella,
równania
transportu
nośników

charakte-
rystyki
elementów

modele
elementów:
RLC,
aktywnych

modele:
liniowy,
o stałych
skupionych

PPOM

W2/3–2

Klasyfikacja obwodów

Obwody elektryczne

O stałych skupionych

(S)

O stałych rozłożonych

(R)

Liniowe

(L)

Nieliniowe

(N)

Stacjonarne

(S)

Niestacjonarne

(N)

PPOM

W2/3–3

Założenia

Podstawowe założenia analizy obwodów:

■

jednoczesność oddziaływań i skutków we wszystkich punktach układu ⇒ struktury o stałych
skupionych (S),

■

idealność (zerowy opór) doprowadzeń elementów.

PPOM

W2/3–4

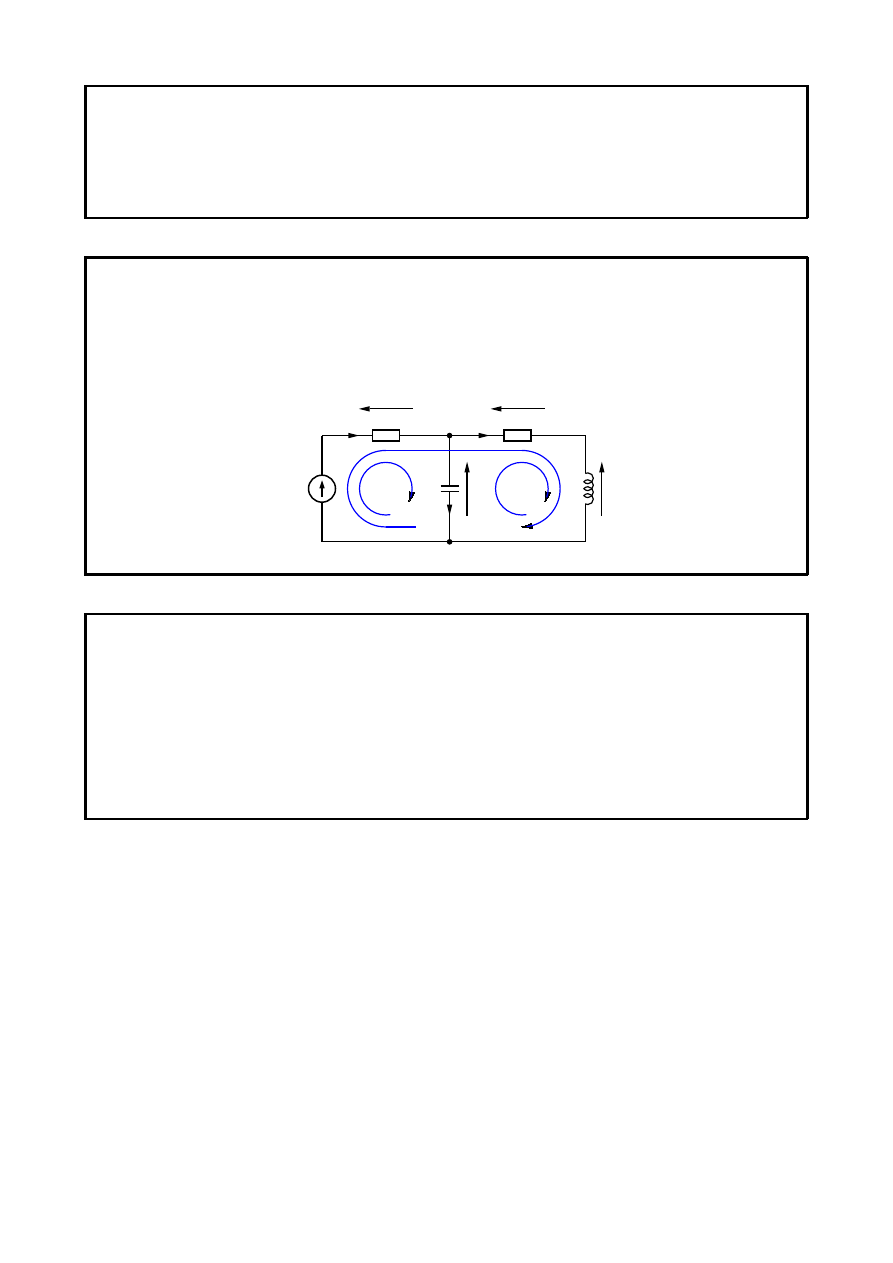
Opis obwodów

Składniki informacji o właściwosciach obwodu:

■

struktura połączeń (topologia obwodu),

■

charakterystyki (równania) elementów obwodu

PPOM

W2/3–5

Topologia obwodu

węzeł

miejsce połączenia trzech lub więcej wyprowadzeń różnych elementów,

gałąź połączenie między dwoma sąsiednimi węzłami złożone z jednego lub więcej elementów,

obwód zamknięty

droga zamknięta złożona z gałęzi (usunięcie dowolnej gałęzi powoduje

otwarcie obwodu).

R

1

i

1

u

1

A

C

i

3

u

3

B

R

2

i

2

u

2

L

u

L

e

b

a

c

PPOM

W2/3–6

Rodzaje elementów obwodów

bierne rozpraszające energię lub zdolne do magazynowania energii dostarczonej z zewnątrz

(reprezentowane przez R, L, C, M itp.)

■

stratne (dyssypatywne),

■

bezstratne (reaktancyjne);

aktywne zdolne do dostarczania energii (reprezentowane przez źródła niezależne, źródła

sterowane itp.).

PPOM

W2/3–7

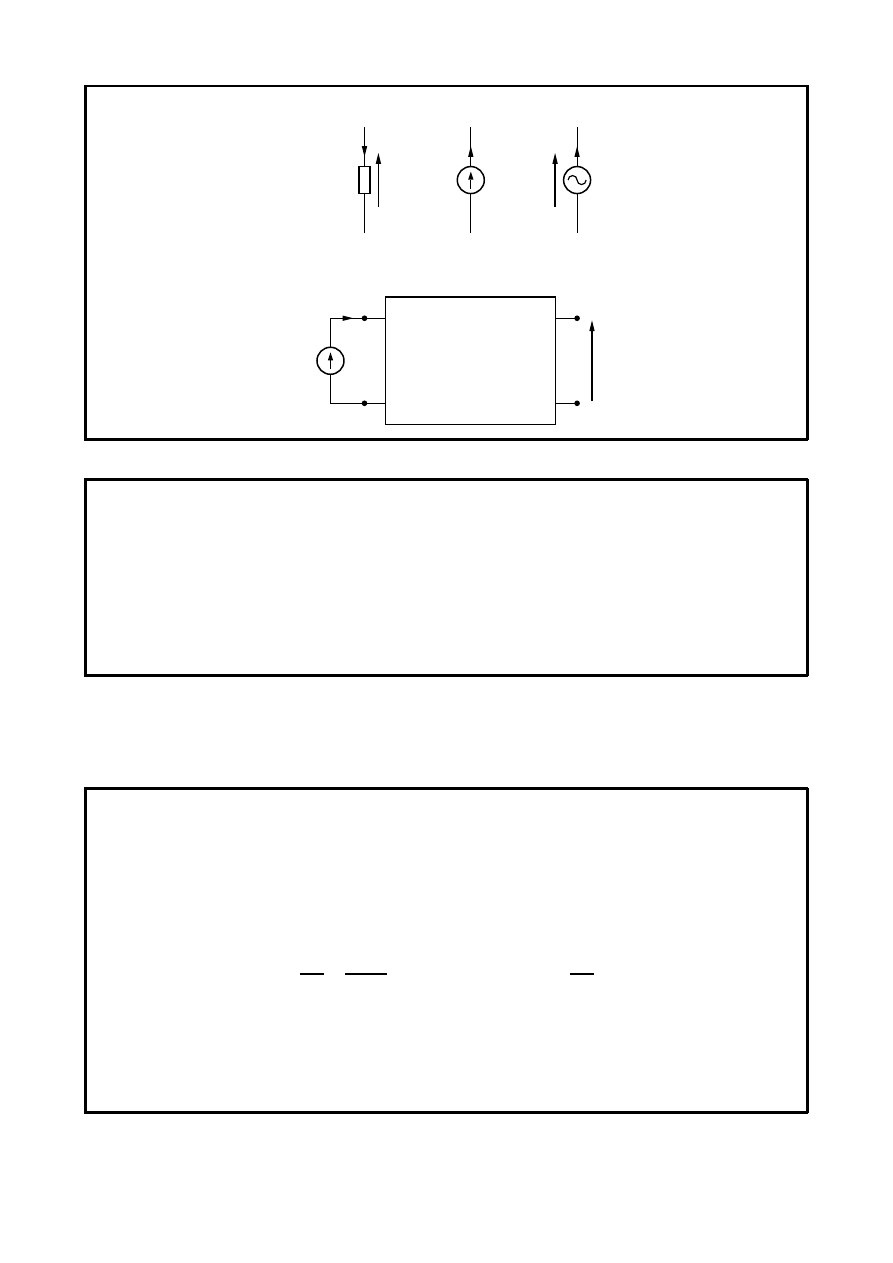
Konwencje oznaczeń elementów obwodów

pobudzenie

wymuszenie

R

i

u

E

I

i

e

e

i

1

1

2

3

4

u

34

odpowiedź

PPOM

W2/3–8

Liniowość

Jeśli odpowiedzią na wymuszenie x

1

jest y

1

, a odpowiedzią na wymuszenie x

2

jest y

2

, to:

1. odpowiedzią na wymuszenie x

1

+ x

2

będzie y

1

+ y

2

(addytywność),

2. odpowiedzią na wymuszenie ax

1

będzie ay

1

(jednorodność) dla dowolnej liczby

rzeczywistej a.

F(ax

1

+ bx

2

) = aF(x

1

) + bF(x

2

)

PPOM

W2/3–9

Elementy bierne

W2/3–10

Opór

Opór (rezystancja): R

Przewodność (konduktancja): G = R

−

1

Wymiar: dim(R) = L

2

MT

−

3

I

−

2

Jednostki: om, simens

1 Ω =

1 V
1 A

=

kg m

2

A

2

s

3

1 S =

1 A
1 V

= 1 Ω

−

1

„Jeden om (Ω) stanowi rezystancję między dwoma punktami przewodnika, przez który płynie

prąd o natężeniu 1 ampera (A), gdy różnica potencjałów między tymi punktami wynosi
1 wolt (V).”

u = Ri

i = Gu

PPOM

W2/3–11

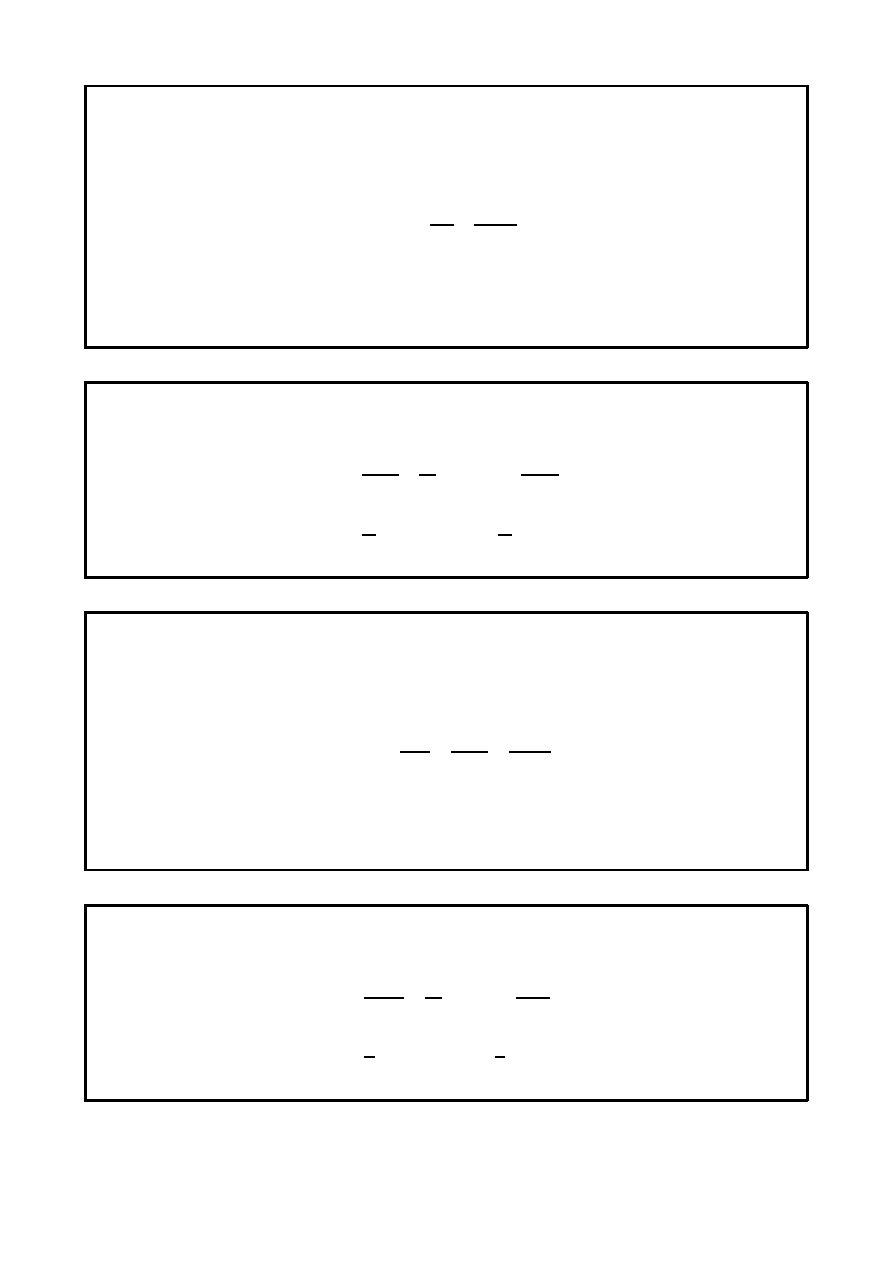
Pojemność

Symbol: C

Wymiar: dim(C) = L

−

2

M

−

1

T

4

I

2

Jednostka: farad

1 F =

1 C
1 V

=

A

2

s

4

kg m

2

„Jeden farad (F) stanowi pojemność kondensatora, w którym miedzy okładkami występuje

napięcie 1 wolta (V), gdy znajdują się na nich różnoimienne ładunki elektryczne o wartości
1 kulomba (C) każdy.”

q = Cu

PPOM

W2/3–12

Pojemność

i(t) =

dq(t)

dt

=

d

dt

[Cu(t)] = C

du(t)

dt

u(t) =

1

C

t

Z

−∞

i(τ) dτ = U

0

+

1

C

t

Z

0

i(τ) dτ

PPOM

W2/3–13

Indukcyjność

Symbol: L

Wymiar: dim(L) = L

2

MT

−

2

I

−

2

Jednostka: henr

1 H =

1 Vs

1 A

=

1 Wb

1 A

=

kg m

2

A

2

s

2

„Jeden henr (H) stanowi indukcyjność obwodu, w którym indukuje się siła elektromotoryczna

1 wolta (V), gdy prąd przepływający przez ten obwód zmienia się jednostajnie o 1 amper (A)
w czasie 1 sekundy (s).”

ψ = Li

PPOM

W2/3–14

Indukcyjność

u(t) =

dψ(t)

dt

=

d

dt

[Li(t)] = L

di(t)

dt

i(t) =

1
L

t

Z

−∞

u(τ) dτ = I

0

+

1
L

t

Z

0

u(τ) dτ

PPOM

W2/3–15

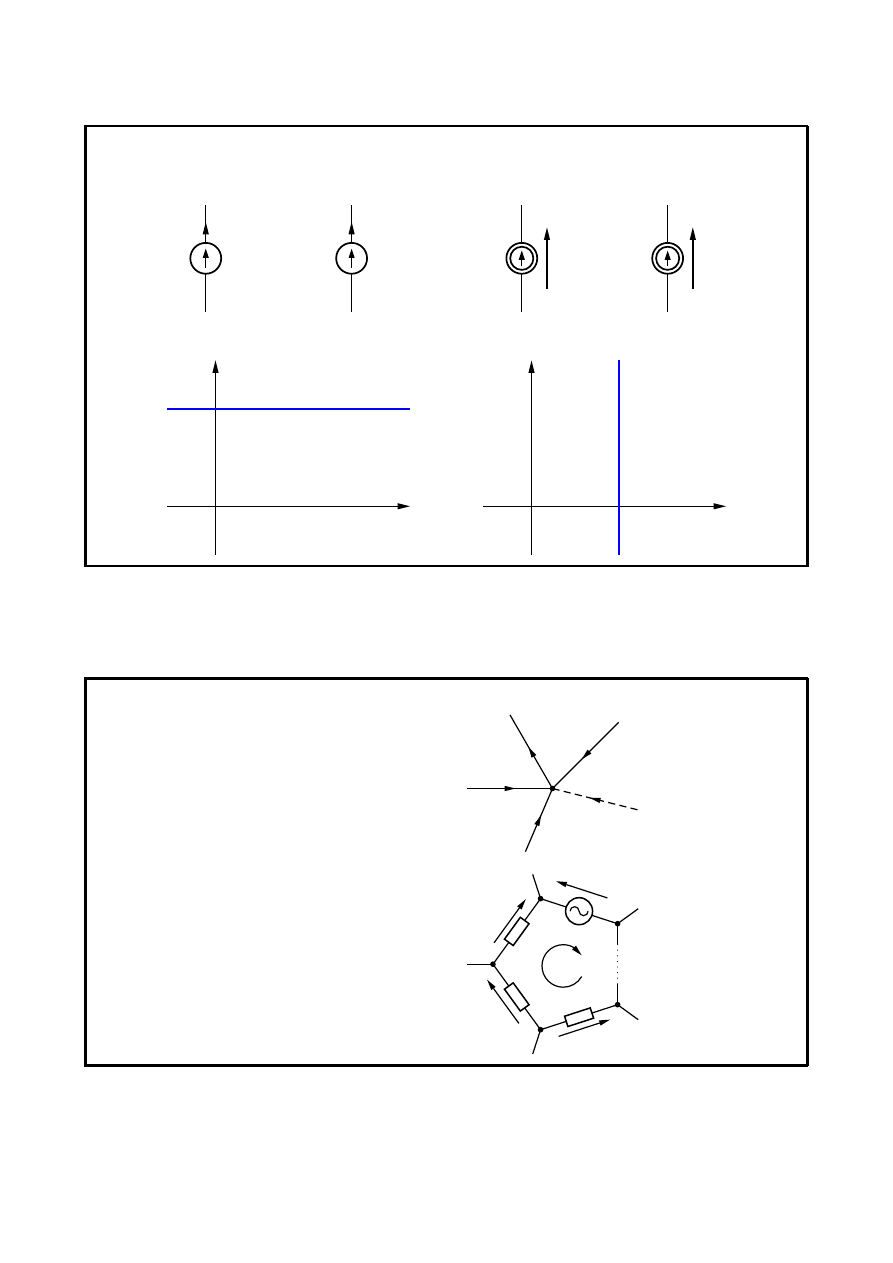
Elementy czynne

W2/3–16

Idealne źródła niezależne

Źródło napięciowe

Źródło prądowe

E

I

e

i

I

U

E

J

U

j

u

I

U

J

PPOM

W2/3–17

Podstawowe prawa obwodowe

W2/3–18

Prawa Kirchhoffa

Prądowe prawo Kirchhoffa

n

X

k=1

I

k

= 0

I

1

I

2

I

3

I

k

I

n

Napięciowe prawo Kirchhoffa

n

X

k=1

U

k

= 0

U

2

E

3

U

n

U

1

PPOM

W2/3–19

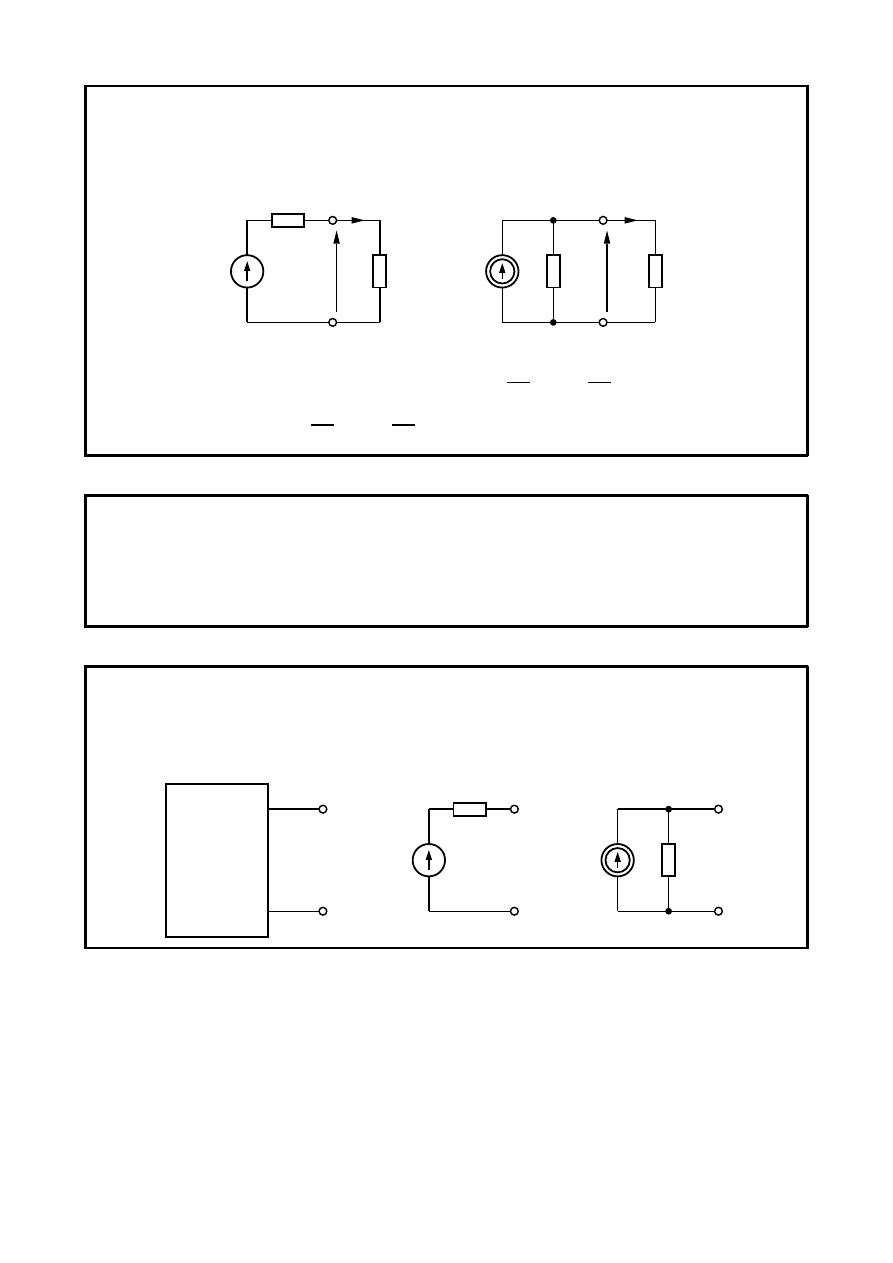
Równoważność źródeł rzeczywistych

Dwa żródła są równoważne, jeżeli wytwarzają identyczny prąd w obwodzie obciążenia przy
dowolnej wartości oporu R.

E

R

w

I

R

U

J

I

U

G

w

R

=⇒

J =

E

R

w

G

w

=

1

R

w

E =

J

G

w

R

w

=

1

G

w

⇐

=

PPOM

W2/3–20

Zasada superpozycji

Prąd (napięcie) w wyróżnionej gałęzi układu liniowego, w którym występuje kilka źródeł
niezależnych, może być obliczony jako suma prądów (napięć) wywołanych w tej gałęzi przez
każde z tych źródeł działających osobno, tzn. po zastąpieniu wszystkich pozostałych
niezależnych źródeł napięciowych zwarciami i niezależnych źródeł prądowych rozwarciami.

PPOM

W2/3–21

Twierdzenie o źródle zastępczym

Twierdzenie Thevénina – Nortona

Obwód

liniowy

1

2

≡

E

T

R

T

1

2

≡

J

N

1

2

G

N

PPOM

W2/3–22

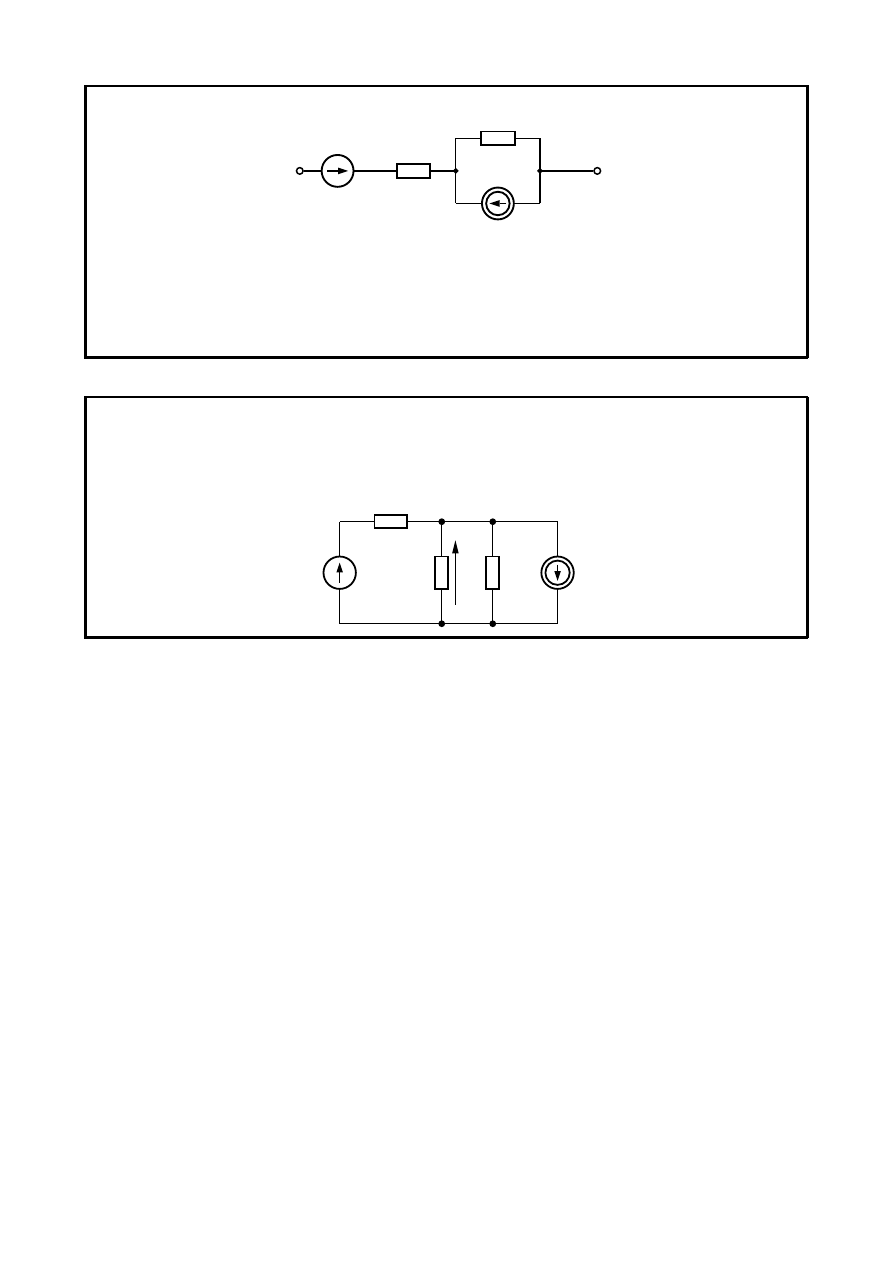
Przykład 4.2

E

1

R

1

G

2

J

2

Źródło napięciowe o sile elektromotorycznej E

1

= 10 V i oporze wewnętrznym R

1

= 1 Ω

połączono szeregowo ze źródłem prądowym o wydajności J

2

= 5 A i przewodności wewnętrznej

G

2

= 0,5 S.

Obliczyć parametry zastępczego źródła napięciowego.

PPOM

W2/3–23

Przykład 4.3

Stosując zasadę superpozycji, obliczyć spadek napięcia na oporze R.
Przyjąć: E = 20 V, J = 5 mA, R

1

= 1 kΩ, R

2

= 2 kΩ, R = 1 kΩ.

E

R

1

R

U

R

2

J

PPOM

W2/3–24