Instytut Mechatroniki i Systemów Informatycznych
do użytku wewnętrznego
Maszyny Prądu Stałego
Zadanie 3
Dla silnika obcowzbudnego o znamionach:
moc
znamionowa
12
P
N
=
kW,
napięcie znamionowe
220
U
N
=
V,
prędkość znamionowa
7
,
16
n
N
=
obr/s,
sprawność
85
,
0
N
=
η
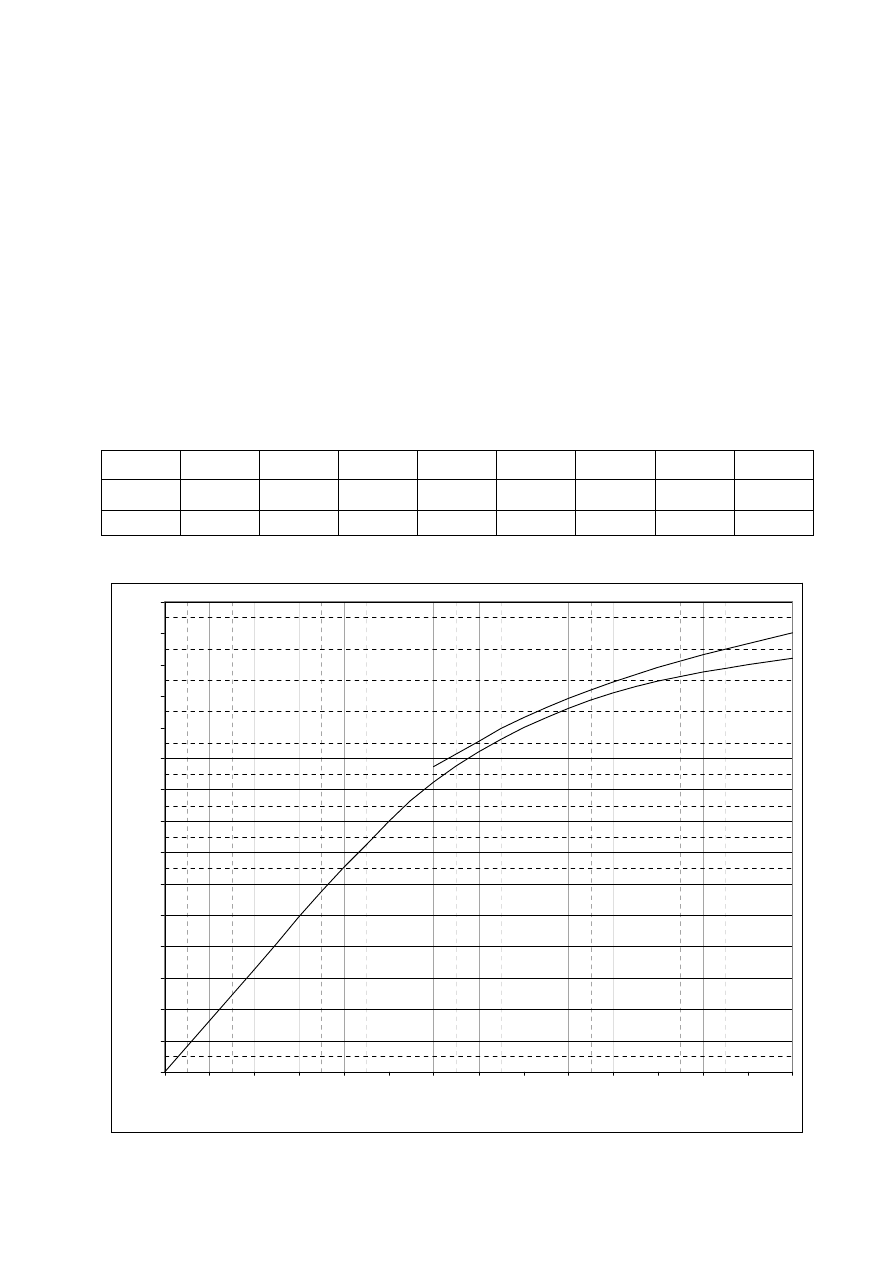
wyznaczono charakterystyki biegu jałowego
( )
f
I
f
E
=
0
dla
N
n
n
=
oraz zewnętrzną
( )
f
I
f
U
=
dla
i
N
n
n
=
aN
a
I
I
=
f
I
A 0,2 0,4 0,6 0,8 1,0 1,2 1,4
0
E
V 65 131 185 220 242 255 264
U
V
-
- 195 226 249 265 280
0
20
40
60
80
100
120
140
160
180
200
220
240
260
280
300
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
I
m
[A]
E
0
[V
],
U
[V
]
Zredagował dr inż. Witold Kubiak - na podstawie materiałów własnych Instytutu
1
Instytut Mechatroniki i Systemów Informatycznych
do użytku wewnętrznego
Ponadto zmierzono:
rezystancję obwodu twornika
2
,
0
R
a
=
∑
Ω,
uzwojenia
wzbudzenia
180
R
2
E
1
E
=
Ω,
spadek
napięcia na szczotkach
2
u
2
tc
=
Δ
V
Należy:
1. oszacować maksymalny prąd jaki popłynąłby przez silnik gdyby włączono go do sieci
o napięciu znamionowym bez rozrusznika, jeżeli
2
1E
E
f
R
R
=
,
2. dobrać rezystancję rozrusznika, tak, aby prąd rozruchowy w tworniku nie przekroczył
wartości znamionowej,
3. określić na jakiej prędkości zakończy się rozruch jeżeli opornik rozruchowy nie
zostanie wyłączony, a silnik nie jest obciążony momentem, jeżeli
,
2
1E
E
f
R
R
=
4. określić moment strat jałowych w znamionowych warunkach pracy,
5. określić rezystancję opornika regulacyjnego włączonego w obwód twornika, aby silnik
zasilany napięciem znamionowym przy
fN
f
R
R
=
i obciążony znamionowym
momentem elektromagnetycznym wirował z prędkością
N
n
9
,
0
n
⋅
=
(jakie będzie
wówczas napięcie na tworniku?),
6. określić prędkość silnika zasilanego znamionowym napięciem, jeżeli
Ω
,
a
,
220
R
f
=
aN
a
I
I
=
7. jaką minimalną prędkość może rozwinąć ten silnik zasilany napięciem znamionowym
w stanie obciążenia
.
aN
a
I
I
=
Rozwiązanie:
Ad. 1 Przy rozruchu
czyli
0
n
=
0
n
c
E
=
⋅
Φ
⋅
=
, stąd:
tc
a
max
as
N
u
2
R
I
U
U
Δ
+
⋅
=
=
∑
1090
2
,
0
2
220
R
u
2
U
I
a
tc
N
max
as
=
−
=
Δ
−
=
∑
A
22
,
1
180
220
R
U
R
U
I
2
E
1
E
N
f
N
f
=
=
=
=
A
1091
1
1090
I
I
I
f
max
as
max
s
=
+
=
+
=
A
W warunkach znamionowych:
17
,
64
220
85
,
0
10
12
U
P
I
3
N
N
N
N
=
⋅
⋅
=
⋅
η
=
A
stąd:
Zredagował dr inż. Witold Kubiak - na podstawie materiałów własnych Instytutu
2
Instytut Mechatroniki i Systemów Informatycznych
do użytku wewnętrznego
17
17
,
64
1091
I
I
N
max
s
=
=
Ad. 2 Znamionowy prąd twornika
Z charakterystyki
,
,
( )
f
I
f
U
=
N
n
n
=
aN
a
I
I
=
odczytujemy prąd wzbudzenia dla
V :
220
U
U
N
=
=
76
,
0
I
f
=
A
41
,
63
76
,
0
17
,
64
I
I
I
f
N
aN
=
−
=
−
=
A
W chwili rozruchu z rozrusznikiem:
(
)
tc
s
a
aN
N
u
2
R
R
I
U
U
Δ
+
+
⋅
=
=
∑
stąd:
24
,
3
2
,
0
41
,
63
2
220
R
I
u
2
U
R
a
aN
tc
N
s
=
−
−
=
−
Δ
−
=
∑
Ω
Ad. 3 Dla prądu wzbudzenia przy znamionowym napięciu
22
,
1
I
f
=
A (patrz wyżej)
odczytujemy z charakterystyki
( )
f
I
f
E
=
0
,
N
n
n
=
:
256
E
U
0
=
≈
V
Prędkość wirowania w stanie jałowym przy napięciu znamionowym:
35
,
14
256
220
7
,
16
U
U
n
E
E
n
n
N
N
0
0
N
=
⋅
=
⋅
≈
⋅
=
∗
∗
obr/s
Ad. 4 SEM w warunkach znamionowych
3
,
205
2
2
,
0
41
,
63
220
u
2
R
I
U
E
tc
a
aN
N
N
=
−
⋅
−
=
Δ
−
⋅
−
=
′
∑
V
moc „wewnętrzna”
0
,
13
13018
41
,
63
3
,
205
I
E
P
tN
N
eN
=
=
⋅
=
⋅
′
=
kW
moment elektromagnetyczny
124
7
,
16
2
10
13
n
2
P
P
M
3
N
eN
N
eN
eN
=
⋅
π
⋅
⋅
=
⋅
π
⋅
=
Ω
=
Nm
moment znamionowy
114
7
,
16
2
10
12
n
2
P
P
M
3
N
N
N
N
N
=
⋅
π
⋅
⋅
=
⋅
π
⋅
=
Ω
=
Nm
moment strat
Zredagował dr inż. Witold Kubiak - na podstawie materiałów własnych Instytutu
3
Instytut Mechatroniki i Systemów Informatycznych
do użytku wewnętrznego
10
114
124
M
M
M
N
eN
dN
=
−
=
−
=
Nm
Ad. 5 Jeżeli
i
, to
fN
f
I
I
=
eN
e
M
M
=
aN
a
I
I
=
Dla prędkości wirowania
N
n
9
,
0
n
⋅
=
8
,
184
3
,
205
9
,
0
E
9
,
0
n
n
9
,
0
E
n
n
E
E
N
N
N
N
N
N
=
⋅
=
′
⋅
=
⋅
⋅
′
=
⋅
′
=
′
∗
∗
V
(
)
tc
ad
a
aN
N
u
2
R
R
I
E
U
Δ
+
+
⋅
+
′
=
∑
∗
stąd:
324
,
0
2
,
0
41
,
63
8
,
184
2
220
R
I
E
u
2
U
R
a
aN
tc
N
ad
=
−
−
−
=
−
′
−
Δ
−
=
∑
∗
Ω
5
,
199
324
,
0
41
,
63
220
R
I
U
U
ad
atN
N
a
=
⋅
−
=
⋅
−
=
V
Ad. 6 Prąd wzbudzenia przy
Ω
i
220
R
f
=
N
U
U
=
1
220
220
R
U
I
f
N
f
=
=
=
A
Z charakterystyki
,
,
( )
f
I
f
U
=
N
n
n
=
aN
a
I
I
=
odczytujemy napięcie dla wzbudzenia
A :
1
I
*
f
=
249
U
*
=
V
Przy prądzie
aN
a
I
I
=
3
,
234
2
2
,
0
41
,
63
249
u
2
R
I
U
E
tc
a
aN
*
=
−
⋅
−
=
Δ
−
⋅
−
=
′
∑
V
W warunkach znamionowych, przy prądzie
aN
a
I
I
=
i
N
U
U
=
,
N
n
n
=
3
,
205
2
2
,
0
41
,
63
220
u
2
R
I
U
E
tc
a
aN
N
N
=
−
⋅
−
=
Δ
−
⋅
−
=
′
∑
V
stąd:
63
,
14
3
,
234
3
,
205
7
,
16
E
E
n
n
N
N
*
=
⋅
=
′
′
⋅
=
∗
obr/s
Ad. 7 Minimalna prędkość występuje przy maksymalnym strumieniu
Φ
22
,
1
180
220
R
U
I
2
E
1
E
N
max
f
=
=
=
A
z charakterystyki
,
,
( )
f
I
f
U
=
N
n
n
=
aN
a
I
I
=
odczytujemy napięcie dla
A:
22
,
1
I
f
=
∗
Zredagował dr inż. Witold Kubiak - na podstawie materiałów własnych Instytutu
4
Instytut Mechatroniki i Systemów Informatycznych
do użytku wewnętrznego
267
U
=
∗
V
przy prądzie
i
aN
a
I
I
=
N
n
n
=
3
,
252
2
2
,
0
41
,
63
267
u
2
R
I
U
E
tc
a
aN
=
−
⋅
−
=
Δ
−
⋅
−
=
′
∑
∗
∗
V
przy prądzie
i
aN
a
I
I
=
N
U
U
=
3
,
205
2
2
,
0
41
,
63
220
u
2
R
I
U
E
tc
a
aN
N
N
=
−
⋅
−
=
Δ
−
⋅
−
=
′
∑
V
stąd:
59
,
13
3
,
252
3
,
205
7
,
16
E
E
n
n
N
N
*
=
⋅
=
′
′
⋅
=
∗
obr/s
0
20
40
60
80
100
120
140
160
180
200
220
240
260
280
300
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
I
m
[A]
E
0
[V
],
U [V
]
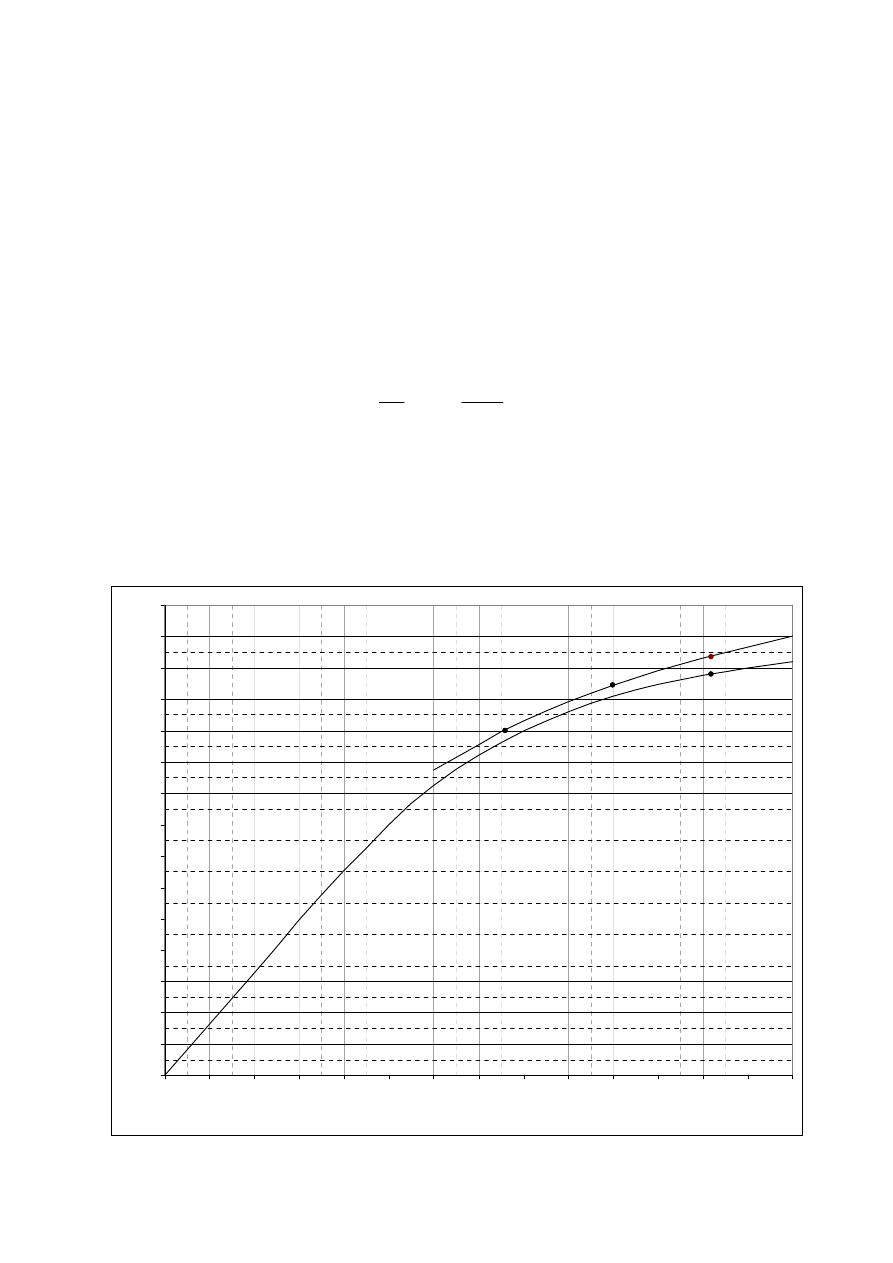
P7
P6
P3
P2
Zredagował dr inż. Witold Kubiak - na podstawie materiałów własnych Instytutu
5