
Cyfrowy zapis
Cyfrowy zapis
Cyfrowy zapis
Cyfrowy zapis
Cyfrowy zapis
Cyfrowy zapis
i f
ji
i f
ji
Cyfrowy zapis
Cyfrowy zapis
i f
ji
i f
ji
informacji
informacji
informacji
informacji
jjjj
6 marca 2011
Wojciech Kucewicz
2

Bit B
Bit Baj
ajt
t Słowo
Słowo
Bit B
Bit Baj
ajt
t Słowo
Słowo
Bit, B
Bit, Baj
ajt,
t, Słowo
Słowo
Kody liczbowe
Kody liczbowe
Bit, B
Bit, Baj
ajt,
t, Słowo
Słowo
Kody liczbowe
Kody liczbowe
Konwersja liczb między różnymi kodami
Konwersja liczb między różnymi kodami
Kod alfanumeryczny
Kod alfanumeryczny
Konwersja liczb między różnymi kodami
Konwersja liczb między różnymi kodami
Kod alfanumeryczny
Kod alfanumeryczny
y
y
y
y
Kody BCD
Kody BCD
Z i li b d ójk
h
ki
Z i li b d ójk
h
ki
y
y
y
y
Kody BCD
Kody BCD
Z i li b d ójk
h
ki
Z i li b d ójk
h
ki
Zapis liczb dwójkowych ze znakiem
Zapis liczb dwójkowych ze znakiem
Dodawanie liczb binarnych ze znakiem
Dodawanie liczb binarnych ze znakiem
Zapis liczb dwójkowych ze znakiem
Zapis liczb dwójkowych ze znakiem
Dodawanie liczb binarnych ze znakiem
Dodawanie liczb binarnych ze znakiem
6 marca 2011
Wojciech Kucewicz
3
Liczby zmiennoprzecinkowe
Liczby zmiennoprzecinkowe
Liczby zmiennoprzecinkowe
Liczby zmiennoprzecinkowe

Bit B
Bit Baj
ajt
t Słowo
Słowo
Bit B
Bit Baj
ajt
t Słowo
Słowo
Bit, B
Bit, Baj
ajt,
t, Słowo
Słowo
Bit, B
Bit, Baj
ajt,
t, Słowo
Słowo
6 marca 2011
Wojciech Kucewicz
4
Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
Bit
Bit
[ang.
[ang.
bi
bi
nary
nary digi
digi
tt
] jest elementem zbioru
] jest elementem zbioru
dwuelementowego używanym do reprezentowania
dwuelementowego używanym do reprezentowania
i f
ji Bit ż i ć
t ść 1 l b 0
i f
ji Bit ż i ć
t ść 1 l b 0
informacji. Bit może mieć wartość 1 lub 0.
informacji. Bit może mieć wartość 1 lub 0.
Bit
Bit
11
00
00
11
11
00
00
00
MSB
MSB
–– bit najbardziej znaczący
bit najbardziej znaczący
LSB
LSB
–– bit najmniej znaczący
bit najmniej znaczący
j
j
ą y
j
j
ą y
LSB
LSB
–– bit najmniej znaczący
bit najmniej znaczący
6 marca 2011
Wojciech Kucewicz
5
Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
11
00
00
11
11
00
00
00
Byte
Byte
BBaj
ajtt ((byte
byte))
ciąg złożony z 8 bitów. Bajt pozwala na zapisanie
ciąg złożony z 8 bitów. Bajt pozwala na zapisanie
w systemie binarnym 2
w systemie binarnym 2
8
8
liczb (0
liczb (0 --255)
255)
Byte
Byte
y
y
y
y
((
))
6 marca 2011
Wojciech Kucewicz
6
Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
11
00
00
11
11
00
00
00
11
00
00
11
11
00
00
00
Word
Word
Słowo (
Słowo (word
word) )
jest informacją złożoną z n bajtów. Słowo
jest informacją złożoną z n bajtów. Słowo
może
może zkładać
zkładać się z
się z 8, 16, 32
8, 16, 32 lub
lub 64
64 bit
bitów.
ów.
Word
Word
S
Słowo
łowo jest
jest traktowane
traktowane przez
przez układy
układy komputera
komputera jako
jako dane
dane
do
do wykonywanej
wykonywanej aktualnie
aktualnie operacji
operacji,, bądź
bądź jako
jako zakodowany
zakodowany
rozkaz
rozkaz..
6 marca 2011
Wojciech Kucewicz
7
Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
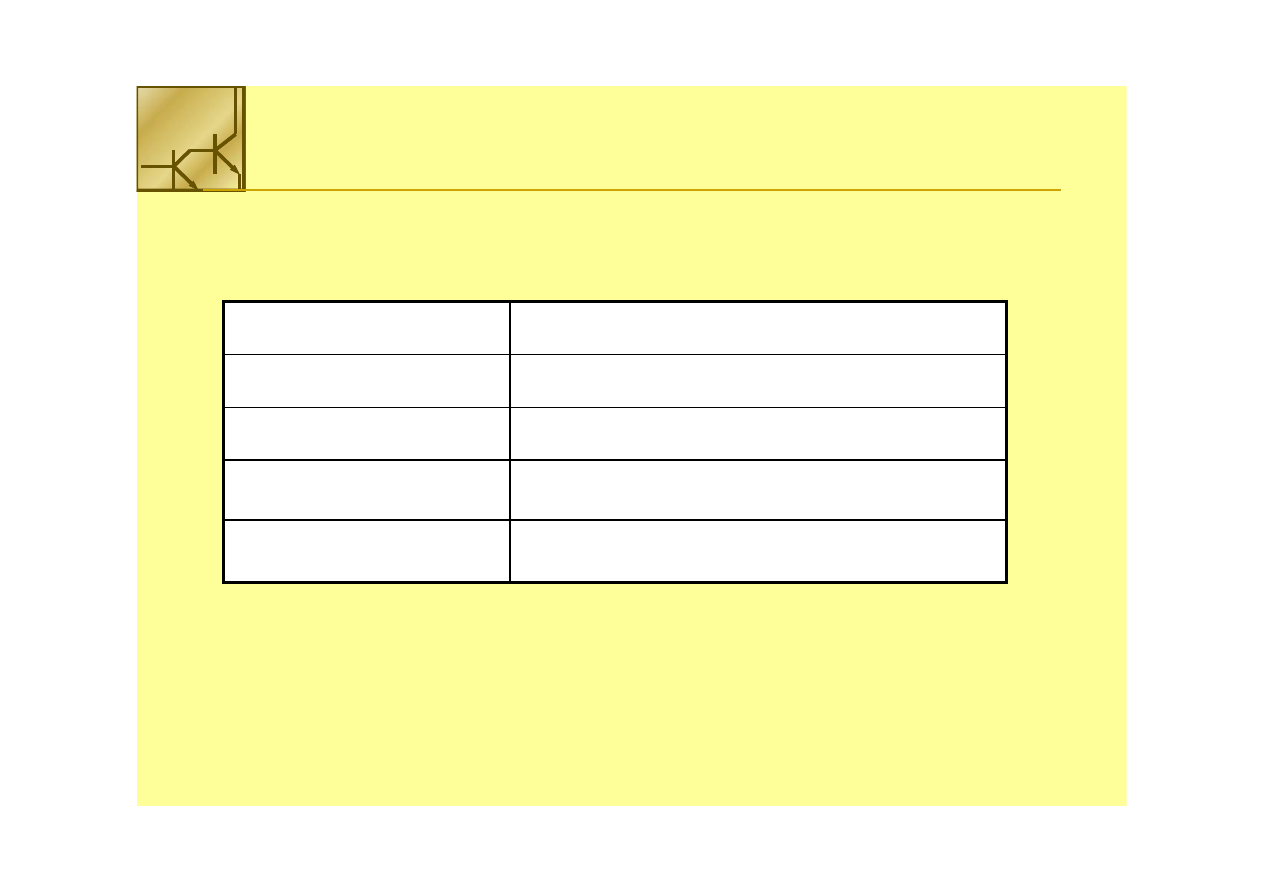
Rozmiar słowa
Rozmiar słowa
Maksymalna liczba możliwa do zapisania
Maksymalna liczba możliwa do zapisania
8 bits
8 bits
255
255
16 bits
16 bits
65535
65535
32 bits
32 bits
4 294 967 295
4 294 967 295
3 b ts
3 b ts
4 94 967 95
4 94 967 95
64 bits
64 bits
18 446 744 073 709 551 615
18 446 744 073 709 551 615
6 marca 2011
Wojciech Kucewicz
8

Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
K d li b
K d li b
K d li b
K d li b
Kody liczbowe
Kody liczbowe
Kody liczbowe
Kody liczbowe
6 marca 2011
Wojciech Kucewicz
9

Kody liczbowe
Kody liczbowe
Kody liczbowe
Kody liczbowe
Najbardziej rozpowszechnionymi kodami liczbowymi są
Najbardziej rozpowszechnionymi kodami liczbowymi są kody
kody
t
l
t
l
naturalne.
naturalne.
Zapis liczb w kodzie naturalnym jest pozycyjny tj. każdy znak
Zapis liczb w kodzie naturalnym jest pozycyjny tj. każdy znak aa
ii
zajmuje ściśle określoną pozycję i, której przyporządkowana jest
zajmuje ściśle określoną pozycję i, której przyporządkowana jest
odpowiednia waga
odpowiednia waga w
w
ii
= p
= p
ii
, gdzie
, gdzie p jest podstawą kodu liczbowego
p jest podstawą kodu liczbowego..
Podstawa kodu określa ilość znaków używanych w kodzie.
Podstawa kodu określa ilość znaków używanych w kodzie.
6 marca 2011
Wojciech Kucewicz
10

Kod dziesiętny
Kod dziesiętny
Kod dziesiętny
Kod dziesiętny
Powszechnie stosowany jest kod (system) dziesiętny. Został
Powszechnie stosowany jest kod (system) dziesiętny. Został
opracowany w Indiach ok. V wieku i poprzez Arabów upowszechnił się
opracowany w Indiach ok. V wieku i poprzez Arabów upowszechnił się
w Europie
w Europie
w Europie.
w Europie.
Oparty jest na dziesięciu znakach (cyfrach):
Oparty jest na dziesięciu znakach (cyfrach):
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Ilość znaków jest podstawą systemu
Ilość znaków jest podstawą systemu ––
p = 10
p = 10
Dowolną liczbę x przedstawia się za pomocą słowa A składającego się
Dowolną liczbę x przedstawia się za pomocą słowa A składającego się
z n cyfr zgodnie ze wzorem:
z n cyfr zgodnie ze wzorem:
y
g
y
g
x = L(A) =
x = L(A) =
aj
aj …a
…a
44
aa
33
aa
22
aa
11
aa
00
. a
. a
--11
aa
--22
gdzie
gdzie
aa
jest jednym z używanych znaków, a indeks
jest jednym z używanych znaków, a indeks
jj
jest potęgą
jest potęgą
6 marca 2011
Wojciech Kucewicz
11
gg
j
j
ym
y
y
,
j
j
ym
y
y
,
jj
j
p ęgą
j
p ęgą
podstawy
podstawy
pp
przez którą znak jest mnożony
przez którą znak jest mnożony
Kod dziesiętny
Kod dziesiętny
Kod dziesiętny
Kod dziesiętny
Liczba
Liczba
aa
jj
… a
… a
11
aa
00
. a
. a
--11
aa
--22
aa
jj
•p
•p
jj
+ ...+
+ ...+ aa
11
•10
•10
11
+
+ aa
00
•10
•10
00
+
+ aa
--11
•10
•10
--11
+
+ aa
--22
•10
•10
--22
P
kł d
P
kł d
Przykład:
Przykład:
Liczbę
Liczbę
4321
4321
można zapisać jako
można zapisać jako::
4321 =
4321 =
4•10
4•10
33
+ 3•10
+ 3•10
22
+ 2•10
+ 2•10
11
+ 1•10
+ 1•10
00
= 4000 +
= 4000 + 300
300 ++ 20
20 ++ 1 = 4321
1 = 4321
10
10
Oznacza kod
Oznacza kod
6 marca 2011
Wojciech Kucewicz
12
Przy pomocy n cyfr możemy zapisać p
Przy pomocy n cyfr możemy zapisać p
n
n
liczb (od 0 do p
liczb (od 0 do p
nn
–– 1)
1)

Kod binarny
Kod binarny
Kod binarny
Kod binarny
W technice cyfrowej najczęściej jest stosowany kod dwójkowy
W technice cyfrowej najczęściej jest stosowany kod dwójkowy
(bi
)
(bi
)
(binarny)
(binarny)
Oparty jest na dwóch znakach:
Oparty jest na dwóch znakach:
0, 1
0, 1
Podstawa systemu
Podstawa systemu ––
p = 2
p = 2
Przykład
Przykład
Liczbę
Liczbę
1000011100001
1000011100001
22
można zapisać jako
można zapisać jako
p
j
p
j
1•2
1•2
12
12
+ 0•2
+ 0•2
11
11
+ 0•2
+ 0•2
10
10
+ 0•2
+ 0•2
99
+ 0•2
+ 0•2
88
+
+
1•2
1•2
77
+
+
1•2
1•2
66
+
+
1•2
1•2
55
+ 0•2
+ 0•2
44
+ 0•2
+ 0•2
33
+ 0•2
+ 0•2
22
+
+
0•2
0•2
11
+
+
1•2
1•2
00
=
=
4096+128+64+32+1
4096+128+64+32+1
= 4321
= 4321
10
10
6 marca 2011
Wojciech Kucewicz
13
10
10

Kod oktagonalny
Kod oktagonalny
Kod oktagonalny
Kod oktagonalny
Kod
Kod oktagonaly
oktagonaly oparty jest na ośmiu znakach:
oparty jest na ośmiu znakach:
0 1
0 1 2 3 4 5 6 7
2 3 4 5 6 7
0, 1
0, 1, 2, 3, 4, 5, 6, 7
, 2, 3, 4, 5, 6, 7
Podstawa systemu
Podstawa systemu ––
p = 8
p = 8
Przykład
Przykład
Liczbę
Liczbę
10341
10341
88
można zapisać jako
można zapisać jako
88
p
j
p
j
1•8
1•8
4
4
+ 0•8
+ 0•8
3
3
+
+
3•8
3•8
22
+
+
4•8
4•8
11
+
+
1•8
1•8
00
= 4096+192+32+1= 4321
= 4096+192+32+1= 4321
10
10
6 marca 2011
Wojciech Kucewicz
14

Kod heksadecymalny
Kod heksadecymalny
Kod heksadecymalny
Kod heksadecymalny
Kod heksadecymalny oparty jest na szesnastu znakach:
Kod heksadecymalny oparty jest na szesnastu znakach:
0 1
0 1 2 3 4 5 6 7 8 9 A B C D E F
2 3 4 5 6 7 8 9 A B C D E F
0, 1
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Podstawa systemu
Podstawa systemu ––
p = 16
p = 16
Przykład
Przykład
Liczbę
Liczbę
10EA
10EA
16
16
można zapisać jako
można zapisać jako
66
p
j
p
j
1•16
1•16
3
3
+ 0•16
+ 0•16
2
2
+
+
14•16
14•16
11
+
+
10•16
10•16
00
= 4096+224+1= 4321
= 4096+224+1= 4321
10
10
6 marca 2011
Wojciech Kucewicz
15

Kody liczbowe
Kody liczbowe
Kody liczbowe
Kody liczbowe
Kod dziesiętny
Kod dziesiętny
Kod binarny
Kod binarny
Kod octagonalny
Kod octagonalny
Kod heksadecymalny
Kod heksadecymalny
00
00
00
00
11
11
11
11
22
10
10
22
22
33
11
11
33
33
44
100
100
44
44
44
100
100
44
44
55
101
101
55
55
66
110
110
66
66
77
111
111
77
77
77
111
111
77
77
88
1000
1000
10
10
88
99
1001
1001
11
11
99
10
10
1010
1010
12
12
A
A
10
10
1010
1010
12
12
A
A
11
11
1011
1011
13
13
BB
12
12
1100
1100
14
14
CC
6 marca 2011
Wojciech Kucewicz
16
13
13
1101
1101
15
15
D
D
14
14
1110
1110
16
16
EE
15
15
1111
1111
17
17
FF

Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
K
j li b i d
K
j li b i d
K
j li b i d
K
j li b i d
Konwersja liczb między
Konwersja liczb między
różnymi kodami
różnymi kodami
Konwersja liczb między
Konwersja liczb między
różnymi kodami
różnymi kodami
różnymi kodami
różnymi kodami
różnymi kodami
różnymi kodami
6 marca 2011
Wojciech Kucewicz
17
Kod dziesiętny
Kod dziesiętny Î
Î
kod binarny
kod binarny
Kod dziesiętny
Kod dziesiętny Î
Î
kod binarny
kod binarny
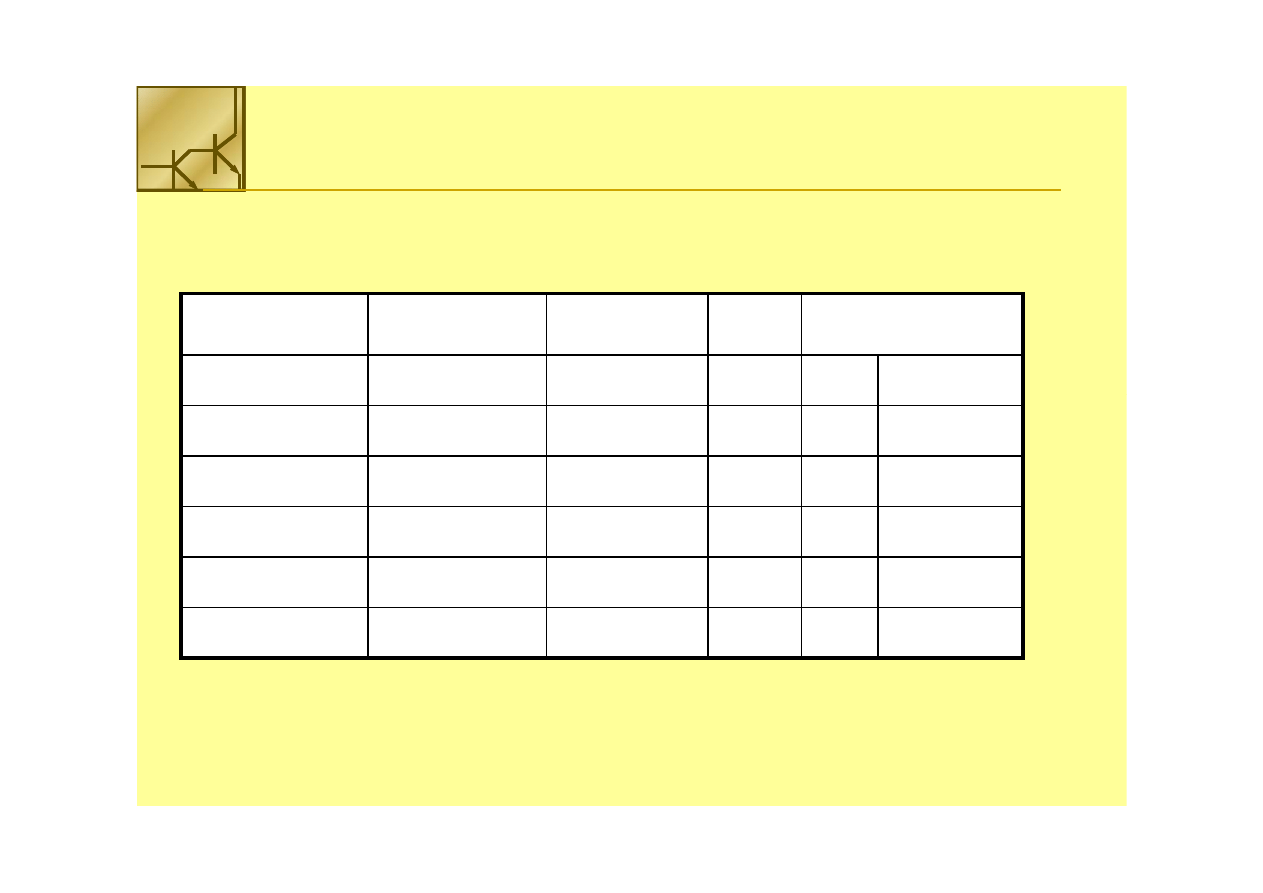
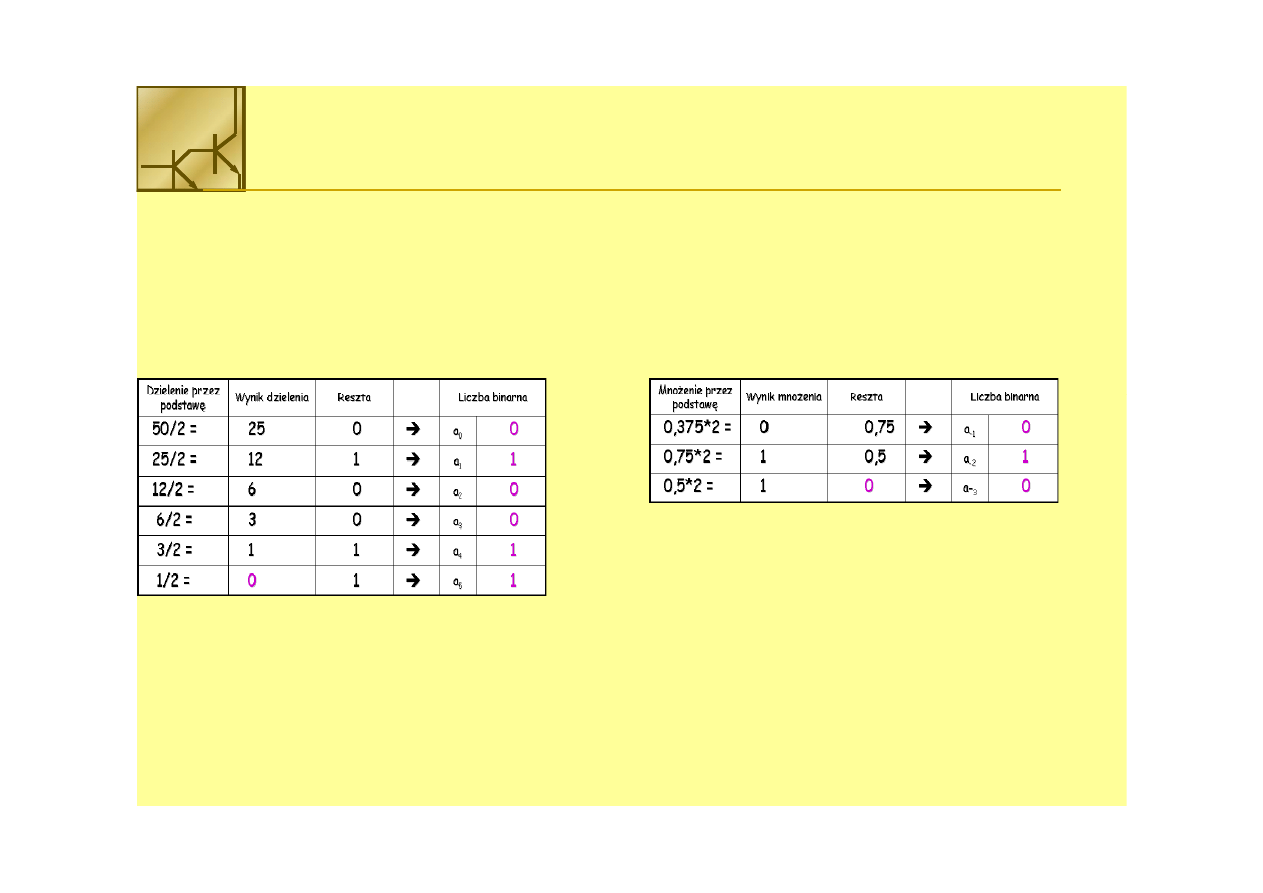
Zamiana liczby całkowitej
Zamiana liczby całkowitej
50
50
10
10
na binarną
na binarną::
Dzielenie przez
Dzielenie przez
podstawę
podstawę
Wynik dzielenia
Wynik dzielenia
Reszta
Reszta
Liczba binarna
Liczba binarna
aa
00
50/2 =
50/2 =
25
25
00
Î
Î
00
aa
11
aa
2
25/2 =
25/2 =
12
12
1
1
Î
Î
11
12/2 =
12/2 =
66
00
Î
Î
00
aa
33
aa
44
6/2 =
6/2 =
33
0
0 Î
Î
00
3/2 =
3/2 =
11
1
1 Î
Î
11
50
50
110010
110010
aa
55
1/2 =
1/2 =
00
1
1 Î
Î
11
6 marca 2011
Wojciech Kucewicz
18
50
50
10
10
= 110010
= 110010
22
Kod dziesiętny
Kod dziesiętny Î
Î
kod binarny
kod binarny
Kod dziesiętny
Kod dziesiętny Î
Î
kod binarny
kod binarny
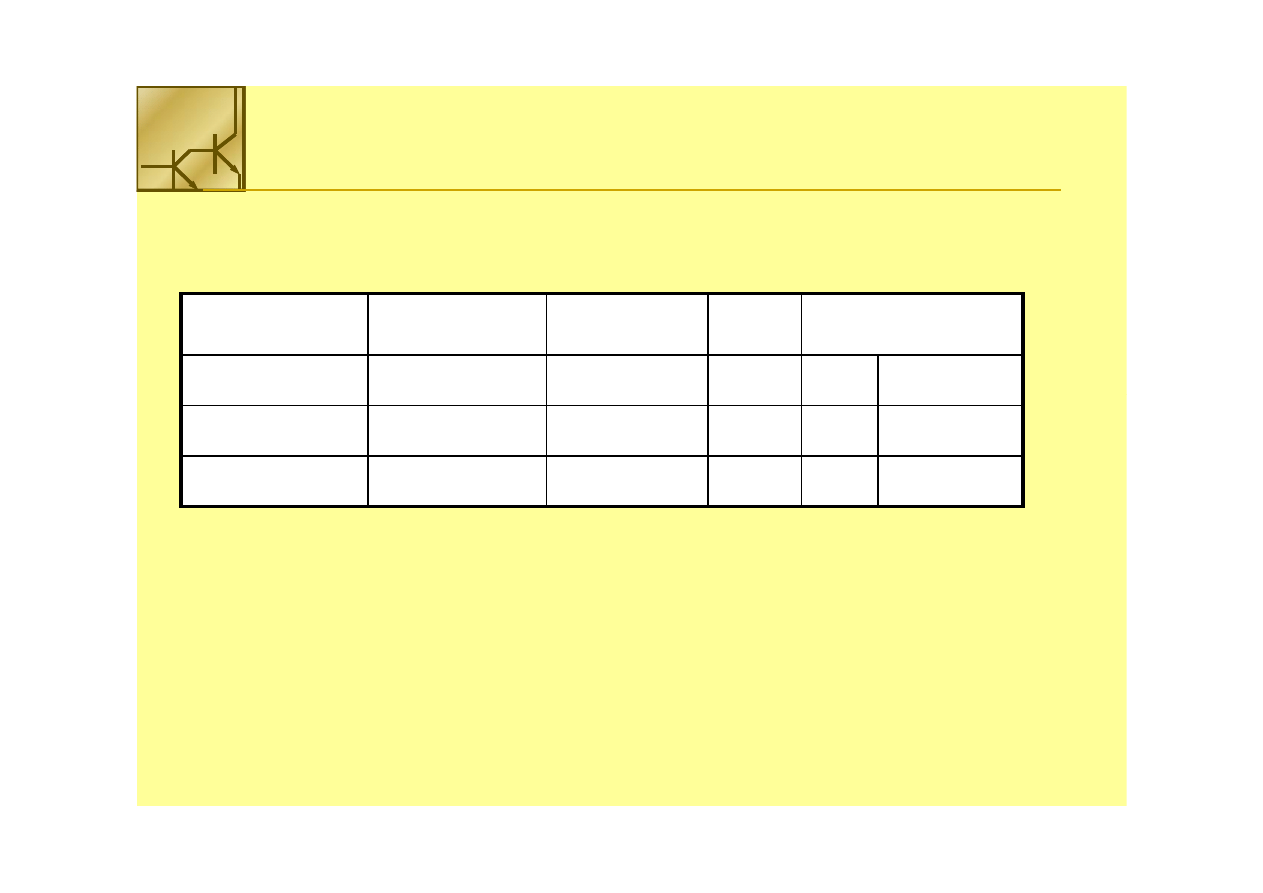
Zamiana liczby ułamkowej
Zamiana liczby ułamkowej
0.375
0.375
10
10
na binarną
na binarną ::
Mnożenie przez
Mnożenie przez
podstawę
podstawę
Wynik mnożenia
Wynik mnożenia
Reszta
Reszta
Liczba binarna
Liczba binarna
aa
--11
0,375
0,375 •• 2 =
2 = 00
0,75
0,75
Î
Î
00
aa
--22
aa--
3
0,75
0,75 •• 2 =
2 =
11
0,5
0,5
Î
Î
11
0,5
0,5 •• 2 =
2 =
11
00
Î
Î
11
0 375
0 375
0 011
0 011
6 marca 2011
Wojciech Kucewicz
19
0.375
0.375
10
10
= 0.011
= 0.011
22
Kod dziesiętny
Kod dziesiętny Î
Î
kod binarny
kod binarny
Kod dziesiętny
Kod dziesiętny Î
Î
kod binarny
kod binarny
Zamiana liczby dziesiętnej
Zamiana liczby dziesiętnej
50.375
50.375
10
10
na binarną wykonuje się w
na binarną wykonuje się w
dwóch krokach:
dwóch krokach:
1)
1) Konwersja części całkowitej
Konwersja części całkowitej
2) Konwersja części ułamkowej
2) Konwersja części ułamkowej
50 375
50 375
10
10
=50 + 0 375 = 110010 + 0 011 = 110010 011
=50 + 0 375 = 110010 + 0 011 = 110010 011
22
6 marca 2011
Wojciech Kucewicz
20
50.375
50.375
10
10
50 + 0.375 110010 + 0.011 110010.011
50 + 0.375 110010 + 0.011 110010.011
22
Kod dziesiętny
Kod dziesiętny Î
Î
kod binarny
kod binarny
Kod dziesiętny
Kod dziesiętny Î
Î
kod binarny
kod binarny
Niektóre ułamki można tylko w przybliżeniu przedstawić w postaci
Niektóre ułamki można tylko w przybliżeniu przedstawić w postaci
binarnej
binarnej
np. 0,3
np. 0,3
::
Mnożenie przez
Mnożenie przez
podstawę
podstawę
Wynik mnożenia
Wynik mnożenia
Reszta
Reszta
Liczba binarna
Liczba binarna
0 3
0 3 2
2
00
0 6
0 6
Î
Î
00
aa
--11
aa
--22
0,3
0,3 •• 2 =
2 =
00
0,6
0,6
Î
Î
00
0,6
0,6 •• 2 =
2 =
11
0,2
0,2
Î
Î
11
0 2
0 2 2
2
00
0 4
0 4
Î
Î
00
aa--
3
aa
--44
0,2
0,2 •• 2 =
2 =
00
0,4
0,4
Î
Î
00
0,4
0,4 •• 2 =
2 =
00
0,8
0,8
Î
Î
00
0 8
0 8 2
2
11
0 6
0 6
Î
Î
11
aa
--55
aa--
6
0 3
0 3
00 010011
010011
0,8
0,8 •• 2 =
2 =
11
0,6
0,6
Î
Î
11
0,6
0,6 •• 2 =
2 =
11
0,2
0,2
Î
Î
11
6 marca 2011
Wojciech Kucewicz
21
0.3
0.3
10
10
=
= 0,
0,010011….
010011….
22

Kod binarny
Kod binarny ÍÎ
ÍÎ
kod oktagonalny
kod oktagonalny
Kod binarny
Kod binarny ÍÎ
ÍÎ
kod oktagonalny
kod oktagonalny
Liczbę binarną należy podzielić na segment 3 elementowe poczynając
Liczbę binarną należy podzielić na segment 3 elementowe poczynając
od przecinka w obie strony a następnie każdy segment zamienić na
od przecinka w obie strony a następnie każdy segment zamienić na
liczbę oktagonalną
liczbę oktagonalną::
liczbę oktagonalną
liczbę oktagonalną::
110010.011
110010.011
22
ÎÎ
110010.011
110010.011
22
ÎÎ
110
110 010.
010. 011
011
22
ÎÎ
ÎÎ
ÎÎ
ÎÎ
110
110 010.
010. 011
011
22
ÎÎ
ÎÎ
ÎÎ
ÎÎ
6 2
6 2..
33
88
ÎÎ
ÎÎ
ÎÎ
ÎÎ
6 2
6 2..
33
88
ÎÎ
ÎÎ
ÎÎ
ÎÎ
62
62..33
88
ÎÎ
62
62..33
88
6 marca 2011
Wojciech Kucewicz
22
Liczbę
Liczbę oktagonalną
oktagonalną zamieniamy na liczbę binarną postępując
zamieniamy na liczbę binarną postępując
odwrotnie
odwrotnie

Kod binarny
Kod binarny ÍÎ
ÍÎ
kod heksadecymalny
kod heksadecymalny
Kod binarny
Kod binarny ÍÎ
ÍÎ
kod heksadecymalny
kod heksadecymalny
Liczbę binarną należy podzielić na segment 4 elementowe poczynając
Liczbę binarną należy podzielić na segment 4 elementowe poczynając
od przecinka w obie strony, a następnie każdy segment zamienić na
od przecinka w obie strony, a następnie każdy segment zamienić na
liczbę heksadecymalną
liczbę heksadecymalną::
liczbę heksadecymalną
liczbę heksadecymalną::
110010.011
110010.011
22
ÎÎ
110010.011
110010.011
22
ÎÎ
00
0011
11 0010.
0010. 011
01100
22
ÎÎ
ÎÎ
ÎÎ
ÎÎ
00
0011
11 0010.
0010. 011
01100
22
ÎÎ
ÎÎ
ÎÎ
ÎÎ
3 2
3 2..
66
16
16
ÎÎ
ÎÎ
ÎÎ
ÎÎ
3 2
3 2..
66
16
16
ÎÎ
ÎÎ
ÎÎ
ÎÎ
32
32..66
16
16
ÎÎ
32
32..66
16
16
6 marca 2011
Wojciech Kucewicz
23
Liczbę heksadecymalną zamieniamy na liczbę binarną postępując
Liczbę heksadecymalną zamieniamy na liczbę binarną postępując
odwrotnie
odwrotnie

Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
Kod alfanumeryczny
Kod alfanumeryczny
Kod alfanumeryczny
Kod alfanumeryczny
6 marca 2011
Wojciech Kucewicz
24

Kod alfanumeryczny ASCII
Kod alfanumeryczny ASCII
Kod alfanumeryczny ASCII
Kod alfanumeryczny ASCII
W komputerach musi być jakiś sposób przedstawiania oprócz liczb
W komputerach musi być jakiś sposób przedstawiania oprócz liczb
także liter i innych symboli. Określenie alfanumeryczny jest
także liter i innych symboli. Określenie alfanumeryczny jest
d
h
b l k ó
k f
d
h
b l k ó
k f
stosowany do tych symboli, które zawierają także cyfry
stosowany do tych symboli, które zawierają także cyfry
dziesiętne.
dziesiętne.
Sposób przyporządkowania odpowiedniego kodu symbolom
Sposób przyporządkowania odpowiedniego kodu symbolom
alfanumerycznym nazywamy kodem
alfanumerycznym nazywamy kodem
ASCII
ASCII
od angielskiej nazwy
od angielskiej nazwy
dokumentu:
dokumentu:
A
A
merican
merican
S
S
tandard
tandard
CC
ode for
ode for
II
nformation
nformation
II
nterchange
nterchange
gg
Kod ASCII jest kodem 7
Kod ASCII jest kodem 7--bitowym, często 8 bit wykorzystuje się
bitowym, często 8 bit wykorzystuje się
do kontroli parzystości lub do kodowania dodatkowych znaków o
do kontroli parzystości lub do kodowania dodatkowych znaków o
do kontroli parzystości lub do kodowania dodatkowych znaków o
do kontroli parzystości lub do kodowania dodatkowych znaków o
numerach od 128 do 255
numerach od 128 do 255
6 marca 2011
Wojciech Kucewicz
25

Kod alfanumeryczny ASCII
Kod alfanumeryczny ASCII
Kod alfanumeryczny ASCII
Kod alfanumeryczny ASCII
Znaki w kodzie ASCII są przyporządkowane liczbom, które można
Znaki w kodzie ASCII są przyporządkowane liczbom, które można
zapisać w dowolnym kodzie numerycznym.
zapisać w dowolnym kodzie numerycznym.
Character
Character
ASCII
ASCII
(bin)
(bin)
ASCII
ASCII
(hex)
(hex)
Decimal
Decimal
Octal
Octal
A
A
1000001
1000001
41
41
65
65
101
101
p
y
y
y
p
y
y
y
BB
1000010
1000010
42
42
66
66
102
102
CC
1000011
1000011
43
43
67
67
103
103
…
…
KK
1001011
1001011
4B
4B
75
75
113
113
aa
1100001
1100001
61
61
97
97
141
141
…
…
11
0110001
0110001
31
31
49
49
61
61
6 marca 2011
Wojciech Kucewicz
26
‘‘
0100111
0100111
27
27
39
39
47
47

Kod alfanumeryczny ASCII
Kod alfanumeryczny ASCII
Kod alfanumeryczny ASCII
Kod alfanumeryczny ASCII
Przykład:
Przykład:
Euro 2012
Euro 2012
Wyrażenie
Wyrażenie
Binarnie
Binarnie
Octagonalnie
Octagonalnie Heksadecymalnie
Heksadecymalnie Decymalnie
Decymalnie
EE
01000101
01000101
105
105
45
45
69
69
EE
01000101
01000101
105
105
45
45
69
69
uu
01110101
01110101
165
165
75
75
117
117
rr
01110010
01110010
162
162
72
72
114
114
rr
01110010
01110010
162
162
72
72
114
114
oo
01101111
01101111
157
157
6F
6F
111
111
00100000
00100000
40
40
20
20
32
32
00100000
00100000
40
40
20
20
32
32
22
00110010
00110010
62
62
32
32
50
50
00
00110000
00110000
60
60
30
30
48
48
00
00110000
00110000
60
60
30
30
48
48
11
00110001
00110001
61
61
31
31
49
49
22
00110010
00110010
62
62
32
32
50
50
6 marca 2011
Wojciech Kucewicz
27
22
00110010
00110010
62
62
32
32
50
50
010001010111010101110010011011110010000000110010001100000011000100110010
010001010111010101110010011011110010000000110010001100000011000100110010
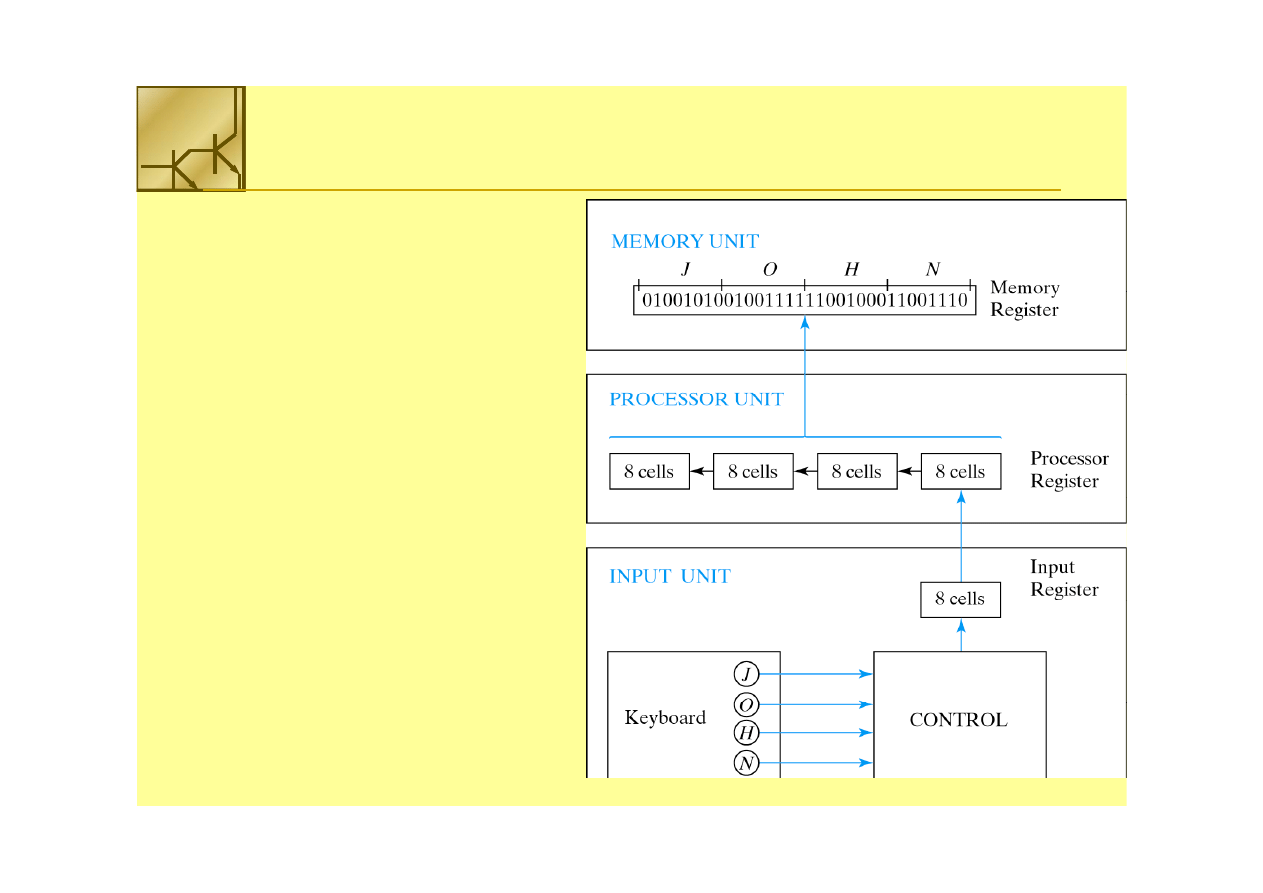
Transmisja informacji
Transmisja informacji
Transmisja informacji
Transmisja informacji
1.
1. Dane w kodzie ASCII wprowadzane
Dane w kodzie ASCII wprowadzane
są z klawiatury
są z klawiatury
ą
y
ą
y
2.
2. Przemieszczane są w blokach
Przemieszczane są w blokach
(bajtach) przy użyciu procesora
(bajtach) przy użyciu procesora
3.
3. Gromadzone są w pamięci
Gromadzone są w pamięci
6 marca 2011
Wojciech Kucewicz
28
Funkcje logiczne 2
Funkcje logiczne 2--argumentowe
argumentowe
Funkcje logiczne 2
Funkcje logiczne 2--argumentowe
argumentowe
Liczba wszystkich możliwych funkcji logicznych dla n zmiennych
wejściowych jest równa 4
n
.
j
y
j
Przy n = 2 otrzymuje się 16 funkcji:
2 funkcje będące stałymi,
4 funkcje unarne
( 2 negacje + 2 przeniesienia),
10 funkcji logicznych
xy
xy
D
D
00
00 01
01 10
10
11
11
Funkcja
Funkcja
10 funkcji logicznych
00
00
00
00
00
00
Stała 0
Stała 0
11
00
00
00
11
xy
xy
Iloczyn logiczny AND
Iloczyn logiczny AND
22
00
00
11
00
xy’
xy’
Iloczyn z zakazem
Iloczyn z zakazem
33
00
00
11
11
xx
Przeniesienie x
Przeniesienie x
44
00
11
00
00
x’y
x’y
Iloczyn z zakazem
Iloczyn z zakazem
55
00
11
00
11
yy
Przeniesienie y
Przeniesienie y
6 marca 2011
Wojciech Kucewicz
29
66
00
11
11
00
(x’y)+(xy’)
(x’y)+(xy’)
Exclusive OR
Exclusive OR
77
00
11
11
11
x+y
x+y
Suma logiczna OR
Suma logiczna OR
Funkcje logiczne 2
Funkcje logiczne 2--argumentowe
argumentowe
Funkcje logiczne 2
Funkcje logiczne 2--argumentowe
argumentowe
Liczba wszystkich możliwych funkcji logicznych dla n zmiennych
wejściowych jest równa 4
n
.
j
y
j
Przy n = 2 otrzymuje się 16 funkcji:
2 funkcje będące stałymi,
4 funkcje unarne
( 2 negacje + 2 przeniesienia),
10 funkcji logicznych
xy
xy
D
D
00
00 01
01 10
10
11
11
Funkcja
Funkcja
10 funkcji logicznych
88
11
00
00
00
(x+y)’
(x+y)’
Negacja sumy NOR
Negacja sumy NOR
99
11
00
00
11
((x’y
x’y’)+(
’)+(xy
xy))
Exclusive NOR
Exclusive NOR
10
10
11
00
11
00
y’
y’
Negacja y
Negacja y
11
11
11
00
11
11
x+y’
x+y’
Implikacja
Implikacja yyÎ
Î
xx
12
12
11
11
00
00
x’
x’
Negacja x
Negacja x
13
13
11
11
00
11
x’+y
x’+y
Implikacja
Implikacja xxÎ
Î
yy
6 marca 2011
Wojciech Kucewicz
30
14
14
11
11
11
00
(xy)’
(xy)’
Negacja iloczynu NAND
Negacja iloczynu NAND
15
15
11
11
11
11
11
Stała 1
Stała 1

Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
K d BCD
K d BCD
K d BCD
K d BCD
Kody BCD
Kody BCD
Kody BCD
Kody BCD
6 marca 2011
Wojciech Kucewicz
31
Kod
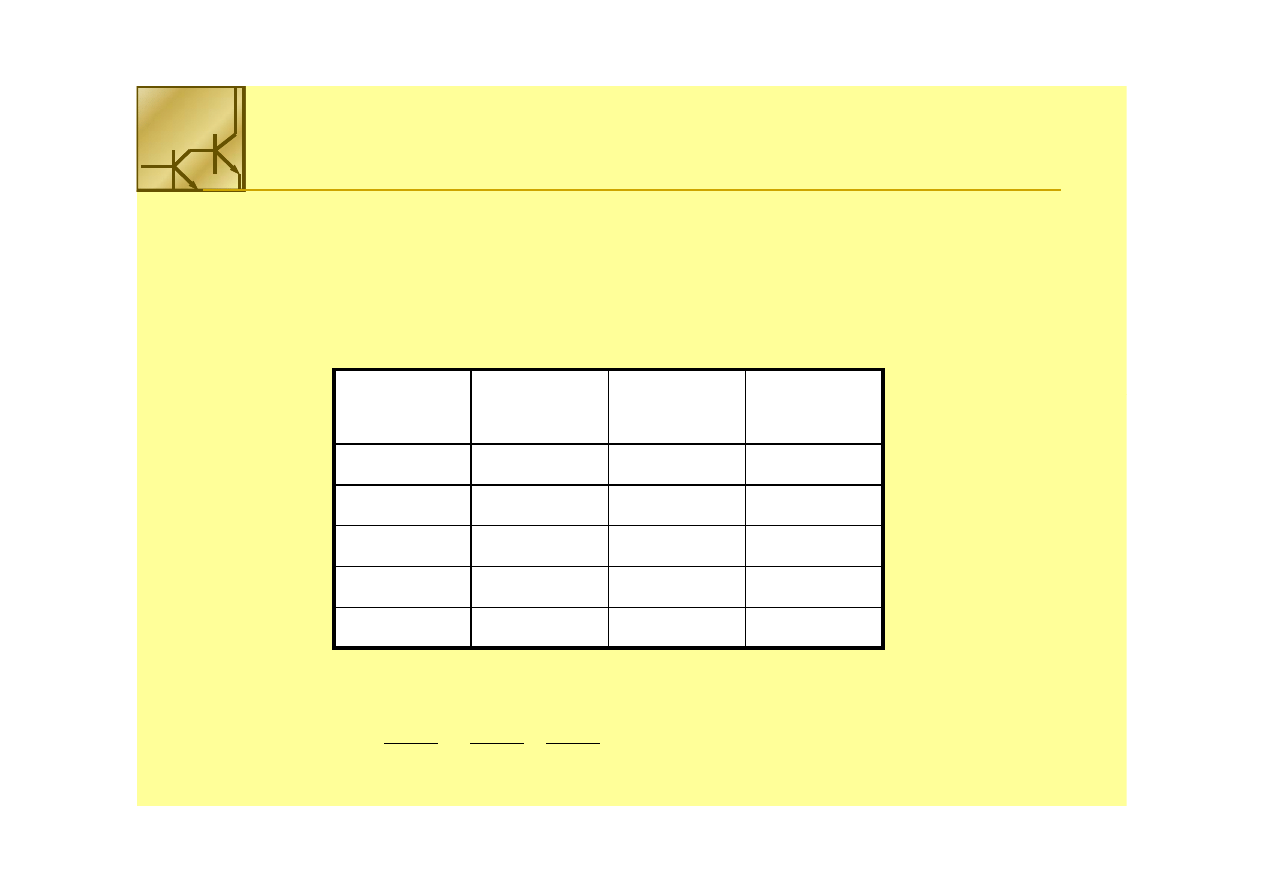
Kod BCD 8421
BCD 8421
Kod
Kod BCD 8421
BCD 8421
W kodzie BCD (ang.
W kodzie BCD (ang. Binary
Binary coded
coded decimal
decimal) każda cyfra liczb
) każda cyfra liczb dziesiętnej
dziesiętnej jest
jest
oddzielnie kodowana dwójkowo w postaci 4
oddzielnie kodowana dwójkowo w postaci 4--bitowego słowa.
bitowego słowa.
Najpopularniejszy jest kod
Najpopularniejszy jest kod BCD 8421
BCD 8421 obejmujący pierwsze 10 liczb z 4
obejmujący pierwsze 10 liczb z 4--
Kod
Kod
Kod
Kod
Najpopularniejszy jest kod
Najpopularniejszy jest kod BCD 8421
BCD 8421 obejmujący pierwsze 10 liczb z 4
obejmujący pierwsze 10 liczb z 4
bitowego naturalnego kodu dwójkowego.
bitowego naturalnego kodu dwójkowego.
Cyfra
Cyfra
Kod
Kod
BCD
BCD8421
8421
Cyfra
Cyfra
Kod
Kod
BCD
BCD8421
8421
00
0000
0000
55
0101
0101
11
0001
0001
66
0110
0110
11
0001
0001
66
0110
0110
22
0010
0010
77
0111
0111
33
0011
0011
88
1000
1000
44
0100
0100
99
1001
1001
Przykładowo liczba 369
Przykładowo liczba 369
10
10
będzie zakodowana następująco:
będzie zakodowana następująco:
6 marca 2011
Wojciech Kucewicz
32
yy
10
10
ę
ęp j
ę
ęp j
0011 0110 1001
0011 0110 1001
To nie jest liczba 0011 0110 1001 !
To nie jest liczba 0011 0110 1001 !
3
3
6
6
9
9
Kod
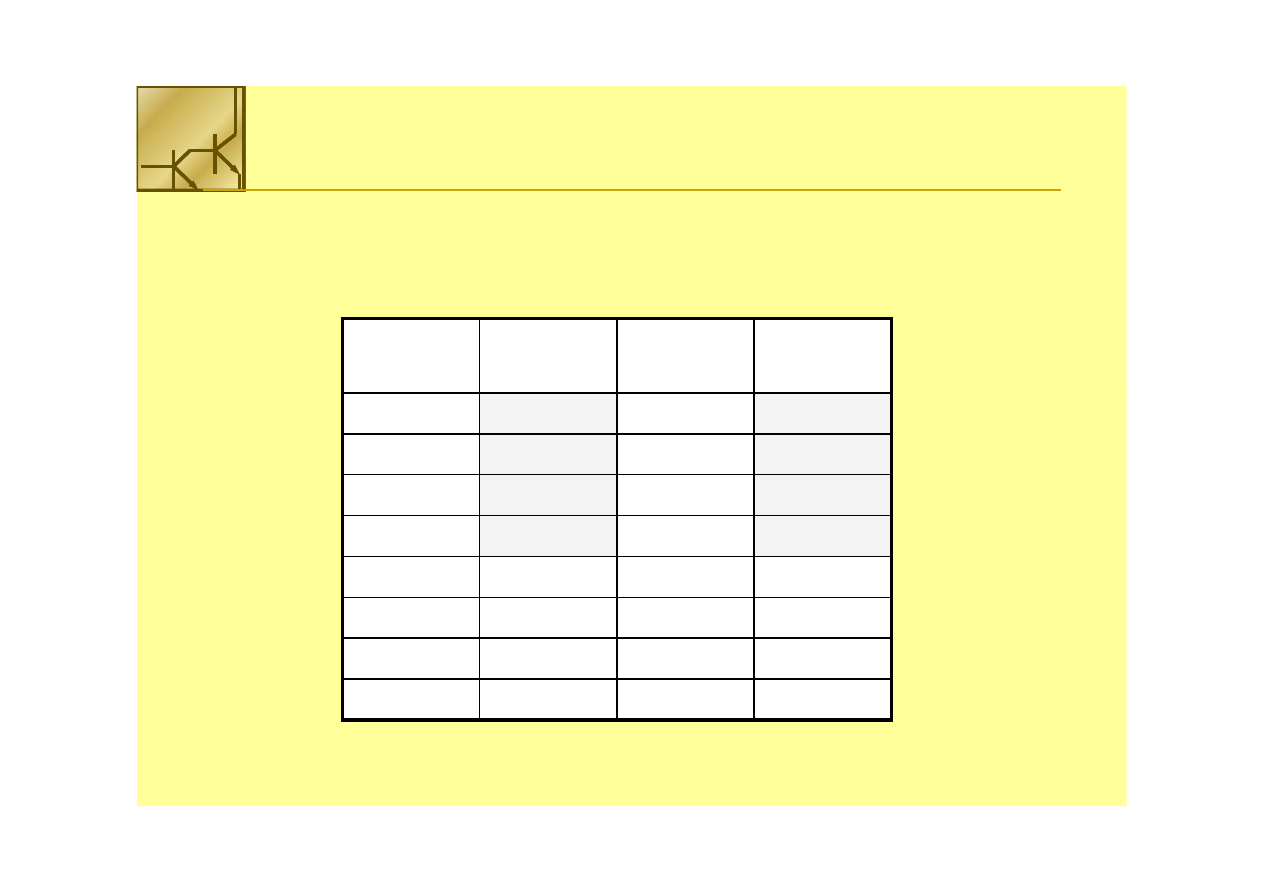
Kod BCD
BCD Gray’a
Gray’a
Kod
Kod BCD
BCD Gray’a
Gray’a
Przykładem
Przykładem kodu BCD jest kod
kodu BCD jest kod Gray’a
Gray’a..
Cyfra
Cyfra
Kod
Kod
Gray’a
Gray’a
Cyfra
Cyfra
Kod
Kod
Gray’a
Gray’a
00
0000
0000
88
111100
00
11
0001
0001
99
111101
01
22
001
00111
10
10
1111
1111
22
001
00111
10
10
1111
1111
33
001
00100
11
11
1110
1110
44
01
011100
12
12
1010
1010
55
01
011111
13
13
1011
1011
66
010
01011
14
14
1001
1001
77
01
0100
00
15
15
1000
1000
6 marca 2011
Wojciech Kucewicz
33
77
01
0100
00
15
15
1000
1000
Kod
Kod Gray’a
Gray’a ma taką właściwość, że jego sąsiednie słowa różnią się tylko jednym bitem
ma taką właściwość, że jego sąsiednie słowa różnią się tylko jednym bitem
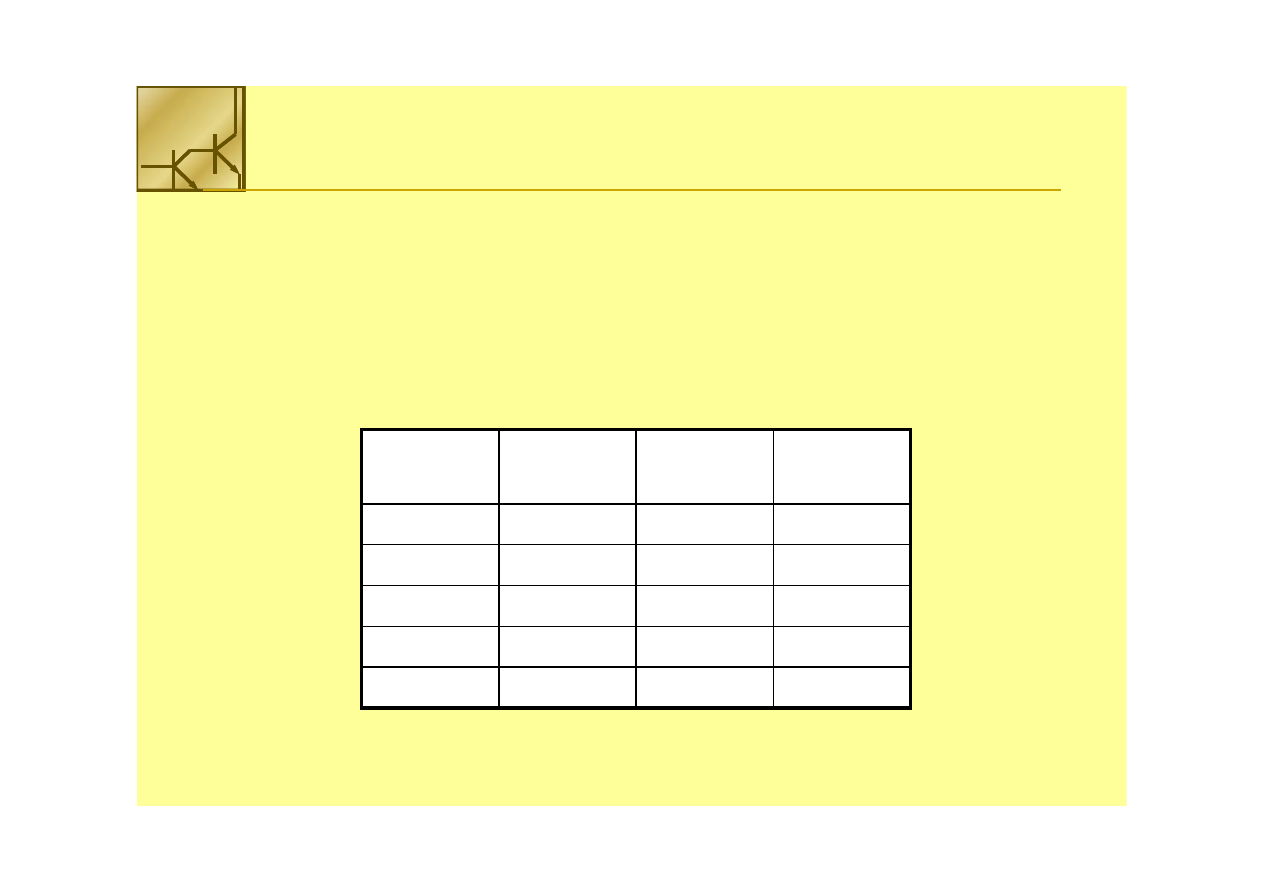
Kod Aikena
Kod Aikena
Kod Aikena
Kod Aikena
W kodzie BCD (ang.
W kodzie BCD (ang. Binary
Binary coded
coded decimal
decimal) ) Aikena
Aikena waga bitów jest
waga bitów jest 22--44--22--1.
1.
Uzupełnienie do 1 liczb binarnych w tym kodzie daje uzupełnienie do 9
Uzupełnienie do 1 liczb binarnych w tym kodzie daje uzupełnienie do 9
odpowiednich liczb dziesiętnych
odpowiednich liczb dziesiętnych
odpowiednich liczb dziesiętnych.
odpowiednich liczb dziesiętnych.
Np. 4
Np. 4 Î
Î
0100
0100 Î
Î
U1=1011
U1=1011 Î
Î
U9=2+2+1=5
U9=2+2+1=5
Kod z taką właściwością nazywamy kodem
Kod z taką właściwością nazywamy kodem samouzupełniającym
samouzupełniającym..
Cyfra
Cyfra
Kod
Kod
Aikena
Aikena
Cyfra
Cyfra
Kod
Kod
Aikena
Aikena
ą
ą
y
y
ą
ą
y
y
p
ją y
p
ją y
00
0000
0000
55
101
10111
11
0001
0001
66
1110
1000
22
001
00100
77
111101
01
22
001
00100
77
111101
01
33
001
00111
88
1111
1100
44
01
010000
99
1111
1111
6 marca 2011
Wojciech Kucewicz
34
Kod z nadmiarem
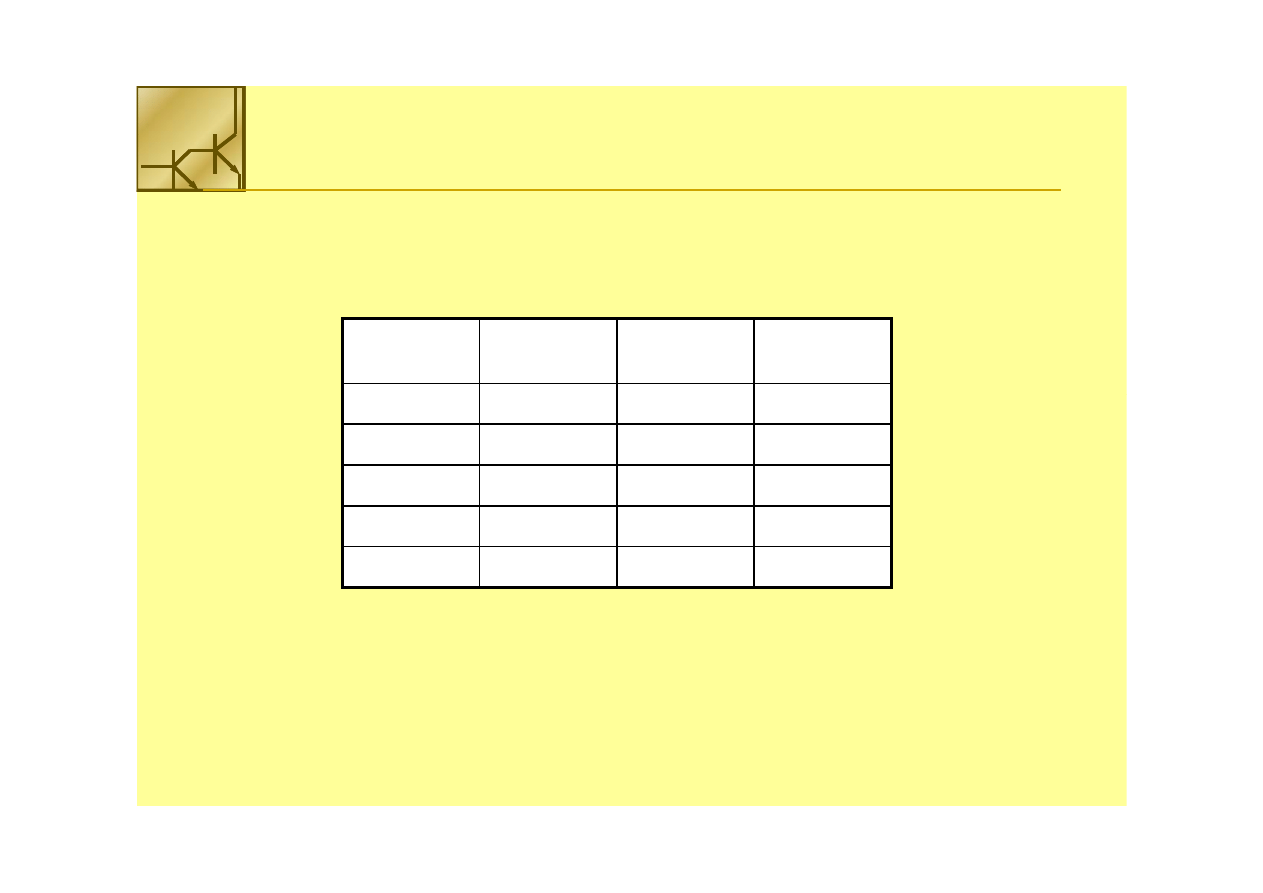
Kod z nadmiarem 3 (XS3)
3 (XS3)
Kod z nadmiarem
Kod z nadmiarem 3 (XS3)
3 (XS3)
W kodzie BCD (ang.
W kodzie BCD (ang. Binary
Binary coded
coded decimal
decimal) z nadmiarem 3
) z nadmiarem 3 liczenie zaczyna
liczenie zaczyna
się od 0011. Nie występuje cztery 0 lub cztery
się od 0011. Nie występuje cztery 0 lub cztery 1.
1.
Jest to kod
Jest to kod samouzupełniający
samouzupełniający
Cyfra
Cyfra
Kod X3
Kod X3
Cyfra
Cyfra
Kod X3
Kod X3
00
00
0011
11
55
1000
1000
Jest to kod
Jest to kod samouzupełniający
samouzupełniający..
00
00
0011
11
55
1000
1000
11
00100
100
66
1001
1001
22
00101
101
77
1010
1010
33
01
0110
10
88
11011
011
44
01
0111
11
99
11100
100
6 marca 2011
Wojciech Kucewicz
35
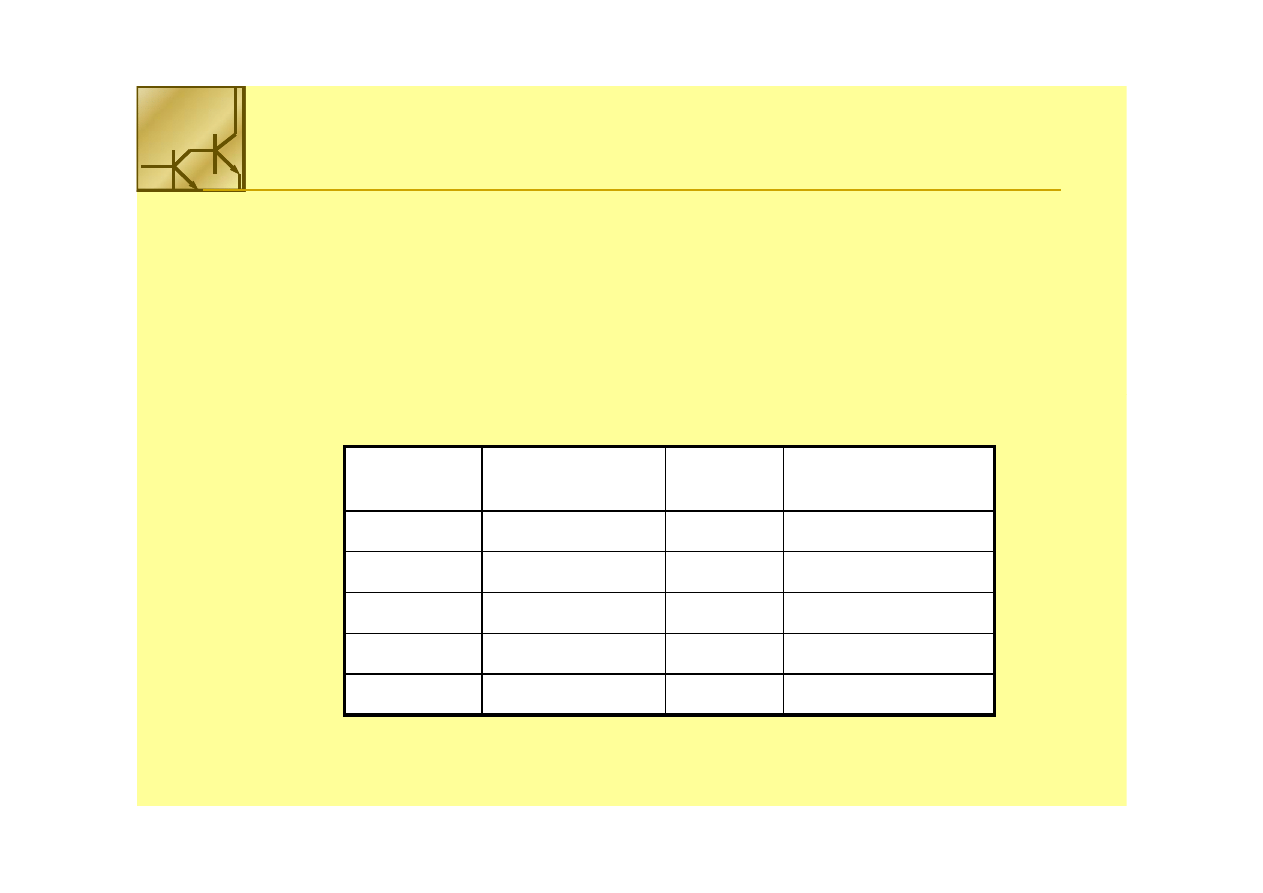
Kod
Kod 1 z 10
1 z 10
Kod
Kod 1 z 10
1 z 10
Kod 1 z 10 jest przykładem kodu k z n. Koncepcyjnie jest to kod do
Kod 1 z 10 jest przykładem kodu k z n. Koncepcyjnie jest to kod do
wprowadzania cyfr kodu dziesiętnego przez 10 dziesięć wzajemnie
wprowadzania cyfr kodu dziesiętnego przez 10 dziesięć wzajemnie
wyłączalnych klawiszy Stosowany jest powszechnie w relacjach człowiek
wyłączalnych klawiszy Stosowany jest powszechnie w relacjach człowiek--
wyłączalnych klawiszy. Stosowany jest powszechnie w relacjach człowiek
wyłączalnych klawiszy. Stosowany jest powszechnie w relacjach człowiek
układ cyfrowy.
układ cyfrowy.
W technice cyfrowej używa się określenia
W technice cyfrowej używa się określenia koder
koder, jako nazwy układu
, jako nazwy układu
służącego do przetwarzania liczb w kodzie 1 z 10
służącego do przetwarzania liczb w kodzie 1 z 10
Cyfra
Cyfra
Kod 1z10
Kod 1z10
Cyfra
Cyfra
Kod 1z10
Kod 1z10
ą g
p
ą g
p
00
00000000001
00000000001
55
0000010000
0000010000
11
00000000010
00000000010
66
0001000000
0001000000
22
00000000100
00000000100
77
0010000000
0010000000
33
0000001000
0000001000
88
0100000000
0100000000
44
0000010000
0000010000
99
1000000000
1000000000
6 marca 2011
Wojciech Kucewicz
36
44
0000010000
0000010000
99
1000000000
1000000000
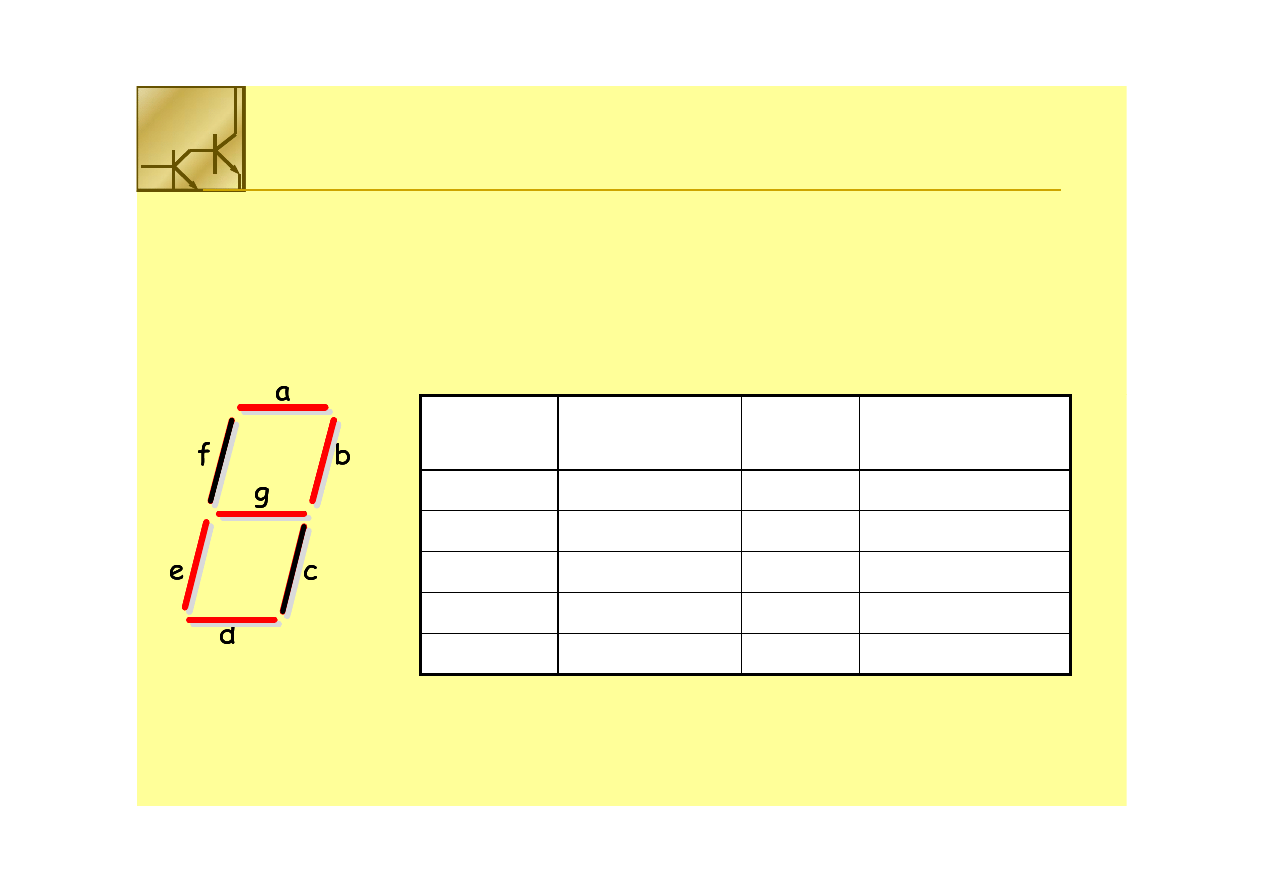
Kod
Kod 77--segmentowy
segmentowy
Kod
Kod 77--segmentowy
segmentowy
Kod 7
Kod 7--segmentowy służy do wyświetlania cyfr na wskaźniku 7
segmentowy służy do wyświetlania cyfr na wskaźniku 7--segmentowym.
segmentowym.
Każda cyfra jest tworzona przez „zapalenie” odpowiednich segmentów
Każda cyfra jest tworzona przez „zapalenie” odpowiednich segmentów
wskaźnika
wskaźnika
wskaźnika.
wskaźnika.
a
a
a
a
Cyfra
Cyfra
Kod 7
Kod 7--segm.
segm.
abcdefg
abcdefg
Cyfra
Cyfra
Kod 7
Kod 7--segm.
segm.
abcdefg
abcdefg
00
1111110
1111110
55
1011011
1011011
a
a
b
b
g
g
f
f
a
a
b
b
g
g
f
f
00
1111110
1111110
55
1011011
1011011
11
0110000
0110000
66
1011111
1011111
22
1101101
1101101
77
1110000
1110000
c
c
g
g
e
e
c
c
g
g
e
e
33
1111001
1111001
88
1111111
1111111
44
0110011
0110011
99
1111011
1111011
d
d
d
d
6 marca 2011
Wojciech Kucewicz
37

Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
Zapis liczb dwójkowych
Zapis liczb dwójkowych
Zapis liczb dwójkowych
Zapis liczb dwójkowych
p
j
y
p
j
y
ze znakiem
ze znakiem
p
j
y
p
j
y
ze znakiem
ze znakiem
6 marca 2011
Wojciech Kucewicz
38

Zapis dwójkowy ze znakiem
Zapis dwójkowy ze znakiem
Zapis dwójkowy ze znakiem
Zapis dwójkowy ze znakiem
W zbiorze liczb rzeczywistych istnieją liczby ujemne, które oznacza się
W zbiorze liczb rzeczywistych istnieją liczby ujemne, które oznacza się
znakiem minus (
znakiem minus (--).).
W dwójkowym systemie liczbowym znak liczby może być wprowadzony tylko
W dwójkowym systemie liczbowym znak liczby może być wprowadzony tylko
w postaci odrębnego
w postaci odrębnego
bitu znaku
bitu znaku
, którego wartość równa 1 reprezentuje
, którego wartość równa 1 reprezentuje
i
k
i
k ”
t ść 0 d
i d
k i ”
”
t ść 0 d
i d
k i ”
umownie znak „
umownie znak „--”, a wartość 0 odpowiada znakowi „+”.
”, a wartość 0 odpowiada znakowi „+”.
Istnieją trzy zasadnicze sposoby kodowania liczb dwójkowych ze znakiem:
Istnieją trzy zasadnicze sposoby kodowania liczb dwójkowych ze znakiem:
•• znak
znak--moduł (ZM)
moduł (ZM)
•• znak
znak--uzupełnienie do 1 (U 1)
uzupełnienie do 1 (U 1)
•• znak
znak--uzupełnienie do 2 (U 2)
uzupełnienie do 2 (U 2)
znak
znak uzupełnienie do 2 (U 2)
uzupełnienie do 2 (U 2)
6 marca 2011
Wojciech Kucewicz
39

Znak
Znak--uzupełnienie do
uzupełnienie do 9
9
Znak
Znak--uzupełnienie do
uzupełnienie do 9
9
Liczba ujemna
Liczba ujemna --53
53
jj
99
99 –– 53 = 46
53 = 46 Î
Î
uzupełnienie do 9
uzupełnienie do 9
99
99 53 46
53 46 uzupełnienie do 9
uzupełnienie do 9
83
83 –– 53 = 30
53 = 30
83 + 46 =
83 + 46 =
11
29
29 Î
Î
29 + 1 = 30
29 + 1 = 30
6 marca 2011
Wojciech Kucewicz
40

Znak
Znak--uzupełnienie do
uzupełnienie do 10
10
Znak
Znak--uzupełnienie do
uzupełnienie do 10
10
Liczba ujemna
Liczba ujemna --53
53
jj
100
100 –– 53 = 47
53 = 47 Î
Î
uzupełnienie do 10
uzupełnienie do 10
100
100 53 47
53 47 uzupełnienie do 10
uzupełnienie do 10
83
83 –– 53 = 30
53 = 30
83 + 47 = 130
83 + 47 = 130
X
X
6 marca 2011
Wojciech Kucewicz
41

Zapis dwójkowy w kodzie ZM
Zapis dwójkowy w kodzie ZM
Zapis dwójkowy w kodzie ZM
Zapis dwójkowy w kodzie ZM
Kod znak
Kod znak--moduł (ang.
moduł (ang. sign
sign--magnitude
magnitude) został utworzony przez dodanie bitu na
) został utworzony przez dodanie bitu na
k k d l b
k
l b
P
k k d l b
k
l b
P
początku każdej liczby reprezentującego znak liczby. Przyjmuje się, że
początku każdej liczby reprezentującego znak liczby. Przyjmuje się, że
gdy liczba jest ujemna, to wartość tego bitu jest równa 1, a dalsze bity
gdy liczba jest ujemna, to wartość tego bitu jest równa 1, a dalsze bity
reprezentują moduł liczby. Gdy liczba jest dodatnia, to wartość tego
reprezentują moduł liczby. Gdy liczba jest dodatnia, to wartość tego
bit j st ó
0
bit j st ó
0
bitu jest równa 0.
bitu jest równa 0.
Za pomocą
Za pomocą nn--bitowego
bitowego słowa (uwzględniając bit znaku) można przedstawić
słowa (uwzględniając bit znaku) można przedstawić
liczby z zakresu:
liczby z zakresu:
--(2
(2
nn--11
--1) ≤ L(A) ≤ +(2
1) ≤ L(A) ≤ +(2
nn--11
--1)
1)
(2
(2
1) ≤ L(A) ≤ +(2
1) ≤ L(A) ≤ +(2
1)
1)
6 marca 2011
Wojciech Kucewicz
42

Zapis dwójkowy ZM
Zapis dwójkowy ZM
Zapis dwójkowy ZM
Zapis dwójkowy ZM
--(2
(2
nn--11
--1) ≤ L(A) ≤ +(2
1) ≤ L(A) ≤ +(2
nn--11
--1)
1)
Np. za pomocą 8
Np. za pomocą 8--bitowego słowa (1
bitowego słowa (1 bajtu
bajtu) można przedstawiać liczby od
) można przedstawiać liczby od --127
127
do 127.
do 127.
Liczba
Liczba
12
12
będzie miała formę
będzie miała formę
00001100
00001100
Liczba
Liczba
--12
12
będzie miała formę
będzie miała formę
10001100
10001100
W zapisie ZM liczba zero może przyjmować dwie formy:
W zapisie ZM liczba zero może przyjmować dwie formy:
00000000 lub 10000000
00000000 lub 10000000
Podwójna reprezentacja O może stwarzać problemy przy realizacji
Podwójna reprezentacja O może stwarzać problemy przy realizacji
algorytmów arytmetycznych (wada).
algorytmów arytmetycznych (wada).
6 marca 2011
Wojciech Kucewicz
43

Zapis dwójkowy w kodzie U 1
Zapis dwójkowy w kodzie U 1
Zapis dwójkowy w kodzie U 1
Zapis dwójkowy w kodzie U 1
W kodzie uzupełnienia do 1 (ang. 1’s
W kodzie uzupełnienia do 1 (ang. 1’s complement
complement) liczby dodatnie
) liczby dodatnie
reprezentowane są jak w kodzie binarnym pod warunkiem, że najbardziej
reprezentowane są jak w kodzie binarnym pod warunkiem, że najbardziej
b
ść
b
b d
b
ść
b
b d
znaczący bit ma wartość 0. Liczby ujemne na najbardziej znaczącej pozycji
znaczący bit ma wartość 0. Liczby ujemne na najbardziej znaczącej pozycji
mają 1, a pozostałe bity mają przeciwne wartości niż w przypadku liczby
mają 1, a pozostałe bity mają przeciwne wartości niż w przypadku liczby
dodatniej.
dodatniej.
U
ł i i li b N k d i U1 j st li b C
U
ł i i li b N k d i U1 j st li b C
Uzupełnieniem liczby N w kodzie U1 jest liczba C:
Uzupełnieniem liczby N w kodzie U1 jest liczba C:
CC
U1
U1
= (2
= (2
nn
–– 1)
1) -- N
N
Za pomocą
Za pomocą nn--bitowego
bitowego słowa (uwzględniając bit znaku) można przedstawić
słowa (uwzględniając bit znaku) można przedstawić
liczby z zakresu:
liczby z zakresu:
--(2
(2
nn--11
--1) ≤ L(A) ≤ +(2
1) ≤ L(A) ≤ +(2
nn--11
--1)
1)
czyli podobnie jak kodzie ZM.
czyli podobnie jak kodzie ZM.
6 marca 2011
Wojciech Kucewicz
44
Zapis dwójkowy w kodzie U 1
Zapis dwójkowy w kodzie U 1
Zapis dwójkowy w kodzie U 1
Zapis dwójkowy w kodzie U 1
Liczba
Liczba
12
12
będzie miała formę
będzie miała formę
00001100
00001100
b
b
b d
f
b d
f
Liczba
Liczba
--12
12
będzie miała formę
będzie miała formę
11110011
11110011
Wartość ujemną wylicza się przez odjęcie modułu liczby od 2
Wartość ujemną wylicza się przez odjęcie modułu liczby od 2
nn
--11
--12 =
12 =
11 11 11 11 11 11 11 11
-- 00 00 00 00 11 11 00 00
-- 00 00 00 00 11 11 00 00
11 11 11 11 00 00 11 11
Liczba 0 ma także dwie reprezentacje: dodatnią
Liczba 0 ma także dwie reprezentacje: dodatnią –– 00000000
00000000
i ujemną
i ujemną -- 11111111
11111111
6 marca 2011
Wojciech Kucewicz
45

Zapis dwójkowy w kodzie U 2
Zapis dwójkowy w kodzie U 2
Zapis dwójkowy w kodzie U 2
Zapis dwójkowy w kodzie U 2
W kodzie uzupełnienia do 2 (ang. 2’s
W kodzie uzupełnienia do 2 (ang. 2’s complement
complement) liczby dodatnie
) liczby dodatnie
reprezentowane są jak w kodzie binarnym pod warunkiem, że najbardziej
reprezentowane są jak w kodzie binarnym pod warunkiem, że najbardziej
b
ść
b
k d
b
ść
b
k d
znaczący bit ma wartość 0. Liczba ujemna X w kodzie U2 reprezentowana
znaczący bit ma wartość 0. Liczba ujemna X w kodzie U2 reprezentowana
takim samym słowem jak liczba X+1 w kodzie U1.
takim samym słowem jak liczba X+1 w kodzie U1.
U
ł i i li b N k d i U2 j st li b C
U
ł i i li b N k d i U2 j st li b C
Uzupełnieniem liczby N w kodzie U2 jest liczba C:
Uzupełnieniem liczby N w kodzie U2 jest liczba C:
CC
U2
U2
= 2
= 2
nn
–– N =
N =
(2
(2
nn
–– 1)
1) -- N
N
+1 = C
+1 = C
U1
U1
+ 1
+ 1
Za pomocą
Za pomocą nn--bitowego
bitowego słowa (uwzględniając bit znaku) można przedstawić
słowa (uwzględniając bit znaku) można przedstawić
liczby z zakresu:
liczby z zakresu:
--22
nn--11
≤ L(A) ≤ +(2
≤ L(A) ≤ +(2
nn--11
--1)
1)
6 marca 2011
Wojciech Kucewicz
46
Zapis dwójkowy w kodzie U 2
Zapis dwójkowy w kodzie U 2
Zapis dwójkowy w kodzie U 2
Zapis dwójkowy w kodzie U 2
Np. za pomocą 8
Np. za pomocą 8--bitowego słowa (1
bitowego słowa (1 bajtu
bajtu) można przedstawiać liczby od
) można przedstawiać liczby od --128
128
do 127.
do 127.
Liczba
Liczba
12
12
będzie miała formę
będzie miała formę
00001100
00001100
Liczba
Liczba
--12
12
będzie miała formę
będzie miała formę
11110100
11110100
Wartość ujemną wylicza się przez odjęcie modułu liczby od liczby 2
Wartość ujemną wylicza się przez odjęcie modułu liczby od liczby 2
nn
--12 =
12 =
11 00 00 00 00 00 00 00 00
-- 00 00 00 00 11 11 00 00
11 11 11 11 00 11 00 00
Liczba 0 ma tylko jedną reprezentację: 00000000
Liczba 0 ma tylko jedną reprezentację: 00000000
6 marca 2011
Wojciech Kucewicz
47
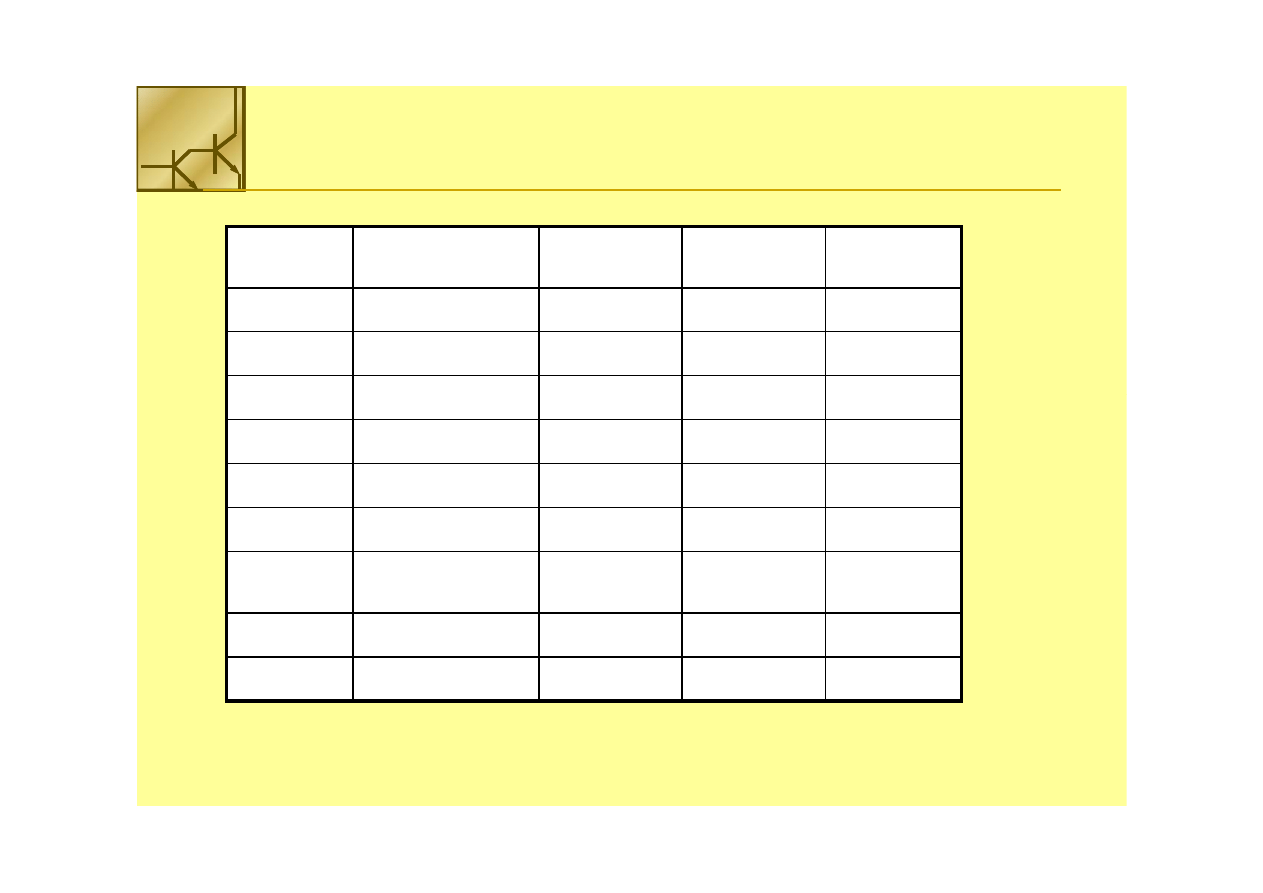
Reprezentacja liczb w różnych
Reprezentacja liczb w różnych
zapisach
zapisach
Reprezentacja liczb w różnych
Reprezentacja liczb w różnych
zapisach
zapisach
Liczba
Liczba
dziesiętna
dziesiętna
Liczba
Liczba
heksadecymalna
heksadecymalna
ZM
ZM
U1
U1
U2
U2
--128
128
80
80
--
--
1000 0000
1000 0000
--127
127
81
81
1111 1111
1111 1111
1000 0000
1000 0000
1000 0001
1000 0001
64
64
C0
C0
1100 0000
1100 0000
1101 11111
1101 11111
1100 0000
1100 0000
--64
64
C0
C0
1100 0000
1100 0000
1101 11111
1101 11111
1100 0000
1100 0000
--16
16
F0
F0
1001 0000
1001 0000
1110 1111
1110 1111
1111 0000
1111 0000
--22
FE
FE
1000 0010
1000 0010
1111 1101
1111 1101
1111 1110
1111 1110
--11
FF
FF
1000 0001
1000 0001
1111 1110
1111 1110
1111 1111
1111 1111
00
00
0000 0000
0000 0000
1000 0000
1000 0000
0000 0000
0000 0000
1111 1111
1111 1111
0000 0000
0000 0000
1000 0000
1000 0000
1111 1111
1111 1111
11
11
0000 0001
0000 0001
0000 0001
0000 0001
0000 0001
0000 0001
127
127
7F
7F
0111 1111
0111 1111
0111 1111
0111 1111
0111 1111
0111 1111
6 marca 2011
Wojciech Kucewicz
48

Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
Dodawanie
Dodawanie
Dodawanie
Dodawanie
liczb binarnych
liczb binarnych
liczb binarnych
liczb binarnych
yy
ze znakiem
ze znakiem
yy
ze znakiem
ze znakiem
ze znakiem
ze znakiem
ze znakiem
ze znakiem
6 marca 2011
Wojciech Kucewicz
49
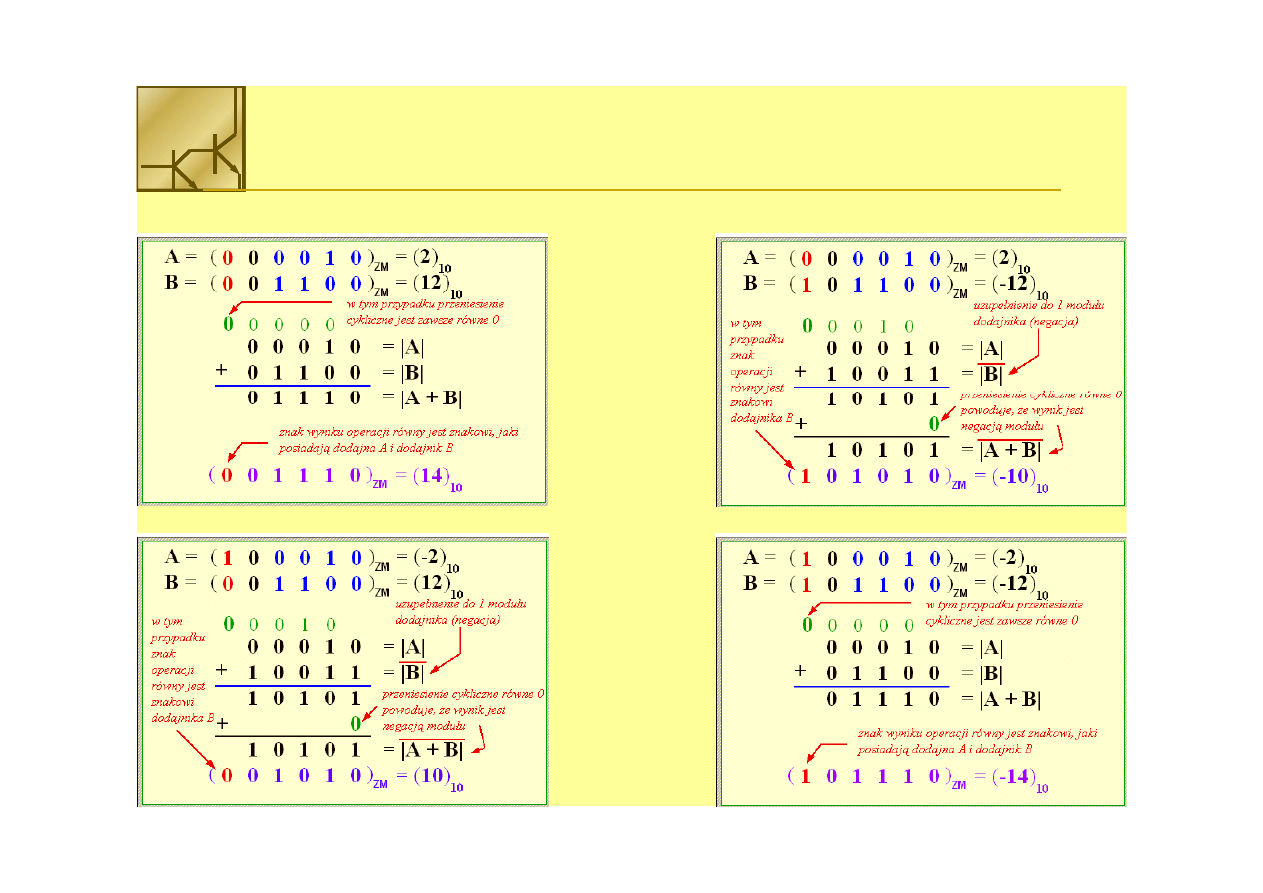
Dodawanie liczb w kodzie ZM
Dodawanie liczb w kodzie ZM
Dodawanie liczb w kodzie ZM
Dodawanie liczb w kodzie ZM
Liczby A i B są dodatnie
Liczby A i B są dodatnie
Liczba A>0 a liczba B<0
Liczba A>0 a liczba B<0
Liczba A<0 a liczba B>0
Liczba A<0 a liczba B>0
Liczby A i B są ujemne
Liczby A i B są ujemne
6 marca 2011
Wojciech Kucewicz
50
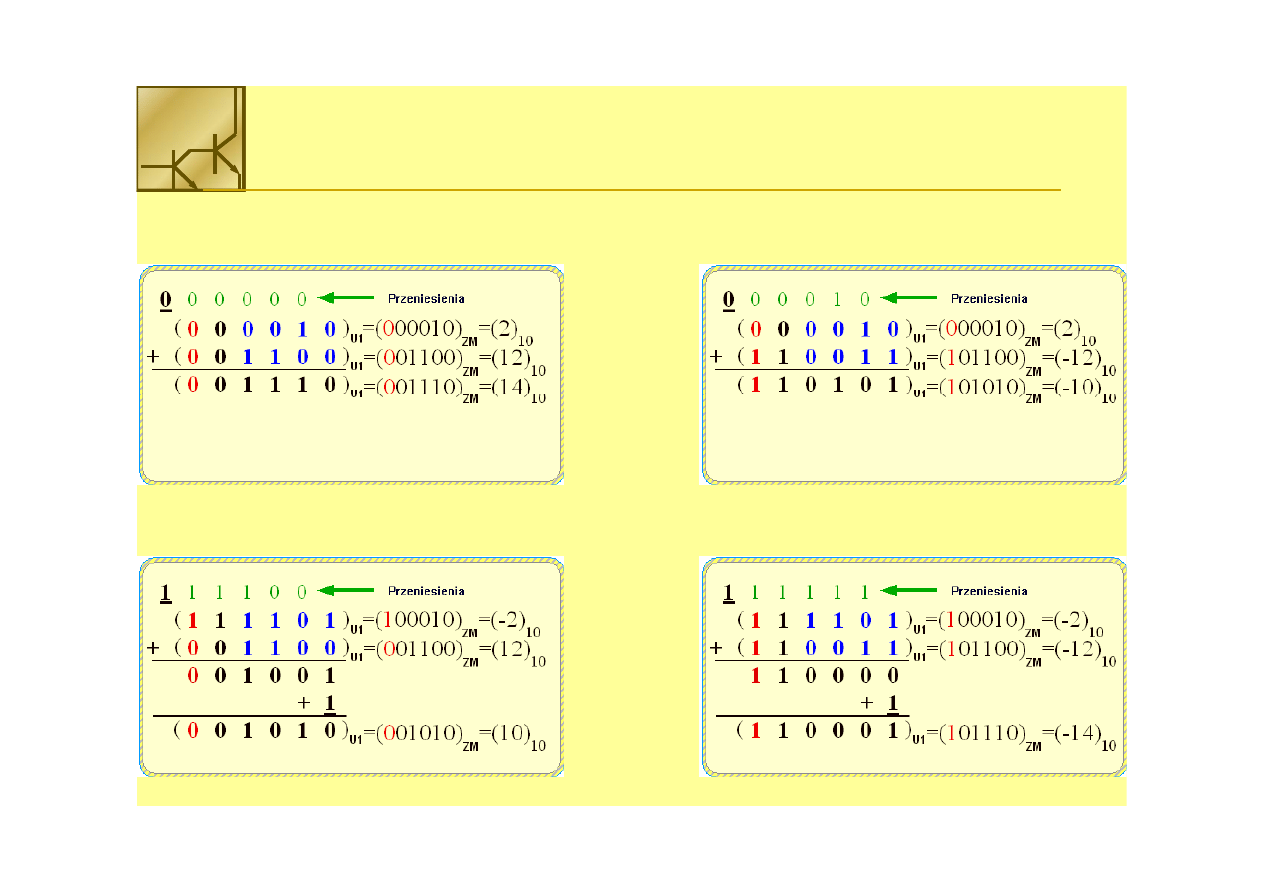
Dodawanie liczb w kodzie U1
Dodawanie liczb w kodzie U1
Dodawanie liczb w kodzie U1
Dodawanie liczb w kodzie U1
Liczby A i B są dodatnie
Liczby A i B są dodatnie
Liczba A>0 a liczba B<0
Liczba A>0 a liczba B<0
Liczba A<0 a liczba B>0
Liczba A<0 a liczba B>0
Liczby A i B są ujemne
Liczby A i B są ujemne
6 marca 2011
Wojciech Kucewicz
51
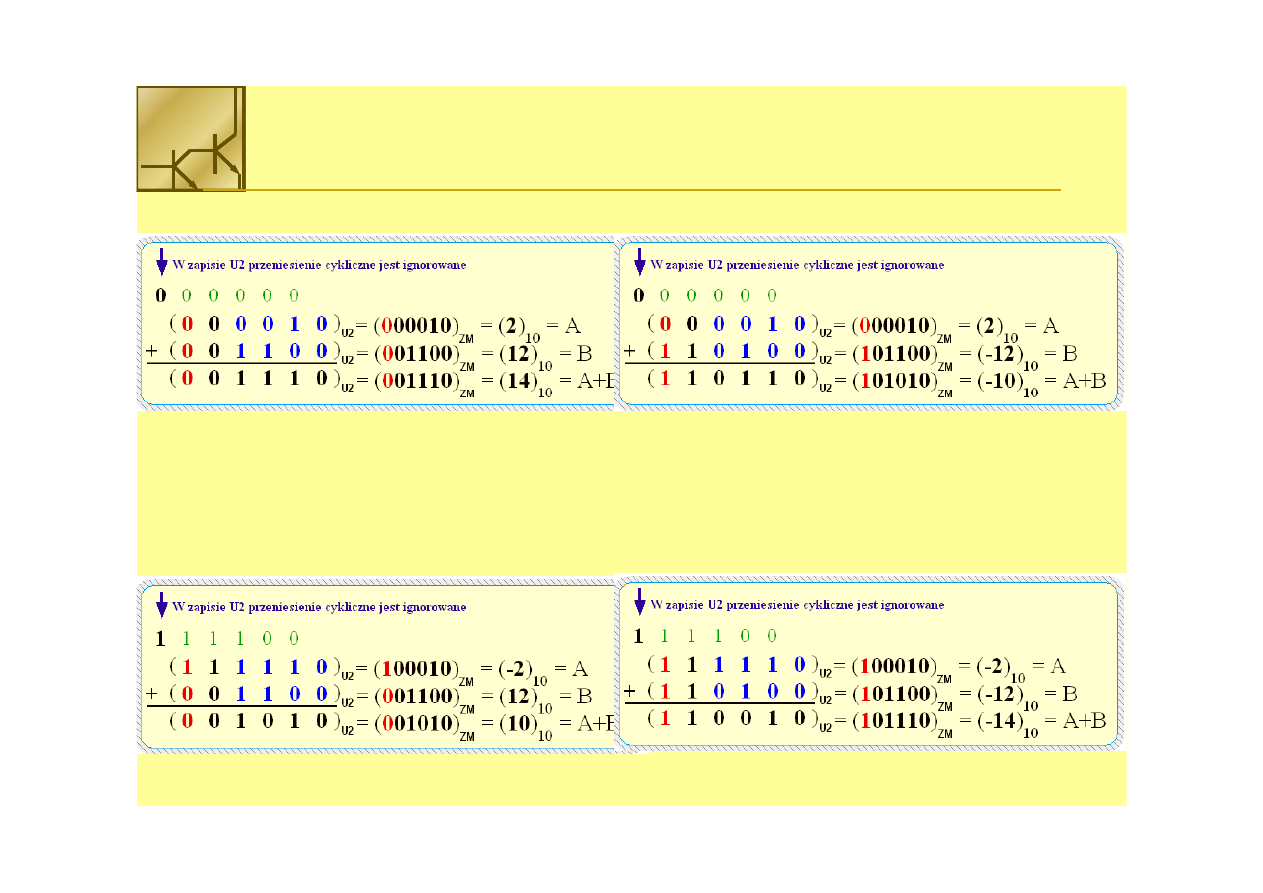
Dodawanie liczb w kodzie U2
Dodawanie liczb w kodzie U2
Dodawanie liczb w kodzie U2
Dodawanie liczb w kodzie U2
Liczby A i B są dodatnie
Liczby A i B są dodatnie
Liczba A>0 a liczba B<0
Liczba A>0 a liczba B<0
Liczba A<0 a liczba B>0
Liczba A<0 a liczba B>0
Liczby A i B są ujemne
Liczby A i B są ujemne
6 marca 2011
Wojciech Kucewicz
52

Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
Cyfrowy zapis informacji
Liczby
Liczby
Liczby
Liczby
yy
zmiennoprzecinkowe
zmiennoprzecinkowe
yy
zmiennoprzecinkowe
zmiennoprzecinkowe
6 marca 2011
Wojciech Kucewicz
53

Liczby zmiennoprzecinkowe
Liczby zmiennoprzecinkowe
Liczby zmiennoprzecinkowe
Liczby zmiennoprzecinkowe
Omawiane do tej pory liczby były przedstawiane w tak zwanej
Omawiane do tej pory liczby były przedstawiane w tak zwanej
reprezentacji stałoprzecinkowej (
reprezentacji stałoprzecinkowej (fixed
fixed point
point notation
notation) w której
) w której
reprezentacji stałoprzecinkowej (
reprezentacji stałoprzecinkowej (fixed
fixed--point
point notation
notation), w której
), w której
położenie kropki jest stałe niezależne od wielkości liczb.
położenie kropki jest stałe niezależne od wielkości liczb.
P
kł d
f
t 8
P
kł d
f
t 8 bit
li b ż
i ć
t
j
bit
li b ż
i ć
t
j
Przykładowo format 8
Przykładowo format 8--bitowy liczby można zapisać następująco:
bitowy liczby można zapisać następująco:
XXXX.XXXX
XXXX.XXXX
J
l l b
d
d
f
d b
J
l l b
d
d
f
d b
Jeżeli liczby wprowadzone do tego formatu znacznie się od siebie
Jeżeli liczby wprowadzone do tego formatu znacznie się od siebie
różnią np.
różnią np.
A=1234,00 i B=0,0005579
A=1234,00 i B=0,0005579
to wiąże się to z dużym błędem
to wiąże się to z dużym błędem
obcięcia liczby B:
obcięcia liczby B:
A = 1234,0000
A = 1234,0000
B = 0000,0005
B = 0000,0005
6 marca 2011
Wojciech Kucewicz
54

Liczby zmiennoprzecinkowe
Liczby zmiennoprzecinkowe
Liczby zmiennoprzecinkowe
Liczby zmiennoprzecinkowe
Aby uniknąć błędów zapisu reprezentacji stałoprzecinkowej (
Aby uniknąć błędów zapisu reprezentacji stałoprzecinkowej (fixed
fixed
point
point notation
notation), stosuje się również zmiennoprzecinkowy zapis liczb
), stosuje się również zmiennoprzecinkowy zapis liczb
((floating
floating poit
poit notation
notation))
((floating
floating--poit
poit notation
notation))
Reprezentację zmiennoprzecinkową liczby L definiuje się jako
Reprezentację zmiennoprzecinkową liczby L definiuje się jako
ł ż i d ó h łó M i W
ł ż i d ó h łó M i W
złożenie dwóch słów M i W
złożenie dwóch słów M i W
L = M *
L = M * pp
W
W
gdzie
gdzie
słowo M (mantysa)
słowo M (mantysa)
–– liczba ułamkowa ze znakiem
liczba ułamkowa ze znakiem
słowo W (wykładnik)
słowo W (wykładnik) –– liczba całkowita ze znakiem
liczba całkowita ze znakiem
yy
pp
-- podstawa kodu zastosowane do zapisu M i W
podstawa kodu zastosowane do zapisu M i W
Przykładowo liczby
Przykładowo liczby
A=1234,0 i B=0,0005579
A=1234,0 i B=0,0005579
można zapisać:
można zapisać:
6 marca 2011
Wojciech Kucewicz
55
y
y
y
y
,
,
,
,
m
p
m
p
A = 0,1234 * 10
A = 0,1234 * 10
44
B = 0,5579 * 10
B = 0,5579 * 10
--33

Liczby zmiennoprzecinkowe
Liczby zmiennoprzecinkowe
Liczby zmiennoprzecinkowe
Liczby zmiennoprzecinkowe
Istotną zaletą reprezentacji zmiennoprzecinkowej jest duży zakres
Istotną zaletą reprezentacji zmiennoprzecinkowej jest duży zakres
liczb które można w ten sposób przedstawić
liczb które można w ten sposób przedstawić
liczb, które można w ten sposób przedstawić.
liczb, które można w ten sposób przedstawić.
W przypadku 4 bitowej mantysy i wykładnika, można przedstawić
W przypadku 4 bitowej mantysy i wykładnika, można przedstawić
li b k
i
li b k
i
liczby w zakresie:
liczby w zakresie:
0,0000 * 10
0,0000 * 10
0000
0000
≤ L ≤ 0.9999 * 10
≤ L ≤ 0.9999 * 10
9999
9999
Liczby binarne można przedstawiać w kodzie ZM, U1 lub U2
Liczby binarne można przedstawiać w kodzie ZM, U1 lub U2
0,0000 * 2
0,0000 * 2
0000
0000
≤ L ≤ 0.1111 * 2
≤ L ≤ 0.1111 * 2
1111
1111
6 marca 2011
Wojciech Kucewicz
56

Liczby zmiennoprzecinkowe
Liczby zmiennoprzecinkowe
Liczby zmiennoprzecinkowe
Liczby zmiennoprzecinkowe
Dodawanie liczb zmiennoprzecinkowych wymaga najpierw wyrównania
Dodawanie liczb zmiennoprzecinkowych wymaga najpierw wyrównania
wykładników a następnie właściwa operację dodawania wykonuje się
wykładników a następnie właściwa operację dodawania wykonuje się
wykładników, a następnie właściwa operację dodawania wykonuje się
wykładników, a następnie właściwa operację dodawania wykonuje się
na mantysach jak na stałoprzecinkowych liczbach ze znakiem.
na mantysach jak na stałoprzecinkowych liczbach ze znakiem.
W celu wyrównania wykładników mniejszy z nich odejmuje się od
W celu wyrównania wykładników mniejszy z nich odejmuje się od
i k
i
t
i
t
i j
i
i k
i
t
i
t
i j
i
większego i mantysę związaną z tym mniejszym przesuwa się w prawo
większego i mantysę związaną z tym mniejszym przesuwa się w prawo
o liczbę pozycji równą otrzymanej różnicy. Wynik jest sumą mantys
o liczbę pozycji równą otrzymanej różnicy. Wynik jest sumą mantys
z większym wykładnikiem.
z większym wykładnikiem.
Dodanie liczb binarnych A=0,1101*2
Dodanie liczb binarnych A=0,1101*2
1000
1000
i i B=0,1011*2
B=0,1011*2
0101
0101
wykonujemy
wykonujemy
następująco:
następująco:
jj
1000
1000 –– 0101 = 0011
0101 = 0011
(3)
(3)
B=0,
B=0,
000
000
1011
1011
A B
A B (0 1101000 0 0001011)*2
(0 1101000 0 0001011)*2
1000
1000
0 1111
0 1111
011
*2
*2
1000
1000
011
011
6 marca 2011
Wojciech Kucewicz
57
A+B
A+B = (0,1101000 + 0,0001011)*2
= (0,1101000 + 0,0001011)*2
1000
1000
=0,1111
=0,1111
011
*2
*2
1000
1000
011
011
Wyszukiwarka
Podobne podstrony:
F1 1 Cyfrowy zapis informacji
Internet jako zrodlo informacji Nieznany
biblioteki cyfrowe ocena, Informacja Naukowa i Bibliotekoznawstwo, Materiały
1f Cyfrowe przetwarzanie sygnal Nieznany
Bikony cyfrowe id 85673 Nieznany (2)
Program Strategiczny informacje Nieznany
Grafika inzynierska Informatyka Nieznany
Konstytucyjne prawo do informac Nieznany
Automatyka nkf cyfrowe id 62906 Nieznany (2)
E1Cyfrowy zapis informacji
30 31 ROZ w spr informacji Nieznany (2)
Reprezentacja cyfrowa analogowa informacji
EkonomiaMiedzynarodowa informa Nieznany
Zadanie udzielenia informacji o Nieznany
IO2Cyfrowy zapis informacji
03 Wykorzystanie technik inform Nieznany (2)
więcej podobnych podstron