L

ABORATORIUM FIZYCZNE

Instytut Fizyki Politechniki Krakowskiej

ĆWICZENIE

24

Analiza spektralna gazów

Ćwiczenie 24

2

ĆWICZENIE

24

Analiza spektralna gazów

Barbara Oleś

1.

Wprowadzenie

Celem ćwiczenia jest zapoznanie studentów z techniką spektroskopii optycznej oraz zastoso-

waniem jej do identyfikacji nieznanych gazów.

1.1

Kwantowanie energii promieniowania elektromagnetycznego i
energii atomów

Promieniowanie elektromagnetyczne jest formą energii, która rozprzestrzenia się w postaci oscy-

lującego pola elektromagnetycznego. Składowe tego pola, wzajemnie się przenikające zmienne pola
elektryczne i magnetyczne, są zawsze prostopadłe zarówno do siebie, jak i do kierunku rozchodzenia
się promieniowania.

W niektórych zjawiskach promieniowanie możemy trak-

tować jak falę elektromagnetyczną

1

, ale w oddziaływaniu z

materią w skali atomowej wykazuje ono naturę cząsteczko-
wą, inaczej

korpuskularną

. Pochłanianie (absorpcję)i wysy-

łanie (emisję) promieniowania przez materię można zrozu-
mieć wówczas, gdy traktuje się go jak strumień cząstek zwa-
nych

fotonami

, z których każdy niesie ściśle określoną por-

cję, czyli

kwant

energii związanej z częstotliwością promie-

niowania wzorem

= ℎ , (1)

gdzie

ℎ = 6,626

⋅

10

−

34

J

⋅

s jest to

stała Plancka

, uniwersalna

stała fizyczna.

Promieniowanie, w szczególności światło, jest absorbo-

wane lub emitowane przez ciała tylko w postaci w postaci
porcji energii określonych wzorem (1).

Energie atomów i cząsteczek są również

skwantowane

, czyli przyjmują tylko określone dyskretne

wartości, które nazywamy

poziomami energetycznymi

. Jeśli ich energia przyjmuje najniższą wartość,

mówimy, że znajdują się w stanie podstawowym. Atom (lub cząsteczka) może pochłonąć kwant ener-
gii i przejść do stanu o wyższej energii, czyli stać się atomem wzbudzonym. Musi być przy tym speł-
niony warunek, że energia, jaką niesie foton

ℎ odpowiada różnicy energii ∆ pomiędzy poziomami

energetycznymi atomu, wzbudzonym i podstawowym

∆ = ℎ . (2)

1

Do zrozumienia zjawisk np. interferencji i dyfrakcji światła wystarczy klasyczna teoria falowa oparta na rów-

naniach Maxwella. W teorii tej światło traktuje się jak falę elektromagnetyczną.

Promieniowanie elektroma-

gnetyczne obejmuje bardzo sze-
roki zakres częstotliwości, od ok.
100 Hz do 10

23

Hz (nie istnieje

dolna ani górna granica zakresu).
Dzielimy go na: fale radiowe,
charakteryzujące się najmniej-
szymi częstotliwościami, następ-
nie mikrofale i promieniowanie
podczerwone, światło widzialne
stanowiące wąski przedział czę-
stotliwości od ok. 4,3

⋅

10

14

Hz do

7,5

⋅

10

14

Hz (co odpowiada dłu-

gościom fali od ok. 400 nm do
700 nm), promieniowanie nadfio-
letowe, promieniowanie rentge-
nowskie i gamma.

Analiza spektralna gazów

3

Obserwacje częstotliwości promieniowania absorbowanego i emitowanego przez atomy i mole-

kuły pokazują, że procesy zachodzą tylko przy pewnych dyskretnych częstotliwościach, co jest po-
twierdzenie kwantowania energii promieniowania oraz energii cząstek.

1.2

Klasyfikacja widm optycznych

Jeśli wiązkę światła o różnych częstotliwościach (czyli i długościach fal), przepuścimy przez pry-

zmat lub siatkę dyfrakcyjną, to uzyskamy jego rozszczepienie na poszczególne częstotliwości.

Rozkład natężenia promieniowania elektromagnetycznego emitowanego lub absorbowanego

przez ciała jako funkcji częstotliwości (lub długości fali ) nazywamy

widmem

.

Detekcją i analizą promieniowania emitowanego lub pochłanianego przez obiekty fizyczne zaj-

muje się

spektroskopia

. Do otrzymania widm stosuje się przyrządy zwane spektroskopami lub spek-

trometrami. W przypadku widm z zakresu widzialnego podstawowym elementem tych przyrządów
jest siatka dyfrakcyjna lub pryzmat.

Ciała stałe, ciecze i gazy pod dużym ciśnieniem podgrzane do odpowiednio wysokiej temperatury

emitują światło, którego widmo określamy mianem

widma ciągłego

, ponieważ są w nim obecne

wszystkie częstotliwości promieniowania z zakresu widzialnego, a także nadfioletu i podczerwieni.
Przykład widma ciągłego widzimy na rys.1.

Widmo atomowe

składa się z szeregu linii, wyraźnie oddzielonych od siebie, które odpowiadają

częstotliwościom promieniowania wysłanego lub pochłoniętego podczas zmiany energii atomu o
Δ

=

Δ

ℎ lub =

ℎ

Δ , gdzie = . (3)

Widma takie określamy mianem

widm liniowych

, a ich przykłady przedstawia rys.2a.

W cząsteczkach wieloatomowych energie poziomów niewiele różnią się między sobą, zatem

przejścia wewnątrz zespołów takich poziomów dają całe serie bardzo blisko siebie leżących linii wid-
mowych, tworzących pasma. Są to tzw.

widma pasmowe

(rys.2b).

Pobudzenie próbki substancji do emisji promieniowania można osiągnąć w wyniku wyładowań

iskrowych, w łukach elektrycznych, metodą termiczną przez podgrzewanie oraz w wyniku zderzeń z
elektronami towarzyszącymi wyładowaniom w rozrzedzonych gazach. Ta ostatnia metoda znalazła
zastosowanie w tzw. rurkach Geisslera, które są stosowane w naszym ćwiczeniu. Otrzymane w ten
sposób widma nazywamy

widmami emisyjnymi

.

Jeśli promieniowanie o widmie ciągłym przechodzi przez ciało, które pochłania określone często-

tliwości promieniowania, to w obszarze widzialnym pojawiają się ciemne prążki lub pasma na tle

Rys.1. Widmo ciągłe – barwy przechodzą płynnie jedna w drugą. Źródłem
takiego widma może być rozżarzone, świecące włókno żarówki

Ćwiczenie 24

4

widma ciągłego. Powstaje w ten sposób

widmo absorpcyjne

. Dla atomów i prostych molekuł położe-

nie linii absorpcyjnych pokrywa się z odpowiednimi liniami emisyjnymi.

Każdy pierwiastek posiada swoje charakterystyczne

widmo atomowe, które pozwala go zidentyfikować. Oprócz
tego natężenie linii widmowych zależy od ilości atomów
emitujących (absorbujących) promieniowanie. Stąd spektro-
skopia jest niezastąpionym narzędziem w nauce, medycynie
i przemyśle do określania składu chemicznego oraz ilościo-
wego substancji. W fizyce i chemii jest wykorzystywana do
badania atomowych oraz cząsteczkowych poziomów ener-
getycznych i struktury cząsteczek. Techniki spektralne po-
zwalają na określenie składu chemicznego oraz ruchów od-
ległych ciał niebieskich.

1.3

Widma liniowe

Wśród widm liniowych na szczególną uwagę zasługuje widmo atomowe wodoru, najprostszego

pierwiastka zbudowanego tylko z jednego protonu – jądra i elektronu. Współczesna fizyka (mechani-
ka kwantowa) podaje dokładne rozwiązanie modelu tego atomu i dostarcza informacje o dozwolo-
nych energiach oraz o rozmieszczeniu elektronu wokół jądra (strukturze elektronowej). Według po-
dejścia kwantowego przypisywanie elektronowi ruchu po kołowych orbitach, jak to ma miejsce w
modelu Bohra, jest niepoprawne. Można wyliczyć jedynie prawdopodobieństwo, z jakim cząstka ta
znajdzie się w pewnej odległości od jądra. Wyznaczona energia atomu wodoru

2

zależy od kwadratu

liczby kwantowej , przyjmującej wartości całkowite i możemy podać ją wzorem

= −

ℎ

, (4)

gdzie

ℎ to stała Plancka, – szybkość światła w próżni, - stała Rydberga

3

,

= 1, 2, 3, …. .

2

Takie samo wyrażenie na energię otrzymuje się rozwiązując model atomu wodoru Bohra.

3

Stała wyraża się poprzez zredukowaną masę atomu

, ładunek elementarny !, stałą Plancka ℎ, szybkość

światła i przenikalność elektryczną próżni

"

#

:

= !

$

/(8"

#

ℎ

'

).

N

Xe

Rys.2. a. Emisyjne widma liniowe (atomowe) azotu i ksenonu. b. Widmo pasmowe (molekularne) azotu

|

|

|

|

400 [nm] 500

600 700

(a)

(b)

N

2

Przykładem widma absorpcyjne-
go jest widmo Słońca, na które
składają się tzw. linie Fraunhofe-
ra. Promieniowanie słoneczne o
ciągłym

widmie

przechodząc

przez chłodniejsze warstwy at-
mosfery otaczającej gwiazdę, jest
w niej selektywnie pochłaniane.
Na podstawie widma absorpcyj-
nego określono skład atmosfery
Słońca, m.in. obecność helu.

Analiza spektralna gazów

5

Podstawiając wyrażenie na energię dane wzorem (4) do wzoru (2) otrzymamy energię fotonu

wyemitowanego przez atom wodoru przy przejściu ze wzbudzonego stanu kwantowego o energii

(

do stanu kwantowego o energii

)

*+,+ -

=

ℎ

= ℎ .

1

−

1

/

0, (5)

gdzie

2

= 1, 2, 3, …. .

Ze wzoru (5) wyznaczamy odwrotność długości fali

1

= .

1

−

1

/

0 (6)

i możemy teoretycznie przewidzieć, z jakich linii składa się widmo atomu wodoru.

Dla atomów wieloelektronowych, nawet dla atomu helu posiadającego tylko dwa elektrony, do-

kładne rozwiązania równań kwantowych nie istnieją. Struktura ich poziomów energetycznych jest
znacznie bardziej skomplikowana niż w przypadku atomu wodoru. Informacje o strukturze elektro-
nowej i energiach stanów kwantowych tych atomów możemy otrzymać analizując ich widma liniowe.

2.

Metoda pomiaru

Celem pomiarów jest analiza spektralna gazów. Jednym ze sposobów otrzymania widm emisyj-

nych jest przepuszczenie prądu elektrycznego przez rozrzedzone gazy zamknięte w przezroczystych
rurkach, zwanych rurkami Geisslera i pobudzenie ich do świecenia. Ponieważ atomy posiadają ściśle
określony układ poziomów energetycznych, charakterystyczny dla danego pierwiastka, widma gazów
jednoatomowych różnią się między sobą długością fali (częstotliwością) i natężeniem. Pozwala to na
identyfikację rodzaju atomów emitujących promieniowanie przez porównanie uzyskanych w pomia-
rze widm z liniami widmowymi umieszczonymi w tabelach widm pierwiastków.

2.1

Zasada działania spektroskopu

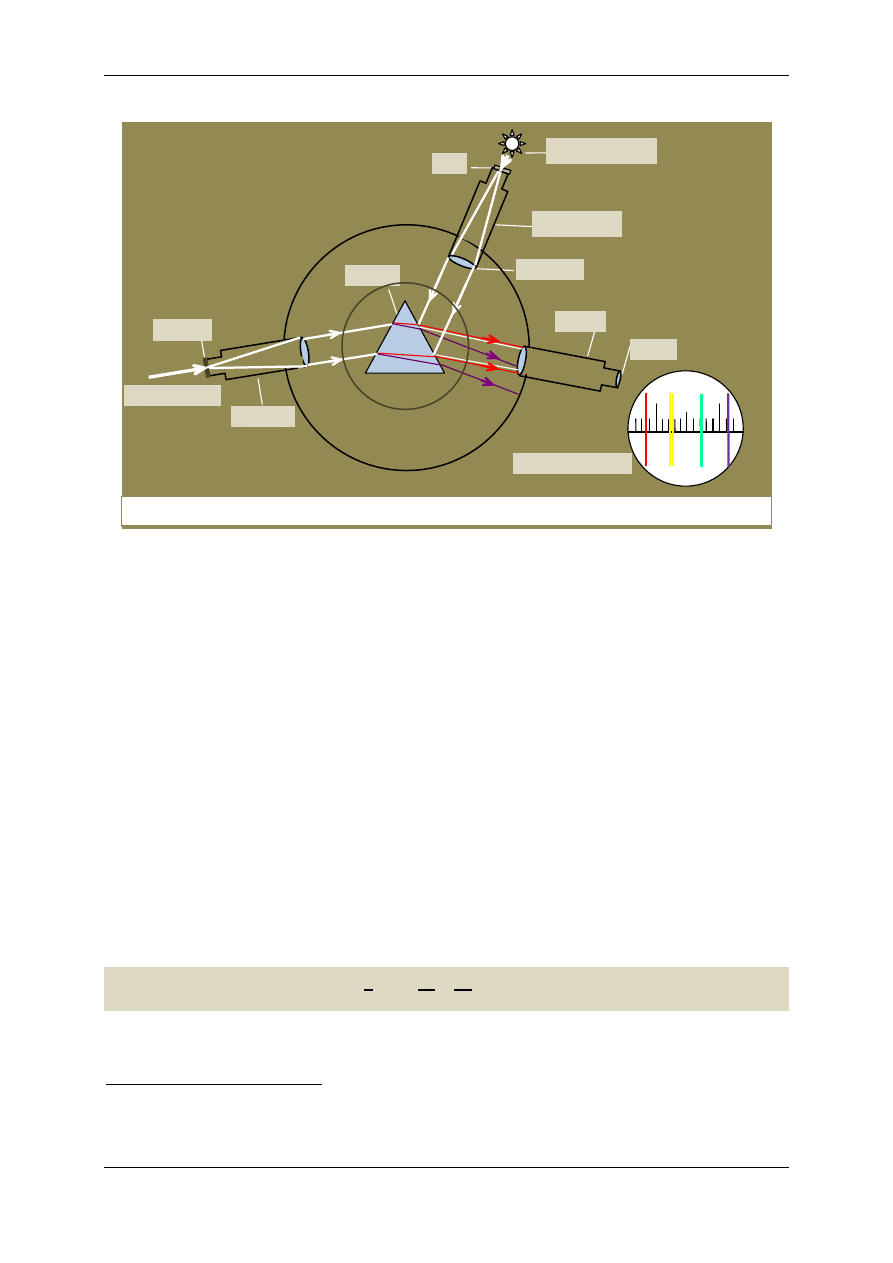
Do otrzymania widm posłużymy się spektroskopem pryzmatycznym, którego schemat przedsta-

wia rys.3. Składa się on z pryzmatu, kolimatora, lunety i rurki ze skalą złożonych na stoliku.

Kolimator jest poczernioną wewnątrz rurką, na której jednym końcu znajduje się szczelina o regu-

lowanej szerokości, a na drugim soczewka skupiająca. Zadaniem kolimatora jest zamiana rozbieżnej
wiązki światła padającej na szczelinę na wiązkę równoległą. Ta równoległa wiązka światła pada na-
stępnie na pryzmat i wnikające do niego światło ulega rozszczepieniu, ponieważ różne długości fal
załamują się pod różnymi kątami

4

. Z pryzmatu wychodzi szereg wiązek równoległych, o różnych bar-

wach, odpowiadających różnym długościom fali, które trafiają one do obiektywu lunety. W lunecie, w
płaszczyźnie ogniskowej obiektywu powstaje szereg rzeczywistych, pomniejszonych i odwróconych
obrazów szczeliny – linii widmowych, które oglądamy przez okular działający jak lupa.

4

Szybkość światła rozchodzącego się w ośrodku

4 jest różna dla różnych długości fali. Stąd współczynnik zała-

mania światła przez ośrodek, zdefiniowany wzorem

= /4 również zależy od długości fali. Światło wnikające

do ośrodka zmienia kierunek rozchodzenia się (z wyjątkiem padania prostopadłego na powierzchnię ośrodka), a
kąt załamania zależy od współczynnika załamania ośrodka i spełnia prawo Snellusa.

Ćwiczenie 24

6

Ustalenie położenia poszczególnych linii widmowych jest możliwe, jeśli są one widoczne na tle

skali. W tym celu spektroskop zaopatrzono w rurkę, na której jednym końcu, oświetlonym światłem
żaróweczki, zamocowana jest podziałka. Podziałka znajduje się w ognisku soczewki umieszczonej na
drugim końcu rurki, a światło, które przeszło przez soczewkę, zamieniane jest na wiązkę równoległą.
Wiązka ta pada na pryzmat i część światła odbitego od pryzmatu wchodzi do lunety, dając w płasz-
czyźnie ogniskowej obiektywu rzeczywisty, odwrócony obraz skali. Patrząc przez okular widzimy jed-
nocześnie linie widmowe i skalę.

Skala spektroskopu nie jest sporządzona w jednostkach pozwalających wprost na odczyt długości

fali. Dlatego przed przystąpieniem do badania widm nieznanych gazów należy spektroskop wycecho-
wać za pomocą widma znanej substancji. Pozwala to otrzymać krzywą dyspersji spektroskopu, czyli
wykres zależności długości fali od położenia jej na skali spektroskopu. Za pomocą krzywej dyspersji
można znaleźć długość każdej linii widmowej, jeśli tylko odczytamy jej położenie na skali.

2.2

Wyznaczanie stałej Rydberga

Widmo wodoru należy do najprostszych widm atomowych. W zakresie widzialnym składają się na

niego cztery linie: czerwona, niebieska i dwie fioletowe, wchodzące w skład tzw. serii Balmera. Moż-
na dla niego podać empiryczny wzór

5

łączący odwrotność długości fali z numerami poziomów energe-

tycznych atomu wodoru, pomiędzy którymi zachodzi przejście elektronu

1

= .

1

2 −

1

2

0,

2

= 3, 4, 5, 6, … (7)

gdzie jest to stała Rydberga,

2

−

liczba kwantowa.

5

Ten empiryczny wzór na odwrotność długości fali w widmie wodoru podał Rydberg, zanim jeszcze powstała

teoria wyjaśniająca zjawiska oddziaływania promieniowania z atomami. Porównanie wzoru (7) ze wzorem (6)
wynikającym z kwantowego modelu atomu wodoru pokazuje, że intuicja nie zawiodła Rydberga.

Rys.3. Schemat spektroskopu pryzmatycznego

skala

pryzmat

rurka ze skalą

oświetlenie skali

badane światło

kolimator

soczewka

szczelina

luneta

okular

widok przez okular

10

11

Analiza spektralna gazów

7

W serii Balmera, obejmującej grupę linii z obszaru widzialnego i bliskiego nadfioletu przejścia za-

chodzą ze wzbudzonych poziomów energetycznych, numerowanych tzw. liczbą kwantową

2

na po-

ziom energetyczny, któremu odpowiada

2

= 2.

Znając długości fal linii widmowych odpowiadające liczbom kwantowym

2

można ze wzoru 6

wyznaczyć stałą Rydberga.

3.

Wykonanie ćwiczenia

3.1

Cechowanie spektroskopu

Zapoznaj się z elementami aparatury używanej w pomiarach, której fotografia przedstawiona jest

na rys.4. Do cechowania spektroskopu użyjemy widma rtęci, które w obszarze widzialnym składa się z
kilkunastu wyraźnych linii widmowych.

Studentom nie wolno samodzielnie regulować spektroskopu. O ustawienie
lampy rtęciowej należy poprosić opiekuna ćwiczenia.

1.

Zanim przystąpisz do pomiarów oświetl szczelinę spektroskopu światłem zwykłej żarówki
i obserwuj przez lunetę otrzymane widmo. Zanotuj swoje spostrzeżenia.

2.

Zwróć się do opiekuna ćwiczenia, aby ustawił lampę rtęciową przed szczeliną kolimatora,
oraz sprawdził oświetlenie i ustawienie skali.
Przy prawidłowym ustawieniu powinieneś widzieć wąskie, wyraźne linie widmowe na tle
również wyraźnych (nierozmytych) linii podziałki. Ostrość obrazu można poprawić przez
wsuwanie i wysuwanie tubusu okularu.

3.

Odczytaj położenia linii widmowych na skali. Zanotuj kolor linii, jej intensywność i poło-
żenie w tabeli.

4.

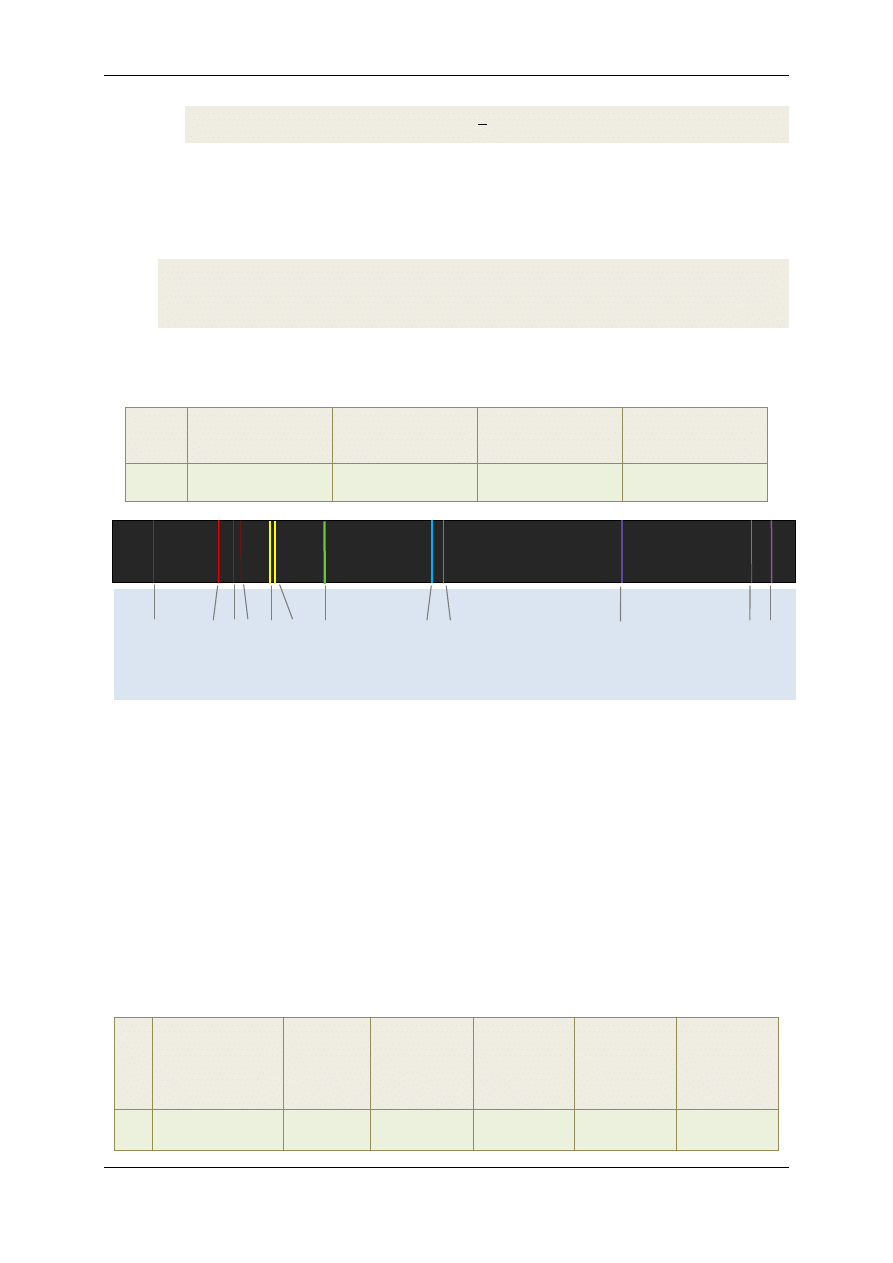
Przyporządkuj każdej linii odpowiadającą jej długość fali posługując się diagramem przed-
stawionym na rys.5.

5.

Korzystając z programu WykresLab sporządź krzywą cechowania spektroskopu. Wpro-
wadź do programu położenia linii

6 oraz długości fali , a następnie do danych pomiaro-

wych dopasuj funkcję

lampa

lampa rtęciowa

kolimator

luneta

rurka ze

skalą

Rys.4. Aparatura używana podczas pomiarów

Ćwiczenie 24

8

7 =

8

6 + :, (8)

Przyjrzyj się otrzymanemu wykresowi – punkty pomiarowe powinny leżeć na dopasowa-
nej krzywej teoretycznej lub w niewielkiej od niej odległości. Jeśli tak nie jest, należy
sprawdzić, czy nie został popełniony błąd podczas odczytu położenia linii lub przyporząd-
kowania długości fali.

6.

Wydrukuj wykres krzywej cechowania. Parametry dopasowania krzywej teoretycznej
umieszczone na wykresie pozwolą na obliczenie długości fal linii widmowych nieznanych
gazów.

7.

Wyłącz lampę rtęciową.

3.2

Identyfikacja nieznanych gazów na podstawie widm

1.

Usuń lampę rtęciową, a w jej miejsce wstaw rurkę Geisslera z pierwszym gazem. Rurkę należy
podłączyć do induktora uważając, aby nie dotknąć przewodów wysokiego napięcia.

2.

Patrząc przez okular ustaw położenie obudowy z rurką tak, aby otrzymać wyraźne i jasne linie
widmowe (w przypadku trudności w ustawieniu rurki, zwróć się do opiekuna ćwiczenia).

3.

Zanotuj położenia wszystkich linii widmowych w Tabeli 2.

4.

Powyższe czynności powtórz dla pozostałych rurek Geisslera, pamiętając o wyłączaniu induk-
tora podczas przełączania rurek.

Tabela 1. Linie widmowe rtęci

L.p.

Położenie linii

6

[jednostki skali]

Barwa linii

Intensywność

(słaba, średnia, silna)

Długość fali

[nm]

Tabela 2. Linie widmowe nieznanego gazu

L.p.

Położenie linii na

skali

6 [jedn.skali]

Barwa

Intensywność

Obliczona

długość fali

[nm]

Obliczona

niepewność

;( ) [nm]

Dopasowana

długość fali z

tablic

[nm]

Widmo rtęci

6

90

.7

6

23

.4

6

12

.3

6

07

.3

5

79

.1

5

77

.0

5

46

.1

4

99

.2

4

91

.6

4

35

.8

4

07

.8

4

04

.7

Rys.5. Diagram linii widmowych rtęci obserwowanych w ćwiczeniu z przypisanymi im długościami fali

Analiza spektralna gazów

9

4.

Obliczenia

4.1

Identyfikacja nieznanych gazów

1.

Oblicz długości fal korzystając ze współczynników dopasowania

8, : (wzór 8) otrzymanych dla

krzywej cechowania w p.3.5 i podstawiając je do wzoru

=

8

6 + :. (9)

Wpisując obliczone do Tabeli 2 powinieneś dokonać poprawnego zaokrąglenia wartości

liczbowych, co możesz zrobić dopiero po oszacowaniu niepewności pomiaru

.

Ogranicz się najpierw do obliczenia trzech linii (np. linii skrajnych i środkowej z pierwszego
widma), a następnie oblicz standardową niepewność złożoną

;

=

( ) pomiaru długości fali

tych linii

6

. Będziesz mógł się wówczas zorientować, ile miejsc dziesiętnych należy zachować

w obliczanych wartościach .

Ponieważ wyprowadzenie wzoru na niepewność złożoną wymaga znajomości pochodnych

7

,

skorzystaj z podanego poniżej gotowego wzoru

;

=

( ) = >?−

8

6 @ ;

A

(6) + B

1

6C ;

D

(8) + ;

D

(:) (10)

Wyniki wpisz do Tabeli 2.

2.

Wykonaj obliczenia długości fal wszystkich pozostałych linii widmowych.

3.

Używając tablic linii widmowych rozpoznaj nieznane gazy.

4.2

Wyznaczanie stałej Rydberga

1.

Wykorzystaj wartości długości fali odpowiadające liniom widmowym wodoru do obli-
czenia stałej Rydberga występującej w teoretycznym wzorze (7).

W tym celu dla każdej z trzech obserwowanych linii oblicz odwrotność długości fali

F/

oraz

G = .

1

2 −

1

2

0.

Ze wzoru (7) widać, że

F/

zależy liniowo od

G (

F/

= G). Zatem można zastosować

metodę regresji liniowej i dopasować teoretyczną funkcję liniową

7 = 86 do naszych da-

6

Jeśli do obliczeń używasz programu Excel, to nie dużym wysiłkiem możesz obliczyć niepewność każdej długości

fali.

7

Ogólny wzór na niepewność złożoną pomiaru długości fali ma postać:

;

=

( ) = >B

H

H6C ;

A

(6) + B

H

H8C ;

D

(8) + B

H

H:C ;

D

(:) .

Ćwiczenie 24

10

nych doświadczalnych. Wyliczona wartość współczynnika kierunkowego

8 będzie równa

szukanej wartości stałej Rydberga .

2.

Wprowadź wartości

F/

oraz

G do programu WykresLab a następnie sporządź wykres i

zapisz obliczoną stałą Rydberga wraz z jej niepewnością.

5.

Dyskusja wyników

1.

Zapisz swoje obserwacje dotyczące widma żarówki.

2.

Oceń dokładność dopasowania obserwowanych linii widmowych do linii widmowych z tablic.

3.

Porównaj wartość wyznaczonej stałej Rydberga z wartością tablicową. Zastanów się, co może
być powodem rozbieżności między tymi wartościami, o ile taka wystąpiła.

4.

Zastanów się, jakie błędy mogły wystąpić w trakcie pomiarów i czy można było ich uniknąć.

6.

Uzupełnienia

Pierwszym modelem, który pozwalał wyjaśnić widmo wodoru, był

model Bohra

. Model ten łączył

elementy fizyki klasycznej z ideą kwantowania wielkości fizycznych. Bohr przyjął, że elektron porusza
się wokół jądra po orbitach kołowych (jak cząstka klasyczna), na których nie wypromieniowuje ener-
gii. Nie wszystkie orbity są jednak dozwolone, a tylko te, na których spełniony jest warunek kwanto-
wania momentu pędu elektronu, tj. może on przyjmować wartości będące wielokrotnością

ℎ/2I

(

J4K = ℎ/2I, = 1,2, …). W modelu tym energia elektronu jest skwantowana, tj. każdej dozwo-

lonej orbicie odpowiada pewna wartość energii elektronu dana wzorem

= − .

2I JL !

$

ℎ

0

1

, = 1, 2, 3, …

który możemy zapisać w postaci

= −ℎ

1

,

gdzie

= (2I JL !

$

)/(ℎ

'

) = 1.097 373 156 852 7 (73) × 10

N

m

F/

to stała Rydberga (cyfry w

nawiasie podają niepewność dwóch ostatnich miejsc dziesiętnych).

Atom może oddawać (lub pochłaniać) energię w postaci promieniowania tylko podczas przejścia

pomiędzy dwoma orbitami (wzór (5)). Z tego ostatniego postulatu Bohra otrzymuje się długości fal
emitowanego (absorbowanego) promieniowania dane wzorem (6).

Tabela 3. Wyznaczanie stałej Rydberga z linii widmowych wodoru

L.p.

Barwa linii

Obliczona dłu-

gość fali

[nm]

Odwrotność

długości fali

F/

[m

−1

]

G = .

1

2 −

1

2

0.

,

;( )

[m

−

1

]

1.

2.

3.

Analiza spektralna gazów

11

Teoria Bora potrafiła przewidzieć linie obserwowane w widmie atomu wodoru oraz jednoelek-

tronowych jonów, np. He

+

, Li

2+

, itp. Zawodziła natomiast przy próbach zastosowania jej do atomów

wieloelektronowych. Współczesna fizyka traktuje elektron jak cząstkę kwantową, która nie może się
poruszać po dobrze określonych torach kołowych. Obecnie do cząstek w skali atomowej, w tym ato-
mu wodoru stosuje się metody obliczeniowe oparte na prawach mechaniki kwantowej, a model
Bohra ma głównie znaczenie poglądowe.

7.

Literatura

[1] J.Brzezowska, Analiza spektralna gazów w pracy zbiorowej pod redakcją B.Oleś i M.Duraj, Ćwicze-
nia laboratoryjne z fizyki, cz.1, Wydawnictwo PK, 2008.
[2] D.Halliday, R.Resnick, J.Walker, Podstawy fizyki, t.5, PWN, 2007.
[3] P.W.Atkins, Chemia fizyczna, PWN, 2001.

Spis treści

1.

Wprowadzenie ................................................................................................................................ 2

1.1

Kwantowanie energii promieniowania elektromagnetycznego i energii atomów ................. 2

1.2

Klasyfikacja widm optycznych ................................................................................................. 3

1.3

Widma liniowe ......................................................................................................................... 4

2.

Metoda pomiaru ............................................................................................................................. 5

2.1

Zasada działania spektroskopu ................................................................................................ 5

2.2

Wyznaczanie stałej Rydberga .................................................................................................. 6

3.

Wykonanie ćwiczenia ...................................................................................................................... 7

3.1

Cechowanie spektroskopu ...................................................................................................... 7

3.2

Identyfikacja nieznanych gazów na podstawie widm ............................................................. 8

4.

Obliczenia ........................................................................................................................................ 9

4.1

Identyfikacja nieznanych gazów .............................................................................................. 9

4.2

Wyznaczanie stałej Rydberga .................................................................................................. 9

5.

Dyskusja wyników ......................................................................................................................... 10

6.

Uzupełnienia .................................................................................................................................. 10

7.

Literatura ....................................................................................................................................... 11