
Ekonometria – ćwiczenia 11 z 24-03-2001 r.
1
Ekonometria – ćwiczenia nr 11 z dnia 24-03-2001 r.
Interpretacja parametrów funkcji produkcji i funkcji popytu. Klasyfikacja zmiennych
w modelu wielorównaniowym.
Zadanie 1.
Oszacowana funkcja produkcji ma postać:
7
,
0
2
,
0
^
0
,
10
M
Z
Y
=
gdzie:
Y- wielkość produkcji
M – wartość majątku produkcyjnego
Z – wielkość zatrudnienia
Proszę odpowiedzieć:
1. o ile wzrośnie wartość produkcji, jeśli wielkość majątku produkcyjnego wzrośnie o
1% ?
2. o ile procent wzrośnie wartość majątku aby przy spadku zatrudnienia o 1% wartość
produkcji utrzymała się na niezmienionym poziomie ?
Odp. 1.
Wartość produkcji wzrośnie o 0,7 %
Odp. 2.
W tym przypadku należy skorzystać z definicji stopy substytucji
29
,
0
7
,
0
2
,
0
−
=
−
=
−
=
−
=
M
Z
j
i
x
x
a
a
a
a
E
j
i
(minus nie jest wartością lecz określa kierunki substytucji)
Jeżeli zatrudnienie spadnie o 1% to majątek winien wzrosnąć o 0,29% aby produkcja nie ule-
gła zmianie.
Zadanie 2.
W pewnym przedsiębiorstwie oszacowana funkcja produkcji typu Cop-Douglasa i otrzymano
wynik:
5
,
0
45
,
0
^
8
,
51
Z
M
P
=
P – produkcja globalna
M- majątek produkcyjny brutto
Z – średnia w roku wielkość zatrudnienia
Proszę określić o ile procent zmieni się zespołowa wydajność pracy jeśli zatrudnienie wzro-
śnie o 5%, a wartość majątku trwałego nie ulegnie zmianie?
Z
Z
M
P
:
/
8
,
51
5
,
0
45
,
0
^
=
5
,
0
45
,
0
^
^
8
,
51
−
=
=
Z
M
Z
P
W
W - spadnie o –2,5%

Ekonometria – ćwiczenia 11 z 24-03-2001 r.
2
Jeśli Z wzrośnie o 5% to W zmieni się o –2,5%
%
5
,
2
)
5
,
0
(
*
%
5
−
=
−
Precyzyjniejsze obliczenia:
(
)
[
]
%
41
,
2
%
100
*
1
05
,
0
1
%
100
*
1
1
5
,
0
−
=
−
+
=
−
∆
+
=
∆
−
β
Z
Z
W
W
Co oznacza, że W spadnie 0 2,41%
Zadanie 3.
Proszę obliczyć elastyczność cenową popytu funkcji:
p
e
cp
D
1
0
γ
γ
=
gdzie: D – popyt
p - cena
D
p
dp
dD
p
dp
D
dD
E
p
*
:
=
=
( )
( )
(
)
(
)
(
)
1
1
0
1
1
0
1
1
0
1
1
0
0
0
0
0
1
0
0
1
1
0
1
0
1
0
1
0
*
*
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
+
=
+
=
=
+
=
+
=
′
+
′
=
−
−
−
−
p
e
cp
p
p
p
ce
p
p
ce
e
cp
e
p
c
e
cp
e
cp
dp
dD
p
p
p
p
p
p
p
(
)
p
e
cp
p
p
e
cp
E
p
p
p
1
0
1
1
0
1
0
1
0
*
γ
γ
γ
γ
γ
γ
γ
γ
+
=
+
=
−
Rozważaną wyżej funkcję można uogólnić:
!
........
6
2
3
3
2
2
0
1
n
p
p
p
e
cp
D
n
n
p
γ
γ
γ
γ
γ
+
+
+
+
=
Wtedy elastyczność cenowa popytu wyniesie:
!
..
..........
6
2
3
3
2
2
1
0
n
p
p
p
p
E
n
n
p
γ
γ
γ
γ
γ
+
+
+
+
+
=
Zadanie 4.
Dany jest następujący model:
3
3
1
33
1
31
31
2
2
22
23
1
1
1
11
13
ε
γ
γ
γ
β
ε
γ
γ
β
ε
γ
γ
β
+
+
+
+
=
+
+
+
=
+
+
+
=
−
−
−
t
t
t
t
t
t
t
t
t
t
K
P
I
K
P
K
Z
P
K
I
a) proszę dokonać klasyfikacji zmiennych ze względu na ich rolę w modelu oraz właści-
wości formalne statystyczne
b) proszę podać postać strukturalną modelu w zapisie macierzowym

Ekonometria – ćwiczenia 11 z 24-03-2001 r.
3
odp. a)
- Podział ze względu na rolę zmiennych w modelu:
zmienne endogeniczne
I, Z, K
zmienne egzogeniczne
P, X
- Podział ze względu na właściwości formalno statystycze:
zmienne łącznie współdzielne I
t
, Z
t
, K
t
zmienne z góry ustalone
P
t-1
, P
t
, K
t-1
, X
t
odp. b)
postać strukturalna w zapisie algebraicznym:
3
3
1
33
1
31
31
2
2
22
23
1
1
1
11
13
ε
γ
γ
γ
β
ε
γ
γ
β
ε
γ
γ
β
=
−
−
−
−
=
−
−
−
=
−
−
−
−
−
−
t
t
t
t
t
t
t
t
t
t
K
P
I
K
P
K
Z
P
K
I
postać strukturalna w zapisie macierzowym:
Ε
=
Γ
+
Z
BY
−
−
−
=
1
0
1
0
0
1
3
2
1
31
23
13
β
β
β
B
K
Z
I
t
t
t
−
−
−
−
−
−
−
=
Γ
−
−
3
33
31
2
22
1
1
1
1
1
0
0
0
0
0
3
2
1
γ
γ
γ
γ
γ
γ
γ
t
t
t
t
X
K
P
P
=
Ε
3
2
1
ε
ε
ε
=
−
−
t
t
t
t
X
K
P
P
Z
1
1
Ε
=
Γ
+
Z
BY
=
−
−
−
−
−
−
−
+
−
−
−
−
−
3
2
1
1
1
3
33
31
2
22
1
1
1
31
23
13
0
0
0
0
0
1
0
1
0
0
1
ε
ε
ε
γ
γ
γ
γ
γ
γ
γ
β
β
β
t
t
t
t
t
t
t
X
K
P
P
K
Z
I
Ekonometria – ćwiczenia 11 z 24-03-2001 r.
4
Zadanie domowe
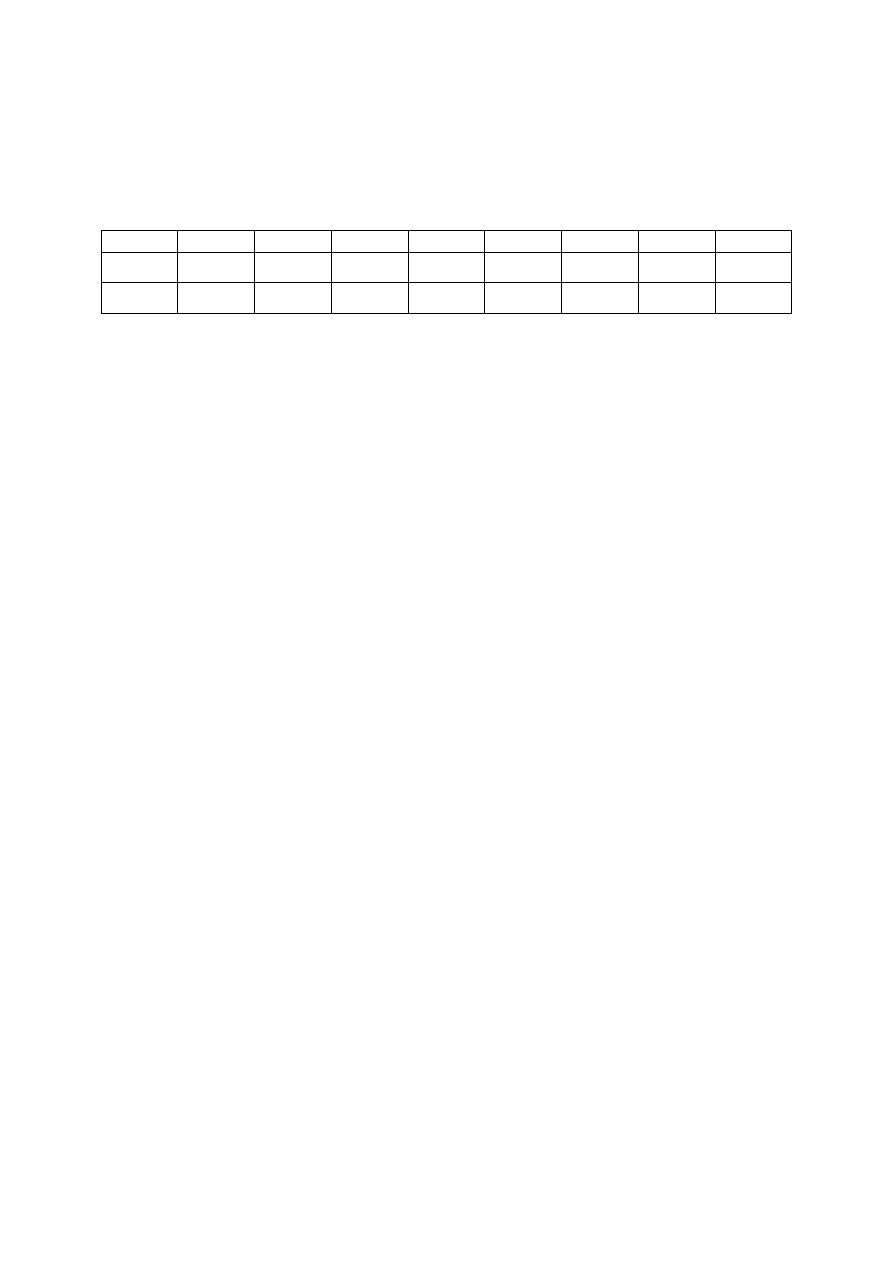
Ilość sprzedanych lodówek w dziesiątkach tysięcy sztuk oraz doprowadzone do porównywal-
ności średnioroczne ceny w setkach złotych uzyskiwane za jedną lodówkę w latach 1992-
1999 przedstawia tabela:
92 93 94 95 96 97 98 99
d
t
10
10
2
10
10
2
10
2
10
3
10
2
10
3
P
t
10
4
10
4
10
3
10
3
10
3
10
2
10
3
10
2
Zakładając, że zależność ceny i popytu ma charakter potęgowy proszę oszacować parametry
modelu opisującego zmiany popytu, ocenić ich istotność na poziomie istotności
γ
= 0,05 oraz
obliczyć współczynnik determinacji modelu opisującego zależność popytu od ceny.
Wyszukiwarka
Podobne podstrony:
Ekonometria ćwiczenia z 24 02 2001
Ekonometria ćwiczenia z 10 03 2001
Ekonometria-ćwiczenia z 10-03-2001
Ekonometria-ćwiczenia z 28-04-2001
Ekonometria-ćwiczenia z 24-09-2000
5 Ekonomia Koszty (24 03 2011)
W1 Wprowadzenie do Ekonomiki Budownictwa 24 03 2011 NOWA
Ekonometria ćwiczenia z 07 04 2001
Ekonometria ćwiczenia z 24 09 2000
mat fiz 2001 24 03
wykład 5- (29. 03. 2001), Ekonomia, Studia, I rok, Finanase publiczne, Wykłady-stare, Wykłady
wykład 2- (08. 03. 2001), Ekonomia, Studia, I rok, Finanase publiczne, Wykłady-stare, Wykłady
FINANSE PUBLICZNE I RYNKI FINANSOWE 24.03.2013, III rok, Ćwiczenia, Finanse publiczne i rynki finans
Ćwiczenia 7 z dn 24 kwietnia 2001
więcej podobnych podstron