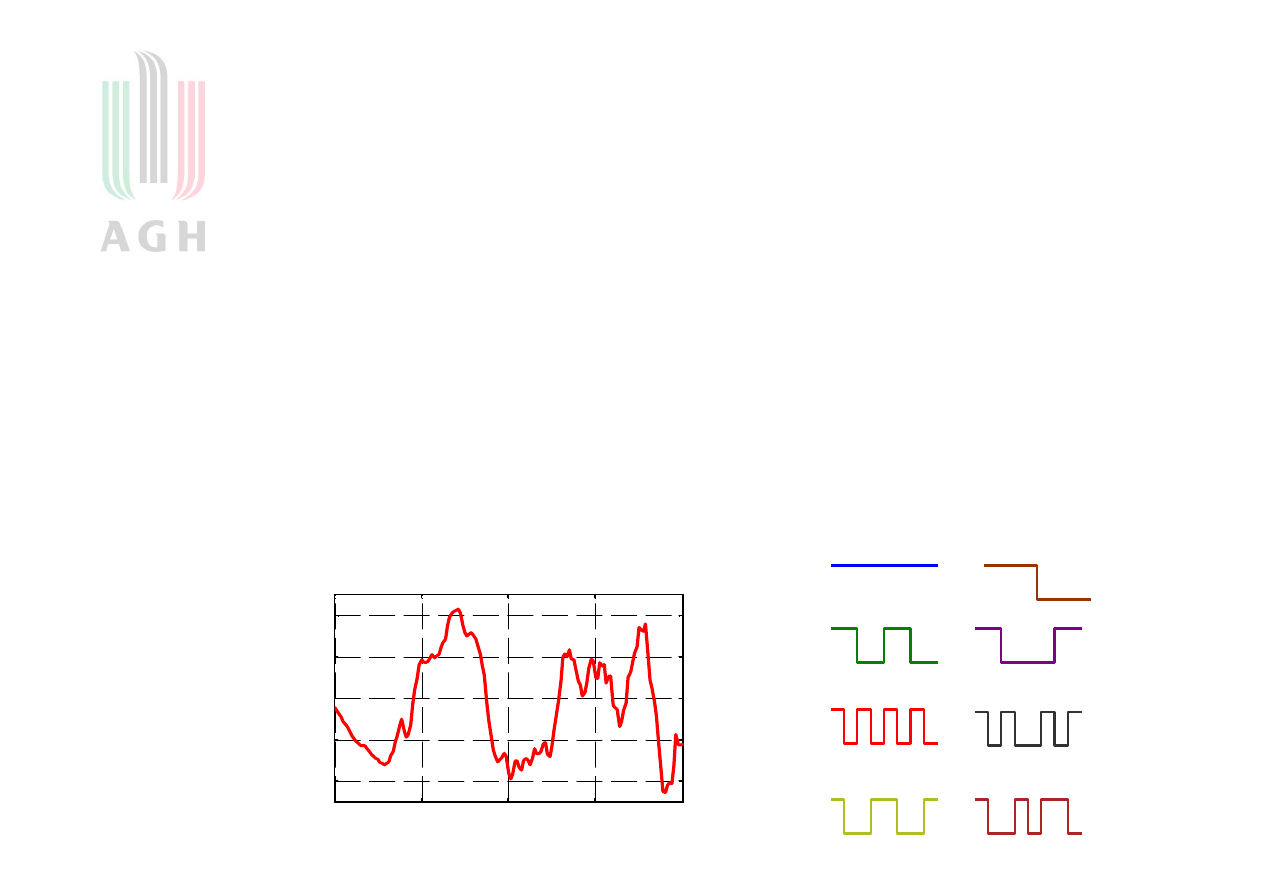
1
REPREZENTACJA SYGNAŁÓW
Spis treści:
1. Bazy sygnałów.
2. Procedura ortonormalizacyjna.
3. Wielomiany, funkcje Haara i Walsha, funkcje
gięte, trygonometryczne.
4. Sygnały dwuargumentowe.
0 .2 1
0 .2 1 5
0 .2 2
0 .2 2 5
0 .2 3
-0 .2
-0 .1
0
0 .1
0 .2
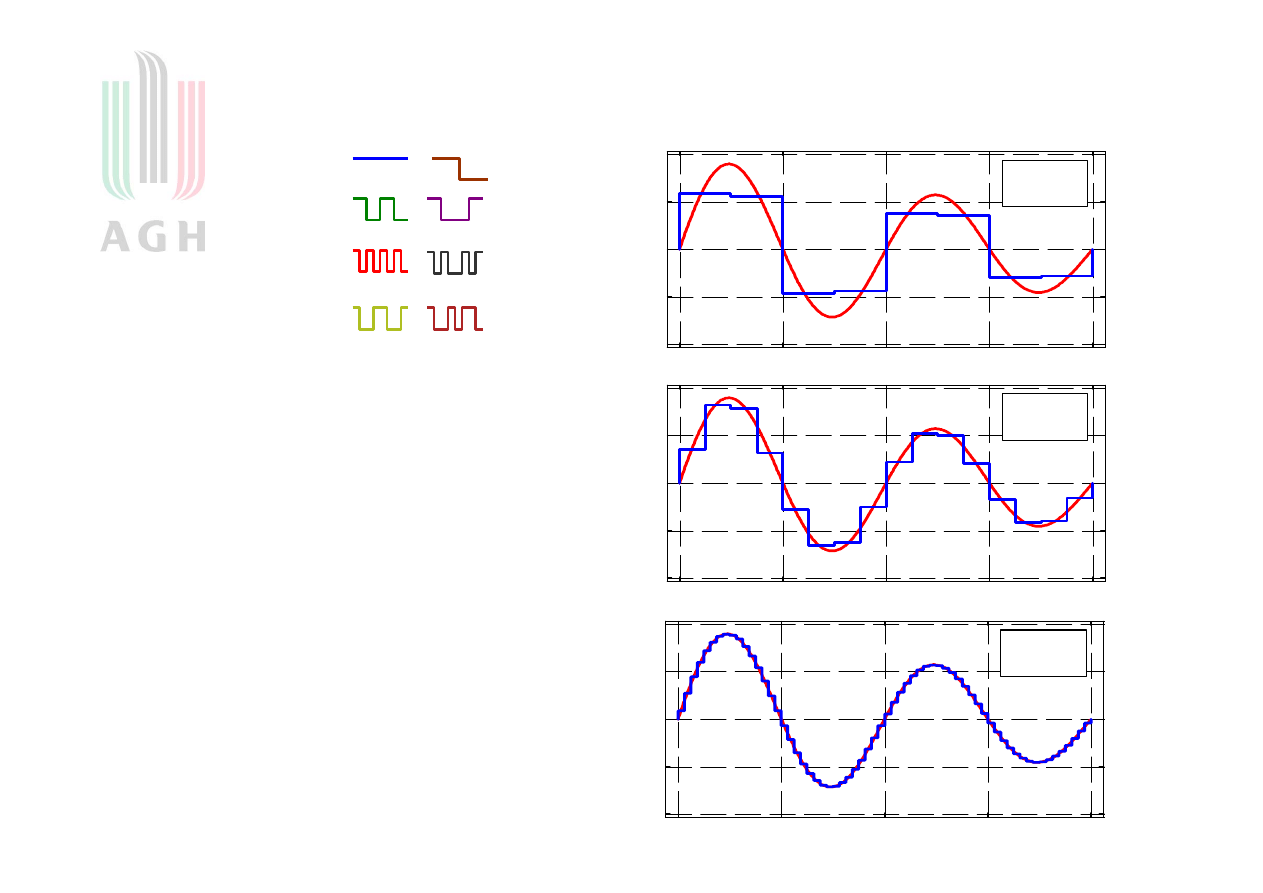
Reprezentacja sygnałami elementarnymi
s
a s
n n
n
N
1
Ciąg jest reprezentacją
sygnału s.
a
n
n
N
1
0
0 .2 5
0 .5
0 .7 5
1
-1
-0 .5
0
0 .5
1
N = 8
= 0 .2 0 9
0
0 .2 5
0 .5
0 .7 5
1
-1
-0 .5
0
0 .5
1
N = 1 6
= 0 .1 0 8
0
0 .2 5
0 .5
0 .7 5
1
-1
-0 .5
0
0 .5
1
N = 6 4
= 0 .0 2 7

3
Liniowa niezależność
Elementy
są
liniowo niezależne
, gdy z warunku zerowania ich
kombinacji liniowej wynikają zerowe wartości współczynników tzn.
s
n
,
n
a
a s
a
n n
n
N
n
N
n
1
1
0
,...,
Definicja 1.

4
Wymiar przestrzeni
Jeżeli przestrzeń S zawiera co najwyżej N elementów liniowo
niezależnych, to S nazywamy
przestrzenią N-wymiarową
a jej wymiar
oznaczamy
.
dim S
N
s
a s
n n
n
N
1
L
T
2
0
( , )
oraz C(0,T) są nieskończenie wymiarowe
Definicja 2.

5
Baza przestrzeni sygnałów
Bazą przestrzeni
S nazywamy dowolny zbiór
s
s
S n
N
S
N
n
n
:
;
,..., ; dim
1
elementów liniowo niezależnych.
Bazę
N-wymiarowej przestrzeni unitarnej S nazywamy
ortogonalną
, jeżeli każde dwa jej elementy są do siebie prostopadłe,
tzn.
{ }
s
n
n
N
1
s s
n
m
,
0
dla
n
m
Definicja 3.
Definicja 4.

6
Baza ortonormalna
Definicja 5.
Jeżeli norma każdego elementu bazy jest jednostkowa, tzn.
s
n
1
to
bazę
nazywamy
unormowaną
.
Definicja 6.
Jeżeli elementy bazowe są zarówno ortogonalne jak i
unormowane, to
bazę
nazywamy
ortonormalną
.

7
Reprezentacja sygnałów w przestrzeniach
skończenie wymiarowych
s
a s
S
n n
n
N
N
1
N
n
n
a
1
reprezentuje
)
,
0
(
2
T
L
S
s
N
s s
s s
a
m
n
m
n
N
n
,
,
1
dla m=1,...,N
gdzie
s s
s t s
t dt
m
m
T
,
( )
( )
0
8
Reprezentacja sygnałów w przestrzeniach
skończenie wymiarowych
a
A
b
gdzie
b
s s
s s
N
,
,
1
a
a
a
N
1
N
N
N
N
N
s
s
s
s
s
s
s
s
s
s
s
s
A
,
,
,
,
,
,
2
1
1
1
2
1
1
a = A b
-1
gdy
0
det
A
s s
s s
a
m
n
m
n
N
n
,
,
1
Układ równań
można zapisać macierzowo
9
Procedura ortonormalizacyjna
Grama-Schmidta
{ }
s
n
n
N
1
ortonormalne
{ }
s
n
n
N
1
s
s
s
1
1
1
v
s
s s s
2
2
2
1
1
,
2
1
2
1
2
1
1
1
,
,
,
,
s
s s
s s
s s
s
v
v
2
2
2
v
s
s s s
s s s
3
3
3
1
1
3
2
2
,
,
3
1
3
1
3
1
1
1
3
2
2
1
,
,
,
,
,
,
s
s s
s s
s s
s s
s s
3
2
3
2
3
1
1
2
3
2
2
2
,
,
,
,
,
,
s
s s
s s
s s
s s
s s
v
s
s s s
n
n
n
m
m
m
n
,
1
1
dowolne

10
Algorytm Grama-Schmidta
1
0
. Dane :
s
1
, s
2
,...,s
N
- dowolna baza,
N - ilość elementów bazy.
2
0
. Obliczyć pierwszy element ortonormalnej bazy
s
s
s
1
1
1
:
i podstawić n:=1.

11
C.d algorytmu Grama-Schmidta
3
0
. Powiększyć numer wskaźnika n:=n+1 i następnie obliczyć
kolejny element
v
s
s s s
n
n
n
m
m
m
n
:
,
1
1
4
0
. Dokonać normalizacji elementu otrzymanego w poprzednim
kroku
s
v
v
n
n
n
:
5
0
. Jeżeli n<N należy przejść do punktu 3
0
. Przeciwny przypadek
oznacza zakończenie procedury ortonormalizacyjnej.

12
Aproksymacja sygnałów w przestrzeniach
nieskończenie wymiarowych
s S
S
S
s
N
ap
N
n
n
n
ap
s
a
s
1
)
,
(
min
)
,
(
1
N
n
n
n
a
ap
s
a
s
s
s
n
)
,
(
)
,
(
*
s
s
s
s
ap
dla każdego
s
S
N
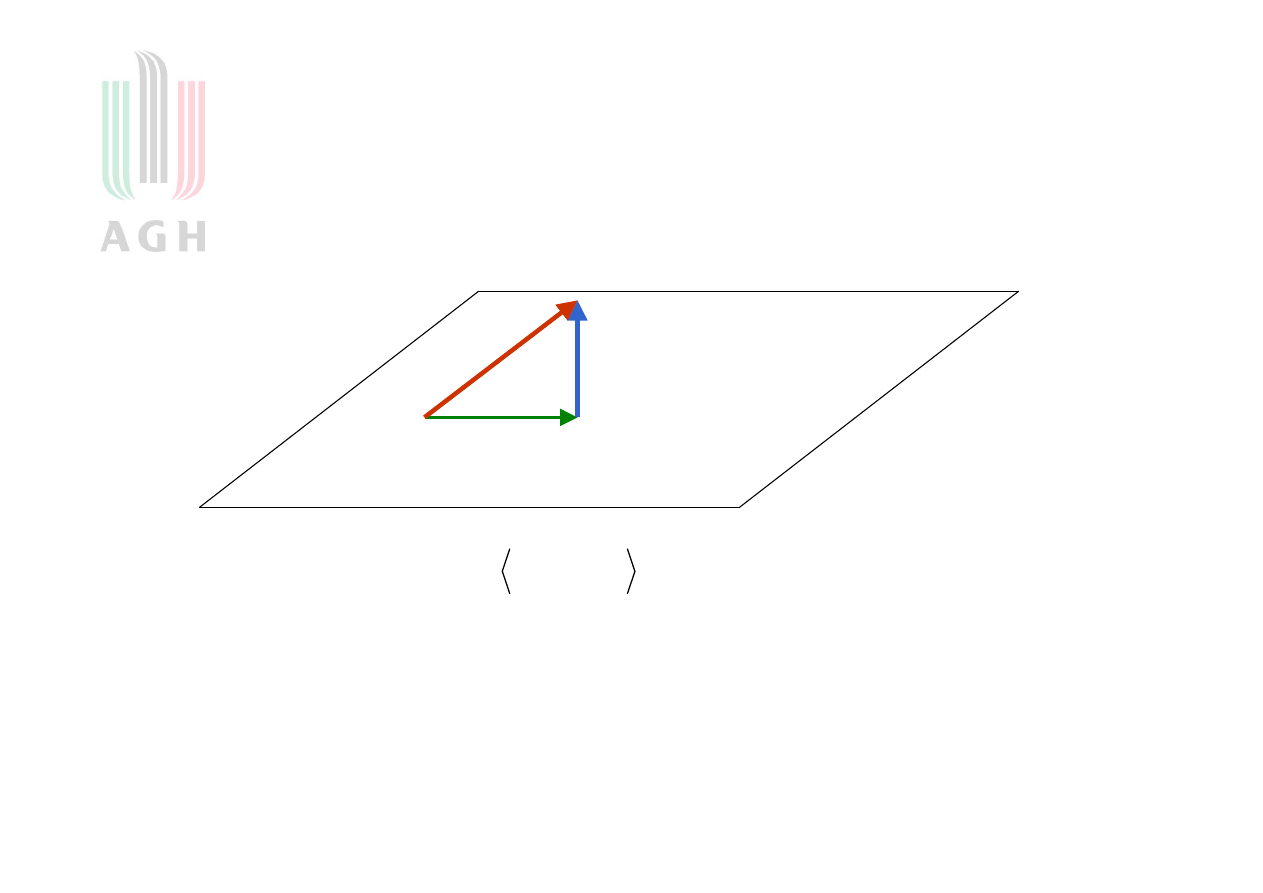
13
Rysunek rzutu ortogonalnego
ap
s
ap
s
s
s
0
,
s
s
s
ap
.
N
S
s

14
Twierdzenie o rzucie ortogonalnym
Niech S będzie przestrzenią unitarną, a
będzie N-wymiarową
podprzestrzenią (tzn.
) rozpiętą na ortonormalnej bazie
.
Dla każdego s istnieje jedyny element
określony wzorem
S
N
S
S
N
s
n
n
N
1
N
ap
S
s
N
n
n
n
ap
s
s
s
s
1
,
taki, że:
1) dla każdego
spełniona jest nierówność
2) element
jest ortogonalny do podprzestrzeni
, tzn.
s
S
N
),
,
(
)
,
(
*
s
s
s
s
ap
ap
s
s
S
N
0
,
s
s
s
ap
.
N
S
s
dla każdego
15
Równość Parsevala
s
a s
a s
a s
a
a
L
n n
n
L
n n L
n
n L
n
l
n
n
n
2
2
2
2
2
2
1
2
2
2
2
2
2
1
1
1
Równość Parsevala
s
a
L
l
2
2
gdzie
s
s
t dt
L
T
2
2
0
( )
a
a
l
n
n
2
2
1
ortogonalność
bazy
baza
unormowana
16
Początek przykładu
W przestrzeni
znaleźć
najlepszą aproksymację sygnału
L
2
0 2
( , )
s t
t
t
t
( )
2
0
1
1
1
2
dla
dla
przy pomocy funkcji:
.
)
(
,
)
(
,
1
)
(
2
3
2
1
t
t
s
t
t
s
t
s
0
1
2
0
1
0
1
2
0
1
2
0
1
2
0
1
2
0
1
2
0
2
4
Funkcje aproksymujące
Sygnał

17
Kontynuacja przykładu
Takie a
1
, a
2
, a
3
aby funkcjonał Q osiągał wartość minimalną.
dt
t
a
t
a
a
dt
t
a
t
a
a
t
a
s
s
)
1
(
2
)
(
2
)
~
,
(
2
3
2
1
2
1
2
3
2
1
1
0
2
1
2
dt
t
t
a
t
a
a
dt
t
t
a
t
a
a
t
a
s
s
)
1
(
2
)
(
2
)
~
,
(
2
3
2
1
2
1
2
3
2
1
1
0
2
2
2
dt
t
t
a
t
a
a
dt
t
t
a
t
a
a
t
a
s
s
2
2
3
2
1
2
1
2
2
3
2
1
1
0
2
3
2
)
1
(
2
)
(
2
)
~
,
(
Kwadrat odległości
1
0
2
1
2
2
3
2
1
2
2
3
2
1
2
2
)
1
(
)
(
)
~
,
(
dt
t
a
t
a
a
dt
t
a
t
a
a
t
s
s
Q

18
Zakończenie przykładu
Po obliczeniu całek, przyrównujemy do zera powyższe pochodne i
otrzymujemy układ równań
,
15
19
4
7
3
2
5
16
2
3
4
4
3
8
2
3
4
1
1
3
2
1
a
a
a
który ma rozwiązanie:
.
4375
,
0
5
,
1
25
,
0
3
2
1
a
a
a
Oznacza to, że aproksymacja zadanego sygnału ma postać
.
16
7
2
3
4
1
)
(
~
2
t
t
t
s
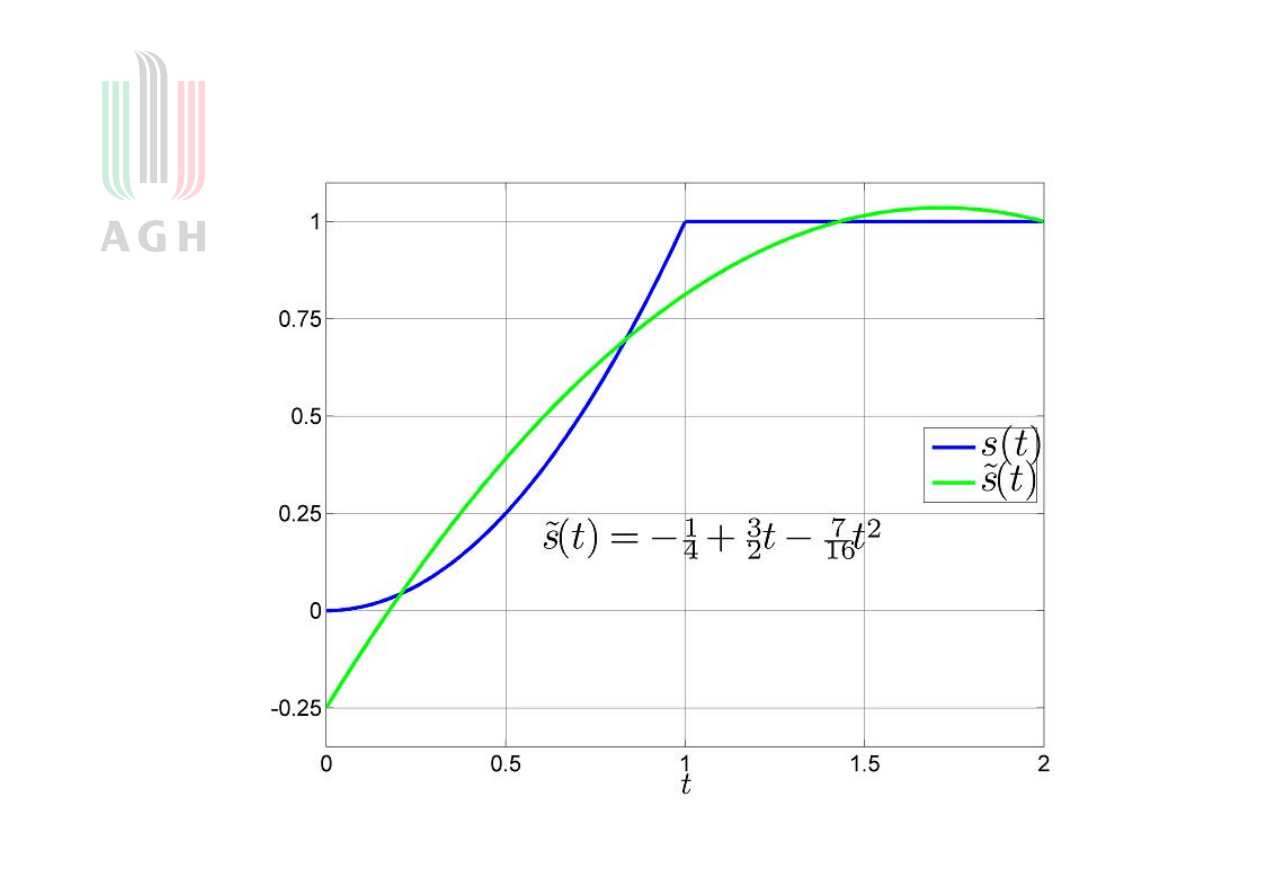
19
Ilustracja rozwiązania

20
Wielomiany ortogonalne
Wielomiany ortogonalne na odcinku [0,1] generowane są wzorem
s
t
n
d
dt
t
t
n
n
n
n
1
2
1
( )
!
n
0 1 2
, , ,....
i spełniają wzór rekurencyjny
).
(
)
2
(
)
(
)
1
2
)(
3
2
(
)
(
)
1
(
2
1
t
s
n
t
s
t
n
t
s
n
n
n
n

21
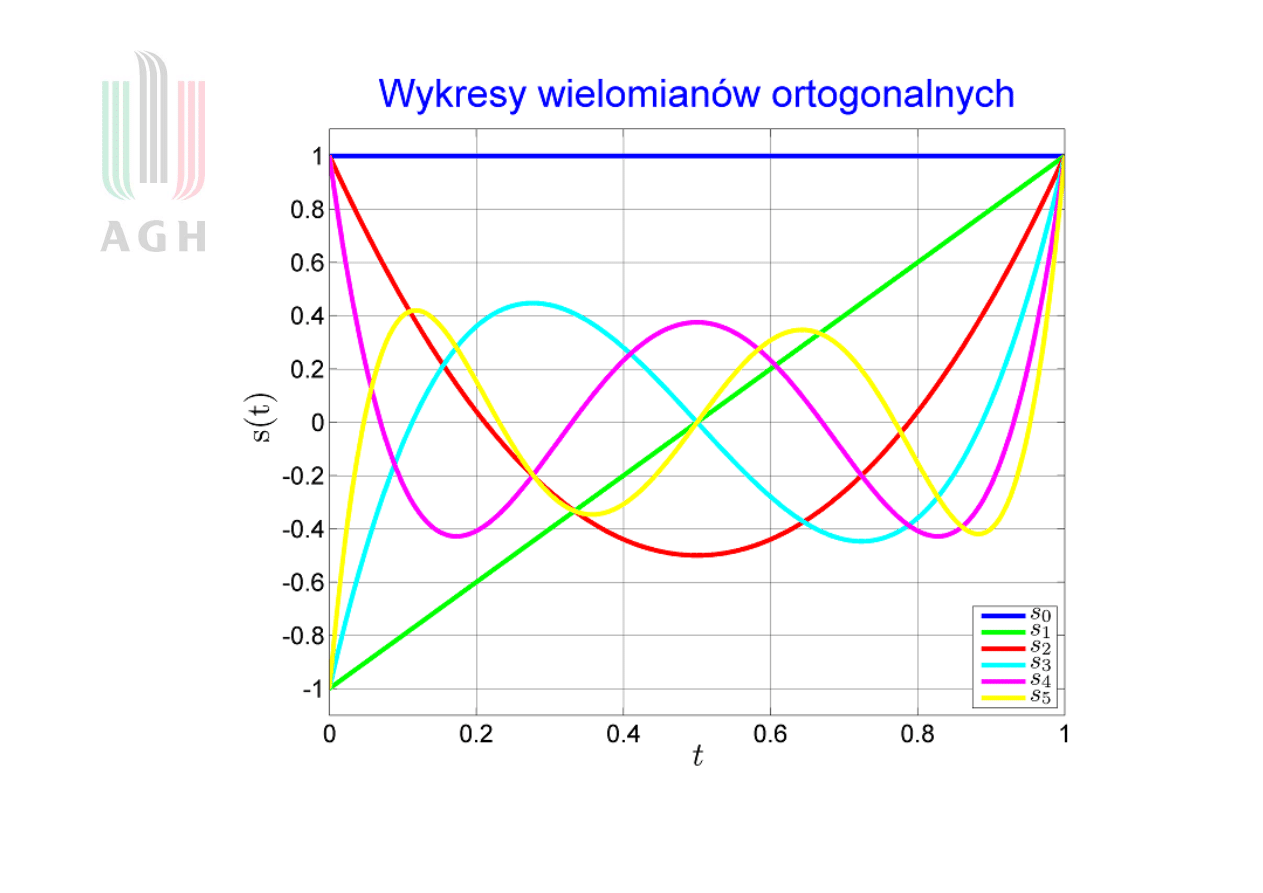
Przykład wielomianów ortogonalnych
Siedem pierwszych wielomianów ortogonalnych na odcinku [0,1]
s t
1
1
( )
s t
t
2
2
1
( )
s t
t
t
3
2
6
6
1
( )
s t
t
t
t
4
3
2
20
30
12
1
( )
s t
t
t
t
t
5
4
3
2
70
140
90
20
1
( )
s t
t
t
t
t
t
6
5
4
3
2
252
630
560
210
30
1
( )
s t
t
t
t
t
t
t
7
6
5
4
3
2
924
2772
3150
1680
420
42
1
( )
s
n
n
1
2
1
22

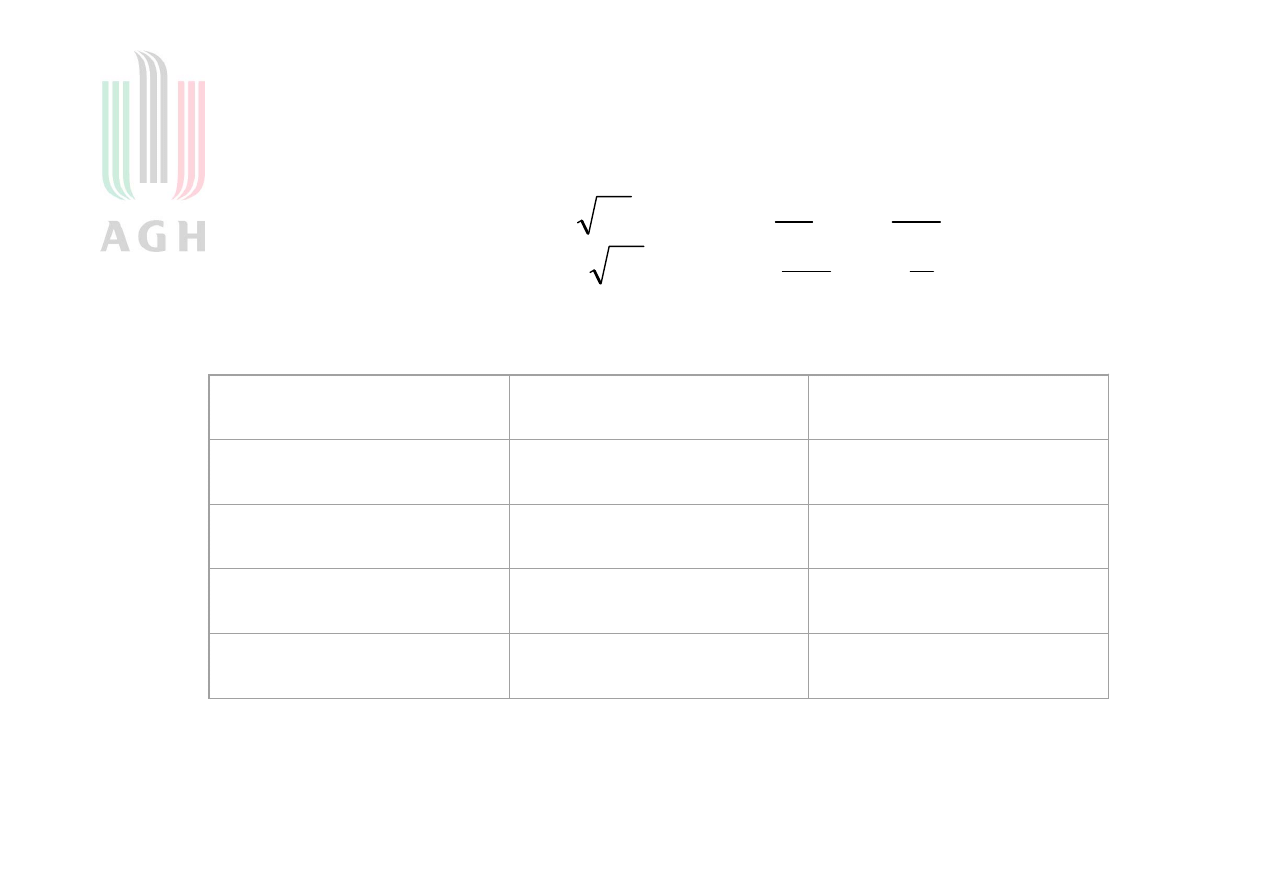
Wykresy funkcji Haara
0
0 .2 5
0 .5
0 .7 5
1
-2
-1
0
1
2
h
0
(t
)
0
0 .2 5
0 .5
0 .7 5
1
-2
-1
0
1
2
h
1
(t
)
0
0 .2 5
0 .5
0 .7 5
1
-2
-1
0
1
2
h
1,
1
(t
)
0
0 .2 5
0 .5
0 .7 5
1
-2
-1
0
1
2
h
1,
2
(t
)
0
0 .2 5
0 .5
0 .7 5
1
-2
-1
0
1
2
h
2,
1
(t
)
0
0 .2 5
0 .5
0 .7 5
1
-2
-1
0
1
2
h
2,
2
(t
)
0
0 .2 5
0 .5
0 .7 5
1
-2
-1
0
1
2
h
2,
3
(t
)
0
0 .2 5
0 .5
0 .7 5
1
-2
-1
0
1
2
h
2,
4
(t
)

24
Funkcje Haara
Haar 1910 rok
Funkcje ortonormalne w
L
2
0 1
( , )
r=0,1,2,... numer grupy
m numer kolejnym funkcji w ramach danej grupy
1
2
m
r
h t
0
1
( )
t
[ , ]
0 1
dla
25
Definicja funkcji Haara
r
m
n
0
1
1
1
1, 2
2, 3
2
1, 2, 3, 4
4, 5, 6, 7
3
1, 2, 3, 4, 5, 6, 7, 8
8, 9, 10, 11, 12, 13, 14, 15
h t
h
t
t
t
t
n
r m
r
r
m
m
m
m
r
r
r
r
( )
( )
,
2
2
0
0 1
1
2
2
1
2
2
1
2
2
1
1
dla
dla
dla pozosta ych [ , ].
l
gdzie n=2
r
+m-1
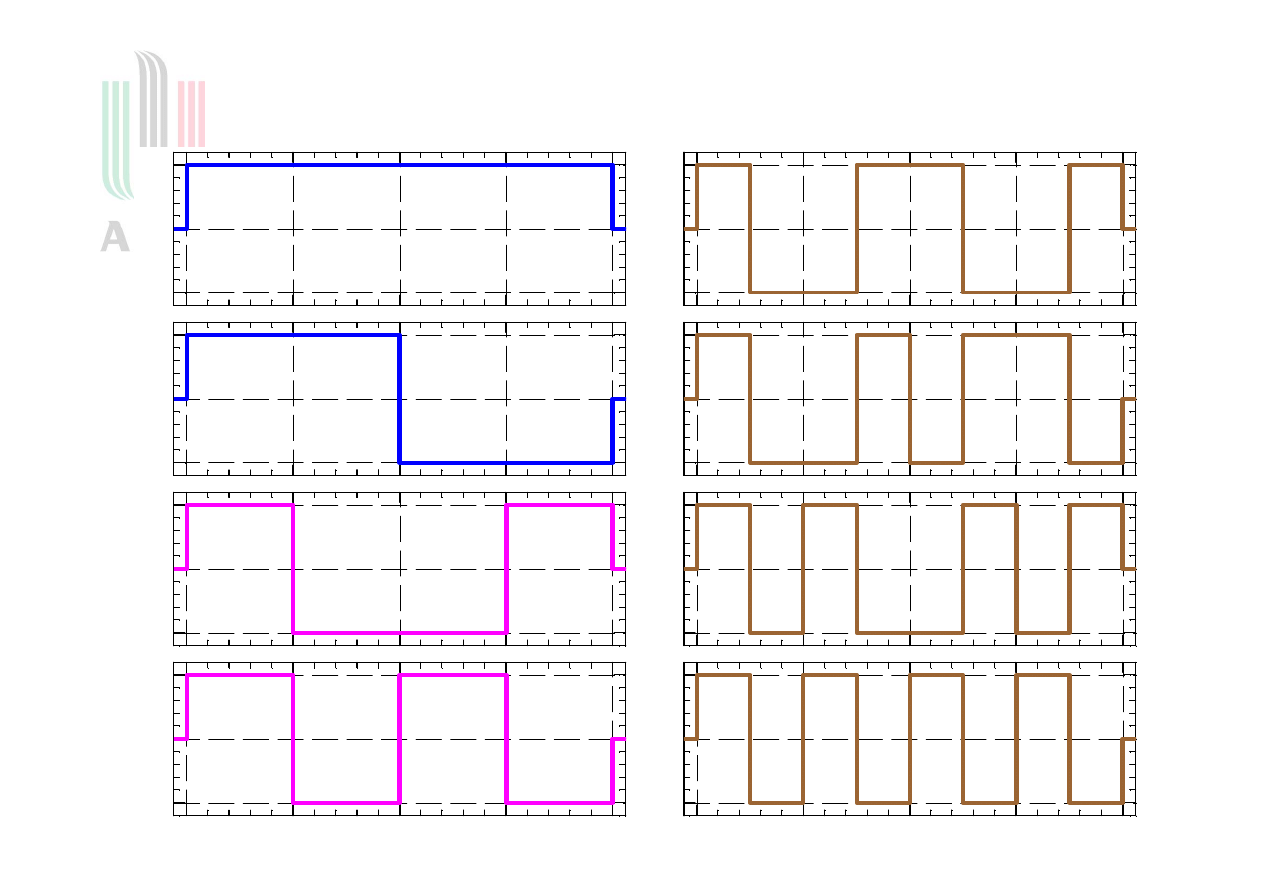
Wykresy funkcji Walsha
0
0 .2 5
0 .5
0 .7 5
1
-1
0
1
w
0
(t
)
0
0 .2 5
0 .5
0 .7 5
1
-1
0
1
w
2,
1
(t
)
0
0 .2 5
0 .5
0 .7 5
1
-1
0
1
w
2,
2
(t
)
0
0 .2 5
0 .5
0 .7 5
1
-1
0
1
w
3,
1
(t
)
0
0 .2 5
0 .5
0 .7 5
1
-1
0
1
w
3,
2
(t
)
0
0 .2 5
0 .5
0 .7 5
1
-1
0
1
w
3,
3
(t
)
0
0 .2 5
0 .5
0 .7 5
1
-1
0
1
w
3,
4
(t
)
0
0 .2 5
0 .5
0 .7 5
1
-1
0
1
w
1
(t
)

27
Funkcje Walsha
Tworzą bazę ortonormalną w
L
2
0 1
( , )
w t
0
1
( )
0
1
t
dla
w t
w
t
t
w
t
t
t
t
1
0
0
2
0
1 2
2
1
1 2
1
1
0
1 2
1
1 2
1
( )
( )
(
)
dla
dla
dla
dla
r = 1,2,... numer grupy
m = 1,...2
r-1
kolejność w ramach m-tej grupy

28
Iteracyjna generacja funkcji Walsha
1
2
1
dla
)
1
2
(
)
1
(
2
1
0
dla
)
2
(
)
(
,
1
,
1
2
,
1
t
t
w
t
t
w
t
w
k
m
k
k
m
k
m
1
2
1
dla
)
1
2
(
)
1
(
2
1
0
dla
)
2
(
)
(
,
,
2
,
1
t
t
w
t
t
w
t
w
k
m
k
k
m
k
m
29
Numeracja funkcji Walsha
w t
w
t
n
r m
( )
( )
,
gdzie n=2
r-1
+m-1
r
m
n
1
1
1
2
1, 2
2, 3
3
1, 2, 3, 4
4, 5, 6, 7
4
1, 2, 3, 4, 5, 6, 7, 8
8, 9, 10, 11, 12, 13, 14, 15

30
Wykresy funkcji giętych
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Przykład jedenastu funkcji giętych pierwszego stopnia

31
Funkcje gięte pierwszego stopnia
,
1
)
1
(
1
gdy
)
1
(
1
1
1
)
1
(
1
gdy
0
)
(
n
t
j
n
t
j
n
t
j
t
j
gdzie
jest założoną ilościa funkcji dla odcinka [0,1]
n
3

32
Iloczyny skalarne funkcji giętych
pierwszego stopnia
1
0
,
h
pozostalyc
,
dla
0
1
lub
1
gdy
6
/
lub
1
gdy
3
/
1
gdy
3
/
2
)
(
)
(
j
i
j
i
j
i
h
n
j
i
j
i
h
n
j
i
h
dt
t
t
a
j
i
j
i
Gdzie
jest długością nośników funkcji giętych
o numerach
h
n
1
1
/ (
)
.
1
,...,
2
n
j

33
Macierzowa prezentacja iloczynów
skalarnych
2
1
1
4
1
1
4
1
1
4
1
1
4
1
1
2
6
h
A

34
Szybka generacja elementów macierzy
odwrotnej do trójprzekątniowej
Macierz A jest trójprzekątniowa, ale macierz do niej odwrotna
jest macierzą pełną z elementami o wartościach
2
1
odw
,
2
j
i
j
i
a
gdzie
i
i
i
3 2
2
3
2
1
1
j
n j
n j
3 2
2
3
2

35
Macierz odwrotna do macierzy iloczynów
skalarnych
0128
,
0
0034
,
0
0009
,
0
0003
,
0
0003
,
0
0256
,
0
0069
,
0
0019
,
0
0005
,
0
0003
,
0
0897
,
0
0241
,
0
0065
,
0
0019
,
0
0009
,
0
3333
,
0
0893
,
0
0241
,
0
0069
,
0
0034
,
0
2436
,
1
3333
,
0
0897
,
0
0256
,
0
0128
,
0
6411
,
4
2440
,
1
3349
,
0
0957
,
0
0478
,
0
3210
,
17
6427
,
4
2500
,
1
3571
,
0
1786
,
0
6427
,
4
3269
,
17
6649
,
4
3328
,
1
6664
,
0
2500
,
1
6649
,
4
4098
,
17
9742
,
4
4871
,
2
3571
,
0
3328
,
1
9742
,
4
5641
,
18
2820
,
9
1786
,
0
6664
,
0
4871
,
2
2820
,
9
6410
,
34
6410
,
34
2820
,
9
4871
,
2
6664
,
0
1786
,
0
0478
,
0
2820
,
9
5641
,
18
9742
,
4
3328
,
1
3571
,
0
0957
,
0
4871
,
2
9742
,
4
4098
,
17
6649
,
4
2500
,
1
3349
,
0
6664
,
0
3328
,
1
6649
,
4
3269
,
17
6427
,
4
2440
,
1
1786
,
0
3571
,
0
2500
,
1
6427
,
4
3210
,
17
6411
,
4
0478
,
0
0957
,
0
3349
,
0
2440
,
1
6411
,
4
3206
,
17
0128
,
0
0256
,
0
0897
,
0
3333
,
0
2436
,
1
6411
,
4
0034
,
0
0069
,
0
0241
,
0
8935
,
0
333
,
0
2440
,
1
0009
,
0
0019
,
0
0065
,
0
0241
,
0
0897
,
0
3349
,
0
0003
,
0
0005
,
0
0019
,
0
0069
,
0
0256
,
0
0957
,
0
0001
,
0
0003
,
0
0009
,
0
0034
,
0
0128
,
0
0478
,
0
1
A

36
Funkcje trygonometryczne
Ortogonalna baza w
oraz baza dla funkcji okresowych
w C(-,)
L
T
2
0
( , )
s t
a
a
nt T
b
nt T
n
n
n
( )
cos(
/ )
sin(
/ )
0
1
2
2
s t dt
a dt
T
T
( )
0
0
0
0
a
T
s t dt
T
0
0
1
( )
37
Współczynniki szeregu
trygonometrycznego
s t
nt T dt
a
nt T dt
n
T
T
( ) cos(
/ )
cos (
/ )
2
2
2
0
0
cos (
/ )
cos(
/ )
sin(
/ )
2
0
0
0
2
1
4
2
2 8
4
2
nt T dt
nt T
dt
t
T
n
nt T
T
T
T
T
otrzymujemy
s t
nt T dt
a
T
T
n
( ) cos(
/ )
2
2
0
a zatem
a
T
s t
nt T dt
n
T
2
2
0
( ) cos(
/ )
podobnie
T
n
dt
T
nt
t
s
T
b
0
)
/
2
sin(
)
(
2

38
Warunki Dirichleta
Jeżeli funkcja spełnia warunki:
1. jest bezwzlędnie całkowalna, tzn.
2. w przedziale jednego okresu ma skończoną liczbę
lokalnych maksimów i minimów,
)
(t
s
,
)
(
0
T
dt
t
s
3. w przedziale jednego okresu ma skończoną liczbę punktów
nieciągłości pierwszego rodzaju, tzn. skończone są granice
lewostronna i prawostronna
)
(
lim t
s
t
t
,
)
(
lim
t
s
t
t
to ma reprezentację w postaci szeregu Fouriera.
)
(t
s

39
Współrzędne biegunowe
Przesunięcie
fazowe
0
i
0
gdy
)
(
tg
arc
0
i
0
gdy
)
(
tg
arc
)
(
sign
0
i
0
gdy
)
(
sign
5
,
0
5
,
0
0
gdy
)
(
sign
5
,
0
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
b
a
a
b
b
a
a
b
b
b
a
a
a
b
amplituda
c
a
b
n
n
n
2
2
wtedy
a
c
n
n
n
cos( )
b
c
n
n
n
sin( )
)
(
tg
arc
n
n
n
a
b

40
Szereg trygonometryczny w postaci
biegunowej
s t
a
c
nt T
c
nt T
n
n
n
n
n
( )
cos( ) cos(
/ )
sin( ) sin(
/ )
0
1
2
2
Korzystając z tożsamości
cos(
) cos(
/ ) sin(
) sin(
/ ) cos(
/
)
n
n
n
nt T
nt T
nt T
2
2
2
otrzymujemy
s t
a
c
nt T
n
n
n
( )
cos
/
0
1
2

41
Funkcje trygonometryczne w postaci
eksponentalnej
cos(
/ )
/
/
2
2
2
2
nt T
e
e
j n t T
j n t T
sin(
/ )
/
/
2
2
2
2
nt T
e
e
j
j n t T
j n t T
gdzie
1
2
j
s t
a
a
e
e
b
e
e
j
n
jnt T
jnt T
n
jnt T
jnt T
n
( )
/
/
/
/
0
2
2
2
2
1
2
2
Oznaczając
s
a
jb
a
a
jb
n
n
n
n
n
n
n
n
1
2
0
1
2
0
0
0
dla
dla
dla
otrzymujemy
s t
s e
n
n
jnt T
( )
/
2
ponieważ
)
/
2
sin(
)
/
2
cos(
/
2
T
nt
j
T
nt
e
T
jnt
s
T
s t e
dt
n
T
j n t T
1
0
2
( )
/
to
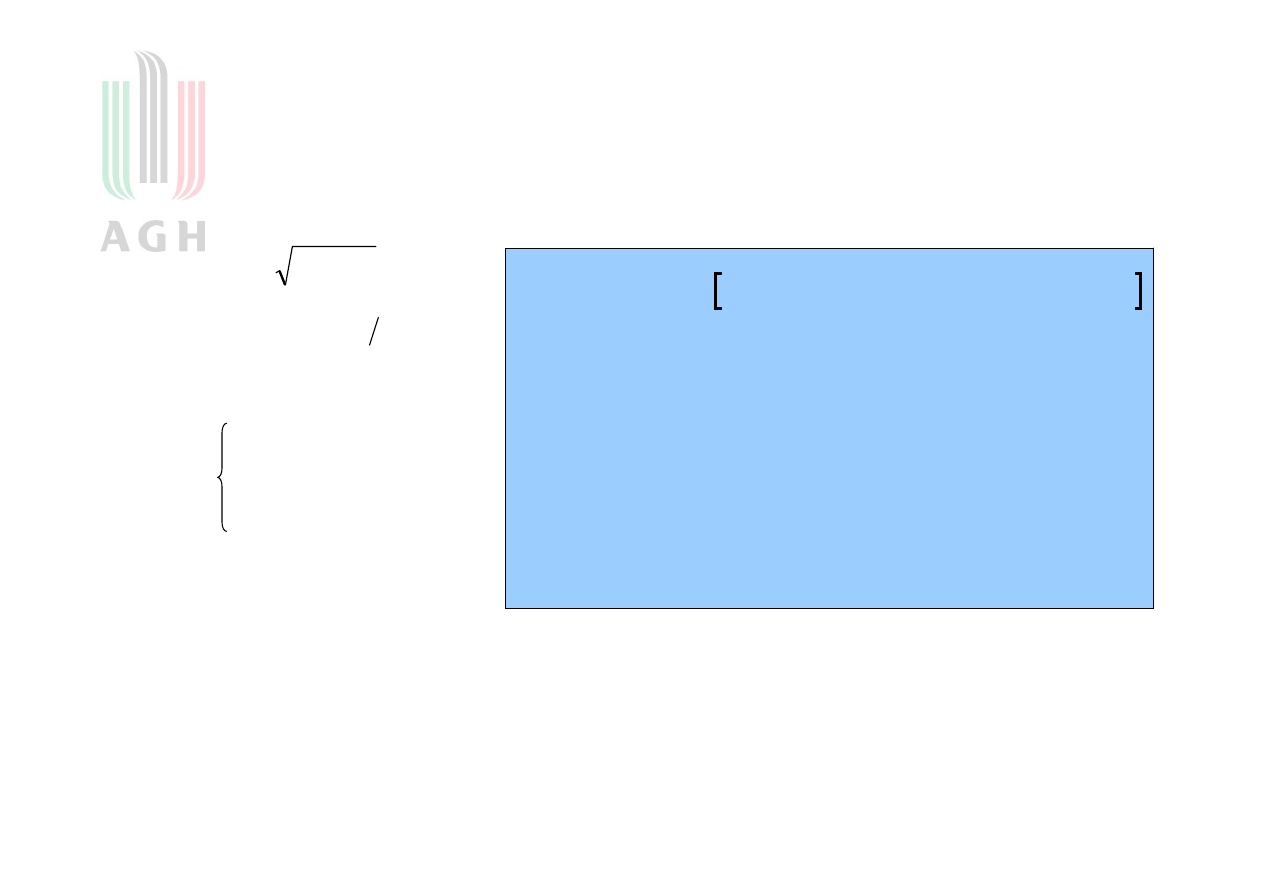
42
Zależności między współczynnikami dla
różnych reprezentacji trygonometrycznych
a
s
s
n
n
n
b
j s
s
n
n
n
c
a
b
n
n
n
2
2
a
c
n
n
n
cos( )
b
c
n
n
n
sin( )
s t
a
c
nt T
n
n
n
( )
cos
/
0
1
2
s t
a
a
nt T
b
nt T
n
n
n
( )
cos(
/ )
sin(
/ )
0
1
2
2
s t
s e
n
n
jnt T
( )
/
2
)
(
tg
arc
n
n
n
a
b

43
Reprezentacja sygnałów dwuwymiarowych
,]
,
0
[
]
,
0
[
2
Y
X
L
s
czyli
s
x y dy dx
Y
X
2
0
0
( , )
s x y
a s
x y
n
n
n
( , )
( , )
1

44
Współczynniki ortonormalnej reprezentacji
sygnałów dwuwymiarowych
s x y s
x y dy dx
n
m
n
m
n
m
Y
X
( , ) ( , )
.
1
0
0
0
dla
dla
s s
a
s
s
n
m
m
n
m
,
,
1
gdzie
s s
s x y s
x y dy dx
n
n
Y
X
,
( , ) ( , )
0
0
a
s s
n
n
,

45
Rozdzielanie zmiennych reprezentacji
sygnałów dwuwymiarowych
s x y
a
x
y
n m
n
m
m
n
( , )
( )
( )
,
1
1
n
m
X
x
x dx
n
m
n
m
( )
( )
1
0
0
dla
dla
n
m
Y
y
y dy
n
m
n
m
( )
( )
.
1
0
0
dla
dla
X
Y
n
m
Y
m
j
X
n
i
m
n
j
i
dy
y
y
dx
x
x
a
dx
dy
y
y
x
s
x
0
0
1
1
0
0
,
)
(
)
(
)
(
)
(
)
(
)
,
(
)
(
a
x
s x y
y dy dx
n m
n
m
Y
X
,
( )
( , )
( )
0
0
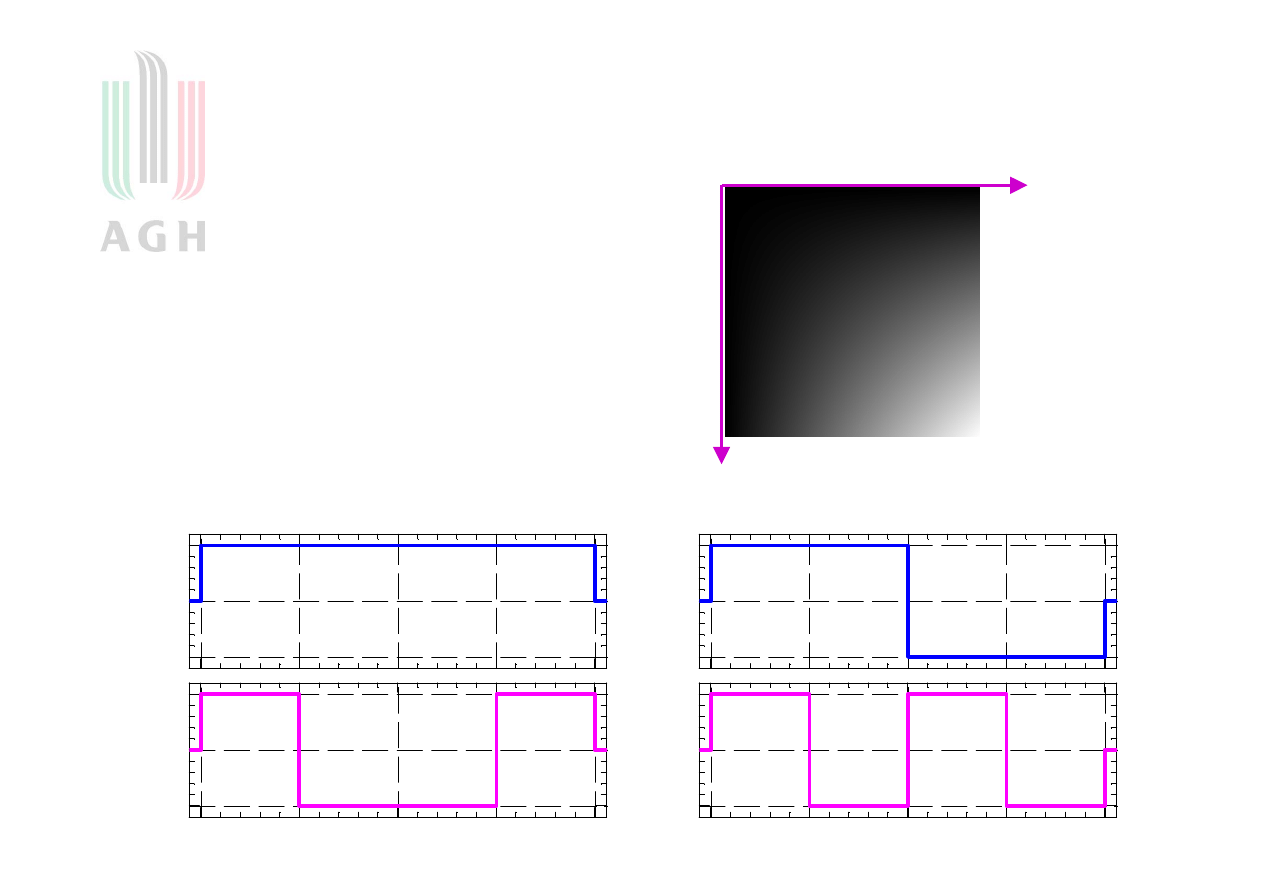
Przykład reprezentacji obrazu przy pomocy
funkcji Walsha
Obraz
Aproksymować przy pomocy czterech pierwszych funkcji Walsha:
1
2
)
,
(
xy
y
x
s
1
s
0
0 .2 5
0 .5
0 .7 5
1
-1
0
1
2
s
0
0 .2 5
0 .5
0 .7 5
1
-1
0
1
4
s
0
0 .2 5
0 .5
0 .7 5
1
-1
0
1
3
s
0
0 .2 5
0 .5
0 .7 5
1
-1
0
1
y
x
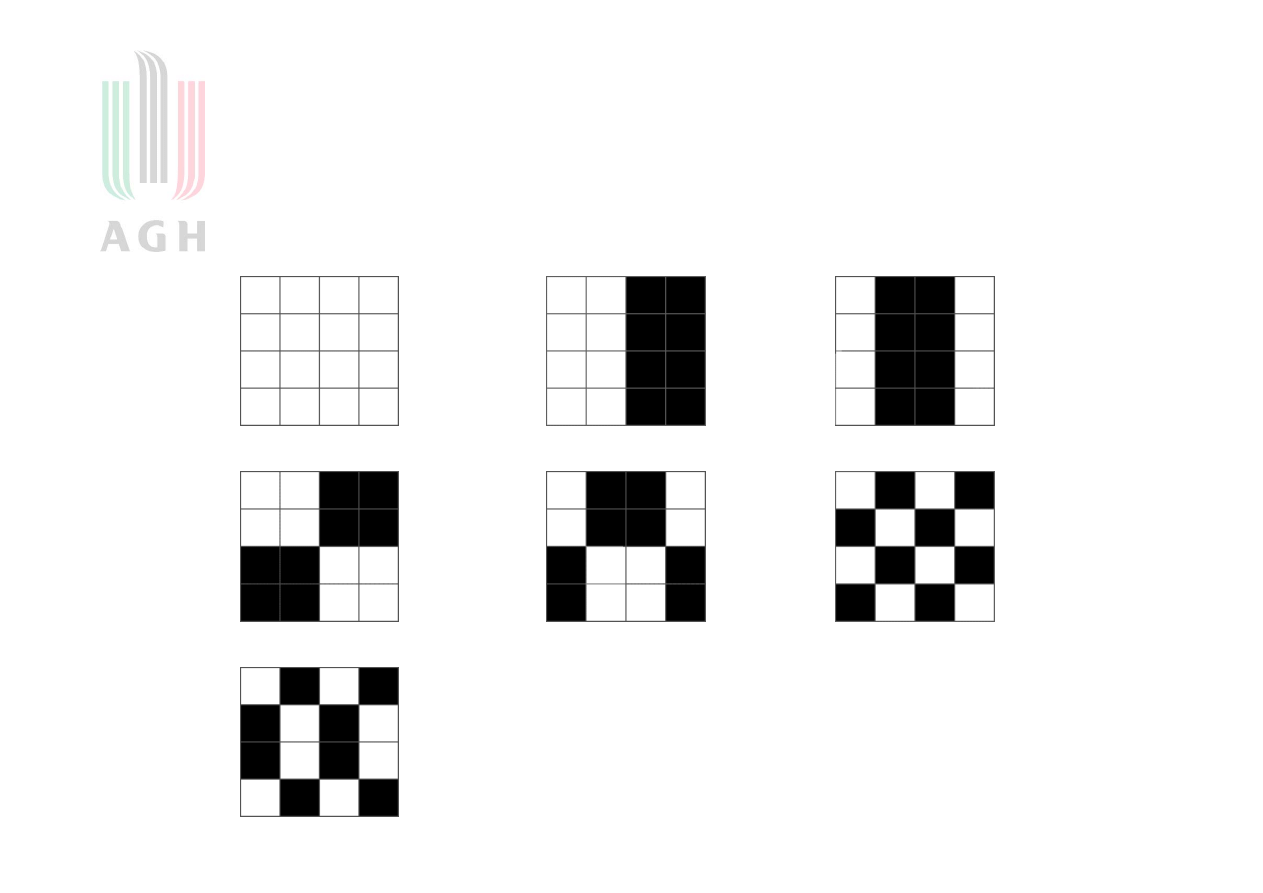
Wybrane obrazy elementarne
Szesnaście obrazów elementarnych
)
(
)
(
)
,
(
,
y
x
y
x
s
m
n
m
n
1
,
1
s
2
,
1
s
3
,
1
s
2
,
2
s
3
,
2
s
3
,
3
s
3
,
4
s
Kolor biały oznacza wartość 1
Kolor czarny to wartość –1 !
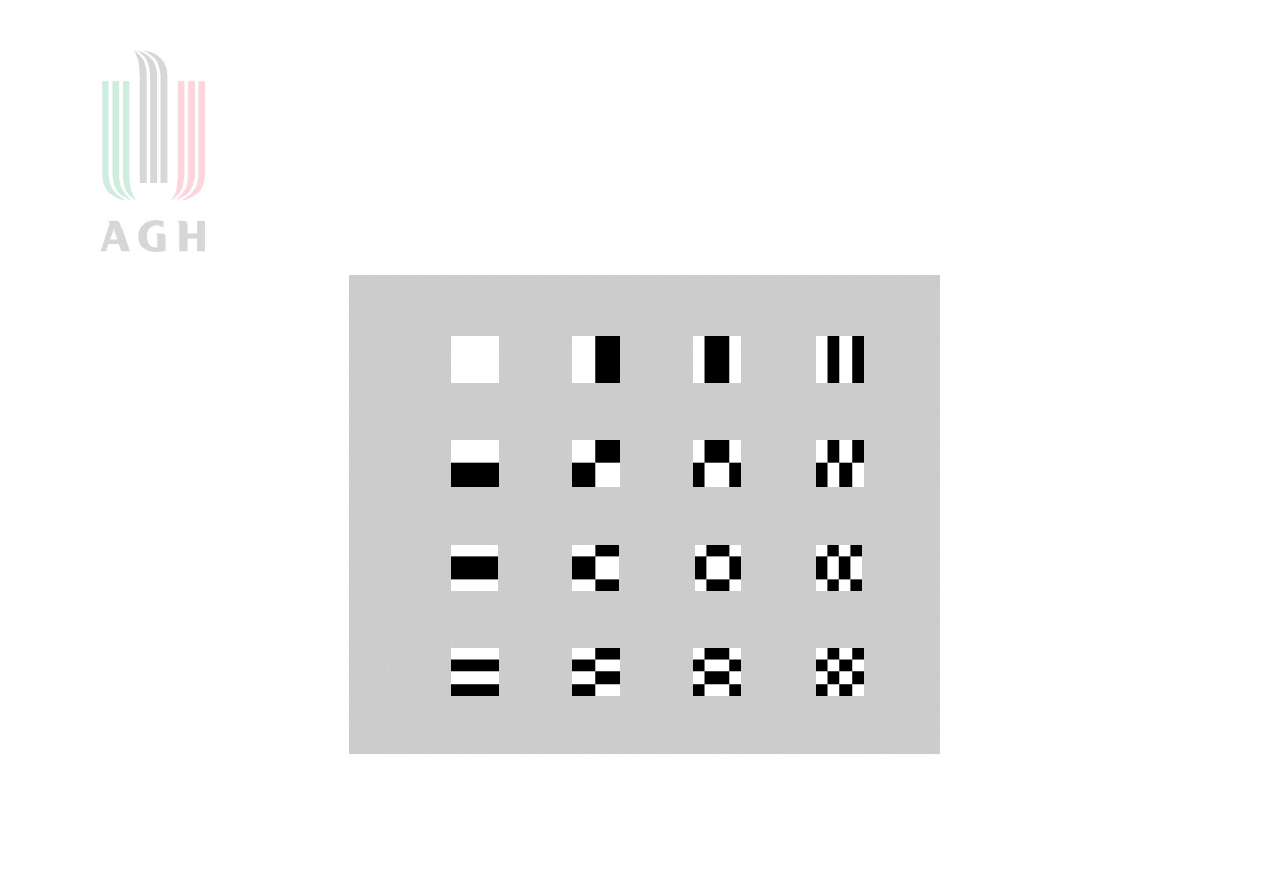
Wybrane obrazy elementarne
Szesnaście obrazów elementarnych
)
(
)
(
)
,
(
,
y
x
y
x
s
m
n
m
n
s
1,1
s
1,2
s
1,3
s
1,4
s
2,1
s
2,2
s
2,3
s
2,4
s
3,1
s
3,2
s
3,3
s
3,4
s
4,1
s
4,2
s
4,3
s
4,4
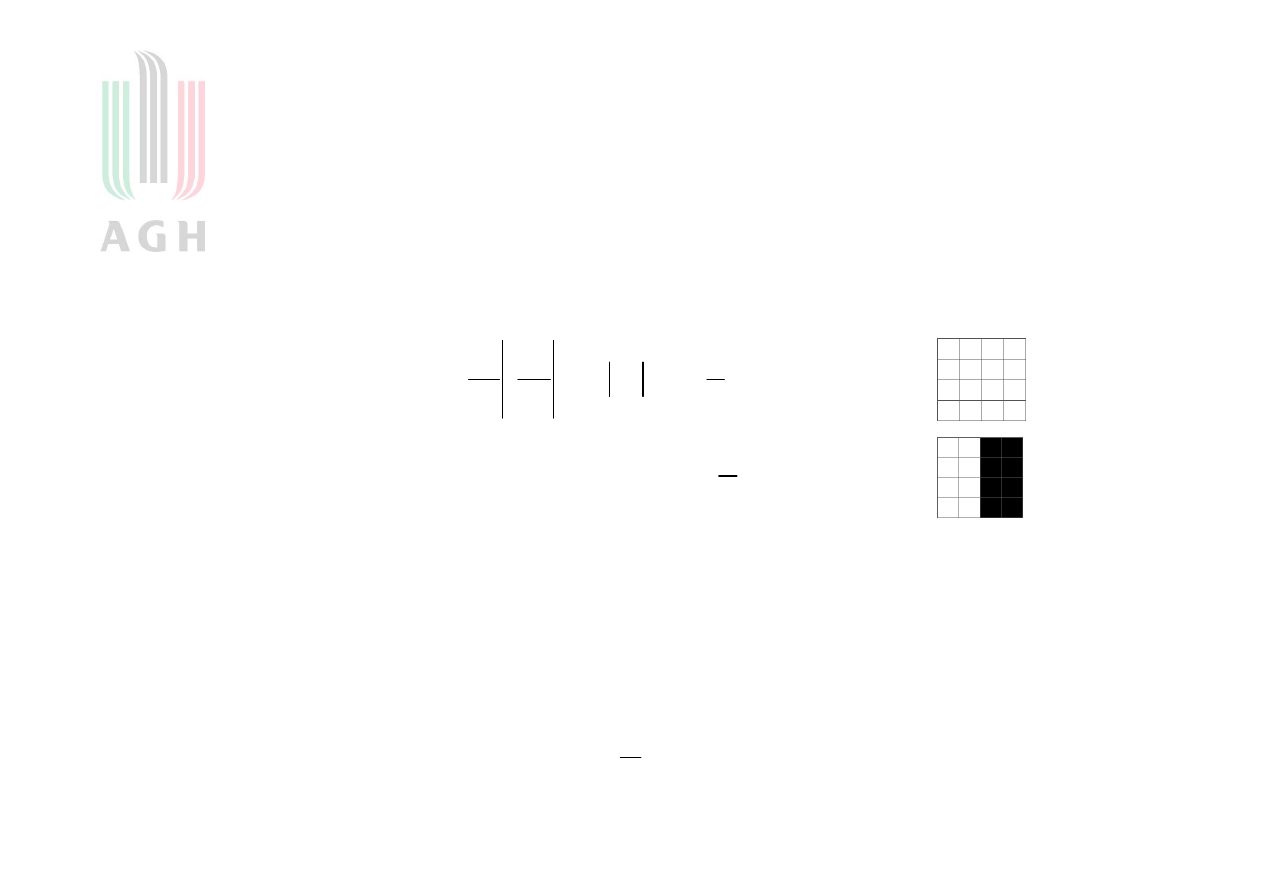
Ciąg dalszy przykładu
Aproksymacja obrazu
s x y
a
s x s
y
n m
n
m
m
n
( , )
( ) ( )
,
1
4
1
4
Współczynniki aproksymacji
2
1
2
2
2
)
1
2
(
1
0
1
0
1
0
2
1
0
2
1
0
1
0
1
,
1
y
x
y
x
dy
dx
xy
a
4
1
)
1
2
(
)
1
2
(
1
0
5
,
0
0
1
0
1
5
,
0
2
,
1
dydx
xy
dydx
xy
a
Symetria obrazu, tzn.
powoduje symetrię
współczynników, tzn.
)
,
(
)
,
(
x
y
s
y
x
s
a
a
n m
m n
,
,
4
1
1
,
2
2
,
1
a
a
dla
dla
C.d. przykładu
0
1
,
3
3
,
1
a
a
3
,
1
s
3
,
2
s
3
,
3
s
3
,
4
s
8
1
1
,
4
4
,
1
a
a
8
1
2
,
2
a
0
2
,
3
3
,
2
a
a
16
1
2
,
4
4
,
2
a
a
0
3
,
4
4
,
3
a
a
0
3
,
3
a
32
1
4
,
4
a
2
,
2
s
2
,
4
s

C.d. przykładu
Obliczone współczynniki możemy zestawić w postaci
symetrycznej macierzy
32
1
16
1
8
1
16
1
8
1
4
1
8
1
4
1
2
1
0
0
0
0
0
0
0
A
17
3
11
25
3
7
17
27
11
17
23
29
25
27
29
31
32
1
s
Ilustracja przykładu
Obraz oryginalny (z lewej) i jego aproksymacja (z prawej)
utworzona przy pomocy funkcji Walsha, niby szesnastu ale w
praktyce tylko dziewięciu
1
2
)
,
(
xy
y
x
s
17
3
11
25
3
7
17
27
11
17
23
29
25
27
29
31
32
1
s
Ilustracja przykładu
1
2
)
,
(
xy
y
x
s
0
0.5
1
0
0.2
0.4
0.6
0.8
1
-1
-0.5
0
0.5
1
0
0.5
1
0
0.2
0.4
0.6
0.8
1
-1
-0.5
0
0.5
1
17
3
11
25
3
11
17
27
11
17
23
29
25
27
29
31
32
1
s
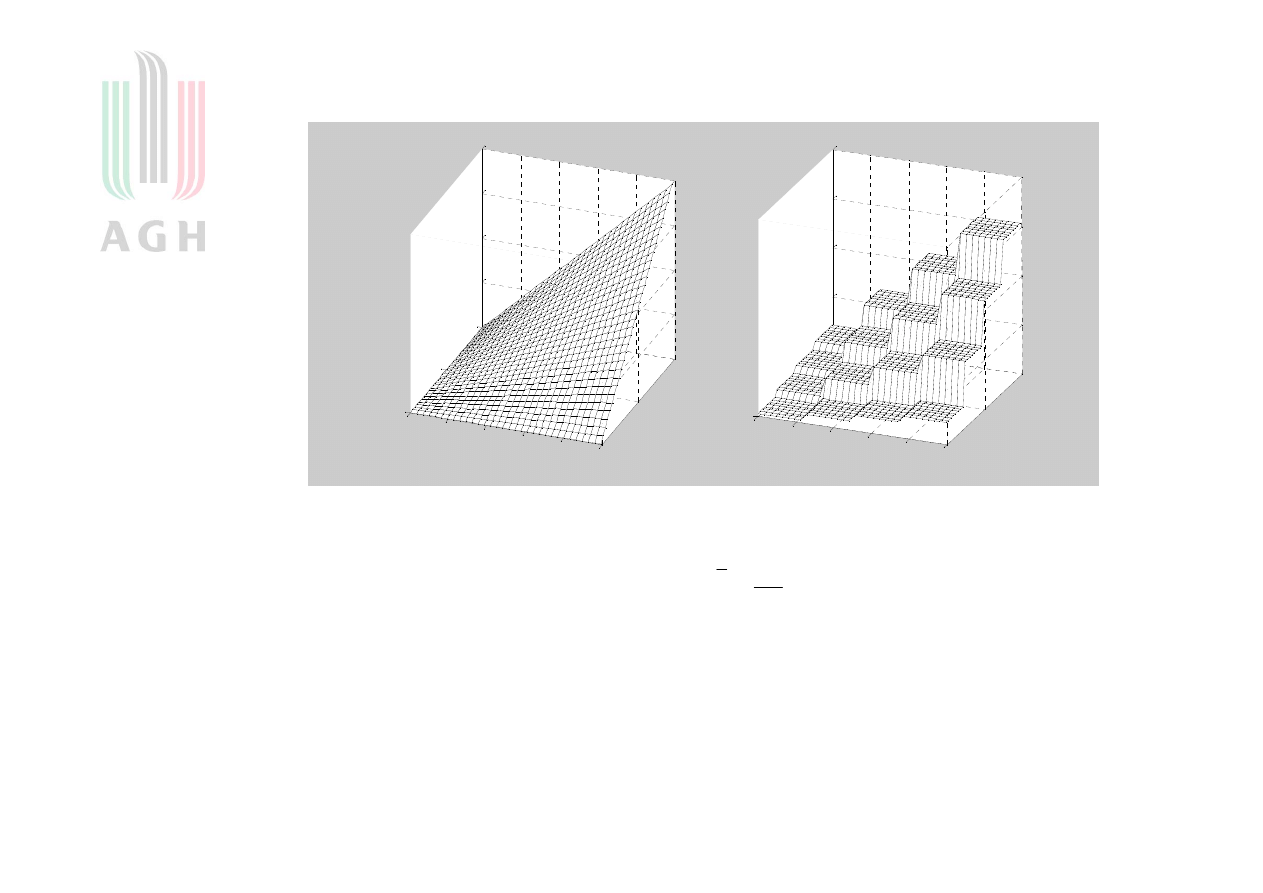
Obraz oryginalny (z lewej) i jego aproksymacja (z prawej)
utworzona przy pomocy funkcji Walsha, niby szesnastu ale w
praktyce tylko dziewięciu
Wyszukiwarka
Podobne podstrony:
10 0 Reprezentacja Binarna
10 Reprezentacja liczb w systemie komputerowymid 11082 ppt
Algorytmy i struktury danych Wykład 1 Reprezentacja informacji w komputerze
01 reprezentacja danychid 2917
02 poznawcza reprezentacje 2009 2010 st2
Reprezentacja
XII. ZASADa reprezentacji politycznej PRAWo WYBORCZE, Studia
Notatki z wykładów, Prawo Konstytucyjne - Wykład 10, 11 - Partie Polityczne, DEMOKRACJA POŚREDNIA (r
pkt 9, Psychologia narracyjna - narracyjne konstruowanie poznawczej reprezentacji rzeczywistości, me
Sysetemy szsnastkowy i inne, Systemy bianrny,dziesietny,szesnastkowy, Reprezentacje liczb
spr3sprawozdanie z DTM w VSD, DEFINICJA I REPREZENTACJA
Reprezentacja cyfrowa analogowa informacji
Formy reprezentacji umysłowych, psych
sprawdzian z reprezentacji liczb gr A
PZPR reprezentował na pogrzebie Stalina Bierut
412 problem reprezentacjihj
więcej podobnych podstron