Strona 1

Ciągi liczbowe - Materiały do druku, Ciąg arytmetyczny, geometryczny, Suma ciągu, różnica, iloraz - Leniwiec.edu.pl

2010-02-08 16:04:12

http://www.leniwiec.edu.pl/index2.php?option=com_content&task=view&id=90&pop=1&page=0&Itemid=88

Ciągi liczbowe - Materiały do druku

Potrzebne definicje, wzory i oznaczenia

1. Niech

i

będą liczbami dodatnimi

liczbę

nazywamy średnią arytmetyczną liczb

i

liczbę

nazywamy średnią geometryczną liczb

i

2. Wzory, które trzeba pamiętać

suma

początkowych liczb naturalnych

suma kolejnych potęg (od zera do

) liczby

3. Niech

będzie funkcją określoną na zbiorze

liczb naturalnych o wartościach w zbiorze liczb rzeczywistych, krótko:

Taką funkcję nazywamy ciągiem liczbowym, "ciągiem

" i zamiast powyższego oznaczenia piszemy

Wartości tej funkcji, czyli

oznaczamy

i nazywamy wyrazami ciągu

4. Ciąg jest rosnący wtedy i tylko wtedy, gdy dla każdej liczby naturalnej dodatniej, każdy następny wyraz ciągu jest większy od poprzedniego, czyli

5. Ciąg jest malejący wtedy i tylko wtedy, gdy dla każdej liczby naturalnej dodatniej, każdy następny wyraz ciągu jest mniejszy od poprzedniego, czyli

6. Definicja rekurencyjna ciągu

Podajemy wartość wyrazu pierwszego lub kilku pierwszych wyrazów oraz regułę wg której można obliczyć wyraz

gdy znamy wyrazy poprzednie.

Np. sławny ciąg, który zwykle definiuje się rekurencyjnie - ciąg Fibonacciego (o nim na naszych stronach w tekście "Ciąg Fibonacciego"). Zdefiniowany jest tak:

Jego początkowe wyrazy to: 1, 1, 2, 3, 5, 8, 13, 21, ...

Ciąg arytmetyczny

Definicja rekurencyjna

jest ciągiem arytmetycznym, jeżeli istnieje taka liczba

, że dla każdego

zachodzi równość:

czyli
Wyraz pierwszy

należy podać.

Każdy wyraz ciągu arytmetycznego - oprócz pierwszego - otrzymujemy dodając do poprzedniego tą samą liczbę

.

Liczbę

nazywa się różnicą ciągu.

W ciągu arytmetycznym różnica między kolejnymi wyrazami jest stała:

Ciąg arytmetyczny jest określony, jeżeli znamy jego wyraz pierwszy

i różnicę

. Wtedy:

...

Strona 2

Ciągi liczbowe - Materiały do druku, Ciąg arytmetyczny, geometryczny, Suma ciągu, różnica, iloraz - Leniwiec.edu.pl

2010-02-08 16:04:12

http://www.leniwiec.edu.pl/index2.php?option=com_content&task=view&id=90&pop=1&page=0&Itemid=88

Otrzymaliśmy wzór na wyraz ogólny ciągu arytmetycznego

Definicja przez podanie wyrazu ogólnego

Ciąg

, którego wyraz ogólny ma postać

, gdzie

jest ciągiem arytmetycznym.

Własności ciągu arytmetycznego

Monotoniczność - ciąg arytmetyczny jest:

- rosnący, gdy

- stały, gdy

- malejący, gdy

Jeżeli

jest ciągiem arytmetycznym, to dla każdej trójki kolejnych wyrazów ciągu

zachodzi równość

która oznacza, że każdy wyraz ciągu arytmetycznego, oprócz pierwszego i ostatniego, jest średnią arytmetyczną wyrazów sąsiadujących - stąd nazwa ciągu.

Suma skończonej liczby kolejnych wyrazów ciągu arytmetycznego

Przez

oznaczamy sumę

kolejnych wyrazów ciągu zaczynając od wyrazu pierwszego

Łatwo jest pokazać, że

Równości te wynikają z tego, że suma wyrazów ciągu arytmetycznego równo odległych od początku i końca ciągu jest taka sama i równa

Piszemy

i po dodaniu stronami otrzymujemy:

a stąd

O pewnych ciągach arytmetycznych (i innych)

Kolejne liczby naturlane 1,2,3, ... ,

, ... tworzą ciąg arytmetyczny o różnicy 1,

Ze wzoru na

otrzymujemy:

czyli wzór na sumę kolejnych liczb naturalnych od 1 do

. Suma taka pojawia się często nie tylko w matematyce, czy fizyce.

Weźmy sumę

kolejnych liczb nieparzystych

oczywiście

W 1837r Lejeune Dirichlet udowodnił bardzo ważne klasyczne twierdzenie o postępie arytmetycznym

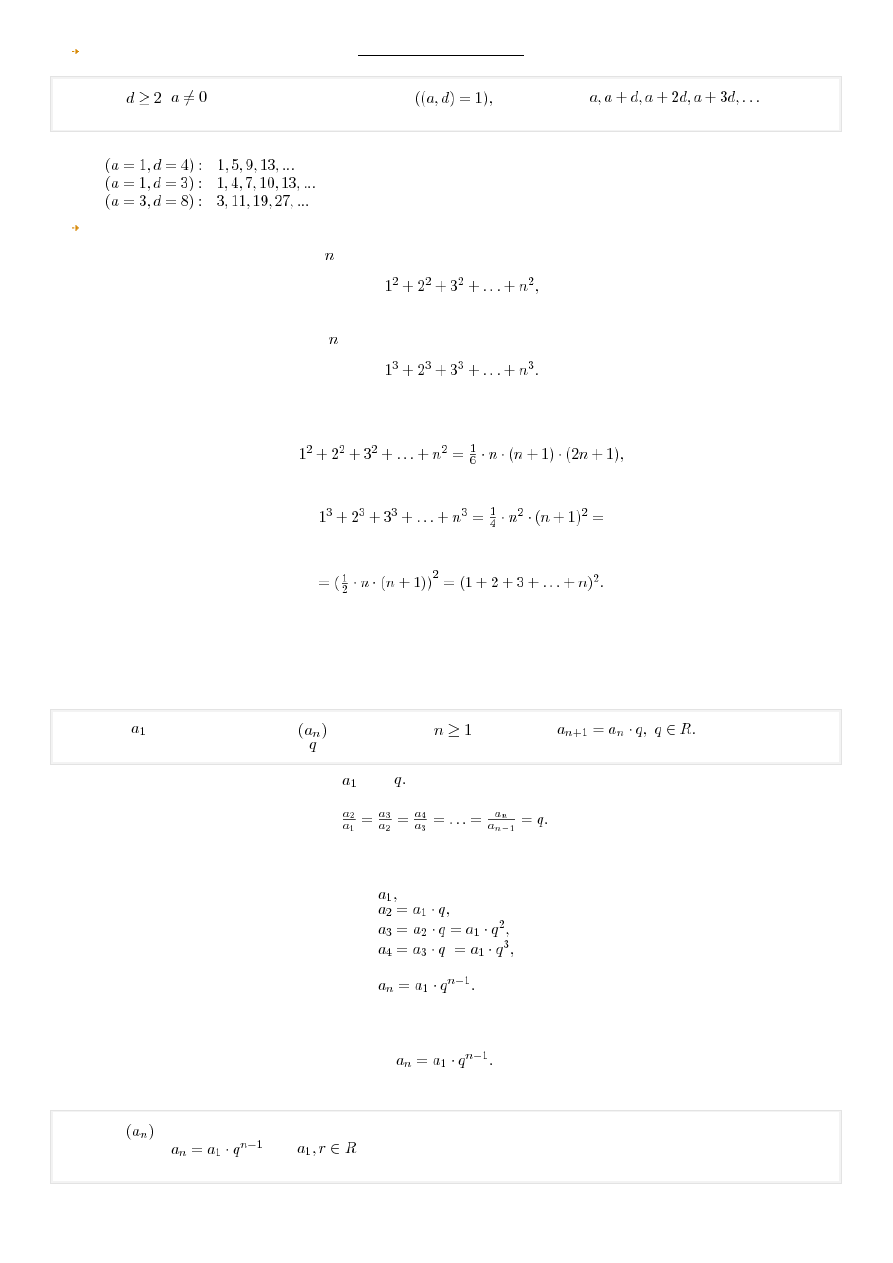
Strona 3

Ciągi liczbowe - Materiały do druku, Ciąg arytmetyczny, geometryczny, Suma ciągu, różnica, iloraz - Leniwiec.edu.pl

2010-02-08 16:04:12

http://www.leniwiec.edu.pl/index2.php?option=com_content&task=view&id=90&pop=1&page=0&Itemid=88

W 1837r Lejeune Dirichlet udowodnił bardzo ważne, klasyczne twierdzenie o postępie arytmetycznym

Jeśli

i

są względnie pierwszymi liczbami całkowitymi

to ciąg arytmetyczny

zawiera

nieskończenie wiele liczb pierwszych.

Np. każdy z poniższych ciągów zawiera nieskończenie wiele liczb pierwszych:
1.

2.

3.

Jeszcze o sumach ciągów, które nie są ciągami arytmetycznymi

1. suma kwadratów kolejnych liczb naturalnych od 1 do

2. suma sześcianów kolejnych liczb naturalnych od 1 do

Takie sumy pojawiają się często w fizyce i różnych działach matematyki. Warto więc pamiętać wyrażające je wzory:

Ciąg geometryczny

Definicja rekurencyjna

Niech

będzie wyrazem pierwszym ciągu

oraz niech dla każdego

zachodzi równość

Tak określony ciąg

nazywamy ciągiem geometrycznym, a liczbę

nazywamy ilorazem ciągu.

Ciąg geometryczny jest określony, gdy znamy jego wyraz pierwszy

i iloraz

Z definicji tej wynika też, że stosunek wyrazu następnego do poprzedniego, dla wszystkich wyrazów, jest stały.

Zgodnie z powyższą definicją mamy:

...

Otrzymaliśmy wzór na wyraz ogólny ciągu geometrycznego

Definicja przez podanie wyrazu ogólnego

Ciąg

, którego wyraz ogólny ma postać

, gdzie

jest ciągiem geometrycznym.

Własności ciągu geometrycznego

Strona 4

Ciągi liczbowe - Materiały do druku, Ciąg arytmetyczny, geometryczny, Suma ciągu, różnica, iloraz - Leniwiec.edu.pl

2010-02-08 16:04:12

http://www.leniwiec.edu.pl/index2.php?option=com_content&task=view&id=90&pop=1&page=0&Itemid=88

Monotoniczność - ciąg geometryczny, którego wyraz pierwszy

jest:

- rosnący, gdy

- stały, gdy

- malejący, gdy

Jeżeli

jest ciągiem geometrycznym o wyrazach dodatnich, to dla każdej trójki kolejnych wyrazów ciągu

zachodzi równość

która oznacza, że każdy wyraz ciągu geometrycznego, oprócz pierwszego i ostatniego, jest średnią geometryczną wyrazów sąsiadujących - stąd nazwa ciągu.

Suma skończonej liczby kolejnych wyrazów ciągu geometrycznego

Przez

oznaczamy sumę

kolejnych wyrazów ciągu zaczynając od wyrazu pierwszego

Łatwo jest udowodnić, że dla kązdego

i

zachodzi

W podręcznikach szkolnych podaje się zwykle następujący dowód

Odejmujemy te równości stronami i otrzymujemy

a stąd mamy

Zbieramy wzory do zapamiętania