Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

POLITECHNIKA POZNAŃSKA
Instytut Konstrukcji Budowlanych
Zakład Mechaniki Budowli

Projekt nr 1

LINIE WPŁYWOWE SIŁ W UKŁADACH STATYCZNIE WYZNACZALNYCH

BELKI

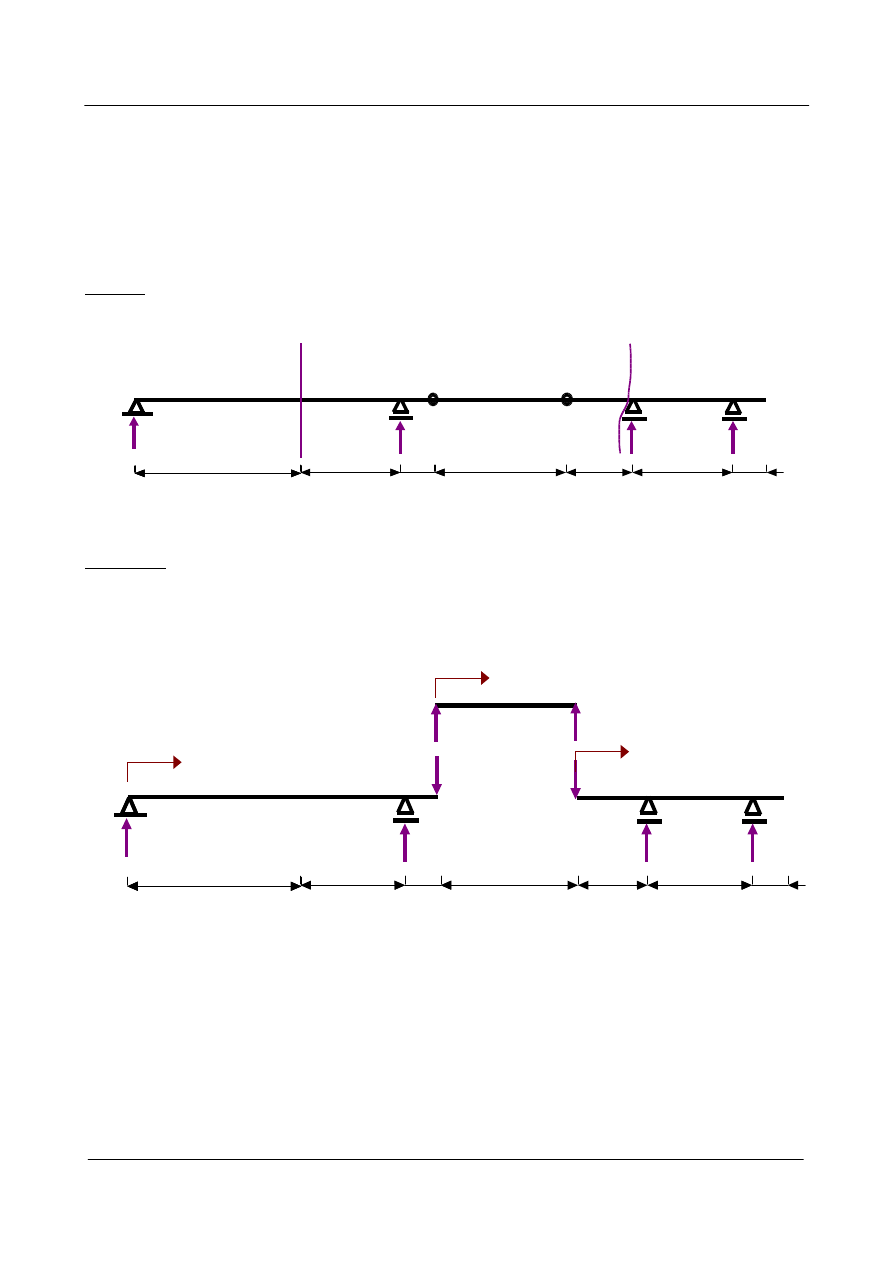
Zadanie 1: Dla belki pokazanej na rys.1.1. wyznaczyć linie wpływowe zaznaczonych wielkości statycznych.

α

α

β

β

5,0 m

3,0 m

1,0 m

5,0 m

5,0 m

4,0 m

2,0 m

3,0 m

1,0 m

A

B

C

D

E

F

Rys.1.1

Rozwiązanie:

1. Przyjmuję współrzędne x

1

, x

2

oraz x

3

określające położenie siły P=1 jak na rys.1.2

R

A

5,0 m

3,0 m

1,0 m

5,0 m

5,0 m

4,0 m

2,0 m

3,0 m

1,0 m

R

B

R

C

R

C

R

D

R

D

R

E

R

F

x

1

x

2

x

3

Rys.1.2

Przy czym :

x

1

∈〈0 ; 9 〉

x

2

∈〈0 ; 4 〉

x

3

∈〈0 ; 6 〉

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

1/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

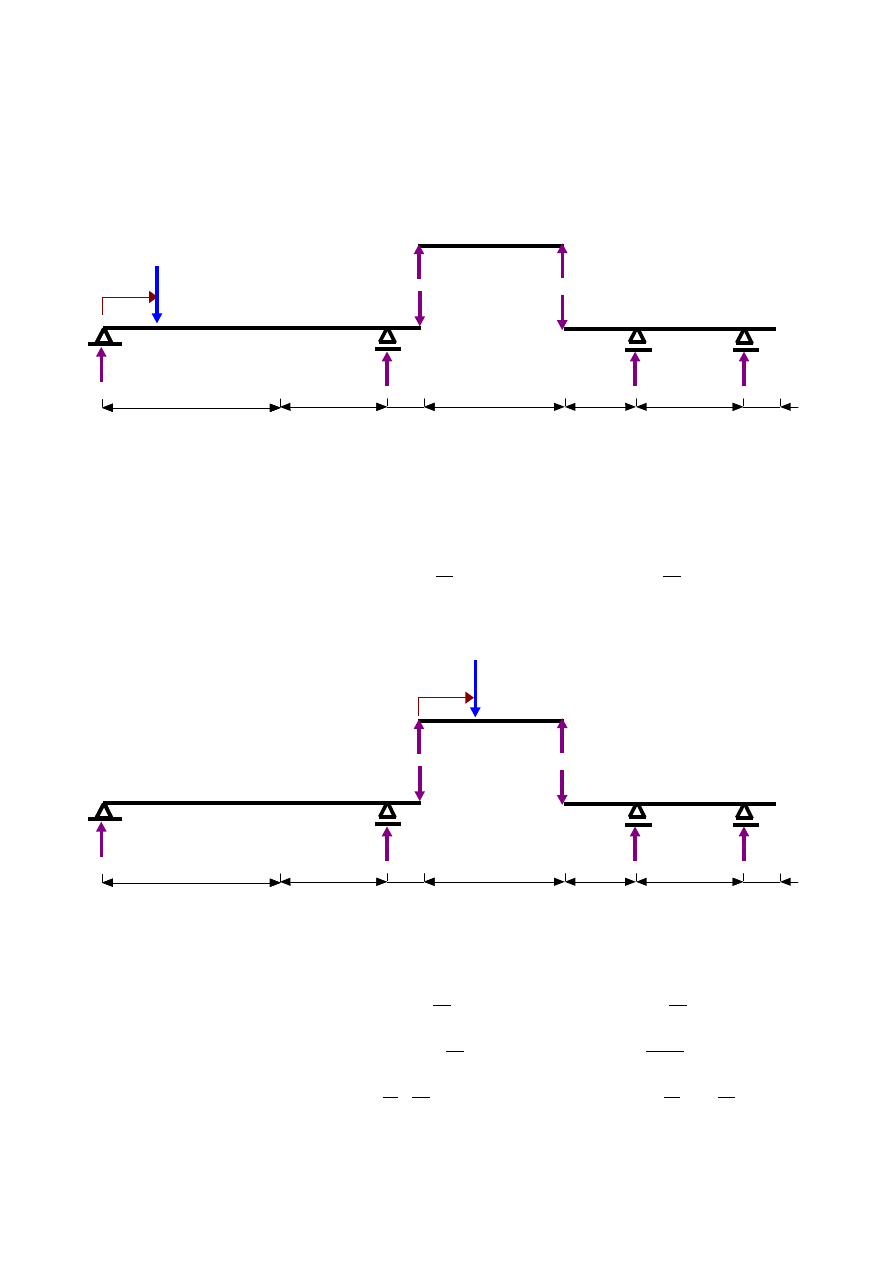
2. Wyznaczenie funkcji reakcji podporowych w zależności od współrzędnej położenia siły P=1 [-]

a)

x

1

∈〈0 ; 9 〉

R

A

5,0 m

3,0 m

1,0 m

5,0 m

5,0 m

4,0 m

2,0 m

3,0 m

1,0 m

R

B

R

C

R

C

R

D

R

D

R

E

R

F

x

1

P=1 [-]

Rys.1.3

Z warunków równowagi dla belki statycznie wyznaczalnej:

•

dla części środkowej belki:

R

C

=0

[-] oraz

R

D

=0

[-]

•

dla części prawej belki:

R

E

=0

[-] oraz

R

F

=0

[-]

•

dla części lewej belki:

∑

M

A

=0 : R

B

=

x

1

8

[-] oraz

∑

Y =0 : R

A

=1−

x

1

8

[-]

b)

x

2

∈〈0 ; 4 〉

R

A

5,0 m

3,0 m

1,0 m

5,0 m

5,0 m

4,0 m

2,0 m

3,0 m

1,0 m

R

B

R

C

R

C

R

D

R

D

R

E

R

F

x

2

P=1 [-]

Rys.1.4

Z warunków równowagi dla belki statycznie wyznaczalnej:

•

dla części środkowej belki:

∑

M

C

=0 : R

D

=

x

2

4

[-] oraz

∑

Y =0 : R

C

=1−

x

2

4

[-]

•

dla części prawej belki:

∑

M

E

=0 : R

F

=−

x

2

6

[-] oraz

∑

Y =0 : R

E

=

5 ⋅x

2

12

[-]

•

dla części lewej belki:

∑

M

B

=0 : R

A

=

1
8

⋅

x

2

4

−1

[-] oraz

∑

M

A

=0 : R

B

=

9
8

⋅1−

x

2

4



[-]

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

2/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

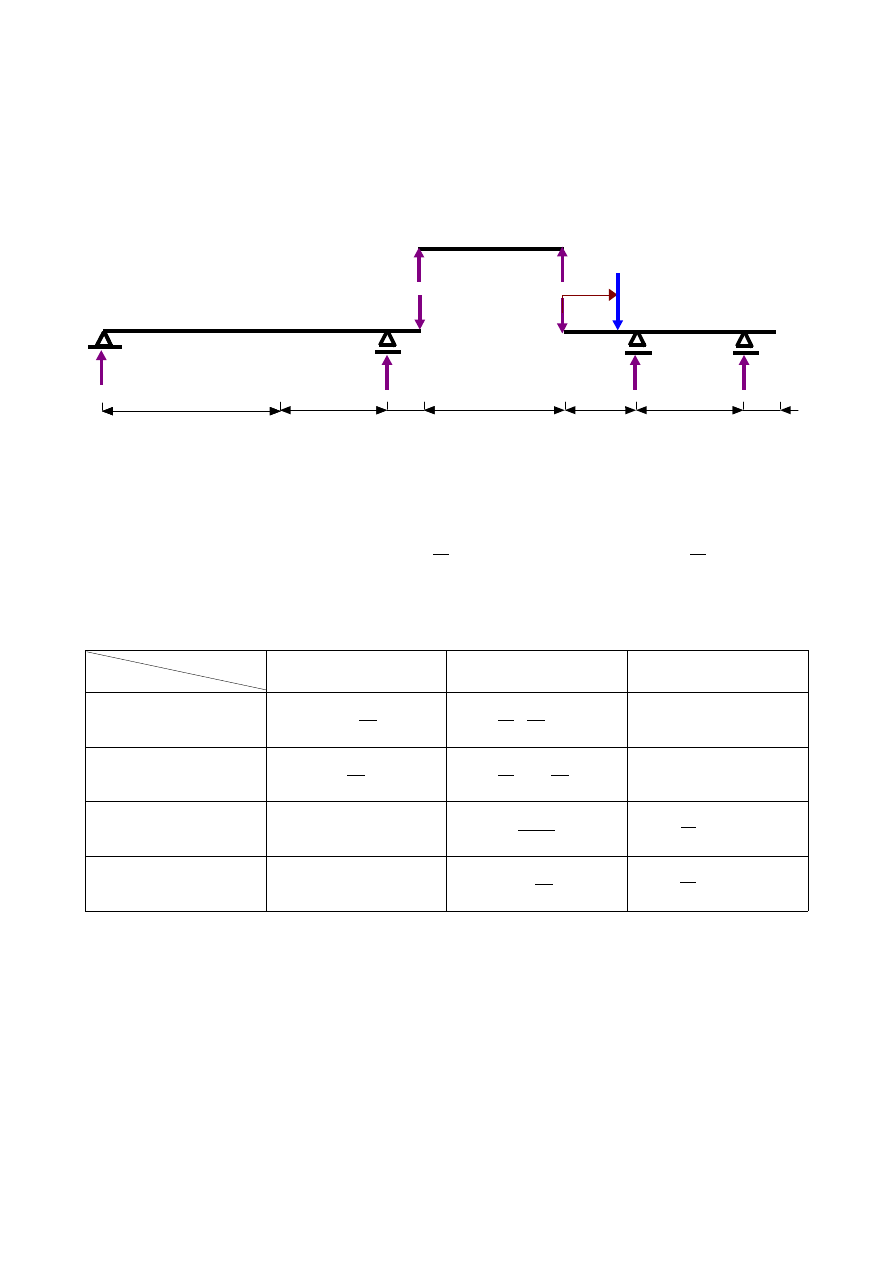
c)

x

3

∈〈0 ; 6 〉

R

A

5,0 m

3,0 m

1,0 m

5,0 m

5,0 m

4,0 m

2,0 m

3,0 m

1,0 m

R

B

R

C

R

C

R

D

R

D

R

E

R

F

x

3

P=1 [-]

Rys.1.5

Z warunków równowagi dla belki statycznie wyznaczalnej:

•

dla części środkowej belki:

R

C

=0

[-] oraz

R

D

=0

[-]

•

dla części prawej belki:

∑

M

E

=0 : R

F

=

1
3

⋅ x

3

−2

[-] oraz

∑

Y =0 : R

E

=

1
3

⋅5− x

3



[-]

•

dla części lewej belki:

R

A

=0

[-] oraz

R

B

=0

[-]

d) zestawienie funkcji reakcji podporowych w zależności od wartości współrzędnej x

współrzędna
reacja

x

1

∈〈0 ; 9 〉

x

2

∈〈0 ; 4 〉

x

3

∈〈0 ; 6 〉

R

A

[-]

1−

x

1

8

1
8

⋅

x

2

4

−1

0

R

B

[-]

x

1

8

9
8

⋅1−

x

2

4



0

R

E

[-]

0

5 ⋅x

2

12

1
3

⋅5− x

3



R

F

[-]

0

−

x

2

6

1
3

⋅ x

3

−2

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

3/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

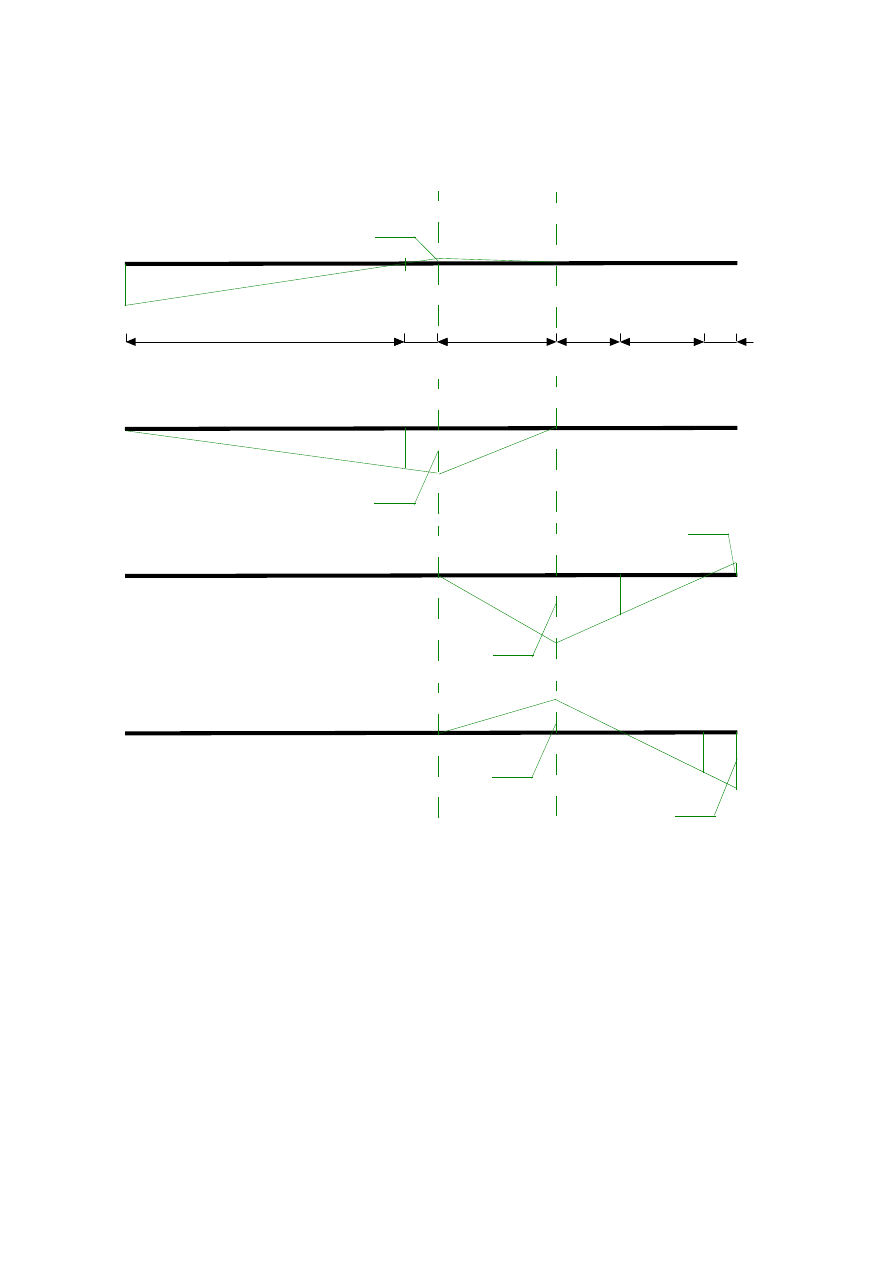
3. Wykreślenie linii wpływowych reakcji podporowych

1

+

-0,125

0

0

1

R

A

(x)[-]

0

+

1,125

0

1

R

B

(x)[-]

+

0

+

1,667

0

1

R

E

(x)[-]

+

-0,333

-

0

-

-0,667

0

1

R

F

(x)[-]

+

1,333

-

8,0 m

4,0 m

2,0 m

3,0 m

1,0 m

1,0 m

Rys.1.6

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

4/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

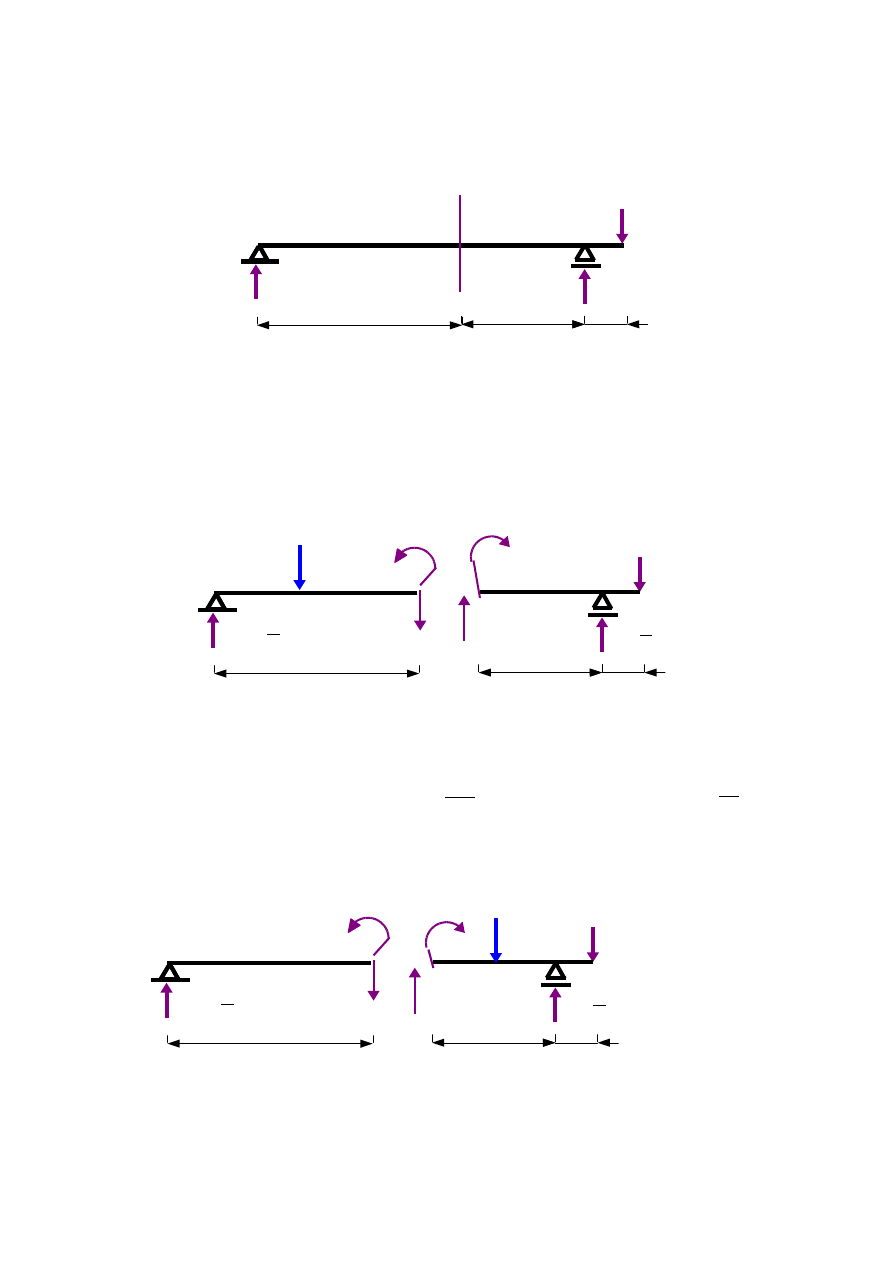
4. Wyznaczenie funkcji sił przekrojowych w przekroju β-β w zależności od współrzędnej położenia siły P=1 [-]

Rachunki przeprowadzam dla belki ABC, na której określony jest przekrój β-β jak na rys.1.7

3,0 m

1,0 m

5,0 m

R

B

R

A

R

C

β

β

Rys.1.7

a)

x

1

∈〈0 ;5 〉

- siła przed przekrojem β-β , rys.1.8

3,0 m

1,0 m

5,0 m

M

β

(x)

M

β

(x)

T

β

(x)

T

β

(x)

R

A

=1−

x

1

8

R

B

=

x

1

8

R

C

=0

P=1 [-]

Rys.1.8

Z warunków równowagi dla belki:

*dla części prawej:

∑

Y =0 : T



 x=

−x

1

8

[-] oraz

∑

M

−

=0 : M



 x=

3

8

x

1

[m]

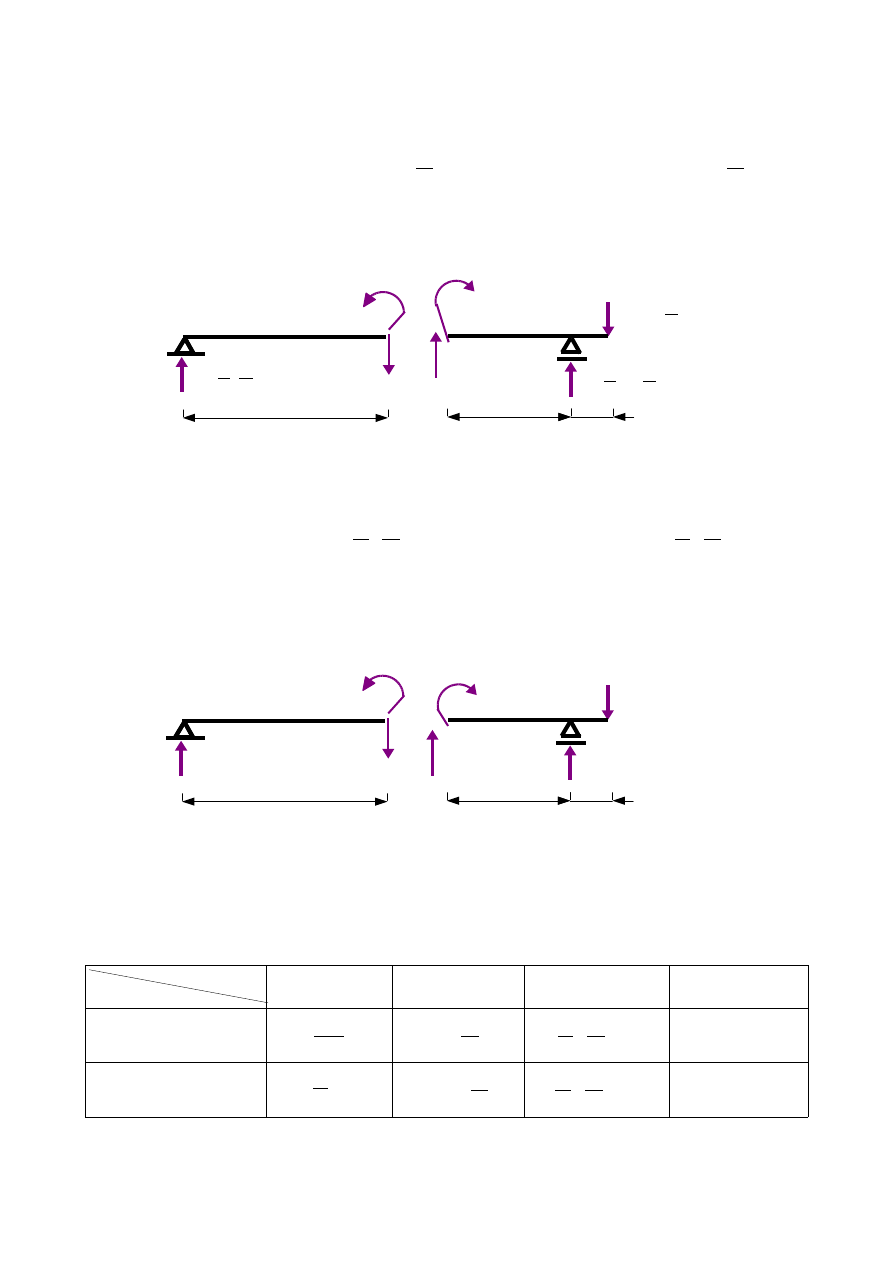
b)

x

1

∈〈5 ; 9 〉

- siła za przekrojem β-β , rys.1.9

3,0 m

1,0 m

5,0 m

M

β

(x)

M

β

(x)

T

β

(x)

T

β

(x)

R

A

=1−

x

1

8

R

B

=

x

1

8

R

C

=0

P=1 [-]

Rys.1.9

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

5/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

Z warunków równowagi dla belki:

*dla części lewej:

∑

Y =0 : T



 x=1−

x

1

8

[-] oraz

∑

M

−

=0 : M



 x=5 ⋅1−

x

1

8



[m]

c)

x

2

∈〈0 ; 4 〉

- rys.1.10

3,0 m

1,0 m

5,0 m

M

β

(x)

M

β

(x)

T

β

(x)

T

β

(x)

R

A

=

1
8

⋅

x

2

4

−1

R

C

=1−

x

2

4

R

B

=

9
8

⋅1−

x

2

4



Rys.1.10

Z warunków równowagi dla belki:

*dla części lewej:

∑

Y =0 : T



 x=

1
8

⋅

x

2

4

−1

[-] oraz

∑

M

−

=0 : M



 x=

5
8

⋅

x

2

4

−1

[m]

d)

x

3

∈〈0 ; 6 〉

- rys.1.11

3,0 m

1,0 m

5,0 m

M

β

(x)

M

β

(x)

T

β

(x)

T

β

(x)

R

A

=0

R

C

=0

R

B

=0

Rys.1.11

Z warunków równowagi dla belki:

*dla części lewej:

∑

Y =0 : T



 x=0

[-] oraz

∑

M

−

=0 : M



 x=0

[m]

e) zestawienie funkcji sił przekrojowych w przekroju β-β w zależności od wartości współrzędnej x

współrzędna
siła wewnętrzna

x

1

∈〈0 ;5 〉

x

1

∈〈5 ; 9 〉

x

2

∈〈0 ; 4 〉

x

3

∈〈0 ; 6 〉

T

β-β

[-]

−x

1

8

1−

x

1

8

1
8

⋅

x

2

4

−1

0

M

β-β

[m]

3
8

x

1

5 ⋅1−

x

1

8



5
8

⋅

x

2

4

−1 

0

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

6/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

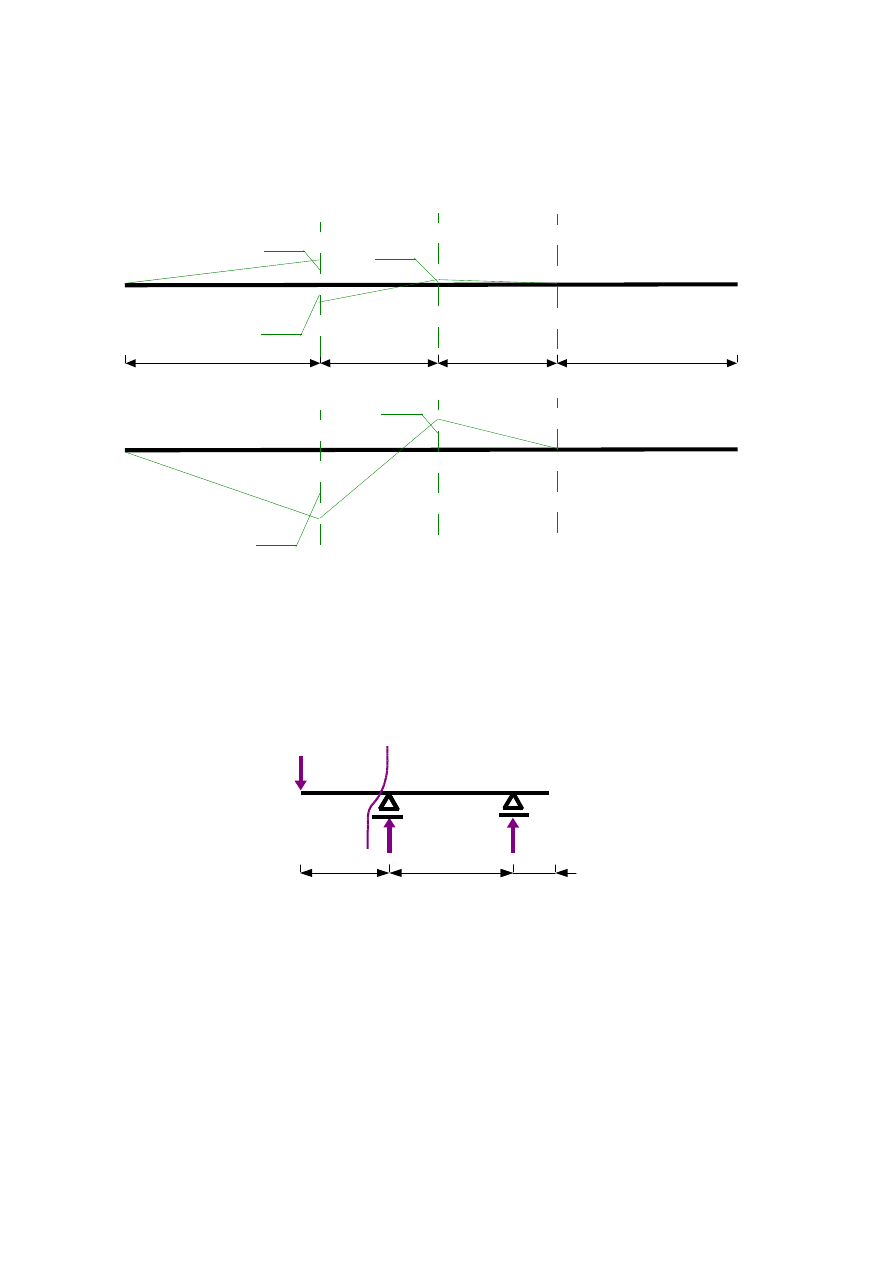
5. Wykreślenie linii wpływowych sił przekrojowych w przekroju β-β

+

-0,125

0

0

T

β-β

(x)[-]

0

+

0

+

5,0 m

4,0 m

6,0 m

4,0 m

-

0,375

-0,625

1,875

-0,625

-

-

M

β-β

(x)[m]

Rys.1.12

6. Wyznaczenie funkcji sił przekrojowych w przekroju α-α w zależności od współrzędnej położenia siły P=1 [-]

Rachunki przeprowadzam dla belki DEF, na której określony jest przekrój α-α jak na rys.1.13

3,0 m

1,0 m

2,0 m

R

F

R

E

R

D

α

α

Rys.1.13

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

7/37

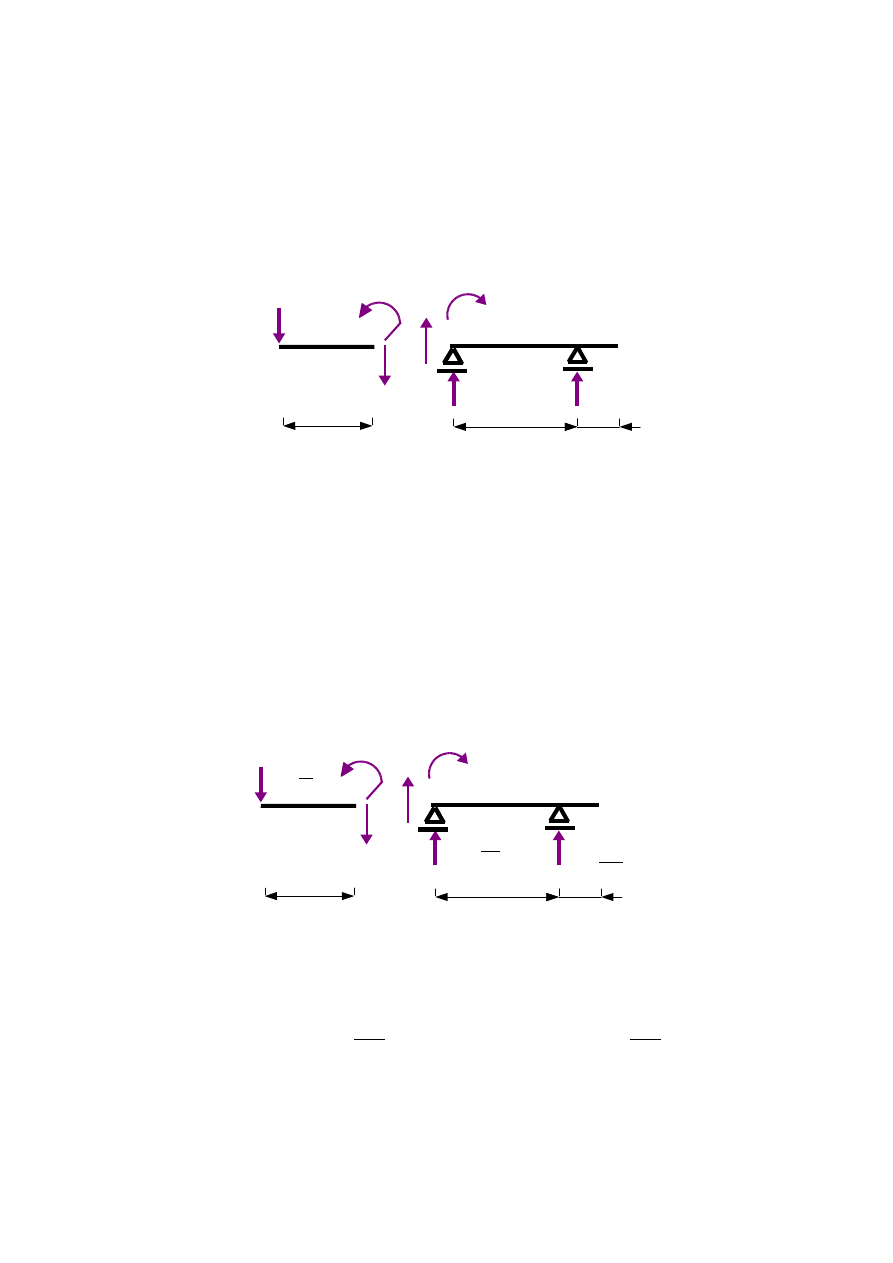
Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

a)

x

1

∈〈0 ; 9 〉

- rys.1.14

3,0 m

1,0 m

2,0 m

M

α

(x)

T

α

(x)

T

α

(x)

M

α

(x)

R

D

=0

R

E

=0

R

F

=0

Rys.1.14

Z warunków równowagi dla belki:

*dla części lewej:

∑

Y =0 : T



 x=0

[-] oraz

∑

M

−

=0 : M



 x=0

[m]

b)

x

2

∈〈0 ; 4 〉

- rys.1.15

3,0 m

1,0 m

2,0 m

M

α

(x)

T

α

(x)

T

α

(x)

M

α

(x)

R

D

=

x

2

4

R

E

=

5

12

x

2

R

F

=

−x

2

6

Rys.1.15

Z warunków równowagi dla belki:

*dla części lewej:

∑

Y =0 : T



 x=

−x

2

4

[-] oraz

∑

M

−

=0 : M



 x=

−x

2

2

[m]

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

8/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

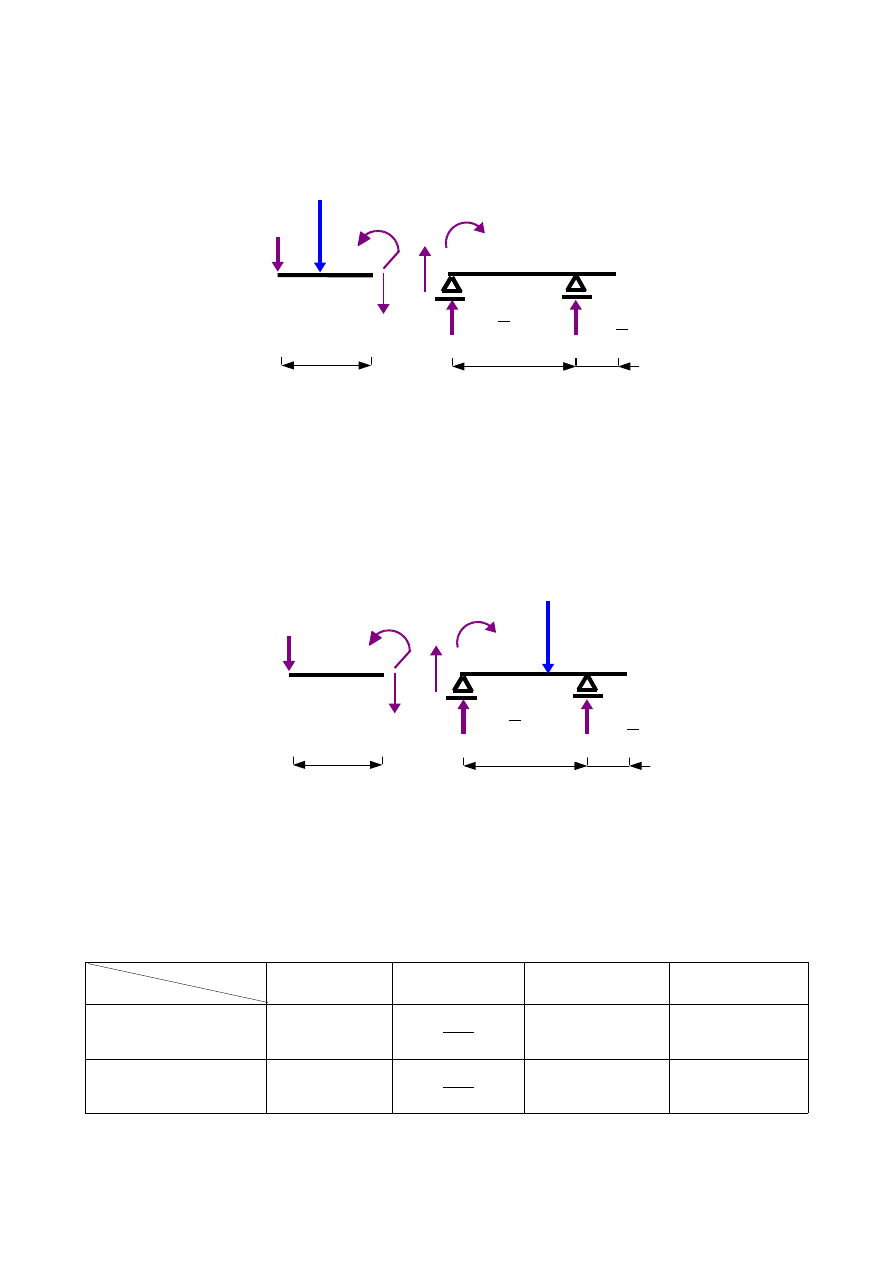
c)

x

3

∈〈0 ; 2 〉

- siła przed przekrojem α-α , jak na rys.1.16

3,0 m

1,0 m

2,0 m

M

α

(x)

T

α

(x)

T

α

(x)

M

α

(x)

R

D

=0

R

E

=

1
3

⋅5−x

3



R

F

=

1
3

 x

3

−2

P=1 [-]

Rys.1.16

Z warunków równowagi dla belki:

*dla części lewej:

∑

Y =0 : T



 x=−1

[-] oraz

∑

M

−

=0 : M



 x= x

3

−2

[m]

d)

x

3

∈〈2 ; 6 〉

- siła za przekrojem α-α , jak na rys.1.17

3,0 m

1,0 m

2,0 m

M

α

(x)

T

α

(x)

T

α

(x)

M

α

(x)

R

D

=0

R

E

=

1
3

⋅5−x

3



R

F

=

1
3

 x

3

−2

P=1 [-]

Rys.1.17

Z warunków równowagi dla belki:

*dla części lewej:

∑

Y =0 : T



 x=0

[-] oraz

∑

M

−

=0 : M



 x=0

[m]

e) zestawienie funkcji sił przekrojowych w przekroju β-β w zależności od wartości współrzędnej x

współrzędna
siła wewnętrzna

x

1

∈〈0 ; 9 〉

x

2

∈〈0 ; 4 〉

x

3

∈〈0 ; 2 〉

x

3

∈〈2 ; 6 〉

T

α-α

[-]

0

−x

2

4

−1

0

M

α-α

[m]

0

−x

2

2

x

3

−2

0

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

9/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

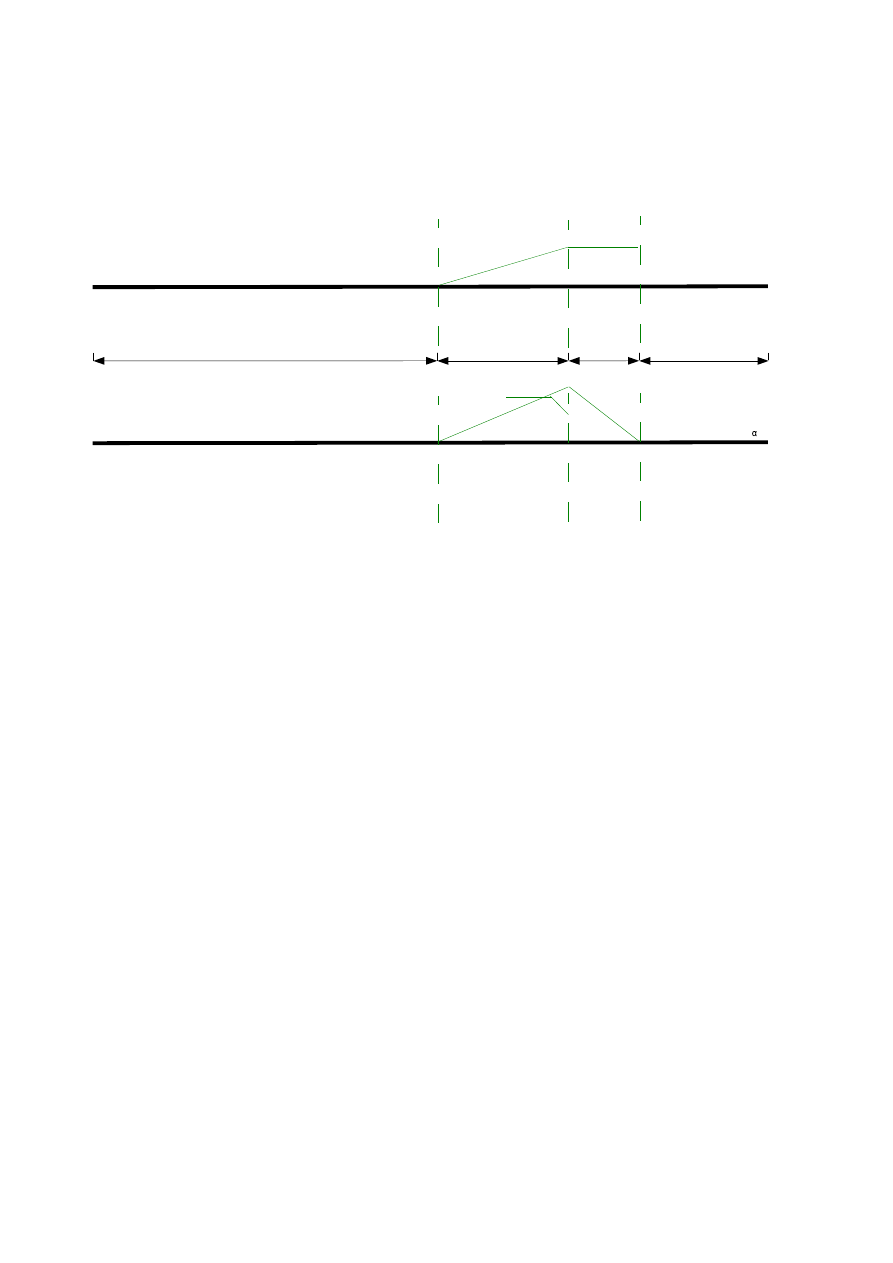
1. Wykreślenie linii wpływowych sił przekrojowych w przekroju α-α

-1

0

0

T

α-α

(x)[-]

0

0

9,0 m

4,0 m

2,0 m

4,0 m

-

-2

-

-

M

-α

(x)[m]

-1

0

0

Rys.1.18

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

10/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

Projekt nr 1

LINIE WPŁYWOWE SIŁ W UKŁADACH STATYCZNIE WYZNACZALNYCH

ŁUKI I RAMY TRÓJPRZEGUBOWE

Zadanie : Dla łuku trójprzegubowego parabolicznego pokazanego na rys.2.1. wyznaczyć linie wpływowe zaznaczonych
wielkości statycznych.

3,0 m

2,0

6,0

5,0

3,0

3,0

α

β

α

β

5

,0

m

A

C

B

Rys.2.1

Rozwiązanie:
1. Przyjmuję układ współrzędnych x,y określających położenie siły P=1 [-] jak na rys. 2.2.

3,0 m

2,0

6,0

5,0

3,0

3,0

α

β

α

β

5

,0

m

R

A

(x)

C

B

x

R

B

(x)

H

A

(x)

H

B

(x)

y

x

Rys.2.2.

Przy czym :

x ∈〈0 ; 16 〉

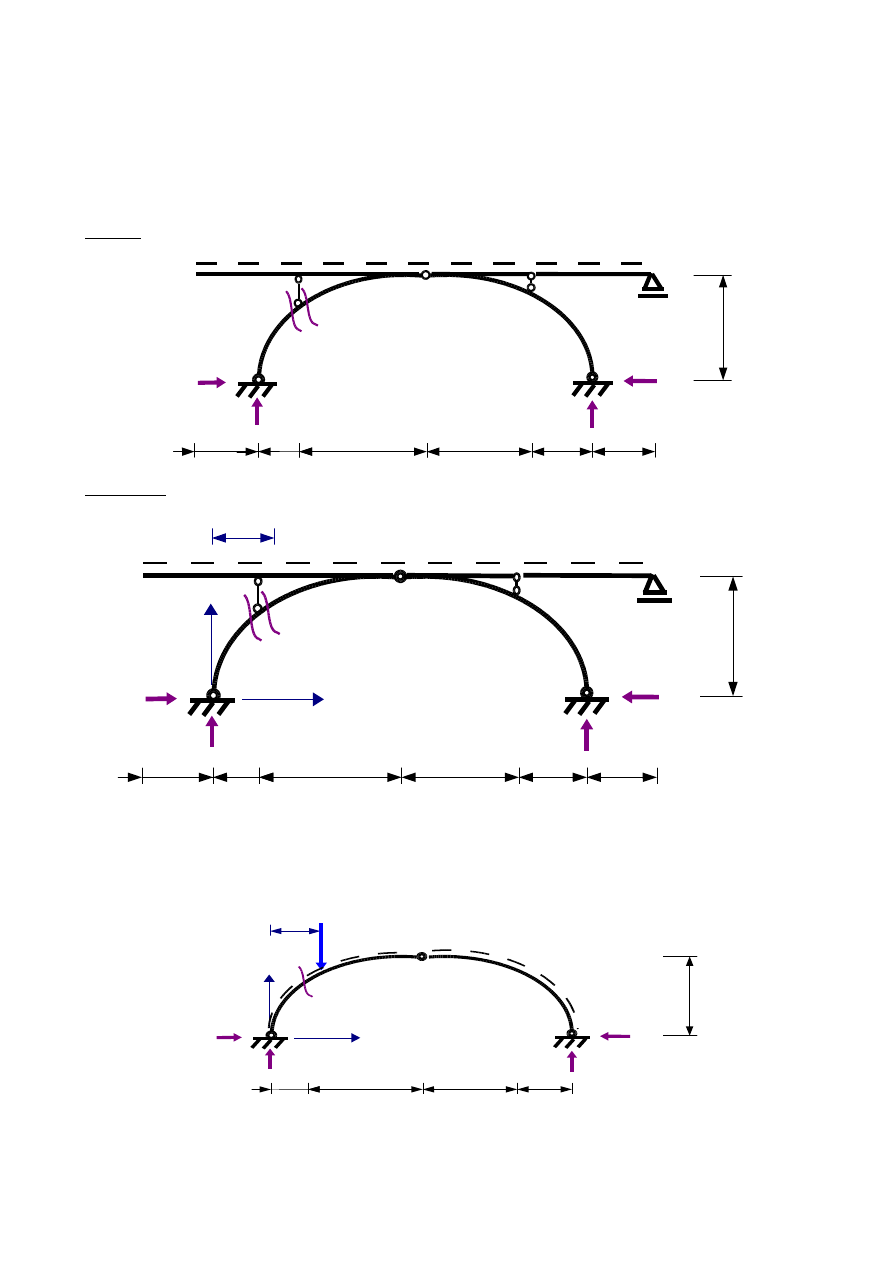
Aby wyznaczyć linie wpływowe wielkości statycznych w przypadku łuku z pomostem pośrednim jako miejscem
działania siły jednostkowej P, początkowo należy przeprowadzić rozważania dla analogicznej konstrukcji bez pomostu
pośredniego, jak na rys.2.3:

2,0

6,0

5,0

3,0

β

β

5

,0

m

R

A

(x)

C

B

x

R

B

(x)

H

A

(x)

H

B

(x)

x

y

P=1[-]

Rys. 2.3.

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

11/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

Wykonanie wykresów linii wpływowych sił reakcji oraz sił przekrojowych dla łuku “uproszczonego” oraz

naniesienie na nich drobnych zmian zgodnie z określonymi zasadami doprowadzi do uzyskania wykresów linii wpływu
sił w wyjściowym układzie.

Ponieważ przekroje α-α oraz β-β w wyjściowym łuku leżą bardzo blisko siebie w przypadku łuku bez pomostu

pośredniego ograniczam sie do wyznaczenia sił przekrojowych w przekroju β-β.

2. Wyznaczenie równania paraboli łuku:

Ogólna postać równania paraboli:

y=ax

2

bxc

W tym przypadku parabola przechodzi przez trzy punkty, których współrzędne łatwo określić:

A0,0

B 16,0

C 8,5

Z układu trzech równań:

0=a⋅0 b⋅0 c

0=a⋅16

2

b⋅16 c

5=a⋅8

2

b⋅8c

Otrzymam współczynniki:

a=

−5

64

b=

5

4

c=0

Stąd równanie paraboli ma postać:

y=

−5

64

x

2



5
4

x

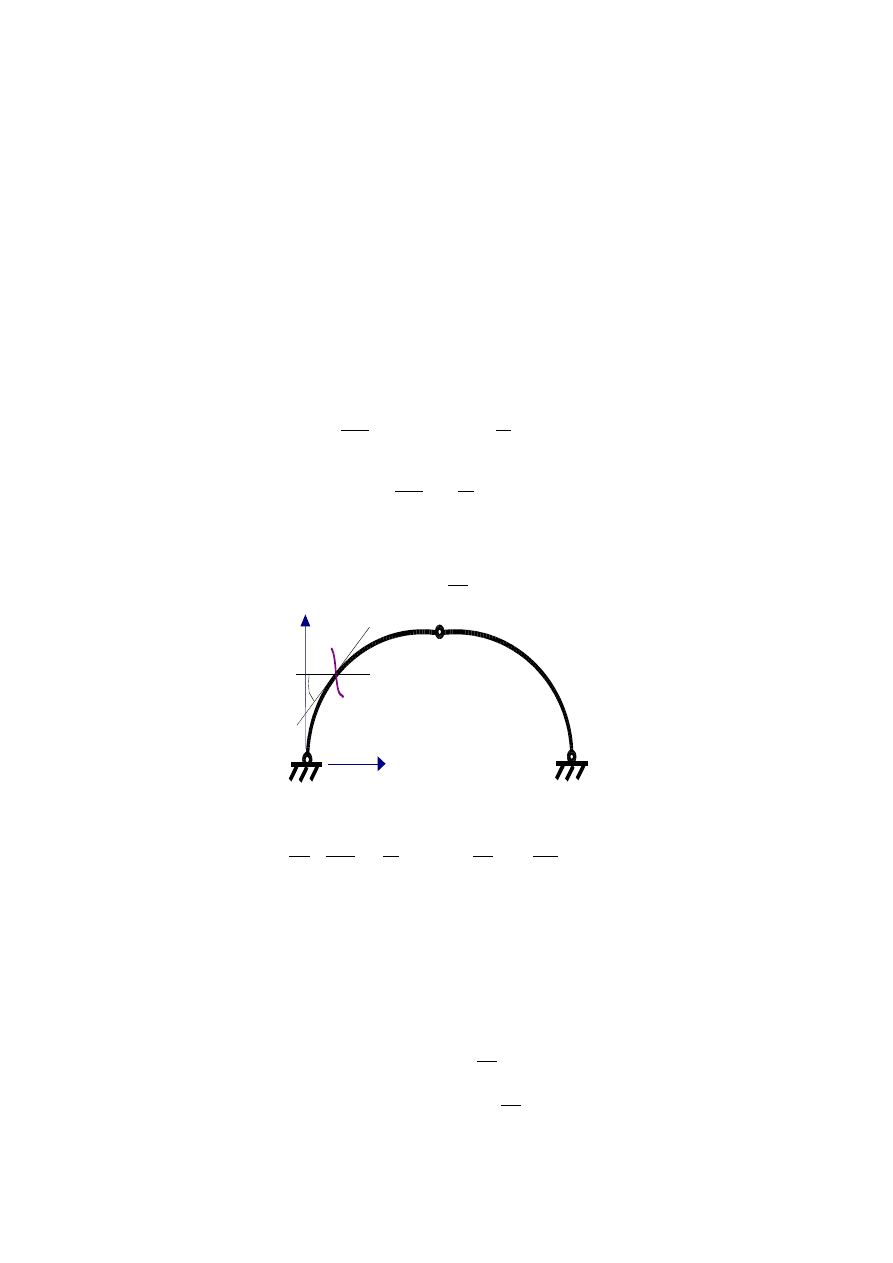
W miejscu przekroju x=2 [m], y=2,1875 [m]

Aby obliczyć kąt φ nachylenia stycznej (rys.2.4) w przekroju β-β korzystam z własności:

tg =

dy
dx

2

β

β

C

B

φ

x

y

Rys.2.4.

dy
dx

=

−5

32

x

5

4

a więc:

dy
dx

2=

15

16

=tg 

stąd:

=43,15

o

oraz

sin =0,6839

cos =0,7295

4. Wyznaczenie funkcji reakcji podporowych w zależności od położenia siły P=1 [-]

4.1.Dla układu jako całości

:

∑

X =0

mamy

H

A

 x=H

B

 x=H  x

[-]

∑

M

A

=0

mamy

R

B

 x=

x

16

[-]

∑

Y =0

mamy

R

A

 x=1−

x

16

[-]

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

12/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

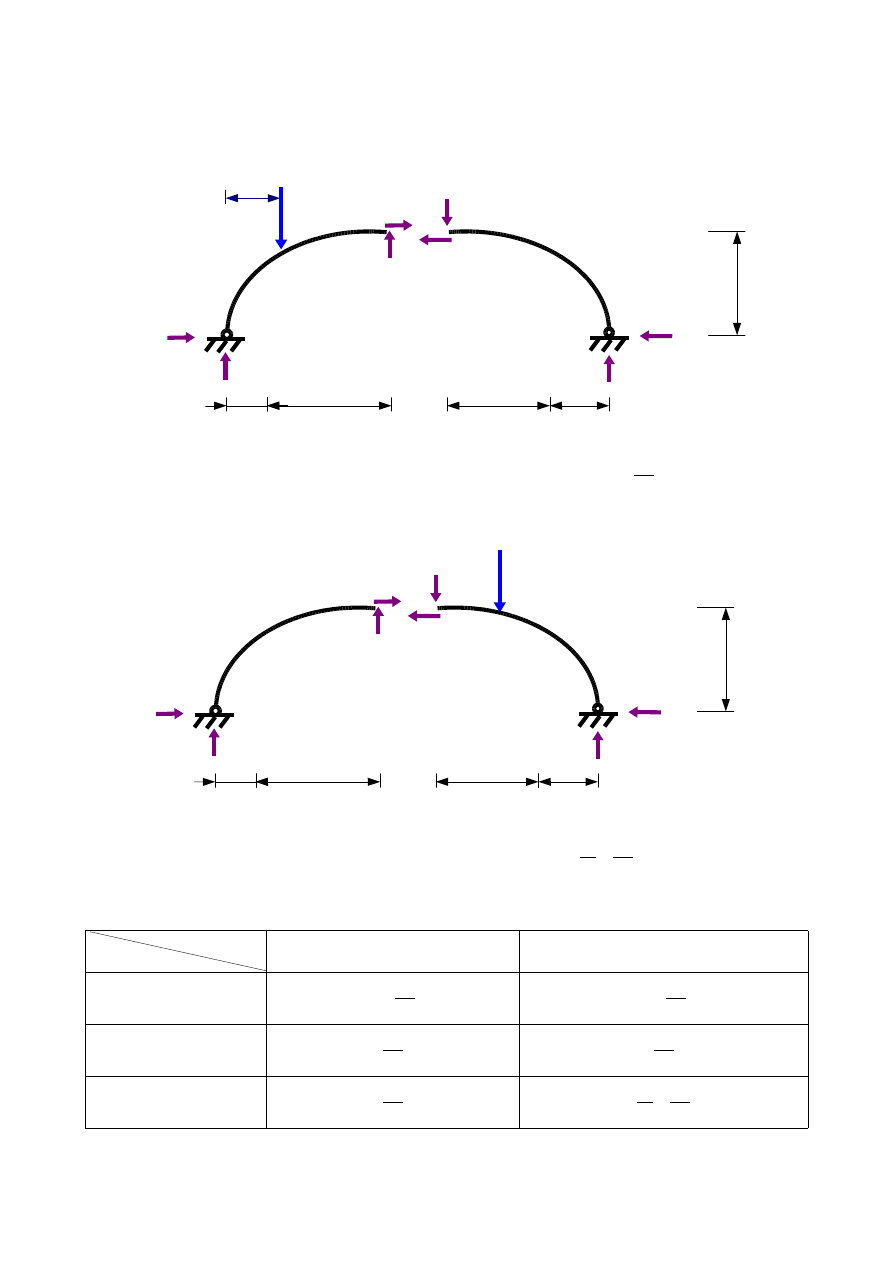
4.2. Dla łuku przeciętego przez przegub:

a)

x ∈〈0 ; 8 〉

2,0

6,0

5,0

3,0

5

,0

m

R

A

(x)

B

x

R

B

(x)

H

A

(x)

H

B

(x)

P=1[-]

V

c

(x)

V

c

(x)

H

c

(x)

H

C

(x)

Rys.2.5.

Z równowagi strony prawej:

∑

M

C

P

=5 H  x=8 R

B

 x

stąd

H  x =

x

10

[-]

b)

x ∈〈8 ; 16 〉

2,0

6,0

5,0

3,0

5

,0

m

R

A

(x)

B

R

B

(x)

H

A

(x)

H

B

(x)

P=1[-]

V

c

(x)

V

c

(x)

H

c

(x)

H

C

(x)

Rys.2.6.

Z równowagi strony lewej mamy:

∑

M

C

L

=0 :5 H  x=8 R

A

 x

stąd

H  x =

8
5

−

x

10

[-]

c) Zestawienie fukcji reakcji podporowych w zależności od wartości współrzędnej x

współrzędna
reakcja

x ∈〈0 ; 8 〉

x ∈〈8 ; 16 〉

R

A

[-]

1−

x

16

1−

x

16

R

B

[-]

x

16

x

16

H [-]

x

10

8
5

−

x

10

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

13/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

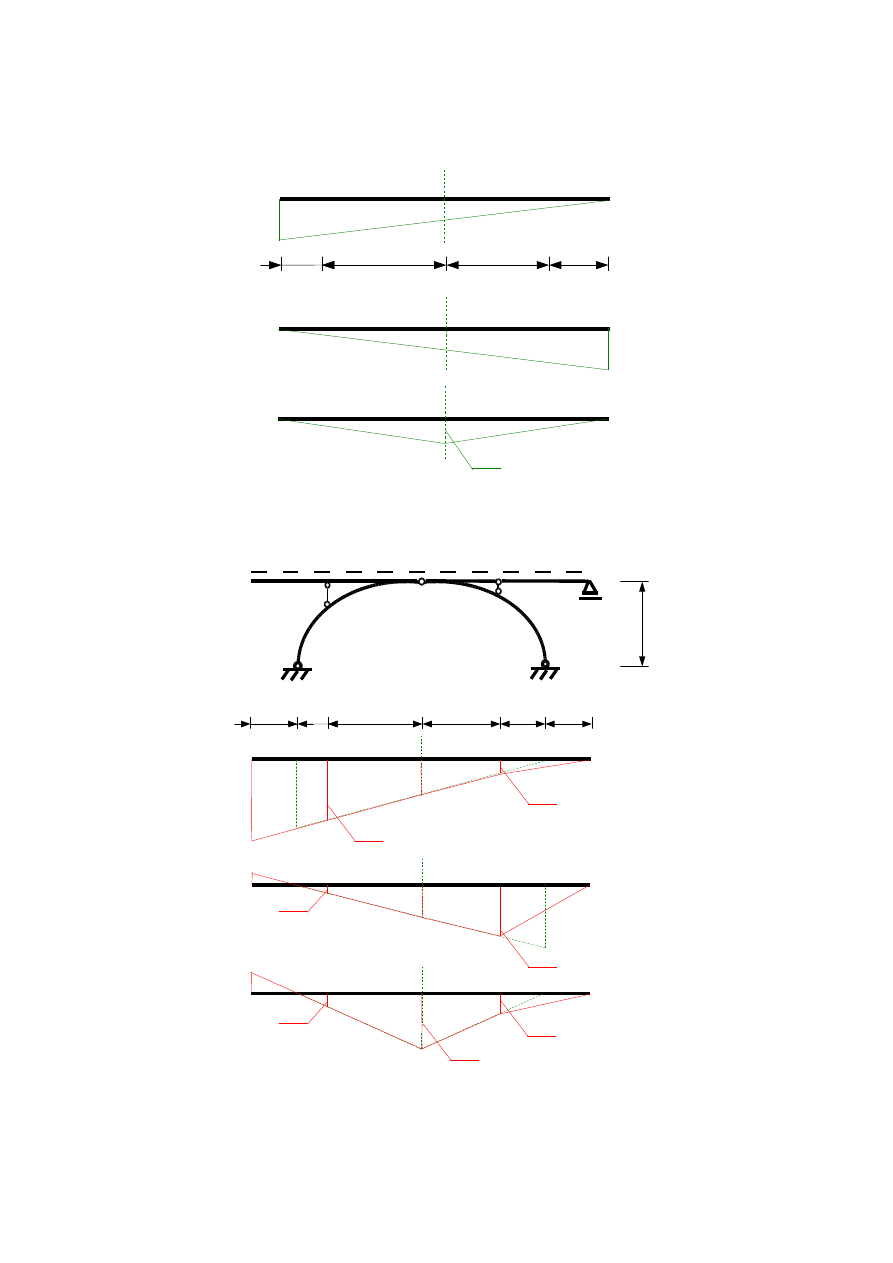
5. Wykreślenie linii wpływowych reakcji podporowych w łuku bez pomostu pośredniego

Rys.2.7

6. Wykreślenie linii wpływowych reakcji podporowych w łuku wyjściowym

3,0 m

2,0

6,0

5,0

3,0

3,0

5

,0

m

A

C

B

R

A

(x) [-]

1

+

R

B

(x) [-]

1

+

H(x) [-]

0,3

+

+

0,2

0

0,55

0,125

0,8125

0,1875

0,875

0

0

Rys.2.8

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

14/37

2,0

6,0

5,0

3,0

R

A

(x) [-]

1

+

R

B

(x) [-]

1

+

H(x) [-]

0,8

+

+

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

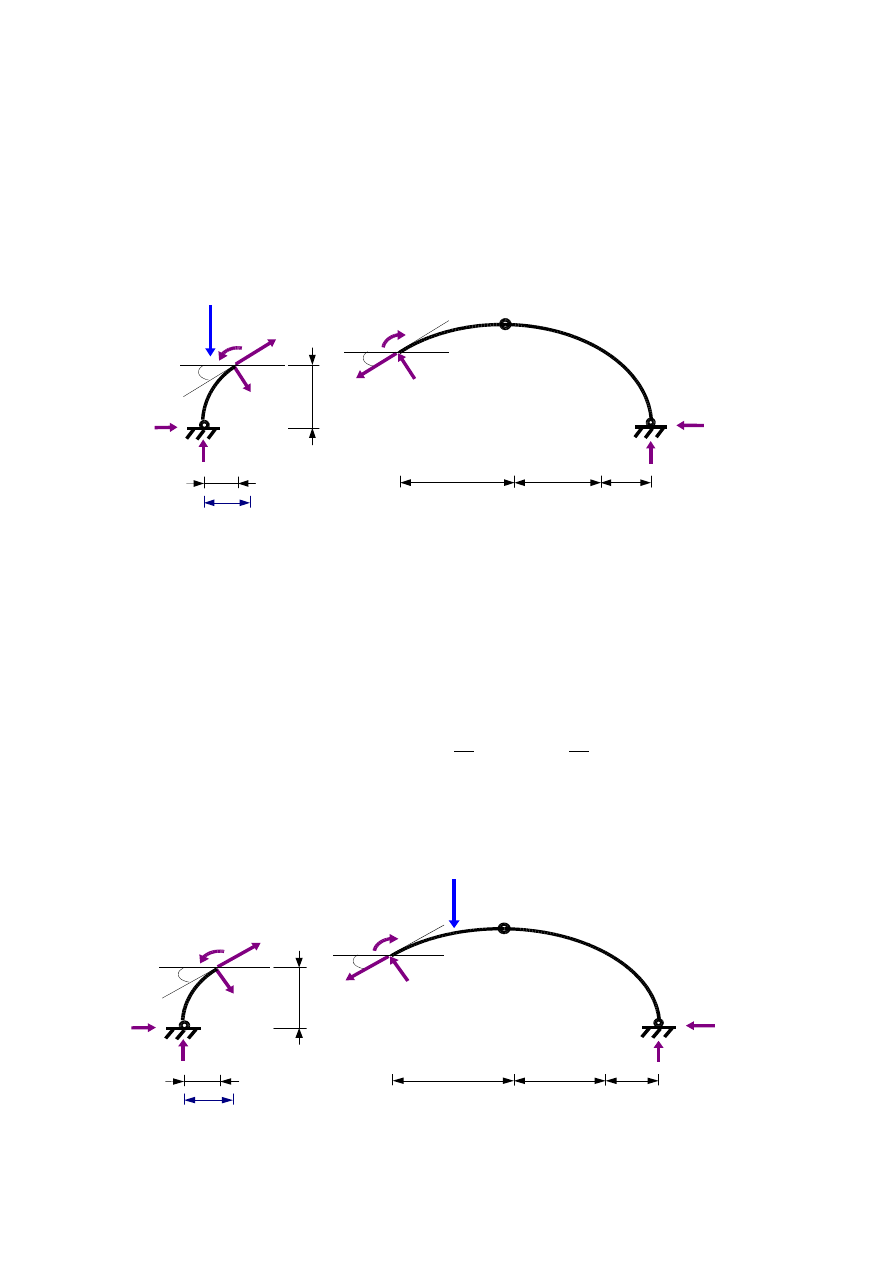
7. Wyznaczenie funkcji sił przekrojowych w zależności od współrzędnej położenia siły P=1[-]

Analogicznie jak w przypadku reakcji naprzód wyznaczamy funkcje sił przekrojowych oraz kreślimy linie wpływu tych
sił dla łuku bez pomostu pośredniego, następnie poprzez odpowiednią modyfikację wykresów otrzymamy linie
wpływowe sił przekrojowych dla łuku z pomostem pośrednim. W zadaniu przekroje α-α i β-β znajdują sie
nieskończenie blisko siebie. Dla łuku bez pomostu pośredniego możemy traktować je jako identyczne, stąd
wystarczające jest określenie funkcji sił przekrojowych tylko dla jednego z nich.

Wyznaczam funkcje sił przekrojowych w przekroju β-β jak na rys.2.3.
a)

x ∈〈0 ; 2 〉

2,0

5,0

3,0

2

,1

8

7

5

m

R

A

(x)

x

R

B

(x)

H

A

(x)

H

B

(x)

P=1[-]

N

β

(x)

T

β

(x)

6,0

φ

M

β

(x)

N

β

(x)

T

β

(x)

φ

M

β

(x)

Rys.2.9

Z warunków równowagi :

* dla strony prawej:

∑

 N



=0 : N



 x=R

B

 xsin −H  xcos 

∑

 T



=0 :T



 x=−R

B

 xcos −H  xsin 

∑

 M



=0 : M



 x=R

B

 x⋅14 −H  x⋅2,1875

Przy czym:

∑

 N



=0

oznacza sumę rzutów na kierunek siły normalnej w przekroju



;

∑

 T



=0

oznacza sumę rzutów na kierunek siły tnącej w przekroju



;

∑

 M



=0

oznacza sumę momentów względem przekroju



dla

sin =0,6839

,

cos =0,7295

,

R

B

 x=

x

16

[-],

H

 x

=

x

10

[-] otrzymujemy:

N



 x=−0,03 x

[-]

T



 x=−0,114 x

[-]

M



 x=0,656 x

[m]

b)

x ∈〈 2 ; 16 〉

2,0

5,0

3,0

2

,1

8

7

5

m

R

A

(x)

x

R

B

(x)

H

A

(x)

H

B

(x)

P=1[-]

N

β

(x)

T

β

(x)

6,0

φ

M

β

(x)

N

β

(x)

T

β

(x)

φ

M

β

(x)

Rys.2.10

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

15/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

Z warunków równowagi :

* dla strony lewej:

∑

 N



=0 : N



 x=−R

A

 xsin − H  xcos 

∑

 T



=0 :T



 x=R

A

 xcos −H  xsin 

∑

 M



=0 : M



 x=R

A

 x⋅2 −H  x⋅2,1875

b.1.)

x ∈〈 2 ; 8 〉

dla

sin =0,6839

,

cos =0,7295

,

R

A

 x=1−

x

16

[-],

H

 x

=

x

10

[-] otrzymujemy:

N



 x=−0,03 x−0,684

[-]

T



 x=−0,114 x0,7295

[-]

M



 x=2−0,344 x

[m]

b.2)

x ∈〈8 ; 16 〉

dla

sin =0,6839

,

cos =0,7295

,

R

A

 x=1−

x

16

[-],

H

 x

=

8
5

−

x

10

[-] otrzymujemy:

N



 x=−1,850,116 x

[-]

T



 x=−0,3650,023 x

[-]

M



 x=−1,50,094 x

[m]

c) zestawienie funkcji sił przekrojowych w zależności od wartości współrzędnej x

współrzędna
siła

x ∈〈0 ; 2 〉

x ∈〈 2 ; 8 〉

x ∈〈8 ; 16 〉

N



[-]

−0,03 x

−0,03 x−0,684

0,116 x−1,85

T



[-]

−0,114 x

−0,114 x0,7295

0,023 x−0,365

M



[m]

0,656 x

2−0,344 x

0,094 x−1,5

8. Wykreślenie linii wpływowych sił przekrojowych w przekroju β-β dla łuku bez pomostu pośredniego:

2,0

6,0

5,0

3,0

N

β

(x) [-]

0

-

T

β

(x) [-]

+

M

β

(x) [m]

1,312

-

+

-0,924

-

-0,744

-0,06

-0,228

-0,06

0,5

-0,18

-

-

-0,75

0

0

0

0

0

Rys.2.11

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

16/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

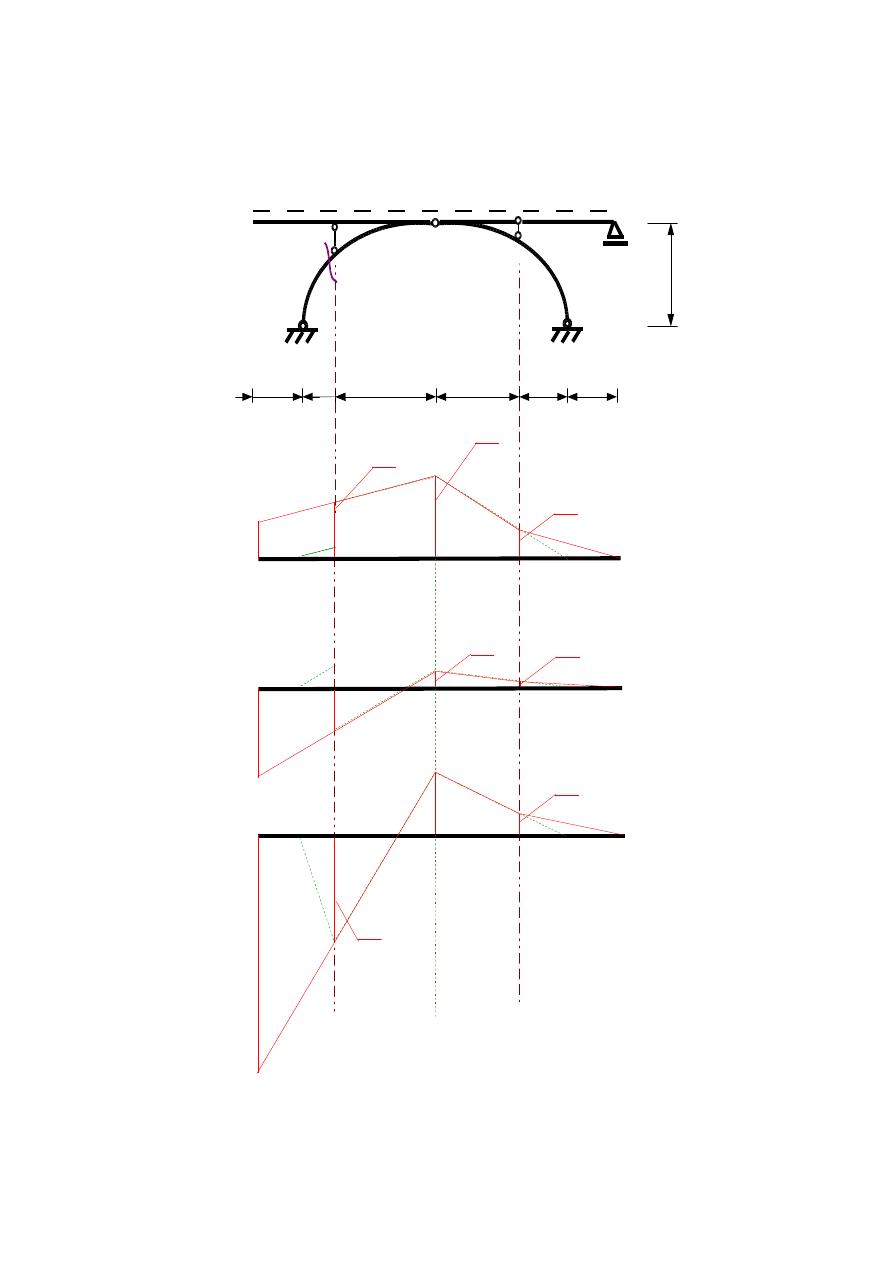
9. Wykreślenie linii wpływowych sił przekrojowych w przekroju β-β (dla tego przekroju pręt wspierający pomost

pośredni znajduje sie po prawej stronie) w łuku danymw zadaniu z pomostem pośrednim.

3,0 m

2,0

6,0

5,0

3,0

3,0

5,

0

m

A

C

B

N

β

(x) [-]

-

T

β

(x) [-]

+

M

β

(x) [m]

1,312

-

+

-0,35

-

-0,744

-0,924

0,5

-

-

-0,28

0

0

0

0

β

β

-0,0675

-0,18

Rys.2.12

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

17/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

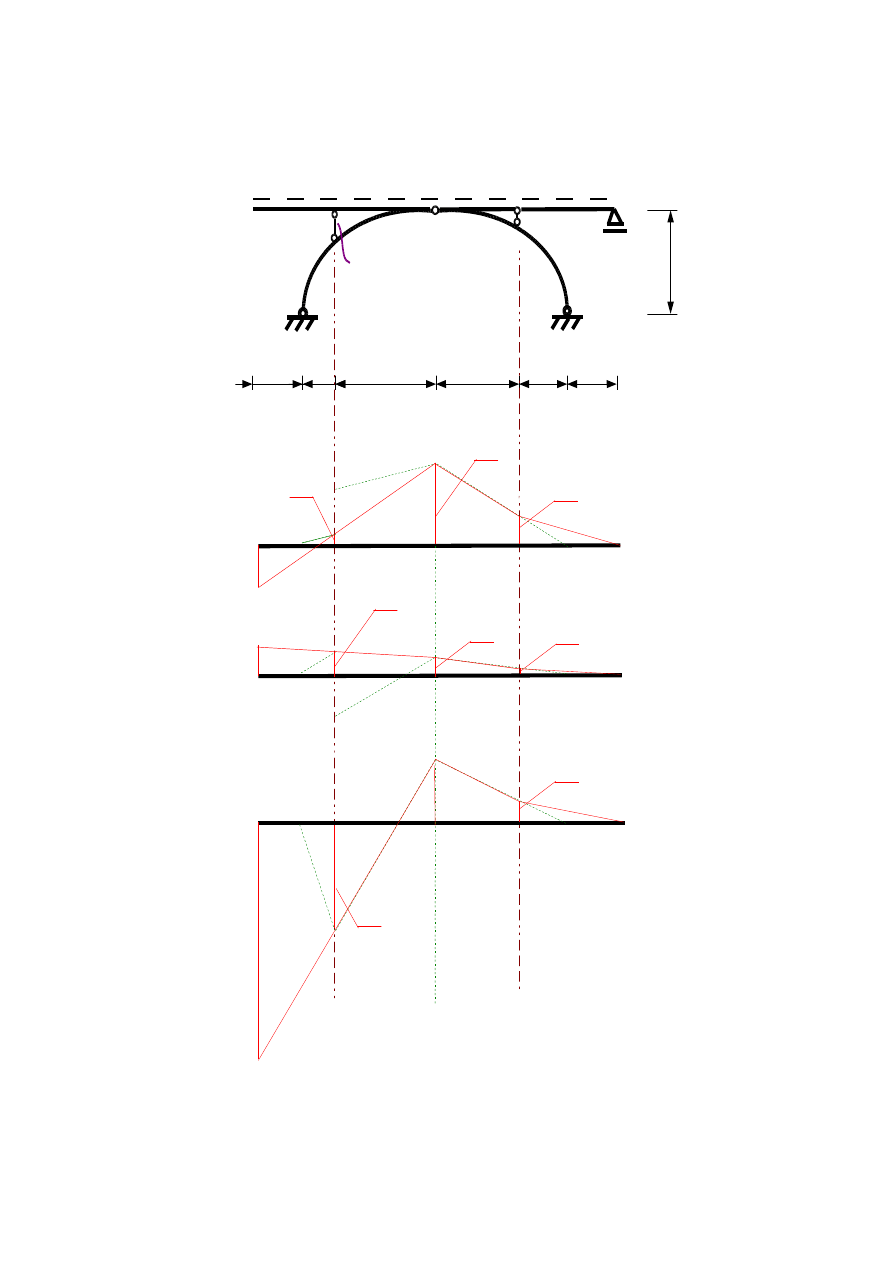
10. Wykreślenie linii wpływowych sił przekrojowych w przekroju α-α (dla tego przekroju pręt wspierający pomost

pośredni znajduje sie po lewej stronie) w łuku danym w zadaniu z pomostem pośrednim.

3,0 m

2,0

6,0

5,0

3,0

3,0

5,

0

m

A

C

B

N

α

(x) [-]

-

T

α

(x) [-]

-

M

α

(x) [m]

1,312

-

+

-0,35

-

-0,06

-0,924

-0,228

-

-

-0,18

0

0

0

0

α

-0,0675

-0,18

α

Rys.2.13

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

18/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

Projekt 1

LINIE WPŁYWOWE W UKŁADACH STATYCZNIE WYZNACZALNYCH

KRATOWNICE

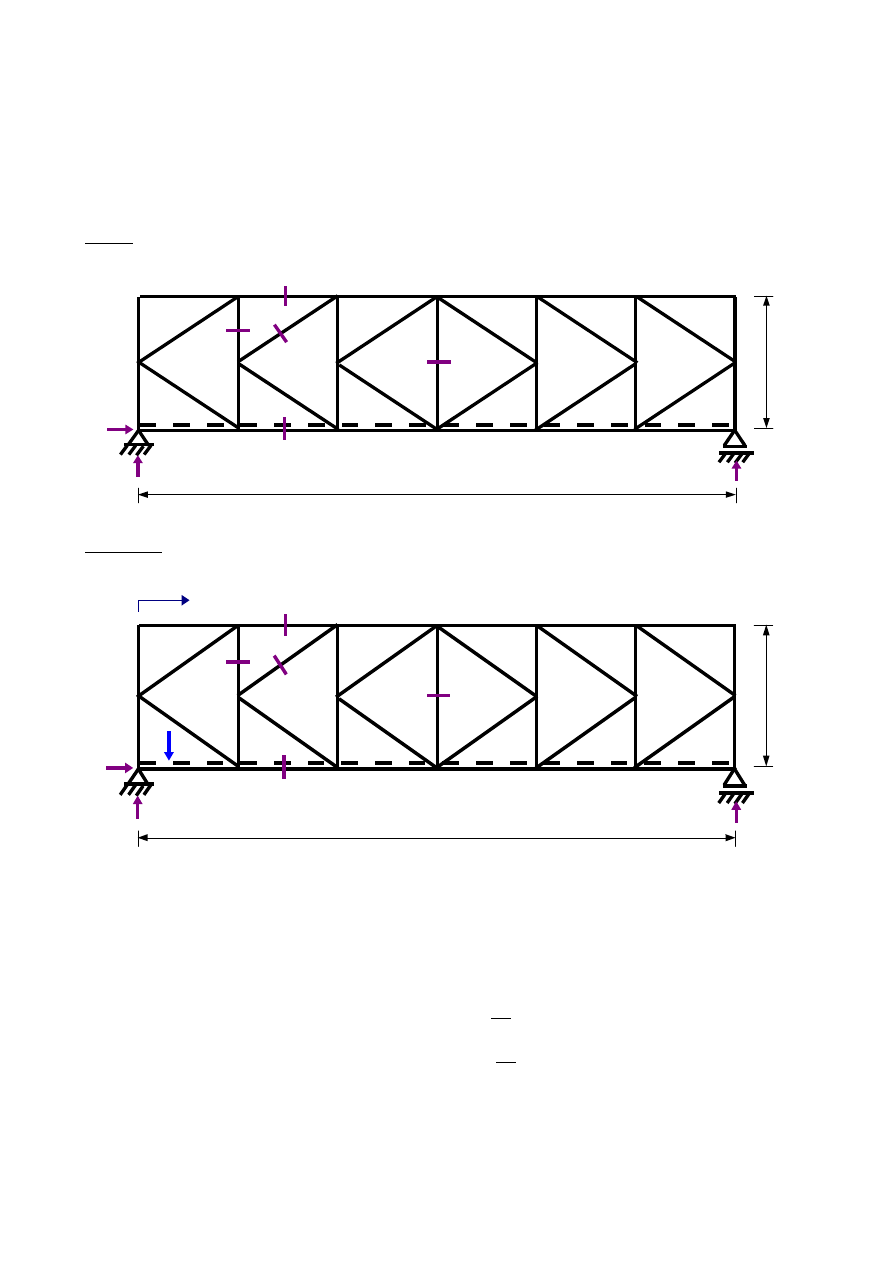
Zadanie: Dla kratownicy pokazanej na rys.3.1. wyznaczyć linie wpływowe zaznaczonych wielkości statycznych.

6 x 3,0 m

2

x

2

,0

m

A

B

Rys.3.1

Rozwiązanie:

1. Przyjmuję układ współrzędnych określających położenie siły P=1 [-] jak na rys.3.2.:

6 x 3,0 m

2

x

2

,0

m

A

B

x

R

A

(x)

R

B

(x)

H

A

(x)

G

1

(x)

D

1

(x)

S

1

(x)

K

1

(x)

S

2

(x)

P=1[-]

Rys.3.2

Przy czym:

x ∈〈0 ; 18 〉

2. Wyznaczenie funkcji reakcji podporowych w zależności od współrzędnej położenia siły P=1[-].

Z warunków równowagi dla kratownicy:

∑

X =0 : H

A

=0

[-]

∑

M

A

=0 : R

B

=

x

18

[-]

∑

Y =0 : R

A

=1−

x

18

[-]

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

19/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

3. Wykreślenie linii wpływowych reakcji podporowych:

+

R

A

(x) [-]

0

1

+

0

1

R

B

(x) [-]

H

A

(x) [-]

0

Rys. 3.3

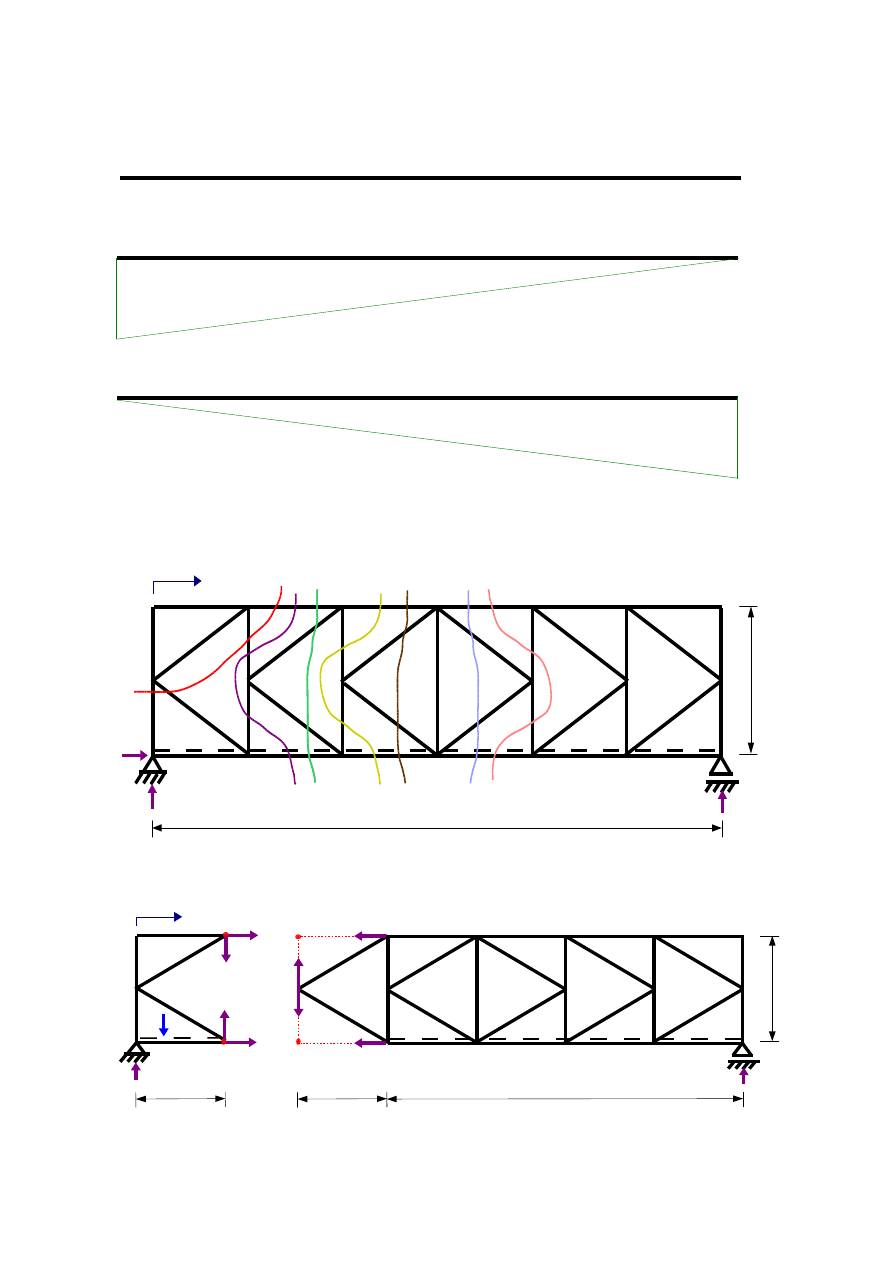
4. Wyznaczenie funkcji sił w określonych prętach w zależności od współrzędnej położenia siły P=1[-]

Przekroje pomocnicze do wyznaczania sił w prętach pokazano na rys. 3.4:

6 x 3,0 m

2

x

2,

0

m

A

B

x

R

A

(x)

R

B

(x)

H

A

(x)

α

α

β

β

γ

γ

λ

λ

δ

δ

ω

ω

φ

φ

S

Rys.3.4

4.1.1. Wyznaczenie funkcji G

1

(x) oraz D

1

(x) – przekrój α-α :

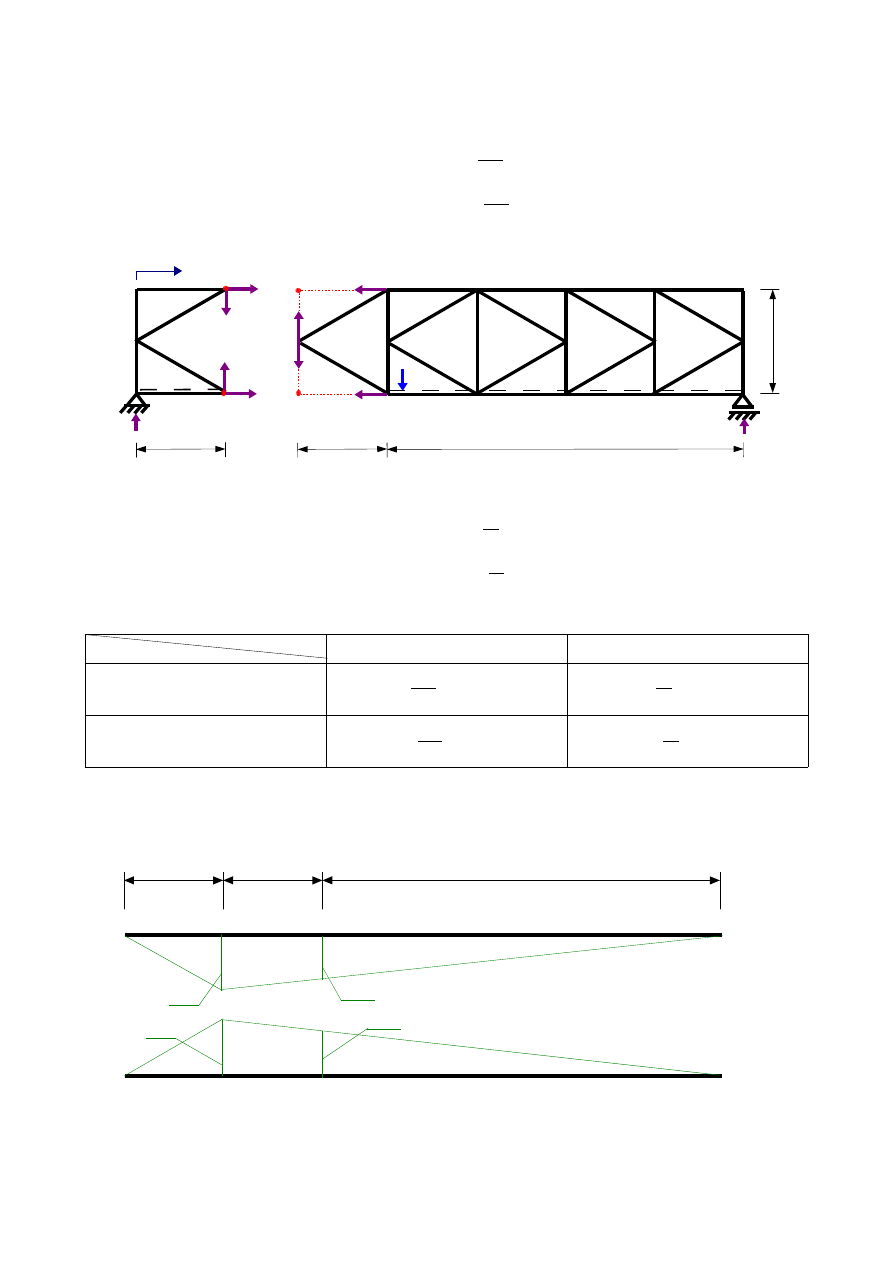
a)

x ∈〈0 ; 3 〉

3,0 m

2

x

2

,0

m

x

R

A

(x)=1-x /18 [-]

R

B

(x)=x /18 [-]

G

1

(x)

D

1

(x)

S

1

(x)

K

1

(x)

P=1[-]

3,0 m

12,0 m

G

1

(x)

D

1

(x)

S

1

(x)

S

2

(x)

S

2

(x)

R

D

R

D

R

G

R

G

Rys.3.5

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

20/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

Z równowagi części prawej:

∑

M

R

D

=0 : D

1

 x=

15

4

R

B

 x

[-]

∑

M

R

G

=0 :G

1

 x=−

15

4

R

B

 x

[-]

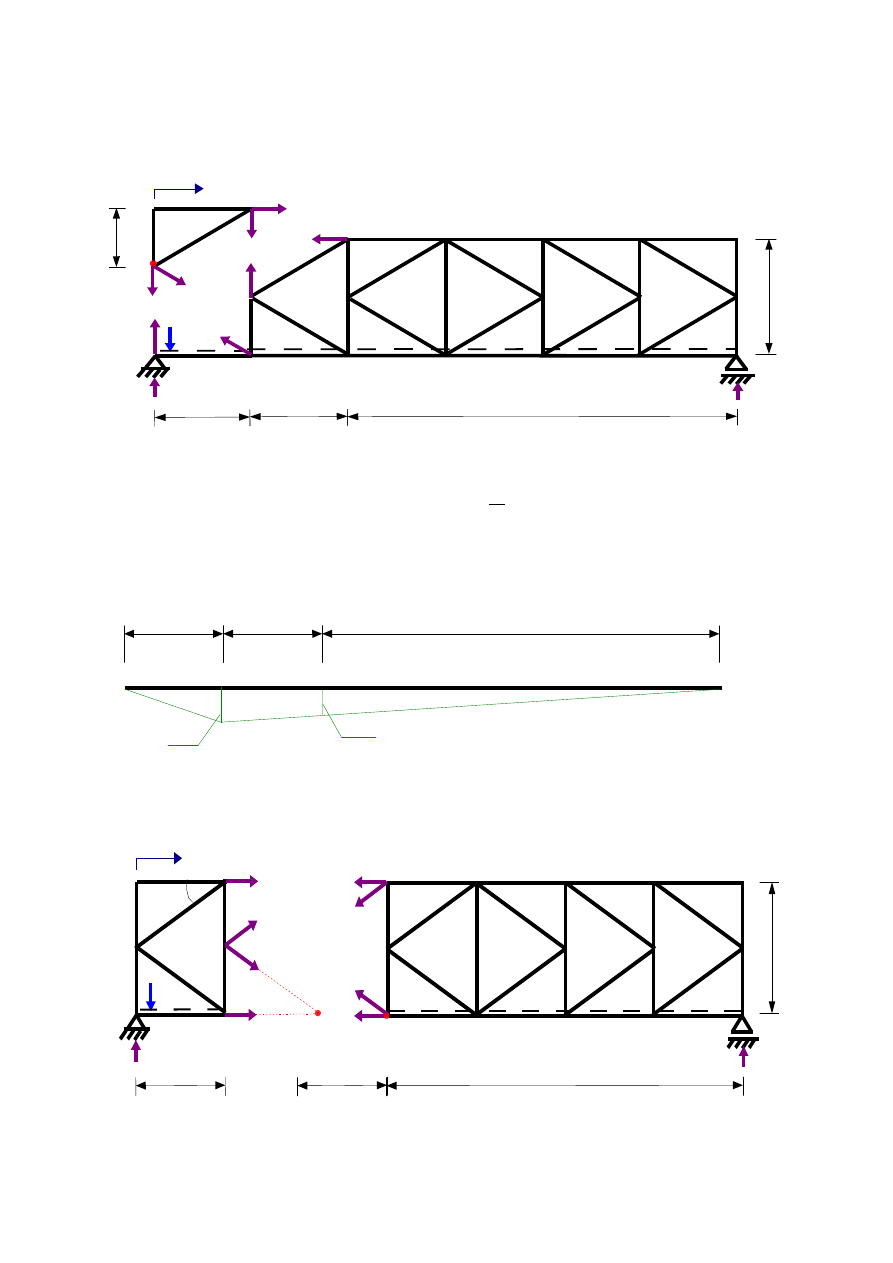
b)

x ∈〈6 ; 18 〉

3,0 m

2

x

2

,0

m

x

R

A

(x)=1-x /18 [-]

R

B

(x)=x /18 [-]

G

1

(x)

D

1

(x)

S

1

(x)

K

1

(x)

P=1[-]

3,0 m

12,0 m

G

1

(x)

D

1

(x)

S

1

(x)

S

2

(x)

S

2

(x)

R

D

R

D

R

G

R

G

Rys.3.6

Z równowagi części lewej:

∑

M

R

D

=0 : D

1

 x=

3
4

R

A

 x

[-]

∑

M

R

G

=0 :G

1

 x=−

3

4

R

A

 x

[-]

4.1.2.Zestawienie funkcji sił w prętach D

1

i G

1

w zależności od współrzędnej x:

pręt współrzędna

x ∈〈0 ; 3 〉

x ∈〈6 ; 18 〉

D

1

[-]

15

4

R

B

 x

3
4

R

A

 x

G

1

[-]

−

15

4

R

B

 x

−

3

4

R

A

 x

4.1.3.Wykreślenie linii wpływowych sił w prętach D

1

i G

1

(z wykorzystaniem linii wpływowych reakcji jak na rys.3.3)

+

D

1

(x) [-]

0

0,625

-

0

0

G

1

(x) [-]

3,0 m

3,0 m

12,0 m

0,5

0

-0,625

-0,5

Rys.3.7

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

21/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

4.2.1.Wyznaczenie funkcji S

1

(x) – przekrój β-β :

3,0 m

2

x

2

,0

m

x

R

A

(x)=1-x /18 [-]

R

B

(x)=x /18 [-]

G

1

(x)

S

1

(x)

K

1

(x)

P=1[-]

3,0 m

12,0 m

G

1

(x)

S

1

(x)

R

s

2

,0

m

Rys.3.8

Z równowagi odciętej części górnej:

∑

M

R

S

=0 : S

1

 x=−

2

3

G

1

 x

[-]

4.2.2.Wykreślenie linii wpływowej siły w pręcie S

1

(z wykorzystaniem linii wpływowej siły w pręcie G

1

jak na rys.3.7)

+

S

1

(x) [-]

0

0,417

3,0 m

3,0 m

12,0 m

0,333

0

Rys.3.9

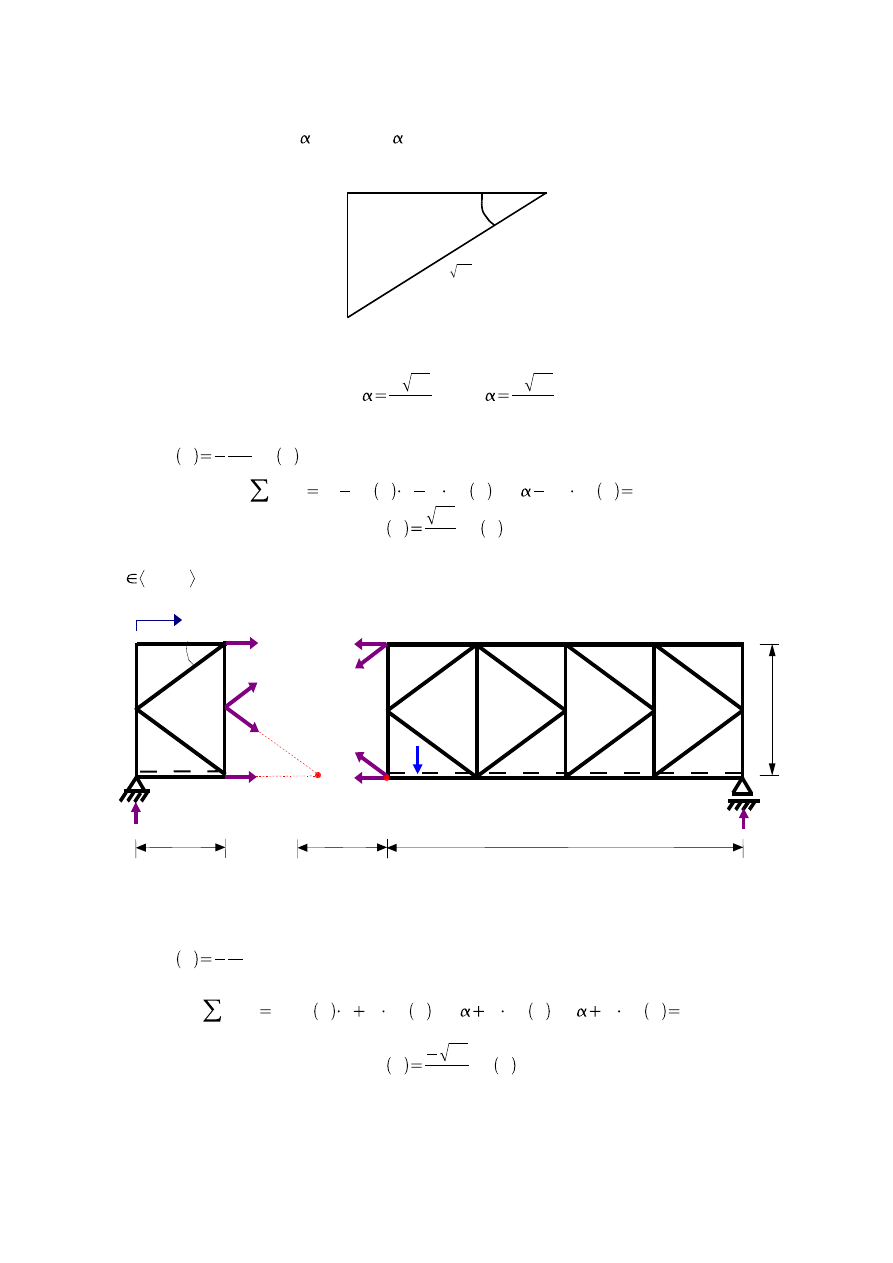
4.3.1.Wyznaczenie funkcji K

1

(x) – przekrój γ-γ :

a)

x ∈〈0 ; 3 〉

3,0 m

2

x

2,

0

m

x

R

A

(x)=1-x /18 [-]

R

B

(x)=x /18 [-]

G

1

(x)

D

1

(x)

α

K

1

(x)

P=1[-]

3,0 m

12,0 m

G

1

(x)

D

1

(x)

R

K

K

2

(x)

K

1

(x)

K

2

(x)

R

K

Rys.3.10

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

22/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

Dla kąta α określam wartości

sin

oraz

cos

:

α

3,0

2,0

13

Rys.3.11

sin

2 13

13

cos

3 13

13

Z równowagi części prawej:

dla

G

1

x

15

4

R

B

x

[-]

M

R

K

0 : G

1

x 4 4 K

1

x cos

12 R

B

x

0

stąd:

K

1

x

13

4

R

B

x

[-]

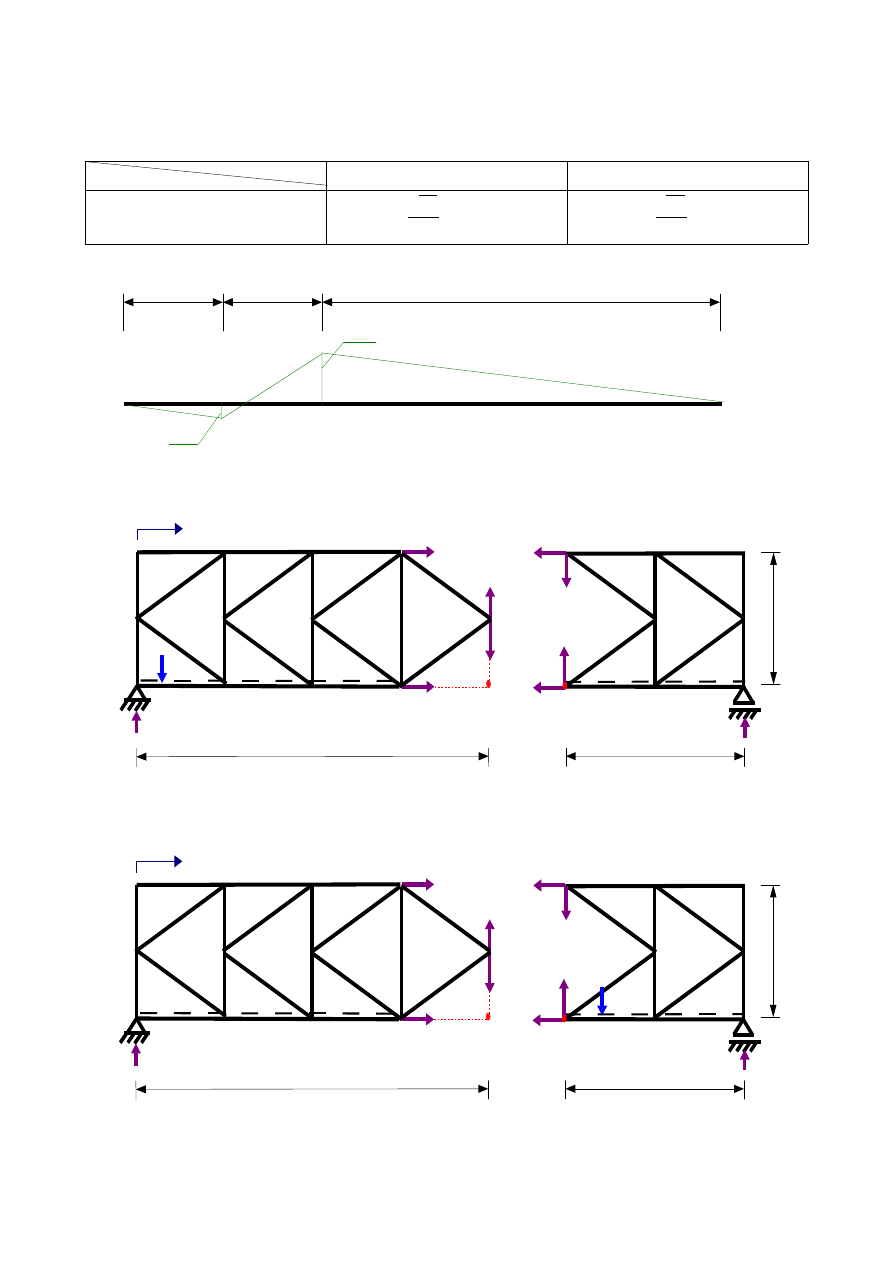
b)

x

6 ; 18

3,0 m

2

x

2,

0

m

x

R

A

(x)=1-x /18 [-]

R

B

(x)=x /18 [-]

G

1

(x)

D

1

(x)

α

K

1

(x)

P=1[-]

3,0 m

12,0 m

G

1

(x)

D

1

(x)

R

K

K

2

(x)

K

1

(x)

K

2

(x)

R

K

Rys.3.12

Z równowagi części lewej:

dla

G

1

x

3

4

R

A

[-]

M

R

K

0 : G

1

x 4 2 K

1

x cos

3 K

1

x sin

6 R

A

x

0

stąd:

K

1

x

13

4

R

A

x

[-]

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

23/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

4.3.2.Zestawienie funkcji siły w pręcie K

1

w zależności od współrzędnej x:

pręt współrzędna

x ∈〈0 ; 3 〉

x ∈〈6 ; 18 〉

K

1

[-]



13

4

R

B

 x

−



13

4

R

A

 x

4.3.3.Wykreślenie linii wpływowej siły w pręcie K

1

(z wykorzystaniem linii wpływowych reakcji jak na rys.3.3):

-

K

1

(x) [-]

0

0,15

3,0 m

3,0 m

12,0 m

-0,6

0

+

Rys. 3.13

4.4.1Wyznaczenie funkcji G

2

(x) – przekrój φ-φ :

a)

x ∈〈0 ; 9 〉

12,0 m

2

x

2,

0

m

x

R

A

(x)=1-x /18 [-]

R

B

(x)=x /18 [-]

G

2

(x)

P=1[-]

6,0 m

G

2

(x)

R

G

R

G

Rys.3.14

Z równowagi części prawej:

∑

M

R

G

=0 :G

2

 x=−1,5 R

B

 x

[-]

b)

x ∈〈12 ; 18 〉

12,0 m

2

x

2,

0

m

x

R

A

(x)=1-x /18 [-]

R

B

(x)=x /18 [-]

G

2

(x)

P=1[-]

6,0 m

G

2

(x)

R

G

R

G

Rys.3.15

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

24/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

Z równowagi części lewej:

∑

M

R

G

=0 :G

2

 x=−3 R

A

 x

[-]

4.4.2.Zestawienie funkcji siły w pręcie G

2

w zależności od współrzędnej x:

pręt współrzędna

x ∈〈0 ; 9 〉

x ∈〈12 ; 18 〉

G

2

[-]

−1,5 ⋅R

B

 x

−3 ⋅R

A

 x

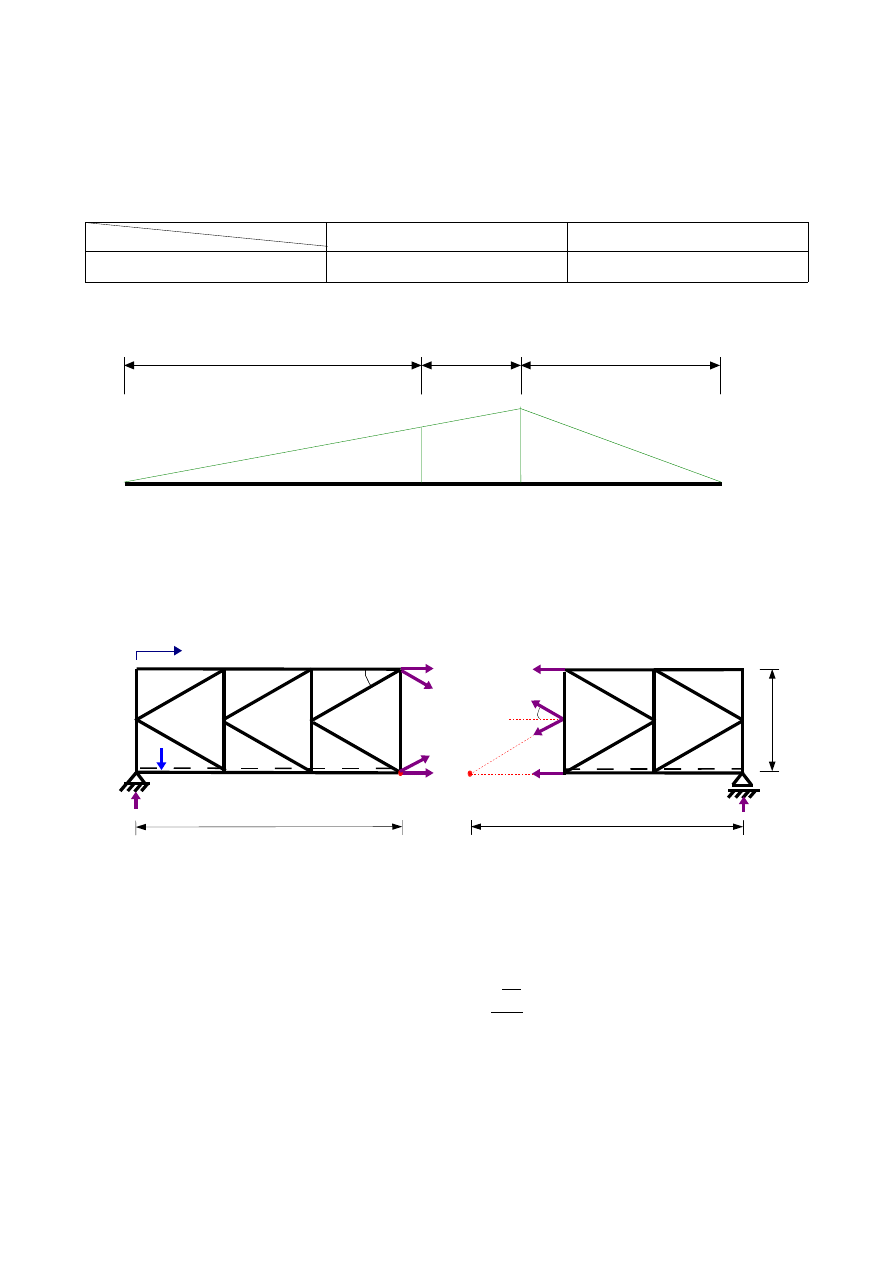
4.4.3.Wykreślenie linii wpływowej siły w pręcie G

2

(z wykorzystaniem linii wpływowych reakcji jak na rys.3.3):

-

G

2

(x) [-]

0

9,0 m

3,0 m

6,0 m

-0,75

-1

0

Rys.3.16

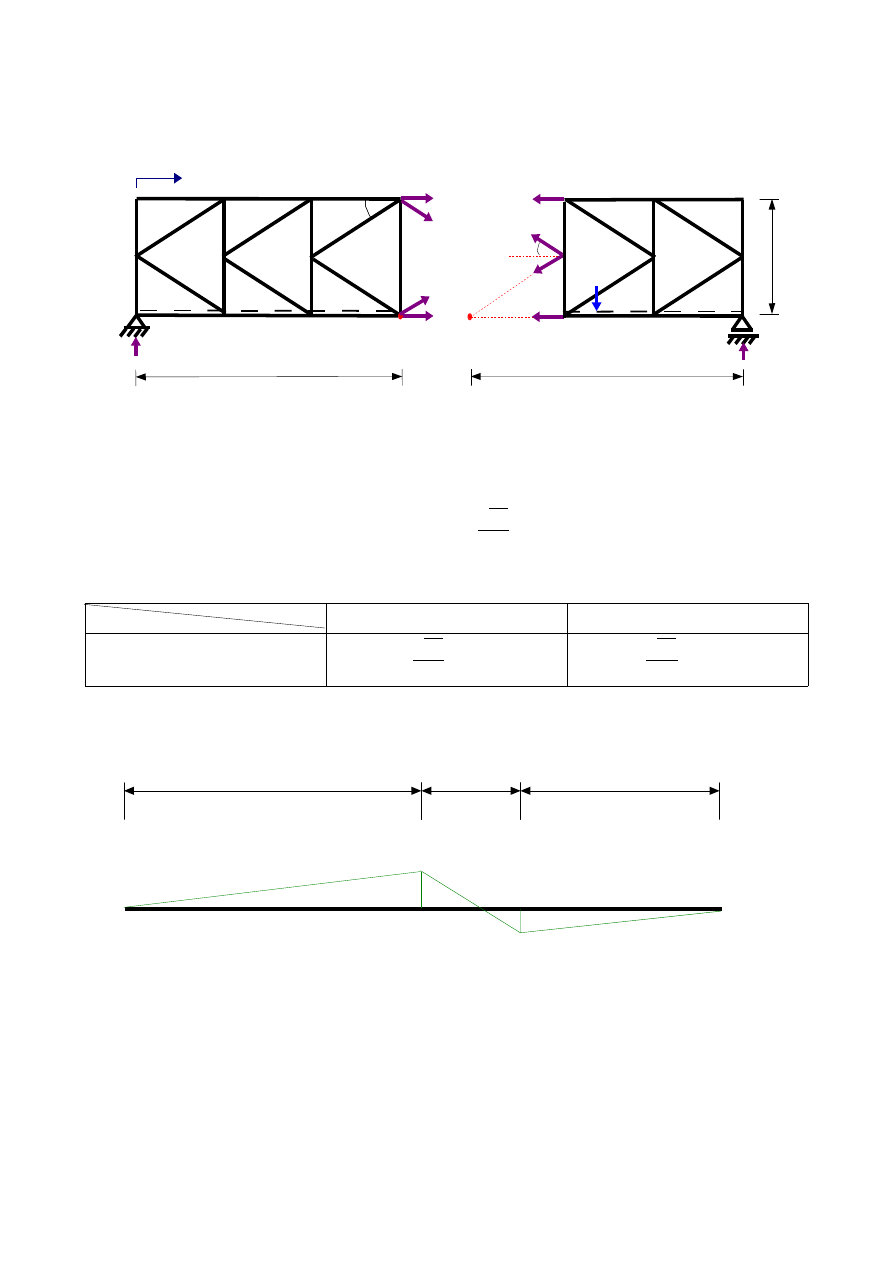
4.5.1Wyznaczenie funkcji K

2

(x) – przekrój ω-ω :

a)

x ∈〈0 ; 9 〉

9,0 m

2

x

2

,0

m

x

R

A

(x)=1-x /18 [-]

R

B

(x)=x /18 [-]

G

2

(x)

P=1[-]

9,0 m

G

2

(x)

R

K

R

K

K

2

(x)

K

2

(x)

α

α

Rys.3.17

Z równowagi części prawej:

∑

M

R

K

=0 :−G

2

 x⋅4 −2 ⋅K

2

 xcos −3 ⋅K

2

 xsin −9 R

B

 x=0

[-]

dla

G

2

 x=−1,5 ⋅R

B

 x

[-]

mamy:

K

2

 x=−



13

4

⋅R

B

 x

[-]

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

25/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

b)

x ∈〈12 ; 18 〉

9,0 m

2

x

2

,0

m

x

R

A

(x)=1-x /18 [-]

R

B

(x)=x /18 [-]

G

2

(x)

P=1[-]

9,0 m

G

2

(x)

R

K

R

K

K

2

(x)

K

2

(x)

α

α

Rys.3.18

Z równowagi części lewej:

∑

M

R

K

=0 : 9 ⋅R

A

 x4 ⋅G

2

 x4 ⋅K

2

 xcos =0

[-]

dla

G

2

 x=−3 ⋅R

A

 x

[-]

mamy:

K

2

 x=



13

4

⋅R

A

 x

[-]

4.5.2.Zestawienie funkcji siły w pręcie G

2

w zależności od współrzędnej x:

pręt współrzędna

x ∈〈0 ; 9 〉

x ∈〈12 ; 18 〉

K

2

[-]

−



13

4

⋅R

B

 x



13

4

⋅R

A

 x

4.5.3.Wykreślenie linii wpływowej siły w pręcie K

2

(z wykorzystaniem linii wpływowych reakcji jak na rys.3.3):

-

K

2

(x) [-]

0

9,0 m

3,0 m

6,0 m

-0,45

0,3

0

+

Rys.3.19

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

26/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

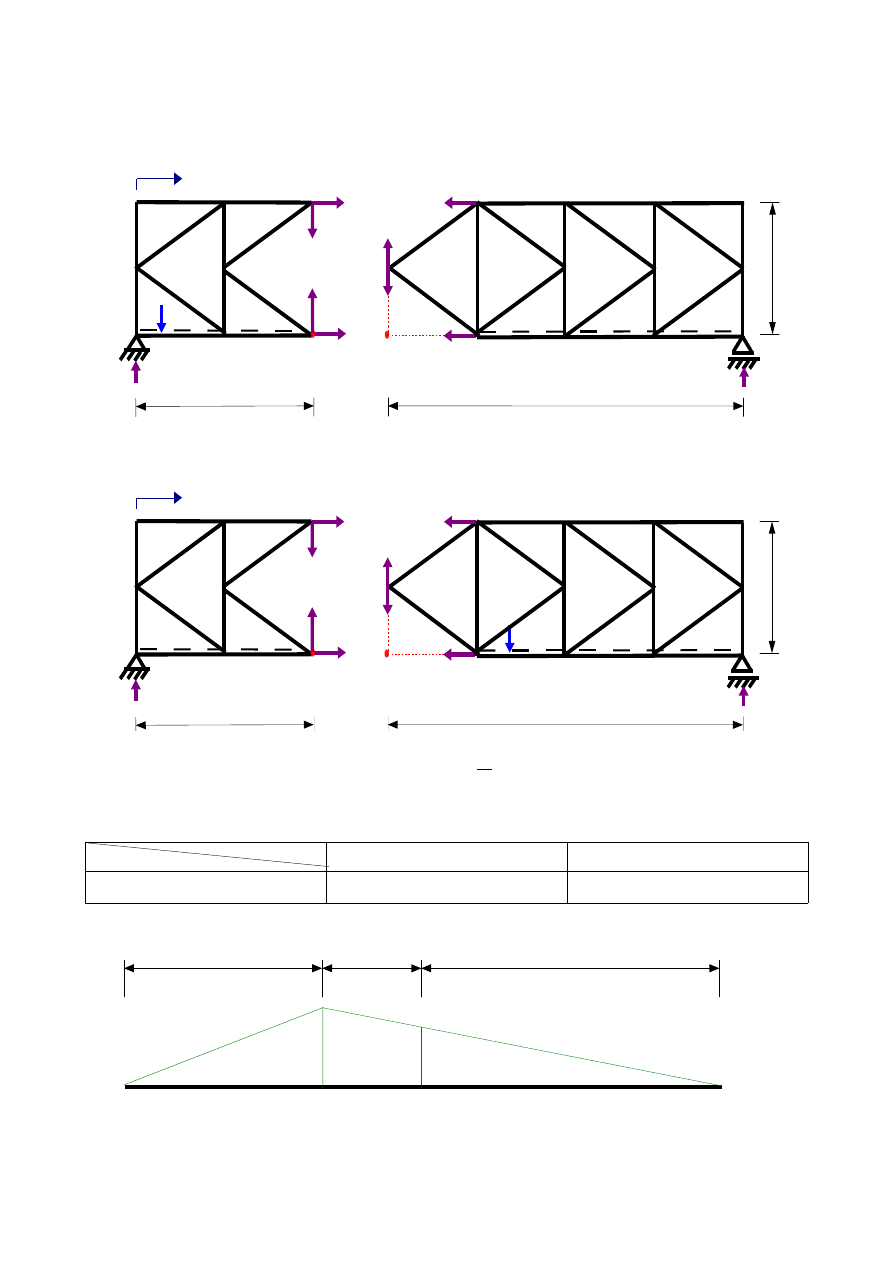
4.6.1.Wyznaczenie funkcji G

3

(x) – przekrój λ-λ :

a)

x ∈〈0 ; 6 〉

6,0 m

2

x

2,

0

m

x

R

A

(x)=1-x /18 [-]

R

B

(x)=x /18 [-]

G

3

(x)

P=1[-]

12,0 m

G

3

(x)

R

G

R

G

Rys.3.20

Z równowagi części prawej:

∑

M

R

G

=0 :G

3

 x=−3 ⋅R

B

 x

[-]

b)

x ∈〈9 ; 18 〉

6,0 m

2

x

2,

0

m

x

R

A

(x)=1-x /18 [-]

R

B

(x)=x /18 [-]

G

3

(x)

P=1[-]

12,0 m

G

3

(x)

R

G

R

G

Rys.3.21

Z równowagi części lewej:

∑

M

R

G

=0 :G

3

 x=−

3

2

⋅R

A

 x

[-]

4.6.2.Zestawienie funkcji siły w pręcie G

3

w zależności od współrzędnej x:

pręt współrzędna

x ∈〈0 ; 6 〉

x ∈〈9 ; 18 〉

G

3

[-]

−3 ⋅R

B

 x

−1,5 ⋅R

A

 x

4.6.3.Wykreślenie linii wpływowej siły w pręcie G

3

(z wykorzystaniem linii wpływowych reakcji jak na rys.3.3):

-

G

3

(x) [-]

0

6,0 m

3,0 m

9,0 m

-0,75

-1

0

Rys.3.22

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

27/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

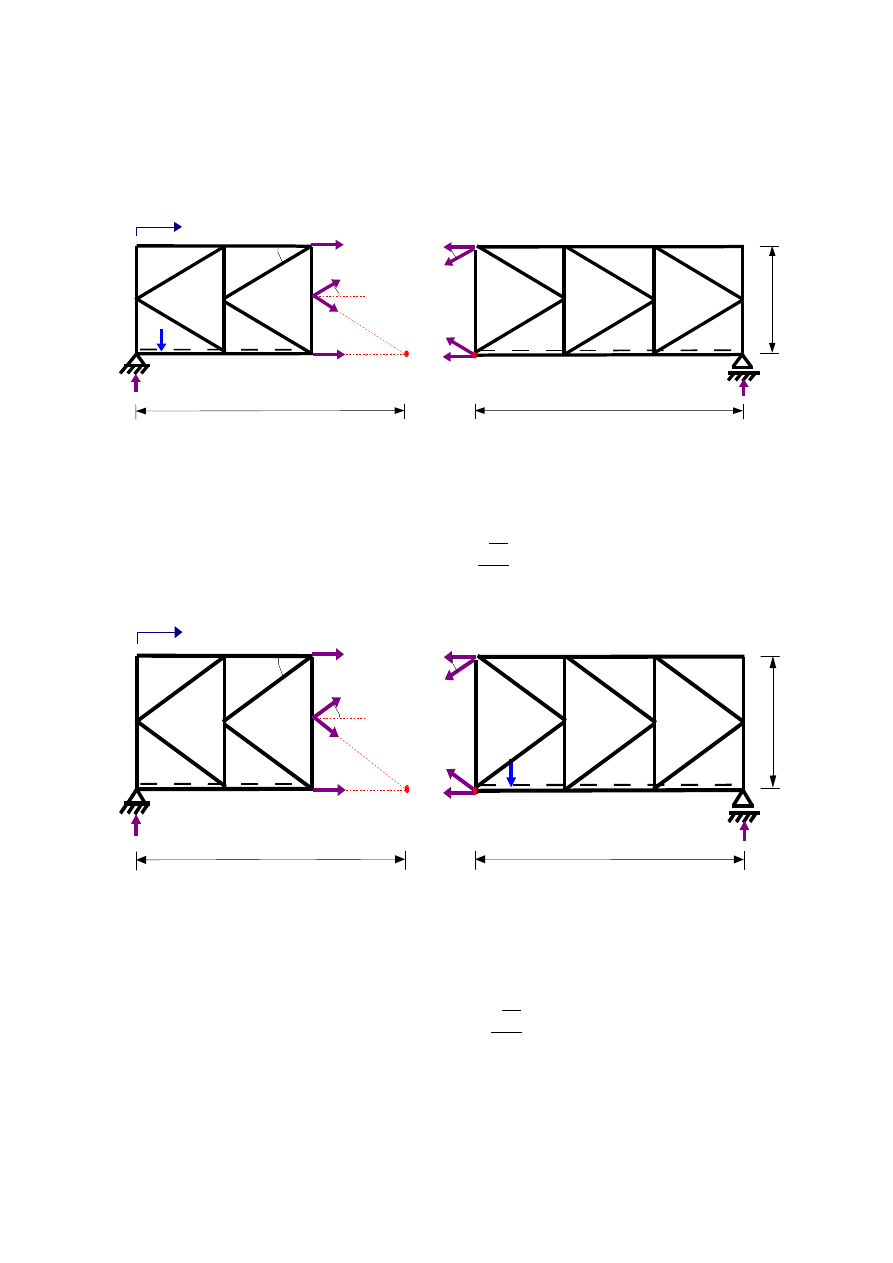
4.7.1.Wyznaczenie funkcji K

3

(x) – przekrój δ-δ :

a)

x ∈〈0 ; 6 〉

9,0 m

2

x

2

,0

m

x

R

A

(x)=1-x /18 [-]

R

B

(x)=x /18 [-]

P=1[-]

9,0 m

G

3

(x)

G

3

(x)

R

K

R

K

K

3

(x)

K

3

(x)

α

α

α

Rys.3.23

Z równowagi części prawej:

∑

M

R

K

=0 :−4 ⋅K

3

 xcos −4 ⋅G

3

 x−9 ⋅R

B

 x=0

dla

G

3

 x=−3 ⋅R

B

 x

[-]

mamy:

K

3

 x=



13

4

⋅R

B

 x

[-]

b)

x ∈〈9 ; 18 〉

9,0 m

2

x

2,

0

m

x

R

A

(x)=1-x /18 [-]

R

B

(x)=x /18 [-]

P=1[-]

9,0 m

G

3

(x)

G

3

(x)

R

K

R

K

K

3

(x)

K

3

(x)

α

α

α

Rys.3.24

Z równowagi części lewej:

∑

M

R

K

=0 : 4 ⋅G

3

 x2 ⋅K

3

 xcos 3 ⋅K

3

 xsin 9 ⋅R

A

 x=0

dla

G

3

 x=−1,5 ⋅R

A

 x

[-]

mamy:

K

3

 x=−



13

4

⋅R

A

 x

[-]

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

28/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

4.7.2.Zestawienie funkcji siły w pręcie K

3

w zależności od współrzędnej x:

pręt współrzędna

x ∈〈0 ; 6 〉

x ∈〈9 ; 18 〉

K

3

[-]



13

4

⋅R

B

 x

−



13

4

⋅R

A

 x

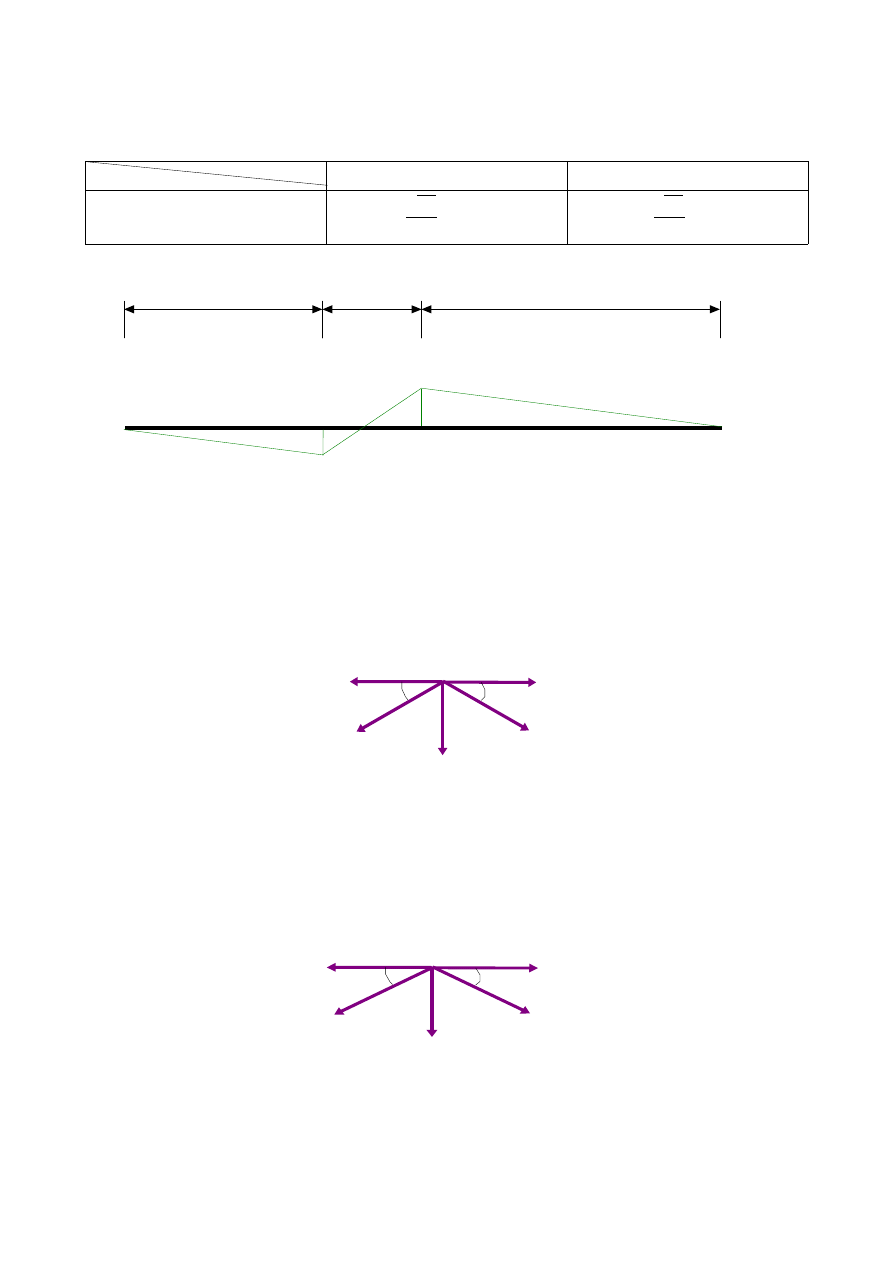
4.7.3.Wykreślenie linii wpływowej siły w pręcie K

3

(z wykorzystaniem linii wpływowych reakcji jak na rys.3.3):

-

K

3

(x) [-]

0

6,0 m

3,0 m

9,0 m

-0,45

0,3

0

+

Rys.3.25

4.8.1.Wyznaczenie funkcji S

2

(x) – z równowagi węzła S [patrz rys.3.4.]

W tym przypadku uwzględniam dwie sytuacje: gdy siła P=1[-] znajduje się w przedziałach

x ∈〈0 ; 6 〉

i

x ∈〈12 ; 18 〉

(wówcza określone są fukcje sił w prętach G

2

, G

3

, K

2

i K

3

) oraz osobno ustawienie siły P=1 [-]

w punkcie x=9 (wówczas mogę określić konkretne wartości ww. prętów w węźle S). Otrzymuję zatem:

a)

x ∈〈0 ; 6 〉

oraz

x ∈〈12 ; 18 〉

G

3

(x)

G

2

(x)

K

3

(x)

K

2

(x)

S

2

(x)

α

α

Rys.3.26

∑

Y =0 :− K

3

 xsin −K

2

 xsin −S

2

 x=0

zatem:

S

2

 x=−sin  K

2

 xK

3

 x

Uwzględniając wartości

K

2

 x

oraz

K

3

 x

na zadanych przedziałach otrzymuję:

S

2

 x=0

[-]

b)

x=9

-0,75

-0,75

-0,45

-0,45

S

2

(x)

α

α

Rys.3.27

∑

Y =0 :−−0,45sin −−0,45sin −S

2

 x=0

zatem

S

2

 x=0,5

[-]

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

29/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

4.8.2.Zestawienie funkcji siły w pręcie S

2

w zależności od współrzędnej x:

pręt współrzędna

x ∈〈0 ; 6 〉

x=9

x ∈〈12 ; 18 〉

S

2

[-]

0

0,5

0

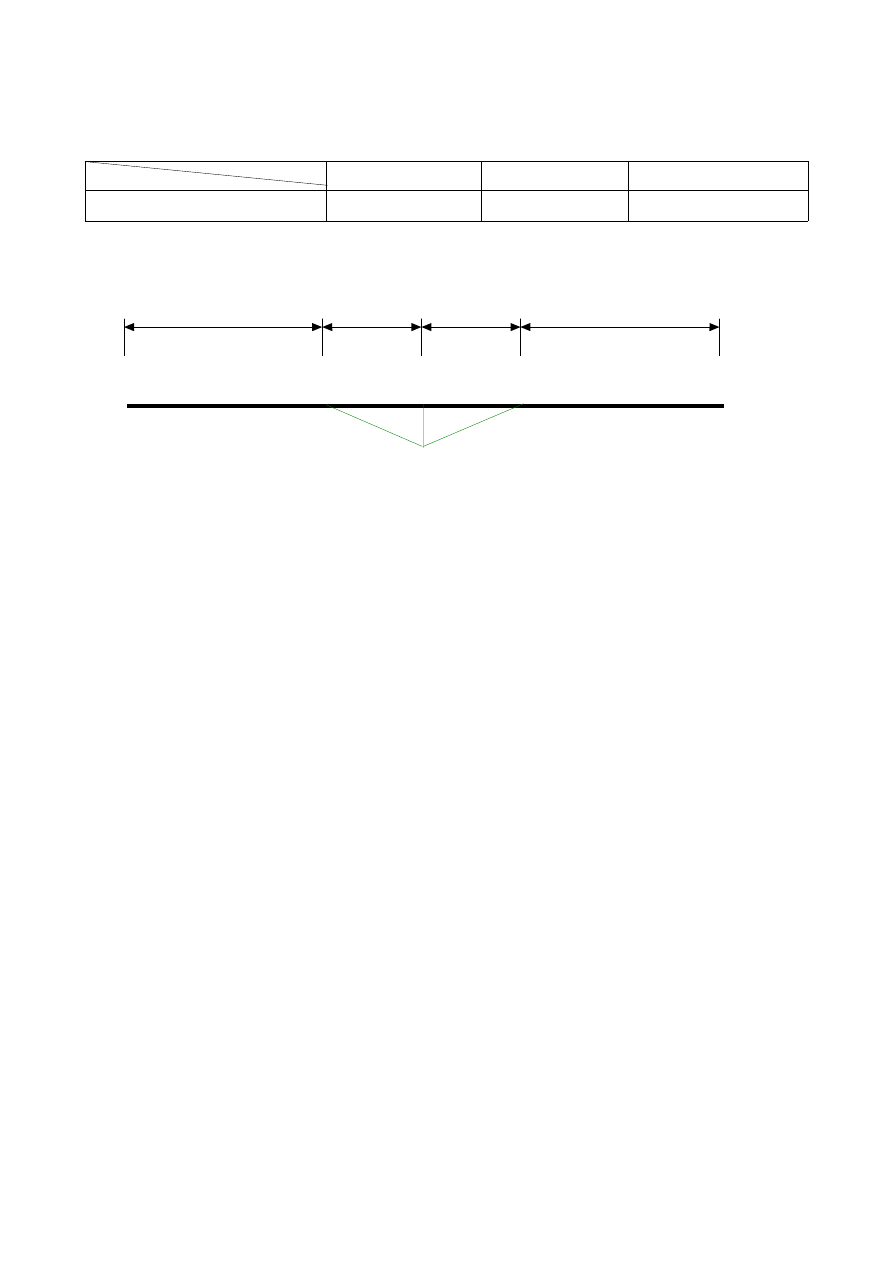
4.8.3.Wykreślenie linii wpływowej siły w pręcie S

2

:

+

S

2

(x) [-]

0

6,0 m

3,0 m

6,0 m

0,5

0

3,0 m

+

Rys.3.28

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

30/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

Projekt nr 1

LINIE WPŁYWOWE SIŁ W UKŁADACH STATYCZNIE WYZNACZALNYCH

EKSTREMALNE WARTOŚCI WIELKOŚCI STATYCZNYCH

Zadanie: Dla belki pokazanej na rys. 4.1. przy obciążeniu zespołem sił ruchomych jak na rys. 4.2. obliczyć ekstremalne

wartości momentu zginającego w przekroju β-β.

β

β

5,0 m

3,0 m

1,0 m

5,0 m

5,0 m

4,0 m

2,0 m

3,0 m

1,0 m

Rys. 4.1.

Zadany zespół sił ruchomych:

30 kN

10 kN/m

1,0 m

2,0 m

Rys.4.2.

Rozwiązanie:

Dana belka jest analogiczna do belki z rys. 1.1, stąd też wykres linii wpływu momentu zginającego w przekroju β-β jest
taki jak na rys. 1.12.
Wykres linii wpływu momentu zginającego w przekroju β-β:

0

+

0

+

1,875

-0,625

-

-

M

β-β

(x)[m]

Rys.4.3.

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

31/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

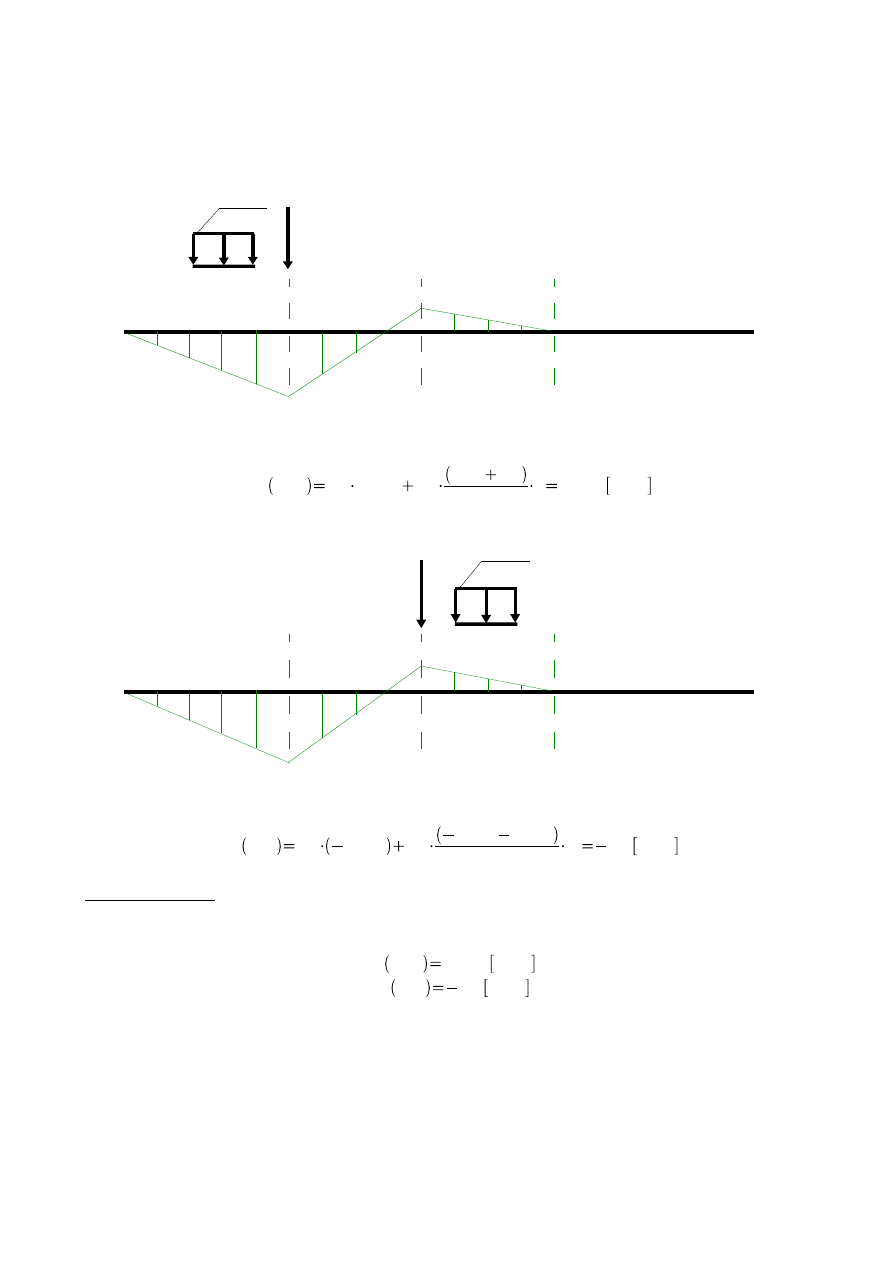
Wyznaczenie ekstremalnych wartości momentu zginającego :

1. Wartość maksymalna momentu wystąpi przy położeniu zespołu sił jak na rys.4.4.:

0

+

0

1,875

-0,625

M

β-β

(x)[m]

30 kN

10 kN/m

1,5

1,125

0,75

0,375

1,25

0,625

0

-0,469-0,313

-0,156

Rys.4.4.

M



max

30 1,875 10

0,75 1,5

2

2 78,75 kNm

2. Wartość minimalna momentu wystąpi przy położeniu zespołu sił jak na rys.4.5.:

0

+

0

1,875

-0,625

M

β-β

(x)[m]

30 kN

10 kN/m

1,5

1,125

0,75

0,375

1,25

0,625

0

-0,469-0,313

-0,156

Rys.4.5

M



min

30

0,625

10

0,469 0,156

2

2

25 kNm

Zestawienie wyników:

Dla zadanej belki, przy obciążeniu zespołem sił jak na rys.4.2 ekstremalne wartości momentu zginającego :

M



max

78,75 kNm

M



min

25 kNm

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

32/37

M

β-β

[m]

M

β-β

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

Projekt nr 1

LINIE WPŁYWOWE SIŁ W UKŁADACH STATYCZNIE WYZNACZALNYCH

OBWIEDNIA MOMENTÓW

Zadanie: Dla belki pokazanej na rys.5.1 obciążonej zespołem sił ruchomych jak na rys. 5.2. wyznaczyć obwiednię

momentów.

3,0 m

4,0 m

2,0 m

Rys.5.1

Zespół obciążeń:

30 kN

10 kN/m

1,0 m

2,0 m

Rys.5.2

Rozwiązanie:

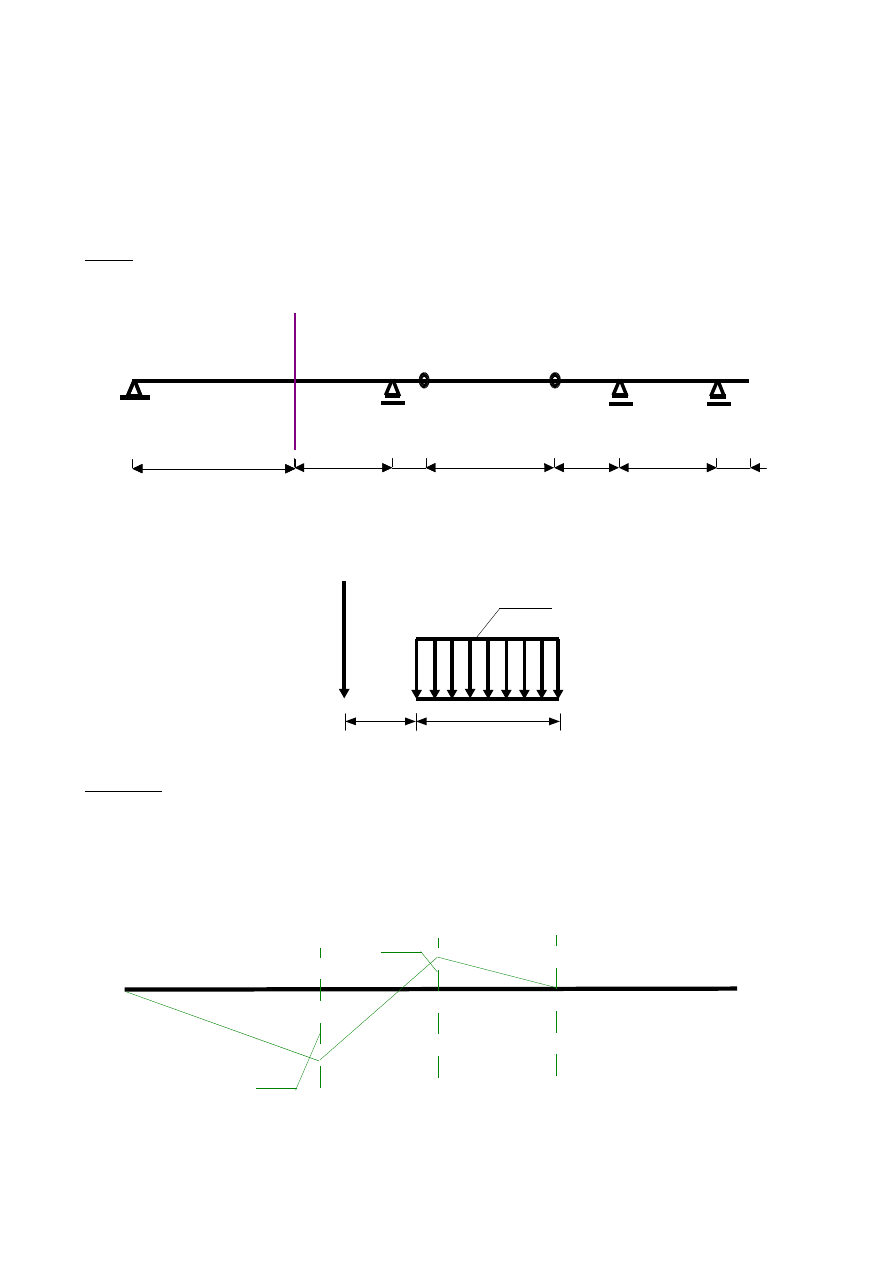
Aby wykreślić obwiednię momentów w pierwszej kolejności wyznaczam linie wpływowe oraz ekstremalne wartości
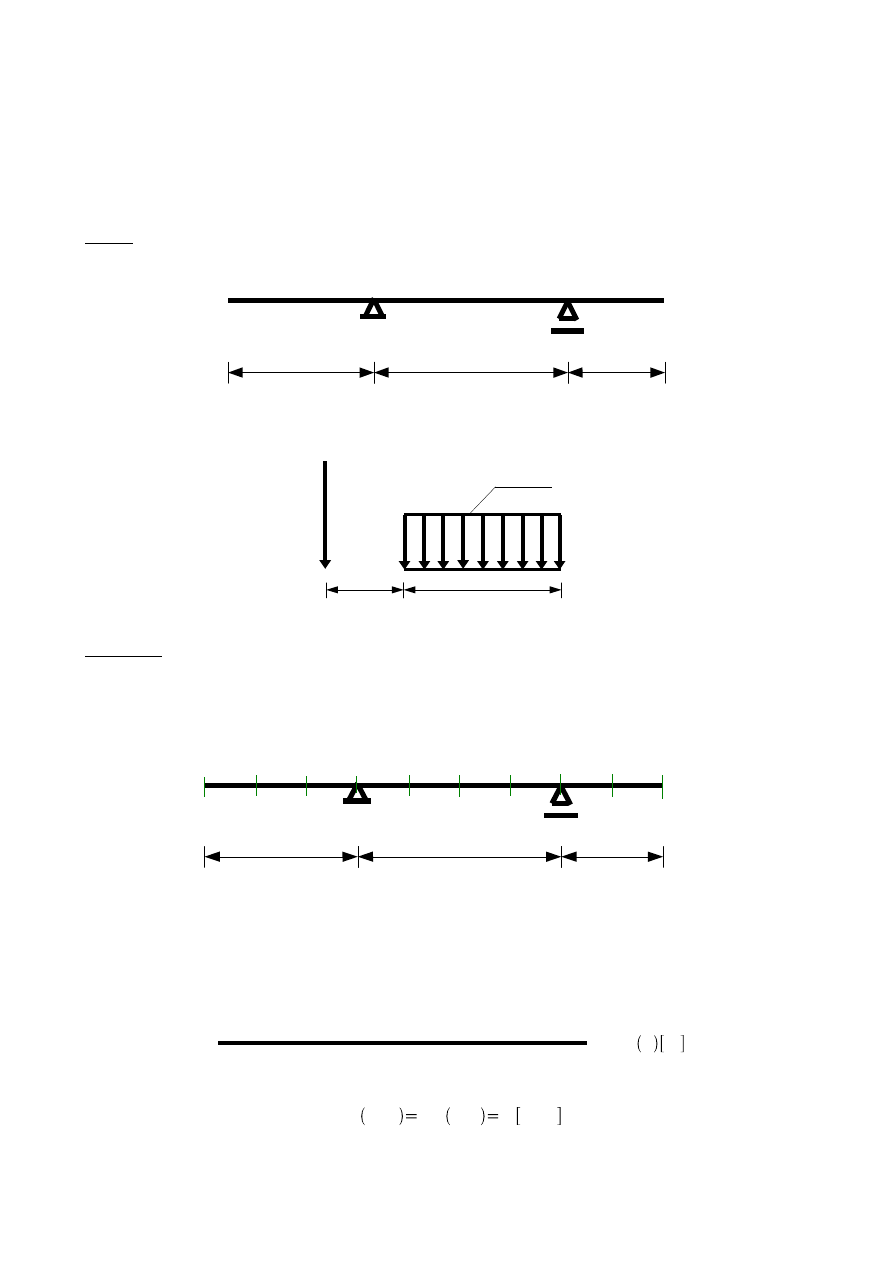
momentu zginającego dla każdego z przyjętych przekrojów. Przekroje ustanawiam co 1m jak na rys. 5.3.:

3,0 m

4,0 m

2,0 m

0

1

2

3

4

5

6

7

8

9

Rys.5.3

Na rysunkach poniżej przedstawiono linie wpływowe momentu zginającego dla każdego z przekrojów 0-9. Kolorem
czarnym przedstawiono położenie danego zespołu obciążeń, przy którym moment zginający ma wartość maksymalną,
natomiast kolorem czerwonym położenie, dla którego moment zginający jest minimalny. Pod każdym z rysunków
wykonano obliczenia ekstremalnych wartości momentu.

Przekrój 0

0

M

0

x m

Rys.5.4

M

0

max

M

0

min

0 kNm

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

33/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

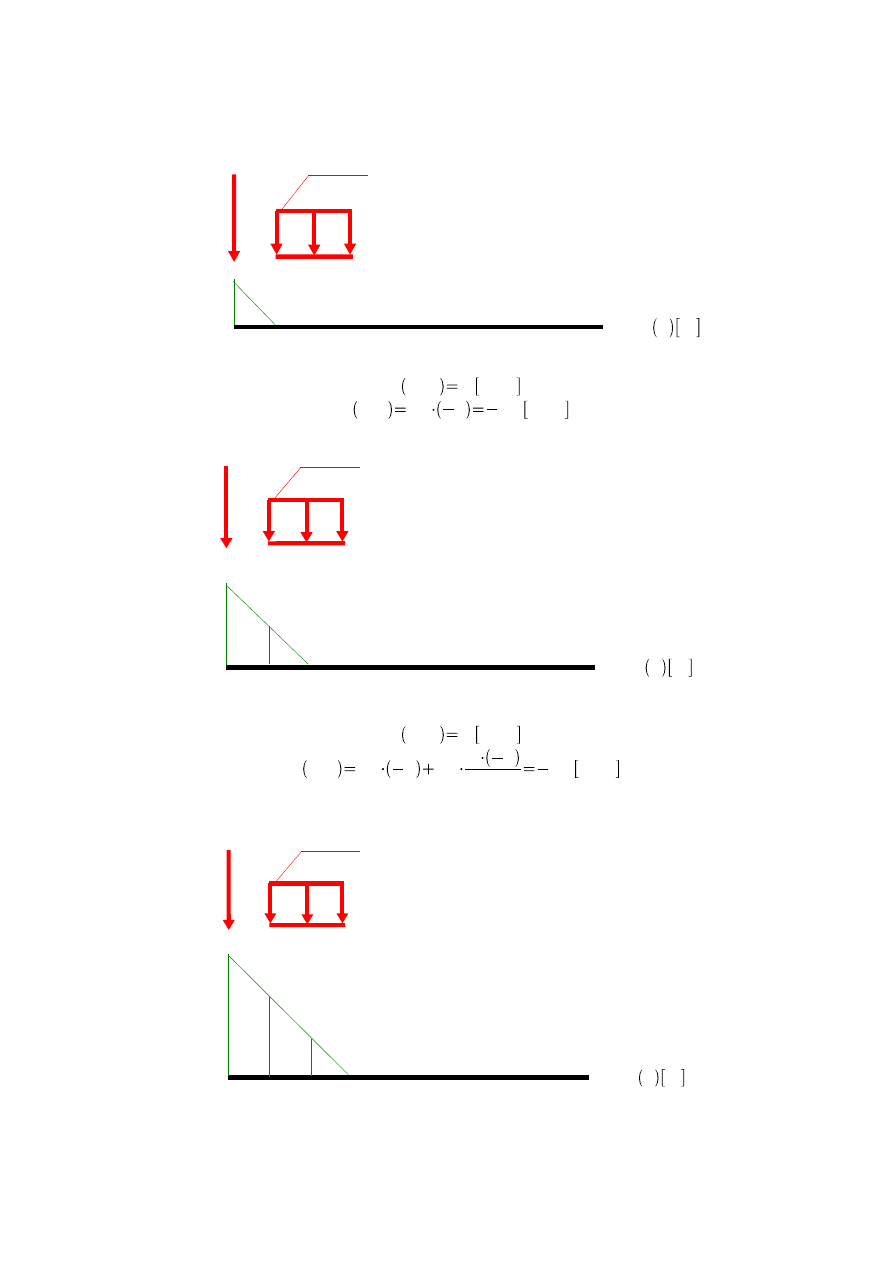
Przekrój 1

0

M

1

x m

-1

30 kN

10 kN/m

Rys. 5.5.

M

1

max

0 kNm

M

1

min

30

1

30 kNm

Przekrój 2

0

M

2

x m

-2

30 kN

10 kN/m

-1

Rys.5.6.

M

2

max

0 kNm

M

2

min

30

2

10

1

1

2

65 kNm

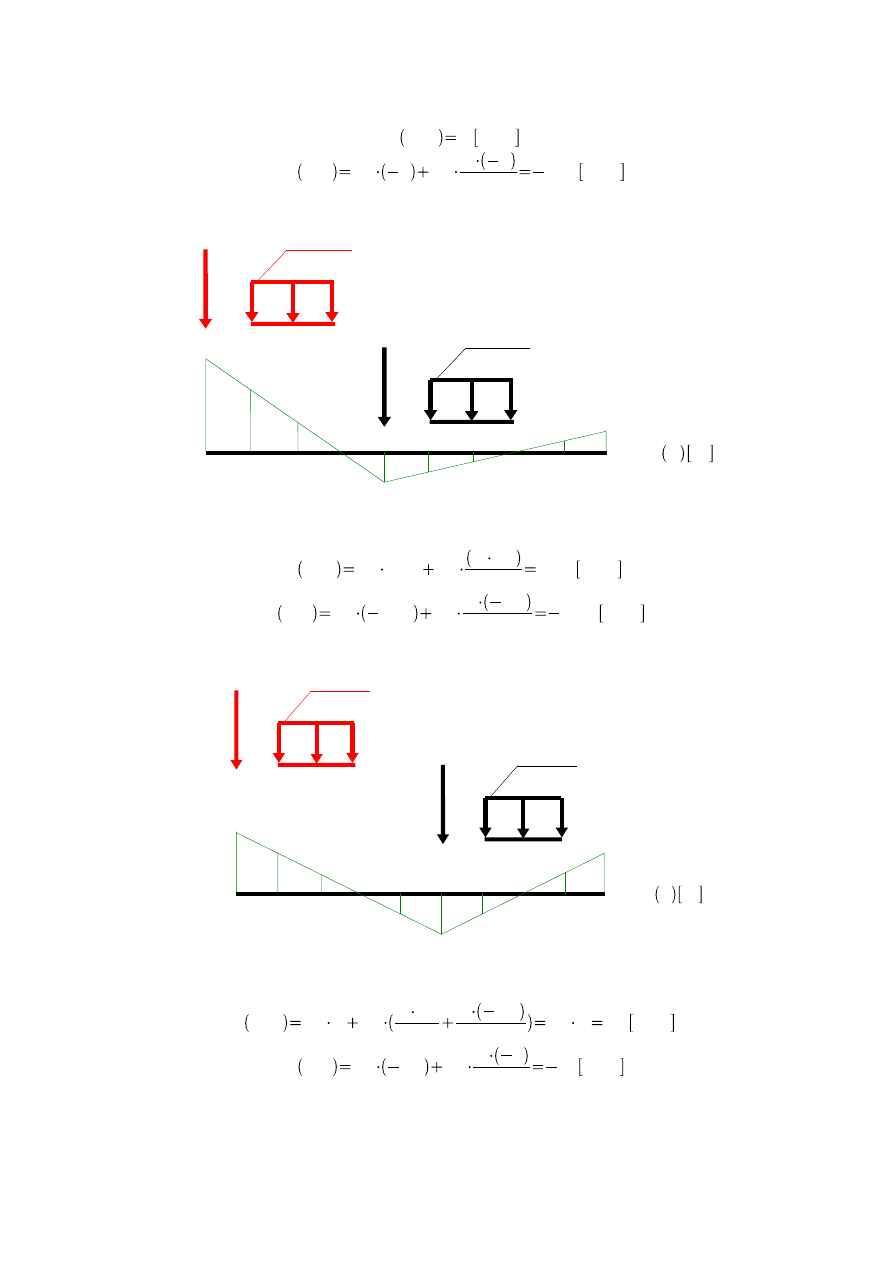
Przekrój 3

0

M

3

x m

-2

30 kN

10 kN/m

-1

-3

Rys.5.7

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

34/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

M

3

max

0 kNm

M

3

min

30

3

10

2

2

2

110 kNm

Przekrój 4

0

M

4

x m

-1,5

30 kN

10 kN/m

-0,75

-2,25

0,75

0,5

0,25

-0,25

-0,5

30 kN

10 kN/m

Rys.5.8

M

4

max

30 0,75 10

2 0,5

2

27,5 kNm

M

4

min

30

2,25

10

2

1,5

2

82,5 kNm

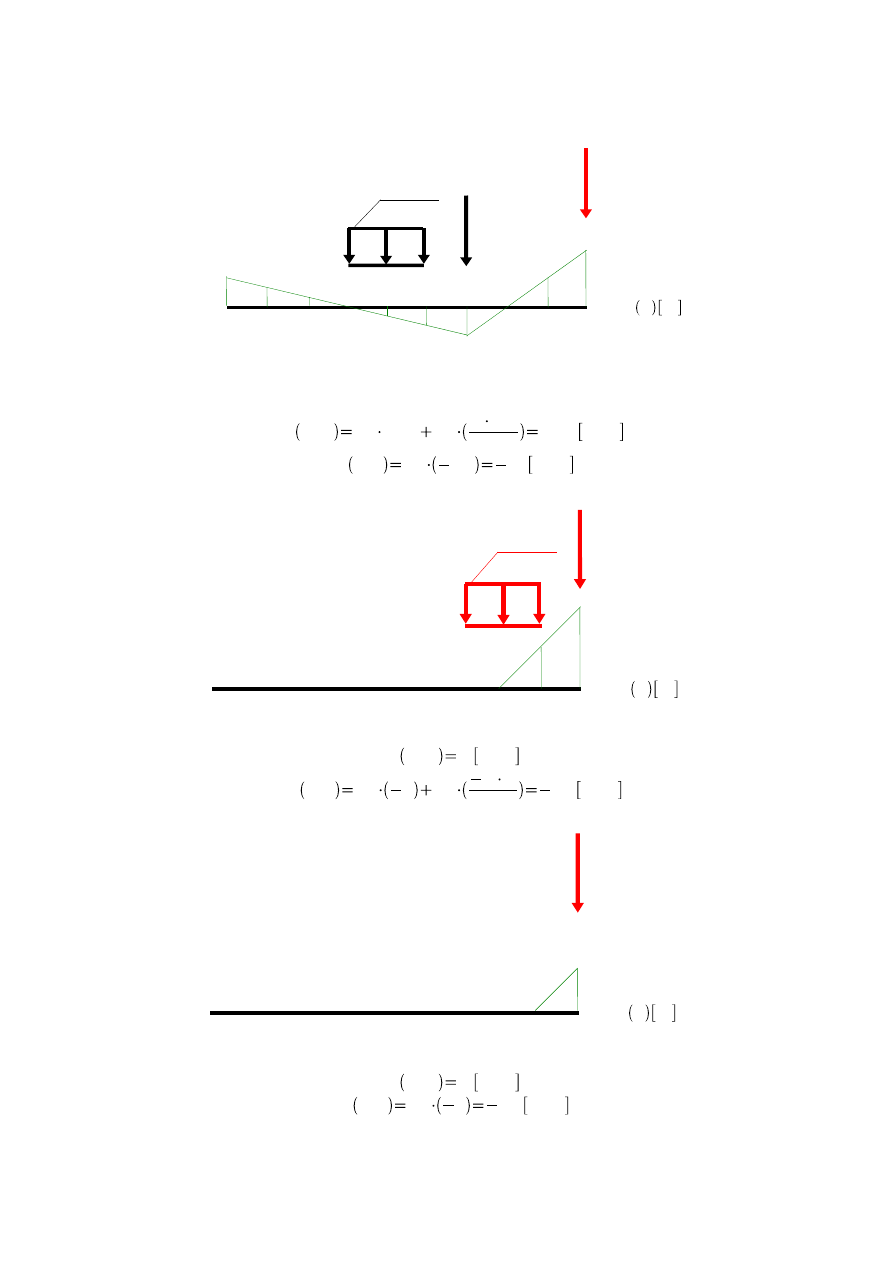
Przekrój 5

0

M

5

x m

-1

30 kN

10 kN/m

-0,5

-1,5

1

0,5

0,5

-0,5

-1

30 kN

10 kN/m

0

Rys.5.9

M

5

max

30 1 10

1 0,5

2

1

0.5

2

30 1 30 kNm

M

5

min

30

1,5

10

2

1

2

55 kNm

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

35/37

Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

Przekrój 6

0

M

6

x

m

-0,25

30 kN

-0,5

-0,75

0,5

0,25

0,75

-0,75

-1,5

30 kN

10 kN/m

0

Rys.5.10

M

6

max

30 0,75 10

2 0,5

2

27,5 kNm

M

6

min

30

1,5

45 kNm

Przekrój 7

M

7

x m

30 kN

0

-1

-2

0

10 kN/m

Rys.5.11

M

7

max

0 kNm

M

7

min

30

2

10

1 1

2

65 kNm

Przekrój 8

M

8

x m

30 kN

0

-1

0

Rys.5.12

M

8

max

0 kNm

M

8

min

30

1

30 kNm

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

36/37

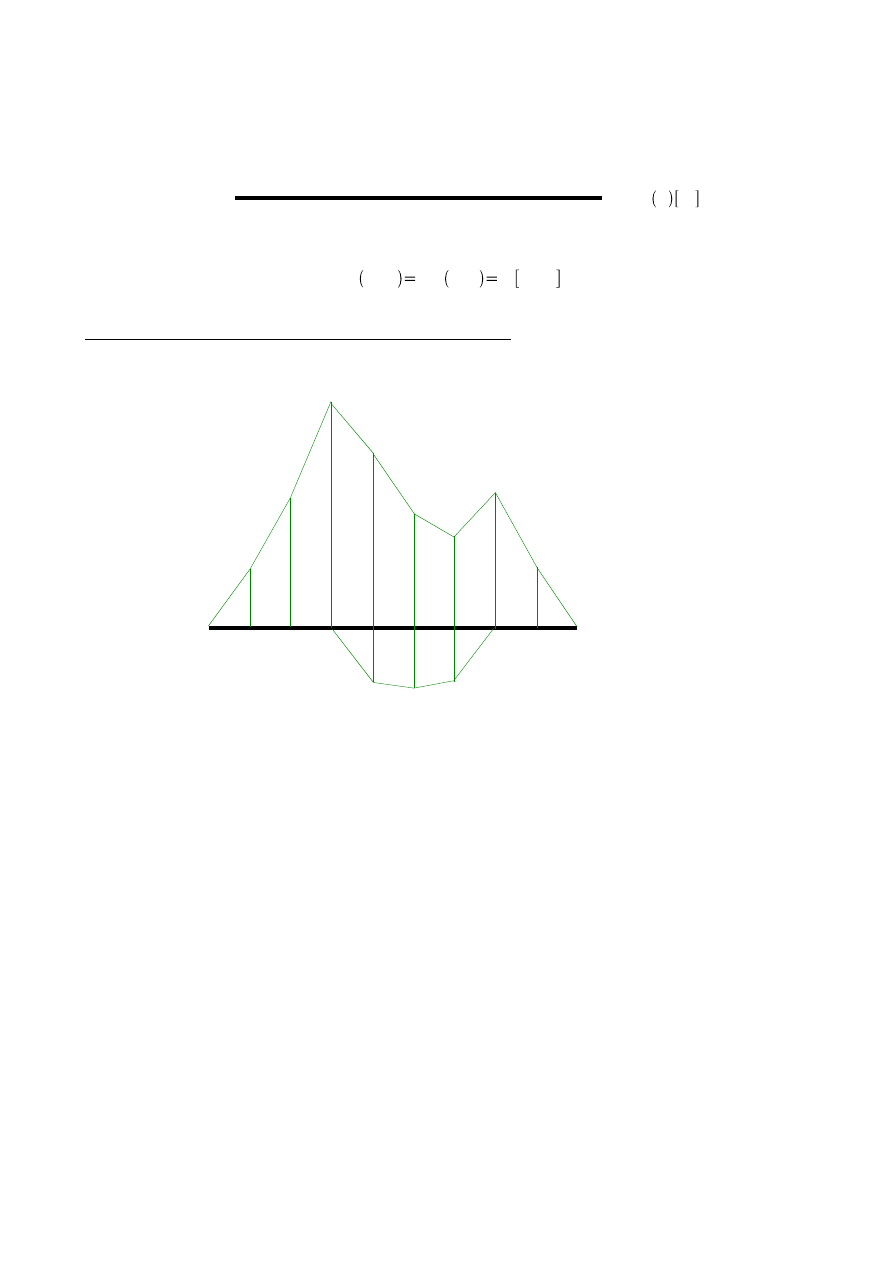
Linie wpływowe w układach statycznie wyznaczalnych

05.11.04

Przekrój 9

0

M

9

x m

Rys.5.13

M

9

max

M

9

min

0 kNm

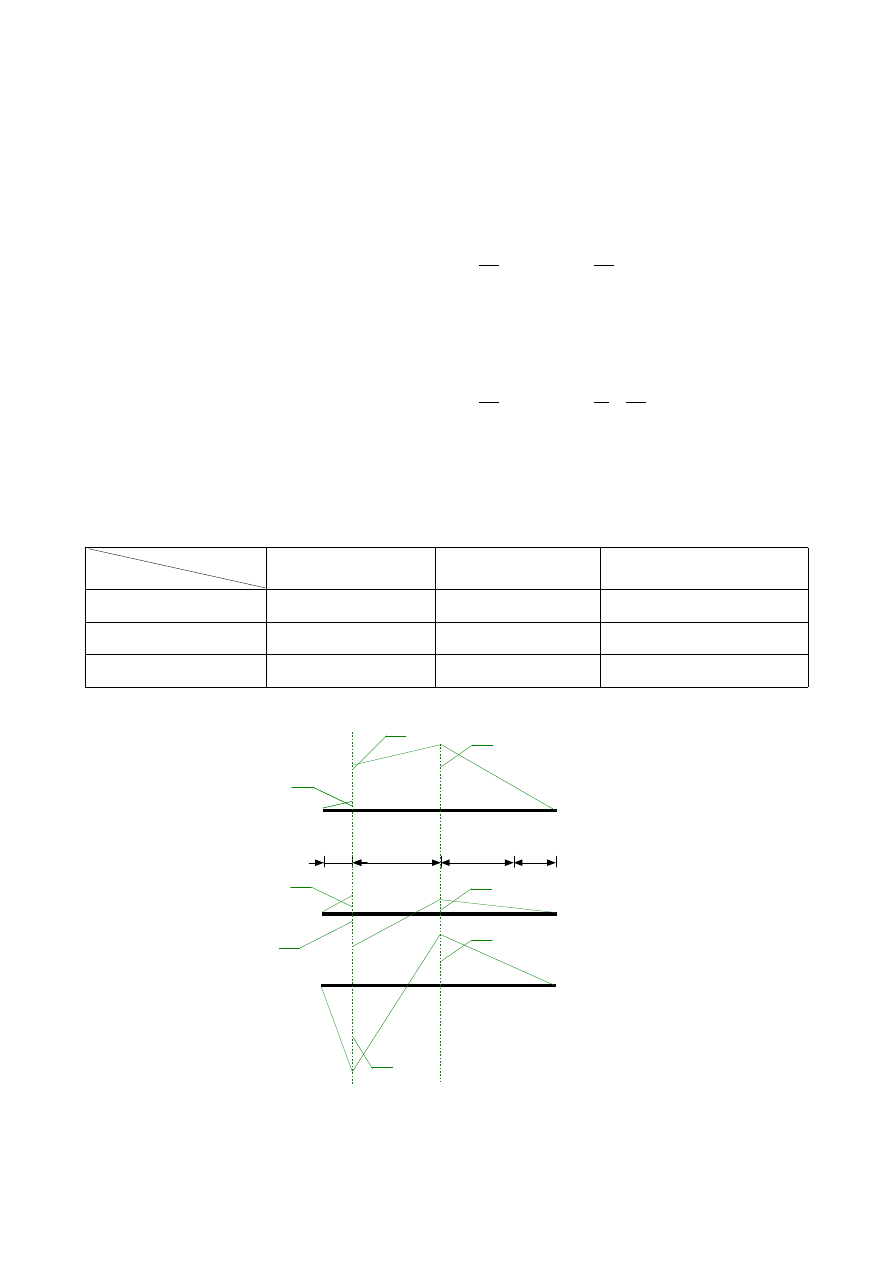
Wykreślenie obwiedni momentów na podstawie powyższych obliczeń:

0

-30

-65

-110

-82,5

-55

-45

-65

-30

0

0

0

0

0

0

27,5

27,5

30

0

0

obw M [kNm]

Rys.5.14

Anna Zielona gr.3 KBI - Linie wpływowe w układach statycznie wyznaczalnych

37/37