α



α

m

a

x









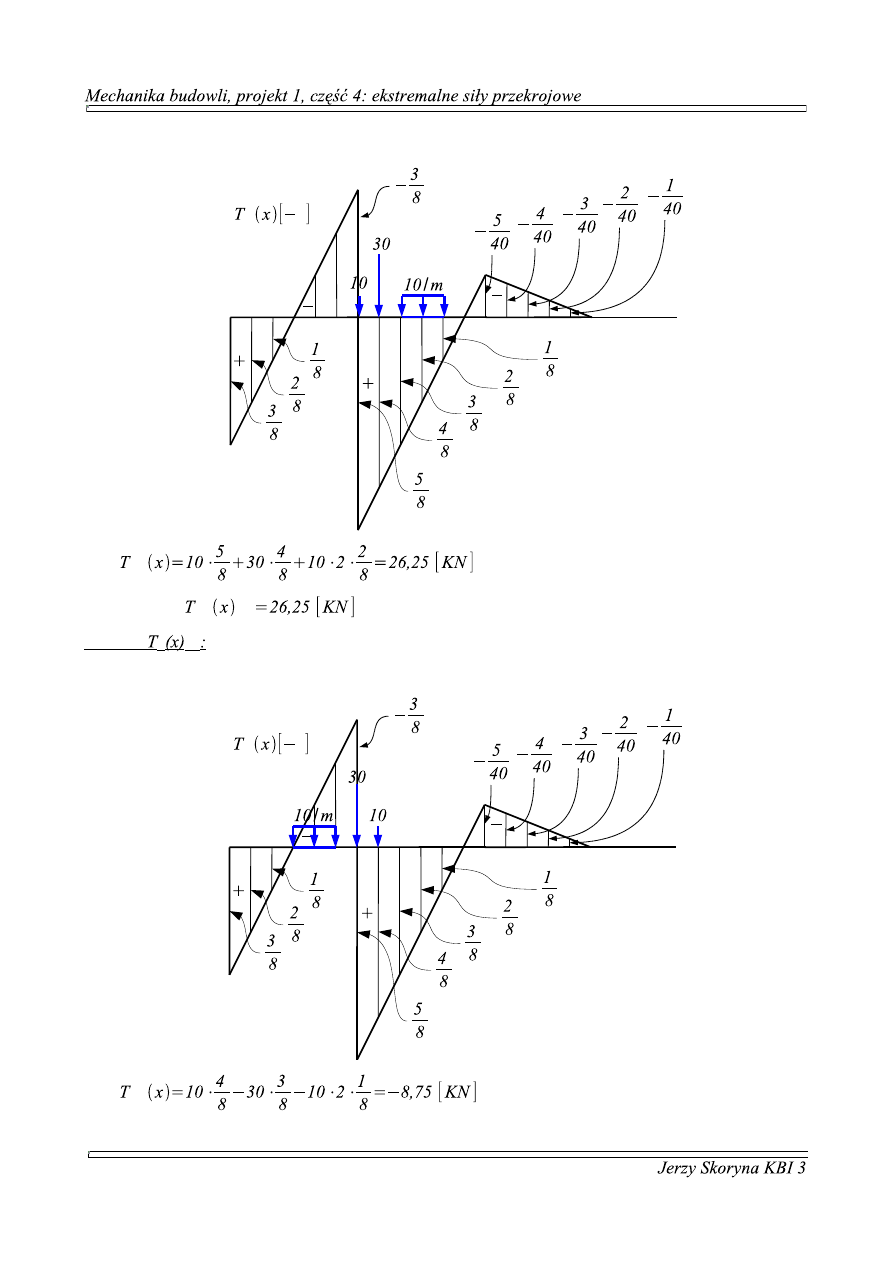
2. położenie 2:









Czyli:







m

a

x

Szukam

α

m

i

n

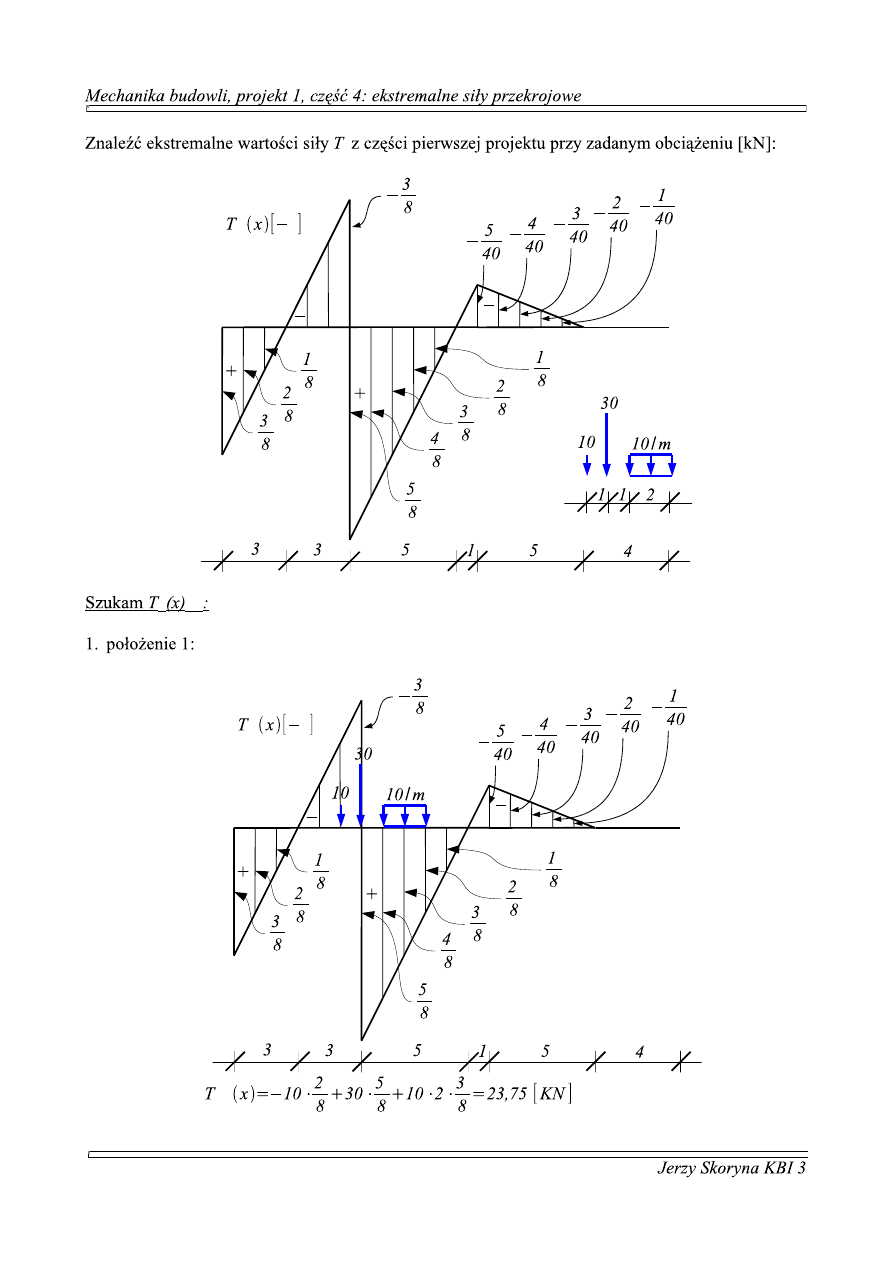
1. położenie 1:









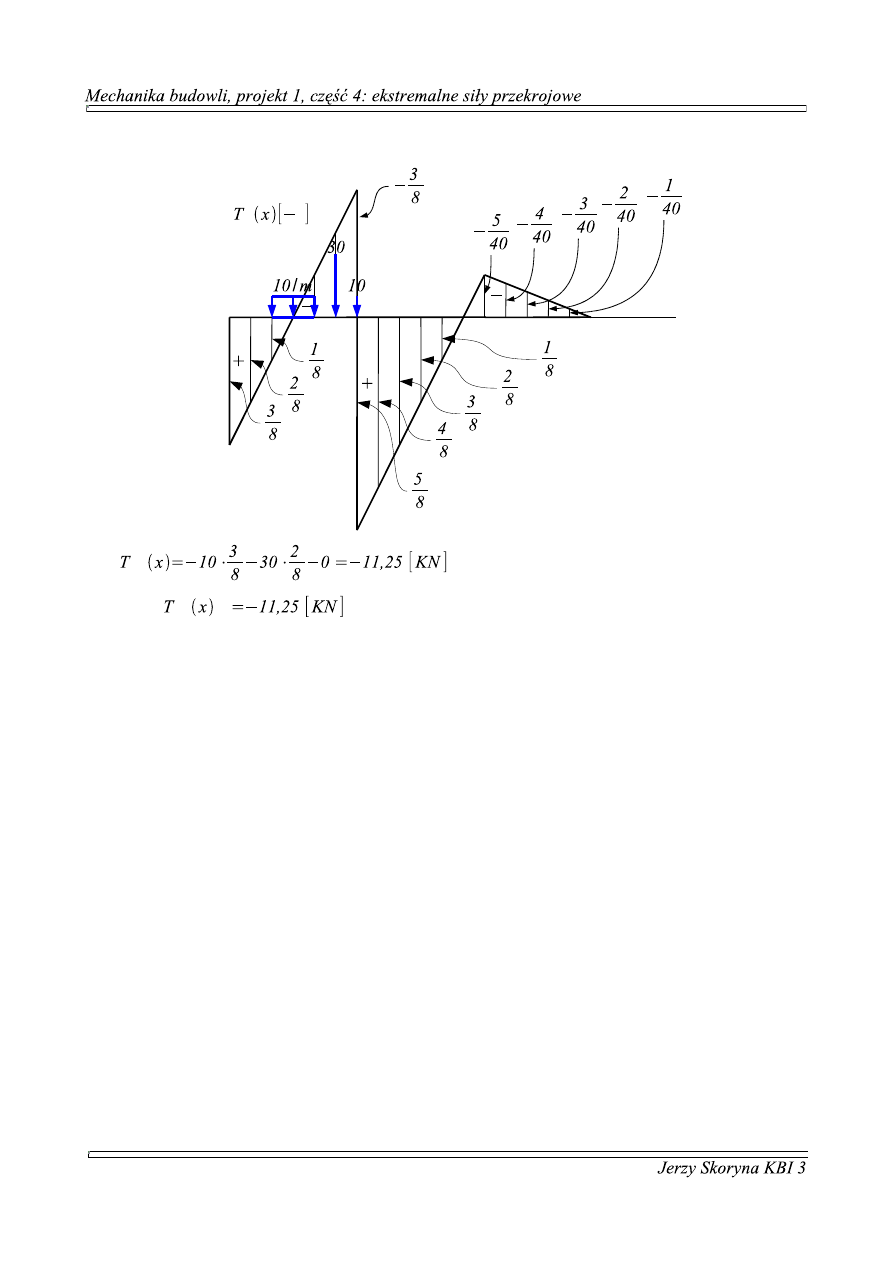
2. położenie 2:









Czyli:







m

i

n

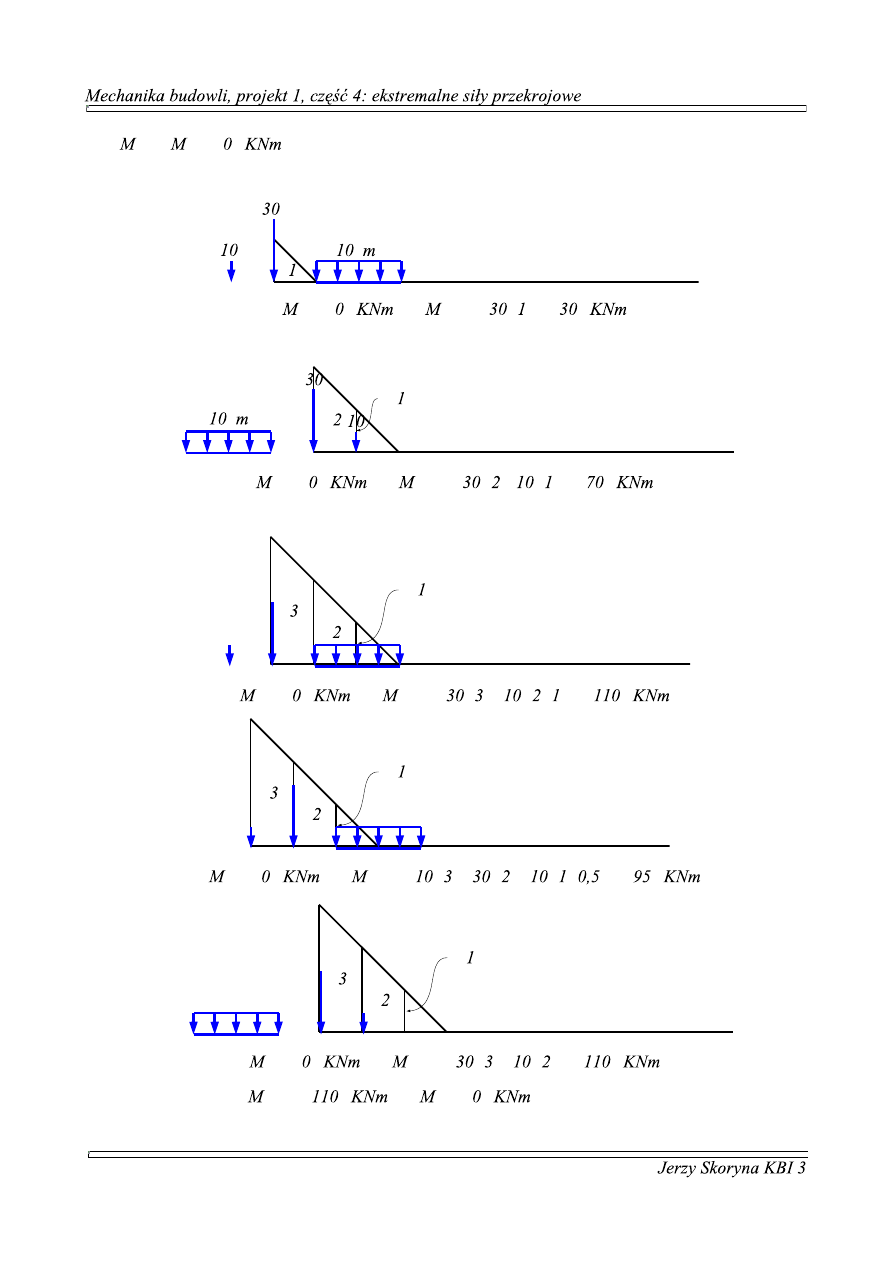
Znaleźć ekstremalne wartości Momentu zginającego dla belki na rysunku przy zadanym
obciążeniu (jak wyżej), naszkicować obwiednię momentów:

linie wpływowe momentów w przekrojach co 1 metr [m]:

−

−







−

−

−

−

−

−

−

−

−

−

−

−

−

−

−

−

−

−

−

−

−



−

−

−

0.

m

i

n

=

m

a

x

=

[

]

1.

−

/

m

a

x

=

[

]

m

i

n

=−

⋅ =−

[

]

2.

−

−

/

m

a

x

=

[

]

m

i

n

=−

⋅ −

⋅ =−

[

]

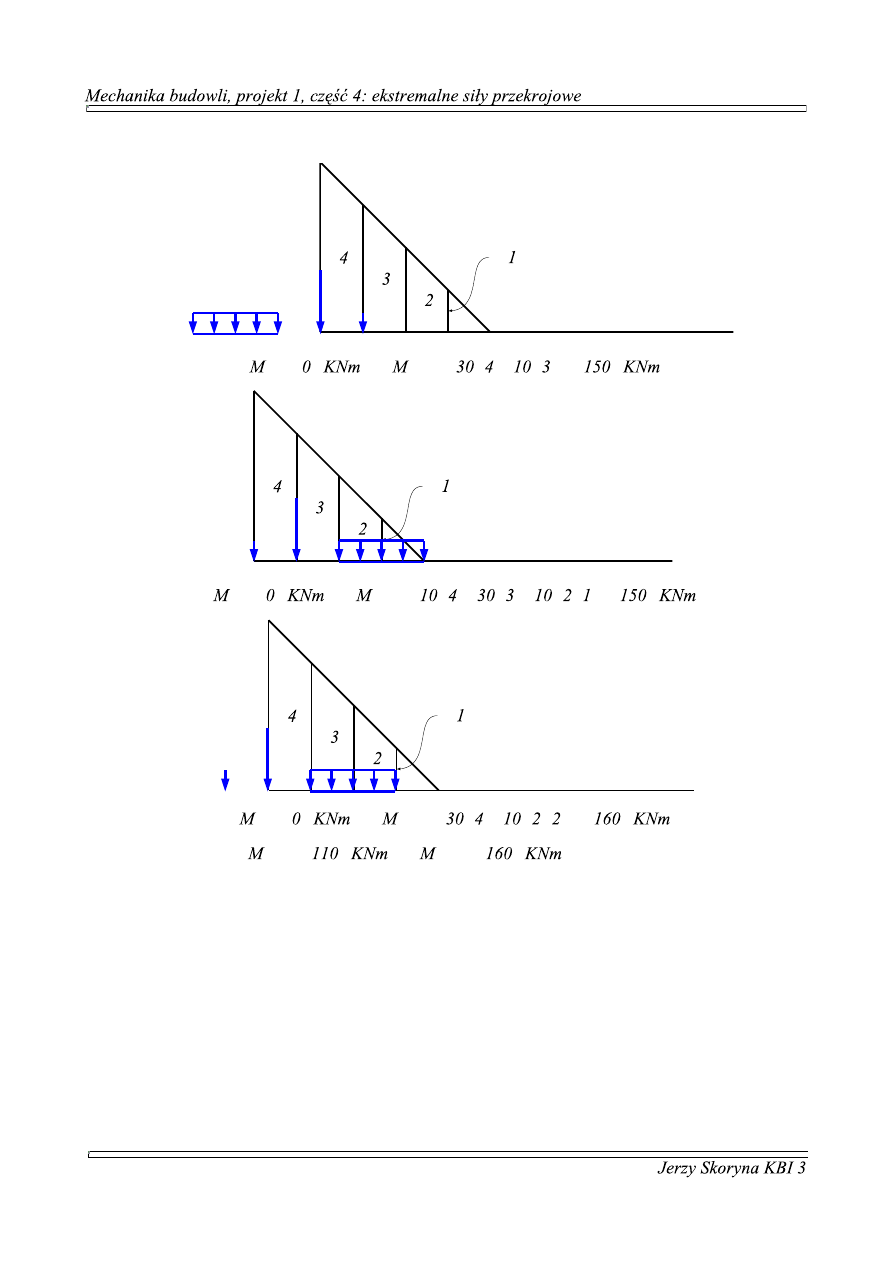
3.

−

−

−

m

a

x

=

[

]

m

i

n

=−

⋅ −

⋅ ⋅ =−

[

]

−

−

−

m

a

x

=

[

]

m

i

n

=−

⋅ −

⋅ −

⋅ ⋅

=−

[

]

−

−

−

m

a

x

=

[

]

m

i

n

=−

⋅ −

⋅ =−

[

]

Czyli ostatecznie:

m

i

n

=−

[

]

m

a

x

=

[

]

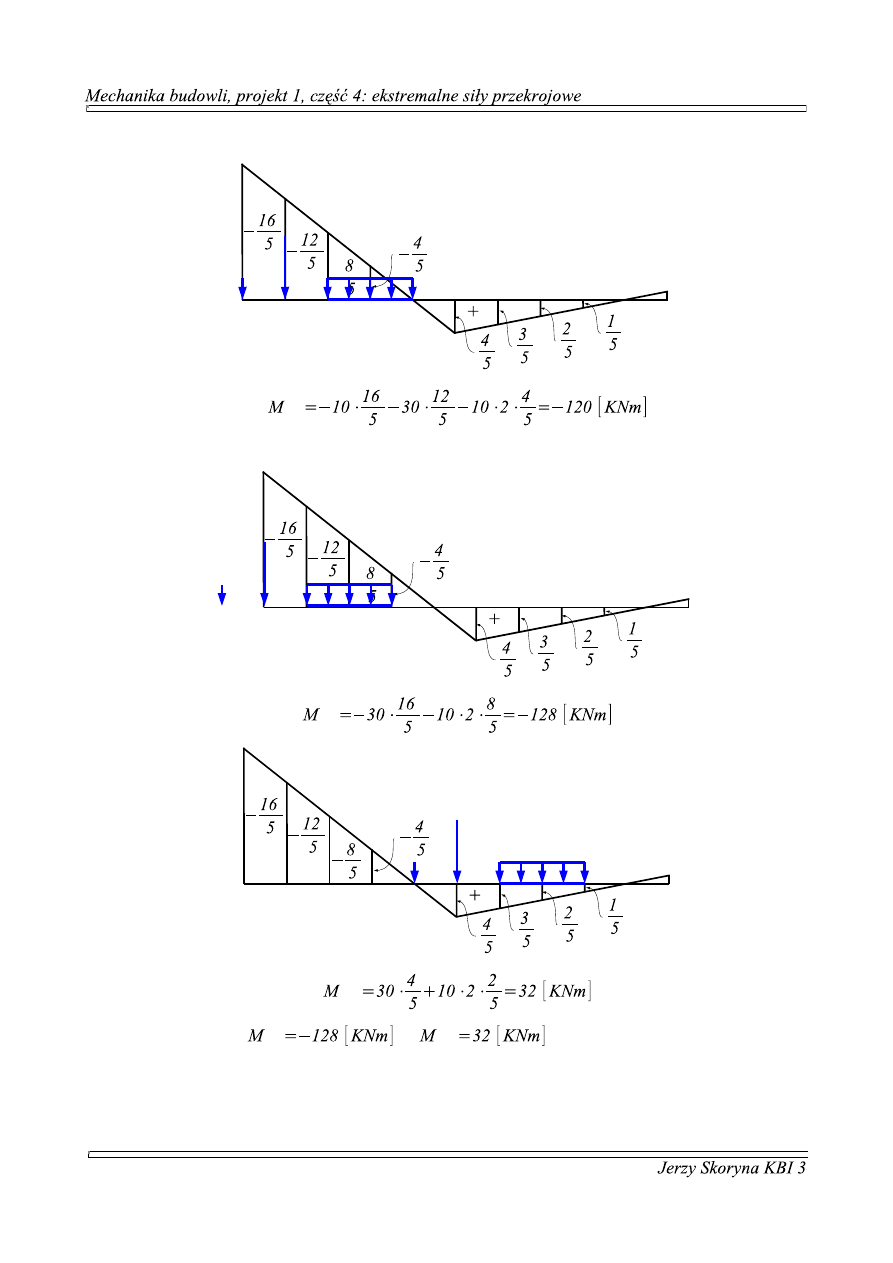
4.

−

−

−

−

m

a

x

=

[

]

m

i

n

=−

⋅ −

⋅ =−

[

]

−

−

−

−

m

a

x

=

[

]

m

i

n

=−

⋅ −

⋅ −

⋅ ⋅ =−

[

]

−

−

−

−

m

a

x

=

[

]

m

i

n

=−

⋅ −

⋅ ⋅ =−

[

]

Czyli ostatecznie:

m

i

n

=−

[

]

m

a

x

=−

[

]

5.

m

i

n

m

i

n

m

a

x

Czyli ostatecznie:

m

i

n

m

a

x

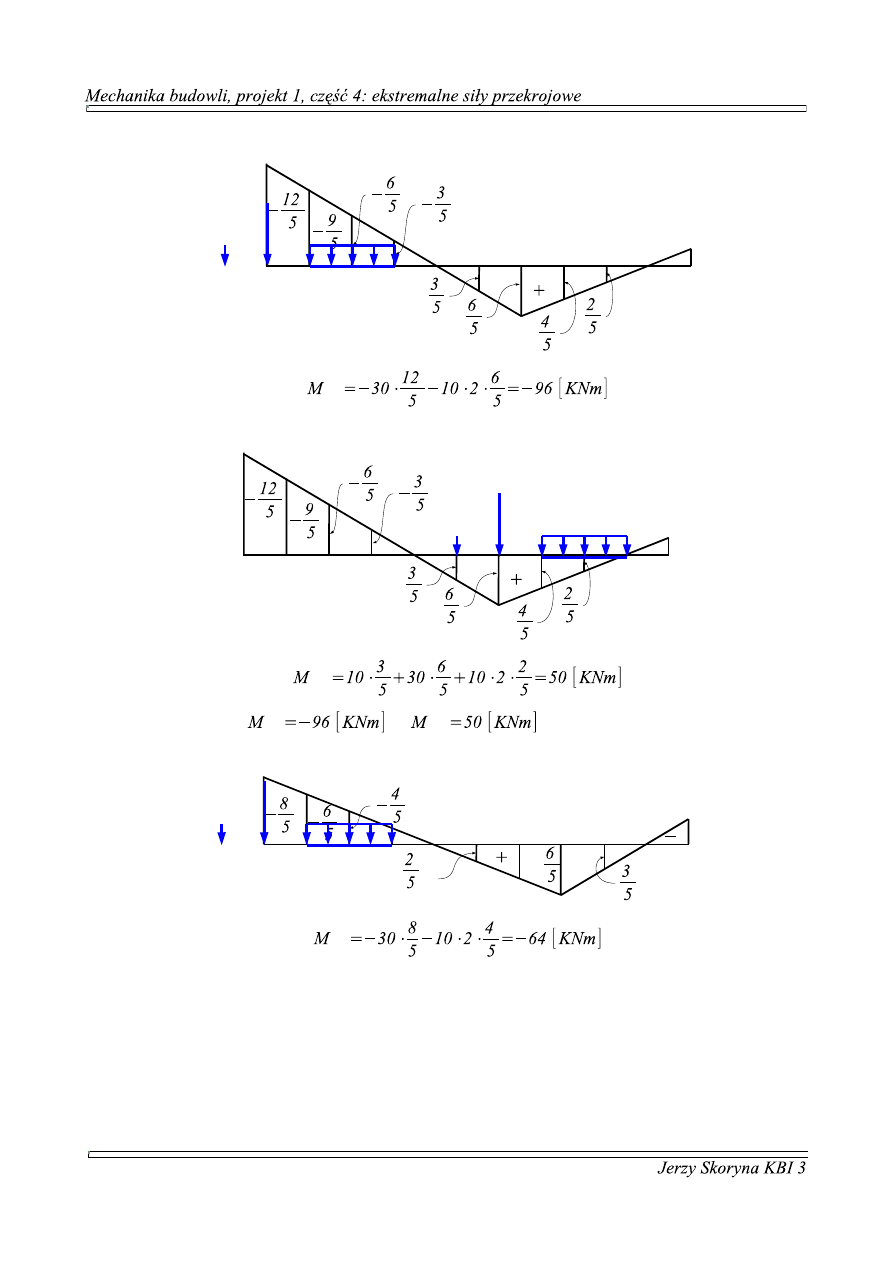
6.

m

i

n

m

a

x

Czyli ostatecznie:

m

i

n

m

a

x

7.

m

i

n

−

−

−

−



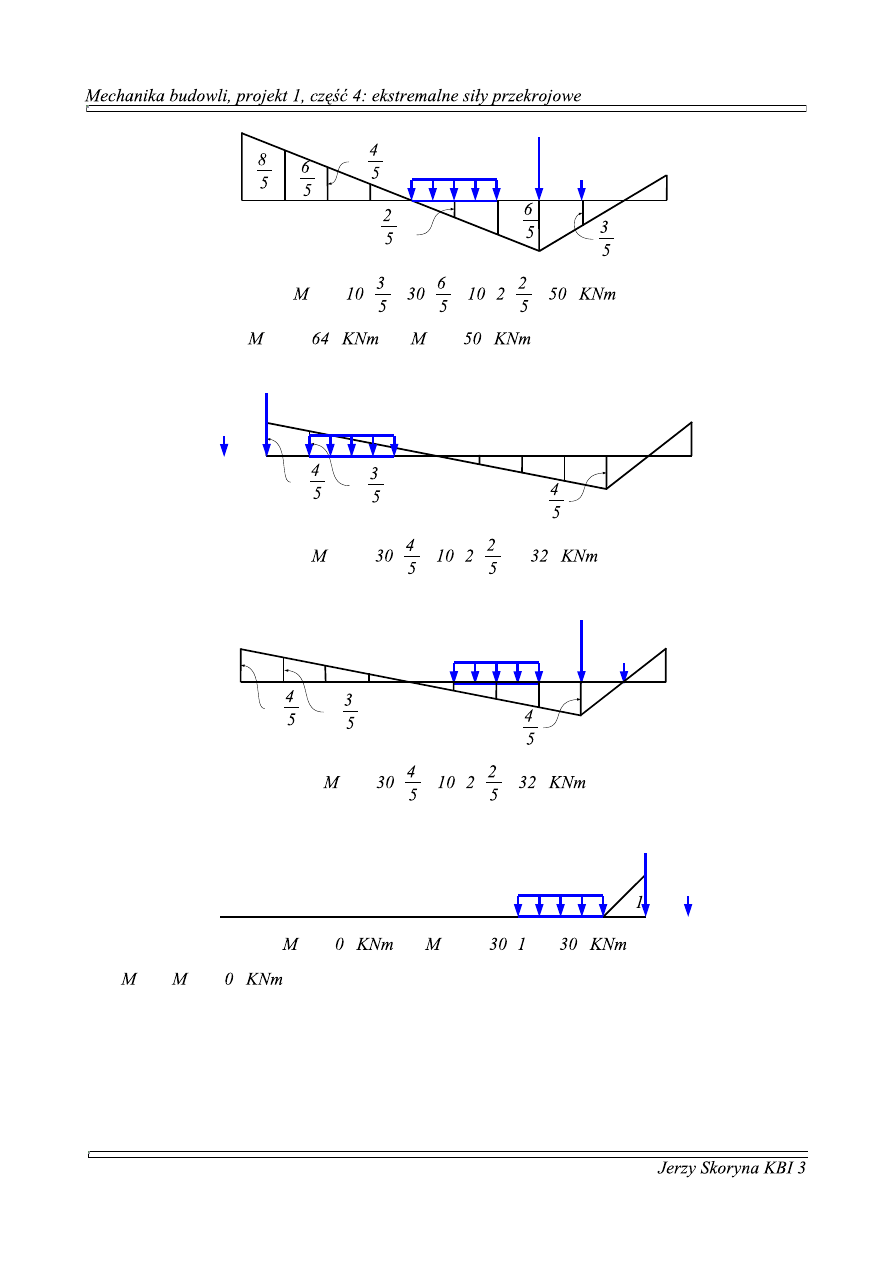
m

a

x

=

⋅ 

⋅ 

⋅ ⋅ =

[

]

Czyli ostatecznie:

m

i

n

=−

[

]

m

a

x

=

[

]

8.

−



−

−

m

i

n

=−

⋅ −

⋅ ⋅ =−

[

]

−



−

−

m

a

x

=

⋅ 

⋅ ⋅ =

[

]

9.

−

m

a

x

=

[

]

m

i

n

=−

⋅ =−

[

]

10.

m

i

n

=

m

a

x

=

[

]

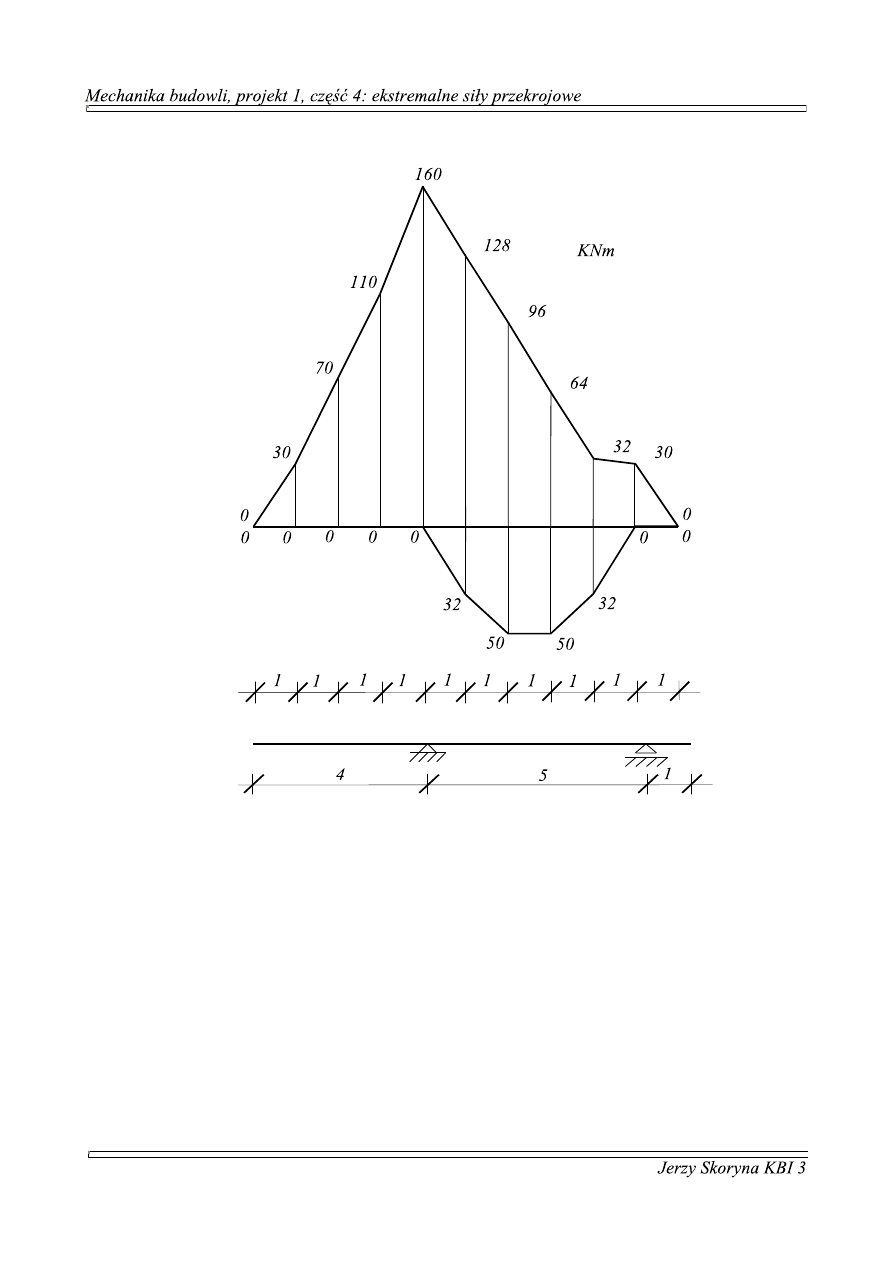
Obwiednia momentów:

−

−

−

−

−

−

−

−

−

[

]