LABORATORIUM FIZYKI I

SPRAWOZDANIE

Ćwiczenie nr : 12
Data : 21.03.2012

Wydział :
WIP

Grupa :
ID-MT-41

Zespół :
2

P

u

n

kt

acja

:

Przygotowanie:

Imię i nazwisko:
Karol Bujalski

Temat ćwiczenia :
Badanie procesów relaksacyjnych w obwodach elektrycznych

Sprawozdanie:

Prowadzący :
Marek Sierakowski

Suma punktów:

1. WSTĘP

Celem ćwiczenia było zapoznanie się z naturą procesów relaksacyjnych, obserwacją zjawiska
drgań relaksacyjnych oraz zbadanie przebiegu procesu ładowania kondensatora. Relaksacja
polega na ustabilizowaniu i przejściu układu do makroskopowego stanu równowagi.
Matematyczny opis procesu relaksacji przedstawiany jest za pomocą równań o postaci:

Gdzie :

y

0

, y

k

– wartość początkowa i końcowa

t – czas
τ – czas relaksacji
e – stała Eulera

Wzór na czas relaksacji w obwodzie RC przyjmuje postać:

2. UKŁAD POMIAROWY

CZĘŚĆ I – BADANIE PROCESU ŁADOWANIA KONDENSATORA

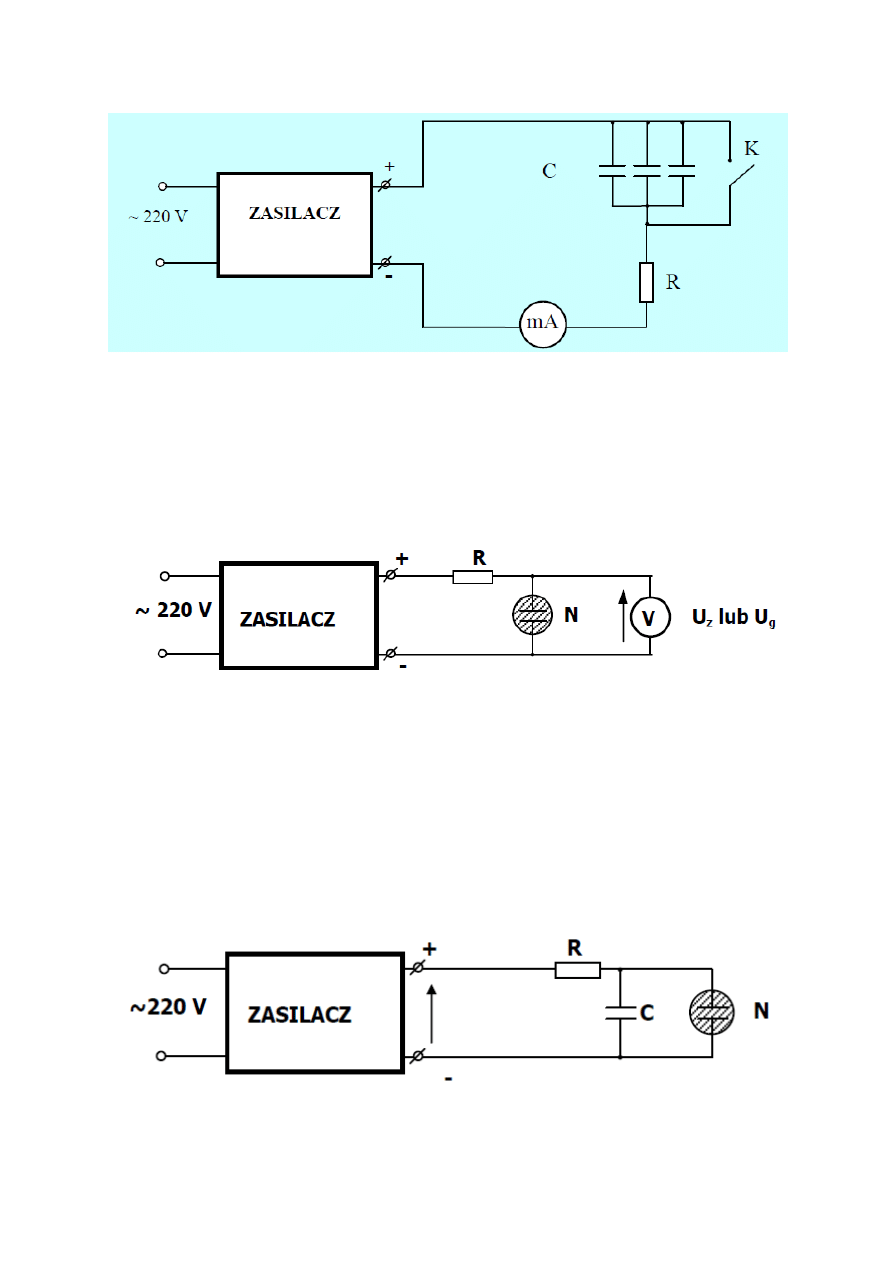
Rys. 1 Źródło: instrukcja do ćwiczenia

R – zestaw oporników
C – zestaw kondensatorów
K – klucz
μA – mikroamperomierz, klasa 0,2, zakres 150 μA, liczba działek – 150

CZĘŚĆ II – POMIAR NAPIĘCIA ZAPŁONU U

z

I GAŚNIĘCIA U

g

NEONÓWKI

Rys. 2 Źródło: instrukcja do ćwiczenia

R – zestaw oporników
N – neonówka
V– woltomierz cyfrowy V543, zakres 100V, c

1

=0,05%, c

2

=0,01%

CZĘŚĆ III – BADANIE ZALEŻNOŚCI OKRESU DRGAŃ RELAKSACYJNYCH OD REZYSANCJI

I POJEMNOŚCI

Rys. 3 Źródło: instrukcja do ćwiczenia

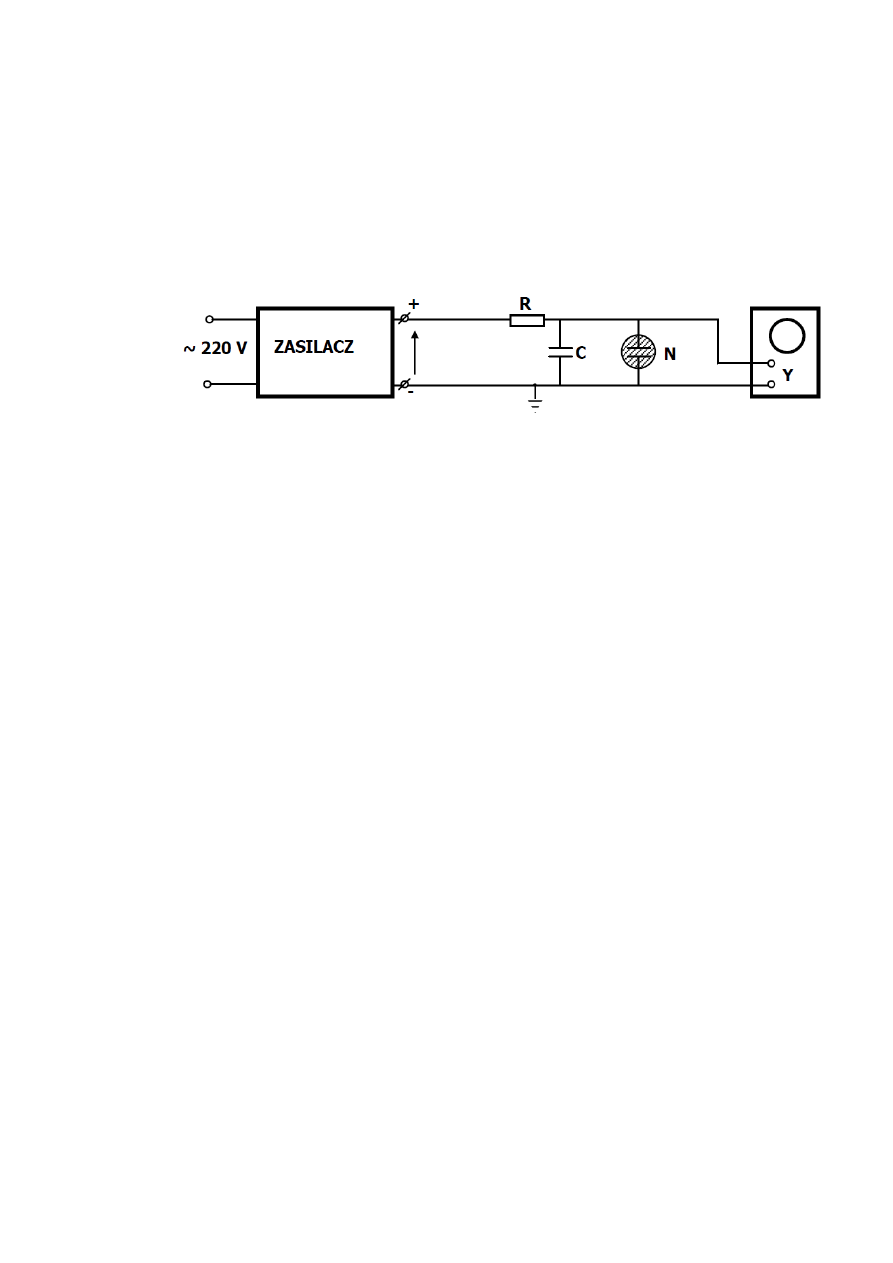
R – zestaw oporników
C – zestaw kondensatorów
N – neonówka

CZĘŚĆ IV – Obserwacja drgań relaksacyjnych na ekranie oscyloskopu

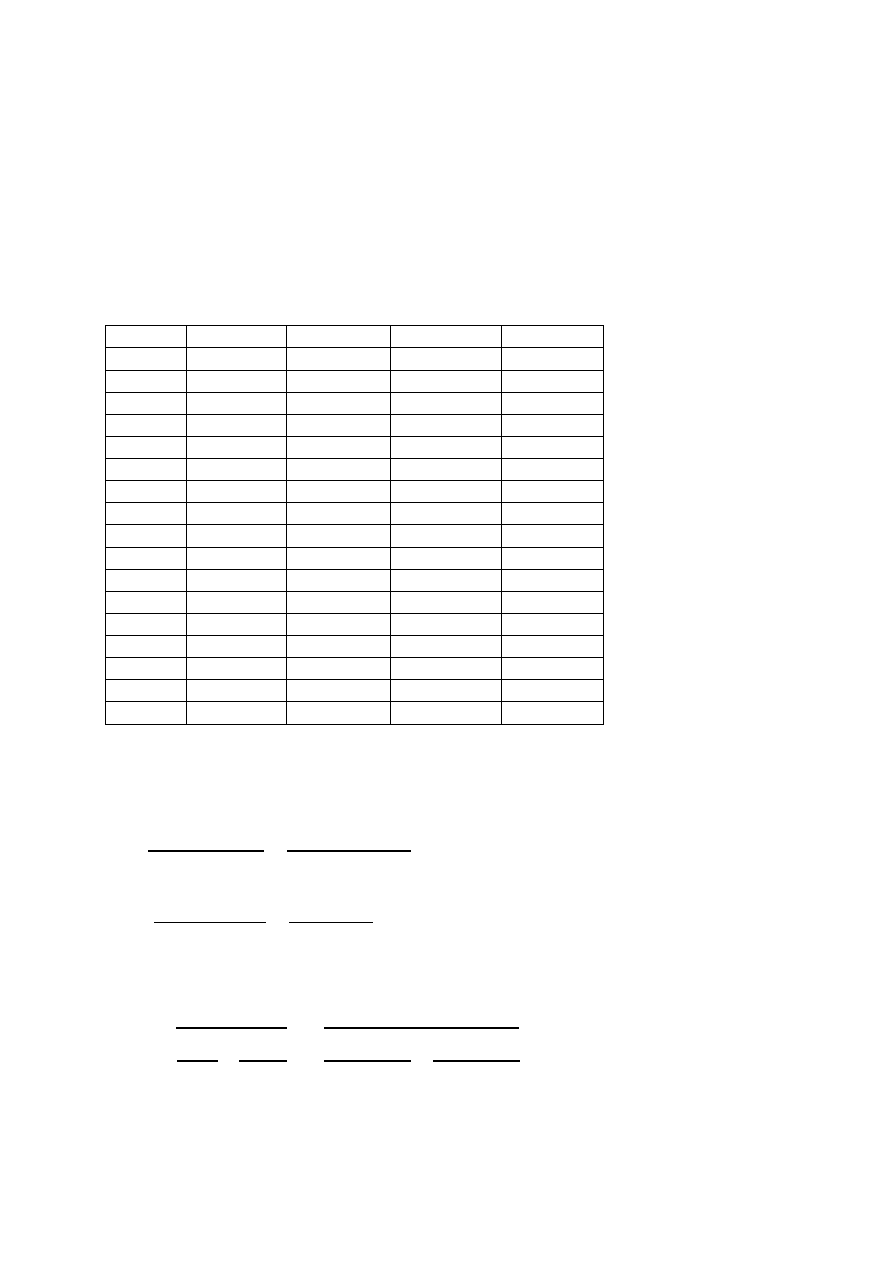
Rys. 4 Źródło: instrukcja do ćwiczenia

R – zestaw oporników
C – zestaw kondensatorów
N – neonówka
Y- oscyloskop

3. WYKONANIE ĆWICZENIA

CZĘŚĆ I

1. Stworzenie obwodu (C=100μF, R=470 kΩ) i uruchomienie urządzeń pomiarowych.
2. Zwieramy klucz w celu ładowania kondensatora.
3. Po naładowaniu kondensatora rozwieramy klucz i co 5 sekund zapisujemy aktualną wartość

natężenia prądu mierzoną mikroamperomierzem.

4. Przy wartości natężenia bliskiej 0 i niewielkich zmianach w natężenia w czasie przerywamy

pomiary.

5. Powtórzono pomiary podłączając inny opornik: R=320 kΩ.
6. Zmieniamy kondensator na C=200μF i powtórzenie pomiarów dla takich samych oporów.

CZĘŚĆ II

1. Stworzenie obwodu jak na Rys. 2, opornik R=50kΩ.
2. Zwiększanie napięcia na zasilaczu aż do uzyskania żarzenia neonówki, odczyt napięcia

żarzenia.

3. Obniżanie napięcia w celu znalezienia napięcia gaśnięcia.
4. Pięciokrotne powtórzenie pomiarów.

CZĘŚĆ III

1. Stworzenie obwodu jak na Rys. 3 C=2,2μF, R=835 kΩ.
2. Pomiar czasu 20 mignięć neonówki.

3.

Powtórzenie pomiarów z wykorzystaniem innych wartości oporów R=760 kΩ, R=680 kΩ,
R=560 kΩ.

4.

Powtórzenie wszystkich pomiarów dla innej pojemności kondensatora C=1μF.

CZĘŚĆ IV

1. Stworzenie obwodu jak na Rys. 4.
2. Obserwacja przebiegu na ekranie oscyloskopu.

4. WYNIKI I ICH OPRACOWANIE

CZĘŚĆ I

C=100[μF]

C=100[μF]

C=200[μF]

C=200[μF]

R=470[kΩ]

C=320[kΩ]

R=470[kΩ]

C=320[kΩ]

t[s]

I[μA]

I[μA]

I[μA]

I[μA]

0

150

150

150

150

5

135

128

142

141

10

120

108

135

129

15

109

94

128

120

20

98

81

122

111

25

87

115

103

30

79

110

96

35

104

88

40

99

82

45

94

76

50

90

55

84

60

80

65

76

T1/2

33

22

66

46

Tabela 1 wyniki pomiarów
Niepewność pomiaru natężenia prądu przy pomocy mikroamperomierza analogowego
obliczamy ze wzorów:

ł

Z prawa propagacji niepewności:

Niepewność logarytmu wartości natężenia:

Niepewność pomiaru czasu:
– najmniejsza działka na używanym stoperze

– szacowana wartość czasu reakcji

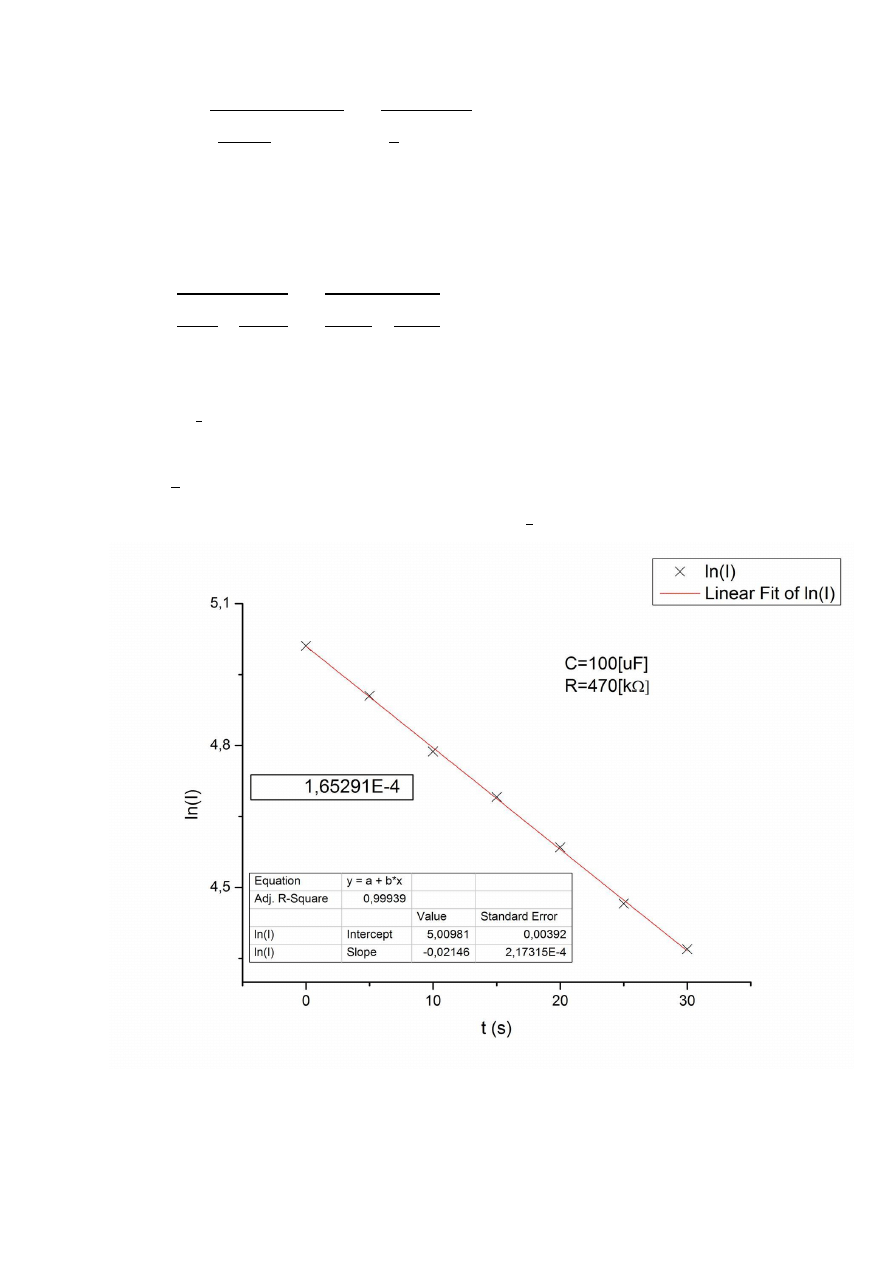
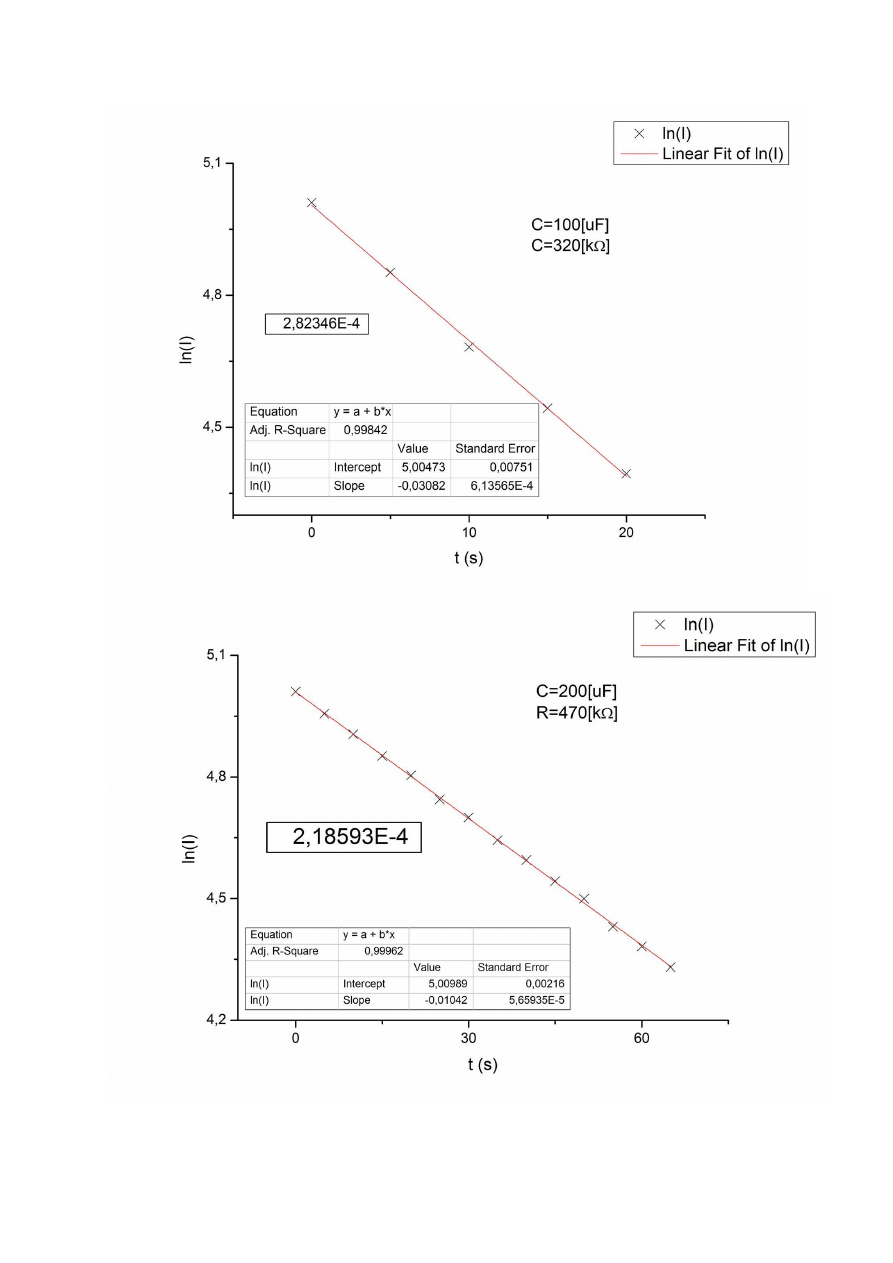
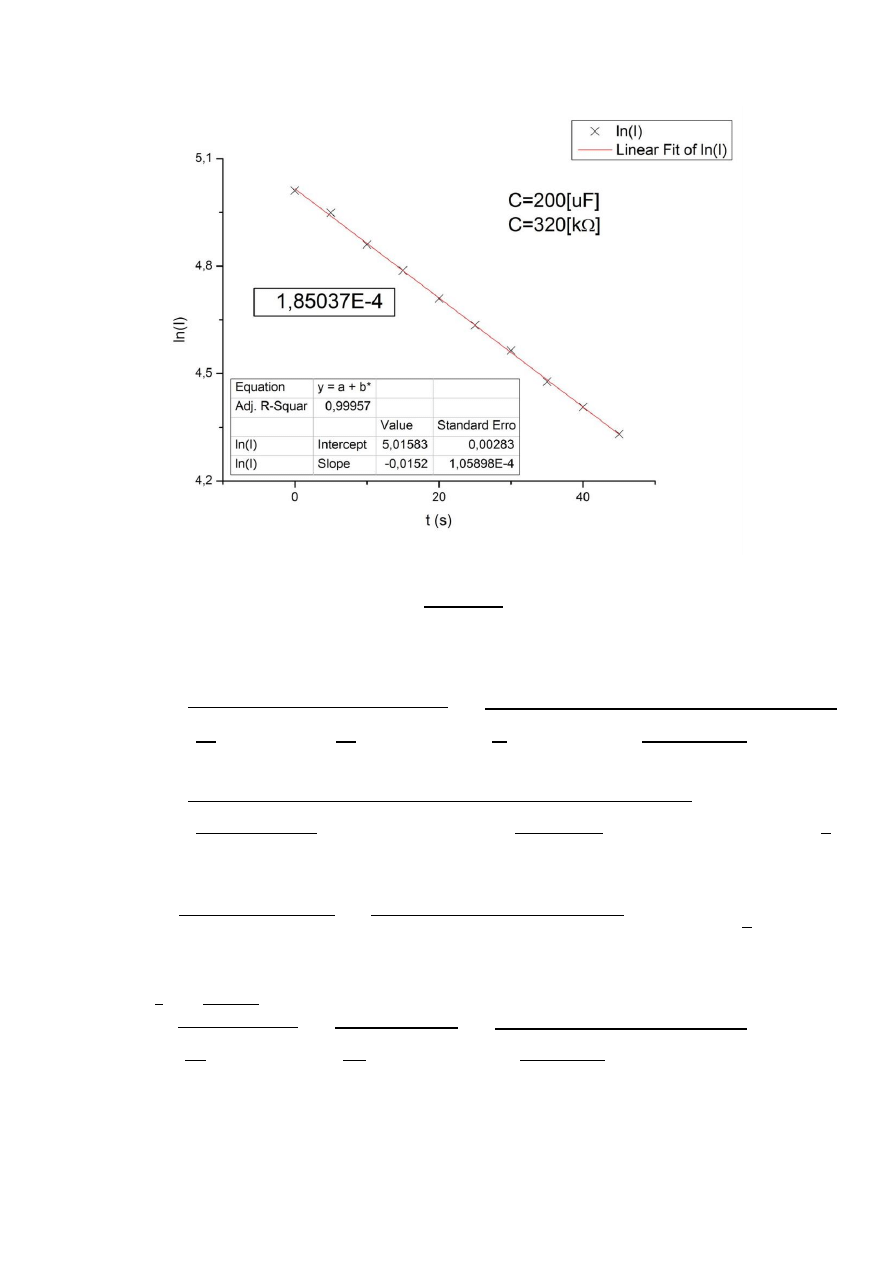
Zależność natężenia prądu od czasu opisana jest wzorem:

Po obustronnym zlogarytmowaniu otrzymujemy:

Jest to równanie liniowe o postaci y = a + bx, gdzie b

, a

.

Niepewność typu B dla współczynnika b wyznaczamy przekształcając równanie do postaci:

Zatem:

Dla punktu pomiarowego C=100[μF], R= 470[kΩ], I = 120μA i t = 10s otrzymujemy:

Niepewność złożona wynosi:

Teraz można wyznaczyć czas relaksacji τ i jego niepewność:

Dla porównania czas relaksacji obliczony ze wzoru wynosi:

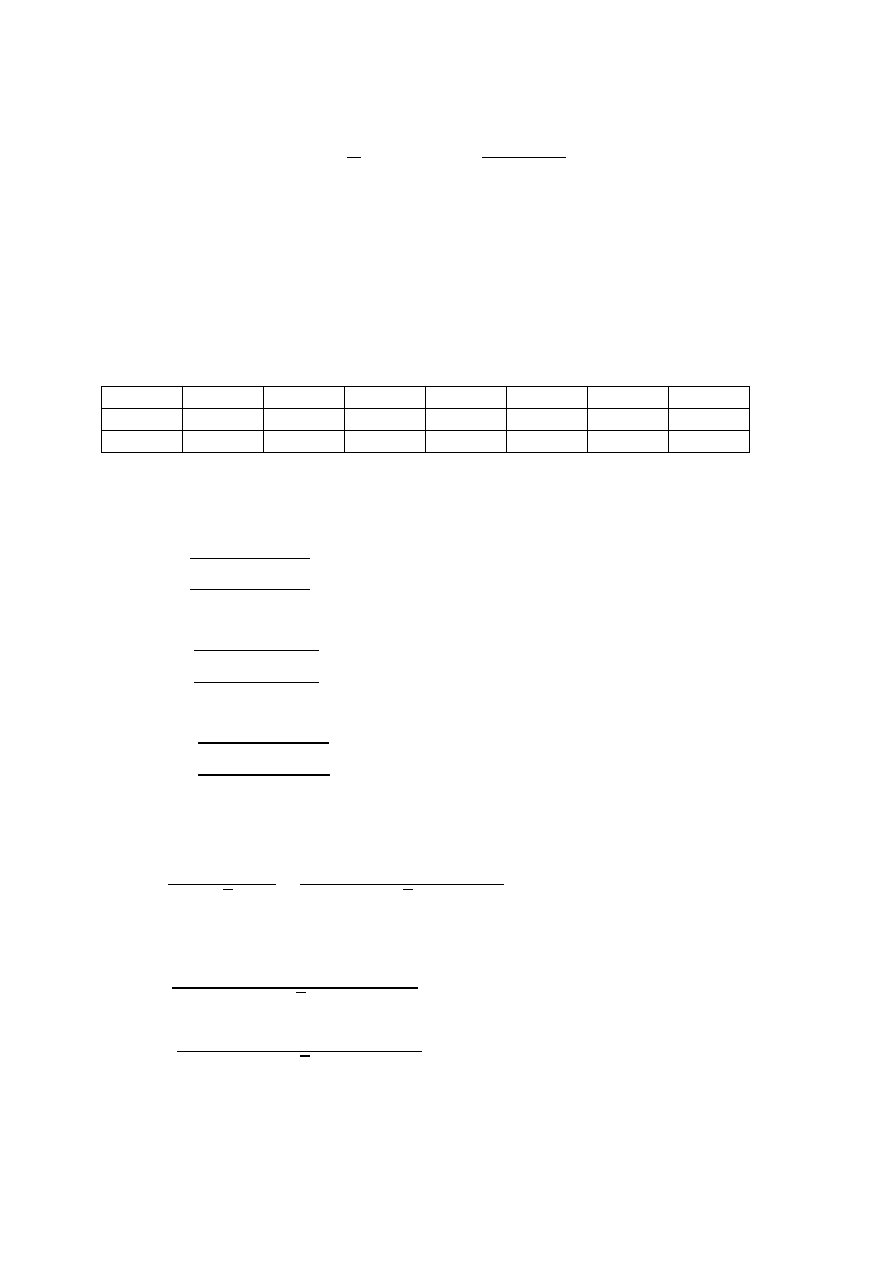
Czas połowicznego zaniku obliczamy ze wzoru:

CZĘŚĆ II
W tej części ćwiczenia dokonywaliśmy sześciokrotnego pomiaru napięć żarzenia i gaśnięcia
neonówki. Wyniki pomiarów przedstawione są w tabeli 2:

Tabela 2: Pomiary napięcia żarzenia i gaśnięcia neonówki

Niepewności typu A wyznaczamy na podstawie odchylenia standardowego:

ś

ż

ż

ś ż

ś

Niepewność typu B dla woltomierza cyfrowego V543:

Podstawiając za U wyznaczoną wartość średnią otrzymujemy:

ż

Z prawa propagacji niepewności:

N

1

2

3

4

5

6 U

śr

Uz

78,53

78,32

78,15

78,23

78,13

78,25

78,26833

Ug

62,73

62,53

62,21

62,01

61,95

62,05

62,24667

ż

ż

ż

ż

CZĘŚĆ III
W tej części ćwiczenia badaliśmy zależność okresu drgań relaksacyjnych od wartości
pojemności kondensatora i rezystancji. Wyniki pomiarów znajdują się w tabeli 3:

Tabela 3. Okres drgań wyznaczony doświadczalnie i teoretycznie

Lp.

C [μF]

R [kΩ]

T

teor

[s]

u(T

teor

) [s]

t

20

[s]

T [s]

1

2,2

835

1,228347

0,010264984

26,72

1,336

2

2,2

760

1,118016

0,00934298

24,39

1,2195

3

2,2

680

1,00033

0,008359508

21,97

1,0985

4

2,2

560

0,823801

0,006884301

18,03

0,9015

5

1

835

0,558339

0,004665902

11,53

0,5765

6

1

760

0,508189

0,004246809

10,91

0,5455

7

1

680

0,454696

0,003799777

9,57

0,4785

8

1

560

0,374455

0,003129228

8,03

0,4015

Niepewność pomiaru T przyjmujemy taką jak ta policzona dla części I, ale należy ją podzielić
dodatkowo przez ilość zliczonych w czasie pomiaru mignięć.

Teoretyczną wartość okresu wyznaczamy ze wzoru:

ż

Gdzie:

ε= 95,1 [V]

ż

Dla jednego pomiaru dokonanego dla danych wartości R i C możemy wyznaczamy tylko
niepewność typu B:

Poniżej przeprowadzone są obliczenia dla C=1 μF i R=835 kΩ. Wyniki dla wszystkich
pomiarów umieszczone są w tabeli 3.

=0,0047

CZĘŚĆ III
W tej części do układu podłączyliśmy oscyloskop. Zaobserwowaliśmy proces ładowania i
rozładowywania kondensora. Wykres znajdujący się na wyświetlaczu oscyloskopu jest
podobny do wykresu teoretycznego przedstawionego w skrypcie.

5. Wnioski

Z dopasowań liniowych otrzymaliśmy wartość

, która jest o wiele mniejsza od wartości

krytycznej, co potwierdza liniowość równania oraz to, że opis rozładowywania kondensatora
za pomocą krzywej ekspotencjalnej jest poprawny. Wyznaczony czas relaksacji jest bardzo
zbliżony do wartości teoretycznej, co potwierdza poprawność pomiarów.
W drugiej części wyznaczyliśmy napięcia żarzenia i gaśnięcia neonówki. Wyniki okazały się
dość precyzyjne, niepewności rzędu 10

-1

V przy wartości napięcia rzędu 50 80 V są

niewielką wartością. W trzeciej części badaliśmy zależność okresu drgań relaksacyjnych dla
neonówki od pojemności kondensatora i rezystancji opornika. Dla mniejszej wartości
iloczynu R i C okres skracał się zgodnie z oczekiwaniami i wzorem teoretycznym. Otrzymany
okres teoretyczny jest bliski wartości wyznaczonej za pomocą stopera. Niedokładność ta jest
spowodowana czasem reakcji eksperymentatora i szybkością sczytywania oraz zapisywania
wyników.