Statystyka, materiały dydaktyczne, IPSiR UW 

 

1

Statystyka 
 
Współczynnik korelacji rangowej R Spearmana 
 
Celem analizy rangowej jest badanie współzależności zmiennych, które są 
niemierzalne, a można je uporządkować według pewnego kryterium, czyli zamienić, 
przekształcić w zmienne rangowe. 
W korelacji rangowej są używane następujące pojęcia: ranga, rangowanie, obiekty 
rangowane, rangujący (sędziowie). 
Rangowanie, inaczej nadawanie rang, to procedura, która polega na ustawieniu 
obiektów rangowanych w porządku od najmniejszego do największego (lub od 
największego do najmniejszego), a następnie przyporządkowanie zajmowanym 
pozycjom kolejnych liczb naturalnych. 
Obiekty rangowane to osoby, przedmioty, zjawiska podlegające ocenie według 
wskazanego, wybranego kryterium, co w konsekwencji prowadzi to ich 
uporządkowania. 
Rangujący (sędziowie) to osoby indywidualne lub grupy osób, których oceny 
obiektów wzięte są pod uwagę. 
Podstawą uporządkowania obiektów w rosnącym ciągu (lub malejącym) są np.  
otrzymane oceny (według pewnego kryterium), zdobyte punkty (w zawodach), liczby 
otrzymanych głosów (w wyborach), itp.  
Obiektowi, który zajął najwyższą pozycję nadajemy rangę 1, kolejnemu – 2 itp. 
Możemy rozpocząć rangowanie od najniższej pozycji i postępować podobnie, 
nadając kolejne rangi pozycjom od najniższej do najwyższej. Wyjątek stanowi 
sytuacja, w której dwa lub więcej obiektów otrzymują takie same oceny, zdobywają 
takie same liczby głosów, wówczas nadajemy im takie same rangi, tzw. rangi 
mieszane.  Rangi mieszane  są równe wartościom  średniej arytmetycznej z 
przypadających na nie pozycji. 

Warto zapamiętać, że w każdym przypadku suma rang powinna być równa 
wartości n*(n+1)/2, czyli sumie n-kolejnych liczb naturalnych. 

Przykład 1. Wyniki badania popularności stacji radiowych przez studentów 
wydziałów pedagogicznego „P” i historycznego „H” są następujące (liczby wskazań; 
każdy mógł wybrać jedną stację). Poranguj stacje radiowe.  
  

Stacje radiowe 

Studenci 

Pedagogiki 

Studenci 

Historii 

R(P) R(H)  di  di^2 

A 20 

17 

3,5 

2,5 

1 

1 

B 20 

15 

3,5 

1 

2,5 

6,25 

C 12 

20 

1 

4,5 

-3,5 

12,25 

D 15 

20 

2 

4,5 

-2,5 

6,25 

E 30 

17 

5 

2,5 

2,5 

6,25 

F 

35 30 6 6 0 0 

suma 

X  X 21 21 X 32 

 

Statystyka, materiały dydaktyczne, IPSiR UW 

 

2

Rangowanie rozpoczęliśmy od najmniejszej liczby wyborów. Wśród studentów „P” 
ranga 1 przypadła stacji C, a według studentów „H” – stacji B. Sumy rang w obu 
przypadkach wynoszą 21, co jest zgodne z wartością [n*(n+1)/2]. 
W obu przypadkach mieliśmy do czynienia z rangami mieszanymi. W ocenie 
studentów Pedagogiki taką samą popularnością cieszyły się stacje A i B, którym 
przypadały w kolejności pozycje 3 i 4. Obie stacje otrzymały takie same rangi 3,5 
(średnia z 3 i 4). Studenci Historii taksami ocenili stacje C i D, w konsekwencji 
przypadały tym stacjom pozycje 4 i 5. Obu stacjom przypisano rangi 4,5 (średnie z 4 i 
5).  
Kolejnym etapem analizy jest zbadanie stopnia zgodności w ocenach i do tego służy 
współczynnik korelacji rang R Spearmana. 

)

1

(

6

1

2

1

2

−

−

=

∑

=

n

n

d

R

n

i

i

 

gdzie: 
di – różnica między rangami 
n – liczba obiektów rangowanych. 
 
Własności i interpretacja współczynnika R 
  

•  R przyjmuje wartości od -1 do 1.  

• Jeśli R zbliża się do +1 mamy do czynienia z całkowitą zgodnością w ocenie 

obiektów. Oceny nie zależą od sędziów oceniających. Te same obiekty mają 
wysokie oceny w oczach obu osób lub grup, które je oceniają.  

• Jeśli R jest bliskie -1, występuje bardzo silna niezgodność. Wyższa lub niższa 

pozycja obiektów zależy od tego kto je ocenia. Te obiekty, które są oceniane 
dobrze przez jednego sędziego (grupę osób), otrzymują niskie oceny u drugiego 
oceniającego. 

• Jeśli wartość R jest bliska 0 – mamy do czynienia z sytuacją, w której trudno 

ocenić czy jest zgodność, czy jej nie ma. 

 
 
Rozróżnienie „zgodności” i „zależności” 
Jeśli  np. oceny mężczyzn i kobiet są w pełni zgodne – to znaczy, że te oceny nie 
zależą od płci, czyli nie ma zależności. Dopiero gdy te oceny są różne dla obu płci, 
możemy powiedzieć, że zależą one od tego, do jakiej płci należeli badani. 
 
Obliczenie współczynnika R Spearmana w przykładzie 1. 
 
R = 1 -  6*32/6*35 = 1- 192/210 = 1 – 0,91 = 0,09  
 
Interpretacja: 
Na podstawie powyższych danych nie można określić stopnia zgodności między 
ocenami stacji radiowych przez studentów obu wydziałów. 

Statystyka, materiały dydaktyczne, IPSiR UW 

 

3

 

Do rozwiązania 
 
Ćwiczenie 1. 
W Polskim Badaniu Przestępczości (PBP) w latach 2007 i 2009 otrzymano 
następujące wyniki dotyczące oceny zagrożenia w swoim miejscu zamieszkania.  
PBP przeprowadzono na próbach losowych 17 tys. Polaków. 
Proszę porangować zagrożenia, obliczyć R i zinterpretować wyniki.  
 

Zagrożenie 

Czego się Pani/Pan najbardziej boi w swoim miejscu 

zamieszkania? 

Wyniki 

PBP’0

9

Wyniki 

PBP’0

7

Ranga 

PBP’07 

Ranga 

PBP’09 

 

di 

 

di

2

 

1  Napadów, rozbojów 

20,1

23,9

4 2 2

4

2  Wymuszeń, okupów 

4,2

4,3

12 12  0

0

3  Bójek i pobić 18,1

20,4

8 7 1

1

4 Włamań (np. do mieszkań, piwnic lub samochodów) 

19,8

22,6

5 4 1

1

5  Kradzieży ( np. kieszonkowych) 

12,5

14,7

9 8 1

1

6  Brawurowo jeżdżących kierowców 

36,8

35,9

1 1 0

0

7 Agresji ze strony osób pijanych lub narkomanów 

20,5

20,7

3 6 

-3

9

8  Handlu narkotykami 

5,9

6,2

11 10  1

1

9  Niszczenia mienia przez wandali 

21,6

21,6

2 5 3

9

10 Zaczepiania przez grupy agresywnej młodzieży 19,7

23,6

6 3 3

9

11 

Hałaśliwych, niekulturalnie zachowujących się sąsiadów

 6,6

5,8

10 11  1

1

12 Innych zagrożeń 1,1

1,3

13 13  0

0

13 Żadnych, niczego nie obawiam się 18,2

14,0

7 9 

-2

4

suma

91 91 

40

 
 
Ćwiczenie 2.  
Poniższa tabela przedstawia wyniki egzaminu z prawa i statystyki 10 studentów 
kierunku Ekonomia. Za pomocą współczynnika korelacji rang Spearmana ustal 
kierunek i siłę korelacji pomiędzy wynikami obu egzaminów i zinterpretuj wynik. 
 
Student Liczba 

punktów z 

prawa 

Liczba 

punktów 

ze 

statystyki 

Ranga 

prawo 

Ranga 

statystyka

Różnica 

rang (d

i

) 

(d

i

 

2

) 

A 2

81 

 

B 8

60 

 

C 18

81 

 

D 12

30 

 

E 12

57 

 

F 15

72 

 

G 7

81 

 

H 5

98 

 

I 14

65 

 

J 14

47 

 

Suma X

X 

 

 
 

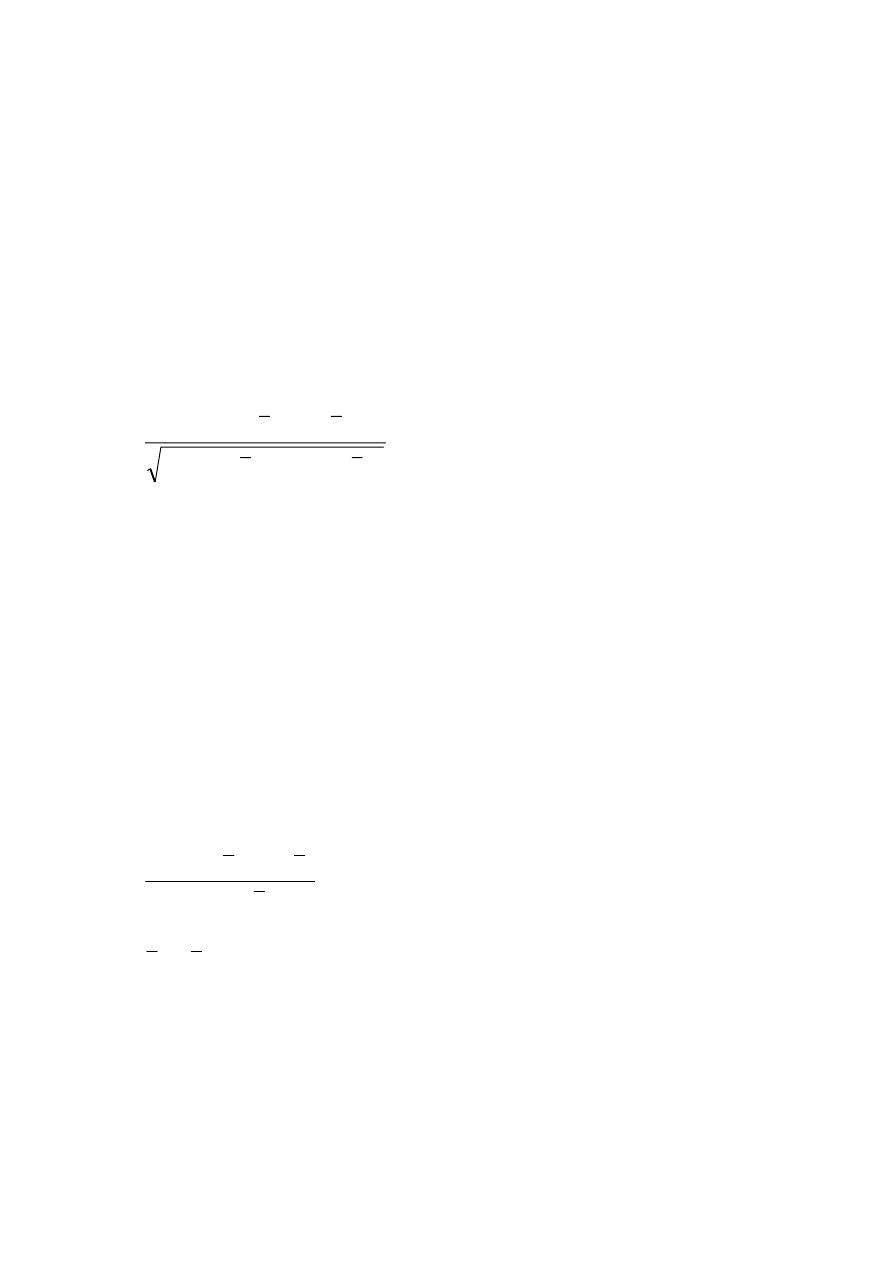
Statystyka, materiały dydaktyczne, IPSiR UW 

 

4

•  Powtórzenie (analiza korelacji i regresji) 

 
Do czego służy analiza korelacji (współczynnik r Pearsona)? 
Jakie są własności r Pearsona?  
Do czego służy analiza regresji? 
Jak interpretuje się współczynnik kątowy w oszacowanej regresji liniowej? 
 
W analizie korelacji z wykorzystaniem współczynnika r Pearsona chodziło o 
zbadanie, czy między dwiema zmiennymi istnienie liniowa zależność – czyli np. czy 
wraz ze wzrostem agresywności (zbadanej na jakiejś skali agresji - zmienna X) 
poziom samokontroli (znowu opisanej na jakiejś skali samokontroli - zmienna Y) 
wzrasta czy maleje, czy też te dwie zmienne nie są ze sobą związane.  
 
Współczynnik korelacji liniowej r Pearsona obliczamy według wzoru: 

∑

∑

∑

−

−

−

−

=

2

2

)

(

)

(

)

)(

(

y

y

x

x

y

y

x

x

r

i

i

i

i

 

 
Wartość tego współczynnika zależała od tych odległości zaobserwowanych punktów 
od teoretycznej linii prostej wyznaczonej przez średnie obu zmiennych – co jest 
uwidocznione we wzorze. 
 
Regresja liniowa 
Zakładamy liniowy model regresji 
 

Y = aX + b + e

 

 
Po oszacowaniu parametrów a i b MNK (metoda najmniejszych kwadratów) 
otrzymujemy: 
  

X

a

b

Y

ˆ

ˆ

ˆ

+

=

 

Wzory służące do oszacowania a i b: 
 

∑

∑

−

−

−

=

2

)

(

)

)(

(

ˆ

x

x

y

y

x

x

a

i

i

i

 

 

x

a

y

b

ˆ

ˆ

−

=