EGZAMIN Z PA

– I termin 1.03.2014

Zad 1.

Rozwiązać rów a ie róż i zkowe: (2p)

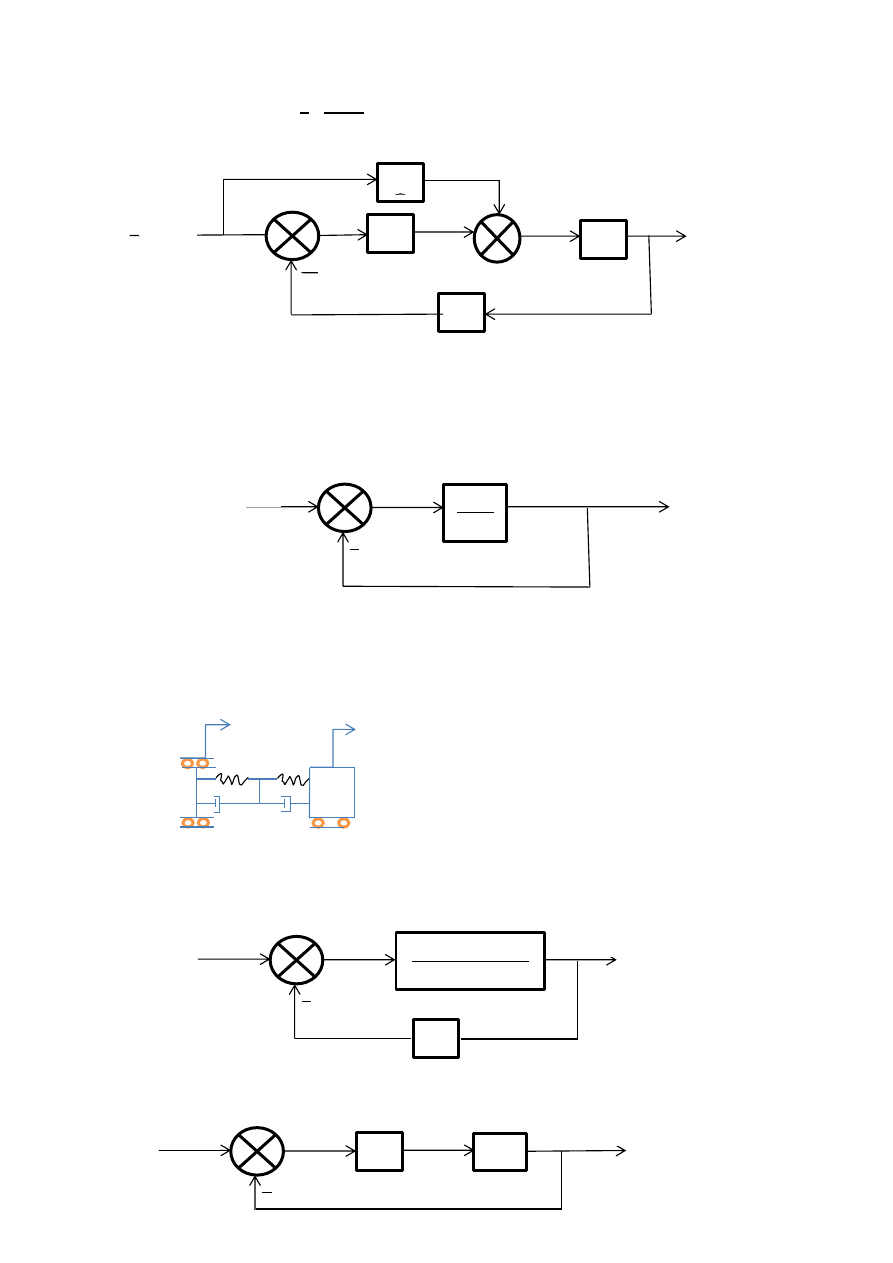
)ad . W z a z ć tra s ita je zastęp zą NIE oż a RÓWNANIAMI : p

)ad . W z a z ć i ar sować logar t i z ą harakter st kę fazowo- zęstotliwoś iową dla układu,
którego s he at lokow przedstawia r su ek. O li z ć wartość wz o ie ia dokład ą w rażo a
w de

ela h dla ω= : p

)ad . W z a z ć rów. Róż i zkowe wejś ia –w jś ia, tra s ita ję operatorową oraz ar sować
schemat blokowy: (3p)

z(t)-

s g ał wejś iow prze iesz ze ie

y(t)-

s g ał w jś iow (przemieszczenie)

)ad . Dla układu określo ego s he ate lokow w z a z ć przedział, do którego powi a

ależeć wartość para etru „k” a układ ł sta il as ptot z ie.

Dodatkowo z adać sta il ość układ dla wartoś i para etru k= : p

)ad . )akłada , że wz o ie ie regulatora P w osi k= , a o iekt a tra s ita ję G s = / s+ .
W z a z ć łąd regula ji e t oraz u h stat zny e

stat

: (3p)

2

H1

H1

H1

U(s)

V(s)

V(s)

U(s)

m

y(t)

x(t)

X(s)

k

k

k

b

b

P

G(s)

Y(s)

Y(s)

R(s)=1/2

)ad . )aprojektuj ra kę sterowa ą. Bra ka posiada:
-

dwa wejś ia da

h i for a je : ,

-

jed o wejś ie sterują e do ko figura ji s,

-

jed o w jś ie .

W zależ oś i od sta u wejś ia sterują ego s, układ a peł ić fu k ję:
->OR dla s=1

->NAND dla s=0
Fu k ję s, , opisują ą działa ie układu przedstaw w posta i i i al ej. Na podstawie
w z a zo ej fu k ji ar suj s he at zaprojektowa ego układu. p

)ad . Nar suj s he at as

hro i z ego li z ika odulo , zli zają ego w przód, zbudowanego z

przerzut ików t pu D w zwala

h z o ze arastają

. Nar suj prze iegi zasowe s g ałów a

wejś ia h posz zegól

h przerzut ików dla ałego klu działa ia li z ika p