Kryptograficzna

przygoda

01010 10001 11000 01111 10011 
01110 00110 10001 00000 00101 

01000 00010 11001 01101 00000
01111 10001 11001 11000 00110

01110 00011 00000

czyli całkiem inne szyfrowanie…

Autor:

phm. Michał Starosta HO

7 DSH „Cerber” im. gen. S.F. Sosabowskiego 

Hufiec ZHP Nowy Tomyśl

cerber7zsh@op.pl

Spis tre

ś

ci

I.

II.

III.

IV.

V.

Czy nie zastanawiali

ś

cie si

ę

?...

Co b

ę

dzie nam potrzebne

Zaczynamy zabaw

ę

Szyfr zmieniaj

ą

cy alfabet

Szyfr Vigenere’a
Szyfr Playfair’a

Robi si

ę

 powa

ż

nie;-)

ECB
CBC
CFB
Szyfr Feistella

Wytaczamy ostatni

ą

 armat

ę

Szyfr afiniczny

Pomoce matematyczne
Dodawanie binarne – dodawanie inaczej
Permutacja – z czym si

ę

 to je

Macierz – to bardzo proste
Modulo – czy kto

ś

 mi grozi?

3
3

4
4
8

13

15
15
19
23
28

33
33

37
37
37
37
38

Czy nie zastanawialiście się?...

www.wedrownik.net 

2

Czy nigdy si

ę

 nie zastanawiali

ś

cie nad pewnymi brakami w rozwoju technik harcerskich? W

zasadzie wi

ę

kszo

ść

 technik harcerskich mo

ż

emy rozwija

ć

 w zale

ż

no

ś

ci od wieku. Wiele, ale

nie   szyfry.   Tak   jak   uczymy   si

ę

  ich   na   samym   pocz

ą

tku   naszej   przygody   harcerskiej,   tak

zazwyczaj  nic nowego ju

ż

 pó

ź

niej nie poznajemy. Proste szyfry harcerskie nie s

ą

 

ż

adnym

wyzwaniem dla harcerzy starszych, nie wspominaj

ą

c o w

ę

drownikach.

Mo

ż

e   pora   to   zmieni

ć

.   Chciałbym   zaproponowa

ć

  mał

ą

  wycieczk

ę

  w   krain

ę

  kryptografii.

Potrzebny przy tym aparat matematyczny nie b

ę

dzie wymagaj

ą

cy – humani

ś

ci nie musz

ą

 si

ę

obawia

ć

.

Do  cz

ęś

ci  szyfrów podam metody ich  łamania. Do  tej  pory przy  harcerskich  szyfrach  nie

mieli

ś

my takiej mo

ż

liwo

ś

ci, gdy

ż

 znajomo

ść

 rodzaju szyfru była równoznaczna z mo

ż

liwo

ś

ci

ą

jego   rozszyfrowania.   Do   nowych   szyfrów   potrzebny   zawsze   b

ę

d

ą

  jakie

ś

  dodatkowe

informacje. I łamanie szyfru b

ę

dzie zazwyczaj równoznaczne z ich kre

ś

leniem.

Co będzie nam potrzebne

Pierwszy grupa nowych szyfrów jakie b

ę

d

ą

 w nast

ę

pnym rozdziale zaprezentowane nie b

ę

d

ą

od nas wymagały 

ż

adnych przekształce

ń

 matematycznych – wystarcz

ą

 odpowiednie tabele i

b

ę

dziemy mogli szyfrowa

ć

 i deszyfrowa

ć

 wiadomo

ś

ci.

Do   szyfrów   z   drugiej   grupy   potrzebna   nam   b

ę

dzie   tabela   zapisu   liter   w   postaci

zerojedynkowej lub mówi

ą

c inaczej binarnej. Na szcz

ęś

cie szyfry te nie b

ę

d

ą

 wymagały od

nas 

ż

adnych skomplikowanych oblicze

ń

. Wystarczy par

ę

 prostych działa

ń

 matematycznych.

Do  pracy  z pozostałymi  szyframi  przyda  si

ę

 nam  kalkulator. My

ś

l

ę

,  

ż

e  nie jest  to  bardzo

uci

ąż

liwe wymaganie, gdy

ż

 wi

ę

kszo

ść

 z nas posiada telefony komórkowe z kalkulatorem w

bonusie. Tutaj potrzebne b

ę

d

ą

 nam tak

ż

e pewne poj

ę

cia z matematyki wy

ż

szej – operacja

modulo (bez strachu to wbrew pozorom bardzo łatwe).
Cała teoria matematyczna zostanie umieszczona dla przejrzysto

ś

ci na ko

ń

cu poradnika – na

pocz

ą

tku mogłaby za bardzo straszy

ć

;-)

Dodam jeszcze, 

ż

e przy opisach działania i łamania szyfrów nie b

ę

d

ę

 rozpisywał  si

ę

 jaka

teoria matematyczna pozwala na takie, a nie inne działania. Nie chc

ę

 aby ten poradnik był

zbyt podobny do ksi

ą

zki z matematyki. Ka

ż

da metoda b

ę

dzie krok po kroku tłumaczona na

konkretnym   przykładzie   –   zamiast   przebijania   si

ę

  przez   teorie   od   razu   zobaczycie   jak

działaj

ą

 konkretne metody.

Ciekawskich zach

ę

cam do poszperania po ksi

ąż

kach (wybór literatury jest naprawd

ę

 du

ż

y,

nawet dla pocz

ą

tkuj

ą

cych), a reszt

ę

 do zabawy nieskr

ę

powanej teori

ą

 matematyczn

ą☺

Zaczynamy zabawę

www.wedrownik.net 

3

Szyfr zmieniający alfabet

Fachowo   powiedzieliby

ś

my   –   szyfr   permutuj

ą

cy   alfabet.   Pierwszy   szyfr   i   ju

ż

  dziwne

matematyczne słowo;-) Ale aby nie bawi

ć

 si

ę

 w nadmierne tłumaczenie definicji permutacji

wystarczy przyj

ąć

, 

ż

e zasada działania szyfru polega na zamianie kolejno

ś

ci liter alfabetu.

Jak to wygl

ą

da?

SZYFROWANIE – DESZYFROWANIE – ŁAMANIE SZYFRU

Aby zaszyfrowa

ć

 wiadomo

ść

 musimy utworzy

ć

 alfabet tajny – czyli zmieni

ć

 kolejno

ść

 liter w

alfabecie. W praktyce wygl

ą

da to tak, 

ż

e zapisujemy najpierw wszystkie litery w klasycznej

kolejno

ś

ci, a pó

ź

niej ka

ż

dej z nich przyporz

ą

dkujemy wybrana przez nas liter

ę

.

Wa

ż

ne 

– nowo przyporz

ą

dkowane litery nie mog

ą

 si

ę

 powtarza

ć

!!!

Poni

ż

sza tabelka jest przykładem takiego nowego przyporz

ą

dkowania.

www.wedrownik.net 

4

a

→

m

f

→

k

m

→

t

ś

→

y

ą

→

c

g

→

i

n

→

ó

t

→

p

b

→

g

h

→

ć

ń

→

ą

u

→

z

c

→

a

i

→

ę

o

→

s

www.wedrownik.net 

5

Wadą tej metody jest to, że każdy przy odrobinie cierpliwości może złamać taki szyfr. Zaletą
zaś jest jej łatwość i możliwość zastosowania w różnych zabawach harcerskich – nawet dla
harcerzy młodszych. 

Szyfr Vigenere’a

Zanim   przejd

ę

  do   omawiania   szyfru   Vigenere’a   przypomn

ę

  szyfrowanie   metod

ą

Cezara. Ten szyfr zna wi

ę

kszo

ść

 harcerzy. W podanym tek

ś

cie, wybieramy jako klucz

cyfr

ę

  nie   wi

ę

ksz

ą

  ni

ż

  26   lub   32   (w   zale

ż

no

ś

ci   czy   stosujemy   angielski   czy   polski

alfabet).   I   wszystkie   litery   naszego   tekstu   przesuwamy   o   t

ą

  warto

ść

  na   prawo   w

alfabecie. Deszyfrowanie analogicznie z tym, 

ż

e przesuwamy litery w lewo.

Ró

ż

nica   pomi

ę

dzy   szyfrem   Cezara,   a   Vigenere’a   jest   taka,  

ż

e   w   tym   drugim

przypadku rol

ę

 klucza pełni nie cyfra ale wyraz. 

Aby nie musie

ć

 co chwila oblicza

ć

 jaka litera jest nast

ę

pn

ą

 o podan

ą

 ilo

ść

 pozycji,

b

ę

dziemy stosowa

ć

 tablic

ę

 Vigenere’a.

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

B

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

C

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

D

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

E

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

F

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

G

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

H

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

I

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

J

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

K

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

L

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

M

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

N

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

O

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

P

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

Q

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

R

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

S

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

T

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

U

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

www.wedrownik.net 

6

V

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

W

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

X

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

Y

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Z

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Wskazówka
-   w   przypadku   tego   szyfru   polecam   stosowanie   alfabetu   angielskiego,   gdy

ż

  dzi

ę

ki

temu mo

ż

emy u

ż

ywaj

ą

c tylko jednej tablicy, by szyfrowa

ć

 teksty w wi

ę

kszo

ś

ci j

ę

zyków

- je

ś

li chcemy szyfrowa

ć

 tekst z polskimi literami musimy odpowiednio rozbudowa

ć

nasz

ą

 tabel

ę

Maj

ą

c ju

ż

 tabelk

ę

 mo

ż

emy przyst

ą

pi

ć

 do nauki jak funkcjonuje ta metoda.

SZYFROWANIE – DESZYFROWANIE – ŁAMANIE SZYFRU

Jak ju

ż

 zostało wspomniane, jako klucza u

ż

ywa

ć

 b

ę

dziemy wyrazu, a nie jednej litery. 

Gdy tekst przeznaczony do szyfrowania jest dłu

ż

szy ni

ż

 nasz klucz, to musimy wyraz klucz

wpisa

ć

 pod naszym tekstem jawnym tyle razy ile si

ę

 zmie

ś

ci.

W poni

ż

szym przykładzie u

ż

ywamy jako klucza słowa 

dom

.

www.wedrownik.net 

7

h
a
r
c
e
r
z

s
z
e
d
l

p
r
z
e
z
…

d
o
m
d
o
m
d

o
m
d
o
m

d
o
m
d
o

Taki zapis oznacza, 

ż

e do szyfrowania litery 

h

 u

ż

yjemy liter

ę

 

d

, 

o

 dla 

a

, 

m

 dla 

r

 itd. Ale jak

teraz   zastosowa

ć

  nasz

ą

  tabel

ę

?   W   pierwszym   wierszu   szukamy   liter

ę

,   któr

ą

  chcemy

zaszyfrowa

ć

, a wi

ę

c w naszym przypadku 

h

. W pierwszej kolumnie szukamy liter

ę

 z klucza,

a wi

ę

c 

d

. Przeci

ę

cie si

ę

 wiersza i kolumny przyporz

ą

dkowuje nam zaszyfrowan

ą

 liter

ę

 – 

k

.

www.wedrownik.net 

8

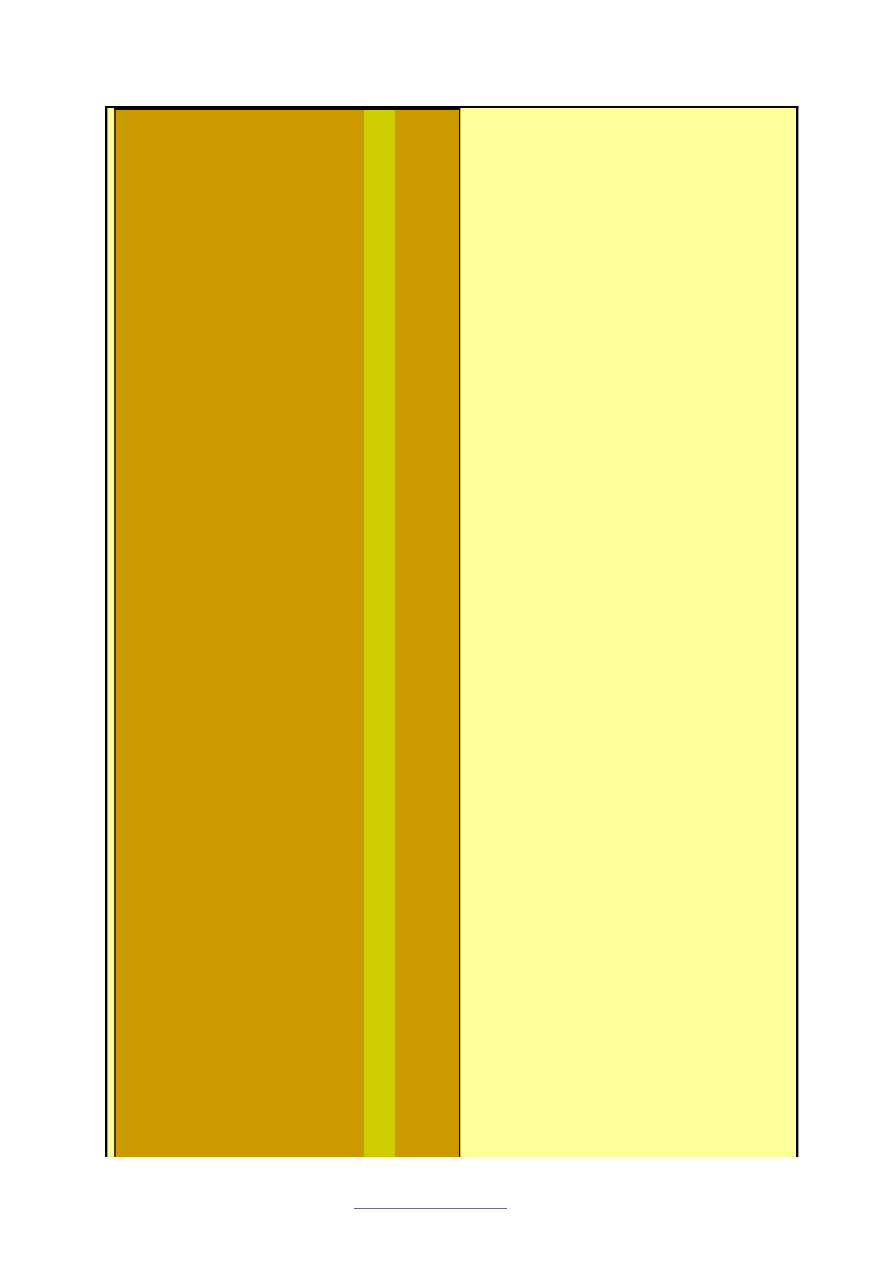
A
B
C
D
E

F

G

H

I

…

A
A
B
C
D
E

F

G

H

I

…

B
B
C
D
E

F

G

H

I

J

…

C
C
D
E

F

G

H

I

J

K

…

D
D
E

F

G

H

I

J

K

L

…

E

www.wedrownik.net 

9

Metoda ta jest do

ść

 pracochłonna, ale po paru próbach łamanie szyfru powinno post

ę

powa

ć

do

ść

 szybko. Istnieje przy niej ryzyko popełnienia pewnej ilo

ś

ci bł

ę

dów literowych lub pomyłki

podczas liczenia. 

www.wedrownik.net 

10

Szyfr Playfaira

B

ę

dzie  to ostatni  szyfr z pierwszej  grupy. Niestety tutaj  nie podam metody jego łamania,

gdy

ż

 jest zbyt pracochłonna. Ale pomimo to jest on wart uwagi.

SZYFROWANIE – DESZYFROWANIE 

Równie

ż

 ten szyfr opiera si

ę

 na stosowaniu odpowiedniej tabelki. Jednak aby j

ą

 stworzy

ć

,

potrzebne  jest  nam  słowo  klucz  . Szyfr  ten powstał  w  oparciu  o  słowo  

playfair

  (st

ą

d   ta

nazwa). Nic nie stoi jednak na przeszkodzie, aby u

ż

ywa

ć

 dowolnego słowa klucza.

Ż

eby   utworzy

ć

  odpowiedni

ą

  tabelk

ę

  (5x5)   wpisujemy   słowo   klucz   z   pomini

ę

ciem

powtarzaj

ą

cych si

ę

 liter. Wa

ż

ne jest tak

ż

e to, 

ż

e litery 

i

 i 

j

 traktujemy jako jedn

ą

. Pozostałe

wolne miejsca w tabeli uzupełniamy (w kolejno

ś

ci alfabetycznej) brakuj

ą

cymi literami.

P

L
A
Y
F

I/J
R
B
C
D

E
G
H
K
M

N
O
Q
S
T

U
V
W
X
Z

Metod

ę

 t

ą

 omówi

ę

 na przykładzie szyfrowania słowa 

konna policja

. Wiem, 

ż

e lepiej brzmi

policja konna, ale na potrzeby prezentacji działania szyfru zamieniłem ogólnie przyjmowan

ą

kolejno

ść

.

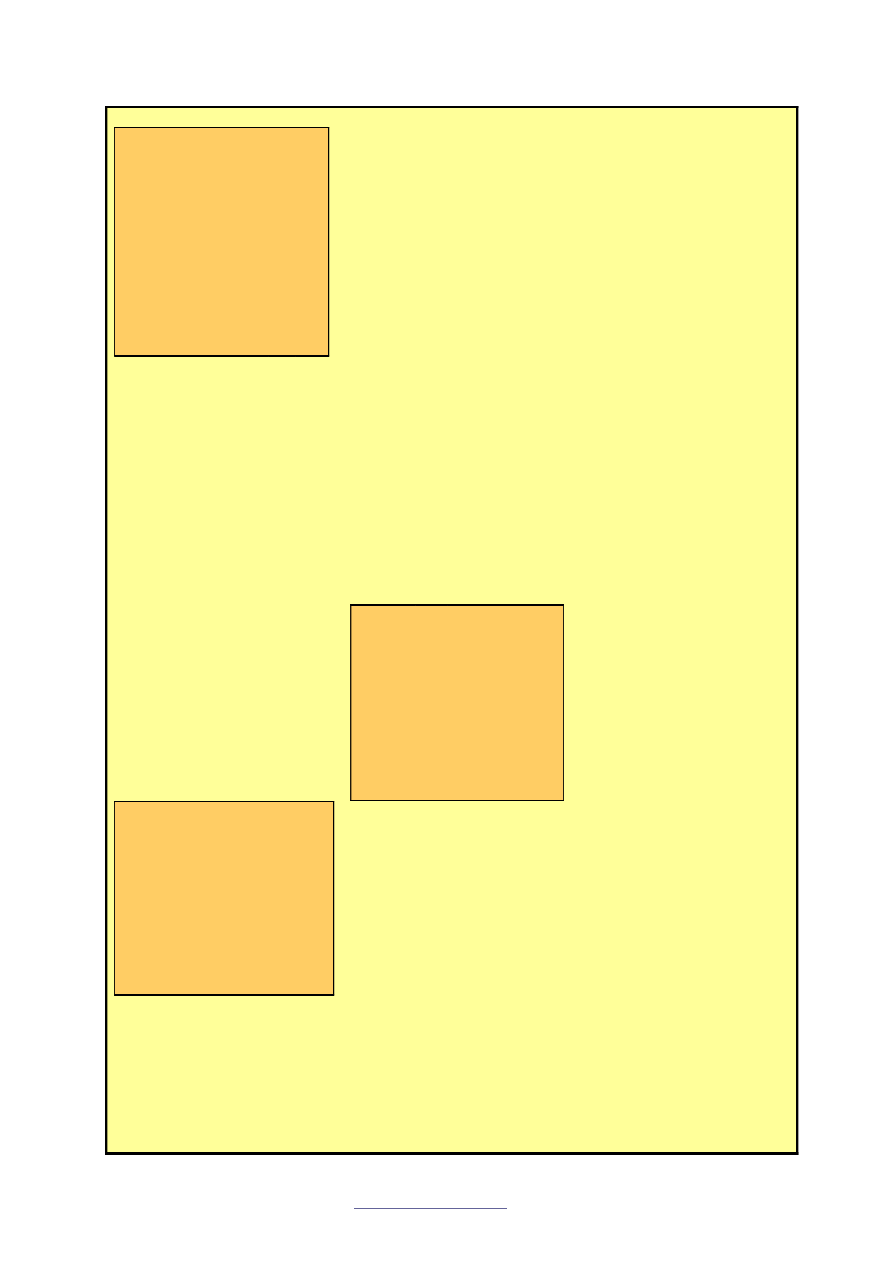
Krok I.
Dzielimy nasz tekst na pary liter. Je

ś

li w parze wyst

ę

puj

ą

 te same litery, to oddzielamy je

liter

ą

 

x

. Gdyby okazało si

ę

, 

ż

e ostatnia litera nie ma pary to tak

ż

e dopisujemy do niej 

x

.

www.wedrownik.net 

11

ko
n

x

n
a
p
o
li
cj
a

x

Krok II.
Teraz stosujemy 3 zasady szyfrowania.

1. Je

ś

li   obie   litery   znajduj

ą

  si

ę

  w   tym   samym   wierszu,   to   zast

ę

pujemy   je   literami

stoj

ą

cymi   po   ich   prawej   stronie.   Je

ś

li   nasza   litera   tekstu   jawnego   jest   na   ko

ń

cu

wiersza, to zamiast niej wstawiamy t

ą

 z samego pocz

ą

tku.

2. Je

ś

li   obie   litery   znajduj

ą

  si

ę

  w   tej   samej   kolumnie,   to   zast

ę

pujemy   je   literami

znajduj

ą

cymi si

ę

 pod nimi. Je

ś

li nasza litera tekstu jawnego jest na dole kolumny, to

zamiast niej wstawiamy t

ą

 z samej góry.

3.

Je

ś

li litery znajduj

ą

 si

ę

 w ró

ż

nych wierszach i kolumnach to zamiast nich wstawiamy

litery z tego samego wiersza, ale z kolumny drugiej litery w parze.

Stosuj

ą

c te 3 zasady otrzymamy nast

ę

puj

ą

cy szyfr.

ko
nx
n
a
p
o
li
cj
ax

⇓

gs
su
q
p
ln
pr
dr
y
w

A wi

ę

c ostatecznym efektem naszego szyfrowania jest tekst 

gssuqplnprdryw

.

●●●

Deszyfrowanie jest zwykłym odwróceniem zasad 1-3. Sprawdzimy to na przykładzie
szyfru 

qbbdgiuz

.

www.wedrownik.net 

12

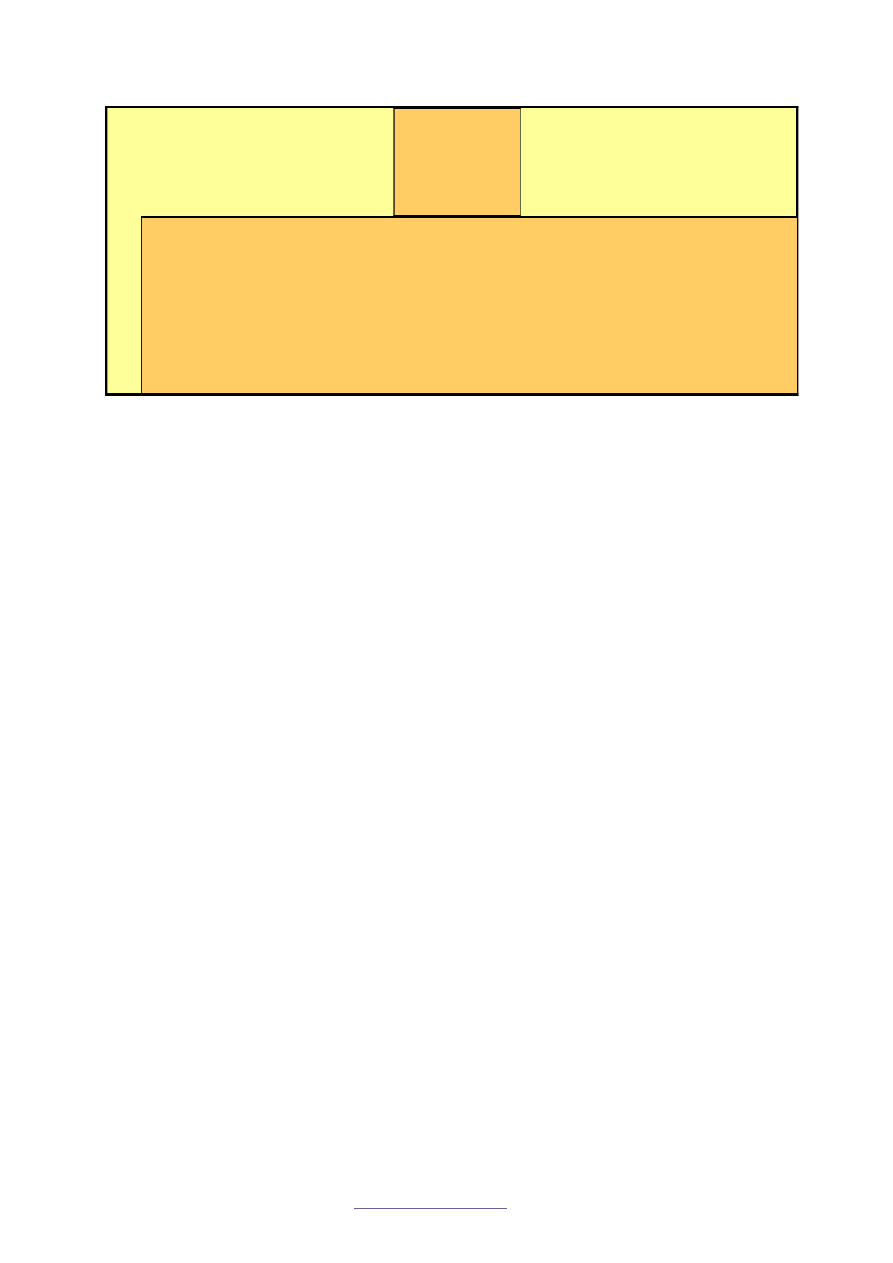
qb
bd
gi
uz

⇓

qb

 – obie litery nale

żą

 do jednej kolumny. Odwracaj

ą

c zasad

ę

 2 przyporz

ą

dkowujemy im litery

b

ę

d

ą

ce nad nimi i otrzymujemy – 

ha

bd

 – obie litery nale

żą

 do jednego wiersza. Odwracaj

ą

c zasad

ę

 1 przyporz

ą

dkowujemy im litery

b

ę

d

ą

ce po ich lewej stronie i otrzymujemy – 

rc

gi

 – obie litery le

żą

 w ró

ż

nych wierszach i kolumnach wi

ę

c stosuj

ą

c zasad

ę

 3 uzyskamy par

ę

 – 

er

uz

 – obie litery nale

żą

 do jednego wiersza. Odwracaj

ą

c zasad

ę

 1 przyporz

ą

dkowujemy im litery

b

ę

d

ą

ce po ich lewej stronie i otrzymujemy –

 zx

Po pozbyciu si

ę

 symboli 

x

 w naszych parach liter, otrzymujemy wiadomo

ść

 – 

harcerz

.

Zalet

ą

  tej   metody   jest   jej   prostota   oraz   fakt,  

ż

e   nie   potrzebujemy   do   niej  

ż

adnych

dodatkowych   pomocy   ani   tabelek.   Potrzebn

ą

  nam   tabelk

ę

  szyfruj

ą

c

ą

  mo

ż

emy   stworzy

ć

sobie sami. Wad

ą

 jest niestety brak mo

ż

liwo

ś

ci łamania tego systemu – niestety wymaga to

zbyt du

ż

ej ilo

ś

ci czasu.

www.wedrownik.net 

13

Robi się poważnie;-)

Szyfry dla zapisu zerojedynkowego

S

ą

 to ciekawe szyfry daj

ą

ce ciekawe mo

ż

liwo

ś

ci. Co bardzo wa

ż

ne nie wymagaj

ą

ce 

ż

adnych

wielkich zdolno

ś

ci  matematycznych  –  a na tym nam przecie

ż

 zale

ż

y:-) Zanim przejd

ę

  do

omawiania dokładnych metod, krótkie wyja

ś

nienie jak zapisujemy wyrazy u

ż

ywaj

ą

c tylko cyfr

0   i   1.   Potrzebujemy   do   tego   tabelk

ę

  przedstawiaj

ą

c

ą

  przyporz

ą

dkowanie   kodu

zerojedynkowego dla ka

ż

dej litery alfabetu.

Litera

Kod

Litera

Kod

Litera

Kod

a

00000

j

01001

s

10010

b

00001

k

01010

t

10011

c

00010

l

01011

u

10100

d

00011

m

01100

v

10101

e

00100

n

01101

w

10110

f

00101

o

01110

x

10111

g

00110

p

01111

y

11000

h

00111

q

10000

z

11001

i

01000

r

10001

Do pierwszych trzech szyfrów nie podam metod ich łamania. Poradnik ten ma by

ć

 w ko

ń

cu

jak najmniej matematyczny. Na szcz

ęś

cie nadrobimy to przy ostatniej metodzie z tej grupy.

ECB (Elektronic Code Book)

Najprostszy z tej grupy szyfrów. Dzi

ę

ki temu jest doskonały nawet dla harcerzy młodszych.

Dobrze tez si

ę

 sprawdza na grach terenowych ze wzgl

ę

du na szybko

ść

 pracy z nim. 

.

SZYFROWANIE – DESZYFROWANIE – ŁAMANIE SZYFRU

Działanie tej metody (tak jak i wcze

ś

niejszych) omówimy na konkretnym przykładzie. Dla

wzrokowców zał

ą

czam jeszcze schemat działania tego szyfru. Cho

ć

 osobi

ś

cie s

ą

dz

ę

, 

ż

e

łatwiej b

ę

dzie pracowa

ć

 nam przy u

ż

yciu tabelki. Ale wszystko po kolei:-)

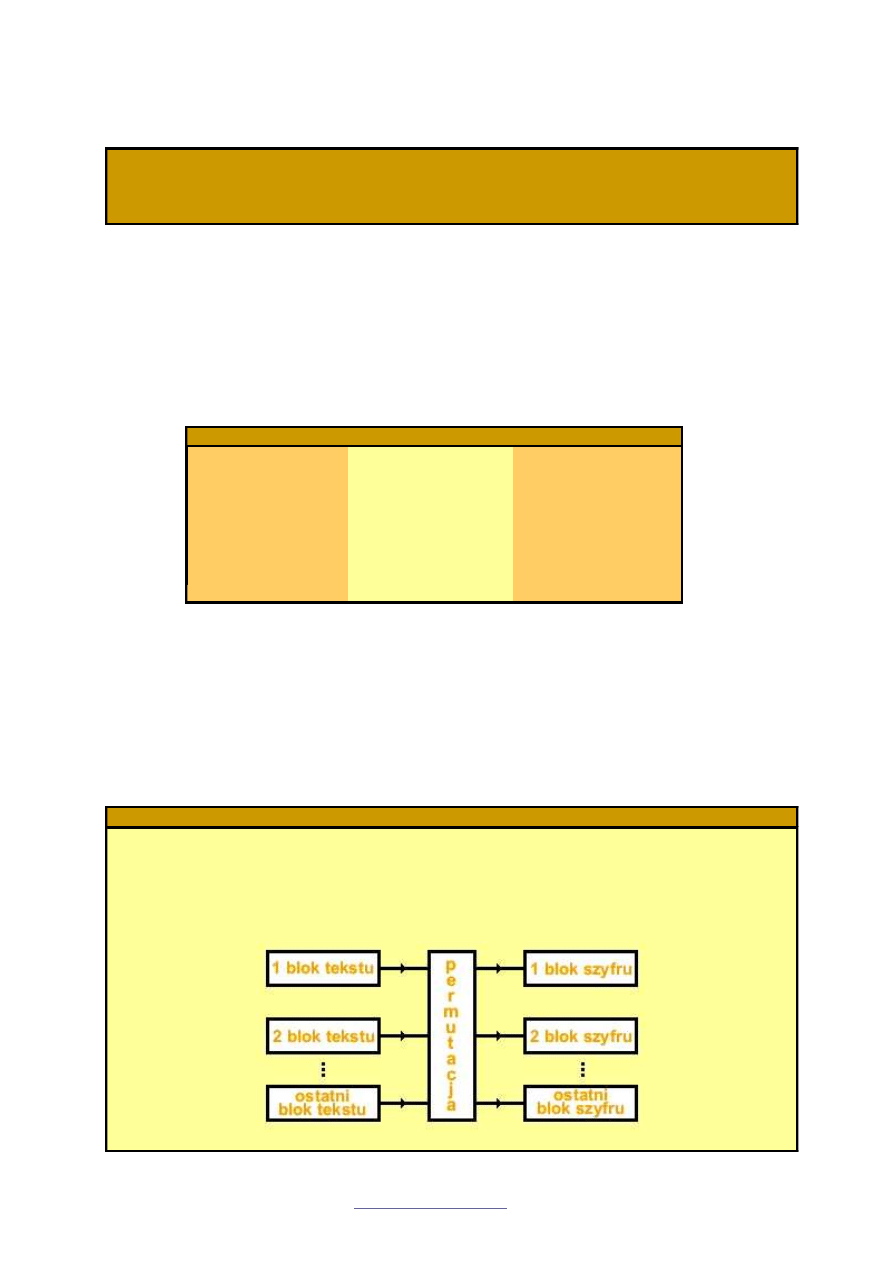
Schemat szyfrowania

www.wedrownik.net 

14

Do zaszyfrowania wybierzemy słowo 

harcerz

. 

Krok I.
Zapisujemy litery w systemie zerojedynkowym.

h
a

r

c

e

r

z

00111
00000
10001
00010
00100
10001
11001

Krok II.
Teraz   pora   na   zaszyfrowanie   naszej   wiadomo

ś

ci.   Dokonamy   tego   zmieniaj

ą

c   kolejno

ść

symboli w blokach tekstu (poddaj

ą

c je permutacji – wyja

ś

nienie poj

ę

cia w rozdziale V na

stronie 37)
W naszym przykładzie u

ż

yjemy nast

ę

puj

ą

cej permutacji –  

(124)

. A wi

ę

c pierwszy symbol

przeniesiemy na drug

ą

 pozycj

ę

, drugi na czwart

ą

, czwarty na pierwsz

ą

, a trzeci pozostanie

na swoim miejscu. Aby tego dokona

ć

 musimy nasz ci

ą

g 0 i 1 podzieli

ć

 na bloki o długo

ś

ci 4

elementów (ilo

ść

 permutowanych elementów).

0011
1000
0010
0010
0010
0010
0100
0111
001

Krok III.
Jak   wida

ć

  ostatni   blok   jest   krótszy.   W   takiej   sytuacji   brakuj

ą

ce   pozycje   uzupełniamy

odpowiedni

ą

 ilo

ś

ci

ą

 zer.

www.wedrownik.net 

15

0011
1000
0010
0010
0010
0010
0100
0111
001

0

Krok IV.
W tym momencie pozostało nam tylko poddanie ka

ż

dego bloku zamianie symboli miejscami

(naszej matematycznej permutacji – wiem, 

ż

e to  słowo nie gryzie, ale wol

ę

 go unika

ć

 aby

nie straszy

ć

 humanistów;-)

0011
1000
0010
0010
0010
0010
0100
0111
0010

⇓

1010
0100
0010
0010
0010
0010
0001
1011
0010

 

I po bólu, nasza wiadomo

ść

 została wła

ś

nie zaszyfrowana:-)

Wa

ż

ne

- powy

ż

ej jest przedstawiony ostateczny wynik szyfrowania. Nie zmieniamy zapisu

zerojedynkowego w literowy, gdy

ż

 podczas szyfrowania mo

ż

emy uzyska

ć

 taki ci

ą

g 0 i 1,

który nie ma odpowiednika literowego

●●●

Schemat deszyfrowania

www.wedrownik.net 

16

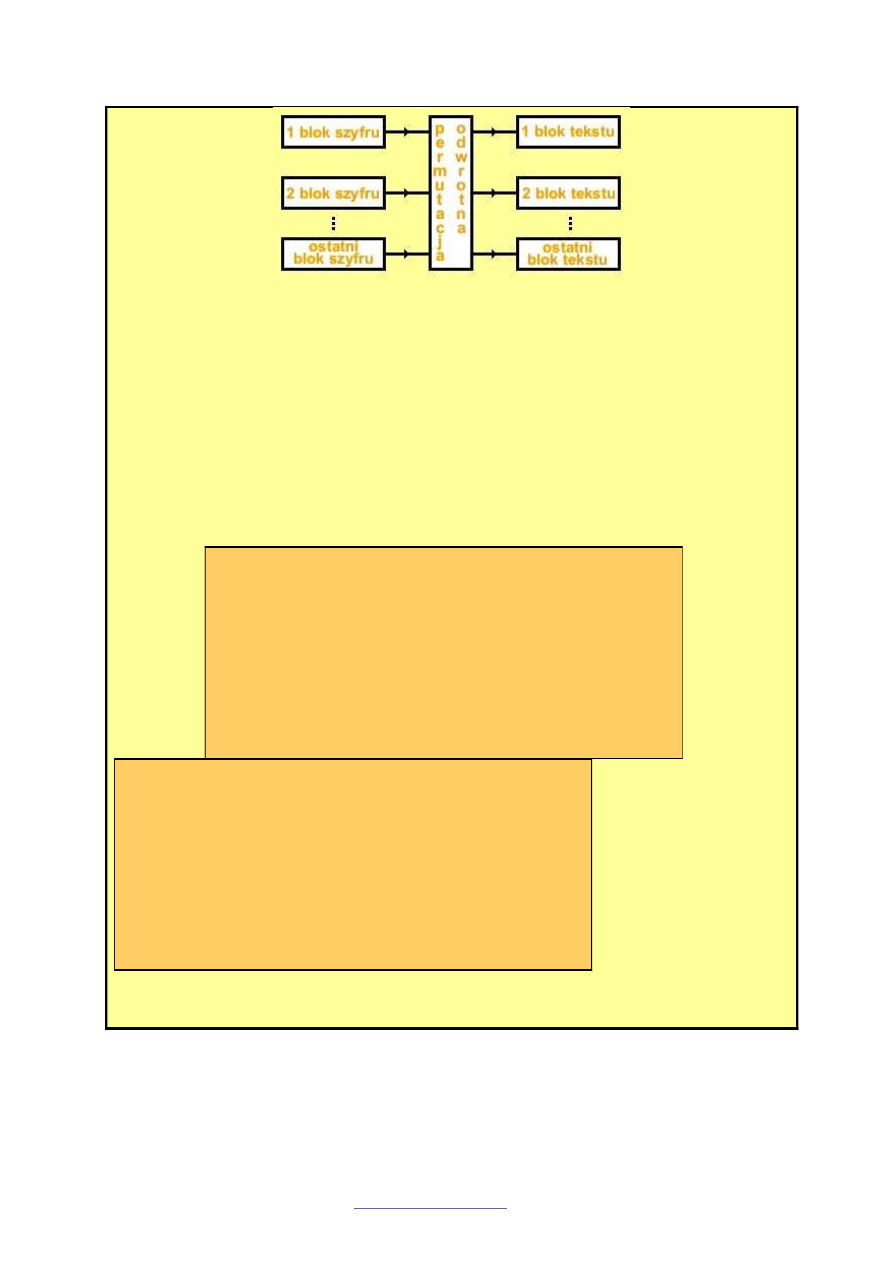
Deszyfrowanie   te

ż

  jest   bezbolesne.   Spróbujemy   teraz   odszyfrowa

ć

  wiadomo

ść

,   któr

ą

dopiero co zaszyfrowali

ś

my. 

Krok I.
Musimy najpierw okre

ś

li

ć

, jak odwróci

ć

 przestawienie symboli (okre

ś

li

ć

 permutacj

ę

 odwrotn

ą

– ponownie odsyłam do rozdziału V na stronie 37)
Dla naszej permutacji szyfruj

ą

cej (124) odwrotn

ą

 jest 

(142)

 – odwrócona kolejno

ść

 (421) z

uwzgl

ę

dnieniem zasady wpisywania zawsze najmniejszej cyfry na pocz

ą

tku – czyli pierwszy

element   umie

ś

cimy   na   czwartej   pozycji,   czwarty   na   drugiej,   drugi   na   pierwszej,   a   trzeci

ponownie pozostaje bez zmian.

Krok II.
W tym momencie mo

ż

emy ju

ż

 zastosowa

ć

 przekształcenie odwrotne na nasz szyfr.

1010
0100
0010
0010
0010
0010
0001
1011
0010

⇓

0011
1000
0010
0010
0010
0010
0100
0111
0010

 

Krok III.
Rozszyfrowan

ą

 wiadomo

ść

 dzielimy na bloki długo

ś

ci 5 symboli, a nadwy

ż

k

ę

 odrzucamy.

www.wedrownik.net 

17

00111
00000
10001
00010
00100
10001
11001

0

Krok IV.
Dokonujemy zamiany zapisu binarnego na nasz normalny alfabet.

00111
00000
10001
00010
00100
10001
11001

h
a

r

c

e

r

z

 

●●●

Łamanie   tego   szyfru   jest   czasochłonne,   ale   nieszczególnie   skomplikowane.   Je

ś

li   znamy

długo

ść

  permutacji   szyfruj

ą

cej   musimy   okre

ś

li

ć

  jej   odwrotno

ść

.   Sprowadza   si

ę

  to   do

sprawdzenia wszelkich mo

ż

liwo

ś

ci – dla 3 elementów musimy sprawdzi

ć

 tylko 6 układów,

dla 4 elementów ju

ż

 24 układy, ale dla 5 elementów niestety a

ż

 120. Z przestawieniem o

długo

ś

ci 2 nie ma najmniejszego problemu, dla (12) odwrotno

ś

ci

ą

 jest (12).

Spróbujmy naszych sił na wiadomo

ś

ci zaszyfrowanej przy pomocy permutacji o długo

ś

ci 3.

001
100
111
001
011

Dla permutacji 3 elementów mamy 6 mo

ż

liwych kolejno

ś

ci –  

(12)

,  

(13)

,  

(23)

,  

(123)

,  

(132)

,

oraz pozostawienie kolejno

ś

ci 

bez zmian

.

Sprawd

ź

my wszystkie 6 mo

ż

liwo

ś

ci. Od razu wynik podzielimy na bloki długo

ś

ci 5 symboli i

podstawimy litery.

www.wedrownik.net 

18

szyfr

001
100
111
001
011

szyfr

001
100
111
001
011

(12)

001
010
111
001
101

(13)

100
001
111
100
110

⇓

długo

ść

 5

00101
01110
01101

długo

ść

 5

10000
11111
00110

tekst

f

o
n

tekst

q

---

g

www.wedrownik.net 

19

szyfr

001
100
111
001
011

szyfr

001
100
111
001
011

(23)

010
100
111
010
011

(123)

100
010
111
100
101

⇓

długo

ść

 5

01010
01110
10011

długo

ść

 5

10001
01111
00101

tekst

k

o

t

tekst

r

p

f

www.wedrownik.net 

20

szyfr

001
100
111
001
011

szyfr

001
100
111
001
011

(132)

010
001
111
010
110

b.z.

001
100
111
001
011

⇓

długo

ść

 5

01000
11110
10110

długo

ść

 5

00110
01110
01011

tekst

i

---

w

tekst

g
o

l

Jak wida

ć

 w paru przypadkach uzyskali

ś

my nawet nieistniej

ą

ce symbole. Jedyne sensowne

wyrazy to  

kot

  i  

gol

  – czyli poprawne permutacje odwrotne to  

(23)

  i kolejno

ść

 

bez zmian

.

www.wedrownik.net 

21

Tak to jest z łamaniem szyfrów, 

ż

e czasem dostajemy par

ę

 sensownych wersji. Gdyby

ś

my

mieli   dłu

ż

szy   szyfr   do   złamania   to   mogliby

ś

my   okre

ś

li

ć

  jednoznacznie   poprawn

ą

deszyfracj

ę

.

Uwaga
- metoda ta działa  równie  dobrze dla normalnego zapisu  literowego (oszcz

ę

dzamy krok z

zamian

ą

 liter na zapis z 1 i 0)

- po podzieleniu tekstu na bloki długo

ś

ci naszej permutacji uzupełniamy w razie potrzeby

ostatni blok – mo

ż

emy dowolnymi literami (tak aby nie zmieniły sensu szyfrowanego tekstu)  

CBC (Cipher Block Chaining)

Pomi

ę

dzy CBC, a ECB s

ą

 dwie ró

ż

nice. Poza permutacj

ą

 posiadamy jeszcze klucz

pocz

ą

tkowy. Klucz ten zmienia si

ę

 po ka

ż

dym zaszyfrowanym bloku – wła

ś

nie ten

zaszyfrowany blok jest nowym kluczem. Brzmi gro

ź

nie, ale na szcz

ęś

cie nie jest to tak

trudne.

SZYFROWANIE – DESZYFROWANIE 

Najpierw zaprezentuj

ę

 schemat tej metody. 

Schemat szyfrowania

www.wedrownik.net 

22

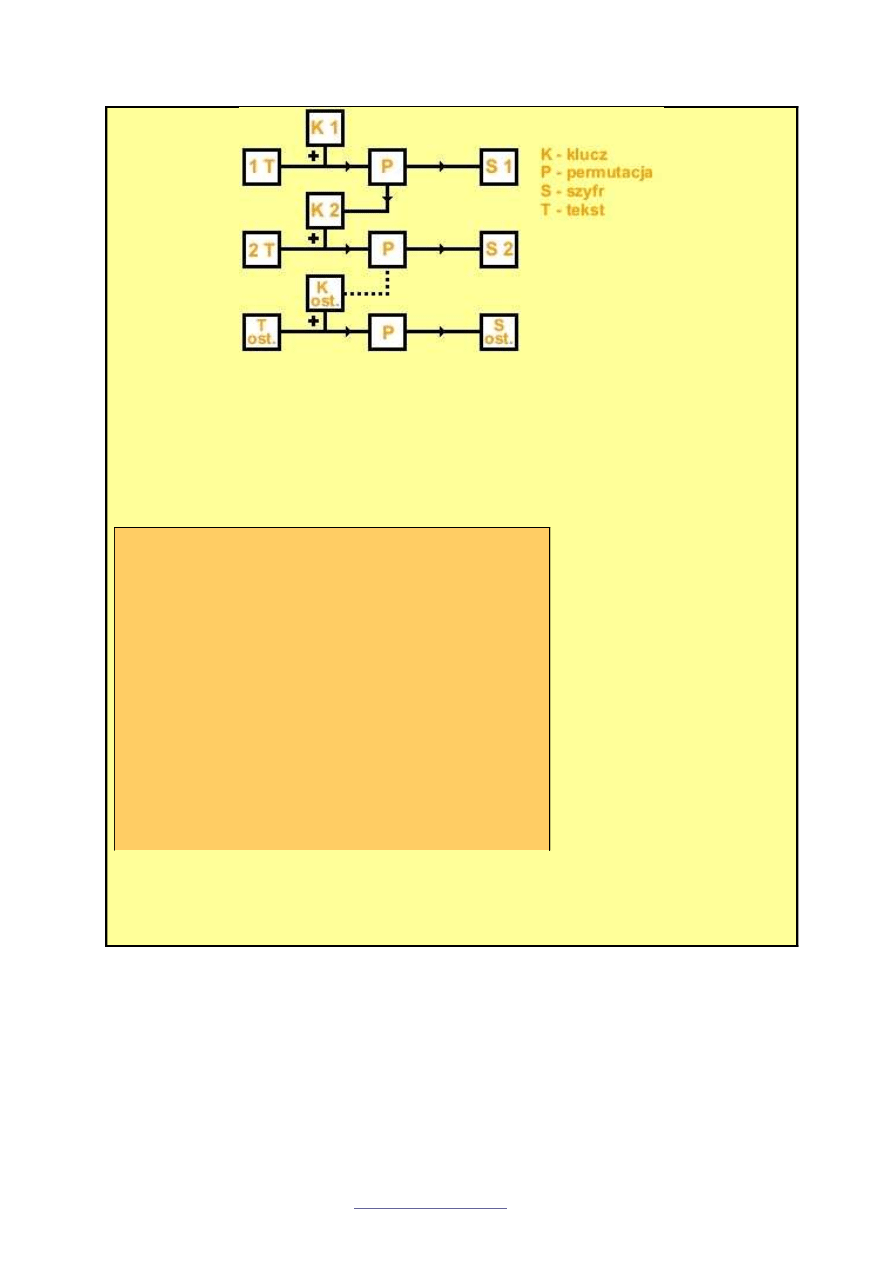
A   teraz   jak   zwykle   przykład   dla   zilustrowania   działania   szyfru.   Ponownie   u

ż

yjemy   słowa

harcerz

. Potrzebujemy te

ż

 funkcj

ę

 zmieniaj

ą

ca kolejno

ść

 elementów – 

(13)(24)

. Elementem

nowym b

ę

dzie klucz startowy – 

0101

. 

Krok I.
Zapisujemy nasz tekst w postaci zerojedynkowej.

h
a

r

c

e

r

z

00111
00000
10001
00010
00100
10001
11001

Krok II.
Dzielimy tekst na bloki długo

ś

ci równej ilo

ś

ci permutowanych elementów – czyli długo

ś

ci 4 –

i ewentualnie uzupełniamy ostatni blok.

www.wedrownik.net 

23

0011
1000
0010
0010
0010
0010
0100
0111
001

0

Krok III.
Tworzymy   tabelk

ę

  z   4   kolumnami   –   1   kolumna   zawiera   wszystkie   bloki   tekstu,   2   w

pierwszym wierszu klucz startowy. Ostatnie dwie na razie pozostawimy puste

www.wedrownik.net 

24

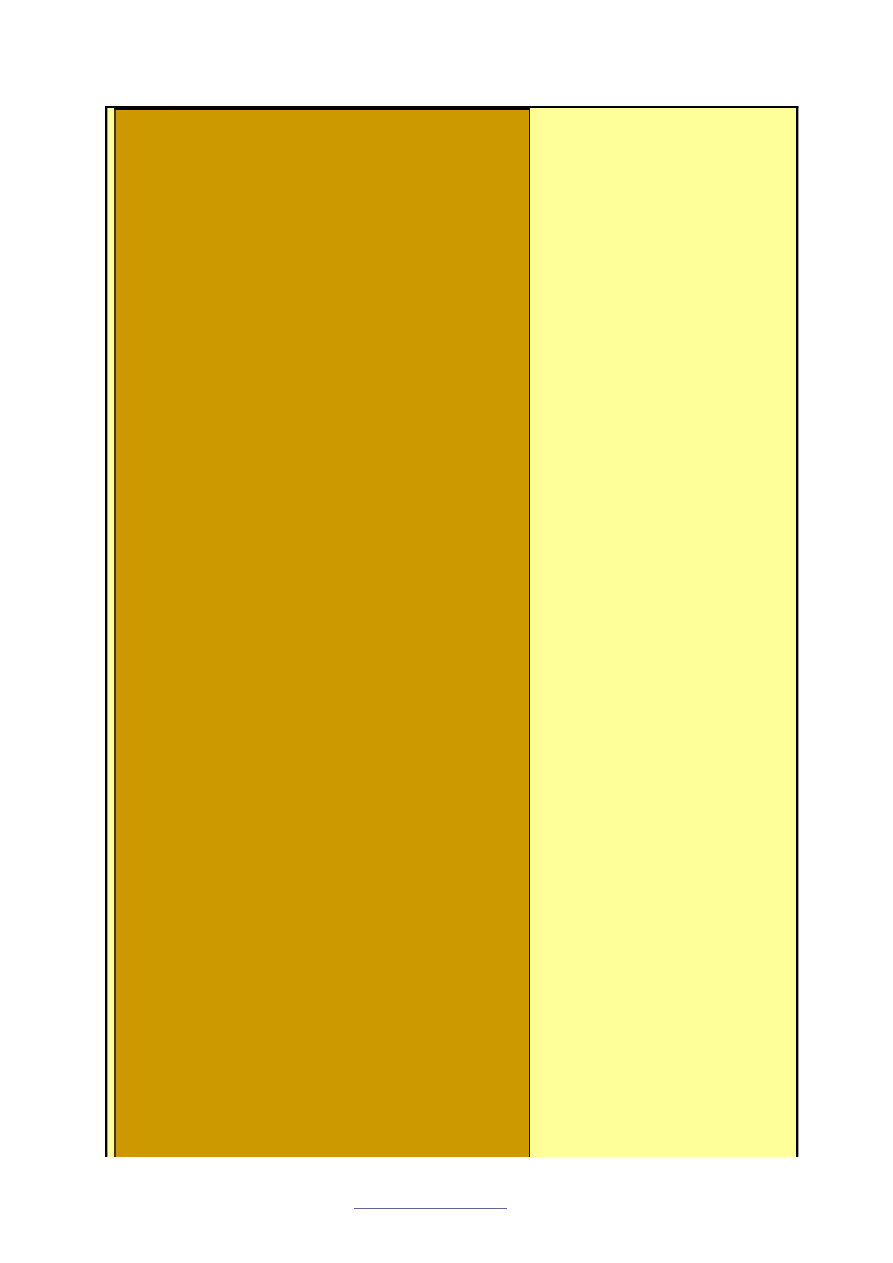
Tekst

Kluc

z

Tekst

+

Kluc

z

Szyfr

(po

perm

utacji

)

0011
0101

1000

0010

0010

0010

0010

0100

0111

0010

www.wedrownik.net 

25

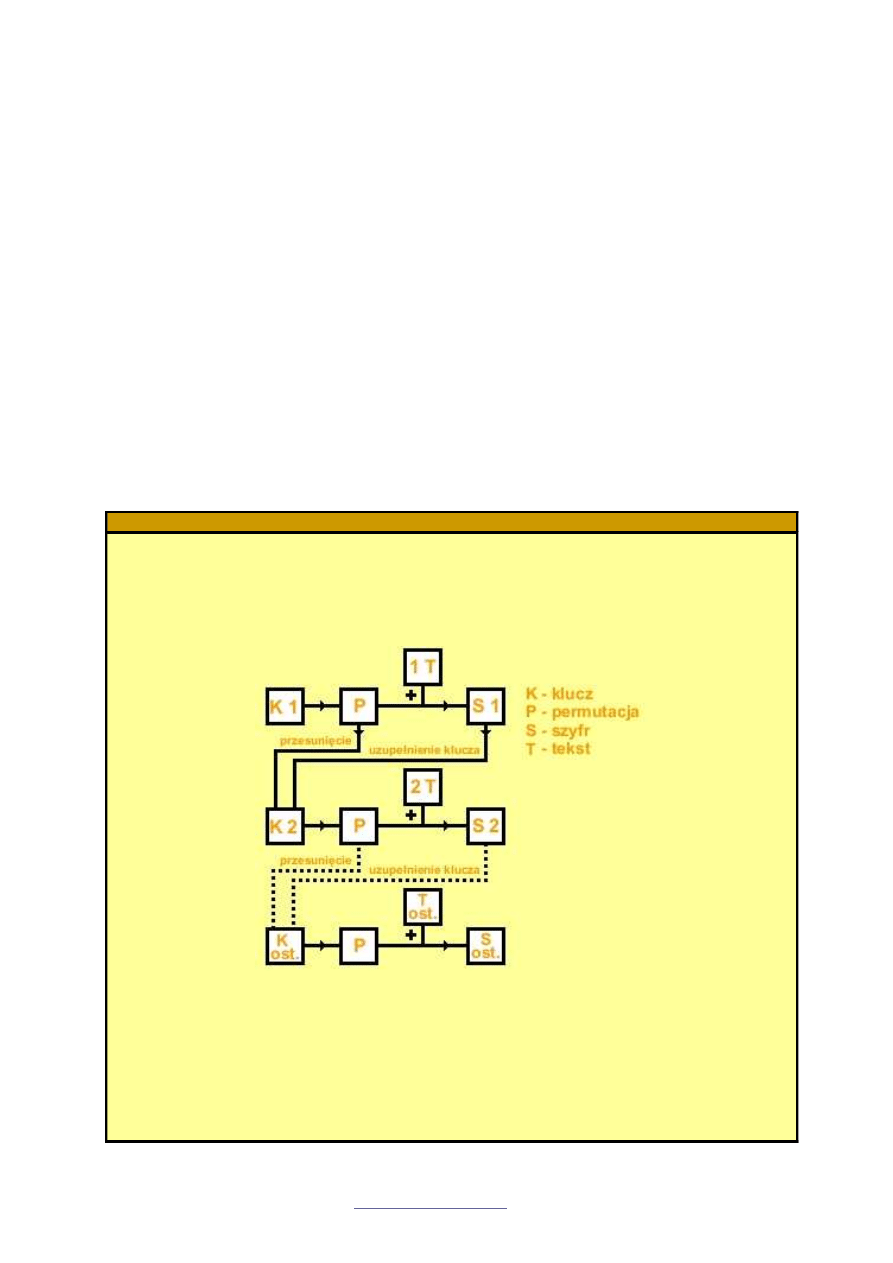
Metoda ta wymaga troszk

ę

 wi

ę

cej pracy ni

ż

 szyfr ECB. Mam jednak nadziej

ę

, 

ż

e pomimo

tego jest ona interesuj

ą

ca.

Uwaga
- w tej i nast

ę

pnej metodzie istnieje ciekawy sposób ukrycia klucza. Po prostu zał

ą

czamy go

na pocz

ą

tku wiadomo

ś

ci. Adresat naszego tekstu wiedz

ą

c jaka jest jego długo

ść

 wyodr

ę

bni

klucz z szyfru i przyst

ą

pi do odczytywania przesyłki.

CFB (Cipher Feedback)

CFB jest kolejnym bardziej skomplikowanym szyfrem z tej grupy. Podobnie jak dla CBC, dla
ka

ż

dego bloku tekstu dostajemy inny klucz. Jednak dokonujemy jeszcze paru dodatkowych

przekształce

ń

 – prosz

ę

 si

ę

 nie ba

ć

, to nie b

ę

d

ą

 

ż

adne matematyczne przekształcenia.

SZYFROWANIE – DESZYFROWANIE 

Szczególnie   przy   tej   metodzie   warto   zapozna

ć

  si

ę

  z   schematem,   gdy

ż

  wtedy   łatwiej

zapami

ę

ta

ć

 jak ona działa.

Schemat szyfrowania

W   przykładzie   ilustruj

ą

cym   prac

ę

  tego   szyfru,   tradycyjnie   u

ż

yjemy   słowa  

harcerz

.

Potrzebujemy   te

ż

  funkcj

ę

  permutuj

ą

c

ą

  –  

(13)

  oraz   klucz   startowy   –  

1101

.   Dodatkowym

parametrem   jest   warto

ść

  przesuni

ę

cia   –  

1

.     Co   ta   warto

ść

  oznacza   najlepiej   poka

ż

e

przykład.

Krok I.
Zapisujemy nasz tekst w postaci zerojedynkowej.

www.wedrownik.net 

26

h
a

r

c

e

r

z

00111
00000
10001
00010
00100
10001
11001

Krok II.
Teraz   musimy   ustali

ć

  długo

ść

  bloku   tekstu.   Permutacja   mo

ż

e   mie

ć

  minimaln

ą

  ilo

ść

elementów równ

ą

 3, ale klucz pocz

ą

tkowy ma ich 4. Wi

ę

c wychodzi nam długo

ść

 4. Tutaj

jednak wchodzi w gr

ę

 warto

ść

 przesuni

ę

cia i skraca nam blok tekstu – w tym przykładzie o

1.
Ostateczna długo

ść

 bloków przeznaczonych do szyfrowania wynosi 3 symbole.

001
110
000
010
001
000
100
010
010
001
110
01

0

Ostatni blok uzupełnili

ś

my o brakuj

ą

cy element.

Krok III.
Tworzymy teraz nast

ę

puj

ą

c

ą

 tabelk

ę

 – na pocz

ą

tek wpisujemy w 3 kolumn

ą

 wszystkie bloki

tekstu.

www.wedrownik.net 

27

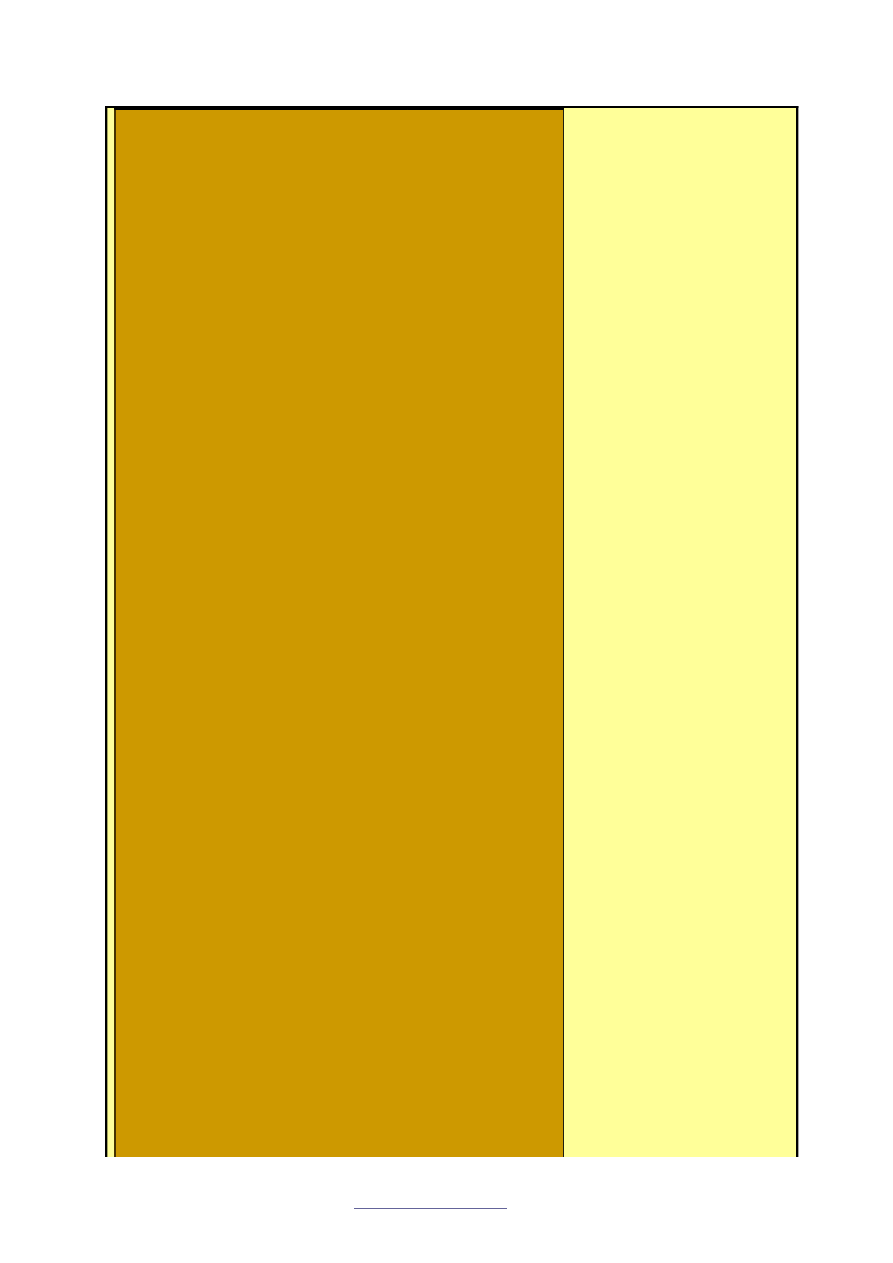
Klucz
Klucz
po
perm
utacji
Tekst
Szyfr

(klucz
+
tekst)

001

110

000

010

001

000

100

010

010

www.wedrownik.net 

28

Niestety,   do   obu   powy

ż

szych   szyfrów   nie   podam   metod   łamania,   gdy

ż

  s

ą

  zbyt

skomplikowane – zainteresowanych odsyłam do fachowej literatury (jednak zalecam wzi

ę

cie

sobie paru dni wolnego;-)

Szyfr Feistella

Ostatni z szyfrów działaj

ą

cych w systemie zerojedynkowym. I to jest jedyne podobie

ń

stwo do

powy

ż

szych szyfrów;-) Stopniem trudno

ś

ci lokuje si

ę

 pomi

ę

dzy dwoma pierwszymi szyframi

z tego rozdziału. Co jednak wa

ż

niejsze, nauczymy si

ę

 w prosty sposób łama

ć

 t

ą

 metod

ę

:-)

SZYFROWANIE – DESZYFROWANIE – ŁAMANIE SZYFRU

Metod

ę

 ta przedstawi

ę

 w najprostszej wersji. Je

ś

li kto

ś

 b

ę

dzie chciał spróbowa

ć

 sił z troch

ę

wy

ż

szym poziomem trudno

ś

ci, to wystarczy zmieni

ć

 warto

ś

ci pewnych parametrów.

Na nasze potrzeby wystarcz

ą

 nast

ę

puj

ą

ce zało

ż

enia – b

ę

dziemy szyfrowa

ć

 bloki tekstu o

długo

ś

ci 4 symboli, ilo

ść

 kroków szyfruj

ą

cych ograniczymy do 2, a stosowanym elementem

szyfruj

ą

cym   b

ę

dzie   macierz   2x2   (kto   nie   zna   tego   poj

ę

cia   to   prosz

ę

  zapozna

ć

  si

ę

  z

rozdziałem  V na stronie 37)

Uwaga
- długo

ść

 bloków jakie podlegaj

ą

 szyfrowaniu jest 

ś

ci

ś

le zwi

ą

zana z wielko

ś

ci

ą

 macierzy –

szyfrowany fragment tekstu jest zawsze dwa razy dłu

ż

szy, ni

ż

 wielko

ść

 macierzy (dlatego

długo

ść

 4 dla macierzy 2x2, 6 dla 3x3, 8 dla 4x4 itd.)

Na potrzeby naszego przykładu zaszyfrujemy słowo  

harcerz

, przy zastosowaniu  

2

  kroków

szyfruj

ą

cych z macierz

ą

 













1

0

1

1

Krok I.

www.wedrownik.net 

29

Tradycyjnie   zapisujemy   nasz   tekst   w   formie   zerojedynkowej   i   dzielimy   na   fragmenty   o
długo

ś

ci 4 elementów z ewentualnym uzupełnieniem ostatniej cz

ęś

ci.

h
a

r

c
e

r

z

00111
00000
10001
00010
00100
10001
11001

⇓

0011
1000
0010
0010
0010
0010
0100
0111
001

0

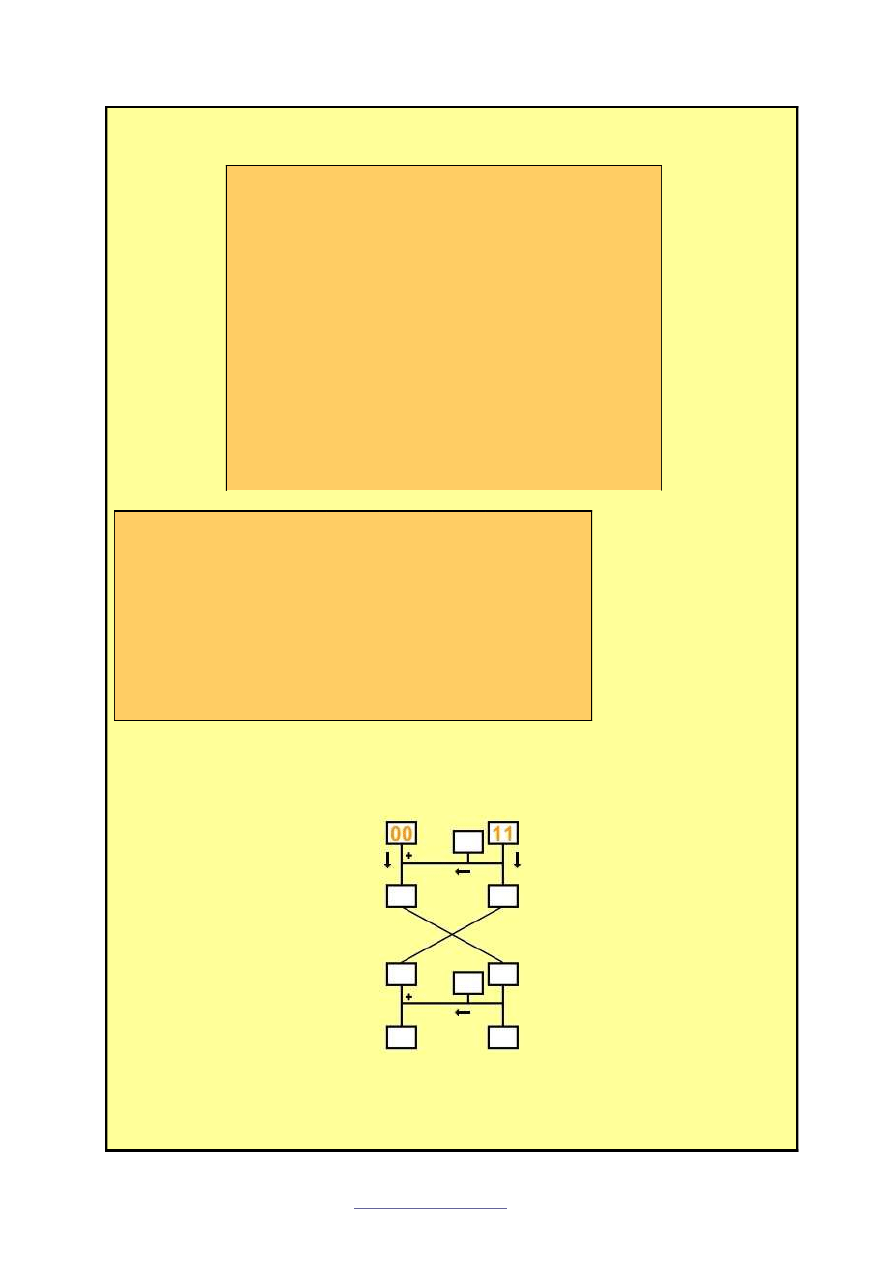
Krok II.
Tym razem działanie  przedstawimy za  pomoc

ą

 rysunku. Najpierw zaszyfrujemy pierwszy

fragment naszego tekstu – 

0011

.

Tekst dzielimy na cz

ęść

 lew

ą

 i praw

ą

.

Krok III.
Zaczynamy   pierwszy   krok   szyfruj

ą

cy.   Cz

ęść

  praw

ą

  mno

ż

ymy   z   nasz

ą

  macierz

ą

  i

przygotowujemy   j

ą

  do   dodania   do   cz

ęś

ci   lewej.   Dodatkowo   niezmienion

ą

  cz

ęść

  praw

ą

przepisujemy poni

ż

ej, aby móc za dwa kroki dokona

ć

 zamiany.

www.wedrownik.net 

30

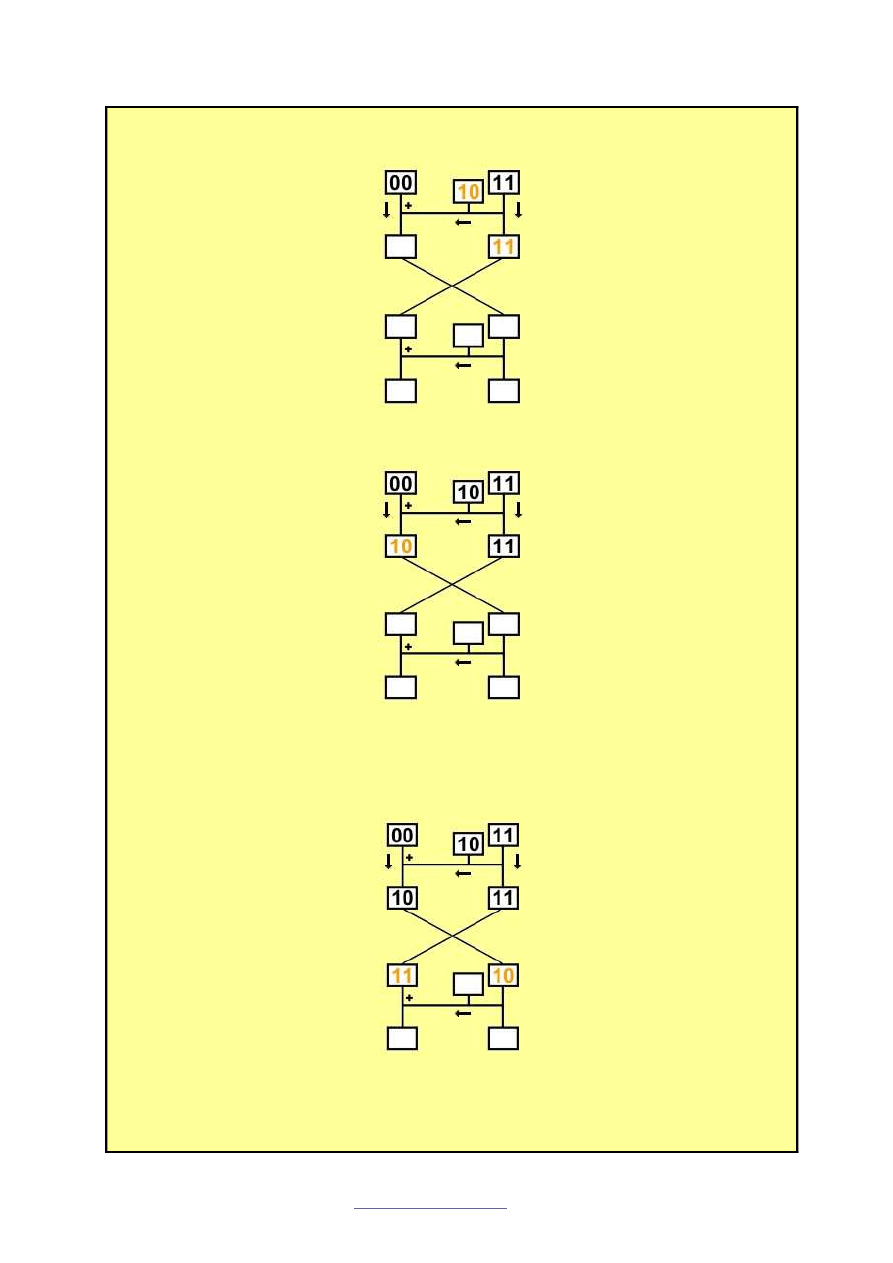
Krok IV.
Dodajemy do siebie cz

ęść

 lew

ą

 i zmodyfikowan

ą

 praw

ą

.

W tym momencie ko

ń

czymy pierwszy krok szyfruj

ą

cy.

Krok V.
Dokonujemy zamiany cz

ęś

ci lewej i prawej.

Krok VI.
Dla nowych cz

ęś

ci tekstu, przeprowadzamy drugi krok szyfruj

ą

cy (dokładnie jak powy

ż

ej).

Po   ostatnim   kroku   szyfruj

ą

cym   nie   dokonujemy   zamiany.   Dlatego   w   naszym   przypadku

drugie powtórzenie daje nam zaszyfrowany pierwszy blok tekstu.

www.wedrownik.net 

31

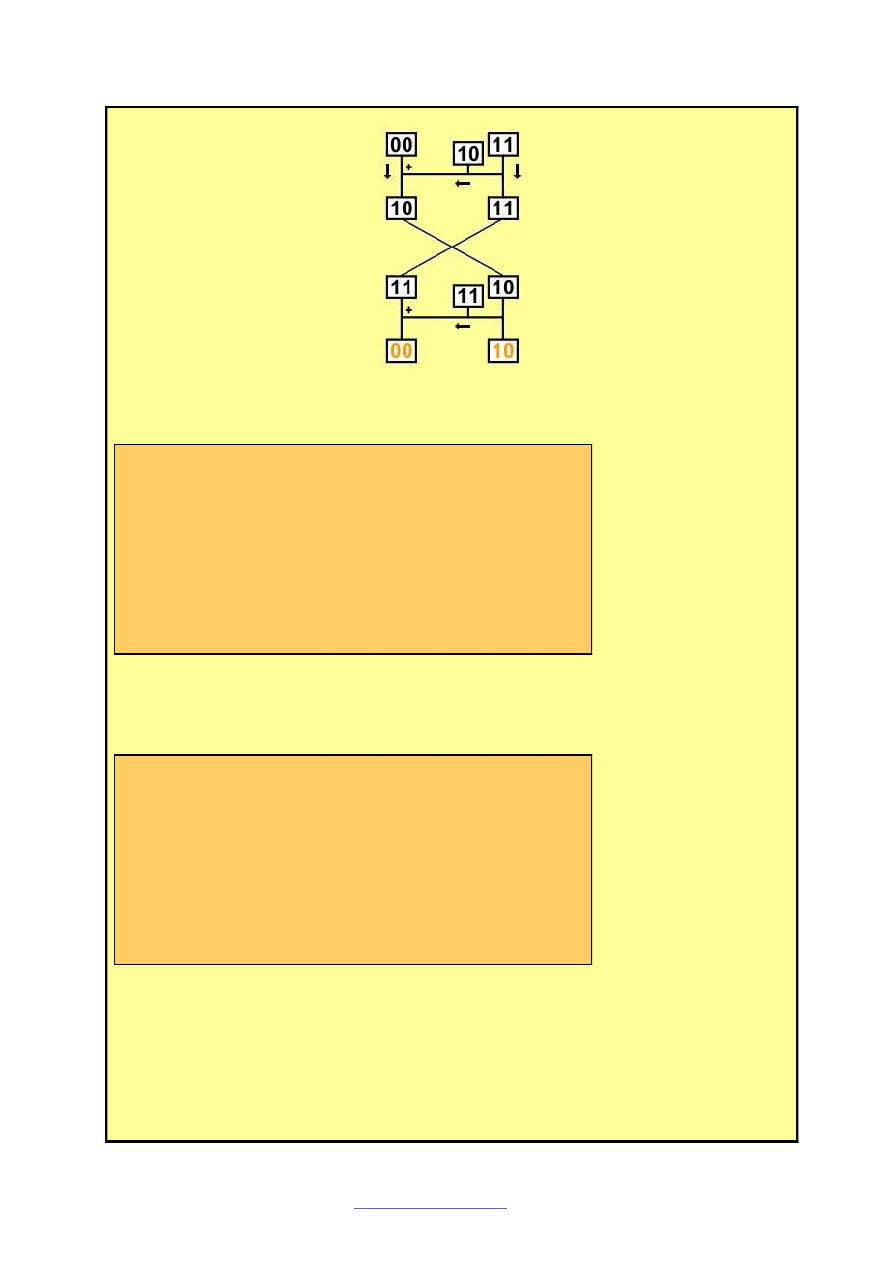
Je

ś

li   powtórzymy   dla   ka

ż

dego   bloku   tekstu   kroki   II   –   VI,   to   jako   zaszyfrowany   tekst

otrzymamy.

0010
1110
0011
0011
0011
0011
0101
0111
0011

●●●

Ta metoda jest kolejn

ą

, przy której dla rozszyfrowania podanego tajnego tekstu, musimy go

ponownie zaszyfrowa

ć

. A wi

ę

c, aby z szyfru

0010
1110
0011
0011
0011
0011
0101
0111
0011

uzyska

ć

  słowo   harcerz,   musimy   na   nim   zastosowa

ć

  opisan

ą

  powy

ż

ej   metod

ę

  wraz   z

ko

ń

cowym   podzieleniem   na   bloki   składaj

ą

ce   si

ę

  z   5   elementów   i   eliminacj

ą

  zb

ę

dnych

symboli – ale te działanie ju

ż

 wielokrotnie 

ć

wiczyli

ś

my.

●●●

Gdy mamy zaszyfrowan

ą

 wiadomo

ść

 i chcemy j

ą

 rozgry

źć

, musimy okre

ś

li

ć

 macierz, która

nam   szyfruje   pojedyncze   bloki.   Wiemy,  

ż

e   macierz   ta   ma   4   elementy,   a   jako   mo

ż

liwe

warto

ś

ci tylko 0 i 1. Je

ś

li znamy jakie

ś

 elementy macierzy to musimy sprawdzi

ć

 wszystkie

mo

ż

liwo

ś

ci i zobaczy

ć

 przy której uzyskujemy sensowne wyniki. Gdy znamy 3 elementy, to

www.wedrownik.net 

32

do sprawdzenia mamy 2 macierze, gdy znamy 2 to ju

ż

 4, przy 1 elemencie a

ż

 8. Gdy nie

znamy 

ż

adnego, to pozostaje nam przetestowa

ć

 wszystkie 16 mo

ż

liwo

ś

ci.

Prób

ę

 przeprowadzamy tak, jak zostało to opisane w cz

ęś

ci po

ś

wi

ę

conej szyfrowaniu.

Ciekawiej   jest,   gdy   oprócz   szyfru   znamy   tekst  jawny   pasuj

ą

cy   do   jednego   bloku   szyfru.

Dzi

ę

ki temu mo

ż

emy okre

ś

li

ć

 poszukiwan

ą

 macierz – gdy znamy jakiekolwiek jej elementy,

to zadanie jest dodatkowo ułatwione.
Jak si

ę

 do tego zabra

ć

?

Trzeba przeanalizowa

ć

, jak wygl

ą

da proces szyfrowania (bo w tej metodzie deszyfrowanie

działa identycznie jak szyfrowanie). Zrobimy to na konkretnym przykładzie.
Dla szyfru 

0110

 znamy tekst jawny 

0111

.

Nasza macierz ma ogóln

ą

 posta

ć

 













d

c

b

a

.

Krok I.
Uzupełniamy schemat szyfru i elementy, które ju

ż

 znamy.

Uzupełnili

ś

my   od   razu  

ś

cie

ż

k

ę

  dla   prawego   elementu   –   wszystko   zgodnie   z   metod

ą

szyfrowania.

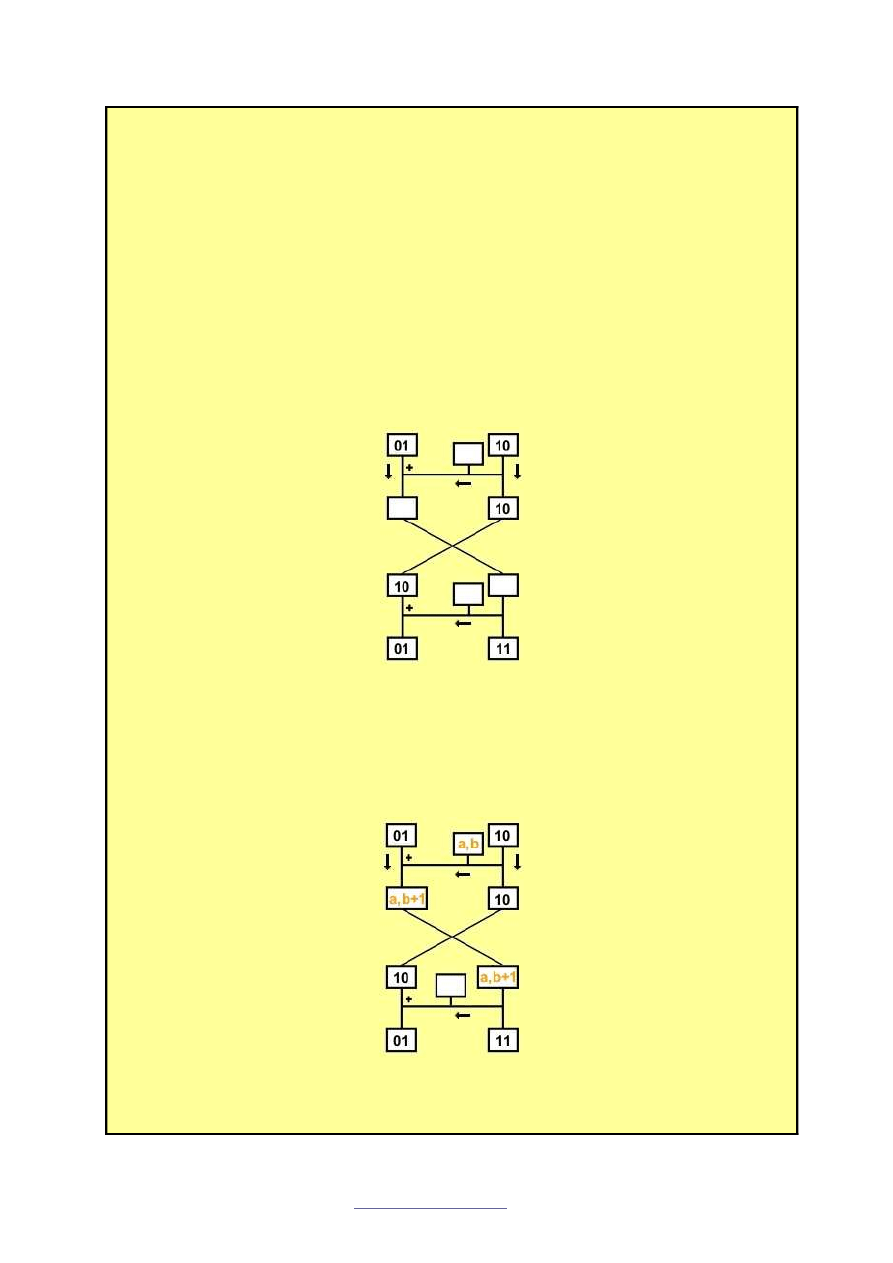
Krok II.
Wymna

ż

amy   praw

ą

  stron

ę

  naszego   szyfru   z   ogóln

ą

  postaci

ą

  macierzy,   a   nast

ę

pnie

dodajemy do lewej strony (i uzupełniamy praw

ą

 stron

ę

 pozycji po zamianie).

Dla przejrzysto

ś

ci u

ż

yłem pisowni z przecinkiem.

W tej chwili mo

ż

emy zacz

ąć

 okre

ś

la

ć

 posta

ć

 naszej macierzy. Z naszego schematu wynika,

ż

e 

(a, b+1) = (11)

. Daje nam to nast

ę

puj

ą

ce warto

ś

ci: 

a = 1

 i 

b = 0

. A wi

ę

c nasza macierz

www.wedrownik.net 

33

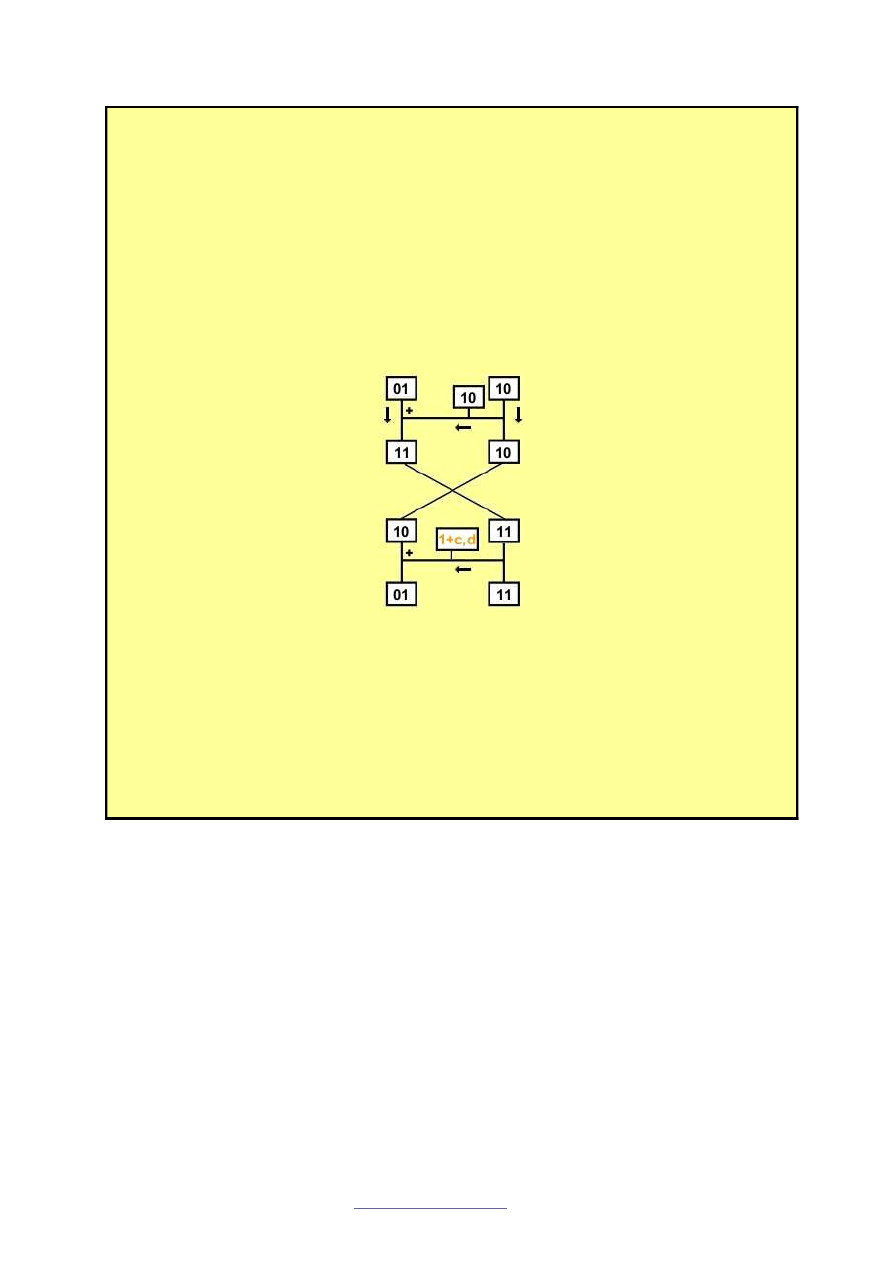
wygl

ą

da nast

ę

puj

ą

co - 













d

c

0

1

.

Krok III.
Teraz wykonujemy drugie mno

ż

enie macierzy z nasz

ą

 praw

ą

 stron

ą

 szyfru (po uprzednim

podstawieniu cyfr).

Aby   okre

ś

li

ć

  ostatnie   elementy   macierzy   dokonujemy   dodawania  

(10)   +   (1+c,   d)

.

Zsumowane   elementy   musz

ą

    (na   podstawie   schematu)   by

ć

  równe   elementowi  

(01)

.

Ostatecznie daje nam to 

(1+1+c, d) = (1, 1)

, a wi

ę

c 

c = 0

, 

d = 1

.  Maj

ą

c wszystkie elementy

wiemy ju

ż

, 

ż

e pozostałe bloki szyfru musimy podda

ć

 działaniu macierzy 













1

0

0

1

.

Czasem mo

ż

e trafi

ć

 si

ę

 nam trudniejsza sytuacja, gdy nie tak łatwo okre

ś

li

ć

 jednoznacznie

elementy   macierzy.   Có

ż

,   pozostaje   nam   wtedy   rozpatrywa

ć

  po   kolei   ró

ż

ne   mo

ż

liwo

ś

ci   i

sprawdza

ć

, które pasuj

ą

 do schematu. 

 

Metoda   ta   jak   pokazuj

ą

  przykłady   mo

ż

e   by

ć

  troszk

ę

  pracochłonna.   Jednak   nie   ma   tutaj

ż

adnej   skomplikowane   matematyki.   Jedynie   sprawdzanie   pewnej   liczby   mo

ż

liwych

kombinacji.

Uwaga
-   metoda   ta   sprawdza   si

ę

  równie

ż

,   gdy   zamiast   macierzy,   u

ż

ywamy   do   szyfrowania

dwuelementowego klucza
- niestety znacznie łatwiej wtedy złama

ć

 t

ą

 metod

ę

, gdy

ż

 do wyboru mamy tylko 4 klucze

(mo

ż

na   zawsze   je   wydłu

ż

y

ć

,   ale   co   za   tym   idzie   dwukrotnie   zwi

ę

kszy

ć

  szyfrowane   lub

deszyfrowane bloki tekstu)

www.wedrownik.net 

34

Wytaczamy ostatnią armatę

Ta grupa szyfrów b

ę

dzie wymagała wprowadzenia pewnej, dla wielu osób na pocz

ą

tku na

pewno niełatwej, teorii matematycznej – działania modulo (proponuj

ę

 zapozna

ć

 si

ę

 z tre

ś

ci

ą

rozdziału V na stronie 38).

Szyfr afiniczny

Jest to mocno utrudniona wersja szyfru Cezara. Tutaj zmiana litery jest okre

ś

lona dwoma

parametrami, a nie jak w metodzie Cezara jednym. 

SZYFROWANIE – DESZYFROWANIE – ŁAMANIE SZYFRU

 
Przy tej metodzie do

ść

 cz

ę

sto pomocnym narz

ę

dziem b

ę

dzie kalkulator.

Aby zobrazowa

ć

 działanie tej metody zaszyfrujemy słowo harcerz.

Krok I.
Zamieniamy litery tekstu jawnego na ich warto

ś

ci liczbowe. Jednak zaczynamy od 0 – czyli

litera a ma warto

ść

 0, 

ą

 – 1, b - 2, itd. 

www.wedrownik.net 

35

h
a

r

c
e

r

z

10

0

22

3
6

22
29

Wa

ż

ne

- wa

ż

ne jest jaki alfabet stosujemy – dla angielskiego mamy 26 liter, a dla polskiego 32

- w tej metodzie szyfrowania, tak

ż

e odst

ę

p mi

ę

dzy wyrazami ma przypisana warto

ść

 – dla

alfabetu angielskiego 26, a dla polskiego 32

Krok II.
Aby zaszyfrowa

ć

 tekst musimy okre

ś

li

ć

 funkcje szyfruj

ą

c

ą

. Jak ju

ż

 wiemy b

ę

dzie ona zale

ż

e

ć

od dwóch warto

ś

ci –  

a

  i  

b

  (b

ę

dziemy je nazywa

ć

 kluczem). Ogólna posta

ć

 funkcji wygl

ą

da

nast

ę

puj

ą

co:

y 

≡

 (ax + b) mod n

a

  oraz  

b

  s

ą

 wybranymi przez nas liczbami,  

n

  jest ilo

ś

ci

ą

 liter w alfabecie + 1,  

x

  warto

ś

ci

ą

liczbow

ą

 szyfrowanej litery, a  

y

  uzyskanym w ten sposób szyfrem. W naszym przykładzie

u

ż

yjemy funkcji 

y 

≡

 (2x + 7) mod 33

Je

ś

li zachcemy zaszyfrowa

ć

 liter

ę

 h, to uzyskamy poni

ż

szy wynik:

h = 10

, a wi

ę

c 

y 

≡

 (2·10 + 7) mod 33

 = 27 mod 33 = 

27 = w

Gdy ka

ż

d

ą

 z liter słowa harcerz tak zaszyfrujemy uzyskamy:

www.wedrownik.net 

36

h
a

r

c

e

r

z

10

0

22

3
6

22
29

⇓

27

7

18
13
19
18
32

w

ę
ń

k
o

ń

●●●

Deszyfracja jest bardziej skomplikowana. Ale wszystko  po kolei.

Poni

ż

szy szyfr został stworzony przy pomocy tej samej funkcji szyfruj

ą

cej: 

y 

≡

 (2x + 7) mod 33

www.wedrownik.net 

37

ę
ą
ę

d
e

ę

d
a

j

ś
ę

7
2
7
5
6
7
5
0
1
2
2
4
7

Krok I.
Aby deszyfrowa

ć

, musimy okre

ś

li

ć

 funkcj

ę

 odwrotn

ą

 do zastosowanej. 

Wa

ż

ne

- aby deszyfrowanie było mo

ż

liwe, musi by

ć

 spełniony warunek NWD (a, n) = 1 (najwi

ę

kszy

wspólny   dzielnik).   Nie   b

ę

d

ę

  si

ę

  rozwodził   dlaczego   akurat   tak,   gdy

ż

  musiałbym   straszy

ć

matematyk

ą

 – zainteresowanych odsyłam do literatury fachowej.

NWD   (2,   33)   =   1,   a   wi

ę

c   mo

ż

emy   jednoznacznie   okre

ś

li

ć

  funkcje   odwrotn

ą

.   Jej   ogólna

posta

ć

 prezentuj

ę

 si

ę

 nast

ę

puj

ą

co:

x 

≡

 a’·(y - b) mod n

a’

  jest   w   tym   przypadku   odwrotno

ś

ci

ą

  a   z   wzoru   na   szyfrowanie.   Nie   jest   to   jednak

odwrotno

ść

,   jak

ą

  znamy   ze   szkoły.   Aby   okre

ś

li

ć

  a’   musimy   zastosowa

ć

 

rozszerzony

algorytm Euklidesa

.

Dla  

x 

≡

 2’(y - 7) mod 33  

całe obliczenie wygl

ą

da jak poni

ż

ej (dlaczego tak, a nie inaczej

wyja

ś

nione jest w rozdziale V na stronie 38).

33 = 16·2 + 1

⇒

1 = 33 - 16·2

A wi

ę

c odwrotno

ś

ci

ą

 

2

 jest 

-16

. Ale -16 odpowiada liczbie 

17

 (33-16=17) w grupie 

mod 33

.

www.wedrownik.net 

38

Nasza funkcja ma posta

ć

:

x 

≡

 17·(y - 7) mod 33

Krok II.
Nasz

ą

 zaszyfrowan

ą

 wiadomo

ść

 poddajemy działaniu funkcji odwrotnej. Daje nam to efekt

jak poni

ż

ej.

ę
ą
ę

d
e

ę

d
a

j

ś

ę

7
2
7
5
6
7
5
0
1
2
2
4
7

⇓

www.wedrownik.net 

39

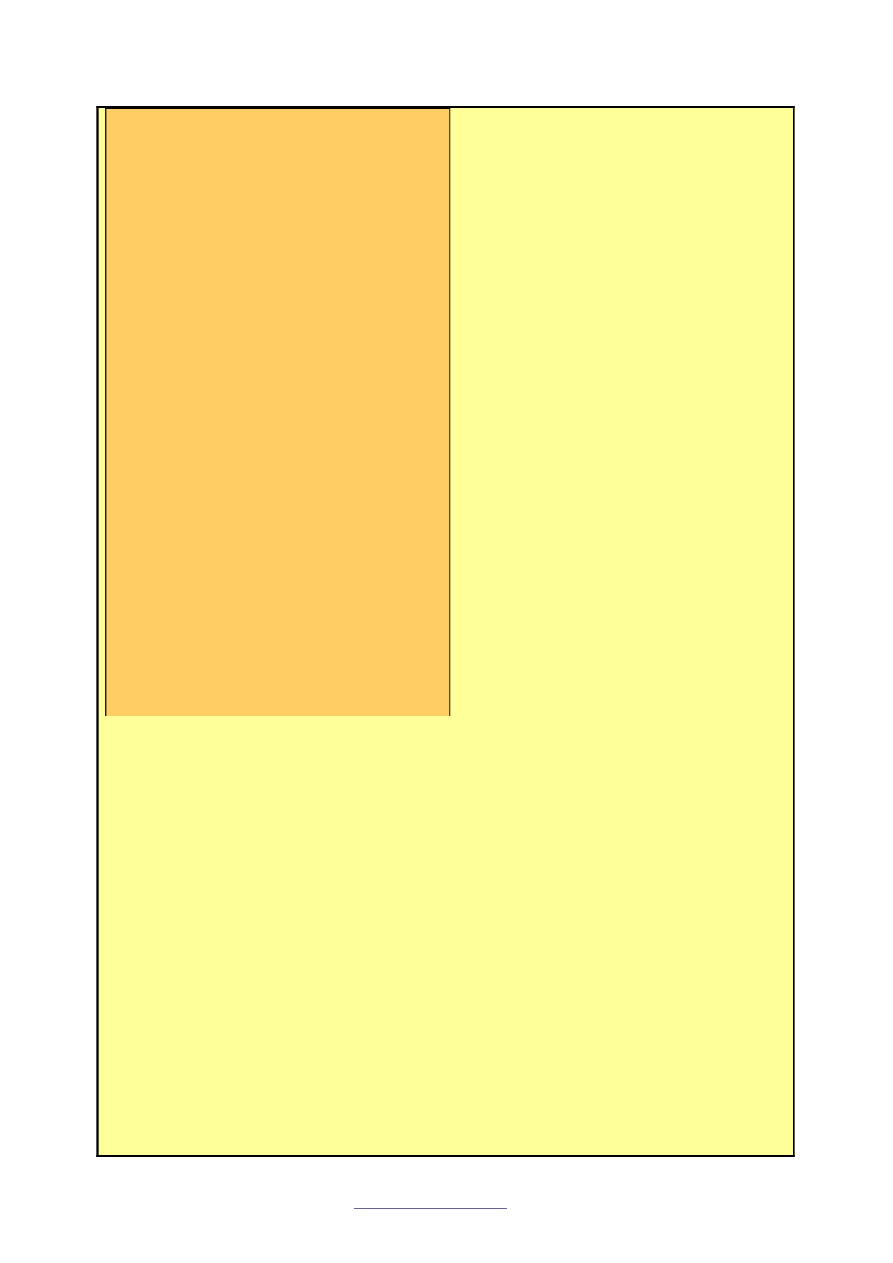
0
1
4
0
3
2
1
6
0
3
2
1
3
1
9
2
5
0

a

l

a

 

m
a

 

k
o

t

a

Metoda ta wymaga wiele uwagi i ci

ą

głej 

ś

wiadomo

ś

ci, 

ż

e liczymy w grupie mod n (u nas w

mod 33).

●●●

Aby  móc  złama

ć

 szyfr  afiniczny  nie znaj

ą

c  funkcji szyfruj

ą

cej,  potrzebujemy informacj

ę

 o

cho

ć

by paru przyporz

ą

dkowaniach liter tekstu jawnego do liter szyfru. Gdy znamy cho

ć

 2 z

nich, mo

ż

emy złama

ć

 t

ą

 metod

ę

 kryptograficzn

ą

. Tak

ż

e w tym przypadku najlepiej łamanie

omówi

ć

 na konkretnym przykładzie, bez zb

ę

dnych teoretycznych wywodów, które sił

ą

 woli

byłyby zbyt techniczne.

Mamy szyfr 

n

ą

ry

ą

l

 i wiemy, 

ż

e 

n

 zostało zaszyfrowane do 

r

, a 

d

 do 

y

. Dzi

ę

ki temu mo

ż

emy

stwierdzi

ć

, 

ż

e

www.wedrownik.net 

40

n

ą

r

y

ą

l

17

1

22
28

1

14

oraz

n

→

r

1
7

→

2
2

d

→

y

5

→

2
8

 

Pozwoli   nam   to   okre

ś

li

ć

,   jak

ą

  funkcj

ą

  zaszyfrowano   tekst,   a   co   za   tym   idzie   wyznaczy

ć

funkcj

ę

 do niej przeciwn

ą

. Gdy ju

ż

 ja uzyskamy, to b

ę

dziemy mogli odszyfrowa

ć

 pozostałe

litery.

Krok I.
Na podstawie drugiej tabelki utworzymy układ równa

ń

 liniowych (w zapisie mod 33).

17a + b 

≡

 22 mod 33

  5a + b 

≡

 28 mod 33

Jak wida

ć

 na naszym przykładzie, warto

ś

ci liczbowe dla 

tekstu jawnego

 wpisujemy przy 

a

,

a 

warto

ś

ci szyfru

 przy 

mod

.

www.wedrownik.net 

41

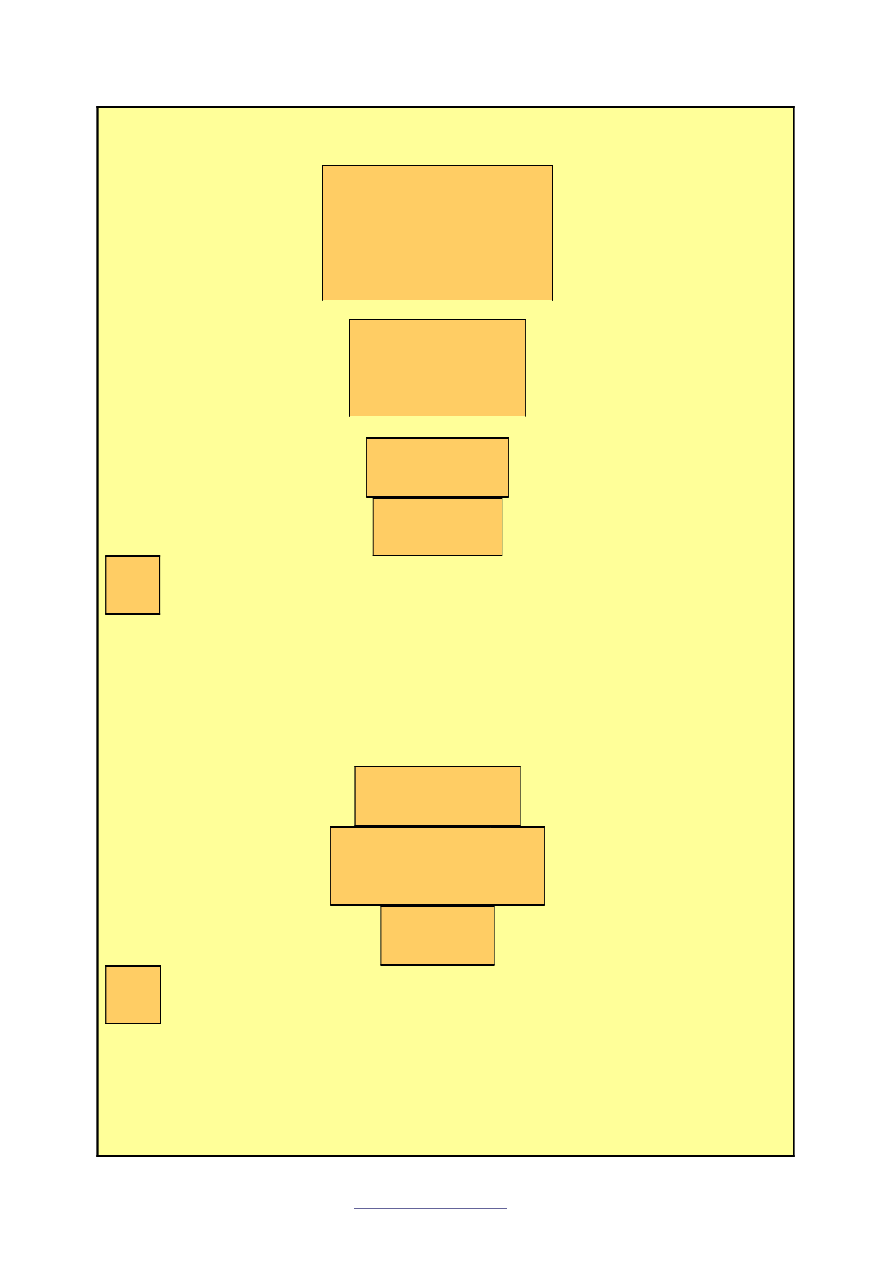
Krok II.
Rozwi

ą

zujemy nasze równanie liniowe (pami

ę

taj

ą

c, 

ż

e liczymy w grupie mod 33).

17a + b 

≡

 22 mod 33

/ · (-1)

  5a + b 

≡

 28 mod 33

⇓

-17a - b 

≡

 -22 mod 33

  5a + b 

≡

 28 mod 33

⇓

-12a  

≡

 6 mod 33

⇓

21a 

≡

 6 mod 33

⇓

a = 5

Pocz

ą

tek rozwi

ą

zania powinien by

ć

 zrozumiały dla wszystkich. Wa

ż

ne jest aby pami

ę

ta

ć

 i

ż

-12

 ma warto

ść

 

21

 w grupie mod 33. 

Wynik 

a = 5

 mo

ż

na uzyska

ć

 jedynie poprzez systematyczne podstawianie liczb (pocz

ą

wszy

od 1) i sprawdzanie czy równanie jest prawdziwe. Wymaga to troch

ę

 cierpliwo

ś

ci i najlepiej

stosowania kalkulatora (jest to du

ż

e udogodnienie).

Teraz musimy wyznaczy

ć

 jeszcze parametr b.

5·5 + b 

≡

 28 mod 33

⇓

25 + b 

≡

 28 mod 33

/ - 20

⇓

b 

≡

 3 mod 33

⇓

b = 3

Maj

ą

c oba parametry wiemy ju

ż

, 

ż

e tekst został zaszyfrowany funkcj

ą

:

y = (4x + 3) mod 33

Krok III.
Do rozszyfrowania wiadomo

ś

ci potrzebujemy, jak ju

ż

 wiemy, funkcj

ę

 odwrotn

ą

 do tej przez

www.wedrownik.net 

42

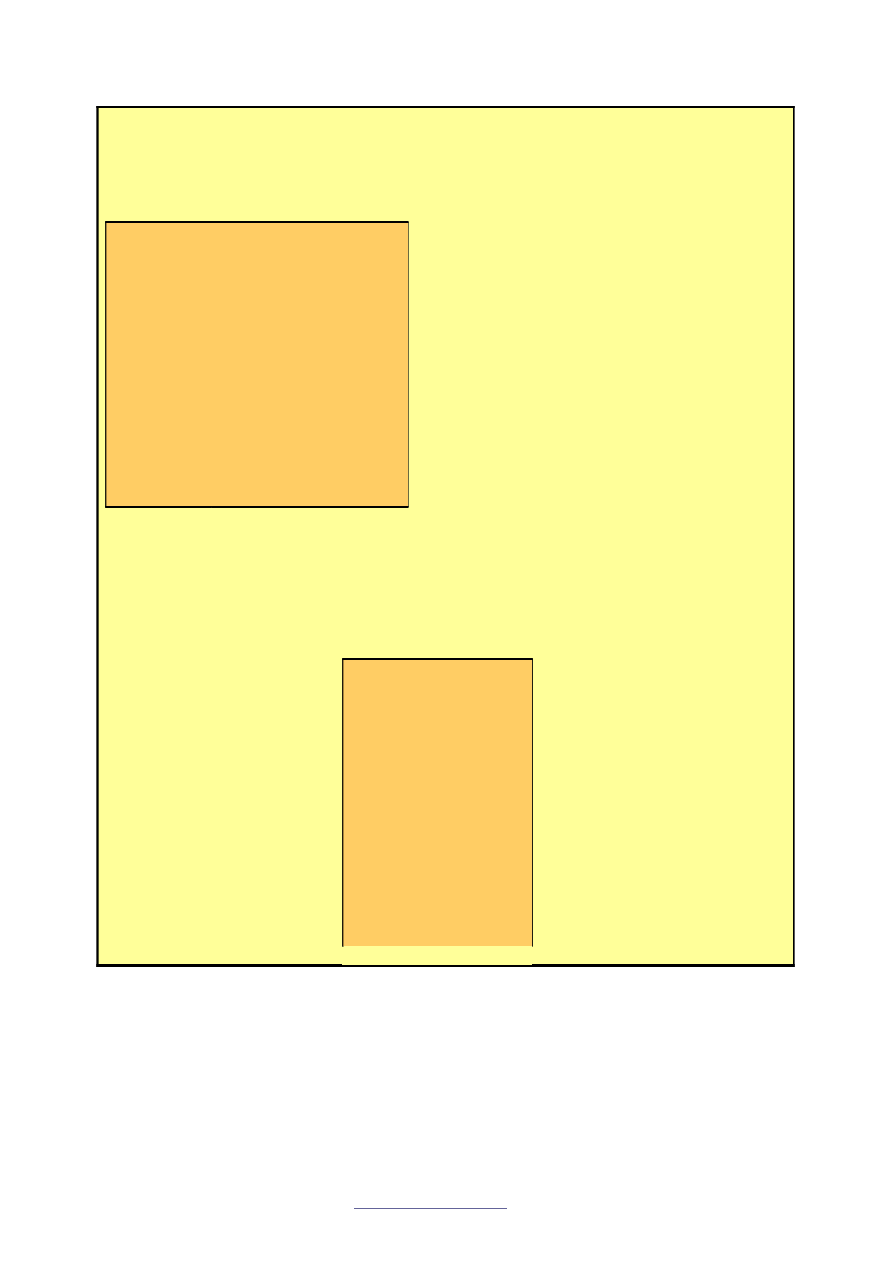
nas okre

ś

lonej. Aby okre

ś

li

ć

 

5’

 z 

x = 5’·(y 

–

 3) mod 33

musimy zastosowa

ć

 rozszerzony algorytm Euklidesa.

33 = 6·5 + 3
  5 = 3 + 2
  3 = 2 + 1

⇒

1 = 3 – 2
1 = 3 – (5 –
3)
1 = 2·3 – 5
1 = 2·(33 –
6·5) – 5
1   =   2·33   –
13·5 

Odwrotno

ś

ci

ą

 5 jest liczba 

- 13

. Jednak -13 w zapisie mod 33 ma warto

ść

 20 (33 – 13 = 20).

Tak wi

ę

c uzyskujemy 

a’ = 20

. Ostatecznie nasza funkcja odwrotna ma posta

ć

:

x = 20·(y 

–

 3) mod 33

Krok IV.
Działamy nasz

ą

 funkcja odwrotn

ą

 na nieznane nam litery szyfru i uzyskujemy tekst jawny:

n

ą

r

y

ą

l

17

1

22
28

1

14

⇓

www.wedrownik.net 

43

16
26
17

5

26
22

m

u
n
d
u

r

W ten sposób przebili

ś

my si

ę

 przez kolejn

ą

 metod

ę

 łamanie szyfru.

Pomoce matematyczne – proszę się nie bać, nie gryzą;-)

Dodawanie binarne - dodawanie inaczej

Brzmi strasznie, ale na szcz

ęś

cie jest prostsze ni

ż

 zwykłe dodawanie, gdy

ż

 mamy tylko 4

mo

ż

liwo

ś

ci:-)

Poni

ż

ej przedstawione s

ą

 wszelkie mo

ż

liwe sytuacje podczas takiego dodawania.

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 0

Permutacja – z czym się to je

Mówi

ą

c   mo

ż

liwie   prosto,   permutacja   to   po   prostu   zmiana   kolejno

ś

ci   elementów   ci

ą

gu.   A

zapis ogólny podaje nam, które pozycje otrzymuj

ą

 nowe przyporz

ą

dkowanie.

Przykładowo  













1

4

4

3

2

2

3

1

oznacza,  

ż

e   pierwszy   element   bloku   o   długo

ś

ci   4   zostanie

przeniesiony na pozycj

ę

 3, drugi pozostanie na pozycji 2, trzeci przesuwamy na pozycj

ę

 4, a

ostatni element l

ą

duje na pocz

ą

tku bloku. Opis mo

ż

e skomplikowany, ale praktyka bardzo

prosta:-)

Inn

ą

 form

ą

 zapisu tej samej permutacji jest (134) – taki jest u

ż

ywany w tym poradniku. Je

ś

li

w   zapisie   tym   brakuje   jakiej

ś

  cyfry,   to   oznacza   to,   i

ż

  symbol   na   tej   pozycji   nie   jest

przenoszony. Jest to opis krótszy a oznacza dokładnie to samo. Czasami mo

ż

emy spotka

ć

nast

ę

puj

ą

cy zapis (13)(24) – oznacza to nic innego jak to, 

ż

e symbol z pozycji 1 przenosimy

na 3, z 3 na 1, a z 2 na 4 oraz z 4 na 2. 
Aby okre

ś

li

ć

 odwrotn

ą

 permutacj

ę

 odwracamy kolejno

ść

 w wersji skróconej czyli otrzymamy

(431). Matematyczna konwencja przewiduje zawsze najmniejszy element  na pocz

ą

tku, wi

ę

c

wersj

ą

 ko

ń

cow

ą

 jest (143).

Permutacje o długo

ś

ci 2 s

ą

 odwrotne same do siebie. A wi

ę

c (23) jest odwrotno

ś

ci

ą

 (23), a

(13)(24) jest odwrotno

ś

ci

ą

 (13)(24). Proste:-)

www.wedrownik.net 

44

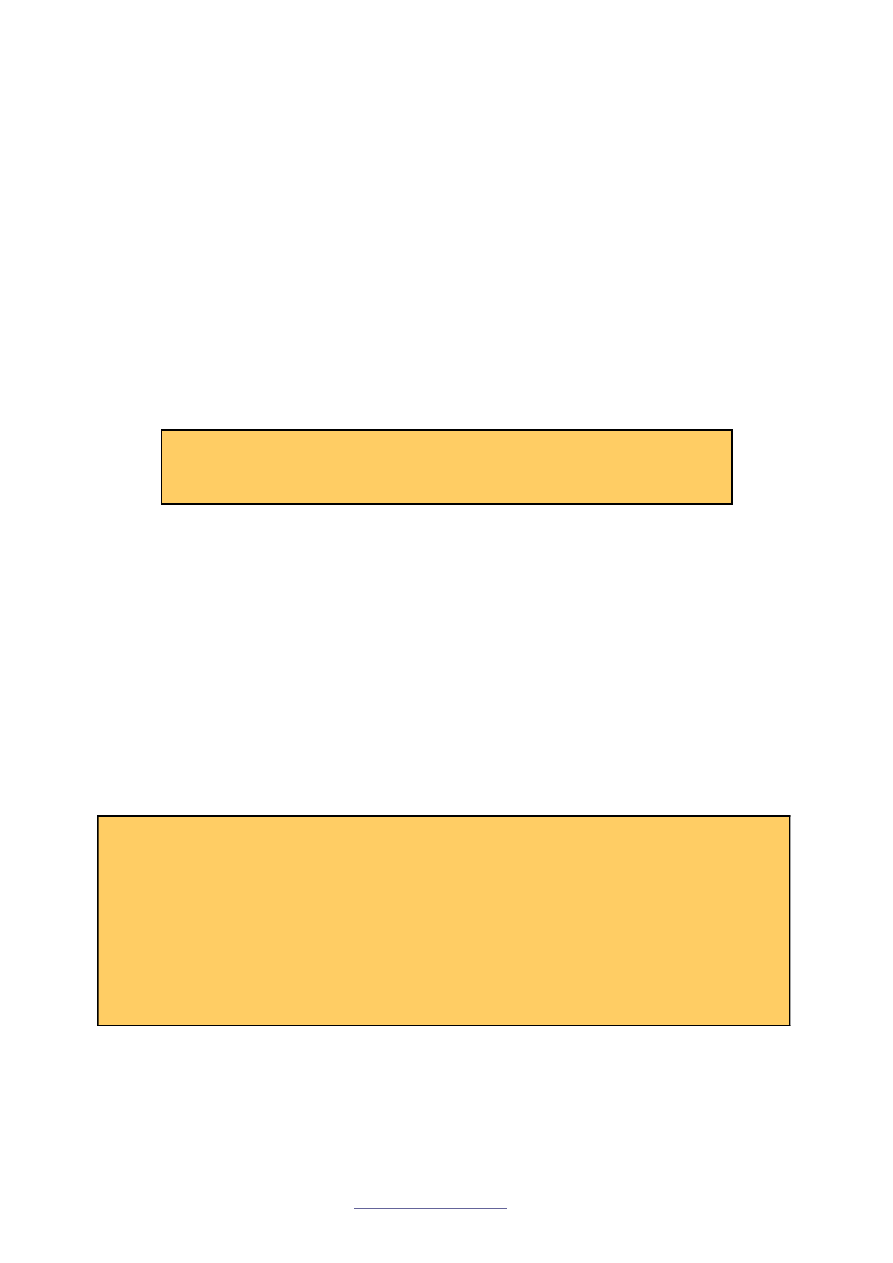
Macierz – to bardzo proste

Nie b

ę

d

ę

 si

ę

 wdawał w opisywanie definicji macierzy. W tym poradniku ograniczymy si

ę

 do

macierzy   kwadratowych   o   rozmiarze   2x2.   Jak   taki   twór   wygl

ą

da?  













d

c

b

a

  jest   ogólnym

zapisem macierzy kwadratowej – prawda, 

ż

e podobne do kwadratu? A zapis 2x2 oznacza,

ż

e mamy po dwa wiersze i dwie kolumny. 

Wektorem z kolei nazwiemy nast

ę

puj

ą

cy element (e, f). Jest to wektor o długo

ś

ci 2. Mno

ż

y

ć

mo

ż

emy z sob

ą

 tylko wektory i macierze kwadratowe o tym samym rozmiarze, a wi

ę

c wektor

o długo

ś

ci 2 z macierz

ą

 2x2.

Jak wygl

ą

da takie mno

ż

enie?

(e  f) 

=













⋅

d

c

b

a

(ea+fc, eb+fd)

(1  1) · 













1

1

1

0

= (1·0 + 1·1   1·1 + 1·1 ) = (0 + 1   1 + 1) = (1  0)

- jest to mno

ż

enie macierzy z uwzgl

ę

dnieniem dodawania zerojedynkowego

Modulo – czy ktoś mi grozi?

Mówi

ą

c   najpro

ś

ciej   jak   si

ę

  da,   jest   to   reszta   z   dzielenia   przez   liczb

ę

  n.   W   zapisie

matematycznym wygl

ą

da to nast

ę

puj

ą

co:

a

≡

b mod n

i   oznacza,  

ż

e   a   przy   dzieleniu   przez   n,   daje   reszt

ę

  b.   Ten  

ś

mieszny   znaczek   pomi

ę

dzy

elementami   traktujcie   jako   zwykły   znak   równo

ś

ci.   Mo

ż

e   nie   jest   to   w   pełni   poprawne

matematycznie, ale nas to nie interesuje, ma by

ć

 łatwo i przyjemnie;-) 

Przy takiej operacji liczba b le

ż

y w przedziale od 0 do n –1, niezale

ż

nie jak du

żą

 liczb

ą

 jest a.

W ramach 

ć

wiczenia par

ę

 przykładów:

22 mod 3 = 1
  4 mod 6 = 4
25 mod 5 = 0

A   co   si

ę

  stanie,   gdy   w   wyniku   naszych   działa

ń

  dostaniemy   liczb

ę

  negatywn

ą

?   Wiemy

przecie

ż

, 

ż

e nasze liczby nale

żą

 do przedziału od 0 do n – 1.

-22 mod 3 = -1 mod 3 = 2    gdy

ż

 3 – 1 = 2

-14 mod 33 = 19    gdy

ż

 33 – 14 = 19

Na  razie   jest miło  prosto  i   przyjemnie.  Niestety teraz  zaczn

ą

 si

ę

 lekkie  schody.   Czasami

musimy   okre

ś

li

ć

  odwrotno

ść

  jakiej

ś

  liczby   w   systemie   modulo   n.   Zapis   matematyczny

przedstawia si

ę

 tak:

ab

≡

1 mod n

www.wedrownik.net 

45

W tym przypadku a i b s

ą

 do siebie odwrotne. Niestety nie s

ą

 to elementy odwrotne tak, jak

si

ę

 do tego przyzwyczaili

ś

my w szkole. 

Do tego nie ka

ż

dy element w systemie mod n ma odwrotno

ść

. Dziwne, ale prawdziwe. Aby

móc wyznaczy

ć

 taki element musi by

ć

 spełniony warunek NWD(a, n) = 1.

Jak mo

ż

na je wyznaczy

ć

? Najprostsz

ą

 metod

ą

 jest rozszerzony algorytm Euklidesa. Jego

działanie najlepiej wytłumaczy

ć

 na przykładzie.

Spróbujmy znale

źć

 odwrotn

ą

 liczb

ę

 dla 18 w systemie mod 41

Szukamy zapisu liczby 41 przy pomocy 18 i ewentualnej reszty:

41 = 2·18 + 5

Teraz 18 przenosimy na lew

ą

 stron

ę

 i szukamy jej zapisu przy pomocy 5 i reszty.

18 = 3·5 + 3

Krok ten powtarzamy tak długo, a

ż

 reszt

ą

 b

ę

dzie liczba 1.

5 = 3 + 2
3 = 2 + 1

W   ten   sposób   zako

ń

czyli

ś

my   pierwsz

ą

  cz

ęść

  szukania   odwrotno

ś

ci.   Druga   polega   na

przedstawieniu   1   za   pomoc

ą

  18   i   41.   Brzmi   troch

ę

  absurdalnie,   ale   jest   to   mo

ż

liwe   i

poprawne matematycznie. Zaczniemy od naszego ostatniego równania – zmieniamy je tak,
aby tylko liczba 1 była po lewej stronie

1 = 3 – 2

Skorzystamy   teraz   z   informacji,   jakie   s

ą

  w   drugim   równaniu   –   po   prostu   w   miejsce   2

wstawimy jej warto

ść

 z drugiego równania.

                                                                 1 = 3 – (5 – 3)

1 = 2·3 – 5 

Wykorzystuj

ą

c równania z pierwszej cz

ęś

ci zamieniamy stopniowo liczby, a

ż

 dojdziemy do

postaci z 18 i 41.

                                                                 1 = 2·(18 – 3·5) – 5
                                                                 1 = 2·18 – 7·5
                                                                 1 = 2·18 – 7·(41 – 2·18)
                                                                 1 = 16·18 – 7·41

Liczb

ą

  odwrotn

ą

  do   18   jest   ta   z,   któr

ą

  jest   ona   wymna

ż

ana   w   ostatniej   linii   naszego

równania. A wi

ę

c jest to liczba 16.

Aby sprawdzi

ć

 nasz rachunek wystarczy wyliczy

ć

, 

ż

e 

16·18 = 288 mod 41 = 1

I to by było na tyle z matematycznych wywodów:-)  

Ż

ycz

ę

 miłej zabawy i całkiem nowych

wra

ż

e

ń

!

www.wedrownik.net 

46