
3. Metoda eliminacji
Dany jest uk
ùad m
r
ównañ liniowych o n
niewiadomych
n
x
x
x
,
,
,
2
1
m
n
mn
m
m
n
n
n
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11
(*)
gdzie
N
n
,
m
a
j
ij
b
,
a
s
¹ liczbami
.
Oznaczmy:
n
m
mn
m
m
n
n
x
x
x
X
b
b
b
B
a
a
a
a
a
a
a
a
a
A
2
1
2
1
2
1
2
22
21
1
12
11
,
,
Wtedy uk
ùad
r
ównañ liniowych
(*) mo
¿na zapisaã
w postaci macierzowej
AX=B
.
Je
¿eli na wierszach
macierzy rozszerzonej
B
A
U
b
êdziemy wykonywaã
podane ni
¿ej
operacje elementarne
, to otrzymamy macierz rozszerzon
¹ ukùadu
r
ównañ równowa¿nego ukùadowi (*)
.
Wyró¿niamy nastêpuj¹ce
operacje elementarne
1.
Mno
¿enie dowolnego
wiersza macierzy rozszerzonej przez liczb
ê ró¿n¹ od zera
.
2.
Dodawanie do dowolnego wiersza macierzy rozszerzonej innego wiersza tej
macierzy pomno
¿onego przez liczbê.
3.
Przestawienie dw
óch dowolnych
wierszy macierzy rozszerzonej.
UWAGA
.
Mo
¿na przestawiaã kolumny ale tylko macierzy wspóùczynników przy niewiadomych
( Patrz Przyk
ùad 12).
operacje
elementarne
..........................................................................................
PRZYK£AD 1
Dla uk
ùad
u r
ównañ
3
6
3
2
1
3
5
7
2
4
3
z
y
x
z
y
x
z
y
x
napisa
ã ukùad równañ równowa¿ny.
id3117125 pdfMachine by Broadgun Software - a great PDF writer! - a great PDF creator! - http://www.pdfmachine.com http://www.broadgun.com
Macierz rozszerzona
U
tego uk
ùadu ma postaã:
3
1
7
|
|
|
6
3
2
3
1
5
2
4
3
U
Do drugiego wiersza tej macierzy dodajmy trzeci wiersz pomno
¿ony p
rzez 4.
Otrzymujemy now
¹ macierz
3
)
3
(
4
1
7
|
|
|
6
3
2
)
6
(
4
3
3
4
1
2
4
5
2
4
3
=
3
11
7
|
|
|
6
3
2
21
11
13
2
4
3
Uk
ùad równañ odpowiadaj¹cy tej nowej macierzy rozszerzonej ma postaã:
3
6
3
2
11
21
11
13
7
2
4
3
z
y
x
z
y
x
z
y
x
i jest on r
ównowa¿ny ukùadowi wyjœciowemu
.
..........................................................................................
Wr
óãmy do ukùadu równañ liniowych (*), zapisanego w postaci macierzowej
AX
=
B
.
Rozwi
¹zywanie takiego ukùadu równañ metod¹ operacji elementarnych polega na
przekszta
ùceniu
macierzy
rozszerzonej
B
A
U
do postaci
D
C
E
,
gdzie
C
jest tzw.
macierz¹ bazow¹
)
(
)
(
)
(
)
(
0
0
k
n
k
m
k
k
m
k
n
k
k
F
I
C
Na bloki macierzy
C
sk
ùadaj¹ siê nastêpuj¹ce macierze:
k
I –
macierz jednostkowa
)
(
k
n
k
F
–
dowolna macierz
k
k
m
)
(
0
,
)
(
)
(
0
k
n
k
m
–
macierze zerowe
przy czym w postaci bazowej tylko macierz jednostkowa
k
I
musi si
ê pojawiã
natomiast pozosta
ùe macierze: zerowe oraz F
nie musz
¹ wystêpowaã.
Z postaci
D
C
E
, gdzie
C
jest macierz
¹ bazow¹ mo¿na natychmiast odczytaã
rozwi
¹zanie ukùadu równañ lub stwierdziã, ¿e ukùad jest sprzeczny.
Operacje elementarne nale
¿y tak dobieraã aby utworzyã zera w miejscu wybranych
element
ów macierzy. W przykùadach zaznaczo
no pogrubion
¹ czcionk¹ utworzone
zera dzi
êki podanej operacji elementarnej.
W przyk
ùadowych zadaniach kolejnoœã tworzenia zer bêdzie miaùa taki sam
przebieg
jak na poni
¿szym schemacie. Pierwsz¹ z zapisanych operacji
1
11
21
2
)
(
w
a
a
w
w tym
schemacie nale
¿y rozumieã nastêpuj¹co: do drugiego wiersza dodajemy wiersz
macierz bazowa
pierwszy pomno
¿ony przez
)
(
11
21
a
a
.
Metoda rozwi
¹zywania ukùadu równañ oparta na pini¿szym schemacie nosi nazwê
metody Gaussa – Jordana
.
Schemat.
4
45
44
43
42
41
3
35
34
33
32
31
2
25
24
23
22
21
1
15
14
13
12
11
b
a
a
a
a
a
b
a
a
a
a
a
b
a
a
a
a
a
b
a
a
a
a
a
1
11
21
2
)
(
w
a
a
w
4
45
44
43
42
41
3
35
34
33
32
31
26
25
24
23
22
1
15
14
13
12
11
b
a
a
a
a
a
b
a
a
a
a
a
b
b
b
b
b
b
a
a
a
a
a
0
1
11
31
3
)
(
w
a
a
w
4
45
44
43
42
41
36
35
34
33
32
26
25
24
23
22
1
15
14
13
12
11
0
b
a
a
a
a
a
b
b
b
b
b
b
b
b
b
b
b
a
a
a
a
a
0
1
11
41
4
)
(
w
a
a
w
46
45
44
43
42
36
35
34
33
32
26
25
24
23
22
1
15
14
13
12
11
0
0
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
a
a
a
a
a
0
2
22
12
1
)
(
w
b
a
w
46
45
44
43
42
36
35
34
33
32
26
25
24
23
22
16
15
14
13
11
0
0
0
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
c
c
c
c
a
0
2
22
32
3
)
(
w
b
b
w
46
45
44
43
42
36
35
34
33
26
25
24
23
22
16
15
14
13
11
0
0
0
0
b
b
b
b
b
c
c
c
c
b
b
b
b
b
c
c
c
c
a
0
2
22
42
4
)
(
w
b
b
w
46
45
44
43
36
35
34
33
26
25
24
23
22
16
15
14
13
11
0
0
0
0
0
c
c
c
c
c
c
c
c
b
b
b
b
b
c
c
c
c
c
0
3
33
13
1
)
(
w
c
c
w
46
45
44
43
36
35
34
33
26
25
24
23
22
16
15
14
11
0
0
0
0
0
0
c
c
c
c
c
c
c
c
b
b
b
b
b
d
d
d
c
0
3
33
23
2
)
(
w
c
b
w
46
45
44
43
36
35
34
33
26
25
24
22
16
15
14
11
0
0
0
0
0
0
0
c
c
c
c
c
c
c
c
d
d
d
b
d
d
d
c
0
3
33
43
4
)
(
w
c
c
w
46
45
44
36
35
34
33
26
25
24
22
16
15
14
11
0
0
0
0
0
0
0
0
d
d
d
c
c
c
c
d
d
d
b
d
d
d
c
0
4
44
14
1
)
(
w
d
d
w
46
45
44
36
35
34
33
26
25
24
22
16
15
11
0
0
0
0
0
0
0
0
0
d
d
d
c
c
c
c
d
d
d
b
e
e
c
0
4
44
24
2
)
(
w
d
d
w
46
45
44
36
35
34
33
26
25
22
16
15
11
0
0
0
0
0
0
0
0
0
0
d
d
d
c
c
c
c
e
e
b
e
e
c
0
4
44
34
3
)
(
w
d
c
w
46
45
44
36
35
33
26
25
22
16
15
11
0
0
0
0
0
0
0
0
0
0
0
d
d
d
e
e
c
e
e
b
e
e
c
0
1
11
1
w
c
,
2
22
1
w
b
,
3
33
1
w
c
,
4
33
1
w
d
46
45
36
35
26
25
16
15
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
f
f
f
f
f
f
f
f
metoda Gaussa
–
Jordana
W praktyce cz
êsto przeksztaùcamy macierz U
do postaci
*
E
podobnej do
E
gdzie
zamiast macierzy jednostkowej
k
I
jest macierz tr
ójk¹tna
k
ale tak
¹
, w kt
ór
ej
wszystkie elementy na gùównej przek¹tnej s¹ ró¿ne od zera
.
)
(
)
(
)
(
)
(
*
*
0
0
k
n
k
m
k
k
m
k
n
k
k
F
E
*
D
Macierz
)
(
*
k
n
k
F
jest to dowolna macierz.
Po uzyskaniu macierzy
*
E
nie mo
¿na odczytaã r
ozwi
¹zania ukùadu. Mo¿na tylko
stwierdzi
ã czy ukùad jest rozwi¹zalny czy sprzeczny. Dla uzyskania rozwi¹zania
trzeba jeszcze wykona
ã kilka przeksztaùceñ wykorzystuj¹c metodê podstawiania.
Spos
ób uzyskania macierzy trójk¹tnej dolnej zaprezentowany jest na p
oni
¿szym
schemacie. Metoda rozwi
¹zywania ukùadu równañ oparta na tym schemacie to
metoda Gaussa.
Schemat.
4
45
44
43
42
41
3
35
34
33
32
31
2
25
24
23
22
21
1
15
14
13
12
11
b
a
a
a
a
a
b
a
a
a
a
a
b
a
a
a
a
a
b
a
a
a
a
a
1
11
21
2
)
(
w
a
a
w
4
45
44
43
42
41
3
35
34
33
32
31
26
25
24
23
22
1
15
14
13
12
11
b
a
a
a
a
a
b
a
a
a
a
a
b
b
b
b
b
b
a
a
a
a
a
0
1
11
31
3
)
(
w
a
a
w
4
45
44
43
42
41
36
35
34
33
32
26
25
24
23
22
1
15
14
13
12
11
0
b
a
a
a
a
a
b
b
b
b
b
b
b
b
b
b
b
a
a
a
a
a
0
1
11
41
4
)
(
w
a
a
w
46
45
44
43
42
36
35
34
33
32
26
25
24
23
22
1
15
14
13
22
11
0
0
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
a
a
a
a
a
0
2
22
32
3
)
(
w
b
b
w
46
45
44
43
42
36
35
34
33
26
25
24
23
22
1
15
14
13
12
11
0
0
0
b
b
b
b
b
c
c
c
c
b
b
b
b
b
b
a
a
a
a
a
0
2
22
42
4
)
(
w
b
b
w
46
45
44
43
36
35
34
33
26
25
24
23
22
1
15
14
13
12
11
0
0
0
0
c
c
c
c
c
c
c
c
b
b
b
b
b
b
a
a
a
a
a
0
3
33
43
4
)
(
w
c
c
w
46
45
44
36
35
34
33
26
25
24
23
22
1
15
14
13
12
11
0
0
0
0
0
d
d
d
c
c
c
c
b
b
b
b
b
b
a
a
a
a
a
0
metoda Gaussa
..........................................................................................
PRZYK£AD 2
Rozwi
¹zaã ukùad równañ
2
3
2
0
2
3
3
2
2
3
t
z
y
x
t
z
y
x
t
z
y
x
.
Rozwi
¹zanie
Macierz rozszerzona
U
tego uk
ùadu ma postaã
2
0
2
3
2
1
1
2
1
3
3
2
3
1
1
U
.
W pierwszym przyk
ùadzie na ka¿dym etapie rozwi¹zywania przeprowadzimy tylko
jedn
¹
operacjê
elementarn¹. W
celu
wye
liminowania wsp
óùczynnika
przy
niewiadomej x znajduj
¹cego siê w drugim wierszu macierzy U
do drugiego wiersza
tej macierzy dodamy wiersz pierwszy pomno
¿ony przez 2 (zapis symboliczny tej
operacji:
1
2
2 w
w
).

2
2
2
0
1
3
1
2
2
1
1
2
1
)
3
(
2
3
1
2
3
3
1
1
1
2
2
=
2
4
2
3
0
1
1
2
1
3
1
3
1
1
0
Wsp
óùczynnik przy niewiadomej x
znajduj
¹cy siê w trzecim wierszu powstaùej
macierzy zostanie wyeliminowany gdy do trzeciego wiersza tej macierzy dodamy
wiersz pierwszy pomno
¿ony przez –
1 (symbolicznie:
1
3
)
1
(
w
w
).
2
)
1
(
2
4
2
1
)
1
(
3
0
1
)
3
(
)
1
(
1
1
)
1
(
2
3
1
0
3
1
1
1
1)
(
1
=
=
0
4
2
2
0
1
4
1
3
1
0
3
1
1
0
Wsp
óùczynnik przy niewiadomej y w pierwszym wierszu wyeliminujemy gdy do
pierwszego wiersza dodamy drugi (symbolicznie:
2
1
w
w
).
0
4
4
2
2
0
1
4
1
0
3
1
0
)
3
(
3
0
1
1)
(
1
=
0
4
6
2
0
1
4
1
0
3
1
0
6
1
0
Eliminujemy teraz wsp
óùczyn
nik przy niewiadomej y w trzecim wierszu.
W tym celu do trzeciego wiersza uzyskanej macierzy dodamy wiersz drugi
(symbolicznie:
2
3
w
w
).
4
0
4
6
2
0
1
)
3
(
4
0
0
3
1
0
6
0
1
1)
(
1
=
4
4
6
2
0
1
1
0
3
1
0
6
0
1
0
Wsp
óùczynnik przy niewiadomej z w pierwszym równaniu wy
eliminujemy gdy do
pierwszego
r
ównania
dodamy
wiersz
trzeci
pomno¿ony
przez
6
(symbolicznie:
3
1
6w
w
).
4
4
4
6
6
2
0
2
6
1
1
0
0
3
1
0
0
6
0
0
6
1
1
6
6
=
4
4
30
2
0
13
1
0
0
3
1
0
0
1
0
Wyeliminujemy wsp
óùczynnik przy niewiadomej z w drugim wierszu.
Do
drugiego
wiersza
dodamy
wiersz
trzeci
pomno
¿ony
przez
3
(symbolicznie:
3
2
3w
w
).
4
4
3
4
30
2
2
3
0
13
1
0
0
0
3
1
0
3
0
0
0
1
1
3
3
=
4
16
30
2
6
13
1
0
0
1
0
0
0
1
0
Wiersz drugi pomno
¿ymy przez –
1(symbolicznie:
1
)
1
(
w
)
4
)
1
(
16
30
2
)
1
(
6
13
1
0
0
0
1)
(
1
)
1
(
0
0
0
1
=
4
16
30
2
6
13
1
0
0
0
1
0
0
0
1
W otrzymanej macierzy nie wyst
êpuj¹ macierze zerowe. Z wyodrêbnionymi blokami
ma ona posta
ã:
4
16
30
2
6
13
1
0
0
0
1
0
0
0
1
Uk
ùad równañ odpowiadaj¹cy uzyskanej macierzy jest nastêpuj¹cy:
4
2
1
0
0
16
6
0
1
0
30
13
0
0
1
t
z
y
x
t
z
y
x
t
z
y
x
Uk
ùad ten jest
r
ównowa¿ny ukùadowi wyjœciowemu.
Otrzymujemy rozwi
¹zanie ukùadu równañ w postaci
4
2
16
6
30
13
t
z
t
y
t
x
,
R
t
.
Widzimy,
¿e ukùad równañ ma nieskoñczenie wiele rozwi¹zañ zale¿nych od jednego
parametru (w otrzymanym rozwi
¹zaniu parametrem jest t
). Rozwi
¹zanie to mo¿na
by
ùo odczytaã bezp
o
œrednio z ostatniej macierzy.
Kolumna wsp
óùczynników przy
niewiadomej
t
znalaz
ùa siê poza macierz¹ jednostkow¹. Oznacza to, ¿e t
w
rozwi
¹zaniu jest parametrem i musi byã przeniesione na praw¹ stronê równañ
uk
ùadu.
Macierz
jednostkowa
Macierz
F
Macierz
D

..........................................................................................
PRZYK£AD 3
Rozwi
¹zaã ukùad równañ
1
5
5
4
3
5
3
1
2
t
z
y
x
t
z
y
x
t
z
y
x
.
Rozwi
¹zanie
Macierz rozszerzona U tego uk
ùadu ma postaã:
1
3
1
5
1
1
5
4
1
1
5
3
1
2
1
U
.
W dalszych obliczeniach opis operacji elementarnych podany b
ê
dzie symbolicznie.
Np. pierwsz
¹ operacjê
1
2
)
3
(
w
w
nale
¿y rozumieã nastêpuj¹co: do wiersza
drugiego dodajemy wiersz pierwszy pomno
¿ony przez –
3, druga operacja
1
3
w
w
oznacza: do wiersza trzeciego dodajemy wiersz pierwszy.
Wykonujemy kolejno podane operacje:
1
2
)
3
(
w
w
1
3
w
w
1
1
1
)
3
(
3
1
1
5
1
)
3
(
1
1
)
1
(
5
2
4
)
1
(
)
3
(
1
2
)
3
(
5
1
2
1
1
1
1
3)
(
3
=
=
0
0
1
4
2
1
4
2
2
1
1
2
1
0
0
2
1
2 w
w
2
3
)
2
(
w
w
0
0
1
)
2
(
)
2
(
4
2
)
2
(
2
1
2
)
2
(
4
0
2
1
0
2
2
1
1
1)
(
2)
(
2
1)
(
2
2
=
0
0
1
0
2
3
0
0
2
1
0
3
1
0
0
Wiersz drugi pomno
¿ymy przez
–
1 co zapisujemy w skr
ócie:
2
)
1
(
w
0
0
1
0
)
2
(
1
3
0
0
0
2
1
)
1
(
1
0
3
0
1
=
0
0
1
0
2
3
0
0
0
2
1
0
3
0
1
Otrzymana macierz z podzia
ùem ma bloki ma postaã:

0
0
1
0
0
2
2
3
3
0
0
1
0
0
1
Wsp
óùczynniki przy niewiadomych z oraz t nie znalazùy siê w macierzy jedno
stkowej,
zatem
z
oraz
t
b
êd¹ parametrami wystêpuj¹cymi
w rozwi
¹zaniu.
Z tak przekszta
ùconej macierzy rozszerzonej podajemy rozwi¹zanie ukùadu równañ:
t
z
y
t
z
x
2
2
1
3
3
,
R
z
,
R
t
gdzie
z, t
s
¹ to parametry.
Rozwi
¹zanie tego ukùadu równ
a
ñ mo¿na podaã tak¿e w postaci
v
t
u
z
v
u
y
v
u
x
2
2
1
3
3
.
..........................................................................................
PRZYK£AD 4
Rozwi
¹zaã ukùad równañ
13
16
3
4
5
3
7
2
5
2
3
2
t
z
y
x
t
y
x
t
z
y
x
.
Rozwi
¹zanie
Macierz rozszerzona
U
tego uk
ùadu ma
posta
ã
13
3
5
16
7
2
3
4
5
0
1
2
3
2
1
U
.
Wykonujemy kolejno operacje:
1
2
2 w
w
1
3
5 w
w
5
5
13
5
2
3
5
)
2
(
5
16
)
2
(
2
7
2
3
5
3
)
2
(
5
4
3
2
0
)
2
(
2
1
3
2
1
1
5
5
1
2
2
=
Macierz
jednostkowa
Macierze
zerowe
Macierz F
Macierz D

=
12
7
5
6
3
2
12
6
6
3
3
2
1
0
0
2
1
3
2
w
w
2
3
2 w
w
7
)
2
(
12
7
7
3
2
5
3
)
2
(
6
3
3
3
2
2
6
)
2
(
12
0
3
0
6
3
2
3
1
3)
(
2)
(
6
3)
(
3
2
2
6
=
=
2
7
3
1
0
3
4
0
0
3
0
1
1
0
0
6
Nie ma potrzeby wykonywania kolejnych operacji prowadz
¹cych do macierzy
jednostkowej bo w trzecim wierszu widoczna jest sprzeczno
œã w ukùadzie równañ.
Zapiszmy uk
ùad równañ wynikaj¹cy z postaci otrzymanej macierzy:
2
0
7
3
6
3
3
1
4
t
z
y
t
z
x
Uk
ùad równañ
jest sprzeczny.
..........................................................................................
PRZYK£AD 5
Rozwi
¹zaã ukùad równañ
9
4
2
3
13
2
4
5
3
2
10
3
z
y
x
z
y
x
z
y
x
z
y
x
.
Rozwi
¹zanie
Macierz rozszerzona
U
tego uk
ùadu ma postaã
9
4
2
3
13
2
4
1
5
3
1
2
10
1
3
1
U
.
Sprzecznoϋ

Wykonujemy kolejno operacje elementarne:
1
2
)
2
(
w
w
1
3
w
w
1
4
)
3
(
w
w
Otrzymujemy:
)
10
(
)
3
(
9
1
)
3
(
4
)
3
(
)
3
(
2
1
)
3
(
3
)
10
(
13
1
2
)
3
(
4
1
1
)
10
(
)
2
(
5
1
)
2
(
3
)
3
(
)
2
(
1
1
)
2
(
2
10
1
3
1
=
=
21
7
7
0
3
1
1
0
15
5
5
0
10
1
3
1
2
5
1
w
4
7
1
w
7
1
21
7
1
7
7
1
7
0
3
1
1
0
5
1
15
5
1
5
5
1
5
0
10
1
3
1
=
3
1
1
0
3
1
1
0
3
1
1
0
10
1
3
1
2
1
3 w
w
2
3
w
w
2
4
w
w
3
3
)
1
(
1
0
3
3
)
1
(
1
0
3
1
1
0
3
3
10
)
1
(
3
1
1
1
1
1
1
1
3
3
=
0
0
0
0
0
0
3
1
1
0
1
2
1
0
0
0
Uzyskana macierz z podzia
ùem na bloki ma postaã:
0
0
3
1
0
0
1
2
0
0
0
0
1
0
0
1
Wsp
óùczynniki przy niewiadomej z
nie znalaz
ùy siê w macierzy jednostkowej, zatem
Macierz
jednostkowa
Macierze
zerowe
Macierz
F
Macierz
D
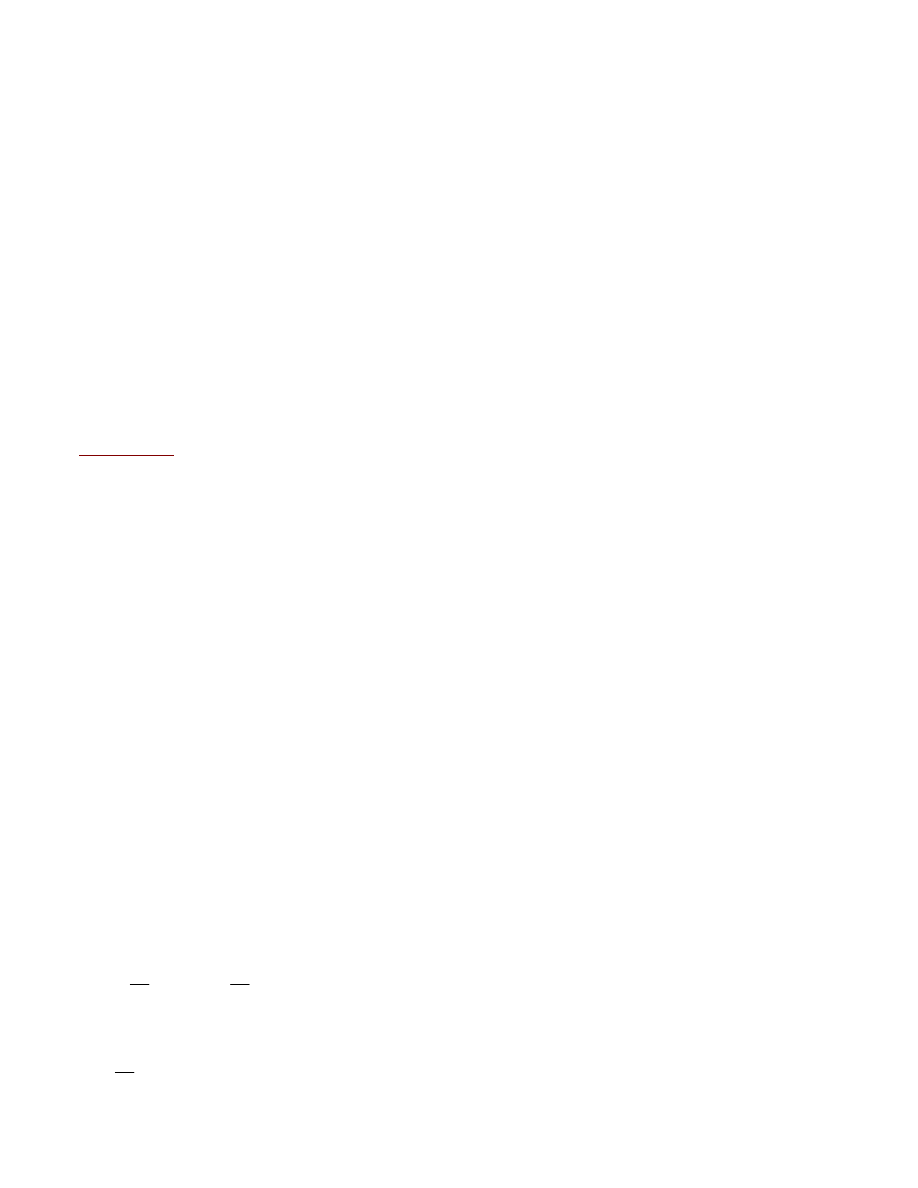
z b
êdzie parametrem wystêpuj¹cym w rozwi¹zaniu.
Z postaci otrzymanej macierzy podajemy rozwi
¹zanie:
3
1
2
z
y
z
x
gdzie
z
to dowolna liczba rzeczywista.
Ostatecznie
3
1
2
z
y
z
x
,
R
z
.
..........................................................................................
PRZYK£AD 6
Rozwi
¹zaã ukùad równañ
0
3
5
11
10
8
5
3
2
6
8
4
z
y
x
z
y
x
z
y
x
z
y
x
.
Rozwi
¹zanie
Macierz rozszerzona
U
tego uk
ùadu m
a posta
ã
0
3
1
5
11
1
10
8
5
3
2
6
8
1
4
1
U
.
Wykonujemy kolejno operacje elementarne:
1
2
6 w
w
1
3
1
3
8
)
8
(
w
w
w
w
1
4
1
4
5
)
5
(
w
w
w
w
Otrzymujemy:
)
8
(
5
0
1
5
3
)
4
(
5
1
)
8
(
8
11
1
8
1
)
4
(
8
10
)
8
(
6
5
1
6
3
)
4
(
6
2
8
1
4
1
1
5
5
1
8
8
1
6
6
=
=
40
2
19
53
9
22
53
9
22
8
1
4
1
0
0
0
2
1
2
1
22
4
)
22
4
(
w
w
w
w
2
3
w
w
2
4
22
19
w
w

)
53
(
22
19
40
9
22
19
2
0
)
53
(
53
9
9
0
53
9
22
0
)
53
(
22
4
8
9
22
4
1
1
22)
(
22
19
19
22)
(
22
22)
(
22
4
4
=
=
22
127
22
127
0
0
0
0
53
9
22
0
22
36
22
14
1
0
0
0
Przestawiamy wiersz trzeci z wierszem czwartym (
4
3
w
w
)
0
0
0
0
22
127
22
127
0
0
53
9
22
0
22
36
22
14
0
1
3
127
22
w
0
0
0
0
1
1
0
0
53
9
22
0
22
36
22
14
0
1
3
1
22
14
w
w
3
2
)
9
(
w
w
0
0
0
0
1
1
0
0
)
1
(
)
9
(
53
1
)
9
(
9
22
0
)
1
(
22
14
22
36
1
22
14
22
14
0
1
=
=
0
0
0
0
1
1
0
0
44
0
22
0
1
0
0
1

2
22
1
w
0
0
0
0
1
1
0
0
2
0
1
0
1
0
0
1
Uzyskana macierz z podzia
ùem na bloki ma postaã:
Z postaci otrzymanej macierzy podajemy rozwi
¹zanie
1
2
1
z
y
x
.
..........................................................................................
PRZYK£AD 7
Rozwi
¹zaã ukùad ró
wna
ñ
1
2
3
11
3
4
13
3
2
z
y
x
z
y
x
z
y
x
.
Rozwi
¹zanie
Macierz rozszerzona
U
tego uk
ùadu ma postaã
1
11
13
1
2
3
3
1
4
3
2
1
U
.
Wykonujemy operacje:
1
2
)
4
(
w
w
1
3
3 w
w
)
13
(
3
1
)
13
(
4
11
13
)
3
(
3
1
2
3
2
1
3
3
)
3
(
4
3
2
4
1
1
4
4
3
2
1
=
0
1
2
1
0
0
0
1
0
0
0
1
0
0
0
1
Macierz
jednostkowa
Macierz zerowa
Macierz D
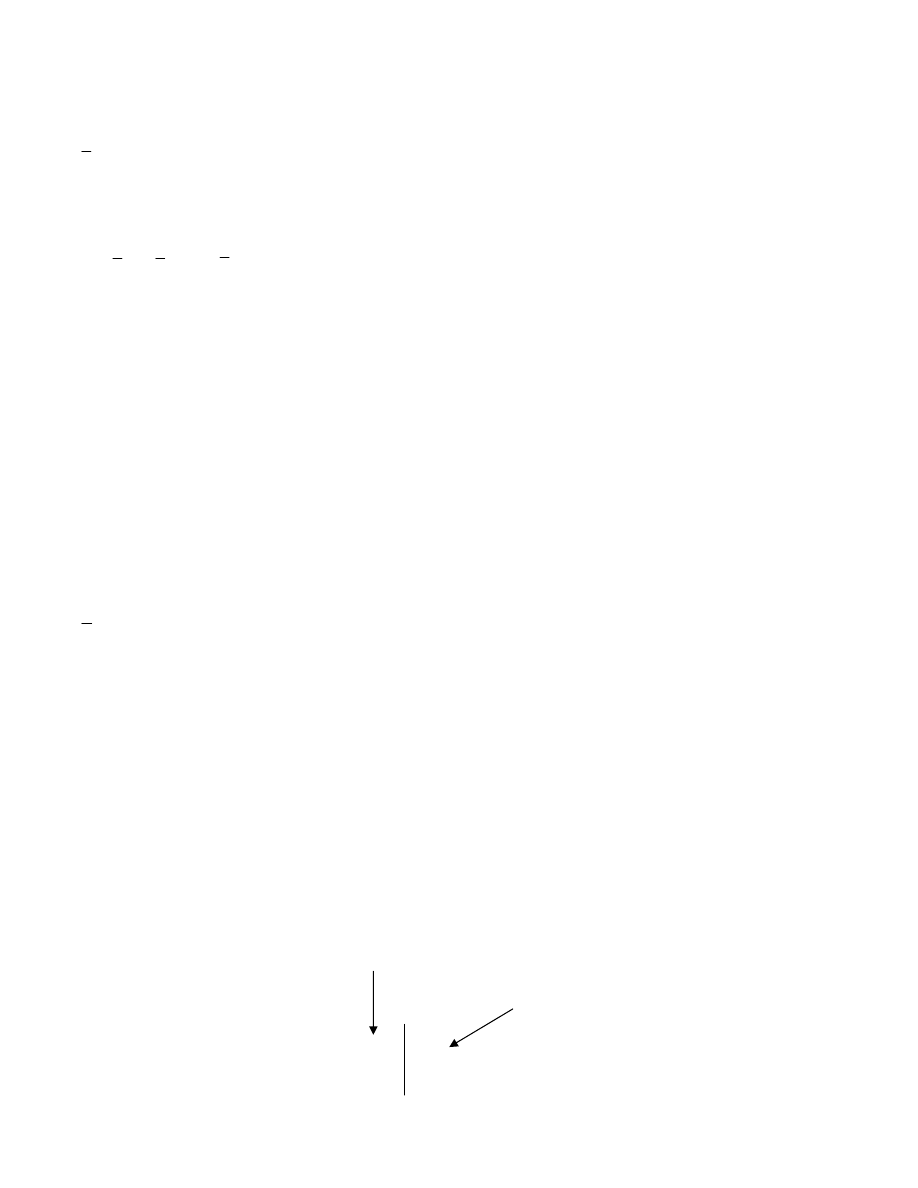
=
40
41
13
8
8
0
9
7
0
3
2
1
3
8
1
w
)
40
(
8
1
41
13
)
8
(
8
1
8
8
1
0
9
7
0
3
2
1
5
41
13
1
1
0
9
7
0
3
2
1
3
2
w
w
41
5
13
9
7
0
1
1
0
3
2
1
2
1
2
1
2
)
2
(
w
w
w
w
1
3
7 w
w
)
5
(
7
41
5
)
5
(
2
13
)
1
(
7
9
1
7
7
0
1
1
0
)
1
(
2
3
1
2
2
1
=
6
5
3
2
0
0
1
1
0
1
0
1
3
2
1
w
3
5
3
1
0
0
1
1
0
1
0
1
3
1
w
w
3
2
w
w
3
3
5
3
3
1
0
0
1
1
1
0
1
1
0
1
=
3
2
0
1
0
0
0
1
0
0
0
1
Otrzymana macierz z podzia
ùem na bloki ma postaã:
3
2
0
1
0
0
0
1
0
0
0
1
Macierz
jednostkowa
Macierz D

Z postaci otrzymanej macierzy podajemy rozwi¹zanie ukùadu równañ
3
2
0
z
y
x
.
..........................................................................................
PRZYK£AD 8
Rozwi
¹zaã ukùad równañ
3
2
2
3
4
5
7
1
2
3
z
y
x
z
y
x
z
y
x
.
Rozwi
¹zanie
Macierz rozszerzona
U
tego uk
ùadu ma postaã
3
3
1
1
2
2
4
5
7
2
3
1
U
.
Wykonujemy operacje:
1
2
1
2
7
)
7
(
w
w
w
w
1
3
1
3
2
)
2
(
w
w
w
w
1
2
3
1
7
3
1
2
2
1
)
3
(
2
2
2
7
4
)
3
(
7
5
2
3
1
1
2
2
1
7
7
=
1
4
1
5
8
10
16
2
3
1
0
0
Zauwa
¿my, ¿e gdy wykonamy operacjê
2
3
2
1
w
w
oka
¿e siê, ¿e rozwi¹zywany
uk
ùad równañ jest sprzeczny i nie wykonujemy ju¿ wtedy dalszych operacji.
)
4
(
2
1
1
4
1
)
10
(
2
1
5
0
10
16
0
2
3
1
16
2
1
8
=
3
4
1
0
0
10
16
0
2
3
1
0
Zapiszmy uk
ùad równañ wynikaj¹cy z postaci uzyskanej macierzy
3
0
4
10
16
1
2
3
z
y
z
y
x
St
¹d u
k
ùad równañ jest sprzeczny
.
..........................................................................................
Sprzecznoϋ

PRZYK£AD 9
Rozwi
¹zaã ukùad równañ
2
2
3
5
8
4
1
6
3
2
z
y
x
z
y
x
z
y
x
.
Rozwi
¹zanie
Przestawmy r
ównanie pierwsze z drugim
, tzn.
2
2
3
1
6
3
2
5
8
4
z
y
x
z
y
x
z
y
x
.
Macierz rozszerzona
U
tego uk
ùadu ma postaã
2
1
5
2
1
3
6
3
2
8
4
1
U
.
Wykonujemy operacje:
1
2
2 w
w
1
3
)
3
(
w
w
5
)
3
(
2
5
2
1
5
8
)
3
(
2
4
)
3
(
1
8
2
6
4
2
3
8
4
1
1
3)
(
3
1
2
2
=
13
11
5
26
13
22
11
8
4
1
0
0
2
11
1
w
3
13
1
w
1
1
5
2
1
0
2
1
0
8
4
1
2
3
w
w
0
1
5
0
0
2
1
0
8
4
1
0

W uzyskanej macierzy mo
¿na wyró¿niã nastêpuj¹ce bloki:
0
1
5
0
2
8
0
0
1
0
4
1
W trzeciej kolumnie tej macierzy znajduj
¹ siê wspóùczynniki przy niewiadomej z
. Jak
wida
ã nie znalazùy siê one w macierzy trójk¹tnej dlatego z bêdzie przeniesione na
praw
¹ stronê równañ, bêdzie wiêc parametrem wystêpuj¹cym w rozwi¹za
niu.
Uk
ùad równañ odpowiadaj¹cy tej macierzy ma postaã
1
2
5
8
4
z
y
z
y
x
.
Po prostych przekszta
ùceniach otrzymujemy
1
2
5
8
)
1
2
(
4
z
y
z
z
x
sk
¹d
1
2
1
z
y
x
,
R
z
..........................................................................................
PRZYK£AD 10
Rozwi
¹zaã ukùad równañ
0
4
2
9
2
3
4
5
3
z
y
x
z
y
x
z
y
x
.
Rozwi
¹zanie
Macierz rozszerzona
U
tego uk
ùadu ma postaã
0
9
4
4
1
2
1
2
3
5
3
1
U
.
Wykonujemy operacje:
1
2
)
3
(
w
w
1
3
)
2
(
w
w
)
4
(
)
2
(
0
)
4
(
)
3
(
9
4
)
5
(
)
2
(
4
3
)
2
(
1
1
)
2
(
2
)
5
(
)
3
(
1
3
)
3
(
2
1
)
3
(
3
5
3
1
=
8
21
4
14
7
0
14
7
0
5
3
1
Macierz
trójk¹tna
Macierze
zerowe
Macierz
*
F
Macierz
*
D
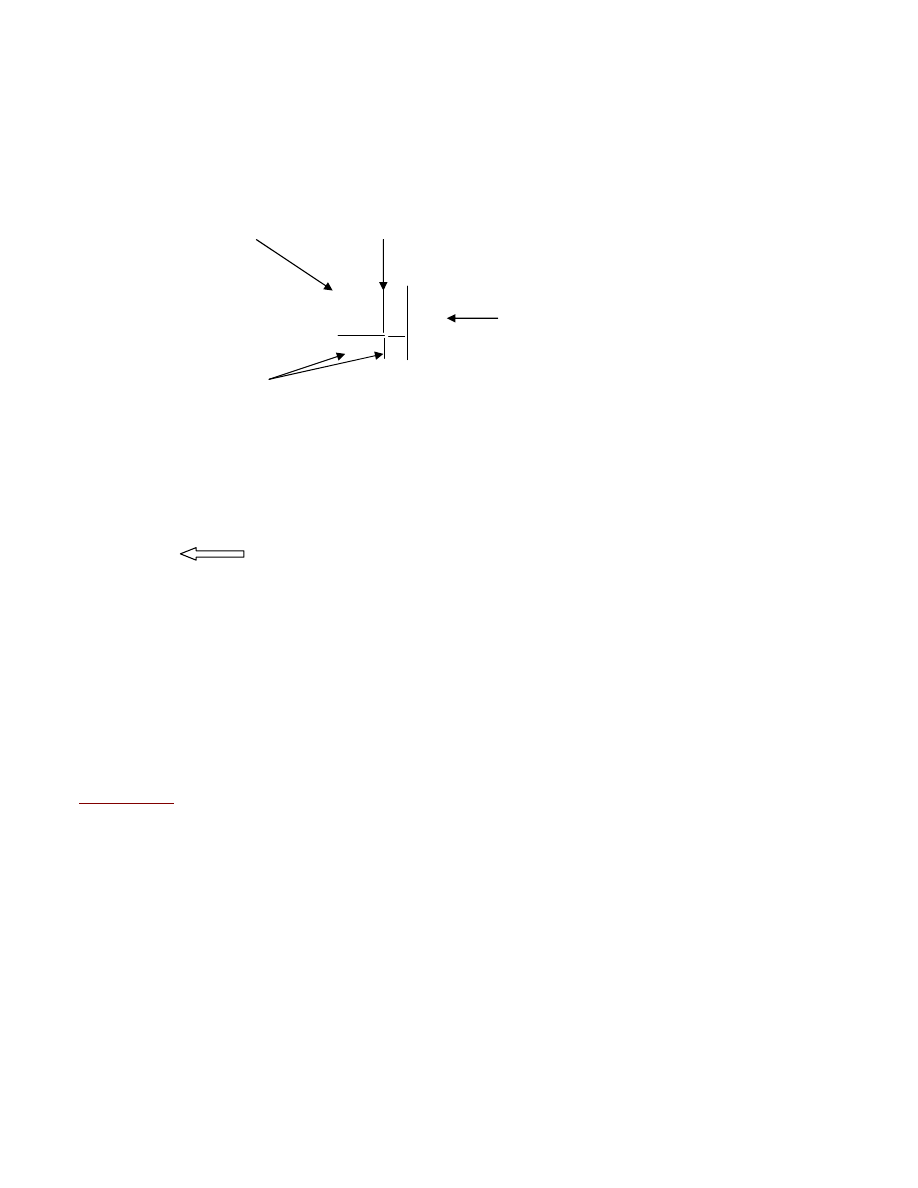
2
3
)
1
(
w
w
21
)
1
(
8
21
4
14
)
1
(
14
)
7
(
)
1
(
7
0
14
7
0
5
3
1
=
13
21
4
0
0
0
14
7
0
5
3
1
Otrzymana macierz z wyodr
êbnionymi blokami ma postaã:
13
21
4
0
14
5
0
0
7
0
3
1
Z postaci tej macierzy wida
ã, ¿e ukùad równañ jest sprzec
zny.
Sprzeczno
œã widaã wyraênie gdy zapiszemy ukùad równañ odpowiadaj¹cy
otrzymanej macierzy:
13
0
21
14
4
4
5
3
z
y
z
y
x
St
¹d u
k
ùad równañ jest sprzeczny
.
..........................................................................................
PRZYK£AD 11
Rozwi
¹zaã ukùad równañ
1
3
3
2
0
2
z
y
x
z
y
x
z
y
x
.
Rozwi
¹zanie
Macierz rozszerzona
U
tego uk
ùadu ma postaã
1
3
0
1
1
3
1
1
2
2
1
1
U
.
Za pomoc
¹ operacji elementarnych przeksztaùcimy macierz U
do postaci
*
E
podobnej do
E
gdzie zamiast macierzy jednostkowej jest macierz tr
ójk¹tna
,
a nast
êpnie dokoñczymy obliczenia metod¹ podstawiania.
Macierz
trójk¹tna
Macierze
zerowe
Macierz
*
F
Macierz
trójk¹tna
Macierz
*
F
Sprzecznoϋ

1
2
)
2
(
w
w
1
3
)
3
(
w
w
0
)
3
(
1
0
)
2
(
3
0
)
2
(
)
3
(
1
1
)
3
(
1
)
2
(
)
2
(
1
1
)
2
(
1
2
1
1
1
3)
(
3
1
2)
(
2
=
1
3
0
5
2
5
1
2
1
1
0
0
2
3
)
2
(
w
w
3
)
2
(
1
3
0
5
)
2
(
5
0
5
1
0
2
1
1
1)
(
2)
(
2
=
5
3
0
5
0
5
1
0
2
1
1
0
W otrzymanej macierzy zamiast macierzy jednostkowej jest macierz tr
ójk¹tna:
5
3
0
5
0
0
5
1
0
2
1
1
Zapiszmy uk
ùad równañ odpowiadaj¹cy tej macierzy
5
5
3
5
0
2
z
z
y
z
y
x
.
Z ostatniego r
ównania wyliczymy z
i podstawimy do pierwszego i drugiego r
ównania:
1
3
1
5
0
1
2
z
y
y
x
Z drugiego r
ównania wyliczymy y
i podstawimy do pierwszego co daje nam
rozwi
¹zanie
1
2
0
z
y
x
.
..........................................................................................
PRZYK£AD 12
Rozwi
¹zaã ukùad równañ
5
3
2
15
6
3
5
2
t
z
y
x
t
z
y
x
t
z
y
x
.
Rozwi
¹zanie
Macierz rozszerzona
U
tego uk
ùadu ma postaã
5
15
5
3
1
1
1
2
1
1
6
3
1
2
1
U
.
Wykonujemy kolejno operacje:
1
2
)
3
(
w
w
,
1
3
w
w
Macierz
trójk¹tna
Macierz
*
D
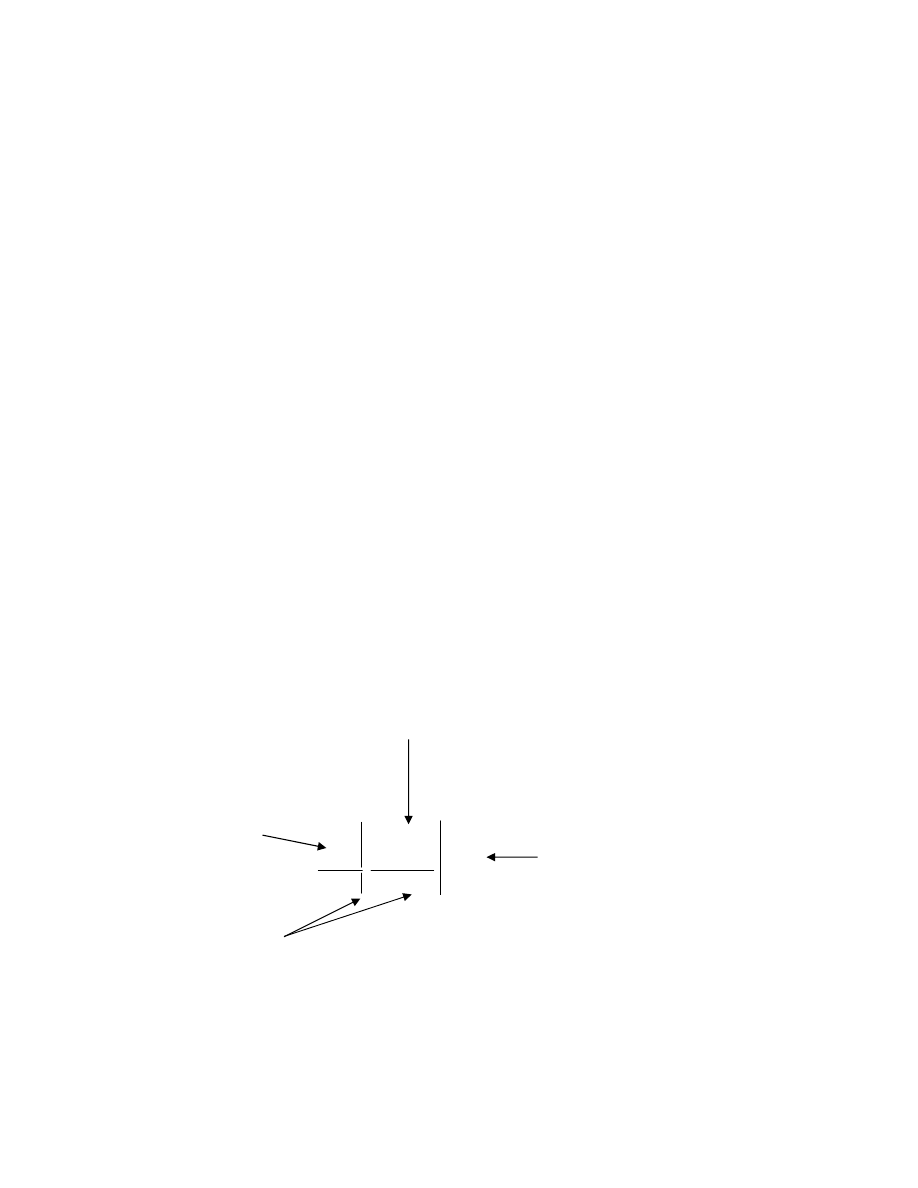
x z y t
)
5
(
)
5
(
5
)
3
(
15
5
1
3
1
)
3
(
1
1
)
1
(
1
)
2
(
2
)
1
(
)
3
(
1
)
2
(
)
3
(
6
1
2
1
1
1
1
3)
(
3
=
=
0
0
5
4
4
1
2
0
2
0
1
2
1
0
0
Zauwa
¿my, ¿e pierwsza, druga i trzecia kolumna tworz¹ wprawdzie macierz
tr
ójk¹tn¹ ale w rozwi¹zywaniu ukùadu równañ metod¹ Gaussa niedopuszczalna jest
macierz tr
ójk¹tna z zerem na gùównej przek¹tnej.
Przestawimy zatem kolumny drug
¹ i tr
zeci
¹ (symbolicznie:
3
2
k
k
)
pami
êtaj¹c o tym, ¿e w kolumnie drugiej s¹ wspóùczynniki przy niewiadomej y
,
a w kolumnie trzeciej wsp
óùczynniki przy niewiadomej z
.
0
0
5
4
4
1
0
2
0
0
2
0
2
1
1
1
3
w
w
0
0
5
)
4
(
4
4
1
0
0
0
2
0
2
1
1
2
2
=
0
0
5
0
4
1
0
0
0
2
0
2
1
1
0
Otrzymana macierz z podzia
ùem
na bloki ma posta
ã:
0
0
5
0
0
4
0
1
2
0
0
2
0
1
1
Wsp
óùczynniki przy niewiadomych y
oraz
t
nie znalaz
ùy siê w macierzy trójk¹tnej,
zatem
y
oraz
t
b
êd¹ parametrami wystêpuj¹cymi w rozwi¹
zaniu.
Mo
¿na oczywiœcie przestawiã kolumny drug¹ i czwart¹, wtedy to y
i
z
b
êd¹
parametrami w rozwi
¹zaniu. Pozostañmy jednak przy ustalonej powy¿ej macierzy
tr
ójk¹tnej.
x z y t
x z y t
x z y t
Macierz
trójk¹tna
Macierze
zerowe
Macierz
*
F
Macierz
*
D

Z przekszta
ùconej macierzy rozszerzonej podajemy ukùad równañ
t
z
t
y
z
x
4
2
5
2
.
Po wyliczeniu
z
w drugim r
ównaniu i podstawieniu do pierwszego otrzymujemy
t
z
t
y
t
x
2
5
2
2
Stad
t
z
t
y
x
2
5
2
R
t
,
R
y
.
..........................................................................................
PRZYK£AD 13
Rozwi
¹zaã ukùad równañ
3
5
4
3
4
10
7
4
2
4
3
2
1
3
2
z
y
x
z
y
x
z
y
x
z
y
x
.
Rozwi
¹zanie
Macierz rozszerzona
U
tego uk
ùadu ma postaã
3
5
4
3
4
10
7
4
2
4
3
2
1
3
2
1
U
.
Wykonujemy kolejno operacje elementarne:
1
2
2 w
w
1
3
1
3
4
)
4
(
w
w
w
w
1
4
3 w
w
Otrzymujemy:
1
3
3
3
3
5
)
2
(
3
4
1
4
4
3
4
10
)
2
(
4
7
1
2
2
3
2
4
)
2
(
2
3
1
3
2
1
1
3
3
1
4
4
1
2
2
=
=
0
4
2
0
2
1
0
2
1
1
3
2
1
0
0
0
2
3
w
w
2
4
2
4
2
)
2
(
w
w
w
w
0
2
2
4
0
0
2
2
0
0
2
1
0
1
3
2
1
1)
(
2
2
1)
(
1
=
0
0
0
0
0
0
0
2
1
0
1
3
2
1
0
0
Uzyskana macierz z podzia
ùem na bloki ma postaã:
0
0
0
1
0
0
2
3
0
0
0
0
1
0
2
1
Wsp
óùczynniki przy niewiadomej z
nie znalaz
ùy siê w macierzy trójk¹tnej, zatem z
b
êdzie parametrem wystêpuj¹cym w rozwi¹zaniu.
Z postaci otrzymanej macierzy podajemy uk
ùad równañ
z
y
z
y
x
2
1
3
2
.
Po wyliczeniu niewiadomej
y
z drugiego r
ównania i wstawi
eniu do pierwszego
otrzymujemy:
z
y
z
z
x
2
1
3
)
2
(
2
Stad
z
y
z
x
2
1
R
z
.
..........................................................................................
PRZYK£AD 14
Rozwi
¹zaã ukùad równañ
4
2
4
3
3
2
4
2
5
2
3
4
6
3
2
t
z
y
x
t
z
y
x
t
z
y
x
t
z
y
x
.
Macierz
trójk¹tna
Macierze
zerowe
Macierz
F
Macierz
D

Rozwi
¹zanie
Macierz rozszerzona
U
tego uk
ùadu ma postaã
4
2
4
1
3
3
1
2
4
2
5
2
3
1
4
6
3
1
2
1
U
.
Wykonujemy kolejno operacje elementarne:
1
2
4 w
w
1
3
1
3
2
)
2
(
w
w
w
w
1
4
1
4
3
)
3
(
w
w
w
w
6
3
4
3
3
2
)
1
(
3
4
2
3
1
6
2
3
3
2
1
)
1
(
2
2
2
2
4
6
4
5
3
4
2
)
1
(
4
3
2
4
1
6
3
1
2
1
1
3
3
1
2
2
1
4
4
=
=
14
7
7
7
15
5
0
0
29
10
1
9
6
3
1
2
1
0
0
0
2
9
1
w
4
7
1
w
2
1
1
1
0
15
5
0
0
0
9
29
9
10
9
1
1
0
6
3
1
2
1
3
4
w
w
9
29
2
9
10
1
9
1
1
0
15
5
0
0
0
9
29
9
10
9
1
1
0
6
3
1
2
1
1
1
=
=
9
11
9
1
9
8
0
15
5
0
0
0
9
29
9
10
9
1
1
0
6
3
1
2
1
0

Przestawmy wiersz trzeci z czwartym
)
(
4
3
w
w
15
5
0
0
0
9
11
9
1
9
8
0
0
9
29
9
10
9
1
1
0
6
3
1
2
1
Dla u
ùatwienia dalszych ob
licze
ñ przeprowadêmy jeszcze trzy operacje
2
9 w
3
9 w
4
5
1
w
3
1
0
0
0
11
1
8
0
0
29
10
1
9
0
6
3
1
2
1
Otrzymana macierz z podzia
ùem
na bloki ma posta
ã:
3
11
29
6
1
0
0
0
1
8
0
0
10
1
9
0
3
1
2
1
Uk
ùad równañ wynikaj¹cy z postaci
tej macierzy:
3
11
8
29
10
9
6
3
2
t
t
z
t
z
y
t
z
y
x
Wyliczmy
t
z ostatniego r
ównania i wstawmy do pozostaùych równañ
3
11
3
8
29
3
10
9
6
3
3
2
t
z
z
y
z
y
x
Z r
ównania trzeciego wyliczmy z
i wstawmy do pierwszego i drugiego r
ównania
3
1
29
3
10
1
9
6
3
3
1
2
t
z
y
y
x
Macierz
trójk¹tna
Macierz D*

zatem
3
1
0
6
3
3
1
2
t
z
y
y
x
st
¹d mamy rozwi¹zanie
3
1
0
2
t
z
y
x
.
..........................................................................................
Wyszukiwarka
Podobne podstrony:
Metoda Eliminacji Gaussa i Gaussa Seidla
Metoda eliminacji Gaussa (1)
Metoda eliminacji Gaussa, Matematyka
Metoda eliminacji Gaussa, mechanika i budowa maszyn, politechnika, polibuda, matma, matma
Metoda eliminacji Gaussa
metoda eliminacji gaussa 2GF64XPQWLQZUSPFSP4MGIKDIVYMP376M7JFZ7Q
Cwiczenia metoda eliminacji
ćw 07 Metoda eliminacji Gaussa
Układ równań liniowych algebra macierzy, metoda eliminacji
Metoda eliminacji gaussa
Metoda magnetyczna MT 14
Metoda animacji społecznej (Animacja społeczno kulturalna)
Metoda Weroniki Sherborne[1]
Metoda Ruchu Rozwijajacego Sherborne
więcej podobnych podstron