3. Funkce

127

3.5. Lineární lomená funkce

Než se začneme zabývat lineární lomenou funkcí, podíváme se krátce na funkci, která jí předchází, je
více ze života. Jedná se o nepřímou úměrnost.

‰

Nepřímá úměrnost

Nepřímá úměrnost je každá funkce na množině

{ }

0

−

R

daná ve tvaru

x

k

y

= ,

kde

{ }

0

−

∈ R

k

.

Řešený příklad

• Máte před sebou cestu dlouhou 20 km. Podle toho, jak rychlý dopravní prostředek si zvolíte, se

bude měnit doba, kterou na cestu budete potřebovat.

Jak dlouho pojedete, bude-li vaším dopravním prostředkem auto, které pojede rychlostí 50 km/h?

A jak dlouho půjdete pěšky rychlostí 5 km/h?

Řešení

Ozn.

s

- dráha

v

- rychlost

t

- čas

Vzorec pro výpočet času:

v

s

t

=

Čas, za který urazíte dráhu v autě:

min

24

4

,

0

/

50

20

=

=

=

h

h

km

km

t

Čas, za který cestu ujdete:

h

h

km

km

t

4

/

5

20

=

=

Je zřejmé, že čím rychleji pojedete, tím méně času na cestu potřebujete. Z našeho příkladu je také
vidět, že v autě rychlostí 10krát větší než při chůzi urazíme dráhu za čas 10krát menší. Stále ale platí,
že součin rychlosti a času je konstantní

t

v.

20

=

.

Mluvíme-li o nepřímé úměrnosti, je to tehdy, platí-li: čím více, tím méně a naopak. Zde, čím menší
rychlost, tím více času na cestě, čím větší rychlost, tím méně času na cestě.

Sestavíme tabulku hodnot a pomocí ní také graf.

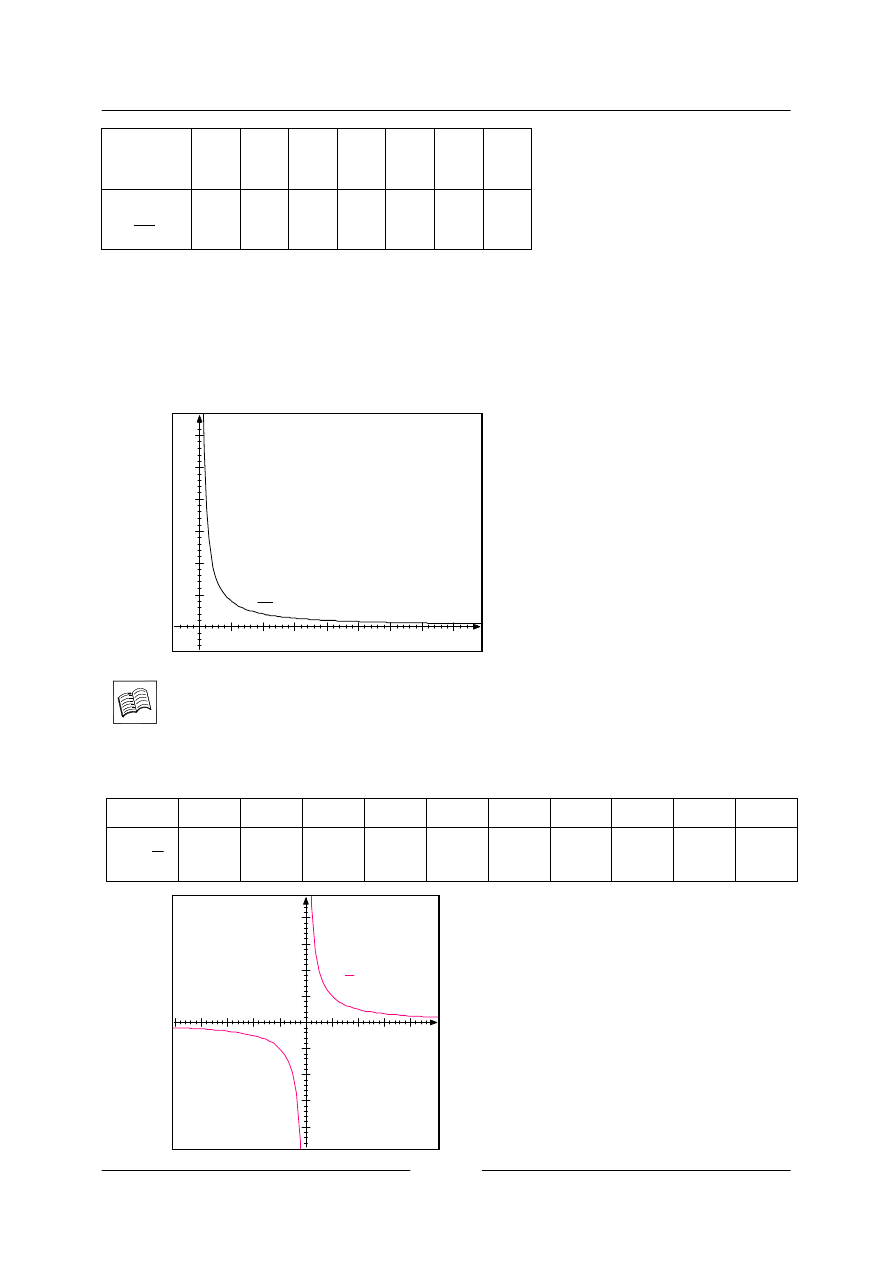
3. Funkce

128

v

)

/

(

h

km

50

)

/

(

h

km

20

)

/

(

h

km

10

)

/

(

h

km

5

)

/

(

h

km

2

)

/

(

h

km

1

)

/

(

h

km

0,5

)

/

(

h

km

h

v

t

20

=

0.4

h

1

h

2

h

4

h

10

h

20

h

40

h

Nyní sestrojíme graf vynesením hodnot z tabulky do soustavy souřadnic.

Rychlost nemůže být rovna nule, protože jmenovatel zlomku nesmí být roven nule. Tedy ani čas
nebude roven nule. Graf funkce proto ani jednu osu soustavy souřadnic neprotíná, pouze se k osám
přibližuje. Rychlost ani čas také nemohou být záporné a tedy graf leží pouze v prvním kvadrantu.

Podíváme se podrobněji na konstrukci grafu nepřímé úměrnosti v závislosti na konstantě

k

.

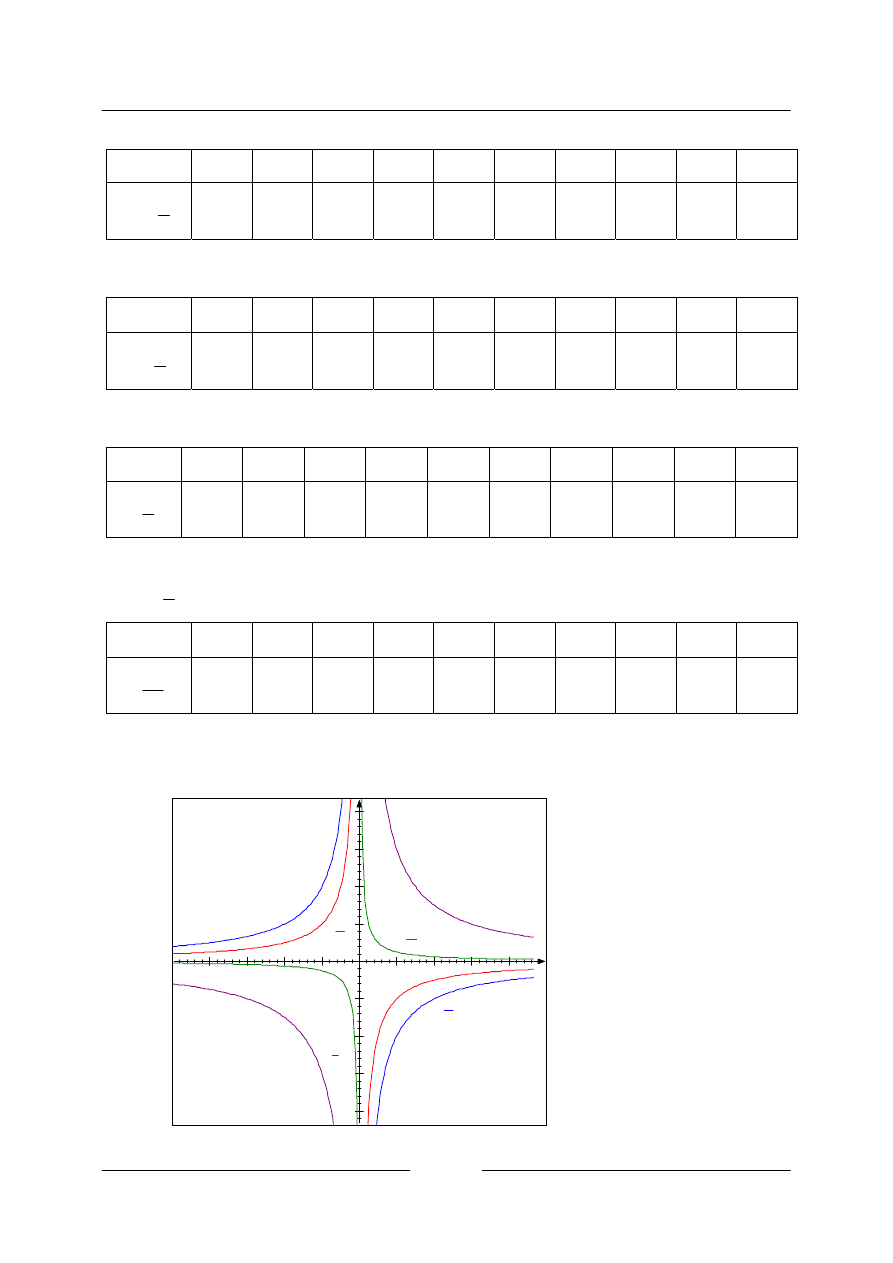
1.

1

=

k

x

1

2

5

,

0

4

1

,

0

1

−

2

−

5

,

0

−

4

−

1

,

0

−

x

y

1

=

1

5

,

0

2

25

,

0

10

1

−

5

,

0

−

2

−

25

,

0

−

10

−

5

10

15

20

25

30

35

40

5

10

15

20

25

0

v

t

5

10

15

20

25

30

35

40

5

10

15

20

25

0

v

t

t=

20

v

-1

-2

-3

-4

1

2

3

4

-1

-2

-3

-4

1

2

3

0

x

y

-1

-2

-3

-4

1

2

3

4

-1

-2

-3

-4

1

2

3

0

x

y

y=

1
x

3. Funkce

129

2.

1

−

=

k

x

1

2

5

,

0

4

1

,

0

1

−

2

−

5

,

0

−

4

−

1

,

0

−

x

y

1

−

=

1

−

5

,

0

−

2

−

25

,

0

−

10

−

1

5

,

0

2

25

,

0

10

3.

2

−

=

k

x

1

2

5

,

0

4

1

,

0

1

−

2

−

5

,

0

−

4

−

1

,

0

−

x

y

2

−

=

2

−

1

−

4

−

5

,

0

−

20

−

2

1

4

5

,

0

20

4.

3

=

k

x

1

2

5

,

0

4

1

,

0

1

−

2

−

5

,

0

−

4

−

1

,

0

−

x

y

3

=

3

5

,

1

6

75

,

0

30

3

−

5

,

1

−

6

−

75

,

0

−

30

−

5.

4

1

=

k

x

1

2

5

,

0

4

1

,

0

1

−

2

−

5

,

0

−

4

−

1

,

0

−

x

y

4

1

=

25

,

0

125

,

0

5

,

0

0625

,

0

5

,

2

25

,

0

−

125

,

0

−

5

,

0

−

062

,

0

−

5

,

2

−

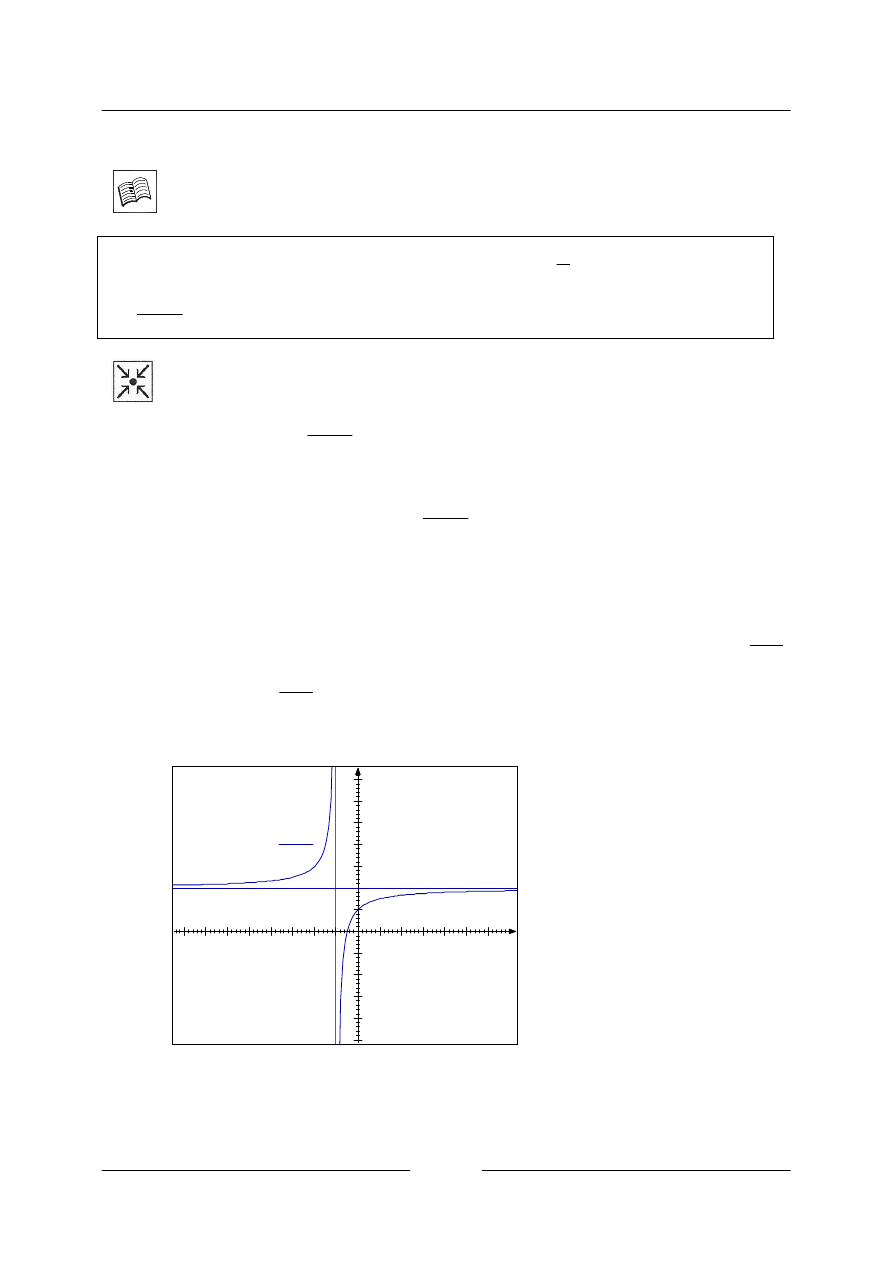
Funkce nakreslíme do jednoho grafu.

-1

-2

-3

-4

1

2

3

4

-1

-2

-3

-4

1

2

3

0

x

y

-1

-2

-3

-4

1

2

3

4

-1

-2

-3

-4

1

2

3

0

x

y

y=

-1

x

y=

-2

x

y=

3
x

y=

1

4x

3. Funkce

130

Grafem je rovnoosá hyperbola, osy souřadnicového systému jsou její asymptoty (hyperbola se k těmto
přímkám přibližuje, ale neprotne je ani se jich nedotkne).

Graf nepřímé úměrnosti je souměrný podle počátku souřadnicového systému a funkce je tedy lichá.

Funkce je prostá.

Je-li

0

>

k

, pak funkce na intervalu

(

)

0

,

∞

−

klesá a klesá také na intervalu

( )

∞

,

0

. Větve hyperboly

se nacházejí v I. a III. kvadrantu.

Je-li

0

<

k

, pak funkce na intervalu

(

)

0

,

∞

−

roste a roste také na intervalu

( )

∞

,

0

. Větve hyperboly se

nacházejí v II. a IV. kvadrantu.

Nemůžeme však říci, že funkce je rostoucí nebo klesající na celém definičním oboru!

Funkce je prostá.

3. Funkce

131

‰

Lineární lomená funkce

Lineární lomená funkce

je každá funkce na množině











−

−

c

d

R

, vyjádřená ve tvaru

d

cx

b

ax

y

+

+

=

, kde

{ }

0

;

,

,

−

∈

∈

R

R c

d

b

a

a

0

≠

− bc

ad

.

Řešený příklad

• Sestrojte graf funkce

1

1

2

+

+

=

x

x

y

Řešení

Zadanou funkci upravíme na tvar

S

S

x

x

k

y

y

−

=

−

, kde

S

S

y

y

x

x

=

= ,

jsou rovnice asymptot

hyperboly a bod

[

]

S

S

y

x

S

,

, jejich průsečík, je střed hyperboly. Definiční obor je

{ }

S

x

−

R

. Jestliže je

0

>

k

, bude graf v I. a III. kvadrantu, pro

0

<

k

, bude ve II. a IV. kvadrantu. Tyto kvadranty neurčují

osy souřadnicového systému, ale asymptoty.

Uvedený tvar dostaneme vydělením čitatele jmenovatelem. Zde po vydělení dostaneme

1

1

2

+

−

+

=

x

y

a hledaný tvar je

1

1

2

+

−

=

−

x

y

. Rovnice asymptot jsou

2

,

1

=

−

=

y

x

, střed má souřadnice

[

]

2

,

1

−

S

,

0

1

<

−

=

k

.

-1

-2

-3

-4

-5

-6

-7

-8

1

2

3

4

5

6

-1

-2

-3

-4

1

2

3

4

5

6

0

x

y

-1

-2

-3

-4

-5

-6

-7

-8

1

2

3

4

5

6

-1

-2

-3

-4

1

2

3

4

5

6

0

x

y

y=

2.x+1

x+1

x=-1

y=2

3. Funkce

132

Úlohy k řešení

Úloha 3.8.

Nakreslete graf funkce:

a)

1

2

−

=

x

x

y

b)

1

+

=

x

x

y

c)

x

x

y

1

+

=

d)

2

3
−

=

x

y

♦

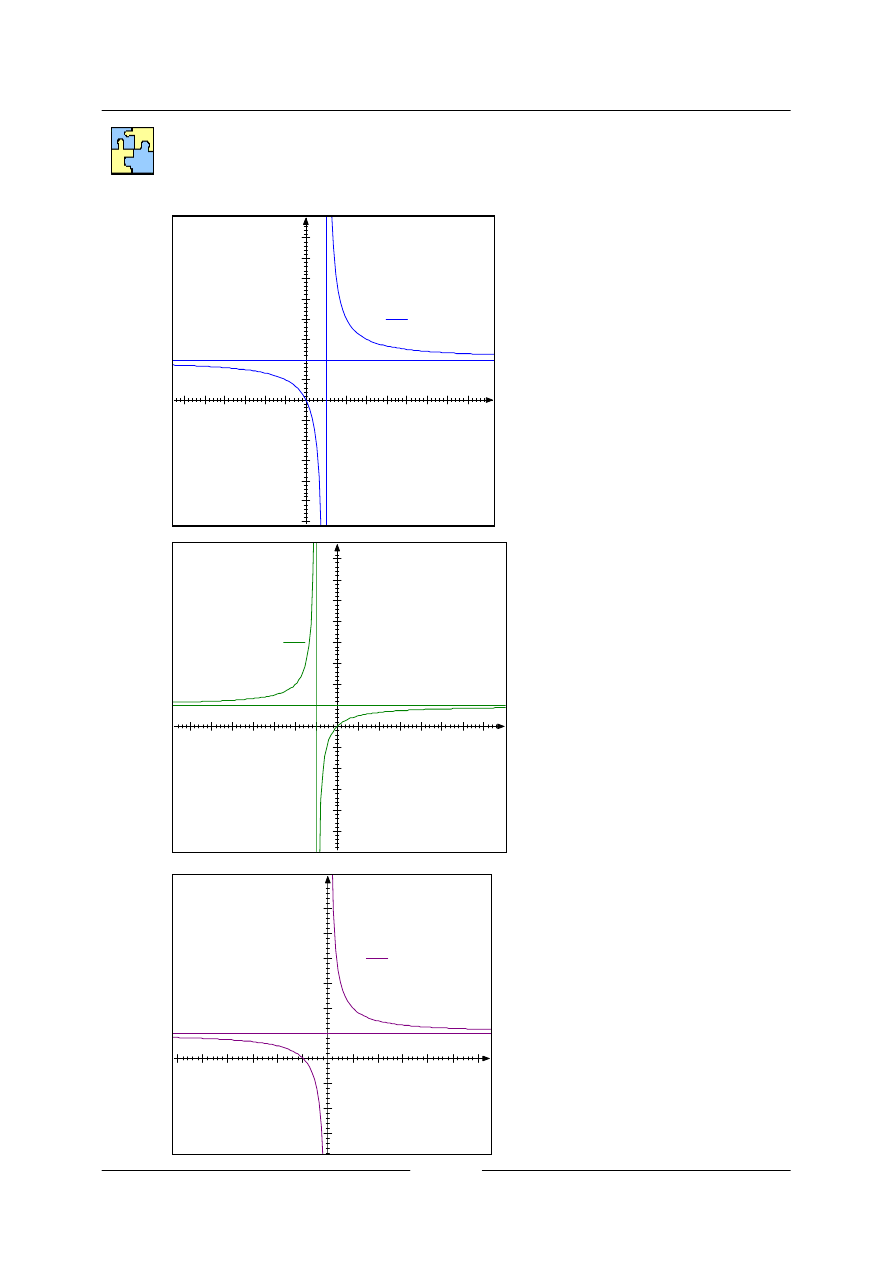
3. Funkce

133

Výsledky

3.8.

a)

b)

c)

-1

-2

-3

-4

-5

-6

1

2

3

4

5

6

7

8

-1

-2

-3

-4

-5

1

2

3

4

5

6

7

0

x

y

-1

-2

-3

-4

-5

-6

1

2

3

4

5

6

7

8

-1

-2

-3

-4

-5

1

2

3

4

5

6

7

0

x

y

y=

2.x
x-1

x=1

y=2

-1

-2

-3

-4

-5

-6

-7

1

2

3

4

5

6

7

-1

-2

-3

-4

-5

1

2

3

4

5

6

7

0

x

y

-1

-2

-3

-4

-5

-6

-7

1

2

3

4

5

6

7

-1

-2

-3

-4

-5

1

2

3

4

5

6

7

0

x

y

y=

x

x+1

x=-1

y=1

-1

-2

-3

-4

-5

-6

1

2

3

4

5

-1

-2

-3

1

2

3

4

5

6

0

x

y

-1

-2

-3

-4

-5

-6

1

2

3

4

5

-1

-2

-3

1

2

3

4

5

6

0

x

y

y=

x+1

x

y=1

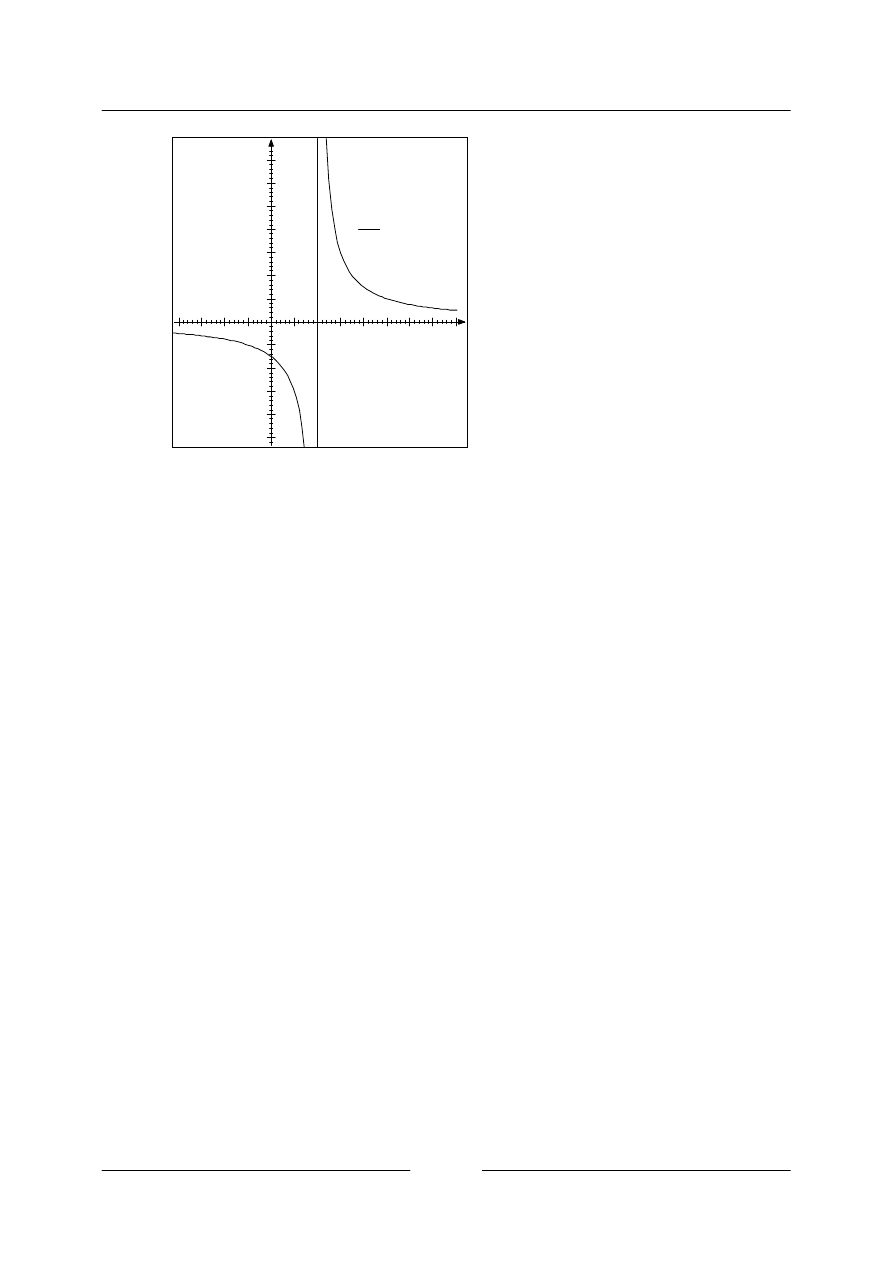
3. Funkce

134

d)

-1

-2

-3

-4

1

2

3

4

5

6

7

-1

-2

-3

-4

-5

1

2

3

4

5

6

0

x

y

-1

-2

-3

-4

1

2

3

4

5

6

7

-1

-2

-3

-4

-5

1

2

3

4

5

6

0

x

y

y=

3

x-2

x=2