3. Funkce

137

3.7. Inverzní funkce

Inverzní funkci můžeme sestrojit téměř ke každé známé funkci, říkám téměř, to znamená, že existuje
jisté omezení, kdy lze inverzní funkci sestrojit.

Inverzní funkce k prosté funkci

f je

1

−

f , pro kterou platí:

( )

( )

f

H

f

D

=

−1

, každému

( )

1

−

∈

f

D

y

je přiřazeno právě to

( )

f

D

x

∈

, pro které je

( )

y

x

f

=

.

Oborem hodnot inverzní funkce je definiční obor původní funkce:

( )

( )

f

D

f

H

=

−1

Grafy obou funkcí jsou souměrné podle osy I. a III. kvadrantu

x

y

=

.

Nyní se podrobněji podíváme na inverzní funkce k funkcím lineárním, kvadratickým, lineárním
lomeným a mocninným. Stále musíme mít na paměti, že funkci inverzní lze sestrojit jen k funkci
prosté, jestliže funkce prostá není, musíme nejdříve určit obor prostoty a na něm vytvářen inverzní
funkci. Více u kvadratických a mocninných funkcí.

‰

Lineární funkce

Řešený příklad

• Do téže soustavy souřadnic zakreslete graf funkce

1

4

3

:

−

= x

y

f

a funkce

1

−

f

k ní inverzní.

Řešení

Sestavíme tabulku pro funkci

1

4

3

:

−

= x

y

f

.

x

0

4

y

1

−

2

Nyní určíme inverzní funkci

1

4

3

:

1

−

=

−

y

x

f

.

Z rovnice vyjádříme

y

.

3

4

4

:

1

+

=

−

x

y

f

Sestavíme tabulku pro funkci

3

4

4

:

1

+

=

−

x

y

f

.

x

1

−

2

y

0

4

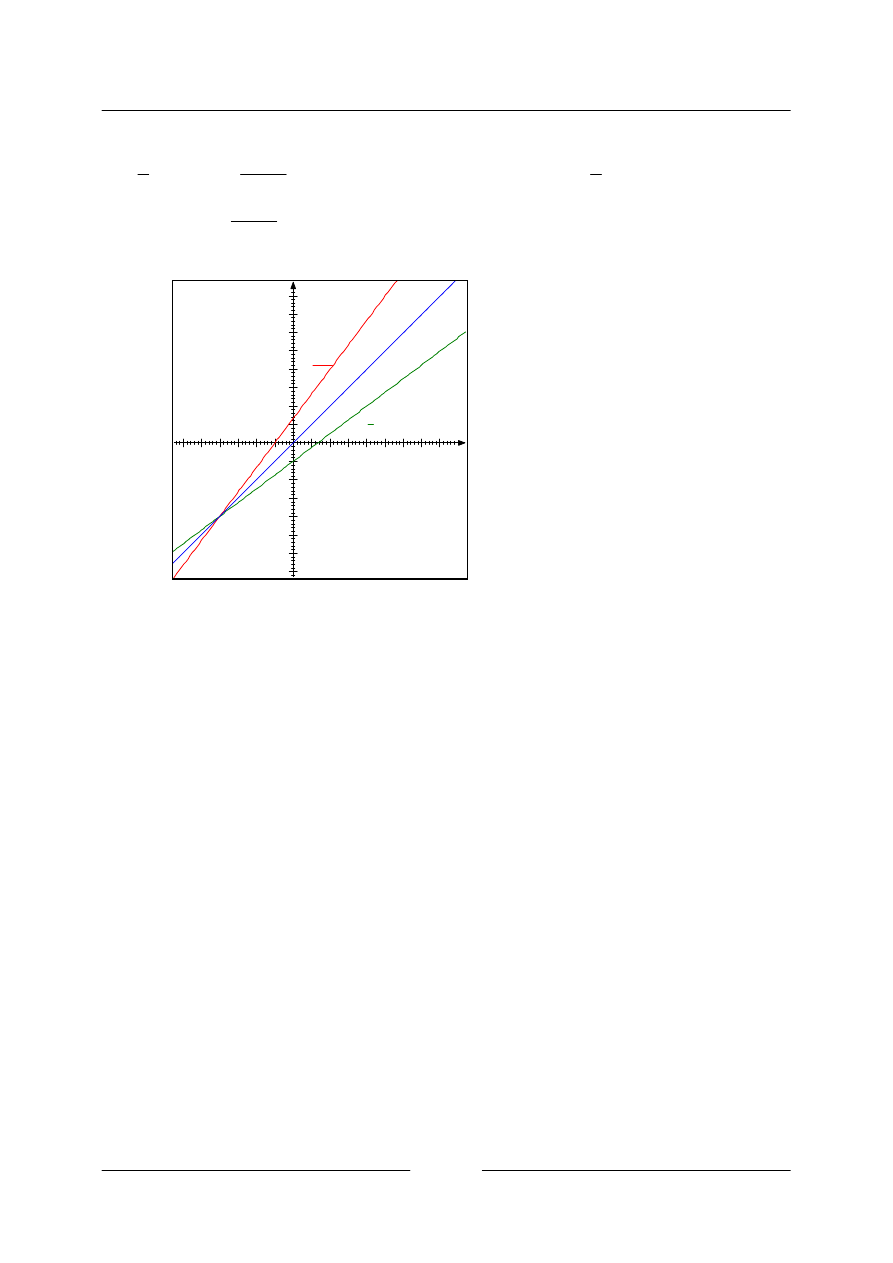
3. Funkce

138

Nyní nakreslíme grafy obou funkcí. V grafu je také vyznačena přímka

x

y

=

, podle které jsou přímky

1

4

3 −

= x

y

a

3

4

4

+

=

x

y

souměrné. Všimněte si, že funkce

1

4

3

:

−

= x

y

f

je rostoucí a funkce

inverzní

3

4

4

:

1

+

=

−

x

y

f

je také rostoucí.

-1

-2

-3

-4

-5

-6

1

2

3

4

5

6

7

8

-1

-2

-3

-4

-5

-6

-7

1

2

3

4

5

6

7

0

x

y

-1

-2

-3

-4

-5

-6

1

2

3

4

5

6

7

8

-1

-2

-3

-4

-5

-6

-7

1

2

3

4

5

6

7

0

x

y

y=

4x+4

3

y=

3
4

x-1

y=x

3. Funkce

139

‰

Kvadratická funkce

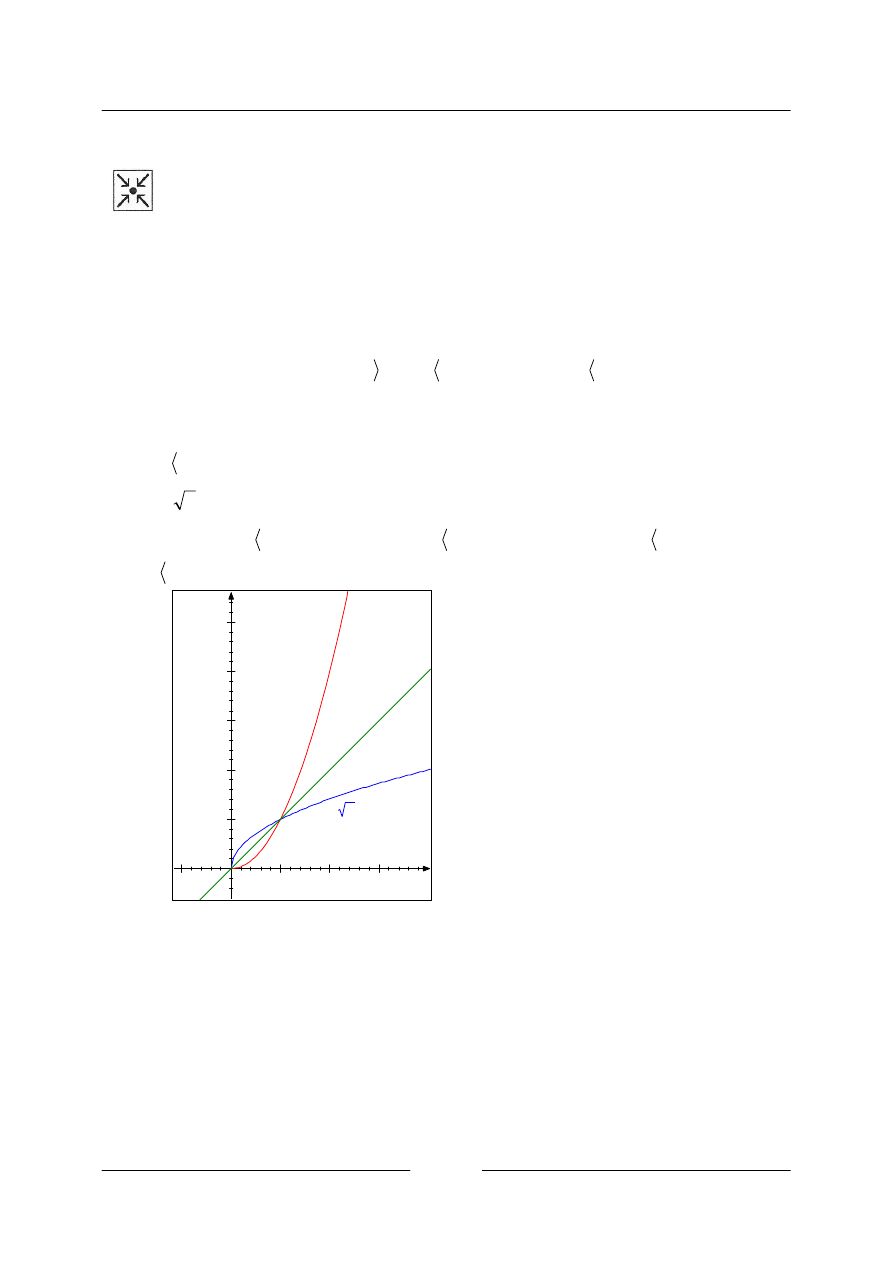
Řešený příklad

• K funkci

2

:

x

y

f

=

vypočítejte inverzní funkci

1

−

f

a nakreslete grafy obou funkcí do téže

soustavy souřadnic.

Řešení

Abychom mohli určit inverzní funkci, musí být funkce prostá. Kvadratická funkce ale prostá není.
Určíme proto nejdříve obor prostoty funkce

f

.

Funkce je prostá na intervalu

(

0

,

∞

−

a na

)

∞

,

0

. Vybereme si

)

∞

,

0

a na tomto intervalu

sestrojíme k funkci

2

:

x

y

f

=

funkci inverzní.

2

y

x

=

rovnici odmocníme (

x

lze odmocnit pokud bude nezáporné tzn.

0

≥

x

a to na zvoleném

intervalu

)

∞

,

0

je)

x

y

f

=

−

:

1

graf bude souměrný s červenou částí grafu funkce

2

:

x

y

f

=

.

Definiční obor

)

∞

= ,

0

f

D

, obor hodnot

)

∞

= ,

0

f

H

. Definiční obor

)

∞

=

−

,

0

1

f

D

, obor hodnot

)

∞

=

−

,

0

1

f

H

.

-1

1

2

3

1

2

3

4

5

0

x

y

-1

1

2

3

1

2

3

4

5

0

x

y

y=x

2

y= x

y=x

3. Funkce

140

‰

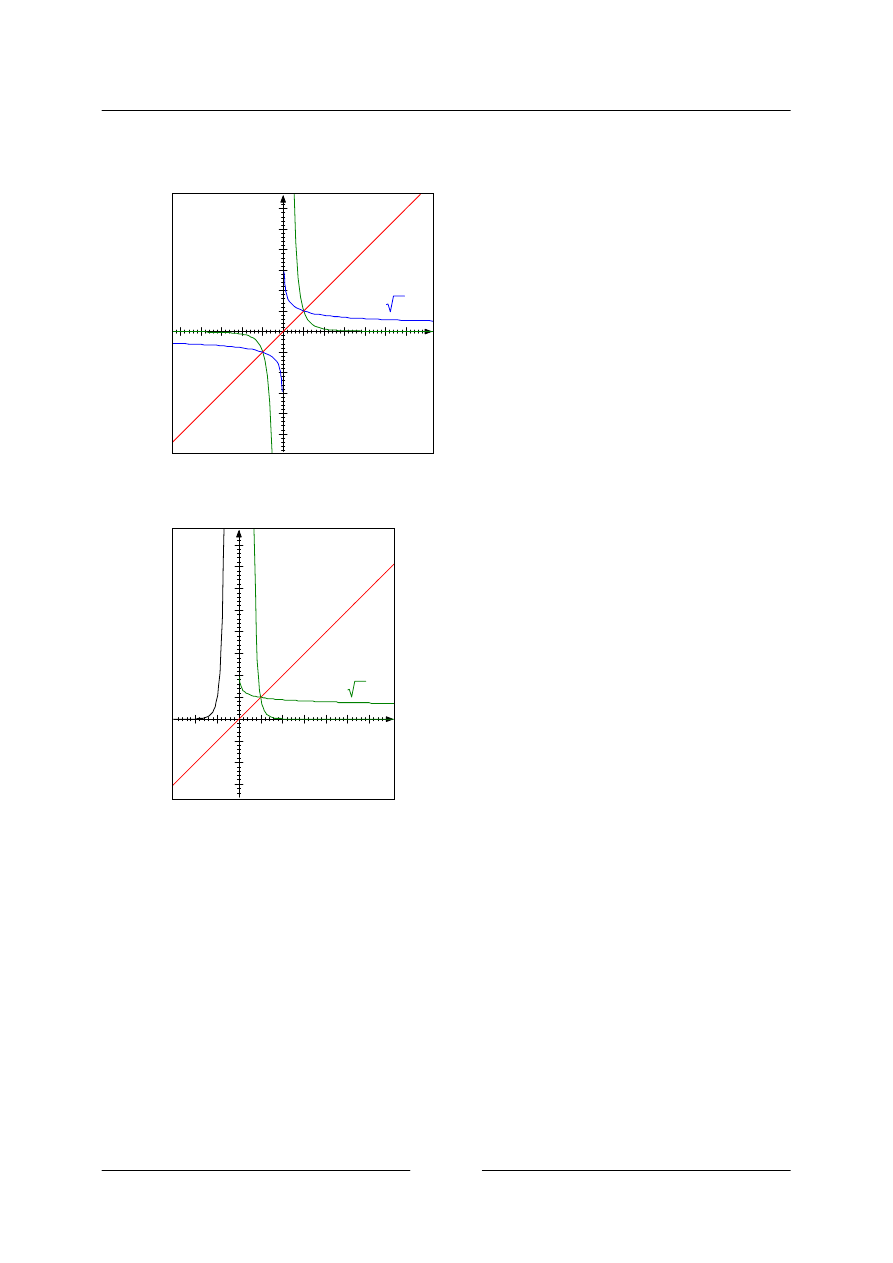
Lineární lomená funkce

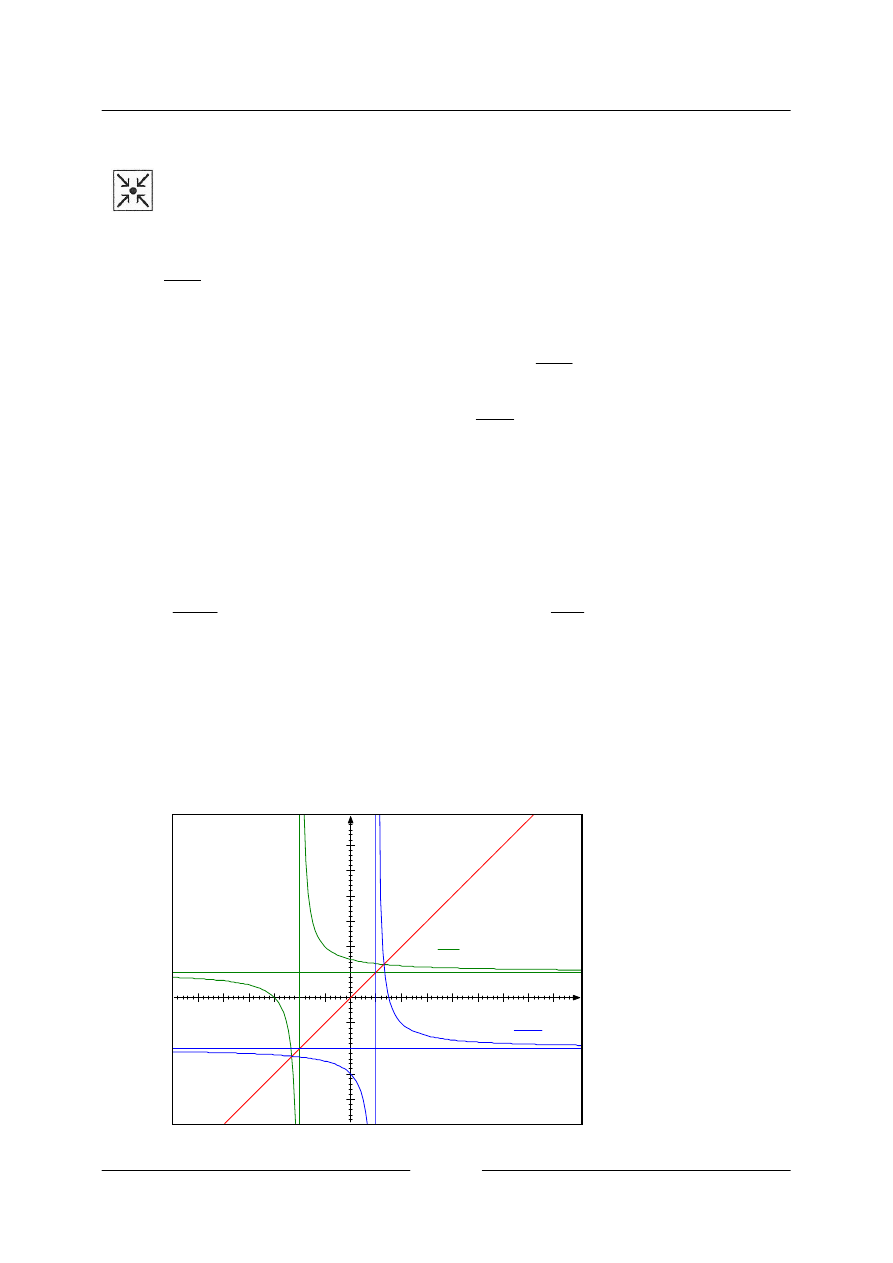
Řešený příklad

• K funkci

f

vypočítejte inverzní funkci

1

−

f

a nakreslete grafy obou funkcí do téhož obrázku.

2

3

+

+

=

x

x

y

Řešení

Upravíme si nejprve zadanou funkci na středový tvar

2

1

1

:

+

=

−

x

y

f

.

Pro výpočet inverzní funkce vyměníme souřadnice

2

3

+

+

=

y

y

x

a vyjádříme

y

.

(

)

3

2

+

=

+

y

y

x

3

2

+

=

+

y

x

xy

x

y

xy

2

3

−

=

−

(

)

x

x

y

2

3

1

−

=

−

1

2

3

:

1

−

−

=

−

x

x

y

f

a nyní ji upravíme na středový tvar

1

1

2

:

1

−

=

+

−

x

y

f

.

Definiční obor

(

) (

)

∞

−

∪

−

∞

−

=

,

2

2

,

f

D

, obor hodnot

(

) ( )

∞

∪

∞

−

=

,

1

1

,

f

H

. Definiční obor

(

) ( )

∞

∪

∞

−

=

−

,

1

1

,

1

f

D

, obor hodnot

(

) (

)

∞

−

∪

−

∞

−

=

−

,

2

2

,

1

f

H

.

Nakreslíme oba grafy do jednoho obrázku, je zde vyznačena také osa I. a III. Kvadrantu, podle které
jsou oba grafy souměrné. Všimněte si, že souměrné jsou také asymptoty obou hyperbol.

-1

-2

-3

-4

-5

-6

1

2

3

4

5

6

7

8

-1

-2

-3

-4

1

2

3

4

5

6

0

x

y

-1

-2

-3

-4

-5

-6

1

2

3

4

5

6

7

8

-1

-2

-3

-4

1

2

3

4

5

6

0

x

y

y=

x+3
x+2

x=-2

y=1

y=x

x=1

y=-2

y=

3-2x

x-1

3. Funkce

141

‰

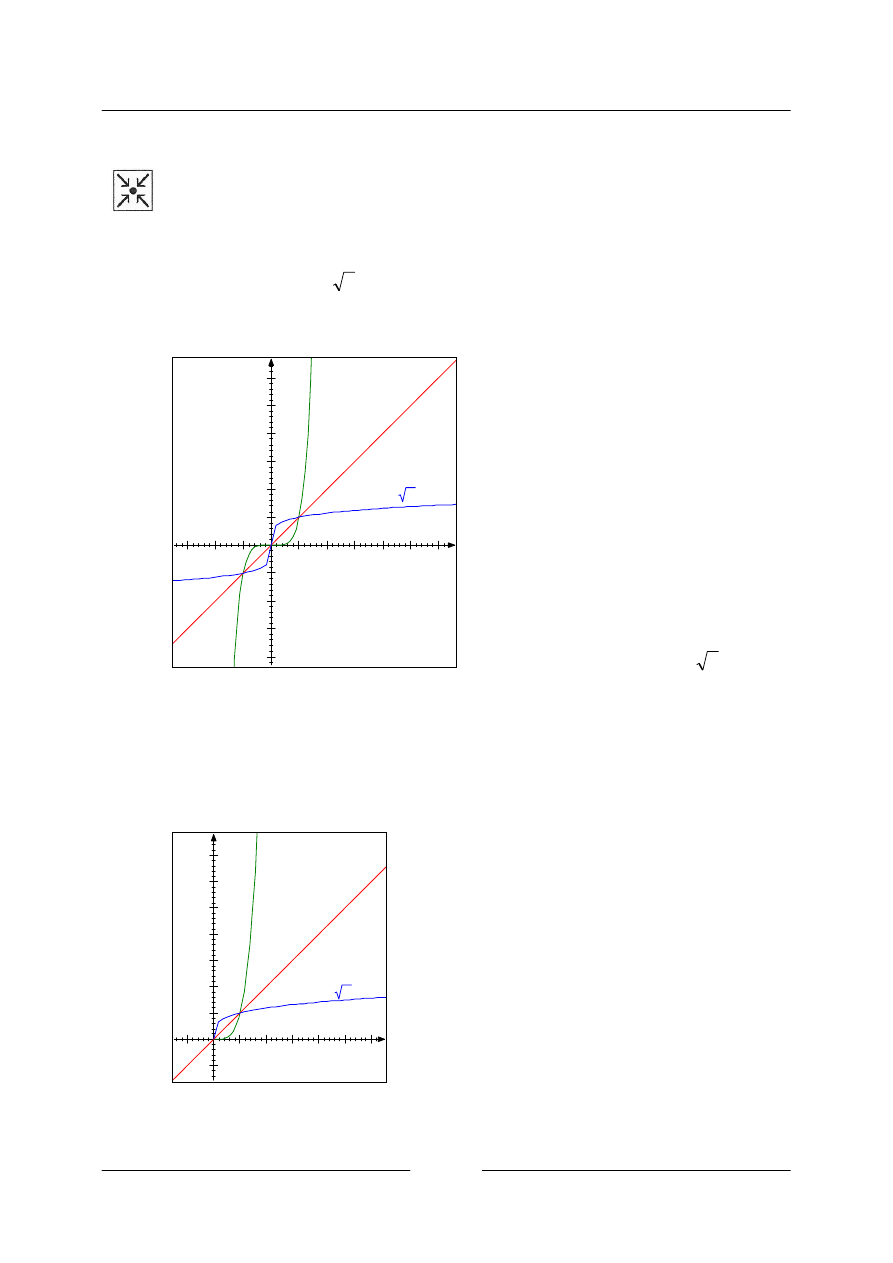
Mocninná funkce

Řešený příklad

• Ukážeme si několik příkladů na sestrojení inverzní funkce k mocninným funkcím. Připomeňte si

vlastnosti těchto funkcí.

a)

5

:

x

y

f

=

5

1

:

x

y

f

=

−

R

H

D

H

D

f

f

f

f

=

=

=

=

−

−

1

1

b)

4

:

x

y

f

=

4

1

:

x

y

f

=

−

4

:

x

y

f

=

není prostá, inverzní funkci sestavíme jen pro tu část, která je prostá.

+

=

=

=

=

−

−

R

H

D

H

D

f

f

f

f

1

1

-1

-2

-3

1

2

3

4

5

6

-1

-2

-3

-4

1

2

3

4

5

0

x

y

-1

-2

-3

1

2

3

4

5

6

-1

-2

-3

-4

1

2

3

4

5

0

x

y

y=x

5

y=x

y=

5

x

-1

1

2

3

4

5

-1

1

2

3

4

5

6

0

x

y

-1

1

2

3

4

5

-1

1

2

3

4

5

6

0

x

y

y=x

4

y=x

y=

4

x

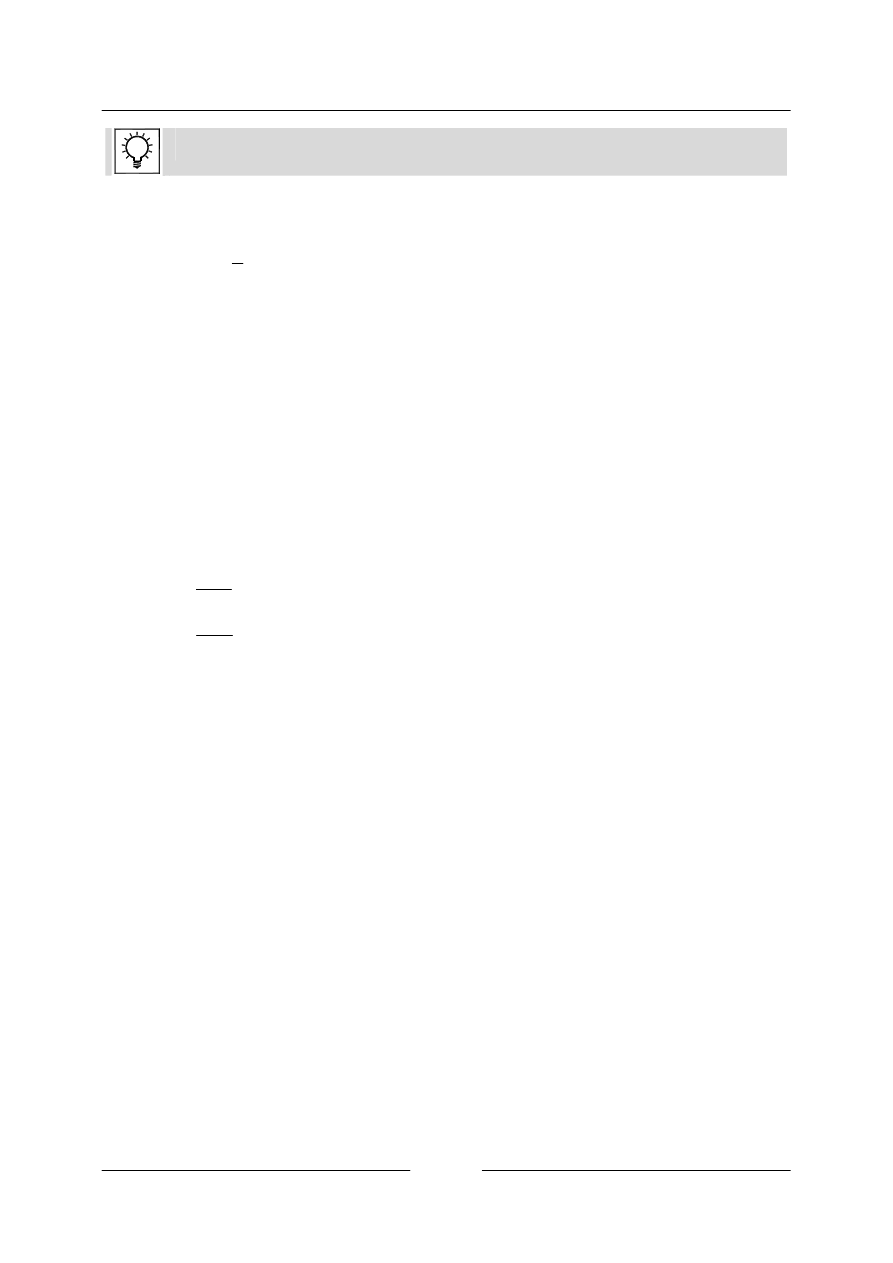
3. Funkce

142

Úlohy k řešení

Úloha 3.9.

Do téže soustavy souřadnic zakreslete graf funkce

f

a funkce

1

−

f

k ní inverzní.

a)

1

2

1

:

−

−

=

x

y

f

b)

1

5

:

+

= x

y

f

c)

1

:

=

y

f

♦

Úloha 3.10.

K funkci

f

vypočítejte inverzní funkci

1

−

f

a nakreslete grafy obou funkcí do téhož obrázku.

a)

(

)

2

1

−

= x

y

b)

2

2

−

= x

y

♦

Úloha 3.11.

K funkci

f

vypočítejte inverzní funkci

1

−

f

a nakreslete grafy obou funkcí do téhož obrázku.

a)

3

2
+

=

x

y

b)

1

2

−

−

=

x

x

y

♦
Úloha 3.12.

Sestrojte graf funkce a funkce k ní inverzní

a)

3

:

−

= x

y

f

b)

6

:

−

= x

y

f

(Funkce není prostá, inverzní funkci sestavíme jen pro tu část, která je prostá.)

♦

3. Funkce

143

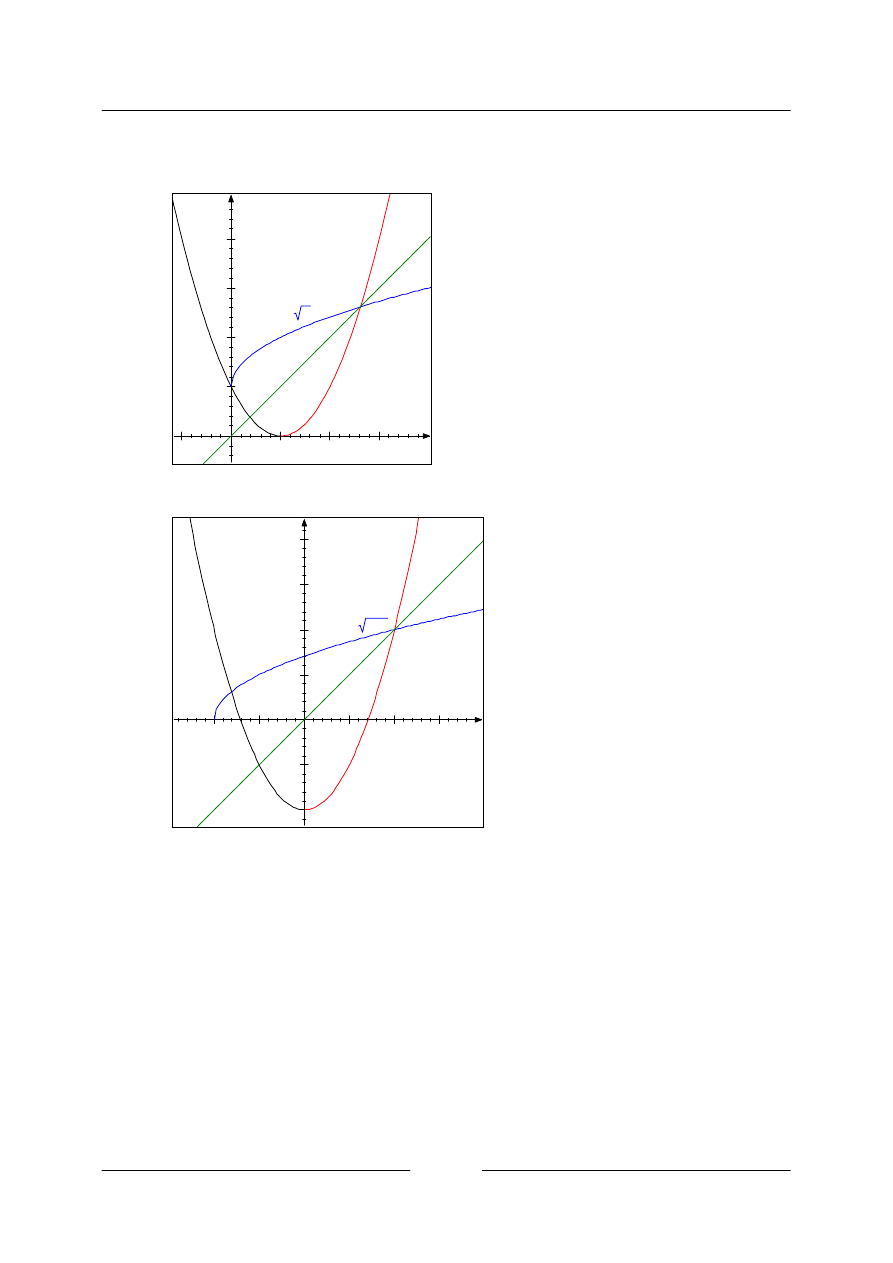
Výsledky

3.9.

a)

b)

c)

Funkce nemá inverzní funkci, protože není prostá

-1

-2

-3

-4

-5

-6

1

2

3

4

5

-1

-2

-3

-4

-5

-6

1

2

3

4

5

0

x

y

-1

-2

-3

-4

-5

-6

1

2

3

4

5

-1

-2

-3

-4

-5

-6

1

2

3

4

5

0

x

y

y=-

1
2

x-1

y=-2x-2

y=x

-1

-2

-3

-4

-5

1

2

3

4

5

6

-1

-2

-3

-4

1

2

3

4

5

6

0

x

y

-1

-2

-3

-4

-5

1

2

3

4

5

6

-1

-2

-3

-4

1

2

3

4

5

6

0

x

y

y=

x-1

5

y=5x+1

y=x

-1

-2

-3

-4

-5

1

2

3

4

5

6

-1

-2

-3

-4

1

2

3

4

5

6

0

x

y

-1

-2

-3

-4

-5

1

2

3

4

5

6

-1

-2

-3

-4

1

2

3

4

5

6

0

x

y

y=1

y=x

3. Funkce

144

3.10.

a)

b)

-1

1

2

3

1

2

3

4

0

x

y

-1

1

2

3

1

2

3

4

0

x

y

y=(x-1)

2

y= x +1

y=x

-1

-2

1

2

3

-1

-2

1

2

3

0

x

y

-1

-2

1

2

3

-1

-2

1

2

3

0

x

y

y=x

2

-2

y= x+2

y=x

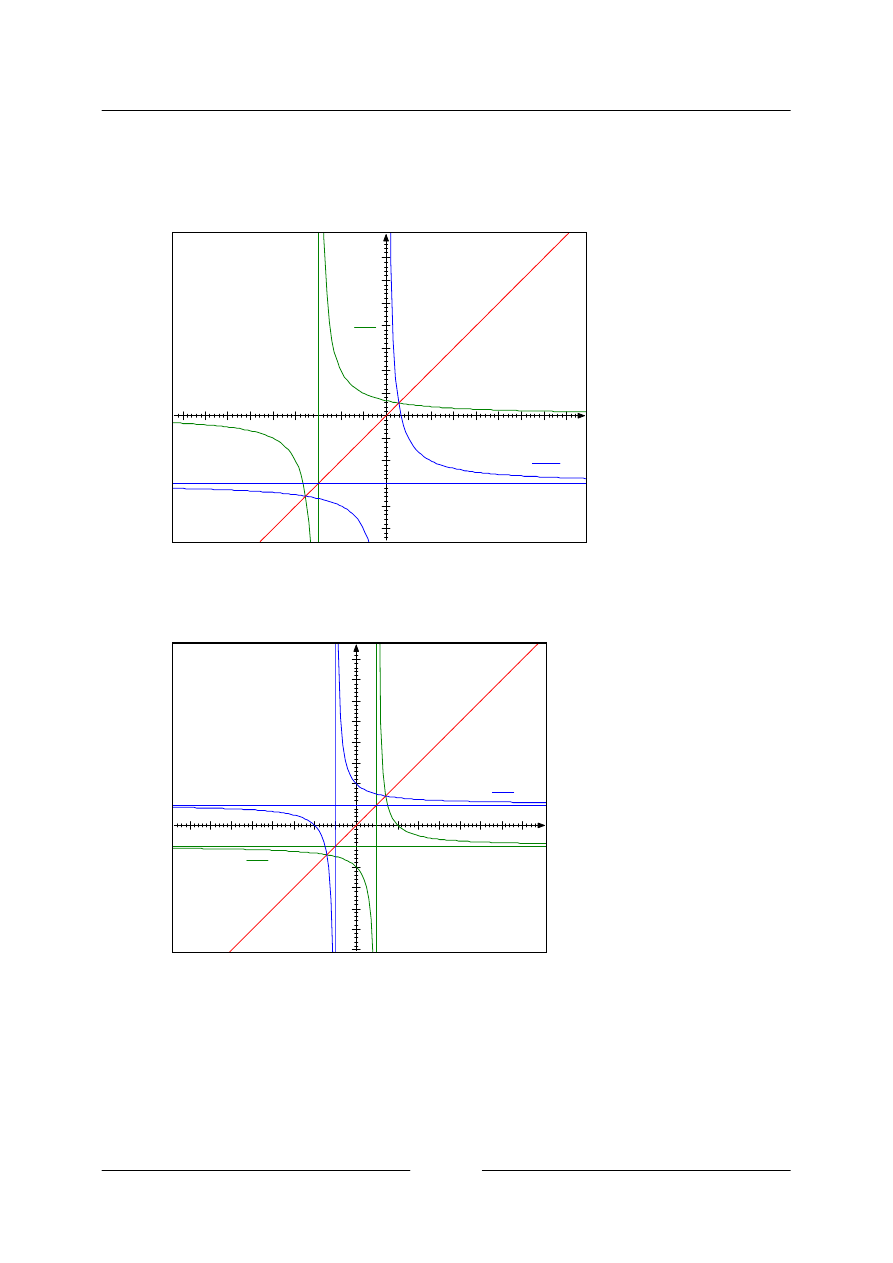
3. Funkce

145

3.11.

a)

b)

-1

-2

-3

-4

-5

-6

-7

-8

-9

1

2

3

4

5

6

7

8

-1

-2

-3

-4

-5

1

2

3

4

5

6

0

x

y

-1

-2

-3

-4

-5

-6

-7

-8

-9

1

2

3

4

5

6

7

8

-1

-2

-3

-4

-5

1

2

3

4

5

6

0

x

y

y=

2

x+3

x=-3

y=x

y=-3

y=

2-3x

x

-1

-2

-3

-4

-5

-6

-7

-8

1

2

3

4

5

6

7

8

-1

-2

-3

-4

-5

1

2

3

4

5

6

7

0

x

y

-1

-2

-3

-4

-5

-6

-7

-8

1

2

3

4

5

6

7

8

-1

-2

-3

-4

-5

1

2

3

4

5

6

7

0

x

y

y=

2-x
x-1

x=-1

y=-1

y=x

x=1

y=1

y=

x+2
x+1

3. Funkce

146

3.12.

a)

b)

-1

-2

-3

-4

-5

1

2

3

4

5

6

-1

-2

-3

-4

-5

1

2

3

4

5

0

x

y

-1

-2

-3

-4

-5

1

2

3

4

5

6

-1

-2

-3

-4

-5

1

2

3

4

5

0

x

y

y=x

-3

y=x

y=

3

x

-1

-2

1

2

3

4

5

6

-1

-2

-3

1

2

3

4

5

6

7

0

x

y

-1

-2

1

2

3

4

5

6

-1

-2

-3

1

2

3

4

5

6

7

0

x

y

y=x

-6

y=x

y=

6

x