3. Funkce

147

3.8. Exponenciální funkce

Exponenciální funkce o základu

a

je funkce na množině R vyjádřená ve tvaru

x

a

y

=

,

kde

1

,

0

≠

> a

a

.

Řešený příklad

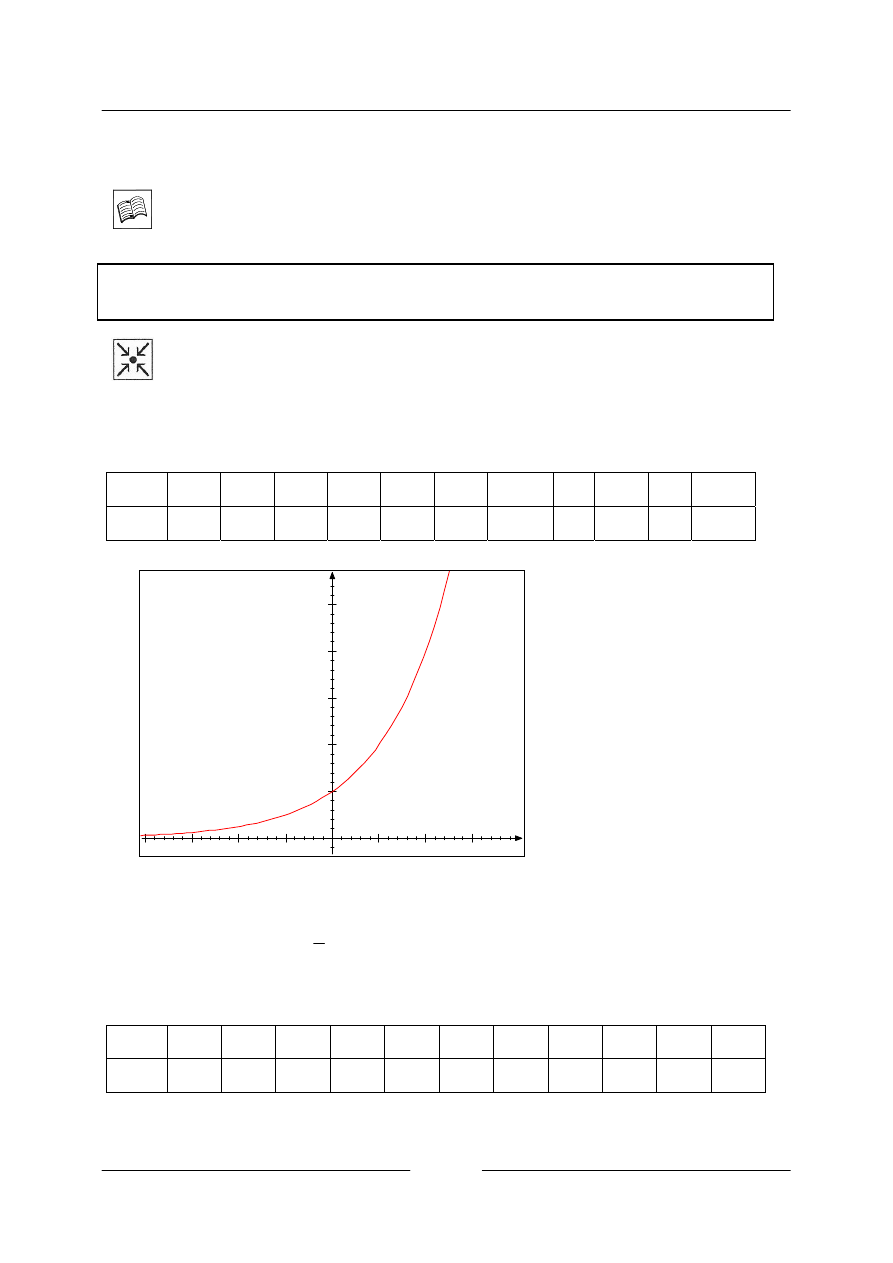
• Sestrojte graf funkce

x

y 2

=

.

Řešení

Sestavíme tabulku hodnot

x

0

5

,

0

5

,

0

−

1

1

−

5

,

1

5

,

1

−

2

2

−

3

3

−

x

y 2

=

1

414

,

1

404

,

0

2

5

,

0

828

2,

354

0,

4

25

,

0

8

125

,

0

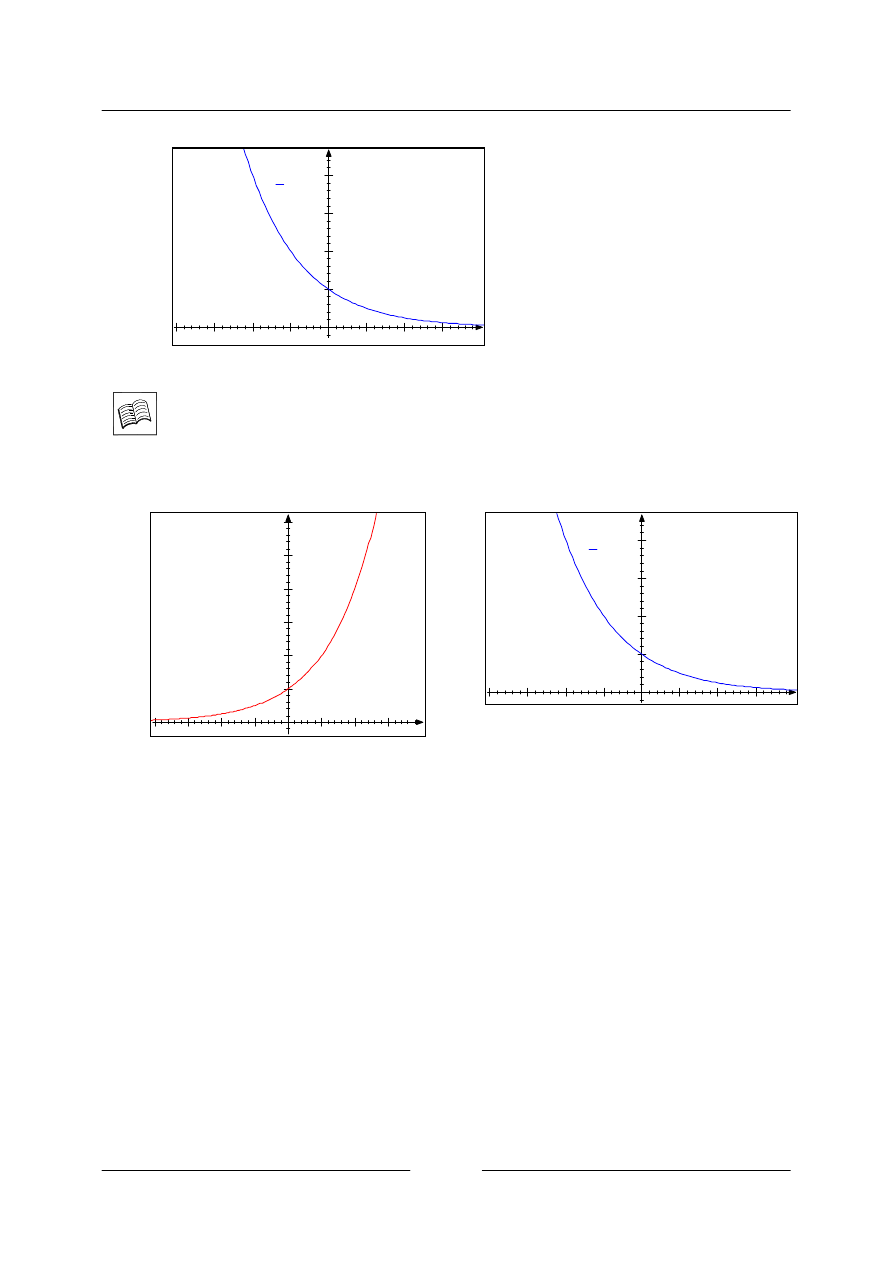
• Sestrojte graf funkce

x

y













=

2

1

Řešení

Sestavíme tabulku hodnot

x

0

1

1

−

5

,

0

5

,

0

−

5

,

1

5

,

1

−

2

2

−

3

3

−

x

y 2

=

1

5

,

0

2

404

,

0

414

,

1

354

,

0

828

,

2

25

,

0

4

125

,

0

8

-1

-2

-3

-4

1

2

3

1

2

3

4

5

0

x

y

-1

-2

-3

-4

1

2

3

1

2

3

4

5

0

x

y

2

x

3. Funkce

148

Srovnáme průběhy funkcí

{}

1

R

,

−

∈

=

+

a

a

y

x

, pro různé hodnoty

a

.

1

>

a

1

0

<

< a

( )

( )

{ }

0

R

,

R

−

=

=

+

f

H

f

D

Je zdola omezená, shora není omezená.

Nemá v žádném bodě ani maximum ani minimum.

Funkční hodnota v bodě

0

je rovna

1

.

Funkce je rostoucí, tedy prostá.

Funkce je klesající, tedy prostá.

-1

-2

-3

1

2

3

1

2

3

4

0

x

y

-1

-2

-3

1

2

3

1

2

3

4

0

x

y

(

1
2

)

x

-1

-2

-3

1

2

3

1

2

3

4

5

0

x

y

-1

-2

-3

1

2

3

1

2

3

4

5

0

x

y

2

x

-1

-2

-3

1

2

3

1

2

3

4

0

x

y

-1

-2

-3

1

2

3

1

2

3

4

0

x

y

(

1
2

)

x

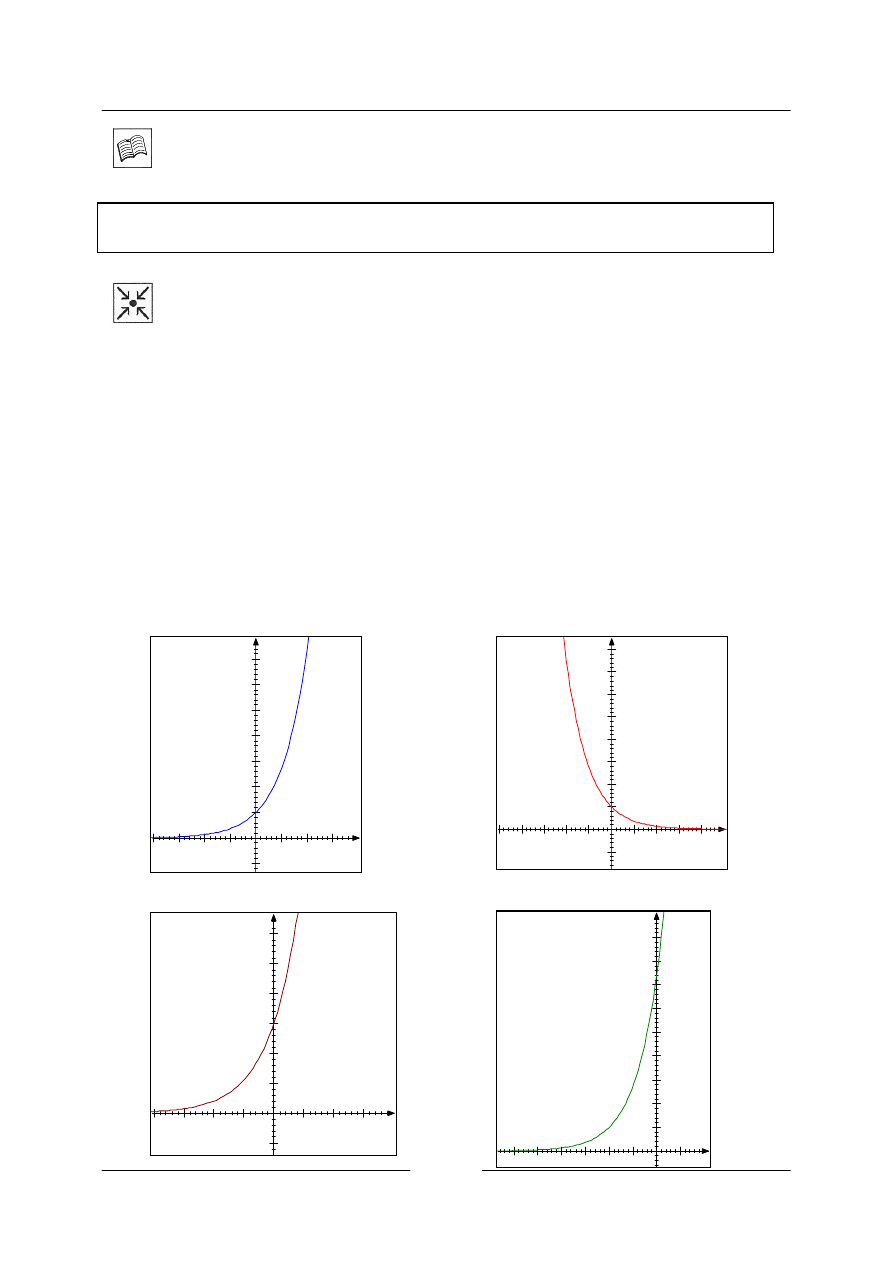
3. Funkce

149

-1

-2

-3

-4

-5

-6

1

1

2

3

4

5

6

7

8

9

0

x

y

-1

-2

-3

-4

-5

-6

1

1

2

3

4

5

6

7

8

9

0

x

y

e

x+2

Je-li základem exponenciální funkce Eulerovo číslo

718281828

,

2

=

e

, mluvíme o

přirozené exponenciální funkci.

Řešený příklad

• Nakreslete graf přirozené exponenciální funkce

a)

x

e

y

=

b)

x

e

y

−

=

c)

x

e

y 3

=

d)

2

+

=

x

e

y

e)

1

−

=

x

e

y

f)

1

−

=

− x

e

y

Řešení

a)

b)

c)

d)

e)

f)

-1

-2

-3

-4

1

2

3

4

-1

1

2

3

4

5

6

7

0

x

y

-1

-2

-3

-4

1

2

3

4

-1

1

2

3

4

5

6

7

0

x

y

e

-x

-1

-2

-3

1

2

3

-1

1

2

3

4

5

6

0

x

y

-1

-2

-3

1

2

3

-1

1

2

3

4

5

6

0

x

y

e

x

-1

-2

-3

1

2

3

-1

1

2

3

4

5

0

x

y

-1

-2

-3

1

2

3

-1

1

2

3

4

5

0

x

y

3e

x

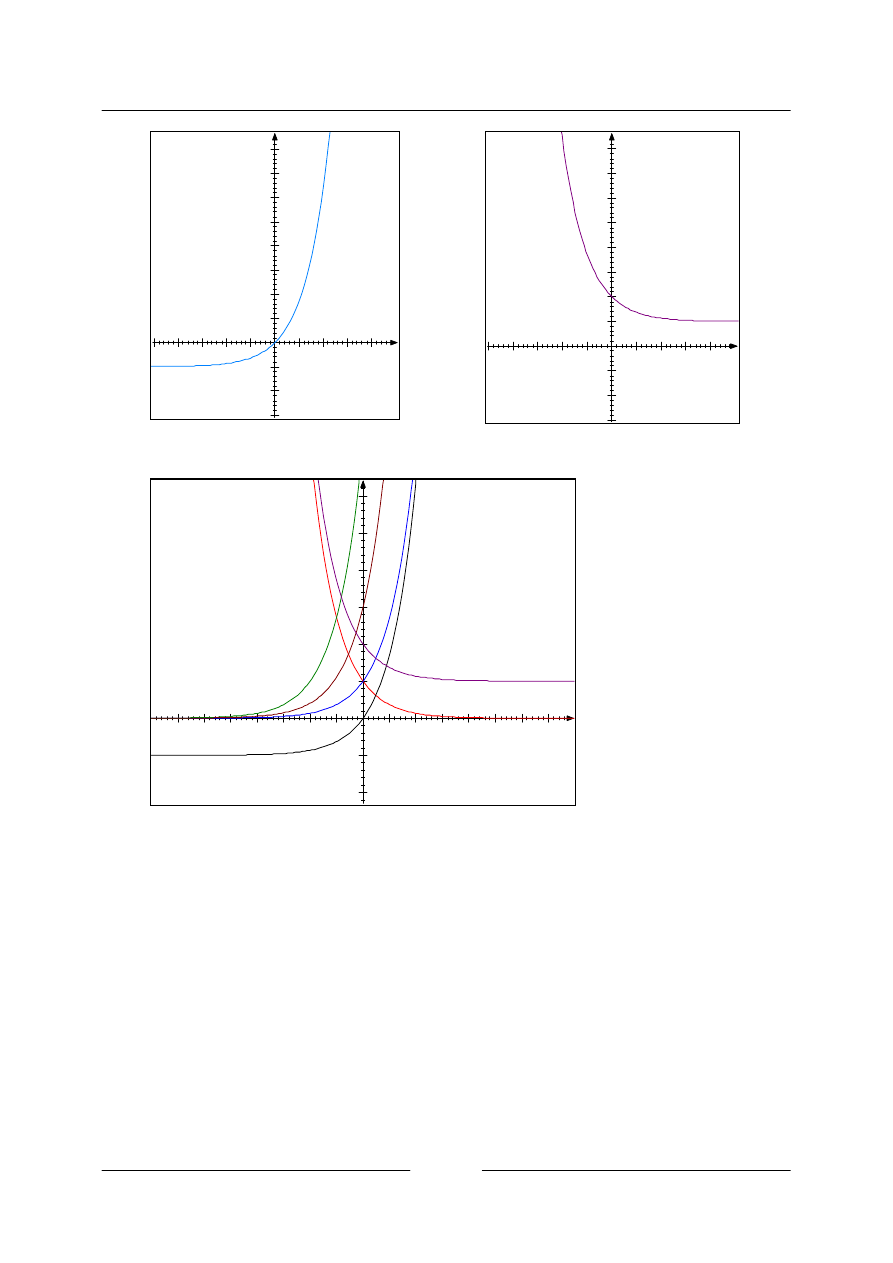
3. Funkce

150

Srovnání průběhu všech funkcí:

-1

-2

-3

-4

-5

-6

-7

1

2

3

4

5

6

7

-1

-2

1

2

3

4

5

0

x

y

-1

-2

-3

-4

-5

-6

-7

1

2

3

4

5

6

7

-1

-2

1

2

3

4

5

0

x

y

e

-x

+1

e

-x

e

x

e

x+2

3e

x

e

x

-1

-1

-2

-3

-4

1

2

3

4

-1

-2

1

2

3

4

5

6

7

0

x

y

-1

-2

-3

-4

1

2

3

4

-1

-2

1

2

3

4

5

6

7

0

x

y

e

x

-1

-1

-2

-3

-4

1

2

3

4

-1

-2

1

2

3

4

5

6

7

0

x

y

-1

-2

-3

-4

1

2

3

4

-1

-2

1

2

3

4

5

6

7

0

x

y

e

-x

+1

3. Funkce

151

Úlohy k řešení

Úloha 3.13.

Nakreslete graf funkce:

a)

x

y 10

=

b)

x

y 5

=

c)

x

y













=

4

1

♦

3. Funkce

152

Výsledky

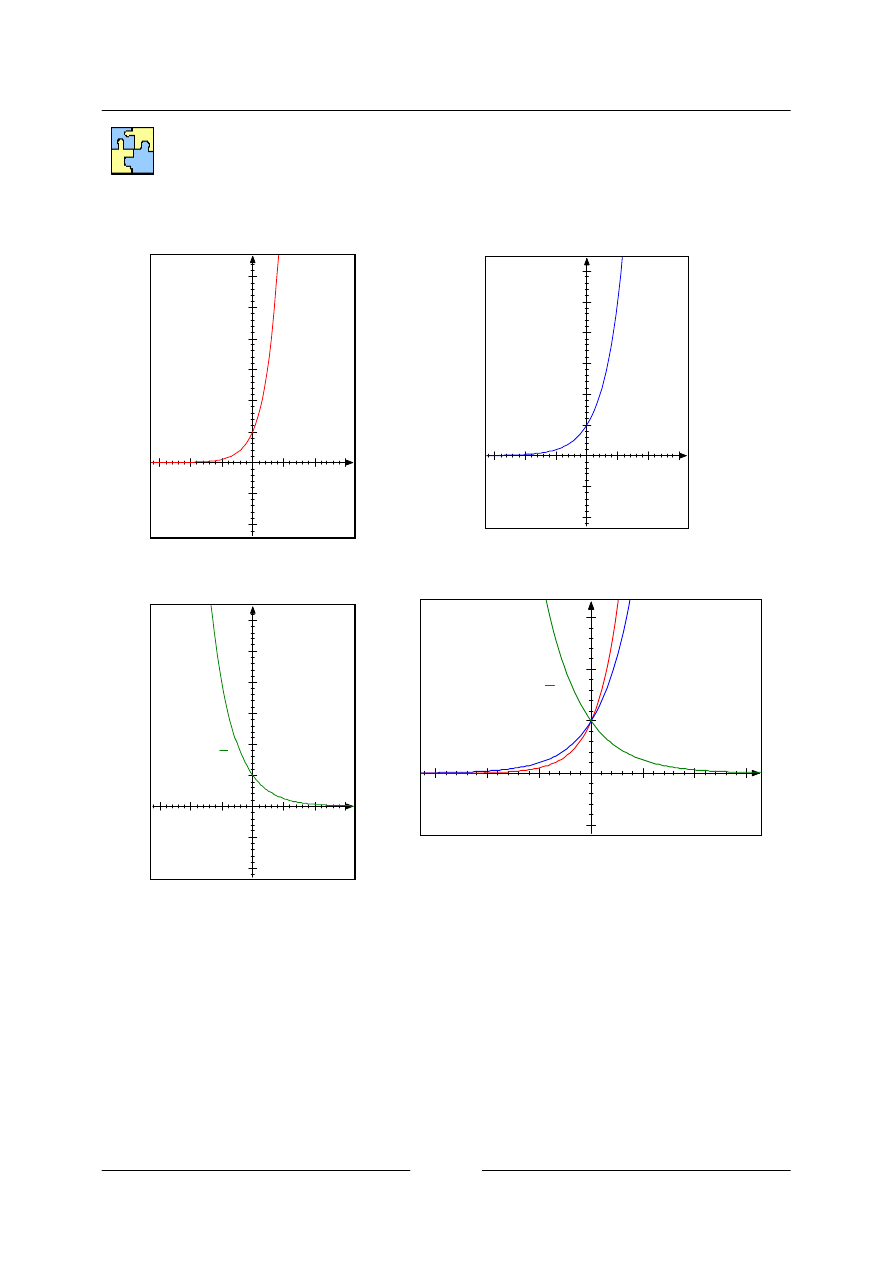
3.13.

a)

b)

c)

Srovnání průběhu grafů

-1

-2

-3

1

2

-1

1

2

0

x

y

-1

-2

-3

1

2

-1

1

2

0

x

y

10

x

5

x

(

1
4

)

x

-1

-2

-3

1

2

-1

-2

1

2

3

4

5

0

x

y

-1

-2

-3

1

2

-1

-2

1

2

3

4

5

0

x

y

(

1
4

)

x

-1

-2

-3

1

2

-1

-2

1

2

3

4

5

0

x

y

-1

-2

-3

1

2

-1

-2

1

2

3

4

5

0

x

y

5

x

-1

-2

-3

1

2

-1

-2

1

2

3

4

5

0

x

y

-1

-2

-3

1

2

-1

-2

1

2

3

4

5

0

x

y

10

x