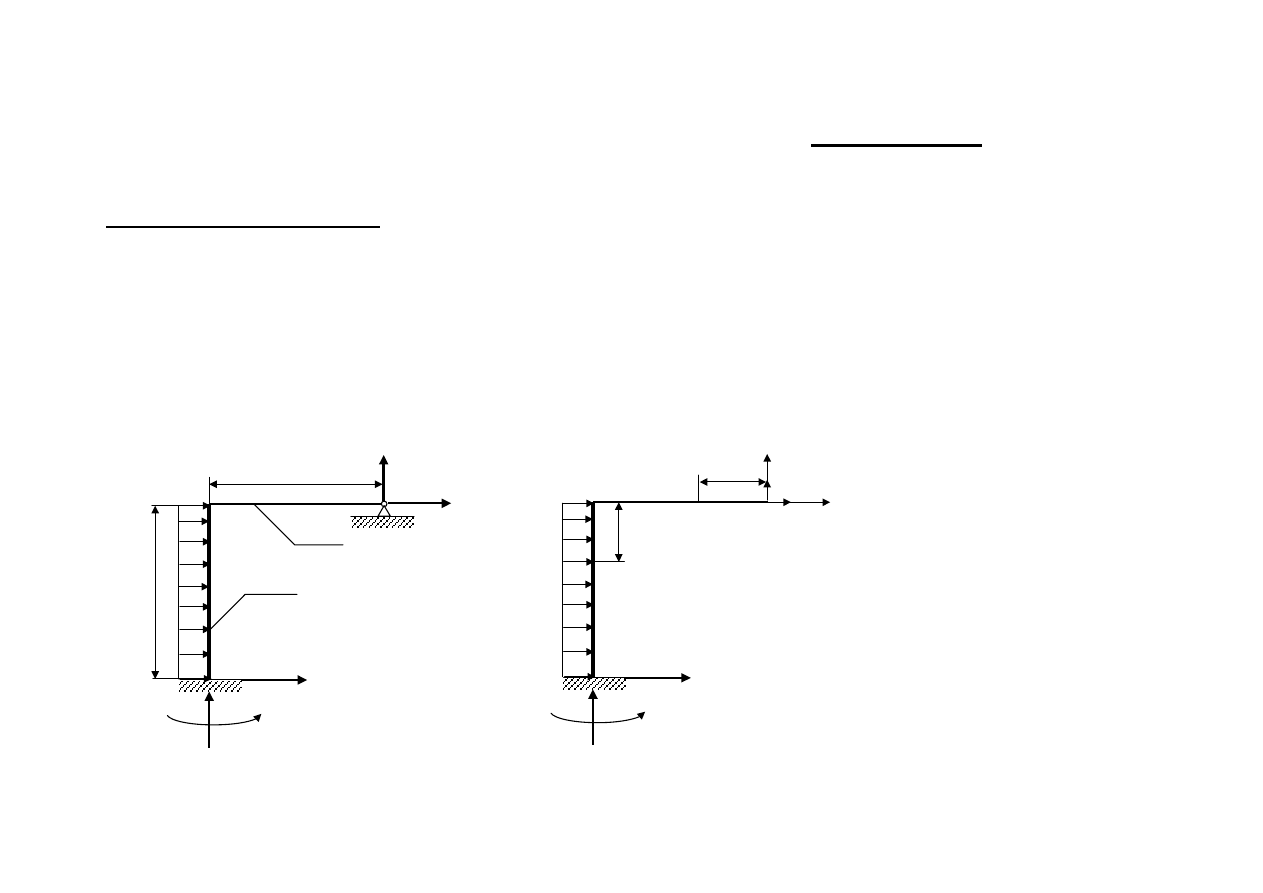
Układy statycznie niewyznaczalne. Metoda sił

Zakres zastosowań. Dowolne układy prętowego statycznie

niewyznaczalne. Implementacje numeryczne.

Przykład zastosowania. Rama płaska.
Dane: q, l, EI.
Wyznaczyć: reakcje podpór, wykresy sił wewnętrznych i kąt obrotu

przekroju C.

M

A

V

A

A

H

A

2EI

l

q

V

C

H

C

EI

l

C

B

M

A

V

A

A

H

A

X

1

q

u

2

X

2

x

C

B

x

u

1

Rzeczywisty układ

pr

ę

towy

Podstawowy układ

pr

ę

towy

Rozwiązanie

1. Określenie rodzaju i liczby wielkości podporowych i sformułowanie

równań równowagi

W punkcie C jest podpora przegubowa, w której występują reakcje H

C

(pozioma) oraz V

C

(pionowa). W punkcie A rama jest utwierdzona, a

więc występują tam reakcje H

A

(pozioma), V

A

(pionowa) i moment

utwierdzenia M

A

. Po oswobodzeniu z więzów rama (rzeczywisty układ

prętowy) jest w równowadze pod działaniem znanego obciążenia
równomiernie rozłożonego q oraz pięciu niewiadomych wielkości
podporowych H

C

, V

C

, H

A

, V

A

, M

A

. Tworzą one płaski układ sił, dla

którego można zapisać trzy równania równowagi statycznej:

0

=

+

+

ql

H

H

C

A

0

=

+

C

A

V

V

0

2

1

2

=

+

−

−

A

C

C

M

ql

l

H

l

V

2. Określenie stopnia statycznej niewyznaczalności i utworzenie

podstawowego układu prętowego

Liczba niewiadomych reakcji wynosi 5, a liczba równań równowagi 3.
Rama jest dwukrotnie statycznie niewyznaczalna (hiperstatyczna). Jako
wielkości hiperstatyczne przyjmujemy X

1

= H

C

i X

2

= V

C

. Usuwamy

więzy, które powodują powstawanie wielkości hiperstatycznych i
tworzymy w ten sposób układ podstawowy (statycznie wyznaczalny).
W przypadku rozważanej ramy oznacza to umożliwienie swobodnego
przemieszczania się punktu C w kierunku poziomym (odpowiadającym
X

1

) oraz pionowym (odpowiadającym X

2

), czyli oswobodzenie tego

punktu.

3. Określenie warunków geometrycznych oraz związków fizycznych

i sformułowanie równań kanonicznych metody sił

Układ podstawowy będzie równoważny układowi rzeczywistemu ramy
przy takich wartościach X

1

i X

2

, dla których są spełnione warunki

geometryczne:

0

,

0

2

1

=

=

u

u

Związki fizyczne, które określają przemieszczenie u

1

i u

2

jako liniowe

funkcje X

1

i X

2

oraz znanego obciążenia równomiernie rozłożonego q:

F

X

f

X

f

u

1

2

12

1

11

1

∆

+

+

=

F

X

f

X

f

u

2

2

22

1

21

2

∆

+

+

=

Po uwzględnieniu związków fizycznych w warunkach geometrycznych
otrzymujemy równania kanoniczne metody sił:

0

1

2

12

1

11

=

∆

+

+

F

X

f

X

f

0

2

2

22

1

21

=

∆

+

+

F

X

f

X

f

f

11

, f

12

– liczby wpływowe X

1

, X

2

na przemieszczenie u

1

f

21

, f

22

– liczby wpływowe X

1

, X

2

na przemieszczenie u

2

∆

1F

, ∆

2F

– część przemieszczeń u

1

, u

2

spowodowana działaniem

znanego obciążenia q.

Równań kanonicznych można napisać tyle, ile jest wielkości
hiperstatycznych.
Przyczyny powstawanie reakcji więzów oraz sił wewnętrznych i
naprężeń w przekrojach prętów układu prętowego statycznie
niewyznaczalnego:
– obciążenia zewnętrzne
– niedokładność wymiarów – naprężenia montażowe
– zmiany temperatury – naprężenia termiczne

4. Wyznaczenie współczynników równań kanonicznych metody sił

Liczby wpływowe f

11

, f

12

, f

21

, f

22

, określają własności sprężyste układu

podstawowego oraz równoważnego układu rzeczywistego.

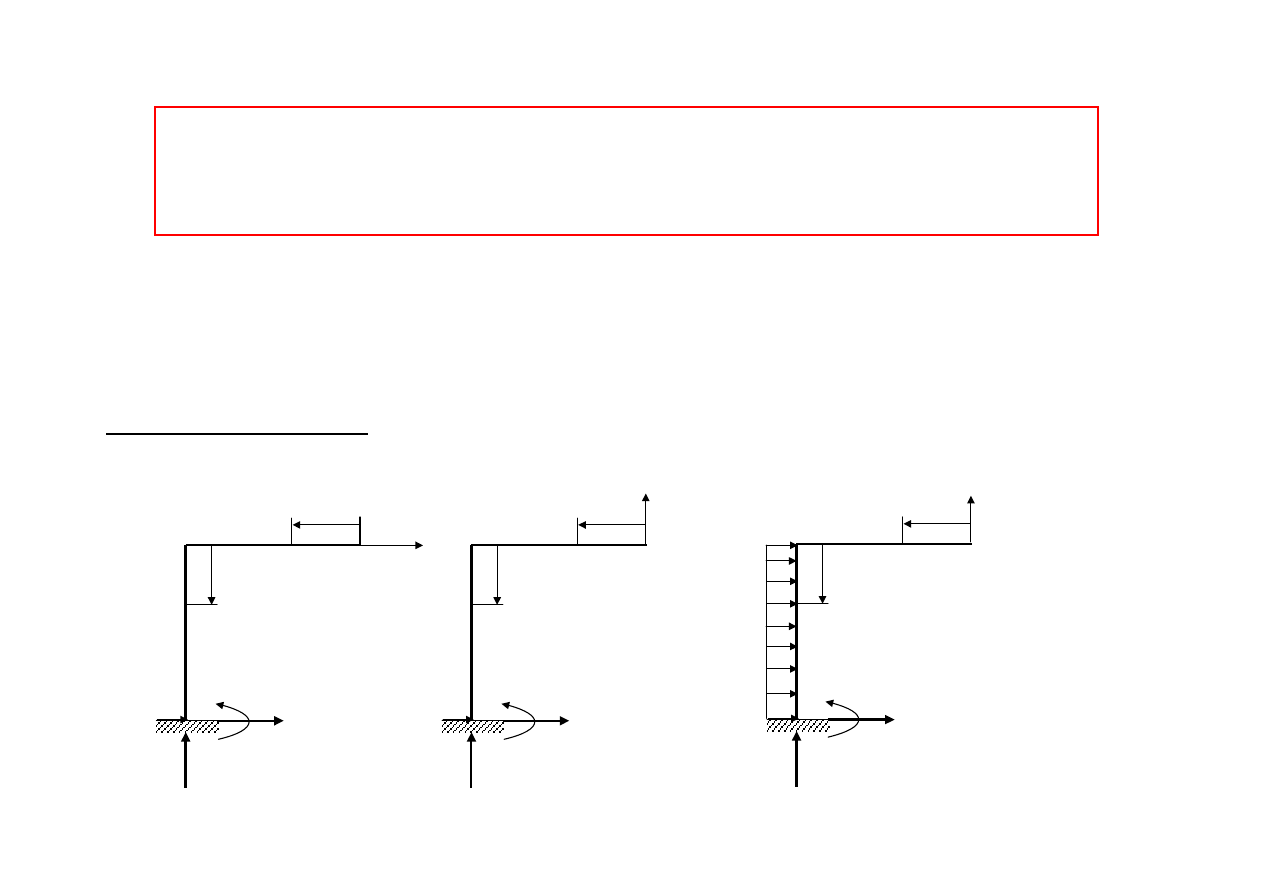
Są one przemieszczeniami w statycznie wyznaczalnym układzie

podstawowym, spowodowanymi jednostkowymi siłami

hiperstatycznymi lub znanymi obciążeniami zewnętrznymi

Można je wyznaczyć metodą Maxwella-Mohra.
Rozważamy układ podstawowy obciążony kolejno siłami X

1

= 1, X

2

= 1

oraz q.
Przypadek ogólny: liczba wariantów obciążeń układu podstawowego o
jeden większa od liczby wielkości hiperstatycznych.

M

A1

V

A1

l,EI

H

A1

X

1

=1

x

l, 2EI

x

M

A2

V

A2

l,EI

H

A2

X

2

= 1

x

l, 2EI

x

M

Aq

V

Aq

H

Aq

q

x

x

l,EI

l, 2EI

Założenia:
– uwzględniamy tylko energię sprężystą zginania
– w każdym wariancie obciążenia identyczne przedziały 1 i 2 oraz

współrzędne x określające położenie przekroju pręta. Przedział 1 –
pręt poziomy BC, przedział 2 – pręt pionowy BA. W obydwu
przedziałach

l

x

≤

≤

0

. Przyjmujemy ponadto, że

– moment gnący M

g

dodatni zakrzywia, a ujemny prostuje ramę.

Rezultat: momenty gnące zależą wyłącznie od X

1

= 1, X

2

= 1 albo q.

Nie ma potrzeby wyliczania pozostałych reakcji

Dla siły hiperstatycznej X

1

= 1 momenty gnące wynoszą:

x

M

M

g

g

=

=

21

11

,

0

Dla siły hiperstatycznej X

2

= 1:

l

M

x

M

g

g

−

=

−

=

22

12

,

Dla obciążenia zewnętrznego q:

2

2

1

2

1

,

0

qx

M

M

F

g

F

g

=

=

Siły X

1

= 1, X

2

= 1

– przyczyna wywołująca moment gnący
– uogólniona siła jednostkowa odpowiadająca przemieszczeniu

Współczynniki równań kanonicznych.

f

12

– siła X

2

= 1 – przyczyna powodująca przemieszczenie (momenty

gnące M

g12

, M

g22

)

– siła X

1

= 1 – siła jednostkowa odpowiadającą przemieszczeniu

(momenty gnące M

g11

, M

g21

).

21

3

0

21

22

0

11

12

12

4

2

1

1

f

EI

l

dx

M

M

EI

dx

M

M

EI

f

l

g

g

l

g

g

=

−

=

+

=

∫

∫

Pozostałe współczynniki równań kanonicznych:

EI

l

dx

M

EI

dx

M

EI

f

l

g

l

g

6

2

1

1

3

0

2

21

0

2

11

11

=

+

=

∫

∫

EI

ql

dx

M

M

EI

dx

M

M

EI

l

g

F

g

l

g

F

g

F

16

2

1

1

∆

4

0

21

2

0

11

1

1

=

+

=

∫

∫

EI

l

dx

M

EI

dx

M

EI

f

l

g

l

g

6

5

2

1

1

3

0

2

22

0

2

12

22

=

+

=

∫

∫

EI

ql

dx

M

M

EI

dx

M

M

EI

l

g

F

g

l

g

F

g

F

12

2

1

1

∆

4

0

22

2

0

12

1

2

−

=

+

=

∫

∫

5. Wyznaczenie z równań kanonicznych metody sił wielkości

hiperstatycznych

Po uwzględnieniu znanych już współczynników w równaniach
kanonicznych można wyznaczyć z nich wielkości hiperstatyczne X

1

i X

2

:

C

C

V

ql

ql

X

H

ql

ql

X

EI

ql

X

EI

l

X

EI

l

EI

ql

X

EI

l

X

EI

l

=

−

≅

−

=

=

−

≅

−

=

⇒

=

−

+

−

=

+

−

023

,

0

44

1

409

,

0

22

9

0

12

6

5

4

0

16

4

6

2

1

4

2

3

1

3

4

2

3

1

3

Równanie kanoniczne metody sił w zapisie rachunku macierzowego

F

F

∆

−

=

⇒

=

∆

+

−

1

F

X

0

FX













=

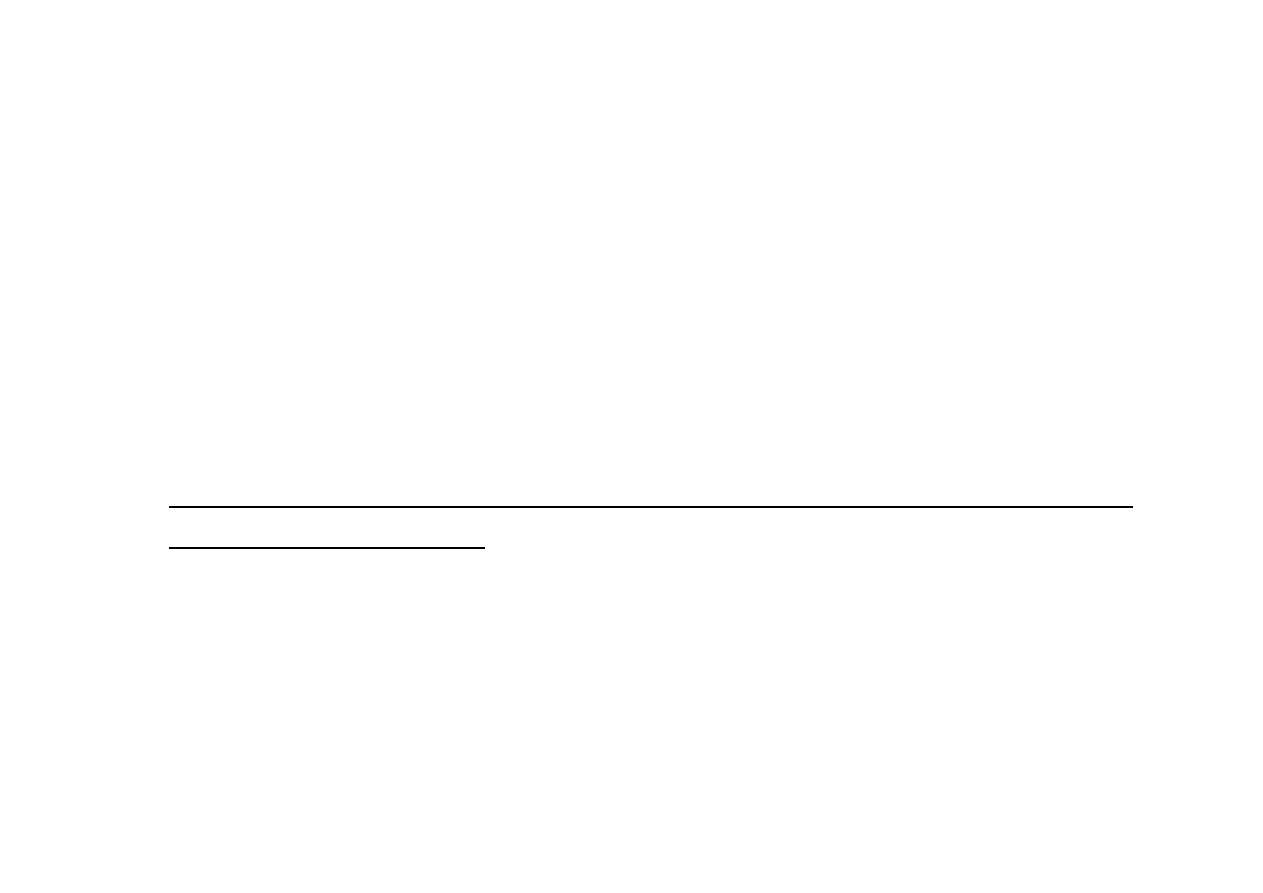
22

21

12

11

f

f

f

f

F

– macierz podatności układu podstawowego

obciążonego tylko siłami X

1

, X

2

X = [X

1

X

2

]

T

– jednokolumnowa macierz wielkości hiperstatycznych

∆

F

= [∆

1F

∆

2F

]

T

– jednokolumnowa macierz przemieszczeń

spowodowanych obciążeniem rzeczywistym,
odpowiadających wielkościom hiperstatycznym.

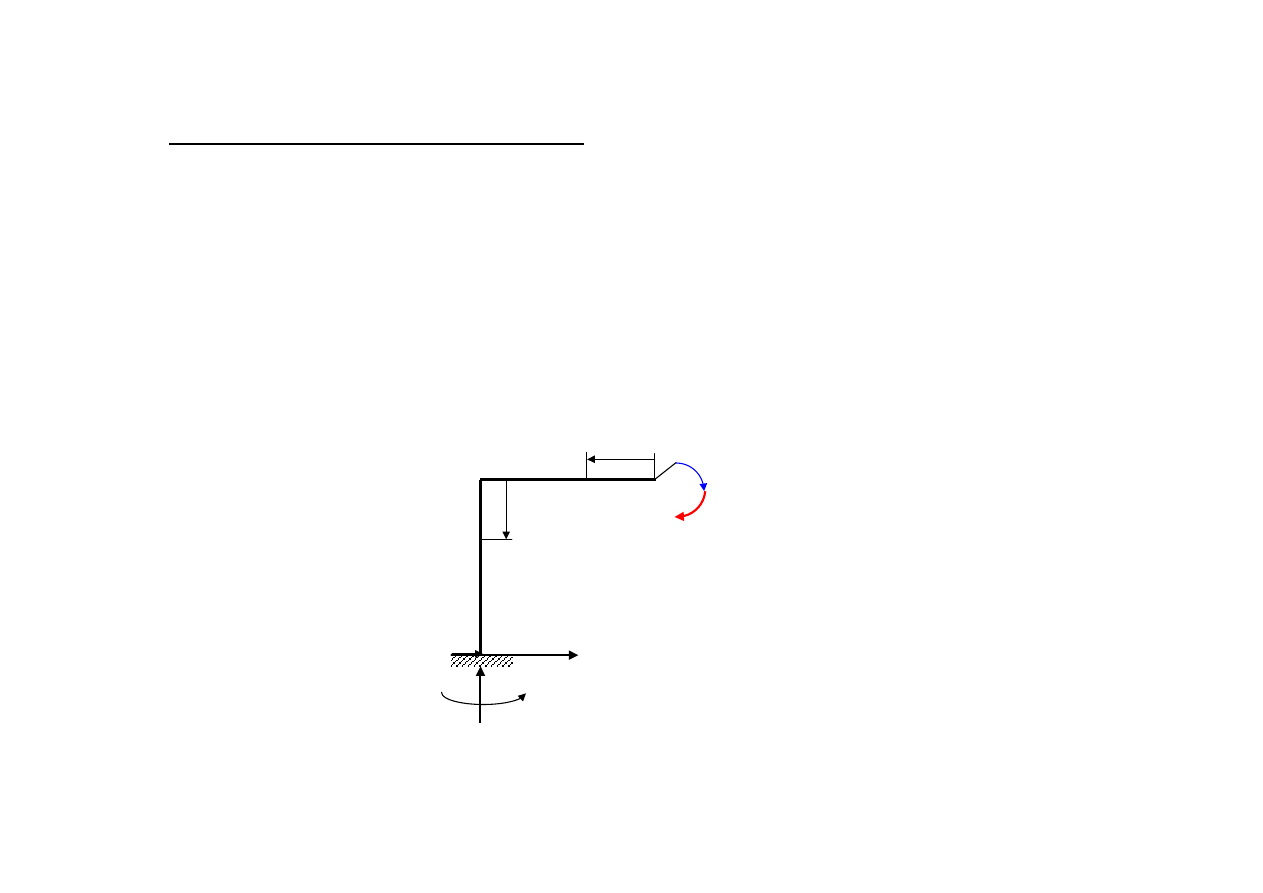
6. Wyznaczenie pozostałych sił niewiadomych, na podstawie równań

równowagi statycznej.

ql

ql

H

H

C

A

591

,

0

−

=

−

−

=

ql

V

V

C

A

023

,

0

=

−

=

2

2

114

,

0

2

1

ql

ql

l

H

l

V

M

C

C

A

=

+

+

−

=

7. Sformułowanie równań i narysowanie wykresów sił wewnętrznych.

Przedział 1 (

l

x

≤

≤

0

)

qlx

x

X

M

g

023

,

0

2

1

=

−

=

dla x = 0, M

g1

= 0, dla x = l,

2

1

023

,

0

ql

M

g

=

ql

X

T

023

,

0

2

1

=

−

=

ql

X

N

409

,

0

1

1

−

=

=

Przedział 2 (

l

x

≤

≤

0

)

2

2

2

2

1

2

2

1

44

1

22

9

2

1

qx

ql

qlx

qx

l

X

x

X

M

g

+

+

−

=

+

−

=

dla x = 0,

2

2

023

,

0

ql

M

g

=

, dla x = l,

2

2

114

,

0

ql

M

g

=

l

x

qx

ql

dx

dM

ekstr

g

409

,

0

0

22

9

2

=

⇒

=

+

−

=

Ponieważ

0

2

2

2

>

=

q

dx

M

d

g

, jest to minimum lokalne

Dla

2

min

2

2

061

,

0

,

409

,

0

ql

M

M

l

x

x

g

g

ekstr

−

=

=

=

=

qx

ql

qx

X

T

+

−

=

+

=

409

,

0

1

2

dla x = 0,

ql

T

409

,

0

2

−

=

dla x = l,

ql

T

591

,

0

2

=

2

2

2

023

,

0

ql

X

N

=

=

0,114ql

2

0,409l

0,023ql

2

-0,061ql

2

Wykres M

g

0,591ql

0,023ql

-0,409ql

Wykres T

-0,023ql

-0,409ql

Wykres N

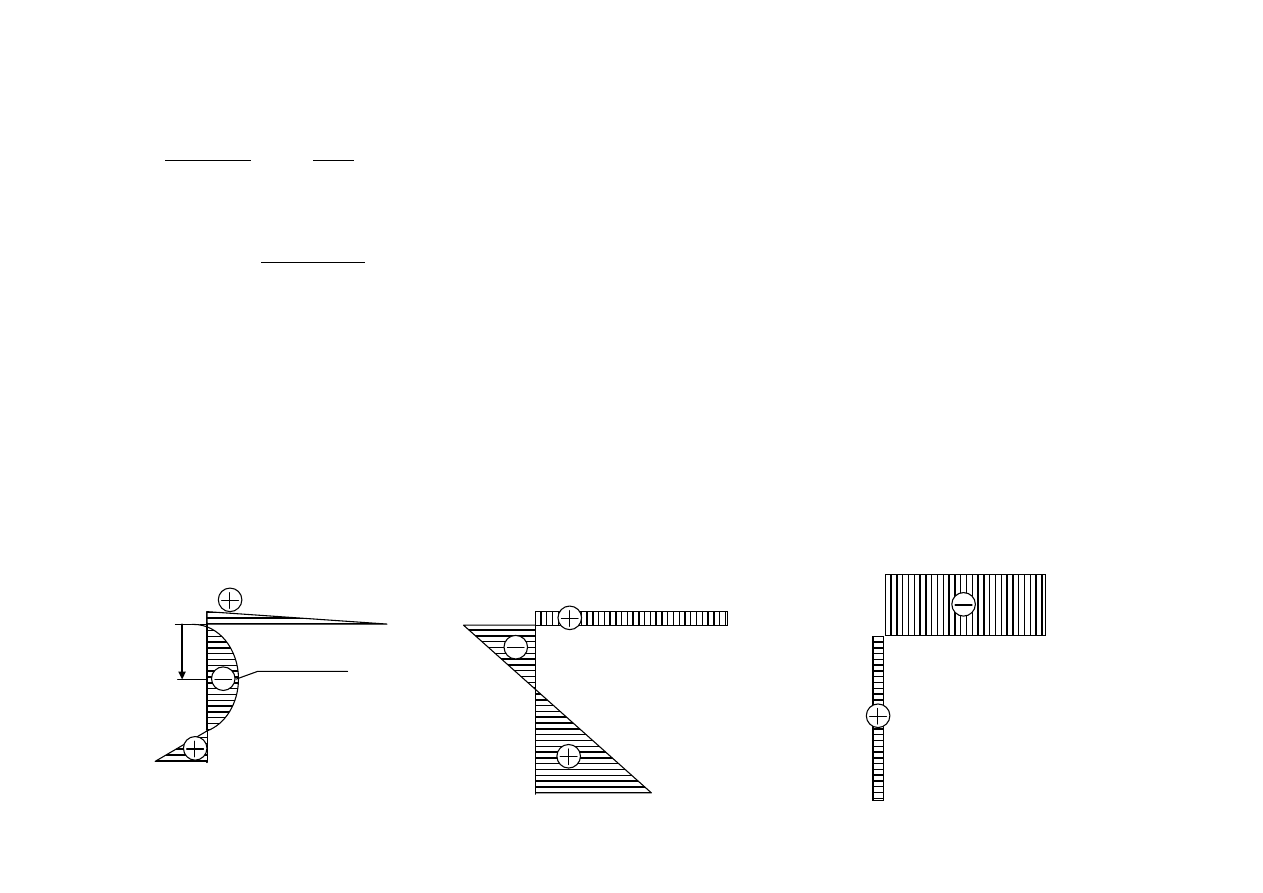
8. Wyznaczenie przemieszczeń

Aby wyznaczyć metodą Maxwella-Mohra kąt obrotu końcowego
prawego przekroju pręta BC, należy w punkcie C przyłożyć moment
jednostkowy i określić spowodowane nim momenty gnące M

’

g1

M

’

g2

w

obydwu przedziałach.
Rozważamy statycznie wyznaczalny układ podstawowy.

M’

A

V’

A

l,EI

H’

A

x

l, 2EI

x

A

B

C

u

1

Momenty gnące spowodowane obciążeniem q i znanymi siłami X

1

, X

2

(M

g1

M

g2

) oraz momentem jednostkowym, odpowiadającym kątowi

obrotu u przekroju C (M

’

g1

M

’

g2

) wynoszą:

1

,

44

1

1

1

=

′

=

g

g

M

qlx

M

1

,

2

1

44

1

22

9

2

2

2

2

=

′

+

+

−

=

g

g

M

qx

ql

qlx

M

Przemieszczenie uogólnione u (kąt obrotu w punkcie C) wyznaczone
metodą Maxwella-Mohra:

EI

ql

dx

M

M

EI

dx

M

M

EI

u

l

g

g

l

g

g

264

2

1

1

3

0

2

2

0

1

1

=

′

+

′

=

∫

∫

Przykład 1.
Rama płaska jest obciążona dwoma równymi, przeciwnie zwróconymi i
leżącymi na jednej prostej siłami F. Narysować wykresy sił
wewnętrznych, jeśli wszystkie pręty mają długość l, a sztywność na

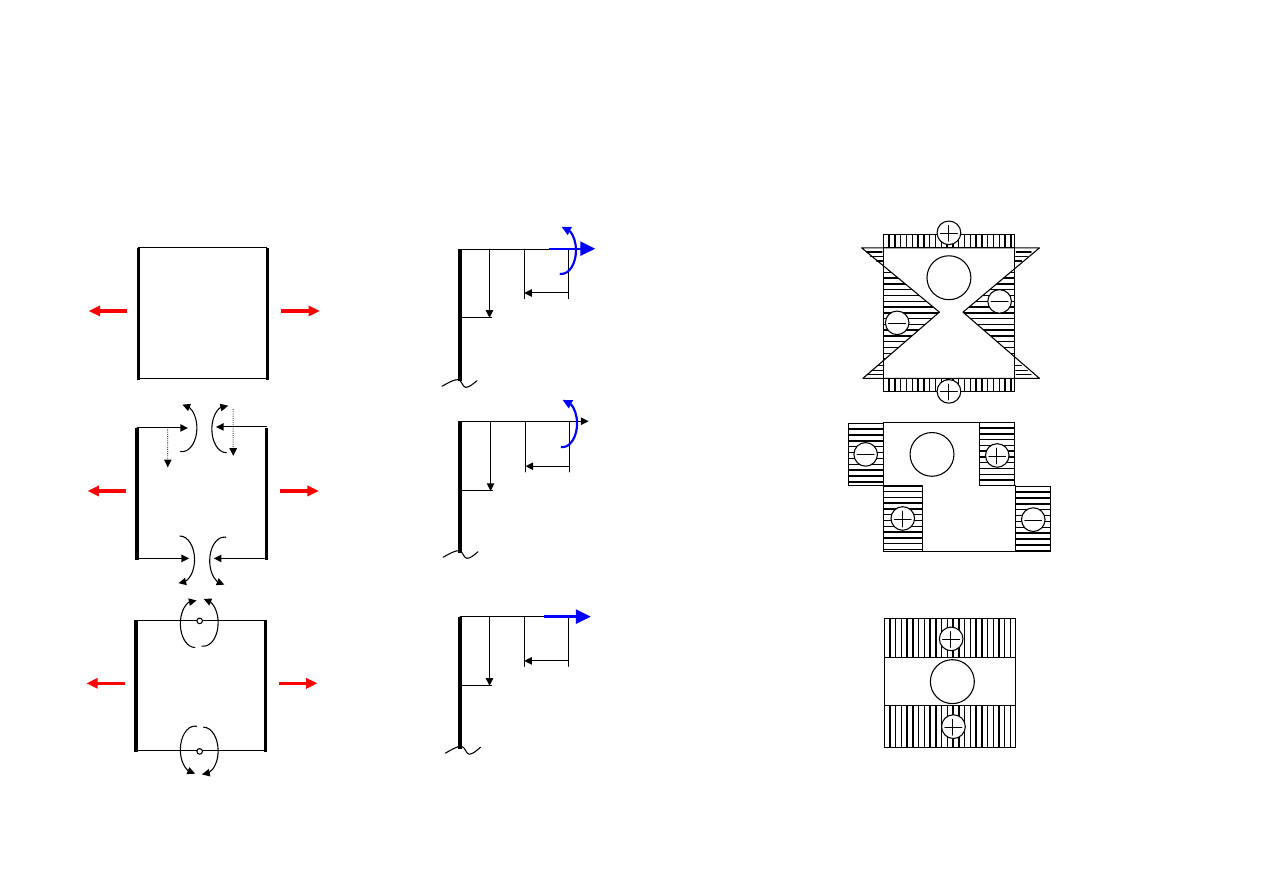
zginanie prętów poziomych oraz pionowych wynoszą odpowiednio EI
oraz 2EI.

F

F

F

F

F

F

M

N

X

M

M

?

?

T = 0

M M

F/2

X

1

x

x

1

l/2

2

l/2

Przedziały w

ć

wiartce ramy

X

1

= 1

x

x

1

l/2

l/2

F/2

x

x

1

l/2

l/2

2

2

M

g

Fl/24

-11Fl/24

-F/2

N

F/2

F/2

-F/2

T

F/2

F/2

Rozwiązanie. „Przecinamy” ramy pionową płaszczyzną symetrii

Z warunków równowagi:

N = F/2

T = 0

Moment gnący M – wielkość hiperstatyczna X

1

.

Układ podstawowy – swobodny wzajemny obrót lewej i prawej strony
rozważanego przekroju.
Warunek geometryczny: przy obciążeniu siłami X

1

i F wzajemny kąt

obrotu u

1

lewej i prawej strony przekroju jest równy zeru

Równanie kanoniczne metody sił:

0

∆

1

1

11

1

=

=

+

u

f

X

F

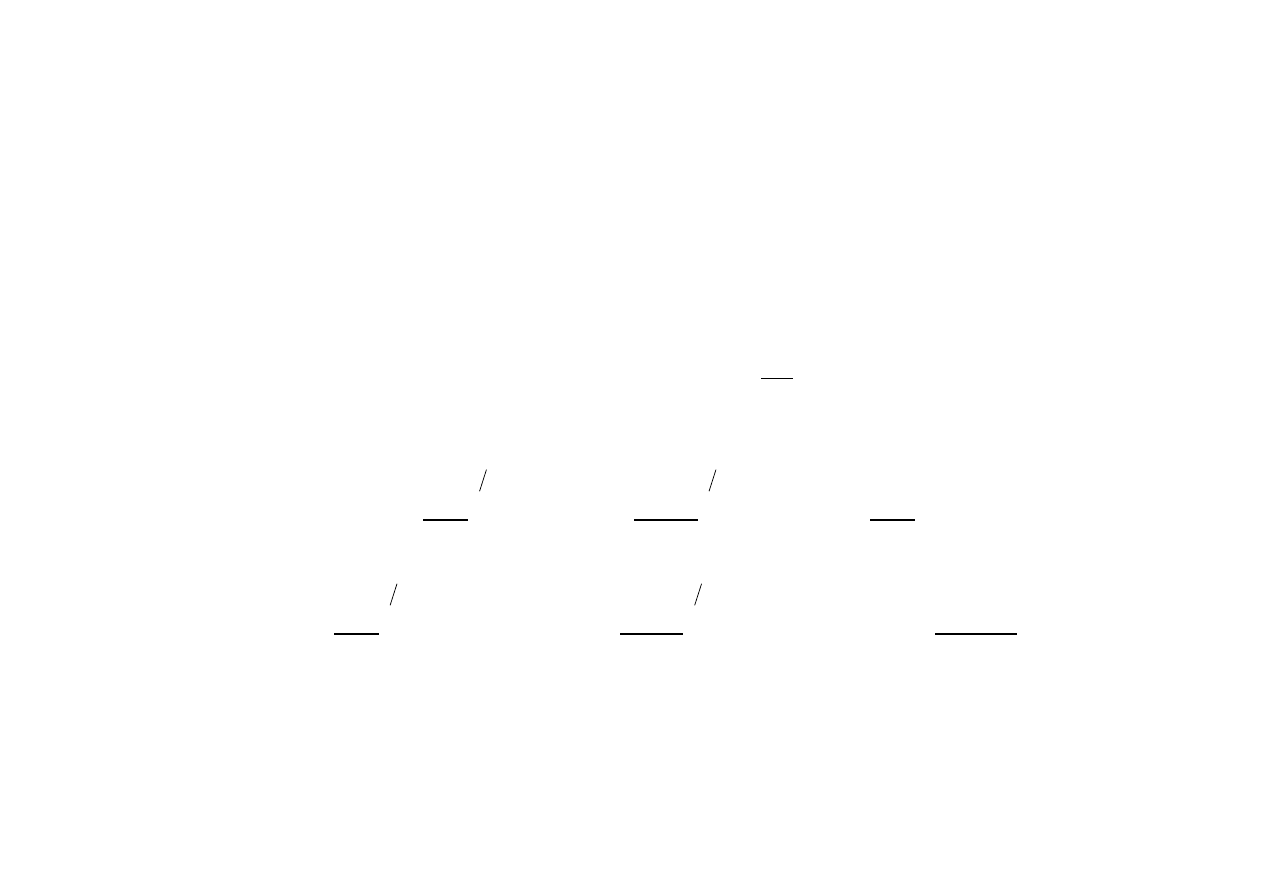
Metoda Maxwella-Mohra – energia dla ćwiartki ramy i wynik mnożymy
przez cztery. Równania momentów gnących wywołanych siłą X

1

= 1

oraz obciążeniem F w przedziałach 1, 2
Dla 0< x< l/2

x

F

M

M

M

M

F

g

F

g

g

g

2

,

0

1

,

1

2

1

21

11

−

=

=

=

=

czyli:

EI

l

dx

M

EI

dx

M

EI

f

l

g

l

g

3

2

4

4

2

0

2

21

2

0

2

11

11

=

+

=

∫

∫

EI

Fl

dx

M

M

EI

dx

M

M

EI

l

g

F

g

l

g

F

g

F

8

2

4

4

∆

2

2

0

21

2

2

0

11

1

1

−

=

+

=

∫

∫

Z równania kanonicznego:

24

0

8

3

1

2

1

Fl

M

X

EI

Fl

EI

lX

=

=

⇒

=

−

−

Równania momentów gnących M

g

sił poprzecznych T i normalnych N

mają postać:

x

F

Fl

M

Fl

M

g

g

2

24

,

24

2

1

−

=

=

2

,

0

2

1

F

T

T

−

=

=

0

,

2

2

1

=

=

N

F

N

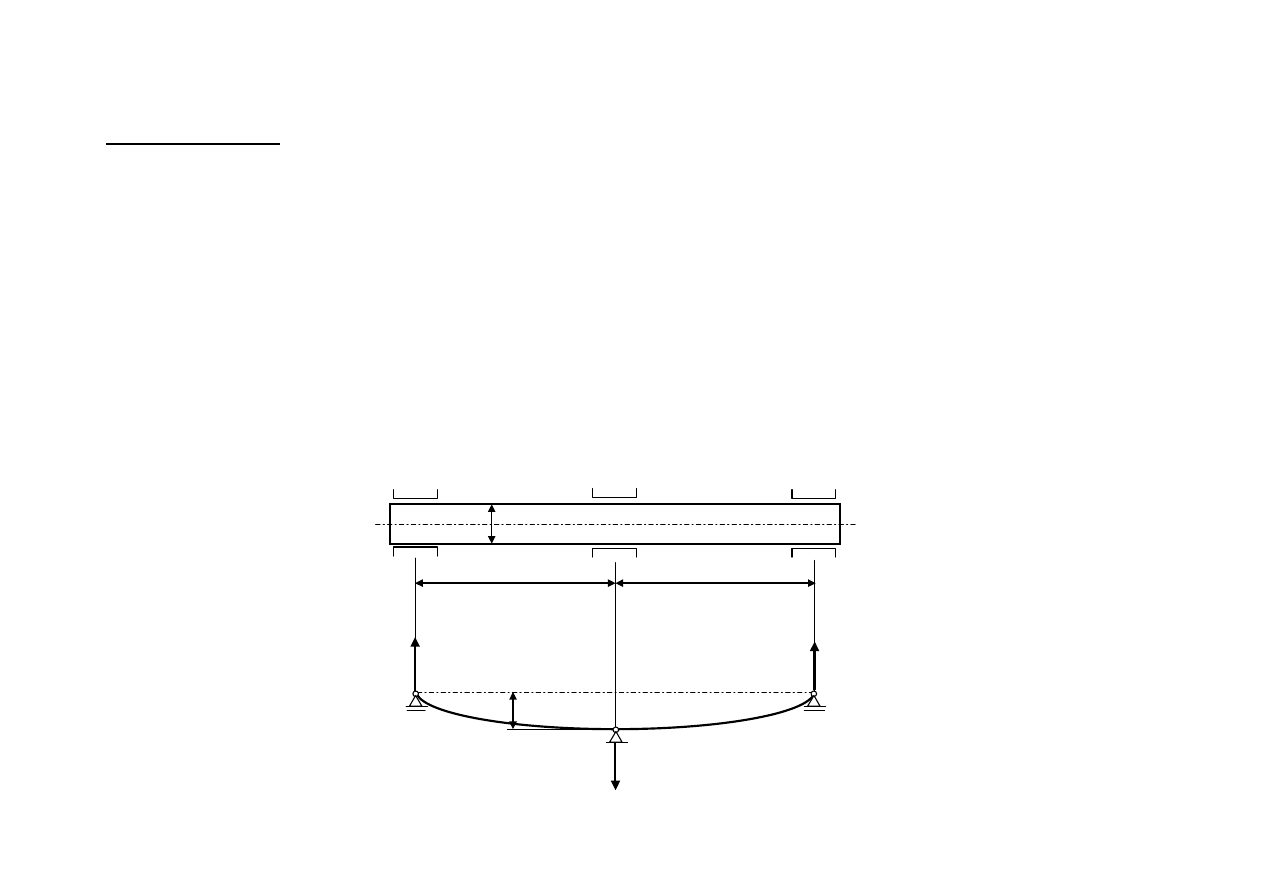
Przykład 2. Wałek o długości l i średnicy d, wykonany z materiału o
współczynniku sprężystości podłużnej E, jest osadzony w trzech
łożyskach. Obliczyć maksymalne naprężenie normalne w wałku po jego
zmontowaniu, jeśli oś łożyska środkowego jest przesunięta o δ
względem osi dwóch pozostałych łożysk.

Rozwiązanie. Wałek modelowany jako belka na trzech podporach.
Wystąpią reakcje R

A

, R

B

, R

C

.

A

d

l/2

l/2

R

A

B

R

B

= X

1

R

C

C

δ

ło

ż

ysko

Warunek równowagi: R

A

= R

C

= R

B

/2

Zadanie jednokrotnie statycznie niewyznaczalne.

Wielkość hiperstatyczna: R

B

= X

1

Równanie kanoniczne metody sił:

δ

=

=

+

1

1

11

1

∆

u

f

X

F

Warunek geometryczny, aby można było zmontować wałek.

Liczba wpływowa f

11

– ugięcie belki o rozpiętości l i sztywności EI

podpartej swobodnie na końcach i obciążonej w środku siłą X

1

= 1

EI

l

f

48

3

11

=

.

Przemieszczenie ∆

1F

= 0 – nie ma obciążenia zewnętrznego:

3

3

1

3

1

24

,

48

48

l

EI

R

R

R

l

EI

X

EI

l

X

C

A

B

δ

δ

δ

=

=

=

=

⇒

=

Moment gnący osiąga wartość maksymalną w przekroju środkowym
wałka i wynosi:

2

max

12

2

l

EI

l

R

M

A

g

δ

=

=

Maksymalne montażowe naprężenie normalne w wałku wynosi:

2

max

max

max

6

2

l

d

E

I

d

M

W

M

g

g

δ

σ

=

=

=