Przewodnik do ćwiczeń kameralnych z dendrometrii

dla studentów Zawodowych Studiów Zaocznych

W trakcie trwania ćwiczeń kameralnych studenci są zobowiązani złożyć dwie prace

kontrolne. Jedną dotyczącą określania miąższości strzał i kłód drzewa leżącego i stojącego oraz

drugą dotyczącą określania elementów miąższości i miąższości oraz przyrostu miąższości

drzewostanu. W przewodniku starano się przedstawić (na konkretnym przykładzie) sposób

wykonania tych prac wraz z pewnymi uwagami. Bardziej szczegółowe wyjaśnienia niektórych

zagadnień można znaleźć w podręczniku "Dendrometria" A. Bruchwalda.

Praca kontrolna nr 1

1. Przedstawić graficznie dokładność teoretyczną wzorów:

Środkowego przekroju, Smaliana i Hossfelda.

2. Obliczyć wzorami: środkowego przekroju, Smaliana i Hossfelda

a) miąższość strzały w korze i bez kory,

b) miąższość kłody odziomkowej (0 - 8 m) w korze i bez kory,

c) miąższość kłody środkowej (8 - 16 m) w korze i bez kory.

3. Ocenić dokładność wzorów na drodze empirycznej.

4. Wyjaśnić przyczyny błędów i wyciągnąć wnioski.

5. Obliczyć pierśnicową liczbą kształtu

a) strzały w korze (F

1

),

b) strzały bez kory (F

2

),

2

c) strzały bez kory (F

3

),

d) grubizny strzały (F

g

).

6. Obliczyć właściwą liczbę kształtu strzały w korze (n = 10).

7. Obliczyć absolutną liczbą kształtu strzały w korze.

8. Obliczyć miąższość strzały w korze

a) wzorem Denzina,

b) tablicami miąższości (B. Radwański).

9. Obliczyć miąższość strzały bez kory tablicami B. Radwańskiego.

10. Obliczyć miąższość grubizny drzewa na podstawie wymiarów pniaka bez kory.

11. Ocenić na drodze empirycznej dokładność zastosowanych sposobów określania miąższości i

wyjaśnić przyczyny błędów.

Do wykonania tej pracy każdy student otrzyma materiał empiryczy dotyczący pomiaru drzewa

leżącego w korze i bez kory w sekcjach 1-merowych, na przykład:

3

Numer drzewa: 112

Wiek: 95 lat

Wysokość 1962: 25,88 m

Odległość środka sekcji

od przekroju ścięcia

Grubość

w korze (w mm)

bez kory (w mm)

0,0
1,3

398
260

308
233

0,5
1,5
2,5
3,5
4,5
5,5
6,5
7,5
8,5
9,5

10,5
11,5
12,5
13,5
14,5
15,5
16,5
17,5
18,5
19,5
20,5
21,5
22,5
23,5
24,5

307
254
247
244
230
223
216
211
209
198
193
190
182
177
170
150
140
131
118
103

88
67
45
29

256
230
225
225
215
215
209
205
203
192
188
185
178
173
163
145
135
126
113

99
81
61
41
25

4

Ad 1. Należy, skorzystać z podręcznika A. Bruchwalda "Dendrometria" i przedstawić

dokładność wzorów na wykresach. Ewentualnie można spróbować, przynajmniej dla jednego

wzoru, przedstawić teoretyczną dokładność dla brył ściętych.

Ad 2a. Miąższość wzorem środkowego przekroju wyliczamy następująco:

L = H, zatem L/2 równa się 12,94 m i na tej wysokości musimy wyinterpolować grubość.

Grubość mamy podaną na wysokościach 12,5 - 182 mm i 13,5 m - 177 mm. Układamy

zależność, że 100 cm (różnica wysokości) : 5 mm (różnica grubości) ma się tak, jak 44 cm

(różnica wysokości) : x (szukana różnica grubości)

zatem x = ok. 2 mm.

Grubość na wysokości 12,94 m równa się grubości na wysokości 12,5 m minus 2 mm,

czyli 182 - 2 = 180 mm.

Grubość tę zamieniamy na pole przekroju (wzorem na pole koła lub za pomocą tablic

powierzchni kół) g = 0,0254 m

2

i mnożymy, zgodnie z wzorem, przez długość strzały

V = 0,0254 × 25,88 = 0,6574 m

3

Podobnie postępujemy przy wyliczaniu miąższości bez kory.

Miąższość wzorem Hossfelda wyliczamy według uproszczonego wzoru dla strzały

L

G

=

V

L/2

•

100

44

5

=

x

•

L

G

4

3

=

V

L/3

•

•

5

L/3 = 25,88 : 3 = 8,63 m. Grubość na wys. 8,5 m = 209 mm, a na wys. 9,5 m = 198 mm,

stąd interpolujemy:

zatem x = 1 mm

Grubość na wys. 8,63 m = grubości na wys. 8,5 m minus 1 mm, czyli 209 - 1 = 208 mm,

co odpowiada polu przekroju g = 0,0340 m

2

Podobnie dochodzimy do miąższości strzały bez kory.

Miąższość wzorem Smaliana wyliczamy także według uproszczonego wzoru dla strzały

Grubość na D

0

= 398 mm co odpowiada g = 0,1244 m

2

Podobnie postępujemy przy wyliczaniu miąższości strzały bez kory.

Uwaga! Proszę zwrócić uwagę na miąższość uzyskaną tym wzorem!

100

13

11

=

x

•

m

0,6599

=

25,88

0,034

4

3

=

V

3

•

•

L

G

2

1

=

V

0

•

•

m

1,6097

=

25,88

0,1244

2

1

=

V

3

•

•

6

Ad 2b. Aby wyliczyć miąższości kłody odziomkowej musimy wyinterpolować grubość w

połowie długości kłody, czyli na wys. 4 m (do wzoru środkowego przekroju); w _ długości

kłody, czyli na wys. 2,67 m (do wzoru Hossfelda) i na wys. 8 m do wzoru Hossfelda i Smaliana.

Grubość na wys. 3,5 m wynosi 244 mm a na wys. 4,5 m wynosi 230 mm, zatem grubość

na wys. 4 m wynosi 237 mm, co odpowiada polu przekroju g = 0,0441 m

2

Miąższość wzorem środkowego przekroju V = 0,0441 × 8 = 0,3528 m

3

Grubość na wys. 2,5 m = 247 mm, a na wys. 3,5 m = 244 mm, zatem grubość na wys. 2,67 m

wynosi po zaokrągleniu do milimetrów - 246 mm, co stanowi g

l/3

= 0,0475 m

2

, natomiast

grubość na wys. 8 m wynosi 210 mm (grubość na wys. 7,5 m = 211 mm, a na wys. 8,5 m = 209

mm) i po zamianie na pole przekroju g

l

= 0,0346 m

2

.

Miąższość kłody wzorem Hossfelda

Miąższość kłody wzorem Smaliana

l

4

g

+

g

3

=

V

l

l/3

•

•

m

0,3542

=

8

4

0,0346

+

0,0475

3

=

V

3

•

•

l

2

g

+

g

=

V

l

0

•

m

0,636

=

8

2

0,0346

+

0,1244

=

V

3

•

7

Ad 2c. Przy wyliczaniu miąższości kłody środkowej postępujemy podobnie jak przy wyliczaniu

miąższości kłody odziomkowej tzn. interpolujemy odpowiednie grubości (na 10,67 m do wzoru

Hossfelda, na 12 m do wzoru środkowego przekroju i na 16 m do wzoru Hossfelda i Smaliana,

ponieważ grubość na wysokości 8 m do wzoru Smaliana mieliśmy już wyliczoną w zadaniu 2b,

zamieniamy je na pola przekroju i podstawiamy do odpowiednich wzorów dla brył ściętych.

Np: miąższość wzorem środkowego przekroju

V = g

l/2

× l; d

l/2

= d

12 m

= 186 mm (grubość na wys. 11,5 m = 190 mm, a na wys.

12,5 = 182 mm), g

12 m

= 0,0272 m

2

,

zatem

Pozostałe miąższości wyliczamy jak w pkt 2b.

Dla ułatwienia wyliczeń miąższości poszczególnymi wzorami dobrze jest wcześniej

wyinterpolować sobie potrzebne grubości i zestawić w tabelce np:

Wysokość

pomiaru

w korze

bez kory

d (grubość) g (pole przekroju)

d (grubość) g (pole przekroju)

Strzała

0,0

8,63

12,94

398

0,1244

308

0,0745

Kłoda odziomkowa

0,0

2,67
4,00
8,00

398
246

0,1244
0,0475

308

0,0745

Kłoda środkowa

8,00

10,67
12,00
16,00

210

0,0346

204

0,0327

m

0,2176

=

8

0,0272

=

V

3

•

8

Ad 3. Ażeby ocenić dokładność wzorów na drodze empirycznej musimy wyliczyć miąższości

rzeczywiste strzał i kłód. Za miąższości rzeczywiste przyjmiemy miąższości wyliczone wzorem

sekcyjnym środkowego przekroju przy długości sekcji 1 m. Ogólna postać wzoru

gdzie:

V

s

- miąższość wyliczona sekcyjnie,

V

w

- miąższość niepełnej sekcji (miąższość wierzchołka),

g

1

, g

2

, - pola przekroju w środku każdej pełnej sekcji.

( )

V

+

g

l

=

V

w

1

s

s

•

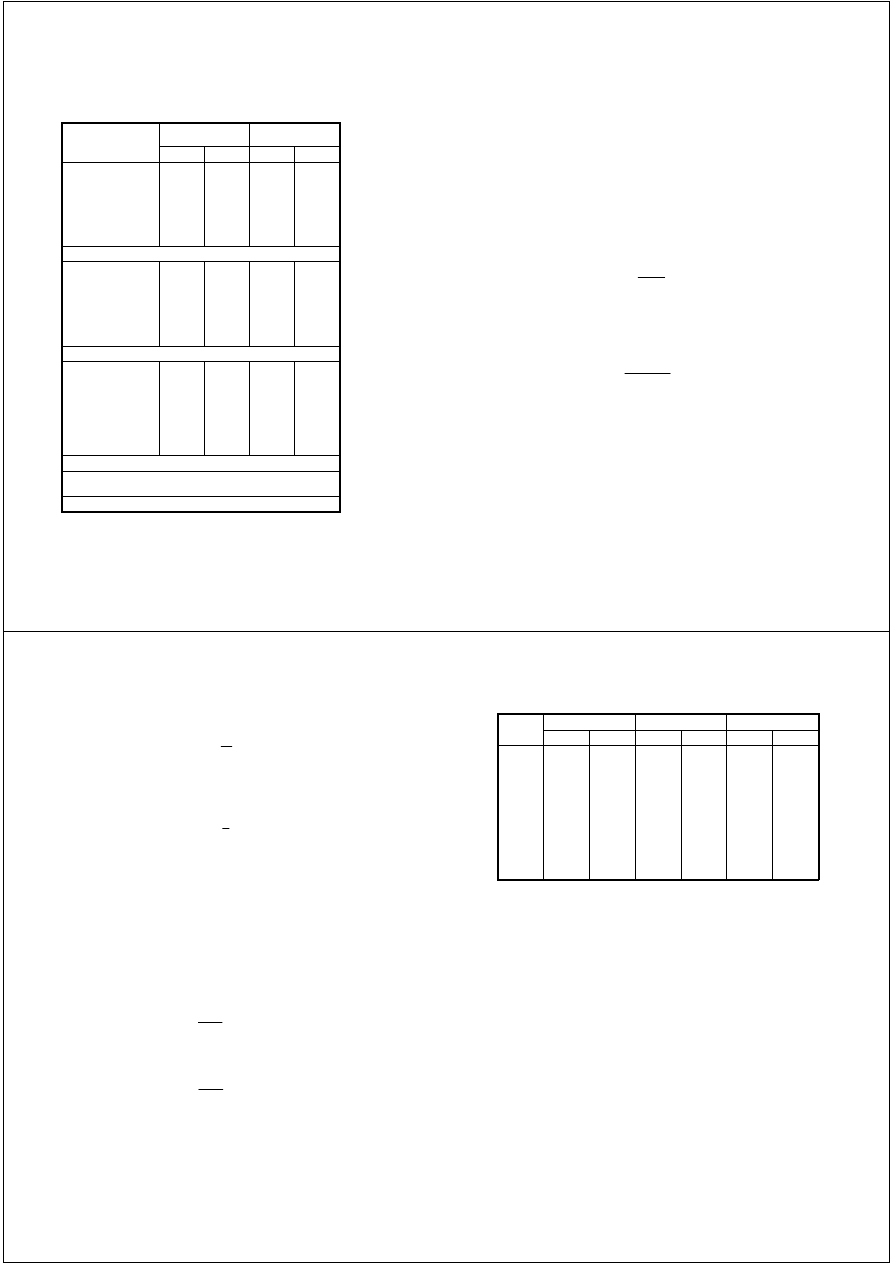
9

Tabela 1. Miąższości rzeczywiste kłód i strzały dla drzewa z przykładu

Odległość środka sekcji

od przekroju ścięcia

w korze

bez kory

grubość

przekrój

grubość

przekrój

0,5
1,5
2,5
3,5
4,5
5,5
6,5
7,5

307
254
247
244
230
223
216
211

0,0740

507
479
468
415
391
366
350

256
230
225
225
216
215
209
205

0,0515

415
398
398
366
363
343
330

suma 0,3346 0,3128

8,5
9,5

10,5
11,5
12,5
13,5
14,5
15,5

209
198
193
190
182
177
170
158

343
308
293
284
260
246
227
196

203
192
188
185
178
173
163
152

324
290
278
269
249
235
209
181

suma 0,2157 0,2035

16,5
17,5
18,5
19,5
20,5
21,5
22,5
23,5
24,5

150
140
131
118
103

88
67
45
29

177
154
135
109

83
61
35
16

7

145
135
126
113

99
81
61
41
25

165
143
125
100

77
52
29
13

5

suma g pełnych sekcji 0,6280 0,5872

V

w

(miąższość niepełnej

sekcji) 0,0001 0,0001

V

s

(miąższość strzały) 0,6281 0,5873

10

Przy okazji wyliczania miąższości strzał wyliczono miąższości kłód. Ponieważ długość

sekcji wynosi 1 m to, zgodnie z wzorem sekcyjnym, suma pól przekrojów pełnych sekcji będzie

jednocześnie miąższością tych pełnych sekcji, a po dodaniu miąższości niepełnej sekcji

otrzymamy miąższość strzały. Miąższość niepełnej sekcji możemy wyliczyć (zwykłym wzorem

ś

rodkowego przekroju) lub wzorem na objętość stożka. Jeśli wyliczamy miąższości wzorem

ś

rodkowego przekroju to musimy wyinterpolować grubość na wysokości 25,44 m, czyli w

ś

rodku niepełnej sekcji, a jeśli wzorem na objętość stożka to interpolujemy grubość na

wysokości 25 m, czyli do podstawy stożka.

Wyinterpolujmy zatem grubość na wysokości 25 m. Grubość na wys. 24,5 m wynosi 29

mm i ma się to do odległości 1,33 m (wys. drzewa 25,88 m minus wysokość ostatniego pomiaru

24,5 m równa się 1,33 m), jak x do 0,5 m (różnica między wysokością podstawy stożka a

wysokością ostatniego pomiaru).

czyli 29 - 11 = 18 mm,

jest to grubość na wys. 25 m, zamieniamy to na pole przekroju g = 0,0003 m

2

i wyliczamy

miąższość wierzchołka

Zaokrąglamy do czterech miejsc po przecinku matematycznie do 0,0001 m

3

.

Jeżeli już wyliczyliśmy miąższości rzeczywiste to możemy przystąpić do empirycznej

oceny dokładności wzorów dla strzał i kłód, to znaczy do wyliczenia błędów absolutnych i

błędów procentowych. Błąd absolutny jest to różnica między miąższością wyliczoną danym

wzorem a miąższością rzeczywistą (czyli wyliczoną wzorem sekcyjnym).

mm

10,9

=

1,33

29

0,5

=

x

•

m

0,000088

=

3

0,88

0,0003

=

V

3

w

•

V

-

V

=

rz

α

11

Błąd procentowy wtórny jest to błąd absolutny wyrażony w procentach miąższości rzeczywistej,

zaś błąd procentowy zasadniczy jest to błąd absolutny wyrażony w procentach miąższości

wyliczonej danym wzorem.

Najczęściej wylicza się błąd procentowy wtórny, pozwala on bowiem porównać dokładność

różnych wzorów.

Przykład. Miąższość strzały w korze wyliczona wzorem środkowego przekroju wynosi 0,6574

m

3

, zaś miąższość rzeczywista (wyliczona wzorem sekcyjnym) wynosi 0,6281 m

3

błąd absolutny

błąd procentowy wtórny

błąd procentowy zasadniczy

W podobny sposób należy wyliczyć błędy dla strzał i kłód dla wszystkich analizowanych

wzorów.

Otrzymane wyniki najlepiej zestawić w tabelce na przykład:

100

V

=

p

rz

•

α

100

V

=

p

,

•

α

m

0,0293

=

0,6281

-

0,6574

=

3

α

4,66%

=

100

0,6281

0,0293

=

p

•

4,46%

=

100

0,6574

0,0293

=

p

,

•

12

Strzała

Kłoda odziomkowa

Kłoda środkowa

w korze

bez kory

w korze

bez kory

w korze

bez kory

V

s

V

ś

V

h

V

sm

a

p

ś

p

,

ś

a

h

p

h

p

,

h

a

sm

p

sm

p

,

sm

0,6281
0,6574
0,6599
1,6097
0,0293

4,66%
4,46%

0,5873

itd.
itd.
itd.
itd.
itd.
itd.

0,3346

0,3128

0,2157

0,2035

Ocena dokładności tych wzorów zawarta jest w tabeli, dotyczy ona jednak tylko jednej

strzały, jednej kłody. Dobrze jest otrzymane wyniki (zawarte w tabeli) porównać z wynikami

uzyskanymi dla liczniejszego materiału (np. dla Puszczy Piskiej). Sprawdzić, czy nasze wyniki

mieszczą się w granicach wyników dla tej puszczy.

Ad 4. Przyczyny błędów są trzy:

a) niedostosowanie wzoru do kształtu strzały w kierunku podłużnym,

b) niedostosowanie wzoru do kształtu strzały w kierunku poprzecznym,

c) błędy pomiarowe.

Ad 4a. Gdyby przekroje wchodzące w skład wzoru były równe przekrojowi przeciętnemu to

wzory byłyby bezbłędne. Gdyby krzywa morfologiczna strzały pokrywała się z tworzącą bryły

regularnej to błąd wynosiłby jak dla teoretycznej dokładności danego wzoru przy określonej

wartości wykładnika kształtu. Na ogół przekroje wchodzące w skład wzoru nie są równe

przekrojowi przeciętnemu a zwykłe wzory dendrometryczne nawet dla brył regularnych nie są

bezbłędne. Krzywa morfologiczna strzały jest linią bardzo skomplikowaną i tylko w większym

lub mniejszym stopniu jest zbliżona do tworzącej bryły równoważnej strzale.

13

Ad 4b. We wszystkich wzorach dendrometrycznych przyjmujemy, że przekrój poprzeczny jest

kołem. Tymczasem przekrój ten jest w większym lub mniejszym stopniu jedynie zbliżony do

koła. Jeżeli w skład wzoru wchodzi przekrój z nieregularnej części strzały (np. przekrój na wys.

0,0 we wzorze Smaliana), a do grubości na tej wysokości dochodzimy poprzez pomiar

ś

rednicomierzem (na 0,0 jest przekrój bardzo nieregularny spowodowany napływamy

korzeniowymi), którym mierzymy najbardziej "wystające" części, to popełniamy duże błędy

dodatnie. Im przekrój jest bardziej zbliżony do koła, tym popełniamy mniejsze błędy.

Ad 4c. Błędy pomiarowe są dwojakiego rodzaju. Jedne wynikają z niedokładnych przyrządów

(wyciągnięta taśma parciana, nierównoległość ramion średnicomierza itd.) a drugie z

systematycznych zaokrągleń np. w dół lub w górę jak również ze zwykłej ludzkiej pomyłki.

Ponieważ w zwykłych wzorach dendrometrycznych tych pomiarów robimy mało (jeden czasem

dwa) to ta ostatnia przyczyna może być powodem czasem nawet dużych błędów.

Wpływ błędu popełnianego przy pomiarze długości na błąd miąższości możemy wyrazić

wzorem

gdzie:

p

v

- procentowy błąd miąższości,

l - absolutny błąd długości,

l - długość strzały.

zaś wpływ błędu grubości na błąd miąższości możemy wyrazić wzorem

gdzie:

d - absolutny błąd grubości,

d - grubość drzewa.

Widzimy zatem, że błąd grubości ma 2-krotnie większy wpływ na procentowy błąd miąższości

niż błąd długości.

100

l

=

p

v

•

λ

200

d

=

p

v

•

δ

14

Ad 5. Pierśnicowa liczba kształtu jest ilorazem miąższości i objętości walca porównawczego

opartego o przekrój pierśnicowy i wysokość drzewa. Miąższość określana jest wzorem

sekcyjnym .

Ad 5a. Pierśnicowa liczba kształtu strzały w korze (F

1

) jest ilorazem miąższości strzały w korze i

objętości walca porównawczego opartego o przekrój na wys. 1,3 w korze i wysokość drzewa

dla przykładowego drzewa

Ad 5b. Pierśnicowa liczba kształtu bez kory (F

2

) jest ilorazem miąższości strzały bez kory i

objętości walca porównawczego bez kory

dla przykładowego drzewa

Ad 5c. Pierśnicowa liczba kształtu strzały bez kory (F

3

) jest ilorazem miąższości strzały bez kory

i objętości walca porównawczego w korze

H

G

V

=

F

wk

wk

1

•

0,4571

=

25,88

0,0531

0,6281

=

F

1

•

H

G

V

=

F

bk

bk

2

•

0,5327

=

25,88

0,0426

0,5873

=

F

2

•

15

dla przykładowego drzewa

Ad 5d. Pierśnicowa liczba kształtu grubizny strzały jest ilorazem grubizny strzały i objętości

walca porównawczego w korze

Należy zatem obliczyć miąższość sekcyjnie grubizny strzały, a więc miąższość od podstawy

drzewa do wysokości, gdzie grubość w korze wynosi 7 cm. Musimy znaleźć najpierw tę

wysokość. W przykładowym drzewie grubość 7 cm drzewo osiągnęło między 21,5 m - 88 mm, a

22,5 m - 67 mm.

Układamy równanie

gdzie:

21 mm - różnica grubości,

100 cm - różnica wysokości,

3 mm - brakujące 3 mm do 7 cm.

H

G

V

=

F

wk

bk

3

•

0,4274

=

25,88

0,0531

0,5873

=

F

3

•

H

G

V

=

F

wk

g

g

•

x

3mm

=

100cm

21mm

14

=

21

300

=

x

16

Ponieważ na wysokości 22,5 m grubość wynosiła 6,7 cm, to 7 cm drzewo miało na wysokości

22,5 - 0,14 = 22,36 m. Po zsumowaniu pól przekroju w środkach metrowych sekcji do

wysokości 21,5 m uzyskamy miąższość do wysokości 22 m czyli 0,6161 m

3

. Musimy jeszcze

wyliczyć miąższość 36 cm niepełnej sekcji wzorem środkowego przekroju. Zatem musimy

wyinterpolować grubość na wysokości 22,18 m. Miąższość rzeczywistą grubizny wyliczamy ze

wzoru

V

g

= 1(g

0,5

+ g

1,5

+ ... + g

21,5

) + g

22,18

× 0,36 m

korzystając z poprzedniego rysunku x = 6,72 » 7 m

lub

x = 3,77 » 4 m

Z pierwszego stosunku grubość na wysokości 22,18 m wynosi 6,7 cm + 0,7 cm = 7,4 cm

Z drugiego stosunku grubość na wysokości 22,18 m wynosi 7 cm + 0,4 cm = 7,4 cm

Zatem obydwie drogi prowadzą do tego samego wyniku. Zamieniamy tę grubość na pole

przekroju i mnożymy przez długość sekcji.

Zatem miąższość grubizny naszej strzały jest równa miąższości pełnych sekcji 0,6222 m

3

+

miąższość niepełnej sekcji 0,0015 m

3

czyli 0,6237 m

3

32

x

=

100

21

18

x

=

86

18

m

0,0015

=

0,36

0,0043

=

l

g

=

V

3

1/2

•

•

17

Ad 6. Właściwa liczba kształtu (F

0,1h

) jest ilorazem miąższości strzały w korze i objętości

odpowiedniego walca porównawczego. Wysokość walca jest równa wysokości drzewa, a jego

przekrój jest równy przekrojowi drzewa z 0,1 wysokości.

dla naszego drzewa

Najpierw należy wyinterpolować grubość na 0,1 m.

Nasze drzewo ma wysokość 25,88 m, wobec tego interesuje nas grubość na 2,59 m. Układamy

stosunek

gdzie

3 mm - różnica grubości między 2,5 i 3,5 m,

9 - różnica wysokości między 2,5, a 0,1 h

czyli przyjmujemy grubość na 2,5 m = 24,7 cm. Pole przekroju na 0,1 h wynosi zatem 0,0479.

0,4539

=

25,88

0,0531

0,6237

=

F

g

•

H

G

V

=

F

0,1

wk

0,1

•

0,5067

=

25,88

0,0479

0,6281

=

F

0,1

•

9

x

=

100cm

3mm

0

100

27

=

x

≈

18

Ad 7. Absolutna liczba kształtu jest ilorazem miąższości strzały w korze i objętości walca

porównawczego opartego o przekrój zerowy i wysokość drzewa

dla naszego drzewa

Ad 8a. Wzór Denzina jest najprostszym sposobem określania miąższości drzewa stojącego

Wystarczy zmierzyć pierśnicę drzewa w cm, podnieść ją do kwadratu i otrzymamy miąższość

drzewa w m

3

. Prostota wzoru niestety wpływa na niewielką jego dokładność. Wzór ten daje

dokładne wyniki dla drzew o wysokości około 30 m lub przy wysokości kształtu 12,73 m.

Ad 8b. Tablice miąższości B. Radwańskiego wymagają znajomości wartości pierśnicy w korze i

wysokości. Miąższość możemy z tych tablic odczytać dla pierśnicy z zaokrągleniem do 1 cm i

wysokości z zaokrągleniem do 1 m. Ponieważ chodzi nam o miąższość pojedynczego drzewa, to

musimy wyinterpolować miąższość i ze względu na grubość i ze względu na wysokość.

Wymiary naszego drzewa - d

1,3

= 26,0 cm i wysokość h = 25,88 m.

V

26;25

= 0,611

V

26;25,88

= 0,634

H

G

V

=

F

0

wk

0

•

0,1951

=

25,88

0,1244

0,6281

=

F

0

•

0,001d

=

V

1,3

2

19

V

26;26

= 0,638

Ad 9. Należy odczytać z tablic miąższości B. Radwańskiego na podstawie pierśnicy w korze i

wysokości miąższość bez kory. Z tego wynika, że w tych tablicach zawarta jest F

3

- czyli

pierśnicowa liczba kształtu strzały bez kory.

Dla naszego drzewa:

V

26;25

= 0,533

V

26;25,88

= 0,555

V

26;26

= 0,558

Ad 10. Za grubość pniaka bez kory przyjmujemy grubość na wysokości 0,0 bez kory. Grubość ta

wynosi 308 mm. Zaokrąglamy ją matematycznie do pełnych centymetrów i przyjmujemy, że

grubość pniaka wynosi 31 cm. Wysokość drzewa wynosi 25,88 m. Tablice dla każdego pniaka bez

kory podają pięć kategorii wysokości. Należy wybrać taką kategorię wysokości azeby różnica

wysokości naszego drzewa i danej kategorii wysokości była najmniejsza i dla tej kategorii odczytać

miąższość grubizny. Wysokość w kategorii drzew wysokich dla wymiaru

pniaka bez kory 31 cm wynosi 23,9 m, a w kategorii drzew bardzo wysokich 26,7 m, zatem różnica

między wysokością mojego drzewa (25,88) jest najmniejsza w porównaniu z kategorią drzew

bardzo wysokich i wynosi około 0,8 m. Dla tej kategorii wysokości odczytuję miąższość grubizny,

która wynosi 0,723 m

3

.

20

Ad 11. Dla załączonego materiału wyliczenia błędu w tabelce

Miąższość rzeczywista

na podstawie

Strzała w korze Strzała bez kory

Grubizna

0,6281

0,5873

0,6237

wzoru Denzina
teblic Radwańskiego
wymiaru pniaka

0,6760
0,6340

0,5550

0,7230

Błąd absolutny

wzoru Denzina
teblic Radwańskiego
wymiaru pniaka

0,0479

0,059

-0,0323

0,0993

Błąd procentowy wtórny

wzoru Denzina
teblic Radwańskiego
wymiaru pniaka

7,63
0,94

-5,50

15,92

Do pola przekroju dochodzimy z pierśnicy (pomierzona) i wysokości (także pomierzyliśmy).

Liczba ksztatu zawarta jest w tablicach miąższości - zatem błąd miąższości będzie wynikał

głównie z różnicy liczby kształtu naszego drzewa i zawartej w tablicach.

21

Praca kontrolna Nr 2

1. Obliczenie pierśnicowej powierzchni przekroju drzewostanu.

2. Obliczenie średniej arytmetycznej pierśnicy oraz przeciętnej pierśnicy drzewostanu na

podstawie średniej powierzchni przekroju.

3. Sporządzenie krzywej wysokości.

4. Obliczenie przeciętnej wysokości drzewostanu wzorem Lorey'a i porównanie jej z

wysokością drzew o średniej grubości.

5. Wyznaczenie błędu standardowego jakim obarczona jest średnia wysokość drzewostanu

(błąd krzywej wysokości).

6. Wyznaczenie współczynnika zmienności wysokości przy wyłączonym wpływie pierśnicy

(z wzorów empirycznych).

7. Obliczenie miąższości grubizny drzewostanu:

a) tablicami IBL,

b) wzorem empirycznym.

8. Za pomocą tablic Radwańskiego obliczyć miąższość drewna wielkowymiarowego I, II i III

klasy wymiarowej oraz miąższość drewna średniowymiarowego z grup S

1

, S

2

i S

3

.

Wymiary krytyczne:

n

W

=

p

H

H.D

H.D

H

1

135,95

+

4,55

=

W

H

•

H

1

42,75

+

4,48

=

W

H.D

•

22

Drewno wielkowymiarowe:

d

c.k.b.k.

ł 14 cm (średnica w cieńszym końcu bez kory)

l

min

6 m

I klasa wymiarowa d

0,5l

do 24 cm

II klasa wymiarowa d

0,5l

25 - 34 cm

III klasa wymiarowa d

0,5l

od 35 cm

grupa S

1

(drewno średniowymiarowe dłużycowe)

d

c.k.b.k.

ł

5 cm

d

0,5l

9 - 16 cm

d

0

Ł 24 cm

grupa S

2

(drewno stosowe użytkowe)

d

c.k.b.k.

ł 5 cm

grupa S

3

(drewno żerdziowe).

d

1

(średnica znamionowa w korze) 7 - 14 cm

9. Określenie miąższości drzewostanu metodą drzew próbnych wybranych jako przeciętne pod

względem pierśnicy i absolutnej grubości kory.

10. Obliczenie miąższości drzewostanu bez kory za pomocą tablic miąższości B. Radwańskiego.

11. Obliczenie przyrostu miąższości drzewostanu

a. Tablicami przyrostu miąższości A. Dudka w wariancie D i H oraz D, H i zd.

b. Tablicami przyrostu miąższości - M. Borowskiego.

12. Porównanie

dokładności

i

pracochłodności

metod

określania

miąższości

i

przyrostu miąższości drzewostanu.

Do wykonania tego tematu każdy student dostanie materiał empiryczny zebrany w

drzewostanie sosnowym. W materiale tym będzie szereg rozdzielczy pierśnic z pomiaru pierśnic

wszystkich drzew. Na 50 drzewach stojących dokonano pomiaru wysokości, grubości kory na

23

pierśnicy i przyrostu pierśnicy, zaś dla 20 drzew próbnych (ściętych) podane są różne dane

łącznie z miąższością każdego drzewa określoną sekcyjnie.

24

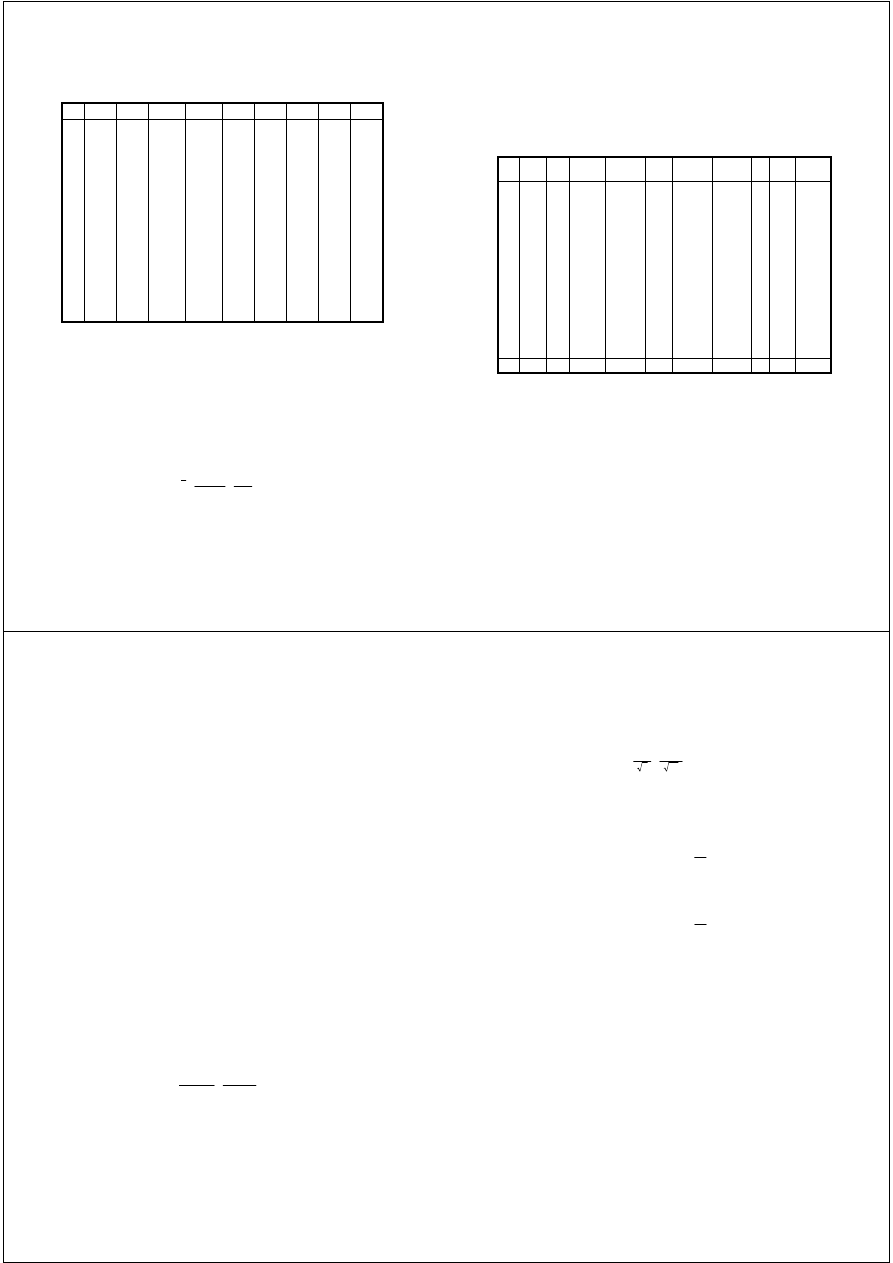
Przykładowy drzewostan:
Wiek: 103 lata
Obszar: 0.48 ha

Część I. Wyniki pomiaru drzew stojących

Część II. Szereg rozdzielczy pierśnic

Lp.

D

1,3

H

z

d

K

D (i)

n (i)

1
2
3
4
5
6
7
8
9

10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

10,8
13,1
14,0
15,0
15,3
15,9
17,0
17,4
17,8
18,4
18,8
19,3
19,7
19,8
20,2
20,5
20,8
20,9
21,1
21,3
21,5
21,6
21,9
22,3
22,5
22,7
22,9
23,2
23,4
23,8
24,0
24,5
24,8
25,0
25,4
25,7
26,0
26,3
26,5
26,9
27,5
27,8
28,3
28,4
29,1
29,5
30,1
30,5
31,3
32,2

16,0
18,0
19,0
19,5
19,5
18,5
19,5
20,0
19,0
19,5
20,0
19,5
21,5
20,0
20,0
20,5
19,5
19,5
21,0
21,0
22,0
21,5
20,5
22,0
21,5
21,5
20,5
22,0
21,5
22,0
22,0
21,0
21,0
22,5
21,0
22,5
22,0
22,0
20,5
22,0
22,0
23,5
22,5
22,0
22,0
22,0
23,0
22,0
22,5
23,0

2
4
3
2
4
2
3
5
3
6
7
7

16
12

7
9
3
5
7
4
6
5
9
6
5
7
4
2
5
9
6

10
21

8
8

10

9
7

10

2
5
3
8

12

7

10

7
6
8
7

14

4

17

6

11

2

35
12
23
22
16
17
35
18
22
27
30
15
28
21
26
26
22
26
26
35
13
26
28
20
21
28
18
21
19
49
19
28
30
41
26
32
24
31
30
39
38
26
37
33

10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
40

2
5

13
19
30
44
60
44
43
31
24
13
11

6
1
2

25

Część III. Wyniki pomiaru drzew próbnych (ściętych)

Nr D

H

V

wk

V

bk

z

d

z

h

K

D

L/3

d

l/3

1
2
3
4
5
6
7
8
9

10
11
12
13
14
15
16
17
18
19
20

129
135
148
166
183
181
200
212
215
217
234
252
250
264
278
282
277
282
192
282

16,00
18,11
17,20
20,71
18,73
20,62
22,05
20,40
20,29
21,77
22,00
21,30
21,06
19,37
20,90
22,07
23,03
25,20
21,07
22,19

0,0845
0,1199
0,1333
0,1748
0,2320
0,2397
0,2823
0,3476
0,3186
0,4291
0,4151
0,4534
0,5076
0,4216
0,5303
0,6309
0,6548
0,7220
0,6174
0,6611

0,0652
0,1029
0,1233
0,1477
0,2010
0,2098
0,2538
0,3039
0,2677
0,4040
0,3620
0,3850
0,4634
0,3401
0,4205
0,5502
0,5962
0,6547
0,5405
0,5961

2
3
2
3
6
6
5
9
8

11

8

13
11
10

9

14

8

11

8
9

0,30
1,07
0,45
1,05
1,26
1,22
0,97
0,92
1,10
1,47
1,06
1,62
1,10
1,36
0,98
1,45
1,10
1,17
1,17
1,19

23
18
10
25
28
23
23
23
34
12
28
36
21
41
50
33
25
26
36
30

84
96

109
110
137
131
136
162
150
175
164
173
190
170
184
206
209
210
208
214

82
94

107
107
132
125
133
157
143
172
159
165
183
163
178
195
205
205
201
209

Ad 1. Aby obliczyć pole przekroju drzewostanu należy, korzystając z tablic powierzchni kół,

zamienić wartości środkowe stopni pierśnic na pole przekroju. Pole przekroju wartości

ś

rodkowej stopnia pierśnicy pomnożone przez liczbę drzew w stopniu da nam pole przekroju

stopnia pierśnicy. Suma pól przekrojów stopni pierśnic daje nam pole przekroju naszego

drzewostanu. Możemy ewentualnie przeliczyć pole przekroju na jednostkę powierzchni (na

1 ha). Średnią pierśnicę drzewostanu wyliczymy z ilorazu - w liczniku suma iloczynów wartości

ś

rodkowych stopni pierśnic i częstości w tych stopniach do liczby drzew drzewostanu w

mianowniku.

23,5

=

348

8192

=

n

d

n

=

d

i

K

1

1.3

i

K

1

∑

∑

26

Ad 2. Znając pole przekroju naszego drzewostanu i liczbę drzew w tymże drzewostanie możemy

wyliczyć przeciętne pole pojedyńczego drzewa w naszym drzewostanie jako iloraz pola

przekroju i liczby drzew. Na podstawie przeciętnego pola przekroju możemy, korzystając także z

tablic powierzchni kół, odczytać przeciętną pierśnicę dla naszego drzewostanu.

Tabela 1.

D

nd

n

g

g × n

h

h×n×g

Näslund

h

h

v

n × v

10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
40

20
60

182
304
540
880

1320
1056
1118

868
720
416
374
216

38
80

2
5

13
19
30
44
60
44
43
31
24
13
11

6
1
2

0,0079
0,0113
0,0154
0,0201
0,0254
0,0314
0,0380
0,0452
0,0531
0,0616
0,0707
0,0804
0,0908
0,1018
0,1134
0,1257

0,0158
0,0565
0,2002
0,3819
0,7620
1,3816
2,2800
1,9888
2,2833
1,9096
1,6968
1,0452
0,9988
0,6108
0,1134
0,2514

16,3
17,0
17,8
18,6
19,3
20,0
20,6
21,2
21,6
22,0
22,4
22,6
22,9
23,1
23,3
23,5

0,2575
0,9605
3,5636
7,1033

14,7066
27,6320
46,9680
42,1626
49,3193
42,0112
38,0083
23,6215
22,8725
14,1094

2,6422
5,9079

15,98
17,29
18,32
19,15
19,84
20,42
20,91
21,33
21,70
22,03
22,31
22,57
22,80
23,01
23,29
23,36

16
17
18
19
19
20
21
21
22
22
22
23
23
23
23
23

0,08
0,12
0,14
0,19
0,24
0,30
0,38
0,44
0,54
0,61
0,70
0,83
0,93
1,04
1,16
1,29

0,16
0,60
1,82
3,61
7,20

13,20
22,80
19,36
23,22
18,91
16,80
10,79
10,23

6,24
1,16
2,58

8192

348

15,9761

341,8464

158,68

Ponieważ obszar naszego drzewostanu wynosi 0,48 ha to po przeliczeniu G/ha = 33,2835 m

2

.

Przeciętny przekrój pojedynczego drzewa wynosi

g = G/N = 15,9761 : 348 = 0,0459 m

2

.

Korzystając z tablic powierzchni kół odczytujemy przeciętną pierśnicę odpowiadającą temu

przekrojowi, która wynosi dg = 24,2 cm.

Ad 3. Krzywą wysokości sporządzamy na papierze milimetrowym lub w kratkę nanosząc

najpierw w układzie współrzędnych prostokątnych na oś odciętych wszystkie wartości środkowe

stopni pierśnic naszego drzewostanu (x), a na osi rzędnych skalę wysokości (y). Następnie z I

27

części naszego materiału empirycznego bierzemy co drugą wysokość (razem 25 pomiarów)

nanosząc ją na wykres. Możemy grubości nanoszonych drzew zaokrąglić do

wartości środkowych stopni grubości. Ponieważ zmienność wysokości nie jest zbyt duża

(V = 6-9%) to te 25 wysokości powinno nam wystarczyć do wykreślenia krzywej wysokości.

Gdybyśmy jednak mieli wątpliwości dla niektórych stopni pierśnic, to możemy dla tych stopni

wybrać z niewykorzystanego materiału empirycznego kilka spostrzeżeń i nanieść na wykres.

Przez naniesione na wykres dane prowadzimy linię wyrównującą jednym pociągnięciem tak, aby

mniej więcej tyle samo spostrzeżeń zostało powyżej i poniżej tej linii. Krzywą wysokości

możemy zbudować korzystając z równania Näslunda (wyrównać matematycznie), najlepiej

korzystając z programu komputerowego. Z załączonego materiału empirycznego (część I)

wprowadzamy dane co drugiego drzewa (pierśnice i wysokość) do programu komputerowego

"rkor" i wyliczamy współczynniki równania Näslunda. Współczynniki te dla mojego materiału

wynoszą a = 1,8417; b = 0,0610 i dodatkowo r = 0,9011. Następnie odczytujemy z

zaokrągleniem do 1 cm wysokości dla poszczególnych stopni grubości (tab. 1). Gdybyśmy

wyliczyli Sngh, gdzie h wyliczono z wzoru Näslunda, to ta suma wyniosłaby 344,0282 m

3

a H

L

= 21,534 m. Oczywiście studenci nie muszą dwiema drogami dochodzić do tych wyników,

wystarczy jedną drogą.

Ad 4. Średnia wysokość wyliczona wzorem Lorey

,

a jest średnią ważoną. Wagą jest tu pole

przekroju. Należy zatem wcześniej wykreślić krzywą wysokości jak w punkcie 3 i z tej krzywej

odczytać wysokości dla każdego stopnia grubości z zaokrągleniem do decymetra lub do

centymetra jeśli krzywą wysokości wyrównaliśmy matematycznie, a następnie wymnożyć przez

pole przekroju stopnia i otrzymane iloczyny zsumować dla całego drzewostanu, a następnie dane

podstawić do wzoru na średnią wysokość wzorem Lorey

,

a

Następnie dla wyliczonej przeciętnej pierśnicy z punktu 2 odczytujemy z krzywej wysokości

wysokość, która wynosi 21,2 m, jest to wysokość drzew o przeciętnej (średniej) grubości.

Wyliczone dwoma sposobami średnie wysokości drzewostanu różnią się o niespełna 0,2 m.

m

21,397

=

15,9761

341,8464

=

g

n

h

g

n

=

H

L

•

∑

•

•

∑

28

Ad 5. Do wykonania tego zadania należy wcześniej wyliczyć W

H.D

w punkcie 6, a następnie

dane podstawić do wzoru na liczebność próby

Ad 6. Podstawiając do wzorów empirycznych wcześniej wyliczoną w punkcie 4 średnią

wysokość wzorem Lorey

,

a wyliczamy ogólny współczynnik zmienności i współczynnik

zmienności wysokości z wyłączonym wpływem pierśnicy (wokół krzywej wysokości).

W

H

= 4.55 + 6.3537 = 10.905%

W

H.D

= 4.48 + 1.9979 = 6.4779%

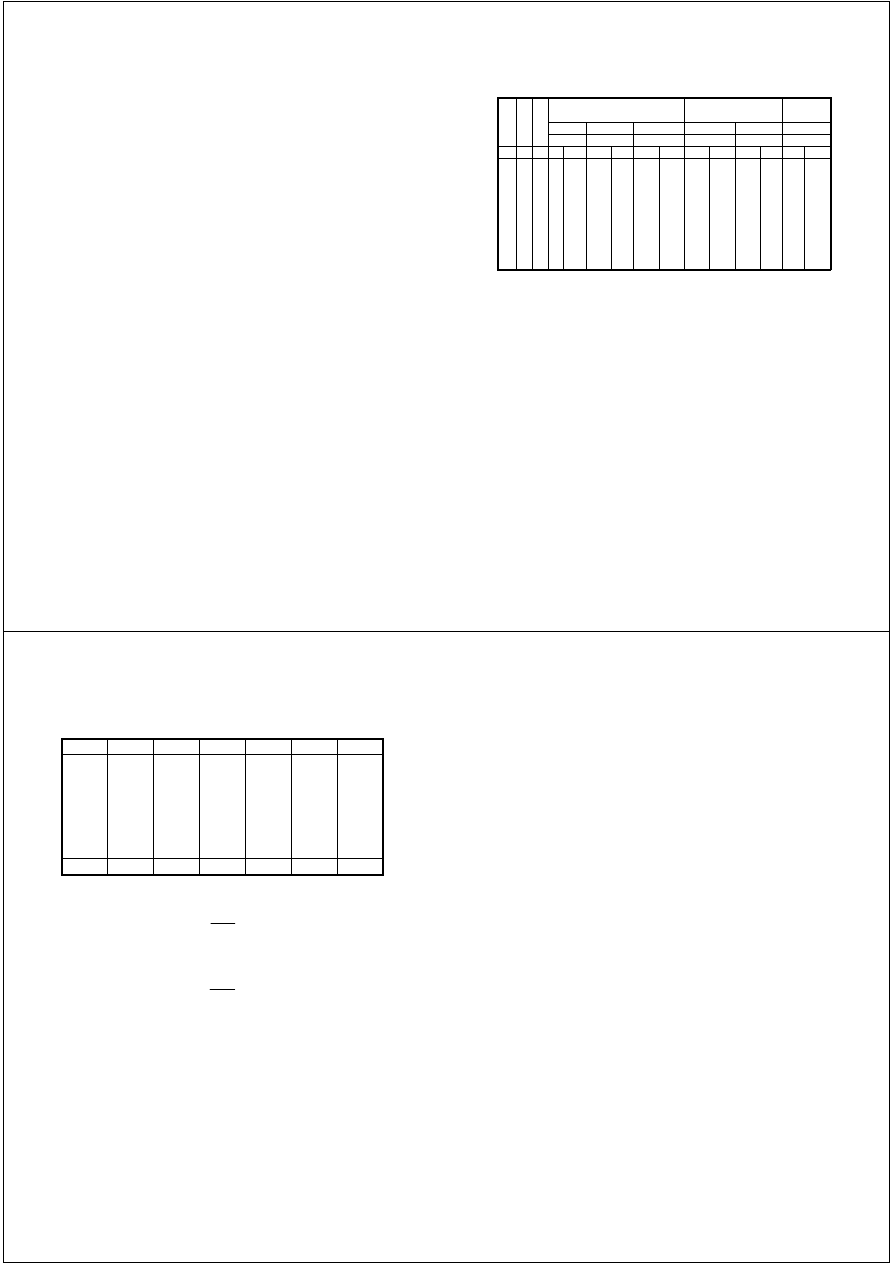
Ad 7a. Tablice miąższości typu bawarskiego podają miąższość pojedyńczego drzewa na

podstawie pierśnicy zaokrąglonej do pełnych centymetrów i wysokości zaokrąglonych do

pełnych metrów. Zatem z krzywej wysokości powinniśmy odczytać jeszcze raz wysokości

zaokrąglone do pełnych metrów i następnie na podstawie wartości środkowej stopnia pierśnicy i

ś

redniej wysokości dla tego stopnia odczytujemy w tablicach miąższość grubizny

pojedyńczego drzewa, po wymnożeniu przez liczebność stopnia miąższość stopnia, a po

zsumowaniu miąższości stopni miąższość drzewostanu (patrz tab. 1). Zadanie to można wykonać

korzystając z tablic miąższości M. Czuraja. Jeżeli, mimo wieku powyżej 80 lat, mamy grubości

poniżej 14 cm, to dla grubości poniżej 14 cm odczytujemy w tablicach miąższości do wieku 80

lat, a od 14 cm w tablicach miąższości ponad 80 lat.

1,296%

=

25

6,48%

=

n

W

=

p

H.D

H.D

H

1

135,95

+

4,55

=

W

L

H

•

H

1

42,75

+

4,48

=

W

L

H.D

•

29

Ad 7b. Obecnie miąższość grubizny drzewostanu coraz częściej oblicza się przy pomocy

wzorów empirycznych. Są to rozwiązania przeznaczone do zastosowań komputerowych, a więc

nowoczesne, bardziej dokładne, a nawet szybsze w użyciu. Z tego względu wzór empiryczny nie

będzie tu przytaczany - należy skorzystać z programu komputerowego. Danymi wejściowymi do

programu "wzór empiryczny" są obliczone wcześniej:

- przeciętna pierśnica drzewostanu (cm), 24,2 cm

- przeciętna wysokość drzewostanu (m), 21,40 m

- szereg rozdzielczy pierśnic.

Po wprowadzeniu tych danych na ekranie komputera otrzymujemy tabelkę zawierającą:

- miąższości pojedynczych drzew w stopniach pierśnic,

- miąższości stopni pierśnic,

- miąższość całego drzewostanu.

Tabelkę tę należy umieścić w sprawozdaniu.

Ad 8. W punkcie tym należy skorzystać z tablic miąższości i zbieżystości dłużyc kłód i

wyrzynków strzały dla sosny B. Radwańskiego i zgodnie z ograniczeniami dla poszczególnych

sortymentów odczytać, na podstawie wartości środkowej stopnia pierśnicy w korze (w cm) i

wysokości dla tego stopnia (w m), miąższość bez kory określonego sortymentu dla pojedyńczego

drzewa, a po wymnożeniu przez liczebność stopnia miąższość sortymentu w stopniu. Tablice w

podstawowej swojej części podają miąższości od 14 cm, zatem dla grubości mniejszych od 14

cm należy skorzystać z tabelek zamieszczonych na końcu tablic. Najpierw w tabeli D (Tablice

miąższości strzały w korze) należy odczytac miąższość w korze i od niej odjąć miąższość

odczytaną w tabeli F (Tablica miąższości kory), a otrzymany wynik wpisać jako miąższość

ż

erdzi w rubrykę S

3

(tabela 2).

30

Tabela 2. Miąższość sortymentów

d

n

h

L>6m D

okbk

>14cm

D

okbk

>5cm

Ż

erdzie

Ds>35

24<Ds<35

Ds<24

9<Ds<16

stosowe

7<Ds<14

W

III

W

II

W

I

S

1

S

2

S

3

V

V×n

V

V×n

V

V×n

V

V×n

V

V×n

V

V×n

10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
40

2
5

13
19
30
44
60
44
43
31
24
13
11

6
1
2

16
17
18
19
19
20
21
21
22
22
22
23
23
23
23
23

0,76
0,85
0,96
1,08

8,36
5,10
0,96
2,16

0,33
0,41
0,48
0,57
0,68

14,52
17,63
14,88
13,68

8,84

0,13
0,17
0,20
0,26
0,33

1,69
3,23
6,00

11,44
19,80

0,05
0,05
0,05
0,03
0,03
0,04
0,04
0,02
0,02

2,20
2,15
1,55
0,72
0,39
0,44
0,24
0,02
0,04

0,055
0,082

0,11
0,41

Wykonujący to zadanie decyduje czy od stopnia grubości 20 cm będzie pozyskiwał WI (drewno

wielkowymiarowe) do 14 cm w cieńszym końcu i S

2

(stosowe) z wierzchołka do 5 cm w

cieńszym końcu czy też jeszcze S

1

(kopalniaki czyli drewno średniowymiarowe dłużycowe) do

grubości 5 cm w cieńszym końcu.

Ad 9. Przed wykonaniem tego zadania powinniśmy najpierw wykreślić zależność podwójnej

grubości kory na pierśnicy od pierśnicy. Praktycznie czynność tę wykonujemy na drzewach

stojących za pomocą koromierza najczęściej łącznie z określaniem przyrostu pierśnicy.

Ponieważ zarówno grubość kory jak i przyrost pierśnicy są cechami znacznie bardziej

zmiennymi niż wysokość, to cechy te powinniśmy określać na liczniejszej próbie niż wysokość

(praktycznie około 50 drzew) (wykres 2). Następnie wybierając drzewo próbne o określonej

grubości powinniśmy sprawdzić, czy ma ono przeciętną grubość kory dla tej grubości. Jeżeli ma,

to je ścinamy i mierzymy celem określenia pierśnicowej liczby kształtu.

31

Tabela 5

Nr

D

H

G

G × H

V

wk

V

bk

1
2
3
4
5
6
7
8
9

10

135
181
200
212
234
252
250
282
282
292

18,11
20,62
22,05
20,40
22,00
21,30
21,06
22,07
22,19
21,07

0,0143
0,0257
0,0314
0,0353
0,0430
0,0499
0,0491
0,0625
0,0625
0,0670

0,2590
0,5299
0,6924
0,7201
0,9460
1,0629
1,0340
1,3794
1,3869
1,4117

0,1199
0,2397
0,2823
0,3476
0,4151
0,4534
0,5076
0,6309
0,6611
0,6174

0,1029
0,2098
0,2538
0,3039
0,3620
0,3850
0,4634
0,5502
0,5961
0,5405

9,4223

4,2750

3,7676

Następnie korzystając z danych z tabeli 5 wyliczamy

i

i podstawiamy do wzoru na miąższość

czyli

V

wk

= 0,4537 × 15,9761 × 21,397 = 155,0931 m

3

V

bk

= 0,3999 × 15,9761 × 21,397 = 136,7021 m

3

0,4537

=

9,4223

4,275

=

F

wk

0,3999

=

9,4223

3,7676

=

F

bk

H

G

F

=

V

•

•

32

Ad 10. Obliczenie miąższości drzewostanu bez kory za pomocą tablic miąższości

Radwańskiego.

Mając szereg rozdzielczy przerśnic i wysokości zaokrąglone do pełnych metrów z tablic B.

Radwańskiego możemy odczytać miąższość bez kory dla pojedynczego drzewa na podstawie

pierśnicy w korze i wysokości. Po wymnożeniu przez liczebność stopnia otrzymamy miąższość

stopnia, a po zsumowaniu miąższości stopni otrzymamy miąższość drzewostanu bez kory.

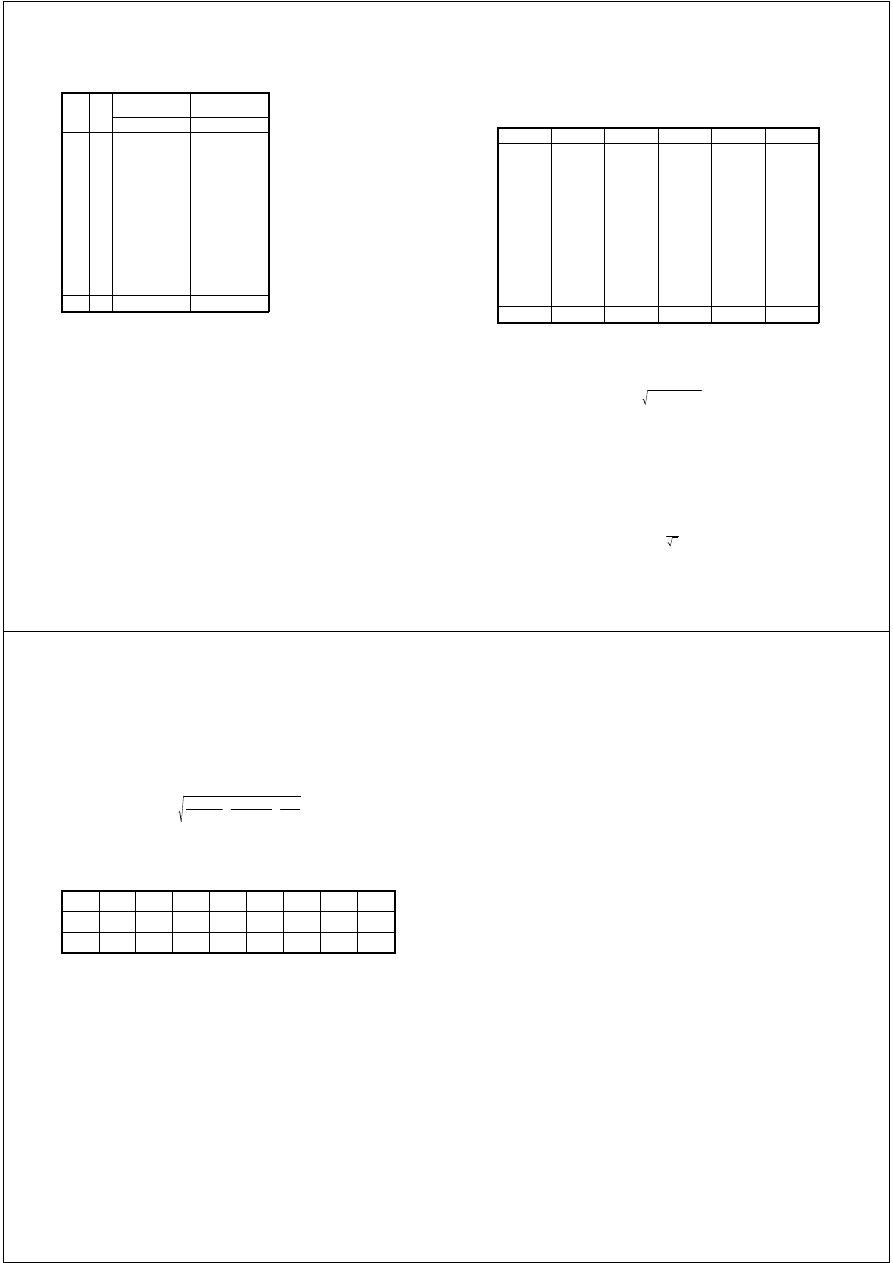
Ad 11a. Do wykonania tego zadania korzystamy z programu komputerowego "tablice przyrostu

miąższości" Dudka. Najpierw wybieramy wariant 2 i ewentualnie jeśli chcemy mieć rozkład

przyrostu miąższości w stopniach pierśnic to wariant 3. W obu tych wariantach wymagana jest

znajomość przeciętnej pierśnicy drzewostanu i średniej wysokości

np. Dg - 24,2 cm; Hg = 21,2 m a G/ha = 33,2835 m

2

Po wprowadzeniu tych danych do wariantu 2 otrzymamy:

Z

v

drzewostanu (m

3

/ha) = 39,2907 m

3

Błąd z

v

na 1 ha ±8,4141 m

3

Po przeliczeniu na powierzchnię naszego drzewostanu:

Z

v

= 18,8595 m

3

W wariancie 3 oprócz przeciętnej pierśnicy i średniej wysokości należy wprowadzić szereg

rozdzielczy i powierzchnię naszego drzewostanu, co pozwoli otrzymać przyrost miąższości w

stopniach grubości i dla całego drzewostanu np: dg = 24,2; h = 21,2; A - 0,48 ha.

33

D

1.3

n

Wariant 3

Wariant 5

n x z

v5

n x z

v5

10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
40

2
5

13
19
30
44
60
44
43
31
24
13
11

6
1
2

0,0178
0,0646
0,2298
0,4411
0,8863
1,6135
2,6766
2,3485
2,7080
2,2762
2,0337
1,2600
1,2099
0,7437
0,1388
0,3092

0,0117
0,0425
0,1517
0,2920
0,5884
1,0741
1,7867
1,5719
1,8172
1,5315
1,3718
0,8520
0,8202
0,5054
0,0946
0,2112

z

v

d-stanu 18,9577

z

v

d-stanu 12,7229

Wariant 4 - dodatkowo podajemy oprócz pierśnicy i wysokości średnią wartość przyrostu

pierśnicy. Wartość tę możemy odczytać dla przeciętnej pierśnicy z linii przyrostu pierśnicy, jeśli

takową mamy zbudowaną, lub wyliczyć jako średnią arytmetyczną zd dla drzew (10-15) o

zbliżonych wymiarach do przeciętnej pierśnicy np.: Dg 24,2 cm; Hg 21,2 m; zd = 7 mm.

Po wprowadzeniu tych danych otrzymamy wynik: z

v

/ha = 26,3043 m

3

po przeliczeniu na 0,48 h

błąd z

v

= ±3,4049 m

3

z

v

= 12,6261 m

3

W wariancie 5 (dane w tabeli) otrzymamy dodatkowo rozkład przyrostu miąższości w stopniach

grubości.

Ad 11b. Z tablic przyrostu miąższości M. Borowskiego można odczytać przyrost miąższości

pojedyńczego drzewa na podstawie wartości środkowej stopnia pierśnicy (w korze), wysokości

dla tego stopnia (z krzywej wysokości z zaokrągleniem do m) i przyrostu pierśnicy (z lini

przyrostu pierśnic z zaokrągleniem do mm). Po wymnożeniu przez liczebność stopnia

otrzymamy przyrost miąższości stopnia a po zsumowaniu przyrostów stopni przyrost miąższości

naszego drzewostanu (tabela 8).

34

Tabela 8

D

n

H

z

d

z

v

n × z

v

10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
40

2
5

13
19
30
44
60
44
43
31
24
13
11

6
1
2

16
17
18
19
19
20
21
21
22
22
22
23
23
23
23
23

2
3
3
4
5
5
6
7
7
8
9
9

10
10
11
12

0,0025
0,0050
0,0067
0,0111
0,0155
0,0191
0,0268
0,0337
0,0395
0,0480
0,0573
0,0650
0,0758
0,0814
0,0934
0,1026

0,0050
0,0250
0,0871
0,2107
0,4650
0,8404
1,6080
1,4828
1,6985
1,4880
1,3752
0,8450
0,8338
0,4884
0,0934
0,2052

11.7515

Ad 12. Miąższość drzewostanu określono metodami pomiarowymi za pomocą tablic miąższości

i za pomocą drzew próbnych. Błąd określania miąższości

Błąd określania wysokości wyliczyliśmy w punkcie 5. Ponieważ mierzyliśmy pierśnice

wszystkich drzew (metoda pomiarowa) to możemy przyjąć, że p

g

= 0. Pozostał nam jedynie do

ustalenia błąd liczby kształtu. W metodzie tablicowej będzie to błąd tablic czyli niezgodność

stałej pierśnicowej liczby kształtu zawartej w tablicach z liczbą kształtu naszego drzewostanu. W

metodach drzew próbnych błąd będzie zależał od liczby drzew próbnych i od cech

pomocniczych, które posłużyły nam do wyboru drzew próbnych.

p

+

p

+

p

=

p

h

2

g

2

f

2

v

n

W

=

p

f

f

35

W przypadku metody drzew próbnych, gdzie drzewa próbne wybiera się jako przeciętne pod

względem pierśnicy i grubości kory

Współczynniki zmienności pierśnicowej liczby kształtu oraz współczynnik korelacji tejże liczby

z różnymi cechami drzewa.

w

W

F

r

FH

r

FD

r

FK

r

q2

R

F(DH)

R

F(DK)

PA

30

7,2

-0,22

-0,45

-0,52

0,83

0,51

0,69

PS

87

7,6

+0,03

-0,19

-0,50

0,87

0,26

0,54

Widzimy zatem, że bardziej pracochłonne są metody drzew próbnych, ale jednocześnie

są one dokładniejsze, ponieważ w tych metodach wszystkie elementy miąższości pochodzą z

pomiaru w drzewostanie. W metodach tablic miąższości liczba kształtu jest cechą stałą tablic

(błąd tablic).

Przyrost miąższości drzewostanu określano dwoma metodami należącymi do grupy

metod pomiarowych, przez jednorazowy pomiar wstecz w końcu okresu. Metoda tablic

przyrostu miąższości jest metodą mniej pracochłonną ale jednocześnie może być metodą mniej

dokładną, ponieważ tablice opierają się o stałe wartości intensywności przyrostu

miąższości. Tablice wielowariantowe Dudka pozwalają na określenie 5-letniego i 10-letniego

przyrostu miąższości drzewostanu w zależności od uzyskanych onformacji o drzewostanie.

Dokładność (błąd) będzie zależał od użytych cech drzewostanu, które wprowadzamy do

komputera celem określenia przyrostu miąższości. Im ściślej wprowadzona cecha będzie

skorelowana z przyrostem miąższości tym błąd będzie mniejszy.

n

W

+

n

W

-

W

+

n

W

-

W

=

p

f

2

f.DK

K

2

f.DK

2

f.D

d

2

f.D

f

2

f.dk