POLITECHNIKA BIAŁOSTOCKA
WYDZIAŁ ELEKTRYCZNY
KATEDRA ENERGOELEKTRONIKI I NAPĘDÓW ELEKTRYCZNYCH
Sprawozdanie zajęć laboratoryjnych
WYDZIAŁU MECHANICZNEGO
studiów dziennych
z przedmiotu:
ELEKTROTECHNIKA I ELEKTRONIKA
ĆWICZENIE 1M
BADANIE OBWODÓW PRĄDU STAŁEGO
Opracowali:
Agnieszka Uklejewska
Kamil Tylewski
Grzegorz Wenda
Sebastian Toczydłowski
BIAŁYSTOK 2010
1. CEL I ZAKRES ĆWICZENIA LABORATORYJNEGO
Praktyczne, tzn. na podstawie pomiarów, sprawdzenie praw Kirchhoffa i
bilansu mocy w rozgałęzionych obwodach prądu stałego. Zastosowanie prawa Ohma
do wyznaczania rezystancji elementów.
W zakres ćwiczenia wchodzi:
-rozwiązywanie obwodów prądu stałego,
-łączenia obwodów z możliwością pomiarów prądów i napięć,
-mierzenie natężenia prądu i napięcia typowymi miernikami o różnych zakresach,
-wykorzystywanie wyników pomiarów do analizy obwodów i wyznaczania
parametrów elementów obwodu.
2. WYNIKI POMIAARÓW I OBLICZEŃ
2 a)Wyznanie parametrów źródeł napięcia.
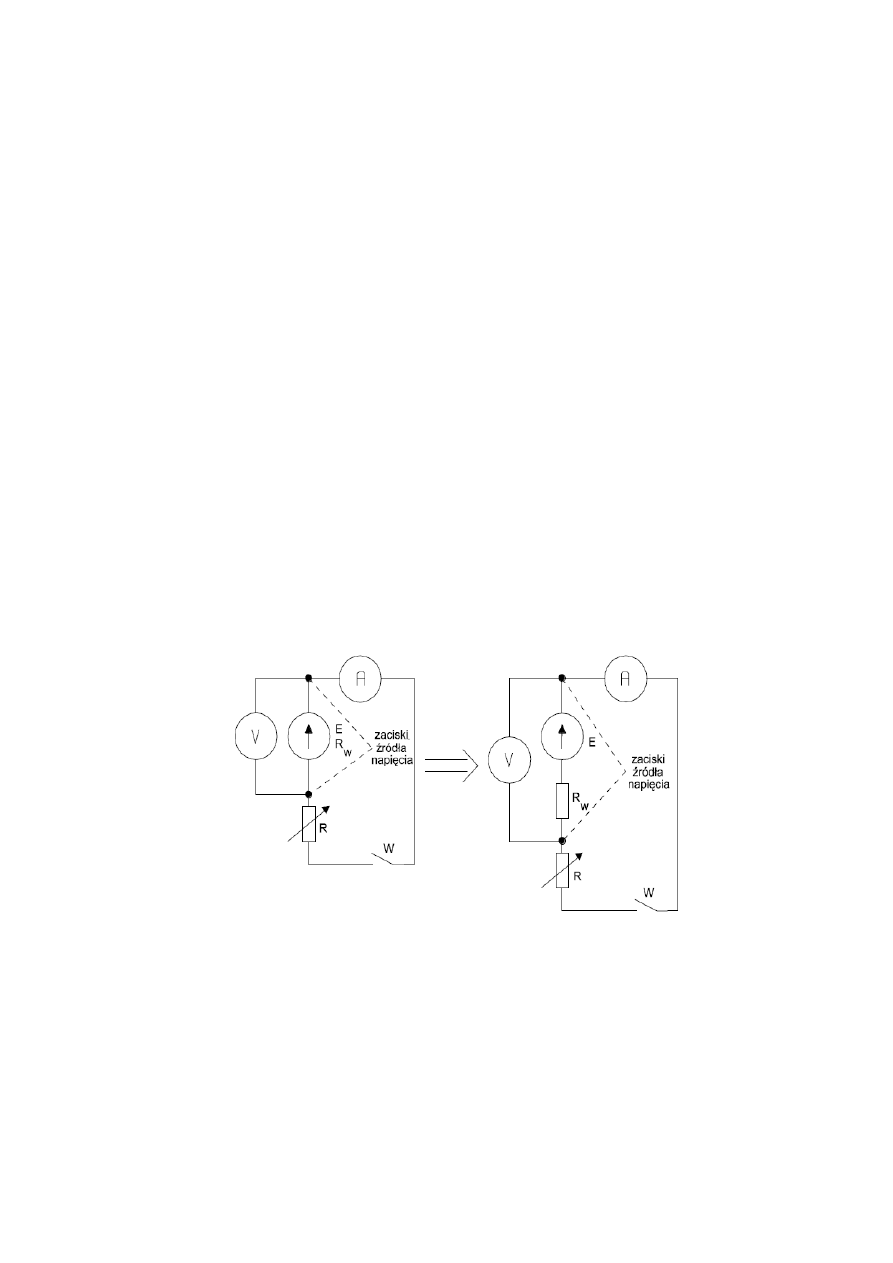
Wykonane zostały dwa układy według schematów na rys.1.
Rys.1
Schemat układu pomiarowego do wyznaczania rezystancji wewnętrznej źródła napięcia
Tabela 1.
Wyniki pomiarów i obliczeń przy wyznaczaniu wartości rezystancji R
w1
akumulatora 1
E
1
U
1
I
1
R
w1
V
V
A
Ω
6,4
6,1
3
0,1
Tabela 2.
Wyniki pomiarów i obliczeń przy wyznaczaniu wartości rezystancji R
w2
akumulatora 2
E
2
U
2
I
2
R
w2
V
V
A
Ω
12,4
11,8
3
0,2
2 b) Badanie rozgałęzionego obwodu prądu stałego
Do badań przyjęty został obwód prądu stałego przedstawiony na rysunku 2
złożony z dwóch źródeł napięcia E
1,
E
2
o rezystancjach wewnętrznych R
w1
R
w2
i
rezystorów R
1
, R
2
, R
3
.
w
IR
E
U
−
=
I
E
U
R
w
−
−
=
Ω
=
−
−
=
−
−
=
1
,
0
3
3
,
0
3
4
,
6
1
,
6
w
R
w
IR
E
U
−
=
I
E
U
R
w
−
−
=
Ω
=
−
−
=
−
−
=
2
,
0
3
6
,
0
3
4
,
12
8
,
11
w
R
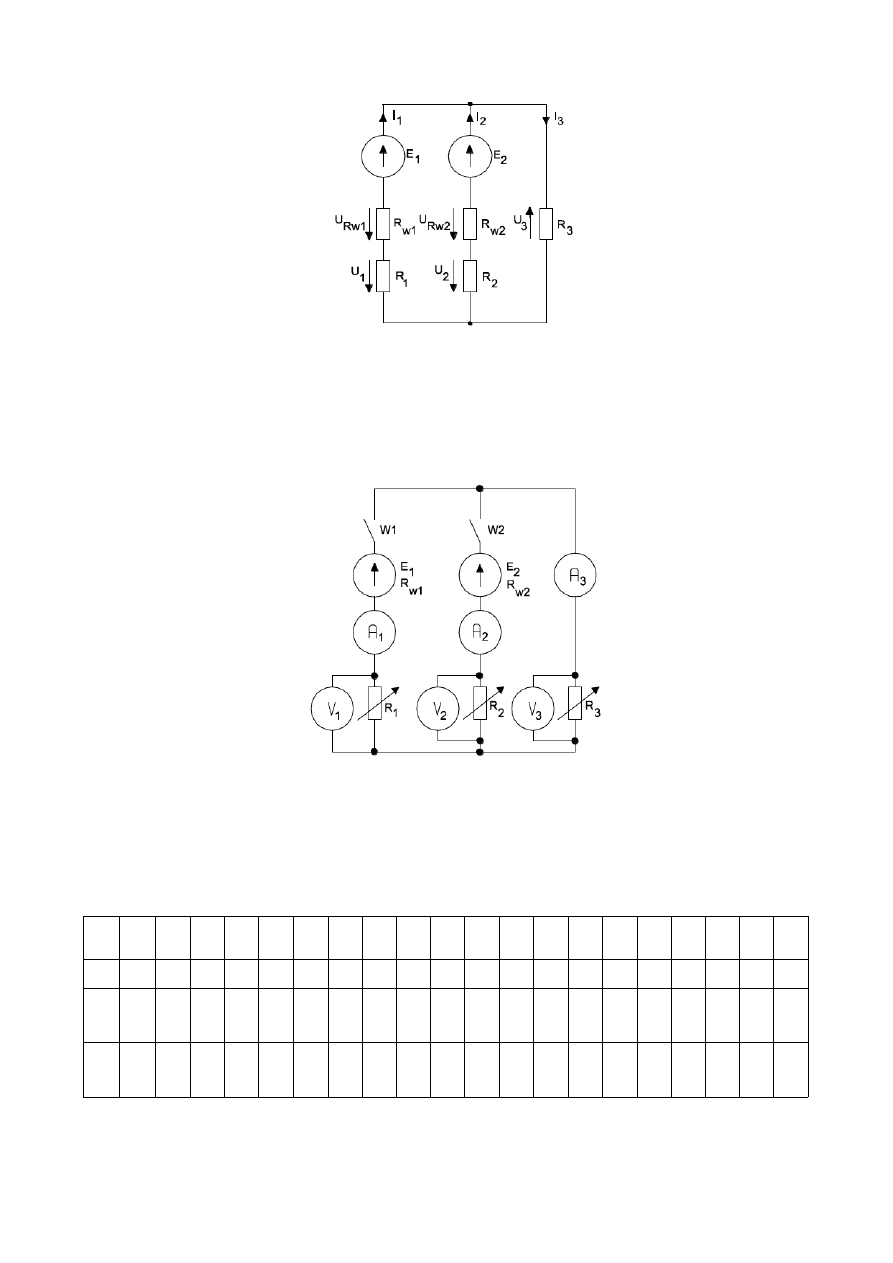
Rys.2. Układ elektryczny o dwóch oczkach i trzech gałęziach
Połączono układ według schematu przedstawionego na rys.3.
Rys.3. Schemat układu pomiarowego
Tabela 3.
Wyniki obliczeń i pomiarów prądów, napięć i mocy.
E
1
E
2
I
1
I
2
I
3
U
1
U
2
U
3
U
Rw
1
U
Rw
2
R
1
R
2
R
3
P
1
P
2
P
3
P
1źr
P
2źr
P
w1
P
w2
V
V
A
A
A
V
V
V
V
V
Ω
Ω
Ω
W
W
W
W
W
W
W
Pom
ierzo
ne
12,4 6,4
0,24 0,04 0,28 7
0,1
6
-0,6 -0,7 29,1 2,5
21,4 1,68 0
1,68 3,47 0,64 0,17 0,18
Obli
czon
e
12
6
0,21 0,06 0,27 6,11 15
5,78 0,1
0,05 29,1 2,5
21,4 1,3
8,7
1,57 2,54 0,36 0,01 0
−
sprawdzenie zgodności wyników pomiarów z prawami Kirchhoffa.
I prawo Kirchhoffa:
II prawo Kirchhoffa:
−
wyznaczanie spadków napięć na rezystancjach wewnętrznych źródeł na
podstawie II prawa Kirchhoffa zastosowanego do oczek obwodu
zawierających jedno źródło:
−
wyznaczenie rezystancji R
1
R
2
R
3
na podstawie prawa Ohma:
0
3
2
1
=
−
+
I
I
I
0
28
,
0
04
,
0
24
,
0
=
−
+
0
1
3
1
=
−
−
U
U
E
1
7
4
,
6
4
,
12
−
=
−
−
0
2
3
2
=
−
−
U
U
E
3
,
0
1
,
0
6
4
,
6
=
−
−
0
1
2
2
1
=
−
+
−
U
U
E
E
9
,
0
7
1
,
0
4
,
6
4
,
12
−
=
−
+
−
1
3
1
1
U
U
E
U
Rw
−
−
=
6
,
0
7
6
4
,
12
1
−
=
−
−
=
Rw
U
2
3
2
2
U
U
E
U
Rw
−
−
=
2
2
2
I
U
R
=
3
3
3
I
U
R
=
1
1
1
I
U
R
=
Ω
=
=
1
,
29
24
,
0
7
1
R
Ω
=
=
5
,
2
04
,
0
1
,
0
2
R
Ω
=
=
4
,
21
28
,
0
6
3
R
7
,
0
1
,
0
7
4
,
6
2
−
=
−
−
=
Rw
U
14
,
2
28
,
0
6
,
0
1
1
1
=
=
=
I
U
R
Rw
w
5
,
17
04
,
0
7
,
0
2
2
2
=
=
=
I
U
R
Rw
w
−
sprawdzenie bilansu mocy:
moce źródłowe:
moce wydzielone na rezystancjach R
1
R
2
R
3
:
moce tracone na rezystancjach wewnętrznych źródeł:
2 c) Rozwiązywanie analityczne obwodu badanego w punkcie 2 b.
2
1
3
2
1
2
1
w
w
źr
źr
P
P
P
P
P
P
P
+
+
+
+
=
+
2
2
2
I
E
P
źr
⋅
=
68
,
1
24
,
0
7
1
1
1
=
⋅
=
⋅
=
I
U
P
004
,
0
04
,
0
1
,
0
2
2
2
=
⋅
=
⋅
=
I
U
P
68
,
1
28
,
0
6
3
3
3
=
⋅
=
⋅
=
I
U
P
472
,
3
28
,
0
4
,
12
1
=
⋅
=
źr
P
64
,
0
1
,
0
4
,
6
2
=
⋅
=
źr
P
17
,
0
14
,
2
28
,
0
2
1
2
1
1
=
⋅
=
⋅
=
w
w
R
I
P
175
,
0
5
,
17
1
,
0
2
2
2
2
2
=
⋅
=
⋅
=
w
w
R
I
P
709
,
3
112
,
4
≠
0
0
1
,
29
6
,
2
6
0
6
,
2
6
6
,
21
12
3
2
1
1
2
2
3
3
2
1
=
−
−
=
⋅
−
⋅
+
=
⋅
+
−
⋅
−
+
=
I
I
I
I
I
I
I
I
I
I
6
6
,
2
1
,
29
6
6
,
21
6
,
2
2
1
3
2
−
=
−
−
−
=
−
I
I
I
I
2706
,
0
059
,
0
2114
,
0
3
2
1
=
=
=
I
I
I
1
1
1
I
E
P
źr
⋅
=
3. Wnioski.
Sprawdzenie zgodności wyników z prawami Kirchhoffa w oparciu o wartości
zmierzone okazało się nie prawidłowe a stało się tak gdyż wartości odczytywane z
woltomierzy mierzących spadki napięcia na rezystorach w dolnym zakresie skali jest
obarczona dużym błędem. Konsekwencjami tej nie prawidłowości stał się nie
prawidłowy bilans mocy. Rozwiązanie analityczne badanego obwodu okazało się
dużo bardziej dokładne. Niestety nie zdarzyliśmy wykonać pomiarów rezystancji
metoda techniczną, ale jak wiadomo z teorii schemat z dokładnym pomiarem prądu
służy do pomiaru dużych rezystancji gdyż rezystancja wewnętrzna amperomierza nie
wprowadza dużych zmian w rezystancji zastępczej, gałęzi pomiarowej na której jest
mierzony spadek napięcia woltomierzem. Do pomiaru małych rezystancji służy układ
z dokładnym pomiarem napięcia gdyż prąd pobierany przez woltomierz jet dużo
mniejszy niż prąd płynący przez obciążenie Rx co również zmniejsza błąd pomiaru
wprowadzany przez rezystancje wewnętrzne mierników analogowych.
0003481
,
0
059
,
0
1
,
0
0083799
,
0
2114
,
0
2
,
0
359
,
0
059
,
0
6
5368
,
2
2114
,
0
12
2
2
1
2
1
≈
⋅
=
≈
⋅
=
≈
⋅
=
≈
⋅
=
w
w
źr
źr
P
P
P
P
567
,
1
2706
,
0
4
,
21
703
,
8
059
,
0
5
,
2
3005
,
1
2114
,
0
1
,
29
2
3
2
2
2
1
≈
⋅
=
≈
⋅
=
≈
⋅
=
P
P
P
2
1
3
2
1
2
1
w
w
źr
źr
P
P
P
P
P
P
P
+
+
+
+
=
+
89
,
2
89
,
2
567
,
1
703
,
8
3005
,
1
0003481
,
0
0083799
,
0
359
,
0
5368
,
2
=
+
+
+
+
=
+
11
,
6
1
,
29
21
,
0
1
1
1
=
⋅
=
=
R
I
U
15
,
0
5
,
2
06
,
0
2
2
2
=
⋅
=
=
R
I
U
778
,
5
4
,
21
27
,
0
3
3
3
=
⋅
=
=
R
I
U
05
,
0
15
,
0
8
,
5
6
1
,
0
1
,
6
8
,
5
12
2
1
=
−
−
=
=
−
−
=
Rw
Rw
U
U