Podstawy modelowania

cybernetycznego systemów

biologicznych

Wykład nr 1 z kursu

Wykład nr 1 z kursu

Biocybernetyki

dla Inżynierii Biomedycznej

prowadzonego przez

Prof. Ryszarda Tadeusiewicza

Na wykładach nr 1, 2 i 3

z Biocybernetyki omawiane były

następujące zagadnienia:

1. Sposób definicji modelu pojedynczego obiektu

biologicznego

2. Sposób łączenia modeli pojedynczych obiektów

celem formowania modeli złożonych systemów

3.
4. Sprzężenie zwrotne i jego właściwości

Dla zagadnień tych nie ma jeszcze komputerowych

slajdów, trzeba więc się tego nauczyć na
podstawie notatek z wykładów

Słowo wstępu

Słowo

Cybernetyka

zostało po raz pierwszy użyte w

książce pt. „Cybernetyka- czyli sterowanie i komunikacja w

zwierzęciu i maszynie

”

„(…)naukowcy uświadomili sobie, że problemy komunikacji,

sterowania i mechaniki statycznej stanowią zasadniczo jedną

„(…)naukowcy uświadomili sobie, że problemy komunikacji,

sterowania i mechaniki statycznej stanowią zasadniczo jedną

całość, niezależnie od tego czy dotyczą maszyny czy istoty

żywej.

(…) Zdecydowaliśmy się nadać całej dziedzinie teorii sterowania

w maszynach i zwierzętach nazwę cybernetyki, którą

utworzyliśmy od grackiego słowa :

κυβενετεσ

, czyli sternik.

Metodą udostępniania technice osiągnięć biologii

może być między innymi

modelowanie cybernetyczne

. Model

jest zawsze sformalizowanym (a więc łatwym do precyzyjnej
analizy przez inżyniera) i bardzo konkretnym opisem
określonego systemu lub procesu. Na podstawie modelu,
dostępnego do rozmaitych badań i symulacyjnych
eksperymentów, można przeprowadzić ścisłe rozumowanie, które
owocować może udaną konstrukcją systemu technicznego
wzorowanego na biologicznym oryginale. Co więcej, model jako
działająca imitacja określonego systemu biologicznego, może być

działająca imitacja określonego systemu biologicznego, może być
bezpośrednio zaangażowany do wykonywania pożądanej
czynności w technice, stając się prototypem poszukiwanego
urządzenia.

Np. Model systemu mięśni dłoni jako element chwytający

robota

Elementy systemu nerwowego i sieci neuronowe.

Podstawowe zasady i używana notacja

Podstawowe zasady i używana notacja

Zwykle modele systemów biologicznych prezentowane są

jako abstrakcyjne odwzorowania, przekształcające zbiory

sygnałów wejściowych

w zbiór sygnałów wyjściowych.

Zbiór –

jest to podstawowe pojęcie (Ich nazwy są dużymi

literami). Ważną cechą zbioru jest jego moc (liczba

literami). Ważną cechą zbioru jest jego moc (liczba

elementów) do zapisu mocy zbioru używany jest symbol

#. Np. moc zbioru zapisujemy następująco : #Ω

Elementy

zbiorów zapisywane są kursywą, przy czym mogą

to być obiekty skalarne lub wektorowe, a także mogą

one być rozważane jako ustalone wartości lub jako jako

funkcje jednej lub wielu zmiennych.

Podstawowe zasady i używana notacja

Podstawowe zasady i używana notacja

Definiuje się zbiór parametrów (stałych ) występujących we zworach,

oznaczone głównie jako C. Elementy tego zbioru oznaczamy
symbolami c

1

, c

2

, c

3

, … , c

k-1

, c

k

.

W razie potrzeby wprowadzić można dodatkowe identyfikatory

używanych sygnałów lub parametrów w postaci dodatkowych
wskaźników dopisywanych u góry odpowiednich symboli

wskaźników dopisywanych u góry odpowiednich symboli
zapisane w nawiasie żeby nie pomylić z potęgowaniem. Np. x

i

(h)

–

jest symbolem sygnału hamowania presynaptycznego w neuronie.

Np. przez dodanie tyldy nad znakiem x ( ) można odróżnić sygnały

wyjściowe od wejściowych w neuronie.

oznacza uśrednianie.

x

~

x

Odwzorowania

Odwzorowania

Opisywane modele traktowane są jako odwzorowania

przekształcające elementy jednego zbioru w elementy
drugiego zbioru. Odwzorowania te zawsze oznaczane są
symbolem ϕ z odpowiednimi indeksami u dołu.
Definiuje się je, podając dwa zbiory: wejściowy i
wyjściowy. W zapisie ogólnym wygląda to następująco:

wyjściowy. W zapisie ogólnym wygląda to następująco:

Ω

⇒

Θ

ϕ :

Co interpretować należy w ten sposób, że elementom
Ξ∈Θ przyporządkowane są za pomocą odwzorowania φ
elementy ω∈Ω

Odwzorowania mogą być składane, w wyniku czego

tworzy się nowe odwzorowanie. Symbolem składania
odwzorowań jest

⊗, a jego znaczenie określić można

następująco: Niech dane będą odwzorowania φ

ω

:

Ω

⇒

Θ

oraz φ

Ξ

: Θ

⇒Ψ. Wówczas odwzorowanie będące złożeniem

φ

=

φ

ω

⊗ φ

Ξ

bezpośrednio przyporządkowuje elementom

ω∈Ω elementy ψ ∈ Ψ.

Formuła typu Θ

Ω

, gdzie Θ i Ω są zbiorami, oznacza

Formuła typu Θ , gdzie Θ i Ω są zbiorami, oznacza

zawsze funkcję argumentu przyjmującego wartości ze
zbioru Ω, o wartościach funkcji dostarczanych ze zbioru
Θ.

Zapis Θ

×Ω oznacza iloczyn kartezjański zbiorów. Zaś K-

krotny iloczyn kartezjański zbioru Ω oznaczamy jako Ω

K

.

Do kompletu informacji na temat notacji dodajemy, że

niekiedy posługiwać się będziemy transformatą
Laplace’a definiowaną jako:

dt

e

)

t

(

p

)}

t

(

p

{

L

)

s

(

P

st

∫

∞

∞

−

−

=

=

Gdzie p(t) ∈ R

R

jest sygnałem zależnym od czasu t ∈T, a

P(s) ∈ C

C

jest jego transformatą, oraz transmitancjami

P(s) ∈ C jest jego transformatą, oraz transmitancjami
operatorowymi oznaczonymi jako G z odpowiednimi
indeksami:

)

s

(

P

)

s

(

P

)

s

(

G

we

wy

=

Gdzie oczywiście P

we

(s)=L{p

we

(t)} oraz

P

wy

(s)=L{p

wy

(t)}

Modelowanie jako wieloetapowy proces

Modelowanie jako wieloetapowy proces

Proces budowy modelu ℳ pewnego systemu

biologicznego ℬ zdefiniujemy formalnie jako

odwzorowanie φ

ℳ

prowadzące od abstrakcyjnie

rozumianej rzeczywistości ℜ do konkretnego modelu

ℳ

:

φ

ℳ

: ℜ

⇒

ℳ

W konkretnych warunkach, realizując odwzorowanie φ

ℳ

dokonujemy czterech, niżej dokładniej

ℜ

ℳ

ℳ

dokonujemy czterech, niżej dokładniej

scharakteryzowanych odwzorowań:

φ

ℳ

= φ

ℜ ℬ

⊗ φ

ℬ

௰

⊗ φ

௰ ℑ

⊗ φ

ℐ ℳ

Istotą tych odwzorowań sprowadza się do zabiegów

ograniczających, których skutkiem modelu ℳ w

stosunku do systemu ℬ. Wynika z tego ograniczona

użyteczność zbudowanego modelu ℳ .

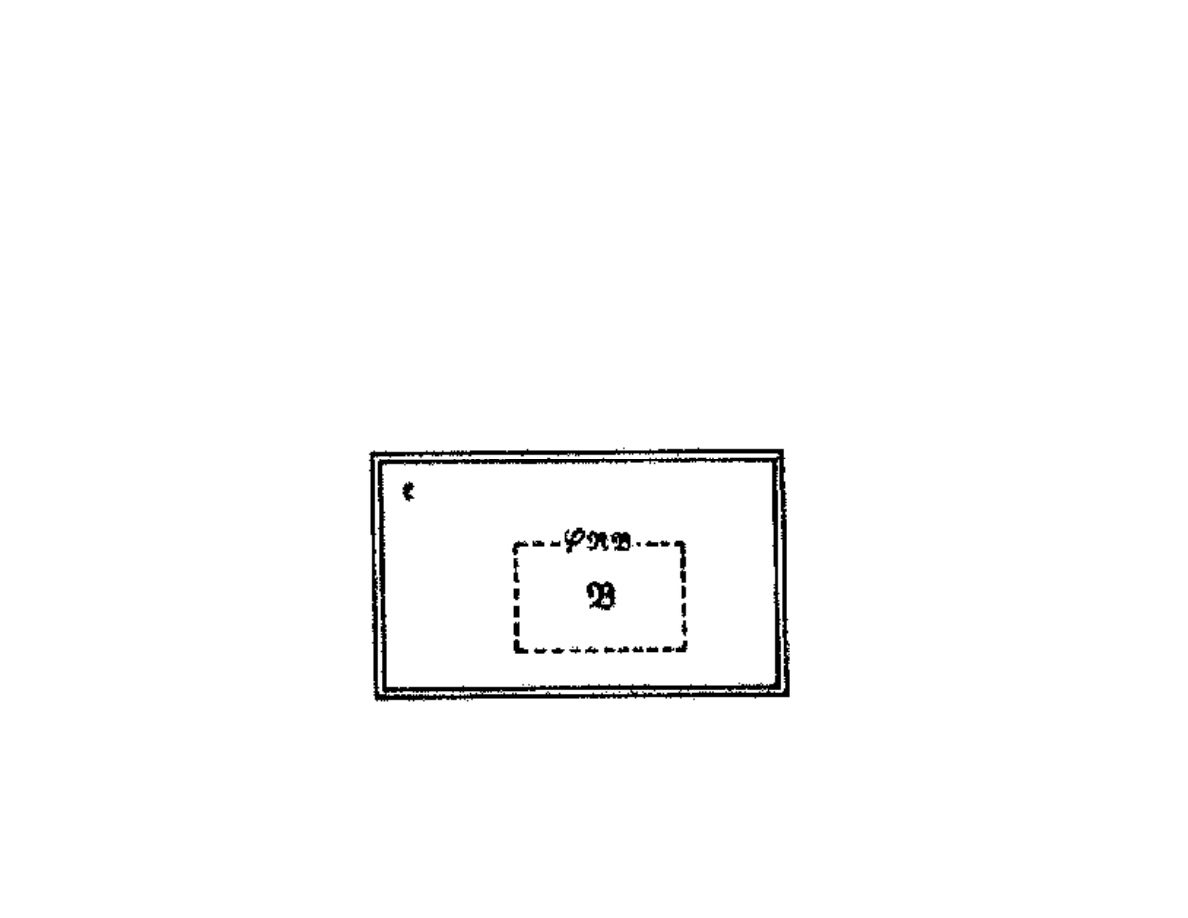
Wybierając obiekt modelowania ℬ dokonujemy pierwszego i

podstawowego ograniczenia, gdyż z – ciągłej w swojej naturze-
rzeczywistości ℜ , wydzielamy interesujący nas obiekt ℬ ,
wstawiając pomiędzy tenże obiekt a pozostałe elementy
rzeczywistości (nazywane umownie otoczeniem ℭ) granice, których
w istocie nie ma. Omawiany zabieg może być symbolicznie
zapisany także jako odwzorowanie

φ

ℜ ℬ

: ℜ ⇒ ℬ,

Przy czym zakładać będziemy, że ℬ ⋂ ℭ =

⌀ oraz że ℬ ⋃ ℭ = ℜ

Rys1. Wydzielenie φ

ℜ ℬ

obiektu modelowania ℬ z ciągłej rzeczywistości ℜ

stanowi pierwszy krok modelowania φ

ℳ

i jest pierwszym źródłem

niedoskonałości modelu ℳ.

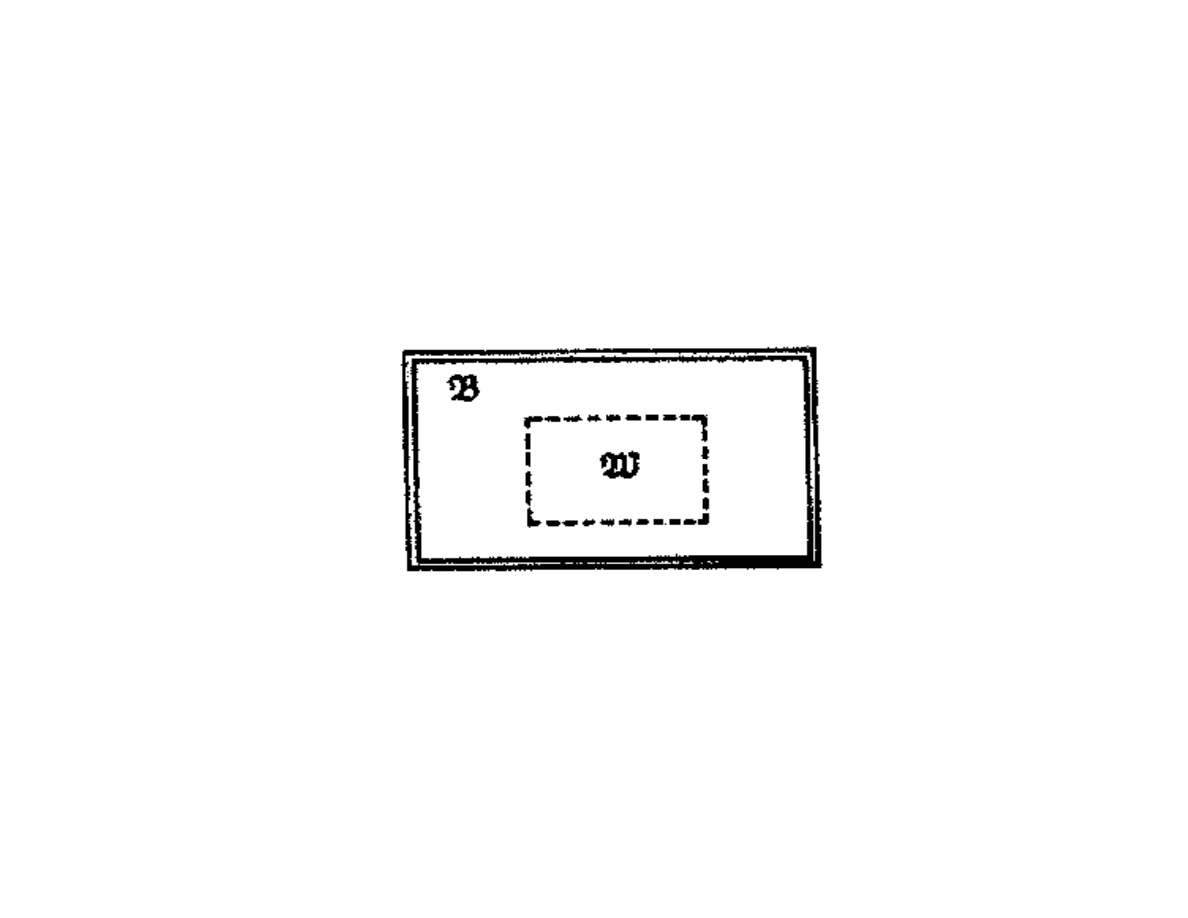
Kolejny czynnik, ważący na doskonałości modelu, wiąże się

z faktem, że modelowaniu nie jest poddawany
rzeczywisty obiekt ℬ, lecz w istocie nasza wiedza o nim,
oznaczana dalej

௰. Występuje więc kolejne odwzorowanie,

dzielące budowany model ℳ od rzeczywistości ℜ.
Odwzorowanie to oznaczamy φ

ℬ

௰

:

φ

ℬ

௰

: ℬ ⇒

௰,

ℬ

ℬ ⇒

Wiedza

௰ jest wzbogacana, zatem można ją wyrazić jako

chwilowy stan dynamicznie zmieniającego się zasobu
wiadomości. Oznaczając przez ℑ zasób informacji o
rozważanym obiekcie biologicznym ℬ możemy to wyrazić
wzorem :

௰= ℑ

T

Mimo, że wiedza

௰ jest stale uzupełniana, to w stosunku

do rzeczywistego obiektu ℬ, z jego potencjalnie nie
skończoną liczbą różnych własności i aspektów (#ℑ

→∞

moc zbioru informacji dąży do nieskończoności) zawsze
będzie niepełna

Przedmiotem modelowania pozostaje wiedza

௰ o

modelowanym obiekcie

ℬ

, a nie on sam; jest to

drugie ważne źródło ograniczeń i
niedoskonałości modelu ℳ

Cel ℑ budowy modelu ℳ wpływa na dobór faktów

௰

1

⊆

௰

, uwzględniających w strukturze modelu, oraz takich

௰

2

⊆

௰ , które zostają pominięte lub których oddziaływanie

jest opisane w sposób uproszczony lub uśredniony. W
praktyce zwykle #

௰

1

< #

௰

2

. Oznaczamy to selekcyjne

działanie zbioru jako kolejne odwzorowanie φ

௰ ℑ

definiując je w następujący sposób:

φ

௰ ℑ

:

௰ ⇒௰

1

,

⊆

௰ ℑ

⇒

1

Gdzie podzbiór

௰

1

⊆

௰ był już określony. Obecność

odwzorowania φ

௰ ℑ

oznacz między innymi, że ten sam

obiekt b ∈ ℬ, modelowany jest dla różnych celów ʓ

1

∈ ℑ,

ʓ

2

∈ ℑ, …, ʓ

k

∈ ℑ, może dostarczać wyrażnie różniących

się modeli m

1

∈ℳ, m

2

∈ℳ, …, m

k

∈ℳ (m

1

≠ m

2

≠… ≠m

k

)

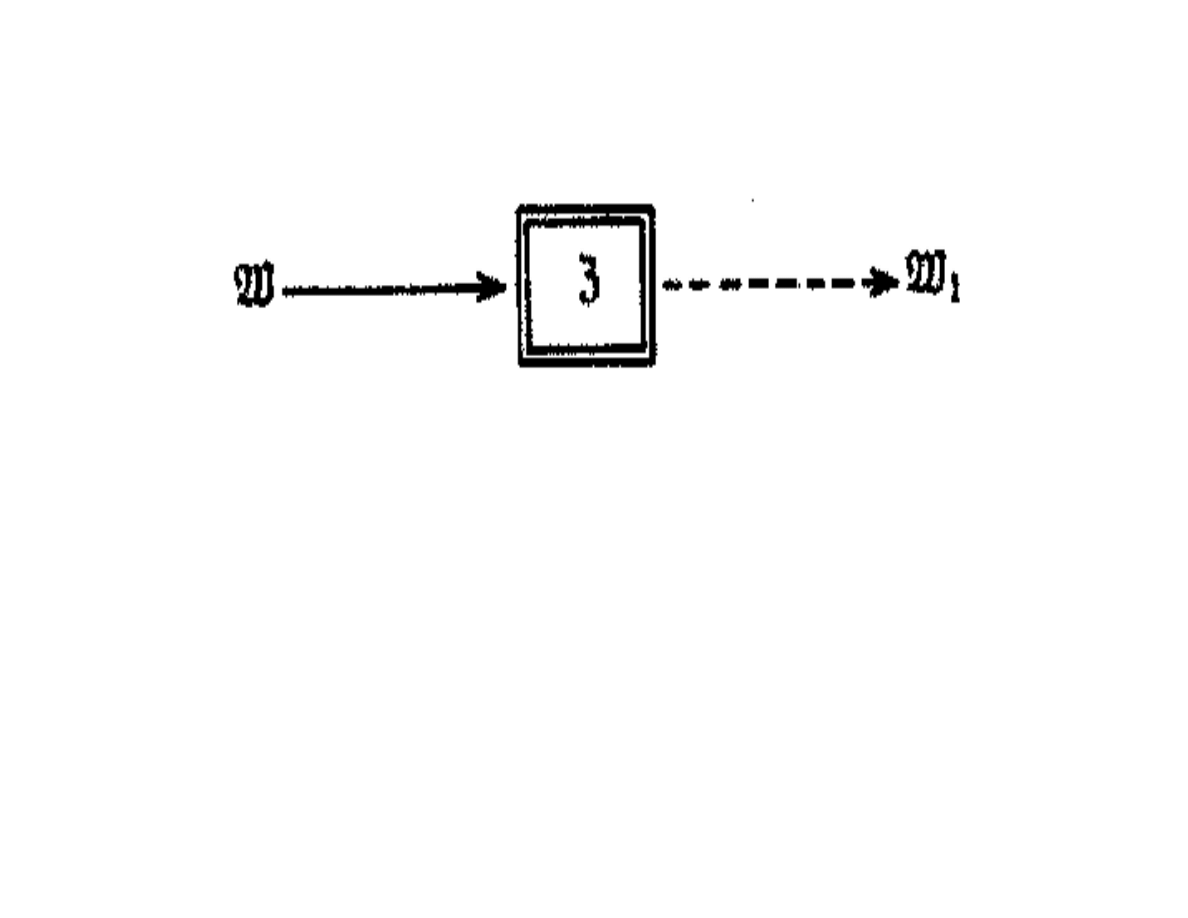
ℑ

ℬ

Cel modelowania ℑ jest „filtrem”, przy użyciu

którego z całości wiedzy

௰ o obiekcie

ℬ

wydobywana jest drobna część

௰

1

, będąca

potem podstawą do modelowania

φ

ℳ

Ostatni składnik, ograniczający wiarygodność modelowania, wiąże się

z używanymi narzędziami ℐ. Rozróżnić można narzędzia
dwojakiego rodzaju, tak jak w procesie modelu, który definiujemy
następująco:

φ

ℐ ℳ

: ℳ

1

⇒ℳ

,

Wyodrębnić można dwa etapy : modelowanie matematyczne

φ

ℐ ℳ

(f)

: ℳ

1

⇒ℳ

f

,

ℐ ℳ

ℳ ⇒ℳ

Oraz symulacja komputerowa

φ

ℐ ℳ

(f)

: ℳ

f

⇒ℳ

s

,

Potrzebne są więc dwojakiego rodzaju narzędzia formalne ℐ

f

⊆ ℐ

i

informatyczne ℐ

s

⊆ ℐ

, konieczne do budowy matematycznych

zrębów modelu ℳ

f

⊆ ℳ

i do jego konkretyzacji w formie modelu

ℳ

s

⊆ ℳ

rys 4. Na ostateczny kształt modelu ℳ mają

wpływ – obok wiedzy

௰ o modelowanym obiekcie

ℬ

- także cele modelowania ℑ i narzędzia
modelowania ℐ

Technika Modelowania

Budowę modelu ℳ określonego systemu ℬ zaczynamy od konstrukcji

opisu matematycznego ℳ

f

. Podstawową rolę odgrywają przy tym

sygnały

ຮ, wśród których wyróżnić można sygnały ຮ

we

i

ຮ

wy

zapewniające więź pomiędzy φ

ℭ ℬ

pomiędzy „odciętym” na wstępie

modelowania obiektem ℬ może być opisany w kategoriach relacji :

φ :

ຮ

we

⇒

ຮ

wy

Przed przystąpieniem do budowy modelu ℳ porządkuje się dostępną

wiedzę

௰ na temat modelowanego obiektu ℬ w formie katalogu

⊆ ℑ

ℳ

wiedzę

௰ na temat modelowanego obiektu ℬ w formie katalogu

typowych koincydencji wejście-wyjście

ຮ

we

× ຮ

wy

⊆ ℑ

, a w trakcie

konstrukcji modelu φ

ℳ

poszukuje się takich formuł i zależności

matematycznych ℳ

f

, które zdolne są te zarejestrowane zależności

wiernie odtwarzać. Do realizacji takiego opisu matematycznego

konieczne jest wprowadzenie do modelu parametrów c ∈ C . Wartości
parametrów nie są na ogół znane w momencie konstruowania modelu

ℳ

i jedynym z ważniejszych zadań twórcy modelu ℳ

f

jest zwykłe

ustalenie tych wartości na drodze analizy obserwacji ℑ rzeczywistego

systemu ℬ.

Dobór parametrów modelu nazywany bywa identyfikacją i

jest przedstawiony w postaci odwzorowania:

φ

id

: ℑ ⇒C ⊆ ℜ,

Prowadzącego ze zbioru ℑ informacji o modelowanym

obiekcie b ∈ ℬ do zbioru parametrów C należącego do
zbioru liczb rzeczywistych ℜ, co odpowiada
przypisywaniu poszczególnym parametrom
konkretnych wartości liczbowych.

Obok parametrów c ∈ C wprowadza się do modelu

ℳ

Obok parametrów c ∈ C wprowadza się do modelu

zmienne stanu s

s

∈

ຮ

s

, które reprezentują wewnętrzna

dynamikę modelu ℳ

f

; jeśli sygnały wyjściowe

ຮ

wy

zależą nie tylko od sygnału wejściowego s

we

∈

ຮ

we

nadchodzącego w danym momencie, lecz os sytuacji
jaka miała miejsce jakiś czas temu ∆t ∈T wcześniej, to
wówczas w modelu ℳ

S

ten efekt „pamięci”

odwzorowywany jest przez wprowadzenie
odpowiednich stanu.

Liczba wprowadzonych zmiennych stanu #

ຮ

s

jest parametrem

decydującym o złożoności modelu ℳ

f

. W przypadku obiektów

technicznych zmiennym stanu s

s

∈

ຮ

s

odpowiadają oddzielne,

znajdujące się w obiekcie magazyny: energii, masy lub dowolnych
innych zasobów. W modelach matematycznych ℳ

f

zmienne stanu

wiążą się z rzędem równań różniczkowych. Np. dla automatyka
liczba zmiennych stanu odpowiada liczbie parametrów, które trzeba
określić w pewnym ustalonym momencie t

0

∈T, aby na ich

podstawie było możliwe określenie zachowania obiektu ℬ w
dowolnej chwili czasowej dla t>t

0

.

ℬ

Właściwie w tym jest problem że żywy organizm wydaje się

charakteryzować potencjalnie nieskończoną liczbą zmiennych
stanu. Każdy element organizmu ma zdolność nabywania nowych
cech i nie da się zaewidencjonować takiego zestawu danych s

s

,

które pozwolą przewidzieć zachowanie obiektu przez dowolne
długi czas ( ∀ t>t

0

). Wprowadzone zmienne stanu s

s

∈

ຮ

s

są

heurystyczną próbą dopasowania zjawisk ℭ w modelu ℳ do
obserwacji ℑ rzeczywistego obiektu ℬ.

Zaprogramowanie gotowego (w sęsie równań

matematycznych) modelu ℳ

f

dla wybranego

komputera, reprezentowane dalej jako odwzorowanie:

φ

p

: ℳ

f

⇒ ℳ

s

,

pozwala przystąpić do prób symulacji φ

ຮ

. W pierwszej

kolejności dokonuje się eksperymentów weryfikacyjnych

φ

ຮ

(w)

. Polegają one na uruchamianiu modelu z takimi

parametrami c∈C i przy takim przebiegu

kontrolowanych sygnałów (głównie wejściowych s

we

∈

ຮ

we

) , które odpowiadają łącznie znanym sytuacjom w∈

௰

ℑ

ℬ

ℭ

we

) , które odpowiadają łącznie znanym sytuacjom w∈

௰

i zachowaniom i∈ ℑ modelowanego systemu ℬ.

Oczekuje się przy tym, że wyniki modelowania σ∈ ℭ

odwzorowywać będą wówczas znane formy zachowania

i∈ ℑ modelowanego obiektu. Porównując sygnały

(głównie wyjściowe

ຮ

wy

) obliczone w czasie

symulacyjnych badań modelu φ

ຮ

(w)

z wartościami tych

sygnałów, znanymi z obserwacji rzeczywistego systemu-

można podejmować decyzję odnośnie wiarygodności i

poprawności funkcjonowania modelu ℳ

s

.

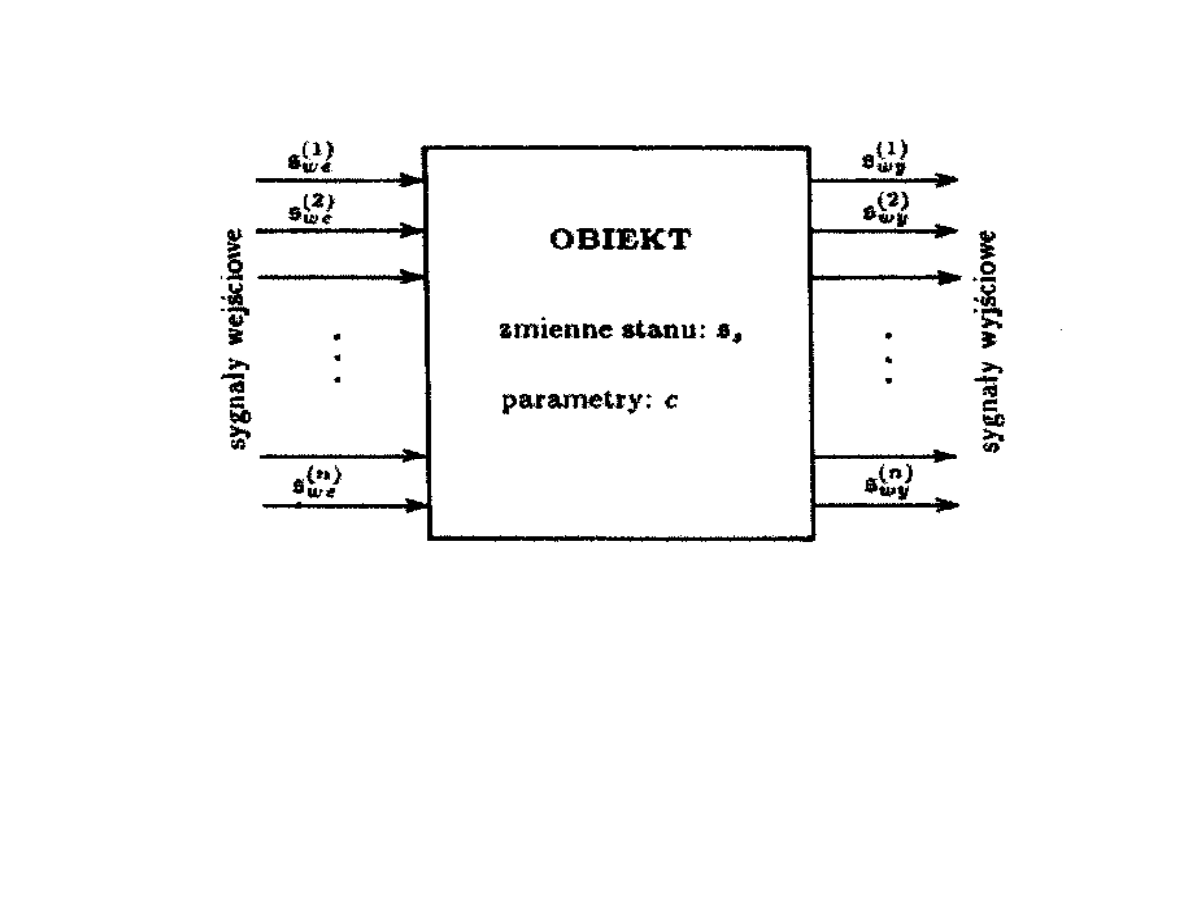
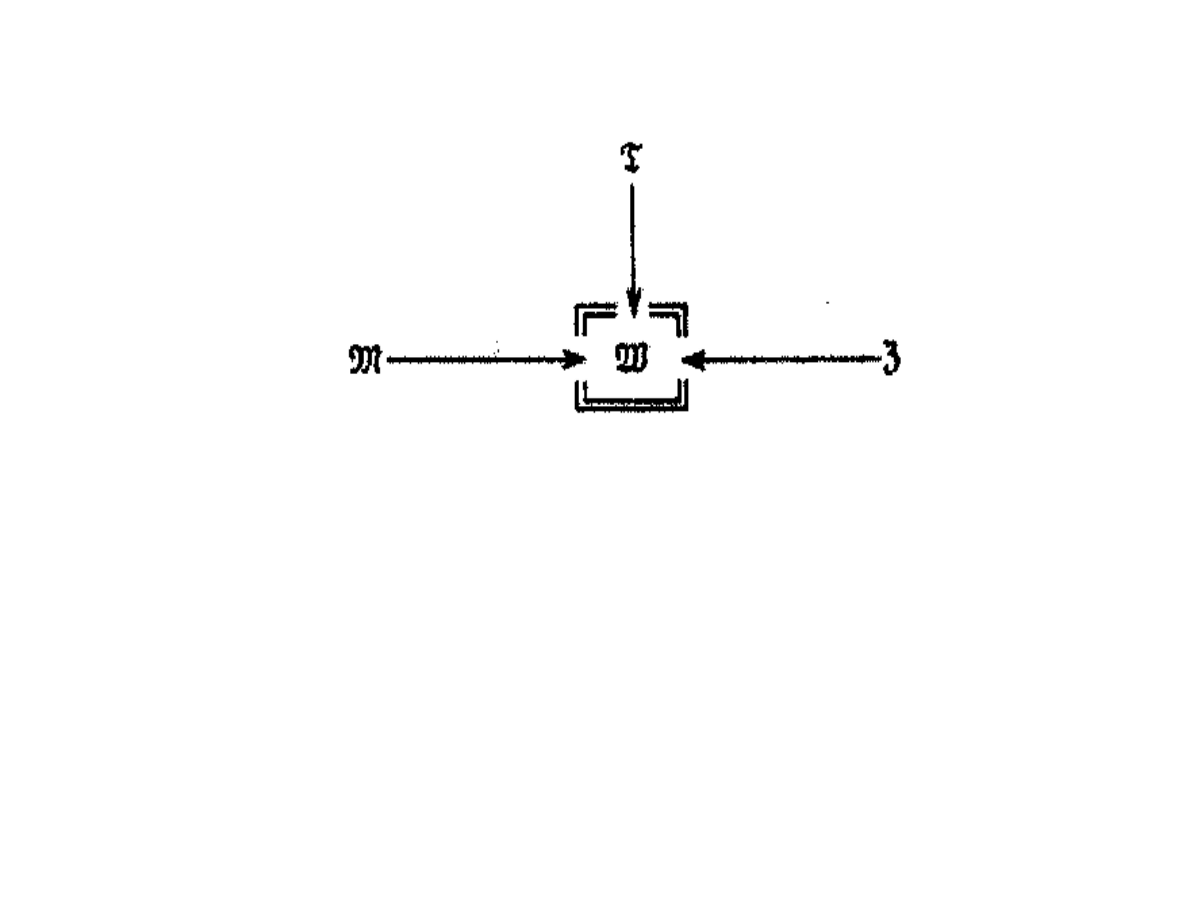
Podstawowe elementy modelu ℳ: sygnały

wejściowe s

we

(i)

∈

ຮ

we

, sygnały wyjściowe

s

wy

(i)

∈

ຮ

wy

, zmienne stanu s

s

∈

ຮ

s

, oraz

parametry c ∈C.

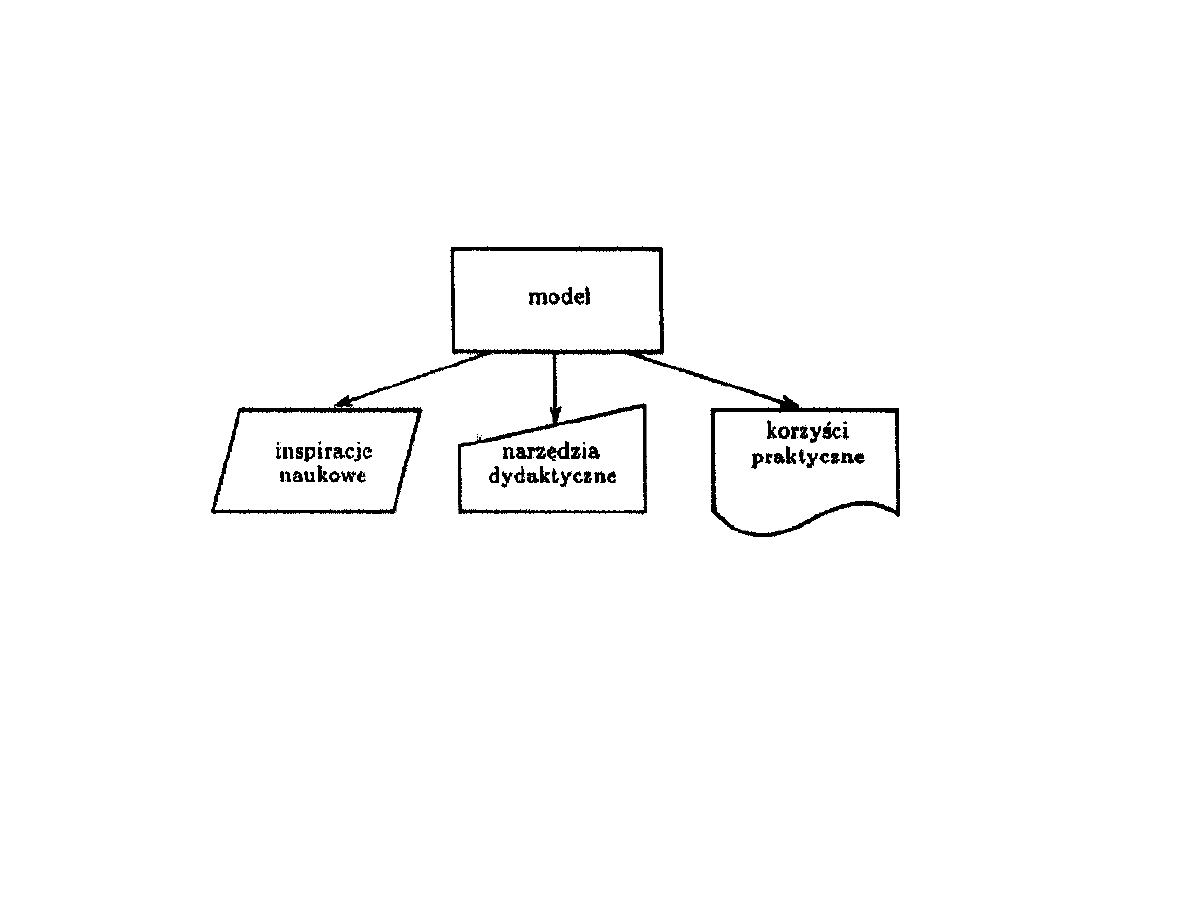
Dopiero gdy upewnimy się, że model działa poprawnie,

można myśleć o jego praktycznym zastosowaniu.

Zbudowany model ℳ może mieć trojakiego rodzaju

zastosowania:

1) Jako źródło inspiracji,
2) Jako narzędzie dydaktyczne,
3) źródło konkretnych korzyści praktycznych.

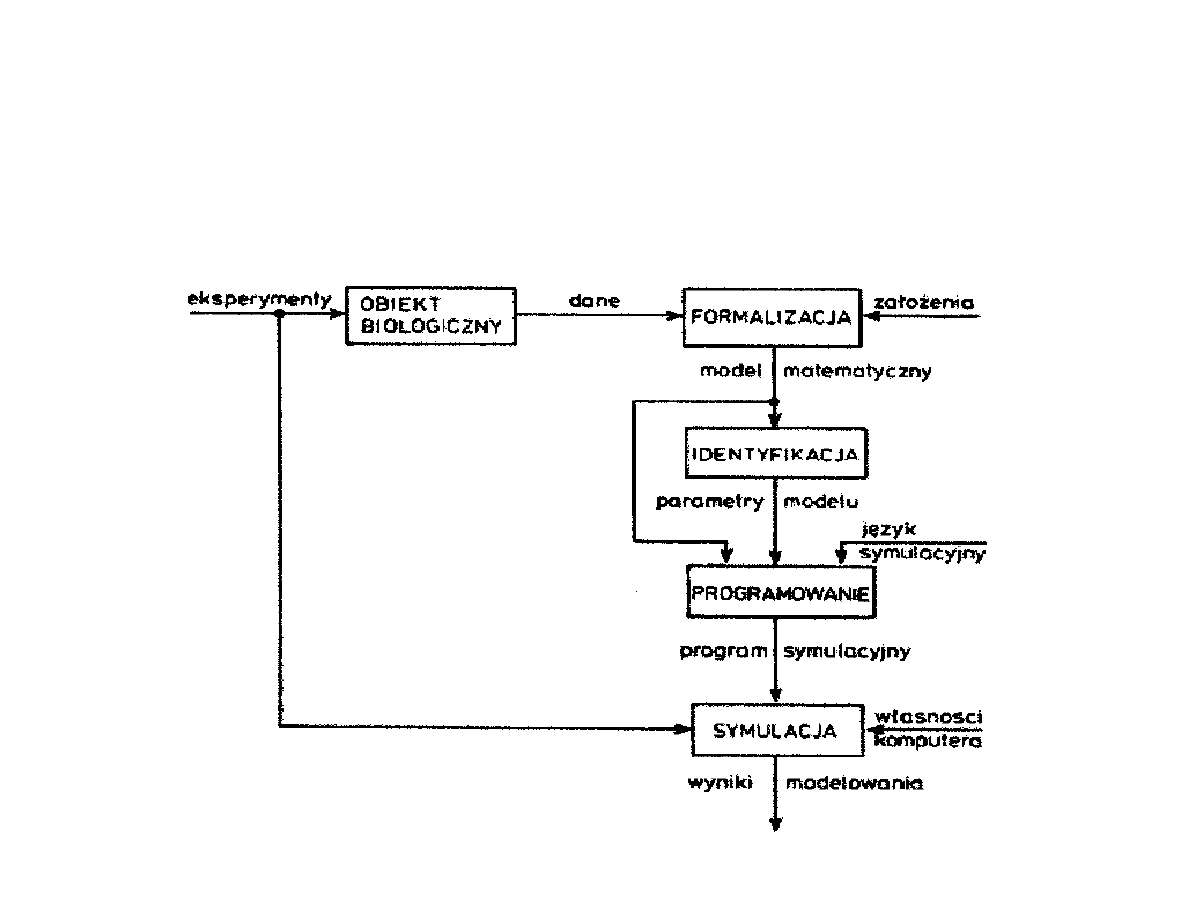
Podsumowanie

Kolejne etapy budowy cybernetycznego modelu systemu

biologicznego.

Przykłady modelów

cybernetycznych

• Układ nerwowy

• Komórka nerwowa

• Model matematyczny
• Model cyfrowy
• Model ciągły

• Model ciągły

• Sieci neuronowe

• Systemy percepcyjne

• System słuchowy
• System wzrokowy

• System hormonalny